Analysis of GNSS-RTK Monitoring Background Noise Characteristics Based on Stability Tests
Abstract
1. Introduction
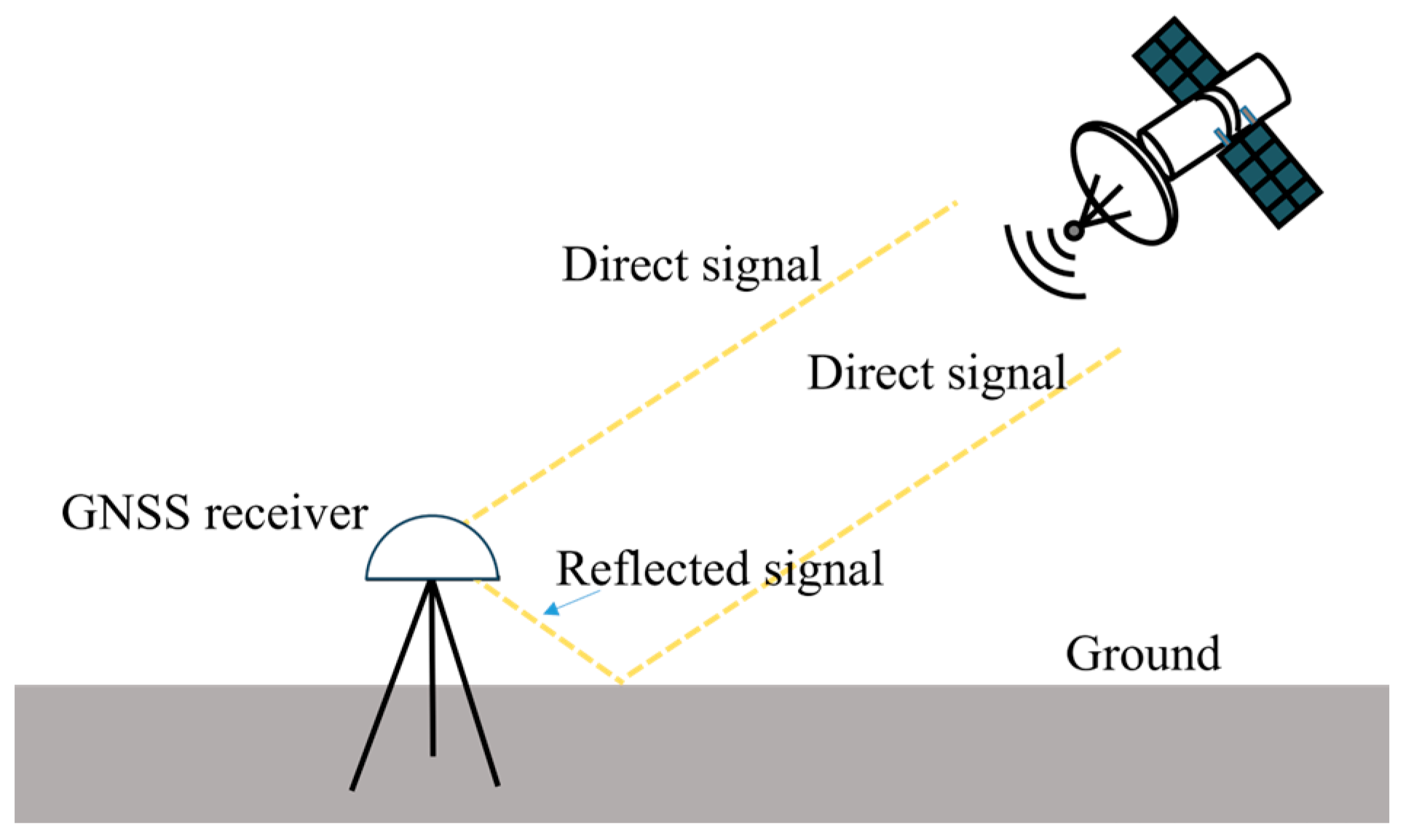
2. Experimental Design
3. Data Processing Methods
3.1. Signal Evaluation Metrics
3.2. Normalized Power Spectral Density Calculation
4. Data Analysis
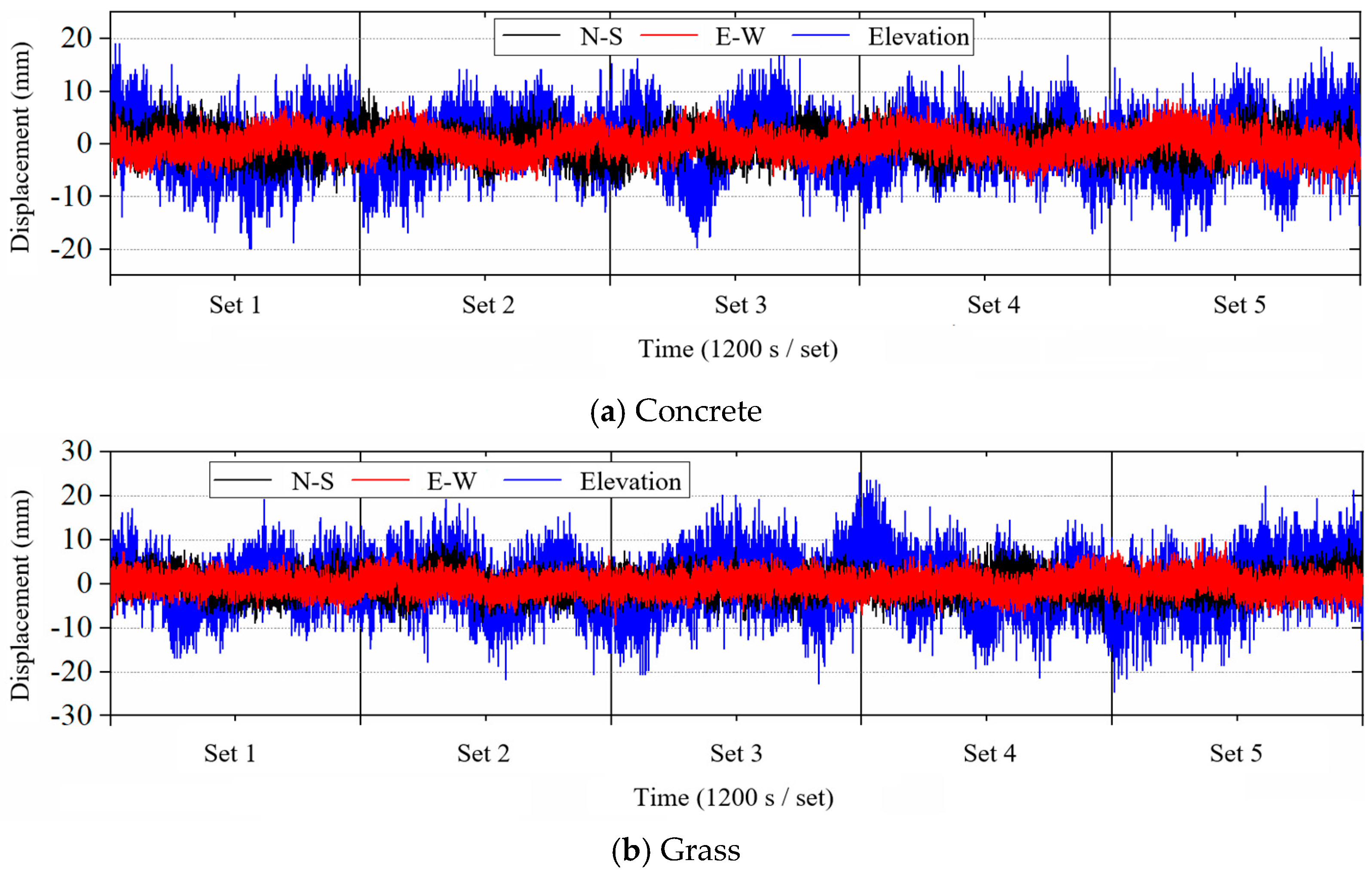
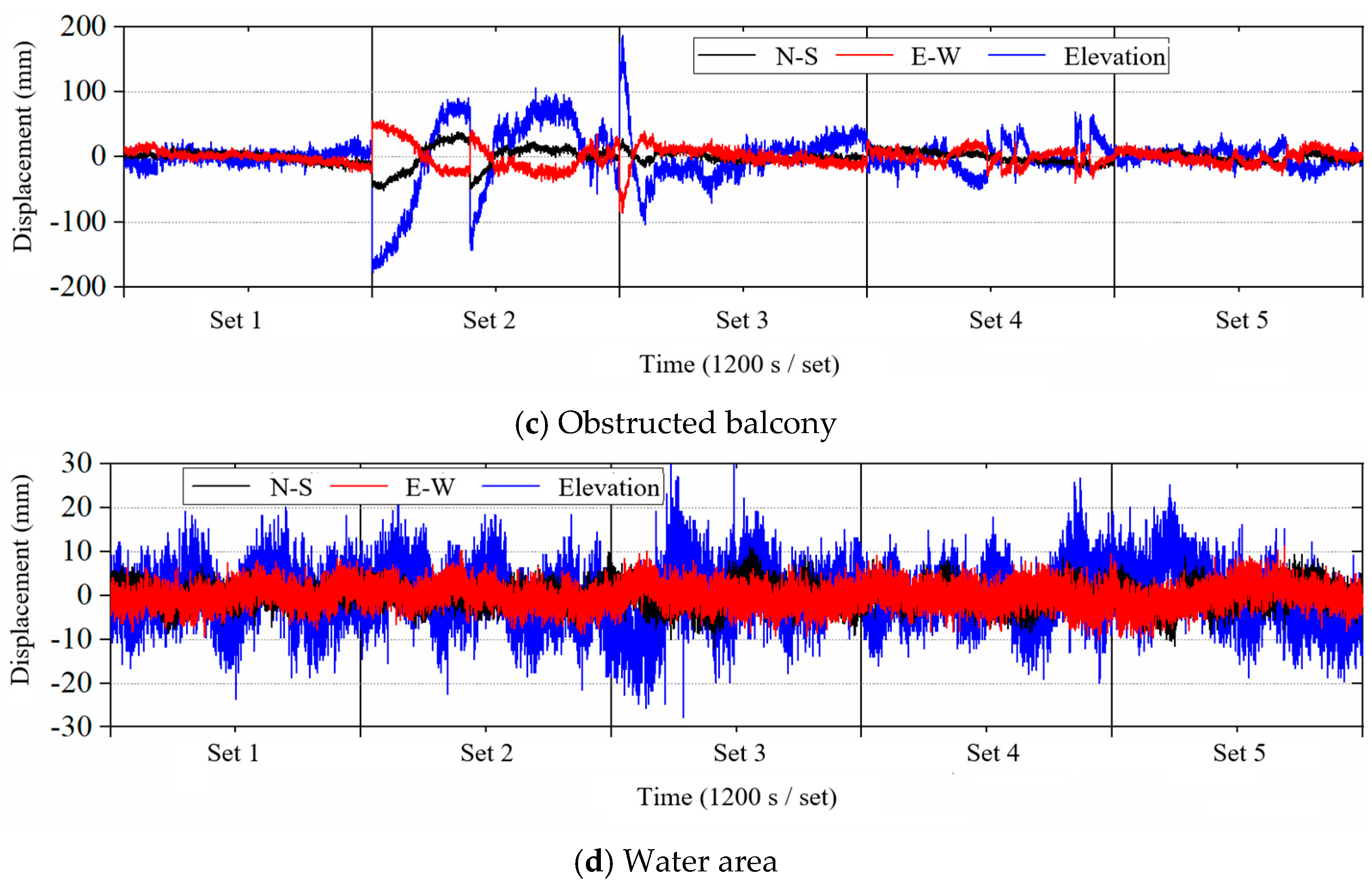
4.1. Time Domain Analysis
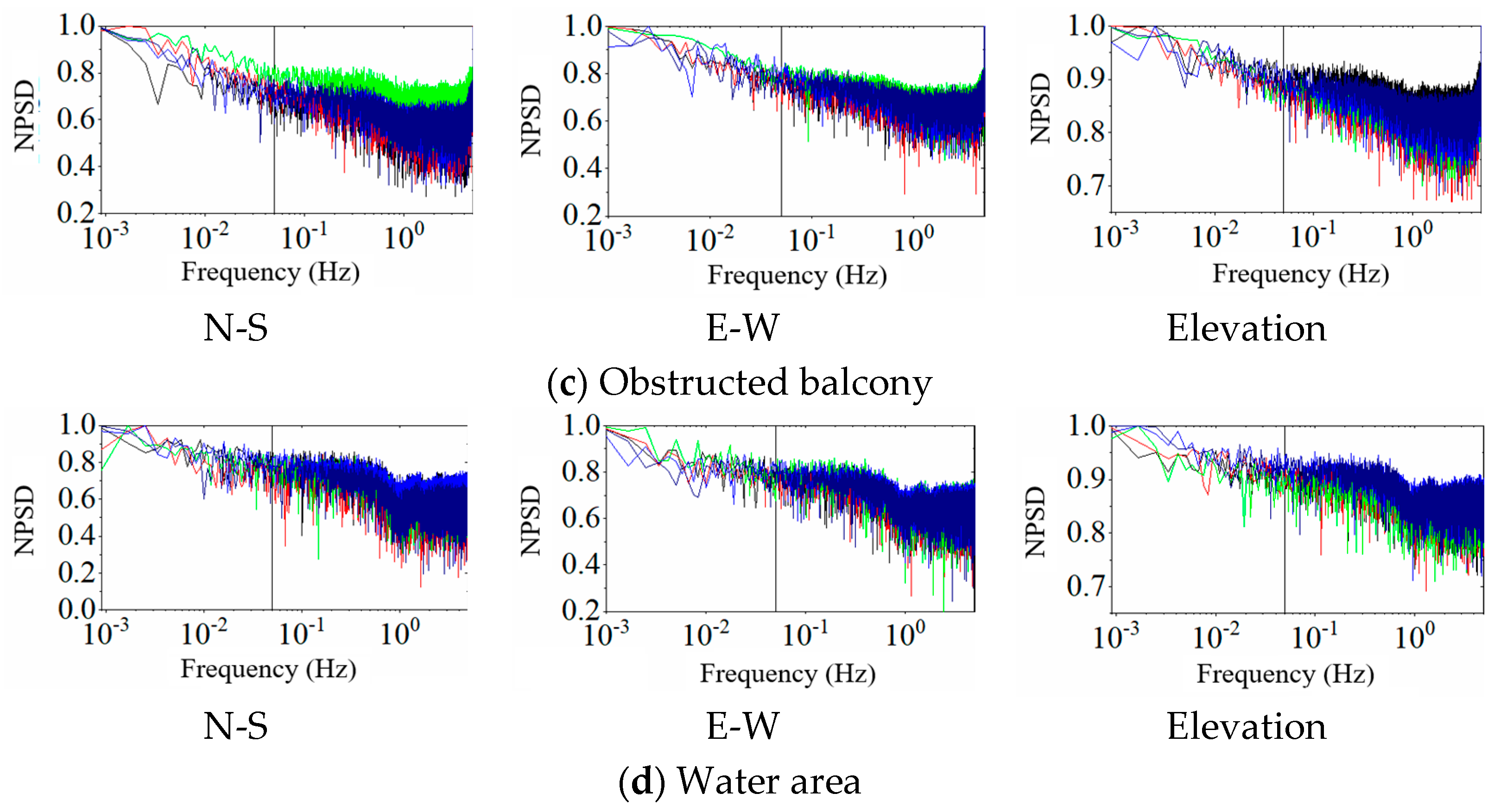
4.2. Frequency Domain Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xi, R.; Zhou, X.; Jiang, W.; Chen, Q. Simultaneous estimation of dam displacements and reservoir level variation from GPS measurements. Measurement 2018, 122, 247–256. [Google Scholar] [CrossRef]
- Yu, J.; Meng, X.; Yan, B.; Xu, B.; Fan, Q.; Xie, Y. Global Navigation Satellite System-based positioning technology for structural health monitoring: A review. Struct. Control. Health Monit. 2020, 27, e2467. [Google Scholar] [CrossRef]
- Yu, L.; Xiong, C.; Chen, W.; Gao, Y.; Ye, Z.; Shi, Q. A combined algorithm for denoising GNSS-RTK positioning solutions with application to displacement monitoring of a super-high-rise building. Meas. Sci. Technol. 2021, 32, 115121. [Google Scholar] [CrossRef]
- Kim, J.; Kim, K.; Sohn, H. Autonomous dynamic displacement estimation from data fusion of acceleration and intermittent displacement measurements. Mech. Syst. Signal Process. 2014, 42, 194–205. [Google Scholar] [CrossRef]
- Xu, Y.; Brownjohn, J.M.W.; Hester, D.; Koo, K.Y. Long-span bridges: Enhanced data fusion of GPS displacement and deck accelerations. Eng. Struct. 2017, 147, 639–651. [Google Scholar] [CrossRef]
- Zheng, F.; Li, Q.; Wang, J.; Gong, X.; Jia, H.; Zhang, C.; Shi, C. GNSS NLOS detection method based on stacking ensemble learning and applications in smartphones. GPS Solut. 2024, 28, 129. [Google Scholar] [CrossRef]
- Xu, B.; Jia, Q.; Luo, Y.; Hsu, L.-T. Intelligent GPS L1 LOS/multipath/NLOS classifiers based on correlator-, RINEX-and NMEA-level measurements. Remote Sens. 2019, 11, 1851. [Google Scholar] [CrossRef]
- Xia, Y.; Pan, S.; Meng, X.; Gao, W.; Wen, H. Robust Statistical Detection of GNSS Multipath Using Inter-Frequency C/N0 Differences. Remote Sens. 2020, 12, 3388. [Google Scholar] [CrossRef]
- Li, L.; Xu, Z.; Jia, Z.; Lai, L.; Shen, Y. An efficient GNSS NLOS signal identification and processing method using random forest and factor analysis with visual labels. GPS Solut. 2024, 28, 77. [Google Scholar] [CrossRef]
- Li, X.; Wang, B.; Li, X.; Huang, J.; Lyu, H.; Han, X. Principle and performance of multi-frequency and multi-GNSS PPP-RTK. Satell. Navig. 2022, 3, 7. [Google Scholar] [CrossRef]
- Yu, J.; Xie, Y.; Fang, Z.; Peng, Z.; Yang, R.; Wang, Y. Identification of bridge modal parameters from GNSS data by integrating IEWT and robust ICA algorithm. Meas. Sci. Technol. 2024, 35, 046124. [Google Scholar] [CrossRef]
- Wang, J.; Wang, J.; Roberts, C. Reducing GPS carrier phase errors with EMD-wavelet for precise static positioning. Surv. Rev. Dir. Overseas Surv. 2009, 41, 152–161. [Google Scholar] [CrossRef]
- Xiong, C.; Wang, M.; Shang, Z.; Liu, T.; Shi, Q. Modal frequencies evaluation of a damaged bridge using RCVMD algorithm based on sensor dynamic responses. Meas. Sci. Technol. 2023, 34, 105013. [Google Scholar] [CrossRef]
- Tao, Y.; Liu, C.; Liu, C.; Zhao, X.; Hu, H. Empirical wavelet transform method for GNSS coordinate series denoising. J. Geovisualization Spat. Anal. 2021, 5, 1–7. [Google Scholar] [CrossRef]
- Li, W.; Guo, J. Extraction of periodic signals in Global Navigation Satellite System (GNSS) vertical coordinate time series using the adaptive ensemble empirical modal decomposition method. Nonlinear Process. Geophys. 2024, 31, 99–113. [Google Scholar] [CrossRef]
- Park, J.C.; Gil, H.B.; Kang, S.G.; Lim, C.W. Dynamic characteristics of a cable-stayed bridge using global navigation satellite system. KSCE J. Civ. Environ. Eng. Res. 2010, 30, 375–382. [Google Scholar]
- Nath, S.; Chetia, B.; Kalita, S. Ionospheric TEC prediction using hybrid method based on ensemble empirical mode decomposition (EEMD) and long short-term memory (LSTM) deep learning model over India. Adv. Space Res. 2023, 71, 2307–2317. [Google Scholar] [CrossRef]
- Hoar, G.; Inglis, D.; MacInnis, M.; Tobin, S. An Autonomous GNSS Wave Sensor Module for Deployment on Existing Buoy Infrastructure: Comparison and Validation of Co-Located GNSS and Accelerometer Directional Wave Sensors. In Proceedings of the 2019 IEEE/OES Twelfth Current, Waves and Turbulence Measurement (CWTM), San Diego, CA, USA, 10–13 March 2019; pp. 1–9. [Google Scholar]
- Xing, L.; Wen, Y.; Thomas DW, P.; Zhang, J.; Zhang, D.; Xiao, J. A Joint time-frequency analytical method for electromagnetic interference in railway GNSS system. In Proceedings of the 2020 International Symposium on Electromagnetic Compatibility-EMC EUROPE, Rome, Italy, 23–25 September 2020; pp. 1–4. [Google Scholar]
- Zhong, P.; Ding, X.; Yuan, L.; Xu, Y.; Kwok, K.; Chen, Y. Sidereal filtering based on single differences for mitigating GPS multipath effects on short baselines. J. Geod. 2010, 84, 145–158. [Google Scholar] [CrossRef]
- Dong, D.; Wang, M.; Chen, W.; Zeng, Z.; Song, L.; Zhang, Q.; Cai, M.; Cheng, Y.; Lv, J. Mitigation of multipath effect in GNSS short baseline positioning by the multipath hemispherical map. J. Geod. 2016, 90, 255–262. [Google Scholar] [CrossRef]
- Ye, S.; Chen, D.; Liu, Y.; Jiang, P.; Tang, W.; Xia, P. Carrier phase multipath mitigation for BeiDou navigation satellite system. GPS Solut. 2015, 19, 545–557. [Google Scholar] [CrossRef]
- Špánik, P.; Hefty, J. Multipath detection with the combination of SNR measurements—Example from urban environment. Geod. Cartogr. 2017, 66, 305–316. [Google Scholar] [CrossRef]
- Ng, H.F.; Zhang, G.; Yang, K.Y.; Yang, S.X.; Hsu, L.T. Improved weighting scheme using consumer-level GNSS L5/E5a/B2a pseudorange measurements in the urban area. Adv. Space Res. 2020, 66, 1647–1658. [Google Scholar] [CrossRef]
- Chen, W.; Xiong, C.; Yu, L.; Lian, S.; Ye, Z. Dynamic monitoring of an offshore jacket platform based on RTK-GNSS measurement by CF-CEEMDAN method. Appl. Ocean. Res. 2021, 115, 102844. [Google Scholar] [CrossRef]
- Xiong, C.; Wang, M.; Chen, W. Data analysis and dynamic characteristic investigation of large-scale civil structures monitored by RTK-GNSS based on a hybrid filtering algorithm. J. Civ. Struct. Health Monit. 2022, 12, 857–874. [Google Scholar] [CrossRef]
- Azarbad, R.M.; Mosavi, R.M. A new method to mitigate multipath error in single-frequency GPS receiver with wavelet transform. GPS Solut. 2014, 18, 189–198. [Google Scholar] [CrossRef]
- Agnew, C.D.; Larson, M.K. Finding the repeat times of the GPS constellation. GPS Solut. 2007, 11, 71–76. [Google Scholar] [CrossRef]
- Choi, K.; Bilich, A.; Larson, K.M.; Axelrad, P. Modified sidereal filtering: Implications for high-rate GPS positioning. Geophys. Res. Lett. 2004, 31, 178–198. [Google Scholar]
- Atkins, C.; Ziebart, M. Effectiveness of observation-domain sidereal filtering for GPS precise point positioning. GPS Solut. 2016, 20, 111–122. [Google Scholar] [CrossRef]
- Wang, M.; Wang, J.; Dong, D.; Li, H.; Han, L.; Chen, W. Comparison of Three Methods for Estimating GPS Multipath Repeat Time. Remote Sens. 2018, 10, 6. [Google Scholar] [CrossRef]
- Wang, M.; Wang, J.; Dong, D.; Chen, W.; Li, H.; Wang, Z. Advanced Sidereal Filtering for Mitigating Multipath Effects in GNSS Short Baseline Positioning. ISPRS Int. J. Geo-Inf. 2018, 7, 228. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, W.; Dong, D.; Wang, M.; Cai, M.; Yu, C.; Zheng, Z.; Liu, M. Multipath mitigation based on trend surface analysis applied to dual-antenna receiver with common clock. GPS Solut. 2019, 23, 1–15. [Google Scholar] [CrossRef]
- JGJ8-2016; Code for Deformation Measurement of Buildings. China Architecture and Building Press: Beijing, China, 2016.



| Environmental Characteristics | Test Grouping | Mean Value | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| Concrete | 2.54 | 2.57 | 2.51 | 2.32 | 2.34 | 2.46 |
| Grass | 2.39 | 2.61 | 2.21 | 2.50 | 2.95 | 2.53 |
| Obstructed balcony | 6.94 | 21.39 | 6.27 | 8.26 | 6.42 | 9.86 |
| Water area | 2.22 | 2.24 | 3.27 | 2.50 | 2.82 | 2.61 |
| Environmental Characteristics | Test Grouping | Mean Value | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| Concrete | 1.99 | 2.15 | 1.90 | 2.08 | 2.46 | 2.12 |
| Grass | 1.80 | 1.91 | 1.89 | 2.09 | 2.30 | 2.00 |
| Obstructed balcony | 7.97 | 23.54 | 16.12 | 11.58 | 9.33 | 13.71 |
| Water area | 2.44 | 2.54 | 2.60 | 2.60 | 2.83 | 2.60 |
| Environmental Characteristics | Test Grouping | Mean Value | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| Concrete | 5.35 | 4.63 | 5.58 | 4.39 | 5.25 | 5.04 |
| Grass | 5.02 | 5.39 | 6.23 | 6.20 | 6.20 | 5.81 |
| Obstructed balcony | 9.01 | 75.01 | 36.92 | 20.63 | 11.26 | 30.56 |
| Water area | 5.80 | 6.09 | 7.34 | 5.79 | 6.56 | 6.32 |
| Environmental Characteristics | Test Grouping | Mean Value | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| Concrete | 15.50 | 17.88 | 23.15 | 17.35 | 21.01 | 23.15 |
| Grass | 17.07 | 20.44 | 17.87 | 20.44 | 19.60 | 19.09 |
| Obstructed balcony | 38.88 | 90.91 | 45.48 | 42.70 | 34.18 | 50.43 |
| Water area | 15.50 | 17.88 | 23.15 | 17.35 | 21.01 | 18.98 |
| Environmental Characteristics | Test Grouping | Mean Value | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| Concrete | 18.07 | 19.14 | 19.50 | 19.72 | 21.04 | 21.25 |
| Grass | 14.56 | 13.58 | 16.33 | 14.93 | 18.45 | 15.57 |
| Obstructed balcony | 49.29 | 96.54 | 126.39 | 68.66 | 53.82 | 78.94 |
| Water area | 18.07 | 19.14 | 19.50 | 19.72 | 21.04 | 19.49 |
| Environmental Characteristics | Test Grouping | Mean Value | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| Concrete | 44.00 | 47.00 | 61.00 | 47.00 | 45.00 | 61.00 |
| Grass | 36.00 | 41.00 | 48.00 | 45.00 | 47.00 | 43.40 |
| Obstructed balcony | 67.00 | 286.00 | 291.00 | 120.00 | 78.00 | 168.40 |
| Water area | 44.00 | 47.00 | 61.00 | 47.00 | 45.00 | 48.80 |
| Environmental Characteristics | Test Grouping | Mean Value | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| Concrete | 13 | 13 | 14 | 13 | 12 | 13 |
| Grass | 13 | 14 | 12 | 13 | 13 | 13 |
| Obstructed balcony | 12 | 11 | 10 | 12 | 13 | 12 |
| Water area | 12 | 11 | 10 | 11 | 11 | 11 |
| Environmental Characteristics | Test Grouping | Mean Value | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| Concrete | 0.9361 | 0.8561 | 0.7836 | 0.7508 | 0.8146 | 0.8282 |
| Grass | 0.8006 | 0.7665 | 0.9036 | 0.8323 | 0.8073 | 0.8221 |
| Obstructed balcony | 1.0245 | 1.1229 | 1.1637 | 1.0030 | 0.9649 | 1.0358 |
| Water area | 0.9354 | 1.0303 | 1.0810 | 0.9545 | 0.9329 | 1.0068 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, W.; Li, F.; Yu, L.; Fan, L.; Zhang, K. Analysis of GNSS-RTK Monitoring Background Noise Characteristics Based on Stability Tests. Sensors 2025, 25, 379. https://doi.org/10.3390/s25020379
Qi W, Li F, Yu L, Fan L, Zhang K. Analysis of GNSS-RTK Monitoring Background Noise Characteristics Based on Stability Tests. Sensors. 2025; 25(2):379. https://doi.org/10.3390/s25020379
Chicago/Turabian StyleQi, Wencong, Feilong Li, Lina Yu, Lilong Fan, and Kai Zhang. 2025. "Analysis of GNSS-RTK Monitoring Background Noise Characteristics Based on Stability Tests" Sensors 25, no. 2: 379. https://doi.org/10.3390/s25020379
APA StyleQi, W., Li, F., Yu, L., Fan, L., & Zhang, K. (2025). Analysis of GNSS-RTK Monitoring Background Noise Characteristics Based on Stability Tests. Sensors, 25(2), 379. https://doi.org/10.3390/s25020379






