1. Introduction
Various gases usually exist in the form of mixtures in the industrial and living environment; it is particularly important to identify the composition and concentration analysis of the gas mixture component, so the detection of the gas mixture component has become a hot research field. There are three methods for gas detection; the first method is sensory evaluation, which is an evaluation method based on the reaction of human sensory organs to gas. However, sensory evaluation is susceptible to the limitations of the human subjective and olfactory system, and some gases can also cause damage to the human body. The second method is chemical analysis, such as spectroscopy, gas chromatography and mass spectrometry; this method uses advanced chemical analysis equipment to measure the composition and concentration of gases. However, the difficulty of sampling, the complexity of operation, the high cost of equipment and the low real-time performance of these methods limit the application of these methods to some extent. The last method is to use gas sensors to detect gases. This method has a low cost and is easy to operate. However, in complex environments or when there are many types of gases, it is difficult to detect the gases using a single sensor. In addition, other influencing factors such as the sensitivity of sensing materials to target gases, the reproducibility of sensor arrays and limitations in the quantity of discriminated gas all impose limitations on the application of the sensor [
1,
2,
3].
Due to the limitations of the above methods, Gardner published a review article on electronic nose, formally proposing the concept of “electronic nose” in 1994 [
4]. Electronic nose, also known as artificial olfactory system, is a new bionic detection technology which can be used to simulate the working mechanism of biological olfactory. It uses sensor array technology, which has the advantages of fast response, high sensitivity, low cost and easy processing. Electronic nose technology not only solves the subjective problems of sensory analysis, but also overcomes the complicated and expensive problems of chemical analysis methods. Electronic nose technology is often used in the analysis and detection of various gas fields, such as pollution control [
5,
6], medical technology [
7,
8], oil exploration [
9], food safety [
10,
11], agricultural science [
12,
13] and environmental science [
14,
15], and the application of electronic noses is very extensive [
16,
17,
18]. Therefore, electronic nose technology has become an important research direction in the field of gas detection. The electronic nose system is mainly composed of gas sensor array, signal preprocessing module and pattern recognition, as shown in
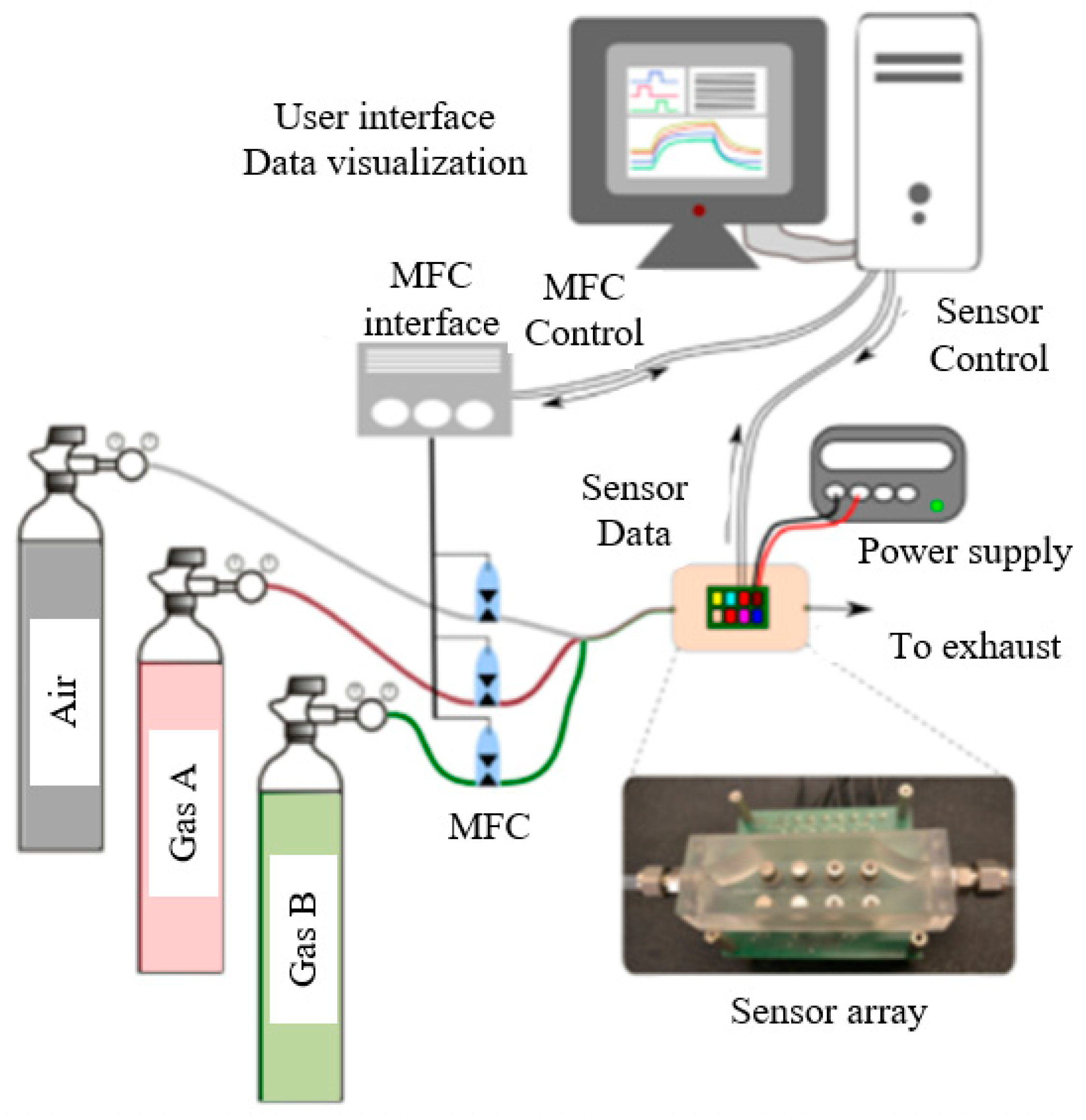
Figure 1.
The sensor array is composed of various types of sensors and converts chemical signals into electrical signals by converting A/D. The signal preprocessing is mainly to remove noise, extract feature and process signal of sensor response signal. The pattern recognition is the classification recognition and concentration estimation of measured gases using machine learning algorithms. At present, the key research directions of electronic nose are mainly the performance improvement of gas sensors and the research of various machine learning methods in gas sensors [
19]. Due to the nonlinear response of MOS gas sensor, it is difficult to improve mixed gas classification and concentration prediction by simply relying on the selection of gas-sensitive materials. Therefore, appropriate machine learning algorithms are needed to solve the current problems [
20]. Machine learning algorithm plays an extremely important role, and its accuracy, time efficiency and anti-interference ability all affect the decision result. Among the research results of many studies, the literature [
21] argues that more intelligent pattern recognition technology is needed to realize the potential of electronic nose technology. Literature [
22] proposes that reasonable improvement of algorithms is an important support for the development of machine olfaction.
Before pattern recognition, data sets need to be preprocessed and feature extraction, which is conducive to providing reasonable data sets for subsequent recognition models. The main steps of data preprocessing are data cleaning, data specification and data transformation. Data cleansing is the “cleaning” of data by filling in missing values, smoothing noise data, smoothing or removing outliers, and resolving data inconsistencies. The average method can solve the problem of missing data, and the averaging method is to fill the average value of all data into the data position to be compensated [
23]. Based on the setting principle, the nearest location data is selected as the compensation data [
24]. The compensation method of regression model is to build a regression model and fill the compensation position with the predicted value of the regression model as the compensation value [
25]. Although the data specification technique is represented by a much smaller data set, it still maintains close data integrity and can be mined on the data set after the specification, and it is more efficient and produces nearly identical analysis results. Common strategies are dimension specification and dimension transformation. Common loss dimension transformation methods include principal component analysis (PCA), linear discriminant analysis (LDA), singular value decomposition (SVD), etc. [
26,
27]. Data transformation includes normalization, discretization and sparse processing of data to achieve the purpose of mining. In the literature [
28], data standardization and baseline processing methods were used as data processing methods to realize the identification of nitrogen dioxide and sulfur dioxide in air pollution. The feature extraction methods include PCA and LDA. When the data is small, the feature extraction effect of PCA is better than that of LDA, but when the data is large, the feature extraction effect of LDA is better than that of PCA [
29].
In the classification study of mixed gases, researchers mostly adopt machine learning methods [
30,
31,
32,
33,
34], and the selection of classification algorithms needs to be based on the characteristics of samples to find a more suitable scheme [
35,
36,
37,
38,
39,
40,
41]. Sunny used four thin film sensors to form a sensor array to identify and estimate the concentration of a gas mixture. PCA was used to extract the features of response signals, and ANN and SVM were used for category recognition, achieving good recognition results [
42]. Zhao studied the recognition of gas mixture components of organic volatiles. An array composed of four sensors was used to identify formaldehyde when the background gas was acetone, ethanol and toluene. PCA was used for dimensionality reduction extraction. MLP, SVM and ELM are, respectively, used in the classifier to identify and classify, among which SVM achieves the best effect and ELM requires the shortest training time to obtain results [
43]. Jang used the SVM and paired graph scheme combined with the sensor array composed of semiconductor sensors to classify CH4 and CO, and obtained a high recognition accuracy [
44]. Jung used sensor array to collect gas and then used SVM and fuzzy ARTMAP network for experimental comparison. The recognition time of SVM was shorter than the fuzzy ARTMAP network [
45]. Zhao adopted a weighted discriminant extreme learning machine (WDELM) as a classification method. WDELM assigns different weights to each specific sample by using a flexible weighting strategy, which enables it to perform classification tasks under unbalanced class distribution [
46].
There are multiple regression [
47], neural network [
48,
49], SVR [
50] and other methods [
51,
52,
53,
54,
55,
56] for gas concentration analysis. Zhang used the WCCNN-BiLSTM model to automatically extract time–frequency domain features of dynamic response signals from the original signals to identify unknown gases. The time domain characteristics of the steady-state response signal are automatically extracted by the many-to-many GRU model to accurately estimate the gas concentration [
57]. Piotr proposed an improved cluster-based ensemble model to predict ozone. Each improved spiking neural network was trained on a set of separate time series; the ensemble model could provide better prediction results [
58]. Liang used AdaBoost classification algorithm to classify the local features of infrared spectrum, and carried out PLS local modeling according to different features to predict the concentration of a gas mixture component. This method solves the problems of difficult identification and inaccurate quantitative analysis of alkane mixture gas components in traditional methods [
59]. Adak used the multiple linear regression (MVLR) algorithm to predict the concentration of a mixture of two gases in acetone. The relative errors of acetone and methanol are lower than 6% and 17%, respectively [
60].
Based on the above literature, most of the methods are suitable for relatively balanced data sets of categories. When the number of samples is extremely unbalanced, the traditional method with the overall classification accuracy as the learning objective will pay too much attention to most categories. As a result, the classification or regression performance of a small number of class samples is degraded, which leads to the failure of traditional machine learning to work well on extremely unbalanced data sets. Secondly, PCA method is often used to solve linear problems in the literature, while most of the problems in the real environment are nonlinear problems. In addition, ML algorithms often have multi-parameter and difficult parameter to determine the problem. In the literature, the parameters of deep learning algorithms such as neural network or ELM are often obtained by trial and error method or experience, and the selection of parameters plays a crucial role in the performance evaluation of algorithms. When the learning algorithm model without optimal parameters is used to detect the mixed gas, it cannot reasonably compare other algorithms with evaluation criteria. To solve the above problems, this paper presents a gas mixture component detection method which is suitable for electronic nose under unbalanced conditions. In view of the problem of extremely unbalanced sample numbers and too few samples, SMOTE, ADASYN, B-SMOTE, S-SMOTE and CSL-SMOTE were put forward for artificial synthesis of new samples by sample expansion methods, so as to alleviate the problem. For nonlinear problems, Kernel Principal Component Analysis (KPCA) method is used for feature extraction, and kernel technique is used to extend PCA to nonlinear problems. To solve the problem of multi-parameter and difficult parameter determination, PSO and GA optimization methods are used to optimize the parameters of classification and regression models, which are convenient for classification and regression methods to identify and classify the mixed gas and estimate the concentration.
The rest of the paper is structured as follows. In Part II, the methods of feature extraction, sample expansion, classification recognition and concentration detection are briefly introduced. In Part III, a new method for detecting mixed gas based on the electronic nose is introduced in detail. The verification experiment is carried out in part IV, and the experimental results are analyzed and discussed. Part V is the summary and outlook.
2. Methods
2.1. Kernel Principal Component Analysis
The KPCA transforms the linearly indivisible sample input space into the divisible high-dimensional feature space through kernel function
and performs PCA in this high-dimensional space. Compared with the linear problem solved by PCA, the KPCA with kernel technique extends the linear problem to the nonlinear problem [
12].
Set
as the observation sample after pretreatment, and contains
samples in
,
represents the
observed sample of the
dimension. The covariance matrix mapping sample
to a high dimensional feature space is expressed as
where
,
is a nonlinear mapping.
Eigenvalue decomposition of covariance matrix
:
where
and
, respectively, represent the eigenvalues and eigenvectors of covariance matrix
, and
is the eigenvector in the eigenspace, that is, the direction of the principal component. There is a coefficient vector
for a linear representation of the eigenvector
:
Substitute (3) into (2) and multiply both ends by
to obtain the following equation:
Define
, then
is the symmetric positive semidefinite matrix of
:
where
represents the elements in row
and column
of matrix
, and the eigenvalue solution problem combined with Equations (3)–(5) is converted to
where
is the eigenvector of
, and principal component analysis (PCA) is performed in the eigenspace to solve the eigenproblem of Formula (6), and the eigenvalue
corresponding to the eigenvector
is obtained;
where
is the number of primary components.
The
th feature of the newly observed sample
is mapped by
to
, where
is the feature vector of the
th feature in the feature space, i.e., the direction of the principal component.
where
is the projection of
onto
. Where
is not satisfied,
is
:
where
is the kernel matrix after centralization, and
is the matrix of
, where each element is
.
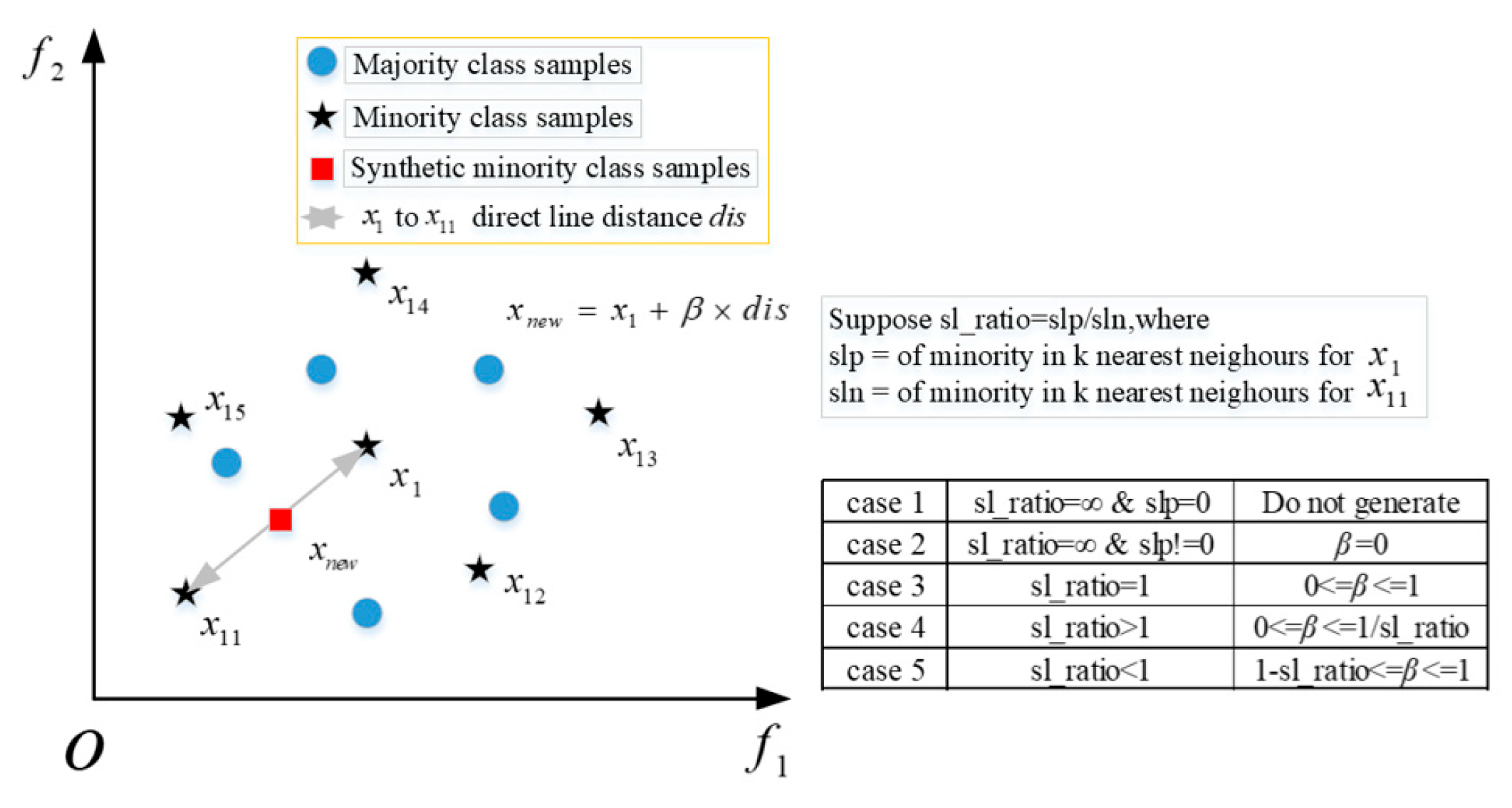
2.2. The Safe-Level-SMOTE Method
The SMOTE method can alleviate the over-fitting problem caused by random oversampling, but it only considers a few types of cases and does not consider the overlap between the synthesized samples and most types of samples; therefore, most researchers tend to adopt the improved Safe-Level-SMOTE method [
61,
62,
63,
64]. The Safe-Level-SMOTE method will select a few classes with a high degree of safety and assign a certain degree of safety to each class separately before combining new classes, which will be closer to the high degree of safety. This method solves the quality problem of the SMOTE class and the problem of fuzzy class boundaries. The schematic diagram of a few class samples synthesized by the Safe-Level-SMOTE algorithm is shown in
Figure 2.
The process of the Safe-Level-SMOTE method is as follows:
- (1)
Find the nearest neighbors of , denoting the number of neighbors in as , and denoting a certain neighbor as .
- (2)
Find the nearest neighbors of , and the number of neighbors in is denoted as .
- (3)
Set the ratio .
where is a sample set of a few classes, and is a sample in .
Case 1: and , that is, the neighbors of the minority class sample are all majority class samples, and no composite data is generated in this case.
Case 2: and , that is, when is very small relative to , the ratio will be 0. The sample point is located in most class samples, and then point is copied.
Case 3: , that is, , at this time to synthesize a new sample between and , synthesis method same as smote.
Case 4: , that is, , at this time, the number of subclass samples around point sample is greater than the number of subclass samples around point sample, consider point as the safe level, and use the smote in between and point to synthesize a new sample, and the synthesized sample position is biased to point.
Case 5: , that is, then the number of subclass samples around point sample is less than the number of subclass samples around point sample, consider point as the safe level, between and point with to synthesize a new sample, the synthesized sample position is biased to point.
2.3. Adaptive Synthetic Sampling Approach (ADASYN)
Many classification problems will face the problem of sample imbalance, most of the algorithms in this case, and classification effect is not ideal. Researchers usually adopt the SMOTE method to address the issue of sample imbalance. Although the SMOTE algorithm is better than random sampling, it still has some problems. Generating the same number of new samples for each minority class sample may increase the overlap between classes and create valueless samples. Therefore, the improved ADASYN method of SMOTE [
65] is adopted. The basic idea of this algorithm is to adaptively generate minority class samples based on their distribution. This method can not only reduce the learning bias caused by class imbalance but also adaptively shift the decision boundary to the difficult-to-learn samples. Then, new samples are artificially synthesized based on the minority class samples and added to the data set.
The process of the ADASYN method is as follows:
Input: Training data set with samples: , where is a sample of dimensional feature space , corresponds to class label . and are defined as minority sample size and majority sample size, respectively, so and .
The algorithm process:
- (1)
Calculate the unbalance degree:
- (2)
If ( is the default threshold of the maximum allowable unbalance rate):
- (a)
Calculate the amount of composite samples that need to be generated for a few classes of samples:
where
is a parameter that specifies the level of balance required after the resultant data is generated, and
indicates that the new data set is completely balanced after the resultant.
- (b)
For each
belonging to the minority class, find
neighbors based on Euclidean distances in
dimensional space, and compute the ratio
, which is defined as
where
is a sample of most classes input in
neighbors, then
.
- (c)
Normalizes according to , so is a density distribution ().
- (d)
Calculate the amount of sample
that needs to be synthesized in each minority sample:
where
is the total sample size of artificial minority samples synthesized according to Formula (11).
- (e)
For each minority sample , the sample is synthesized by following the following steps:
Do the Loop from 1 to ;
- (f)
(i) Randomly select a minority sample from neighbors of ; (ii) Synthetic sample ; where is a difference vector in dimensional space and is a random number.
End Loop
As can be seen from the above steps, the key idea of the ADASYN method is to use density distribution as a criterion to adaptively synthesize the number of artificial samples for each minority class sample. From a physical perspective, the distribution of weights is measured based on the learning difficulty of different minority class samples. The data set obtained by the ADASYN method not only solves the problem of imbalanced data distribution (according to the expected balance level defined by the coefficient), but also forces the learning method to focus on those difficult-to-learn samples.
2.4. The Multi-Output Least Squares Support Vector Regression Machine (MLLSVR)
Support vector regression machine (SVR) is a traditional machine learning method for solving convex quadratic programming problems. The basic idea of the method is to map the input vector to a high-dimensional feature space through a pre-determined nonlinear mapping, and then perform linear regression in this space. Thus, the effect of nonlinear regression in the original space is obtained [
19]. Least squares support vector regression machine is an improved version that replaces inequality constraints in SVR with equality constraints. MLSSVR is a generalization of LSSVR in the case of multiple outputs.
Suppose data set
, where
is the input vector and
is output value. Nonlinear mapping
is introduced to map input to the
dimensional feature space, and the regression function is constructed.
where
is the weight vector and
is the offset coefficient.
In order to find the best regression function, the minimum norm
is needed. The problem can be boiled down to the following constraint optimization problem:
where
is a block vector composed of
,
,
. By introducing the relaxation variable
, the minimization problem of Equation (15) can be transformed into
where
is a vector composed of relaxation variables and
is a regularization parameter.
In the multiple-output case, for a given training set
,
is the input vector,
is the output vector,
and
are composed of block matrices of
and
, respectively. The purpose of MLSSVR is to map from
dimensional input
to
dimensional output
. As in the case of single output, the regression function is
where
is a matrix composed of weight vectors and
is a vector composed of offset coefficients. Minimize the following constrained objective function by finding
and
:
where
is a matrix of relaxation vectors. By solving this problem,
and
are obtained, and the nonlinear mapping is obtained. According to hierarchical Bayes, the weight vector
can be decomposed into the following two parts:
where
is the mean vector,
is a difference vector,
and
reflect the connectivity difference between outputs. That is,
contains the general characteristics of output, and
contains the special information of
th component of the output. Equation (18) is equivalent to the following problem.
where
,
,
,
are two regularization parameters.
The Lagrange function corresponding to Equation (20) is
where
is a matrix consisting of a Lagrange multiplier vector.
According to the optimization theory of Karush–Kuhn–Tucker (KKT) conditions, the linear following equations are obtained:
By canceling
and
in Equation (22), the linear matrix equation can be obtained as follows:
where
,
,
,
,
,
and
. Since
is not positive definite, Equation (23) can be changed to the following form:
where
is a positive definite matrix. It is not difficult to see that Formula (24) is positive definite. The solution
and
of Equation (23) are obtained in three steps:
(1) Solve: , from and ; (2) calculate: ; (3) solve: , .
The corresponding regression function can be obtained as follows:
This article uses the most common RBF kernel functions, as follows.
where
,
is the kernel width.
The MIMO differs from MISO algorithm in input–output mapping system and parameter types. When using this method, an optimization algorithm is needed to optimize the parameters in its model.
3. The Improvement Method
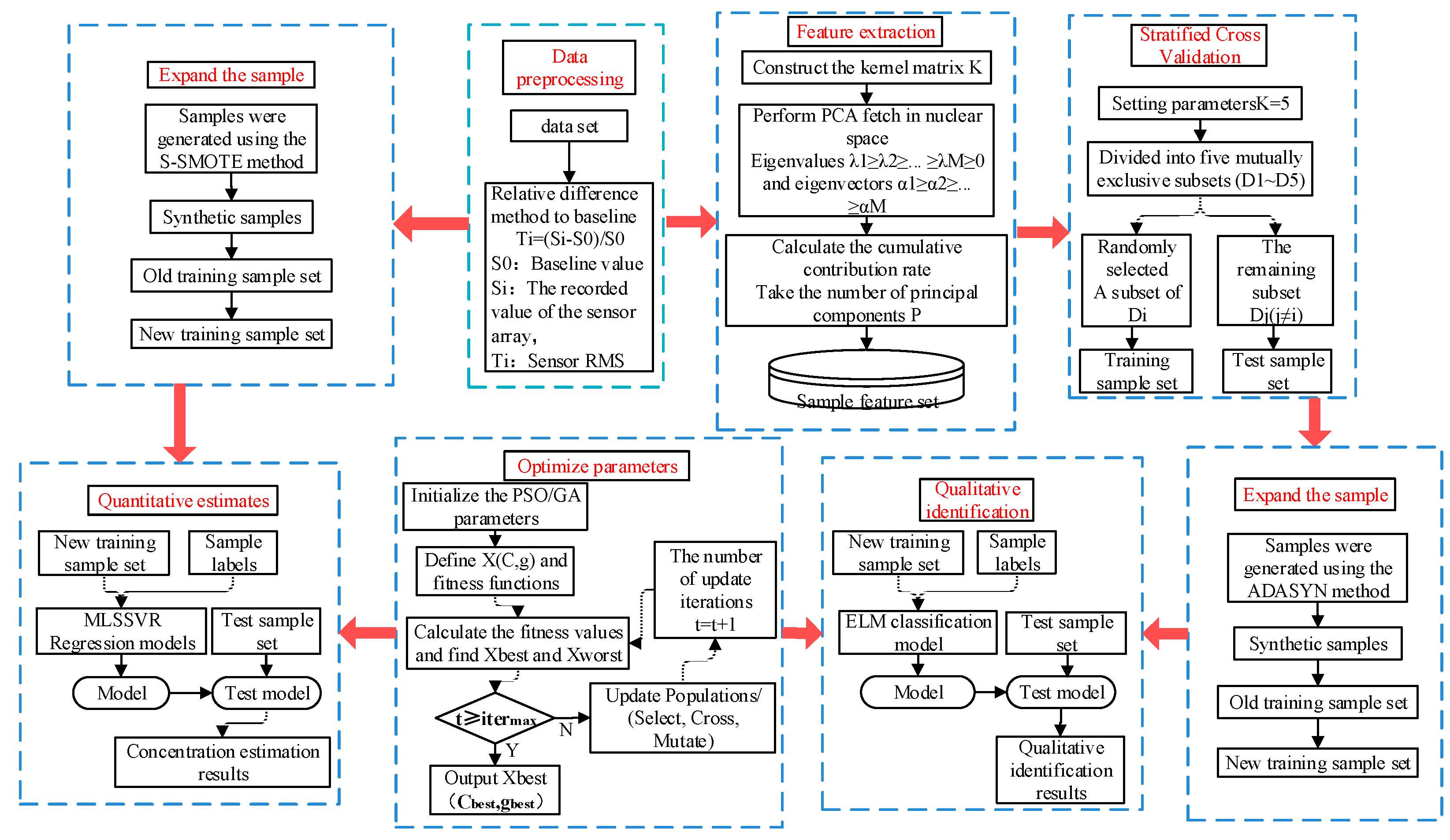
This paper proposes a method of mixture gas identification and concentration detection based on sample expansion. The flow chart of gas identification and concentration detection using the proposed method is shown in
Figure 3.
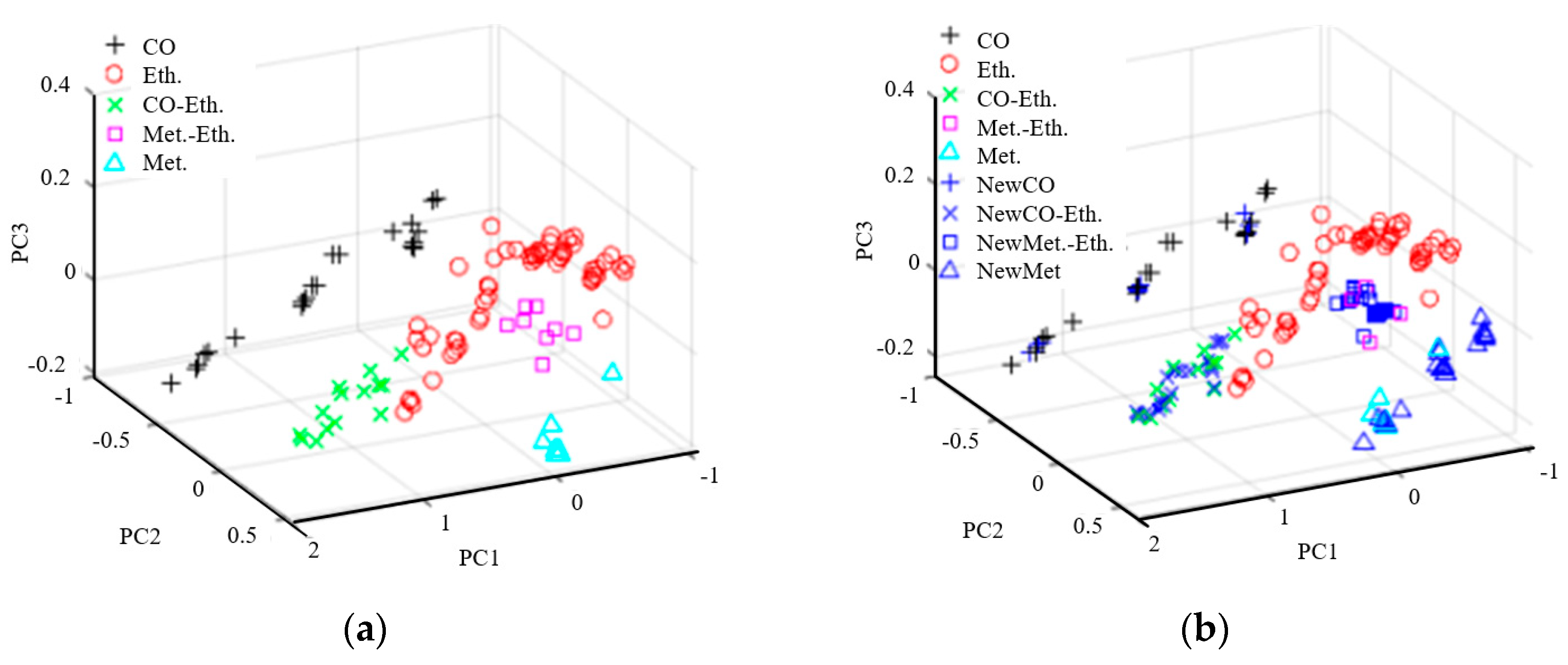
The qualitative analysis of gas mixture is divided into five steps: data preprocessing, feature extraction, stratified cross-validation, sample expansion, parameter optimization and qualitative identification.
Step 1: The raw signal is preprocessed to eliminate the difference caused by the baseline to the raw data.
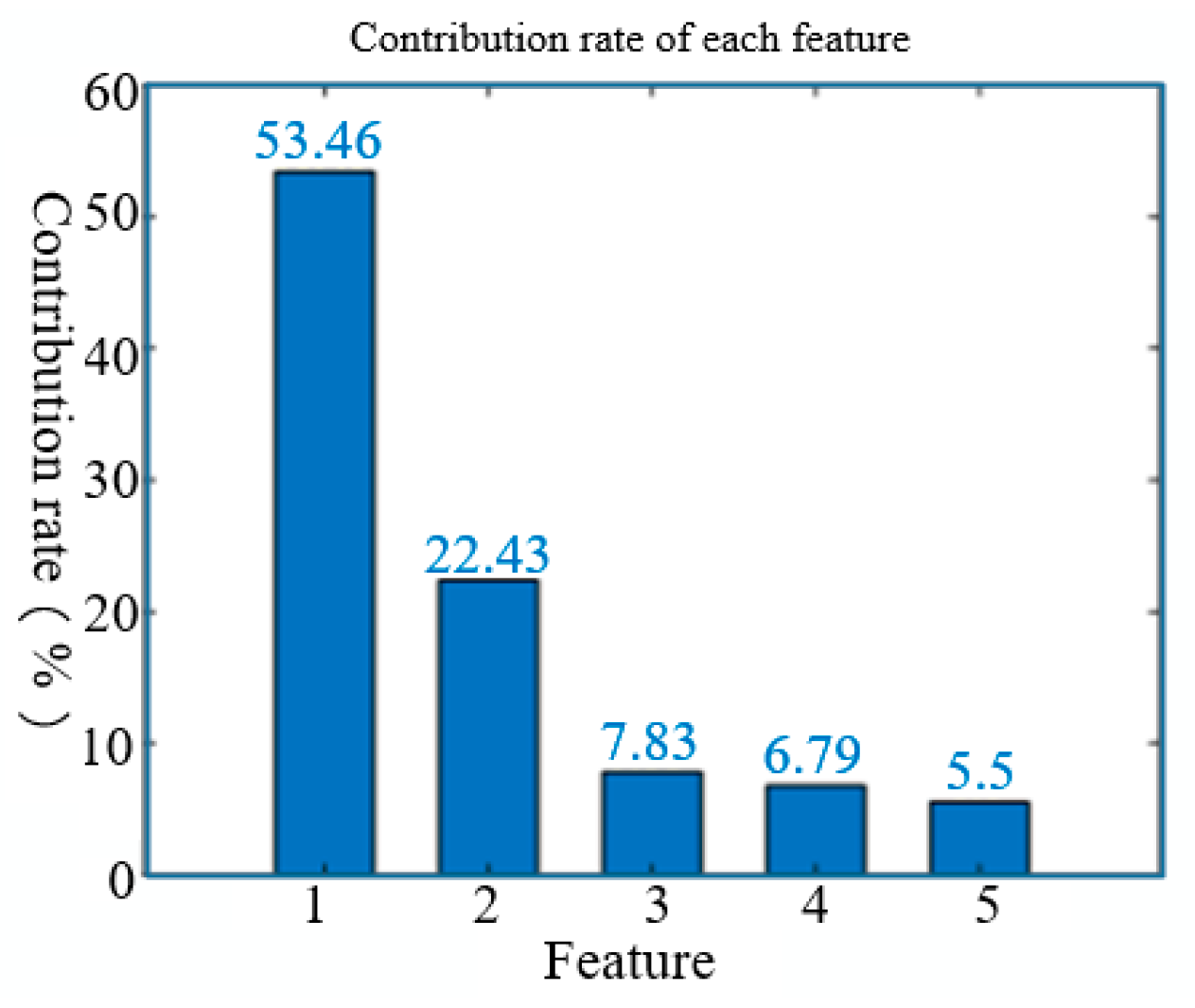
Step 2: The KPCA is used to extract the features of the preprocessed signal. When the cumulative contribution rate of feature values reaches the set threshold, the first features are selected to represent the original features.
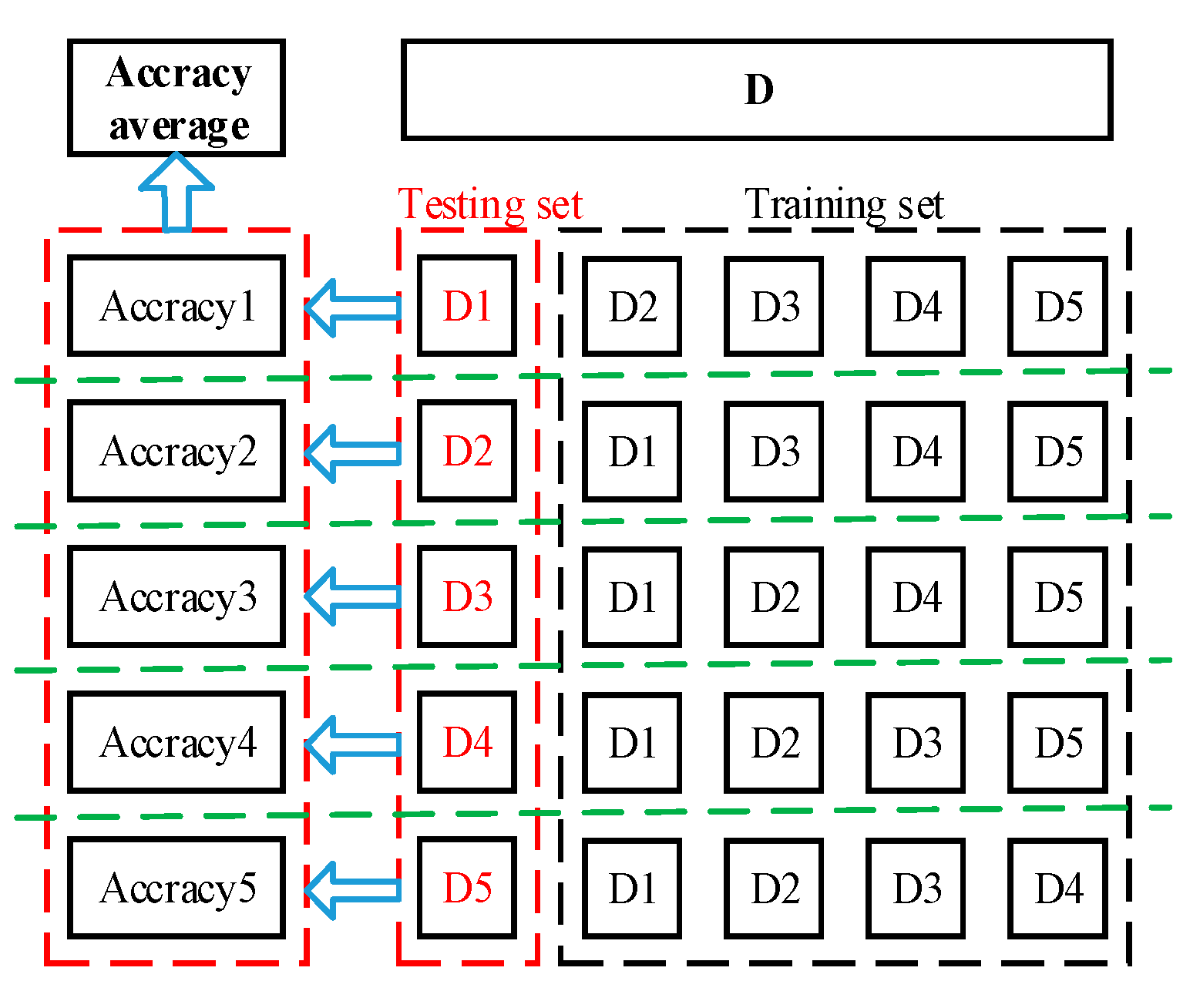
Step 3: After KPCA feature extraction, use hierarchical five-fold cross-validation to divide the data into five mutually exclusive subsets on average. In each experiment, one subset is selected as the test set, the other four subsets are combined as the training set, and the average of the five results is used as the estimation of the algorithm accuracy.
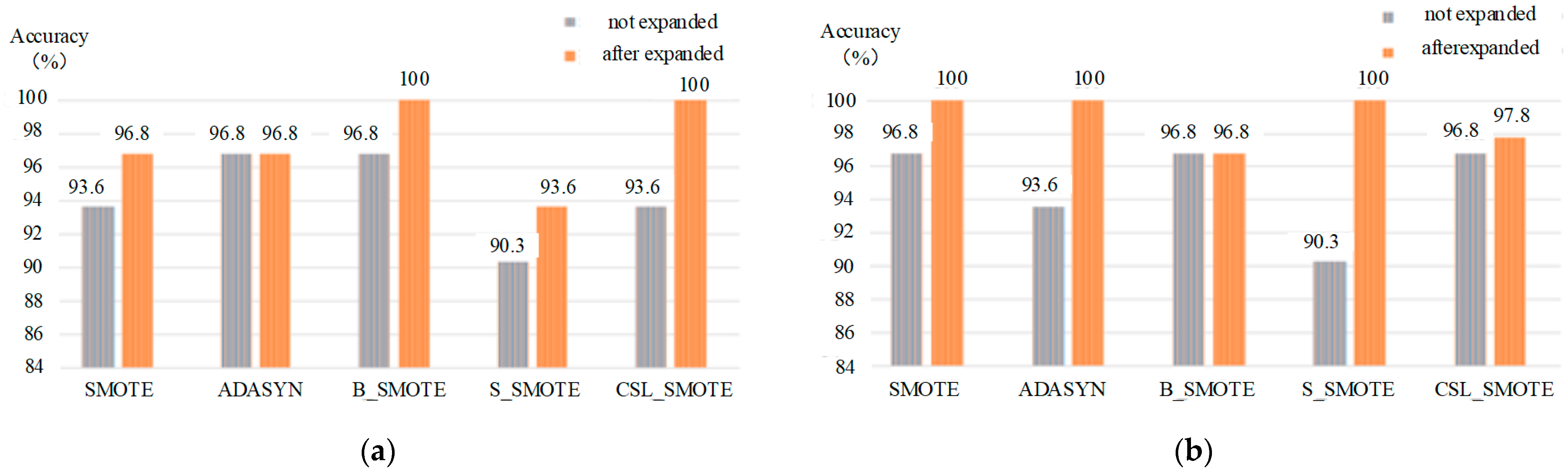
Step 4: In the training set, the ADASYN method is used to artificially synthesize a few class samples in the class imbalance, and the generated new samples are put into the training set to form a new training set.
Step 5: After sample expansion on the class unbalanced data set, The ELM method is adopted as the classification method, the PSO and GA are used to optimize the parameters of the classification method, and the classification model is obtained. The test set is input into the classification model to identify the gas mixture.
The quantitative analysis of a gas mixture component is divided into four steps: data preprocessing, sample expansion, parameter optimization and quantitative estimation.
Step 1: The original signal is preprocessed to eliminate the influence of the baseline.
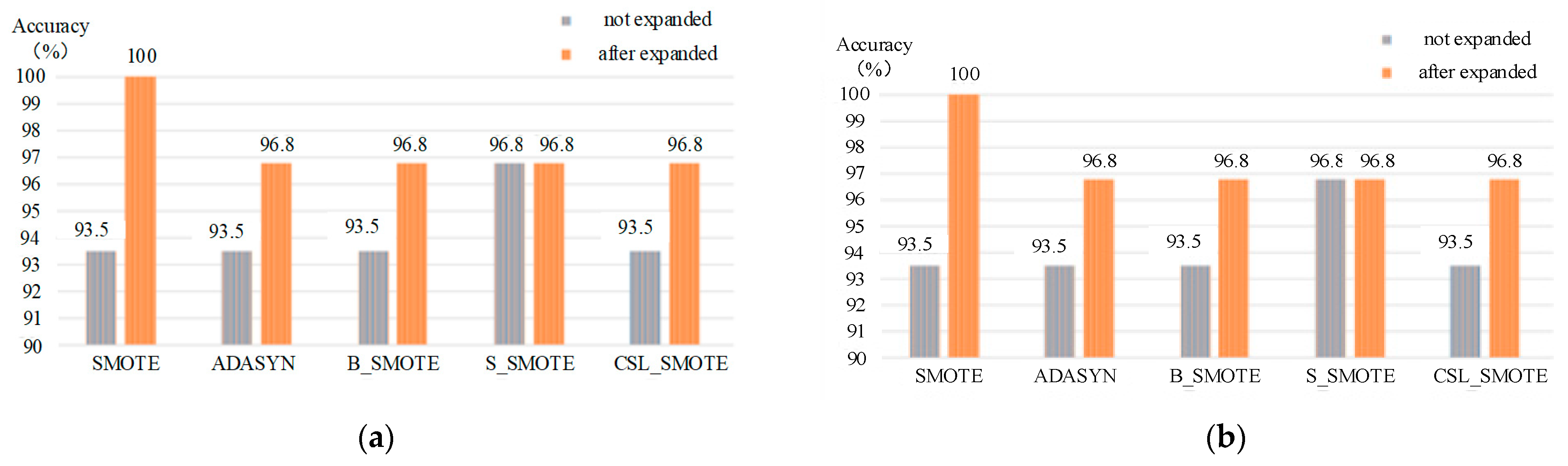
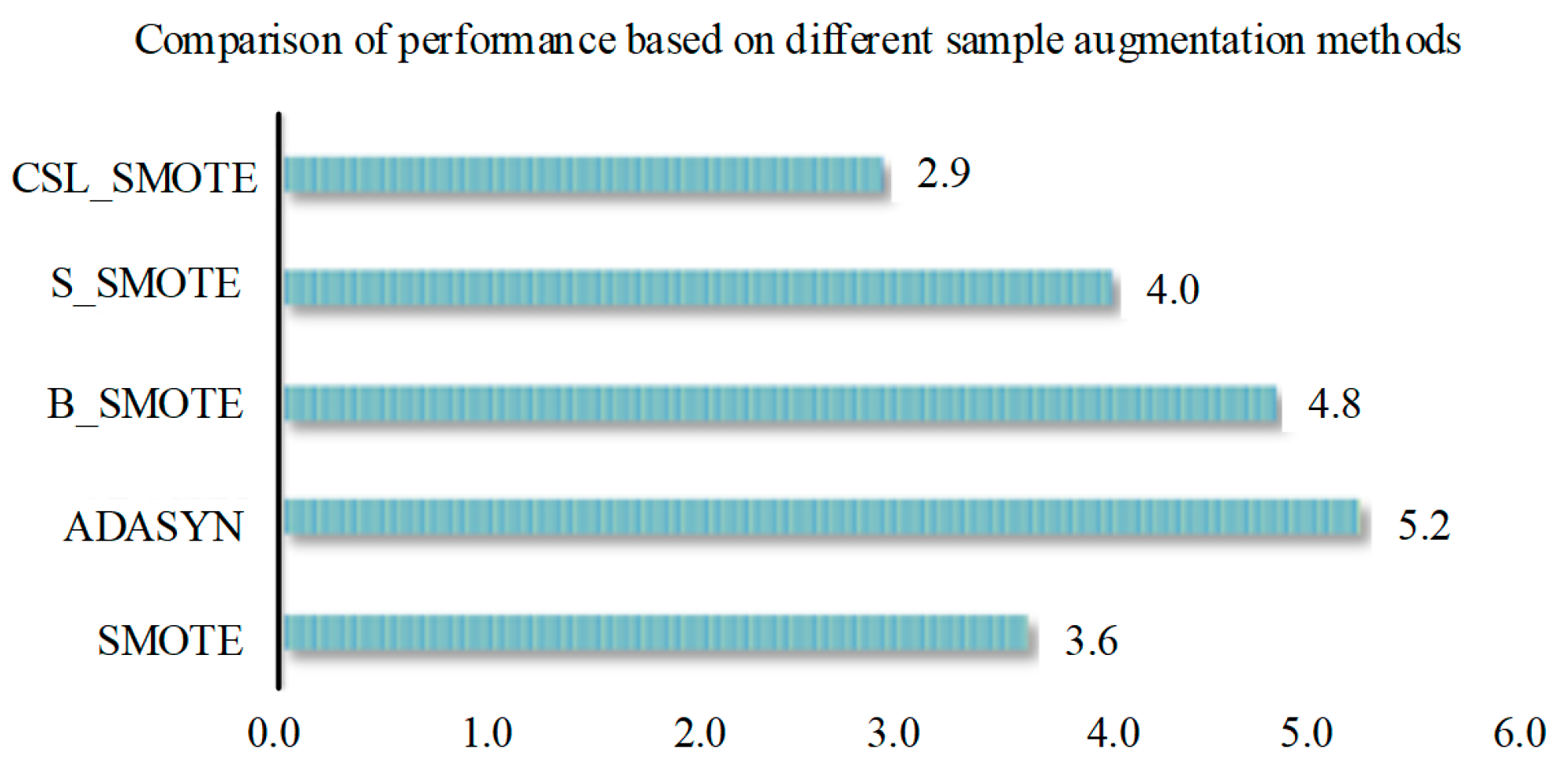
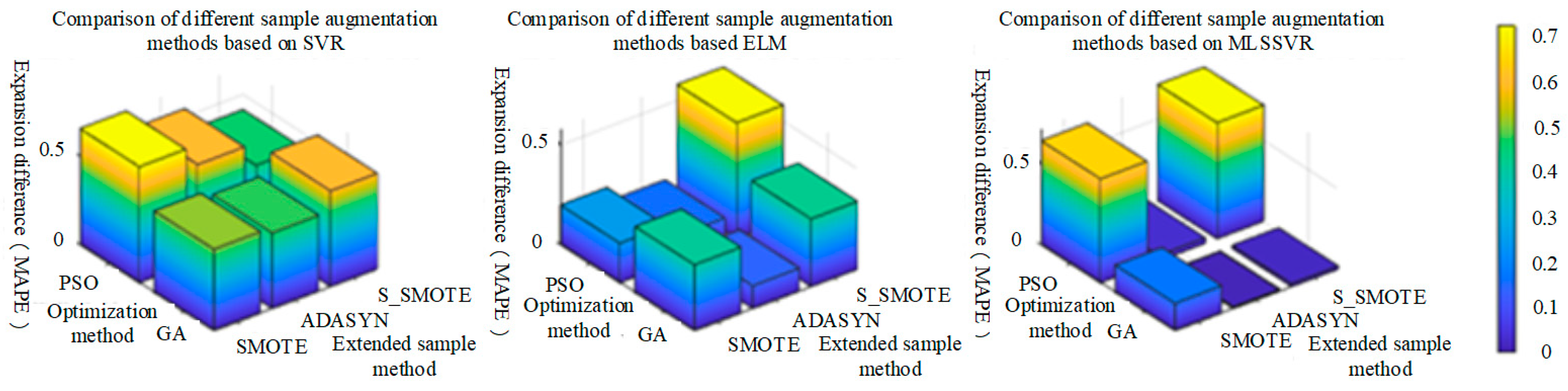
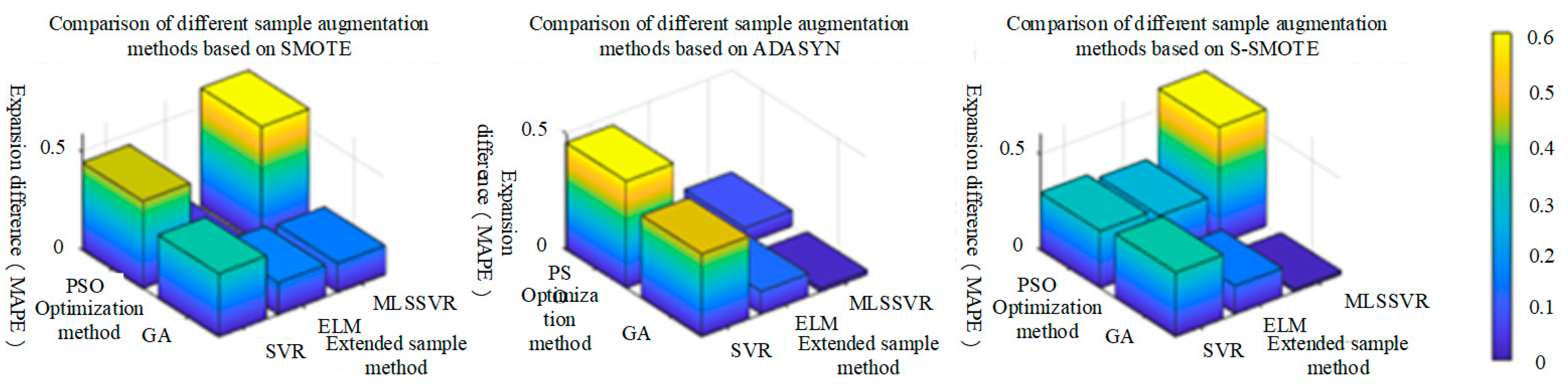
Step 2: Arrange the concentration in ascending order in the pre-treated sample set, and cross-select the samples as the training set and the test set. In the training set, The S-SMOTE method was used to synthesize artificial samples. The generated samples are put into the training set to form a new training set.
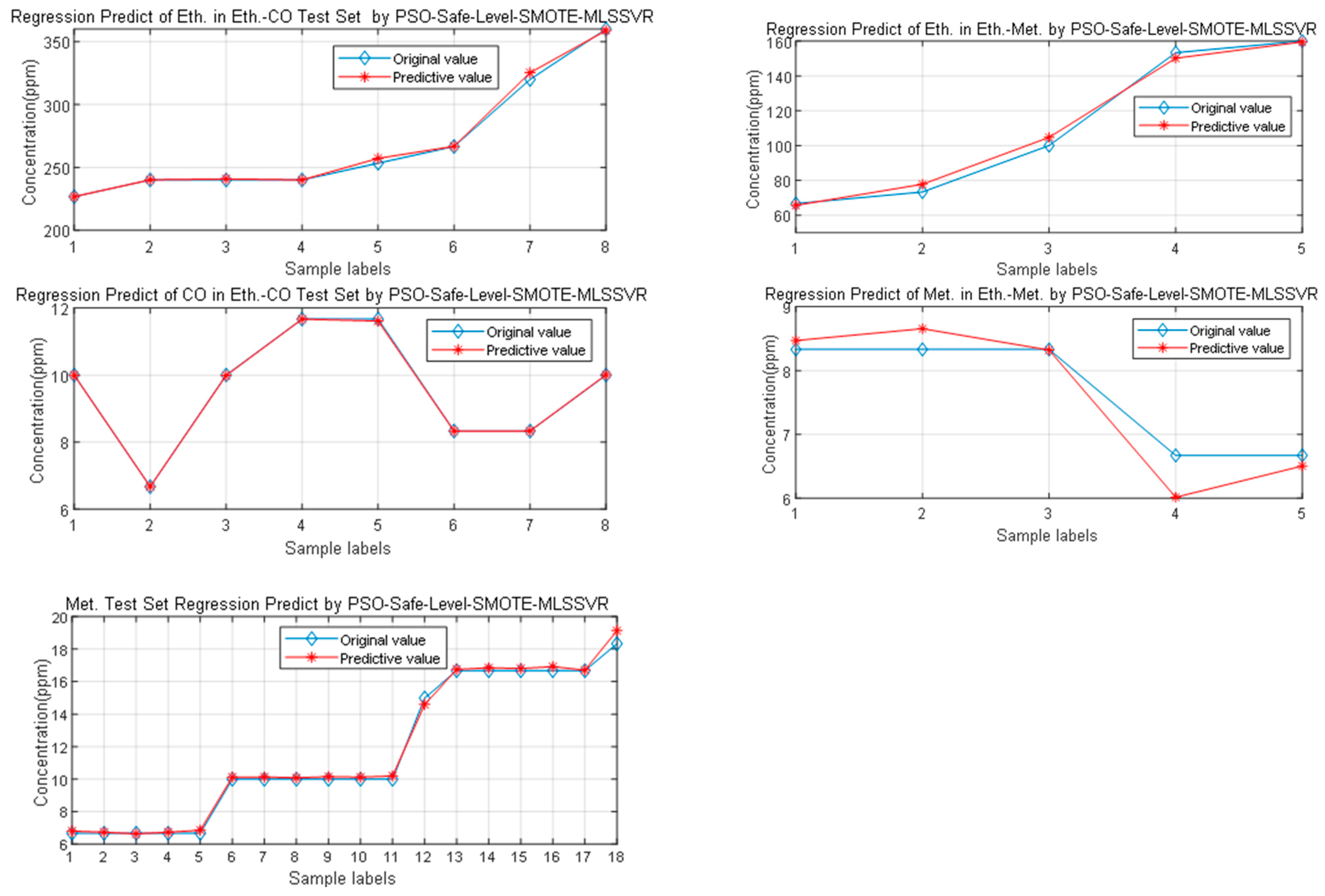
Step 3: After sample expansion, The MLSSVR method is used as the regression, and the PSO and GA methods are used to optimize the parameters of the regression method, and the regression model with the optimal parameters is obtained.
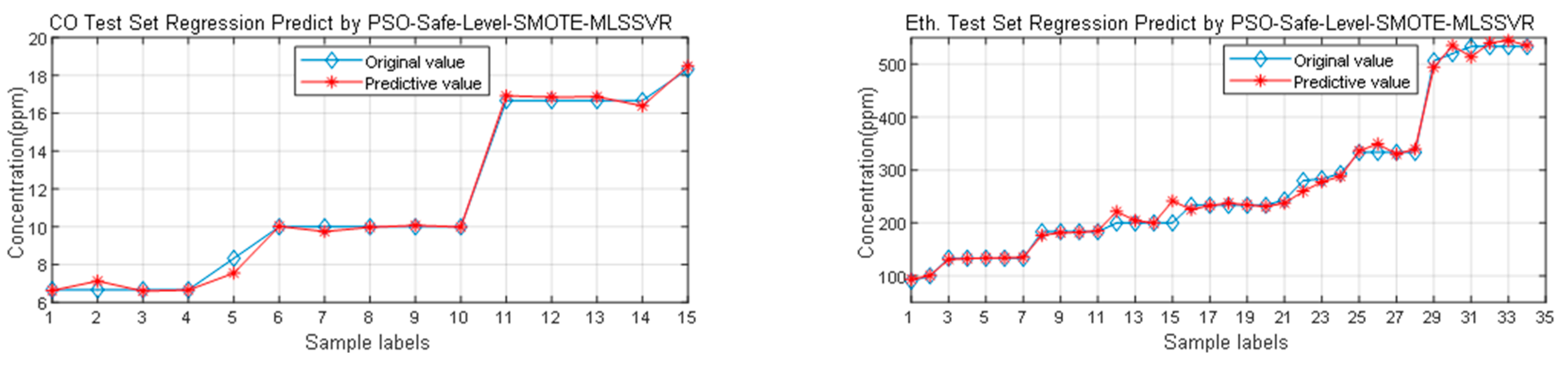
Step 4: Input the test set into the regression model to obtain the estimation of the mixed gas concentration, and use the mean absolute percentage error (MAPE) and root mean square error (RMSE) as the evaluation criteria.