Delay-Compensated Lane-Coordinate Vehicle State Estimation Using Low-Cost Sensors
Abstract
1. Introduction
2. Vehicle Model for Estimator
2.1. Road-Following Vehicle Model in Vehicle Coordinates
2.2. Vehicle Model in Lane Coordinates
3. Vehicle State Estimator in Lane Coordinates
3.1. Lane Detection Algorithm
3.2. Vehicle State Estimator
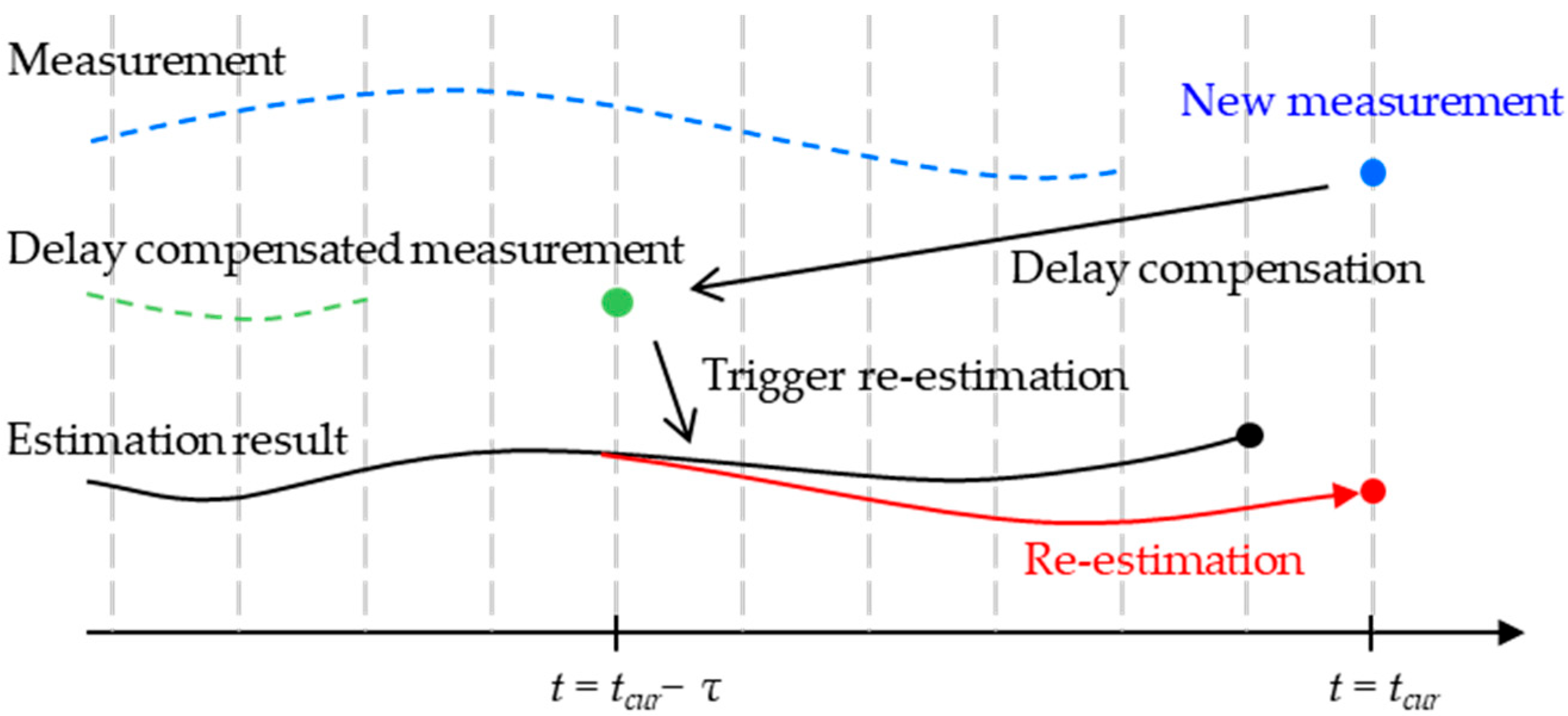
3.3. Compensation for Asynchronous Measurements
3.4. Compensation for Delayed Measurements
4. Validation
4.1. Experiment Configuration
4.2. Experiment Result and Analysis
4.2.1. Computing Efficiency Analysis
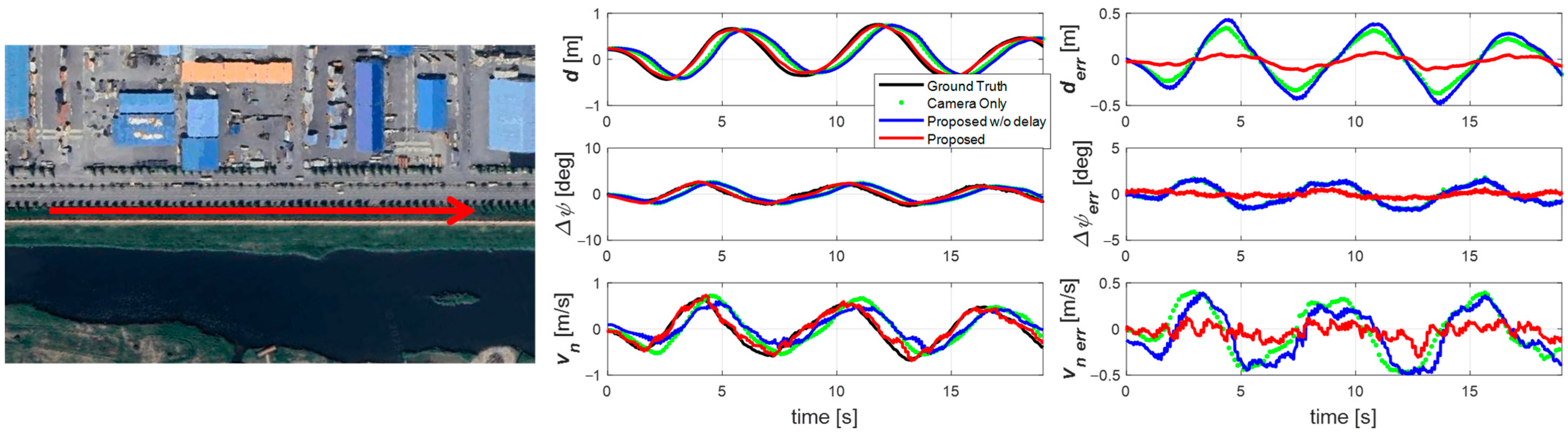
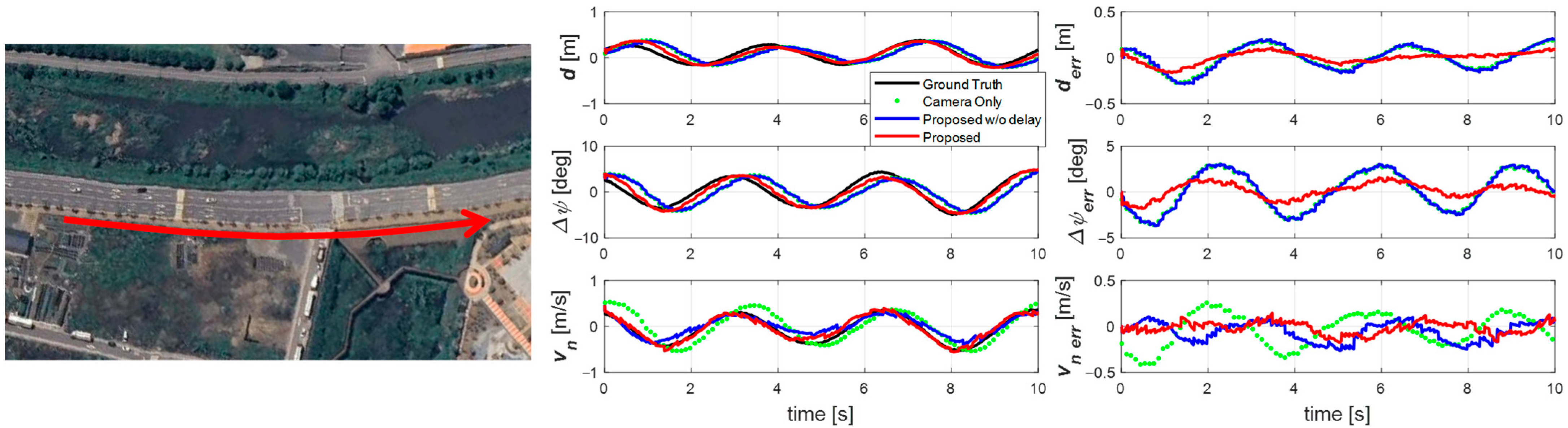
4.2.2. Sine Wave Driving Scenario
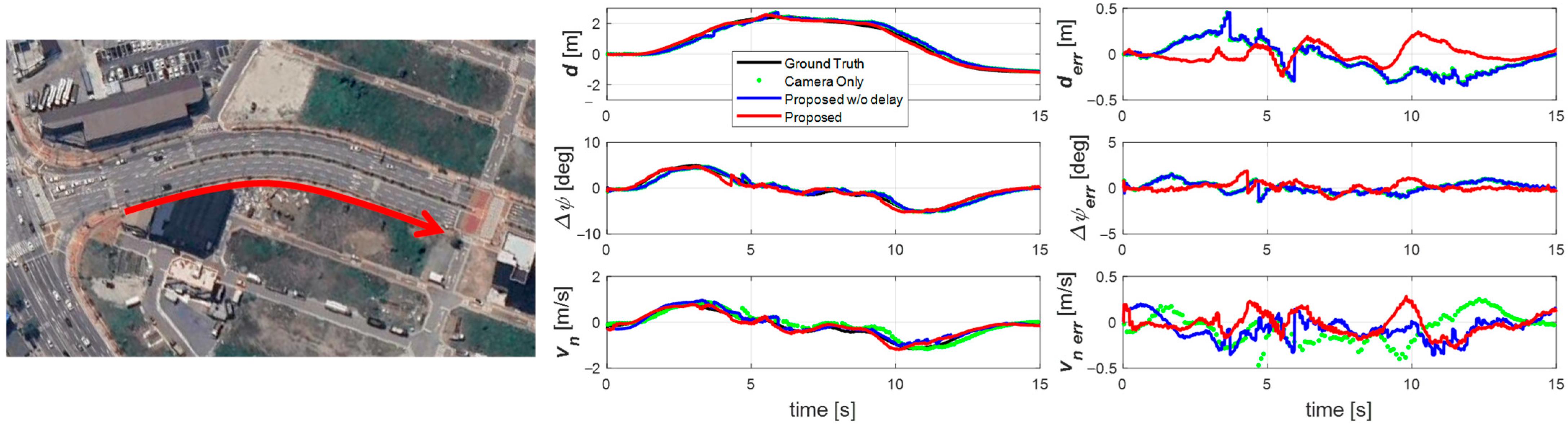
4.2.3. Double-Lane-Change Scenario
4.2.4. Overall Validation Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fayyad, J.; Jaradat, M.A.; Gruyer, D.; Najjaran, H. Deep Learning Sensor Fusion for Autonomous Vehicle Perception and Localization: A Review. Sensors 2020, 20, 4220. [Google Scholar] [CrossRef]
- Yurtsever, E.; Lambert, J.; Carballo, A.; Takeda, K. A Survey of Autonomous Driving: Common Practices and Emerging Technologies. IEEE Access 2020, 8, 58443–58469. [Google Scholar] [CrossRef]
- Ghorai, P.; Eskandarian, A.; Kim, Y.K.; Mehr, G. State Estimation and Motion Prediction of Vehicles and Vulnerable Road Users for Cooperative Autonomous Driving: A Survey. IEEE Trans. Intell. Transp. Syst. 2022, 23, 16983–17002. [Google Scholar] [CrossRef]
- Bersani, M.; Mentasti, S.; Dahal, P.; Arrigoni, S.; Vignati, M.; Cheli, F.; Matteucci, M. An integrated algorithm for ego-vehicle and obstacles state estimation for autonomous driving. Robot. Auton. Syst. 2021, 139, 103662. [Google Scholar] [CrossRef]
- Jo, K.; Lee, M.; Kim, J.; Sunwoo, M. Tracking and Behavior Reasoning of Moving Vehicles Based on Roadway Geometry Constraints. IEEE Trans. Intell. Transp. Syst. 2017, 18, 460–476. [Google Scholar] [CrossRef]
- Kim, J.; Jo, K.; Lim, W.; Lee, M.; Sunwoo, M. Curvilinear-Coordinate-Based Object and Situation Assessment for Highly Automated Vehicles. IEEE Trans. Intell. Transp. Syst. 2015, 16, 1559–1575. [Google Scholar] [CrossRef]
- Levinson, J.; Askeland, J.; Becker, J.; Dolson, J.; Held, D.; Kammel, S.; Kolter, J.Z.; Langer, D.; Pink, O.; Pratt, V.; et al. Towards fully autonomous driving: Systems and algorithms. In Proceedings of the 2011 IEEE Intelligent Vehicles Symposium (IV), Baden-Baden, Germany, 5–9 June 2011; pp. 163–168. [Google Scholar]
- Ghallabi, F.; El-Haj-Shhade, G.; Mittet, M.A.; Nashashibi, F. LIDAR-Based road signs detection For Vehicle Localization in an HD Map. In Proceedings of the 2019 IEEE Intelligent Vehicles Symposium (IV), Paris, France, 9–12 June 2019; pp. 1484–1490. [Google Scholar]
- Vázquez, J.L.; Brühlmeier, M.; Liniger, A.; Rupenyan, A.; Lygeros, J. Optimization-Based Hierarchical Motion Planning for Autonomous Racing. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021; pp. 2397–2403. [Google Scholar]
- Güzel, M.S. Autonomous Vehicle Navigation Using Vision and Mapless Strategies: A Survey. Adv. Mech. Eng. 2013, 5, 234747. [Google Scholar] [CrossRef]
- Tsogas, M.; Polychronopoulos, A.; Amditis, A. Unscented Kalman filter design for curvilinear motion models suitable for automotive safety applications. In Proceedings of the 2005 7th International Conference on Information Fusion, Philadelphia, PA, USA, 25–28 July 2005; p. 8. [Google Scholar]
- Gruyer, D.; Belaroussi, R.; Revilloud, M. Accurate lateral positioning from map data and road marking detection. Expert Syst. Appl. 2016, 43, 1–8. [Google Scholar] [CrossRef]
- Bersani, M.; Vignati, M.; Mentasti, S.; Arrigoni, S.; Cheli, F. Vehicle state estimation based on Kalman filters. In Proceedings of the 2019 AEIT International Conference of Electrical and Electronic Technologies for Automotive (AEIT AUTOMOTIVE), Turin, Italy, 2–4 July 2019; pp. 1–6. [Google Scholar]
- Guo, H.; Cao, D.; Chen, H.; Lv, C.; Wang, H.; Yang, S. Vehicle dynamic state estimation: State of the art schemes and perspectives. IEEE/CAA J. Autom. Sin. 2018, 5, 418–431. [Google Scholar] [CrossRef]
- Liu, H.; Wang, P.; Lin, J.; Ding, H.; Chen, H.; Xu, F. Real-Time Longitudinal and Lateral State Estimation of Preceding Vehicle Based on Moving Horizon Estimation. IEEE Trans. Veh. Technol. 2021, 70, 8755–8768. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y.; Fujimoto, H.; Hori, Y. Vision-Based Lateral State Estimation for Integrated Control of Automated Vehicles Considering Multirate and Unevenly Delayed Measurements. IEEE/ASME Trans. Mechatron. 2018, 23, 2619–2627. [Google Scholar] [CrossRef]
- Yeong, D.J.; Velasco-Hernandez, G.; Barry, J.; Walsh, J. Sensor and Sensor Fusion Technology in Autonomous Vehicles: A Review. Sensors 2021, 21, 2140. [Google Scholar] [CrossRef]
- Nam, H.; Choi, W.; Ahn, C. Model Predictive Control for Evasive Steering of an Autonomous Vehicle. Int. J. Automot. Technol. 2019, 20, 1033–1042. [Google Scholar] [CrossRef]
- Zakaria, N.J.; Shapiai, M.I.; Ghani, R.A.; Yassin, M.N.M.; Ibrahim, M.Z.; Wahid, N. Lane Detection in Autonomous Vehicles: A Systematic Review. IEEE Access 2023, 11, 3729–3765. [Google Scholar] [CrossRef]
- Tang, J.; Li, S.; Liu, P. A review of lane detection methods based on deep learning. Pattern Recognit. 2021, 111, 107623. [Google Scholar] [CrossRef]
- Qin, Z.; Zhang, P.; Li, X. Ultra Fast Deep Lane Detection with Hybrid Anchor Driven Ordinal Classification. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 2555–2568. [Google Scholar] [CrossRef]
- Kao, Y.; Che, S.; Zhou, S.; Guo, S.; Zhang, X.; Wang, W. LHFFNet: A hybrid feature fusion method for lane detection. Sci. Rep. 2024, 14, 16353. [Google Scholar] [CrossRef]
- Valls, M.I.; Hendrikx, H.F.C.; Reijgwart, V.J.F.; Meier, F.V.; Sa, I.; Dubé, R.; Gawel, A.; Bürki, M.; Siegwart, R. Design of an Autonomous Racecar: Perception, State Estimation and System Integration. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 2048–2055. [Google Scholar]
- Byun, Y.-S.; Jeong, R.-G.; Kang, S.-W. Vehicle Position Estimation Based on Magnetic Markers: Enhanced Accuracy by Compensation of Time Delays. Sensors 2015, 15, 28807–28825. [Google Scholar] [CrossRef] [PubMed]
- Wischnewski, A.; Stahl, T.; Betz, J.; Lohmann, B. Vehicle Dynamics State Estimation and Localization for High Performance Race Cars. IFAC-PapersOnLine 2019, 52, 154–161. [Google Scholar] [CrossRef]
- Bai, S.; Hu, J.; Yan, Y.; Pi, D.; Ding, H.; Shen, L.; Yin, G. An Adaptive UKF for Vehicle State Estimation with Delayed Measurements and Packet Loss. IEEE/ASME Trans. Mechatron. 2025, 30, 236–251. [Google Scholar] [CrossRef]
- Wang, Z.; Gao, Y.; Fang, C.; Liu, L.; Zeng, D.; Dong, M. State-Estimation-Based Control Strategy Design for Connected Cruise Control with Delays. IEEE Syst. J. 2023, 17, 99–110. [Google Scholar] [CrossRef]
- Reina, G.; Paiano, M.; Blanco-Claraco, J.-L. Vehicle parameter estimation using a model-based estimator. Mech. Syst. Signal Process. 2017, 87, 227–241. [Google Scholar] [CrossRef]
- Anderson, R.; Bevly, D.M. Using GPS with a model-based estimator to estimate critical vehicle states. Veh. Syst. Dyn. 2010, 48, 1413–1438. [Google Scholar] [CrossRef]
- AIHub. Lane/Crosswalk Recognition Images (Capital Area). Available online: https://www.aihub.or.kr/aihubdata/data/view.do?currMenu=115&topMenu=100&aihubDataSe=realm&dataSetSn=197 (accessed on 25 September 2025).
- PyTorch. resnet50. Available online: https://docs.pytorch.org/vision/main/models/generated/torchvision.models.resnet50.html#torchvision.models.ResNet50_Weights (accessed on 25 September 2025).
- Konatowski, S.; Kaniewski, P.; Matuszewski, J. Comparison of Estimation Accuracy of EKF, UKF and PF Filters. Annu. Navig. 2016, 23, 69–87. [Google Scholar] [CrossRef]
- Ribeiro, M.I. Kalman and Extended Kalman Filters: Concept, Derivation and Properties; Institute for Systems and Robotics: Lisbon, Portugal, 2004. [Google Scholar]






| Description | Description | ||
|---|---|---|---|
| d | Lateral offset about the lane [m] | m | Vehicle mass [kg] |
| ψ | Heading angle in global [rad] | Iz | Yaw moment of inertia [Nm] |
| ψd | Heading angle of the lane [rad] | a | Distance from front axle to CG [m] |
| Δψ | Heading angle from the lane [rad] | b | Distance from rear axle to CG [m] |
| u | Longitudinal velocity [m/s] | Cαf | Front tire cornering stiffness [N/rad] |
| v | Lateral velocity [m/s] | Cαr | Rear tire cornering stiffness [N/rad] |
| vn | Lateral velocity about the lane [m/s] | δf | Front Steer angle [rad] |
| r | Yaw rate [rad/s] | τ | Amount of signal delay [sec] |
| rd | Desired yaw rate along the lane [rad/s] | z | Measurements from the sensor |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| m | 1850 [kg] | Iz | 2800 [Nm] |
| a | 1.35 [m] | Cαf | 86,000 [N/rad] |
| b | 1.45 [m] | Cαr | 92,000 [N/rad] |
| Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cam. 1 | Est. 2 | Prop. 3 | Cam. 1 | Est. 2 | Prop. 3 | Cam. 1 | Est. 2 | Prop. 3 | Cam. 1 | Est. 2 | Prop. 3 | ||
| d (m) | RMSE | 0.201 | 0.256 | 0.055 | 0.121 | 0.131 | 0.061 | 0.171 | 0.177 | 0.090 | 0.183 | 0.192 | 0.077 |
| PE | 0.369 | 0.490 | 0.122 | 0.273 | 0.288 | 0.160 | 0.454 | 0.454 | 0.233 | 0.418 | 0.450 | 0.196 | |
| Δψ (deg) | RMSE | 1.003 | 1.008 | 0.269 | 2.040 | 2.059 | 0.821 | 0.577 | 0.559 | 0.481 | 0.486 | 0.511 | 0.332 |
| PE | 1.803 | 1.773 | 0.671 | 3.565 | 3.626 | 1.724 | 1.522 | 1.442 | 1.811 | 1.224 | 1.242 | 1.150 | |
| vn (m/s) | RMSE | 0.271 | 0.267 | 0.079 | 0.185 | 0.127 | 0.068 | 0.170 | 0.143 | 0.117 | 0.166 | 0.216 | 0.081 |
| PE | 0.475 | 0.525 | 0.288 | 0.414 | 0.261 | 0.162 | 0.469 | 0.345 | 0.281 | 0.357 | 0.513 | 0.196 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, M.; Kang, W.; Ahn, C. Delay-Compensated Lane-Coordinate Vehicle State Estimation Using Low-Cost Sensors. Sensors 2025, 25, 6251. https://doi.org/10.3390/s25196251
Kim M, Kang W, Ahn C. Delay-Compensated Lane-Coordinate Vehicle State Estimation Using Low-Cost Sensors. Sensors. 2025; 25(19):6251. https://doi.org/10.3390/s25196251
Chicago/Turabian StyleKim, Minsu, Weonmo Kang, and Changsun Ahn. 2025. "Delay-Compensated Lane-Coordinate Vehicle State Estimation Using Low-Cost Sensors" Sensors 25, no. 19: 6251. https://doi.org/10.3390/s25196251
APA StyleKim, M., Kang, W., & Ahn, C. (2025). Delay-Compensated Lane-Coordinate Vehicle State Estimation Using Low-Cost Sensors. Sensors, 25(19), 6251. https://doi.org/10.3390/s25196251






