Review of Research Advances in Gyroscopes’ Structural Forms and Processing Technologies Viewed from Performance Indices
Abstract
1. Introduction
2. Basic Mechanics Principle and Indices of Gyroscope
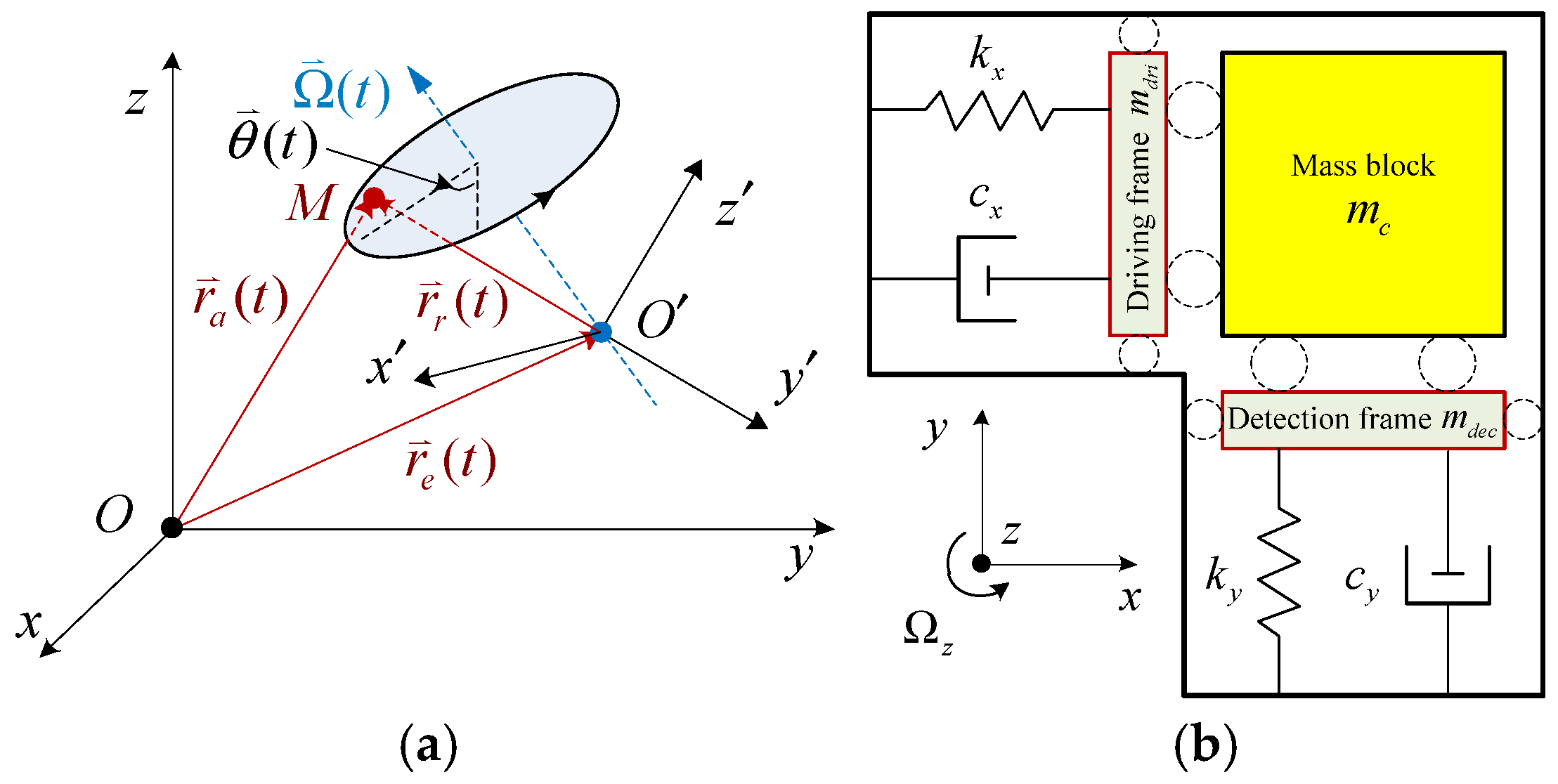
2.1. Coriolis Force Effect and Coriolis Acceleration
2.2. Principle of the Resonant Gyroscope
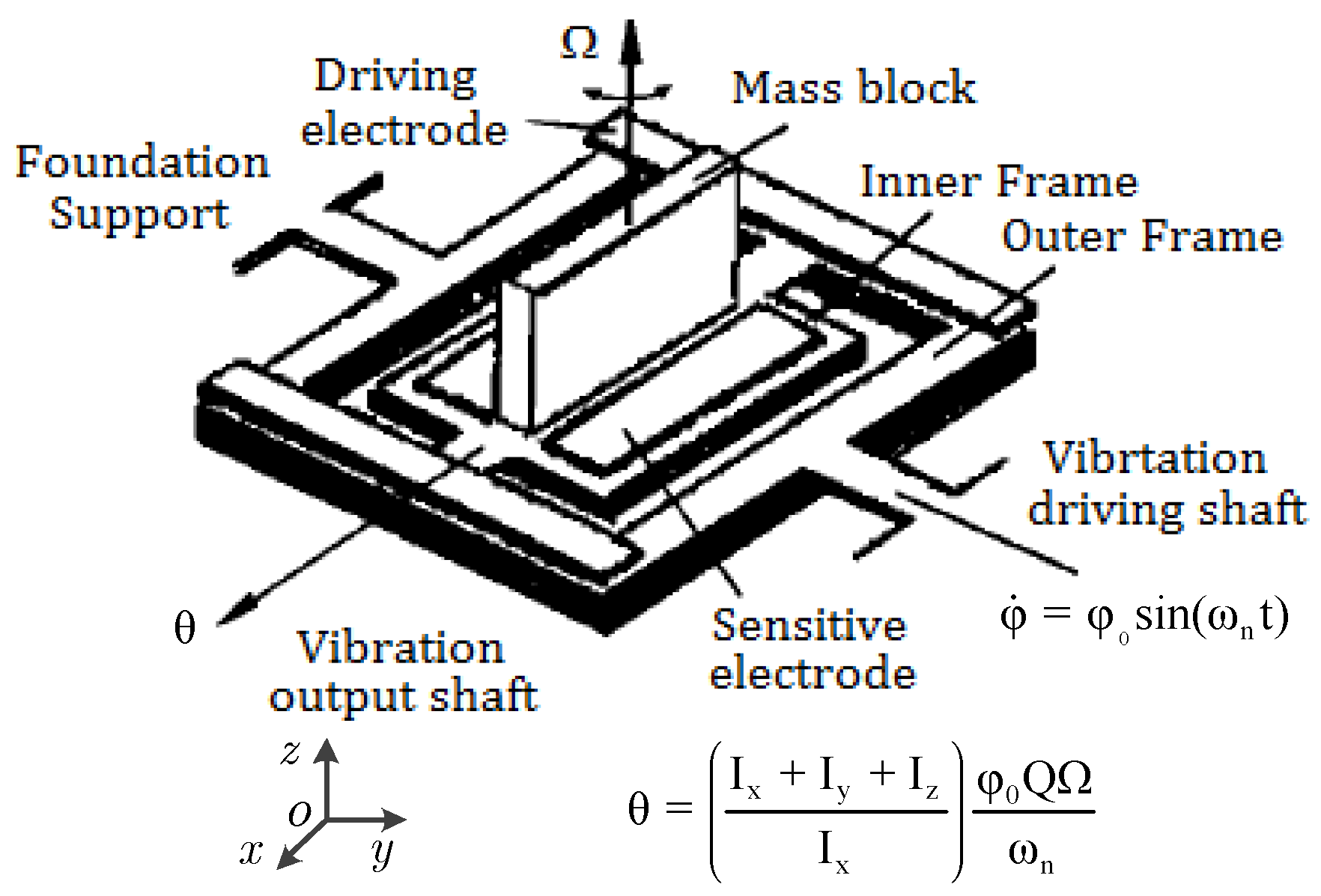
2.2.1. Typical Structure of a Resonant MEMS Gyroscope
2.2.2. Principle of Resonance Detection
- The detection amplitude is directly proportional to the rotation angular velocity of the base (system).
- The mechanical sensitivity of the system is proportional to the amplitude of the driving mode and inversely proportional to the difference in frequency between the driving frequency ωd and the detection frequency ωy.
- Mechanical sensitivity can be enhanced by increasing the driving quality factor, deducing the driving mass, and decreasing the difference frequency.
2.3. Performance Indices of the Gyroscope
2.3.1. Scale Factor
2.3.2. Threshold Value/Resolution
2.3.3. Measuring Range
2.3.4. Zero-Bias Stability
2.3.5. Angle Random Walk (ARW)
2.3.6. Band Width (BW)
2.4. Quantitative Analysis of the Impact of MEMS Gyroscope Structures, Closed-Loop Control, and Phase Alignment Accuracy
3. Research Advances in the Field of Gyroscopes’ Structural Form and Processing Technologies
3.1. Typical Development of Gyroscope
3.1.1. Division of Structural Development Stages
3.1.2. Several Impacts Caused by Structural Evolution
3.2. Performance of Different Structure Forms and Machining Processing in MEMS Gyroscopes
3.2.1. Single-Mass Block Configuration
3.2.2. Dual-Mass-Block Configuration
3.2.3. Quadruple-Mass Block Structure


3.2.4. Ring/Disc Structure


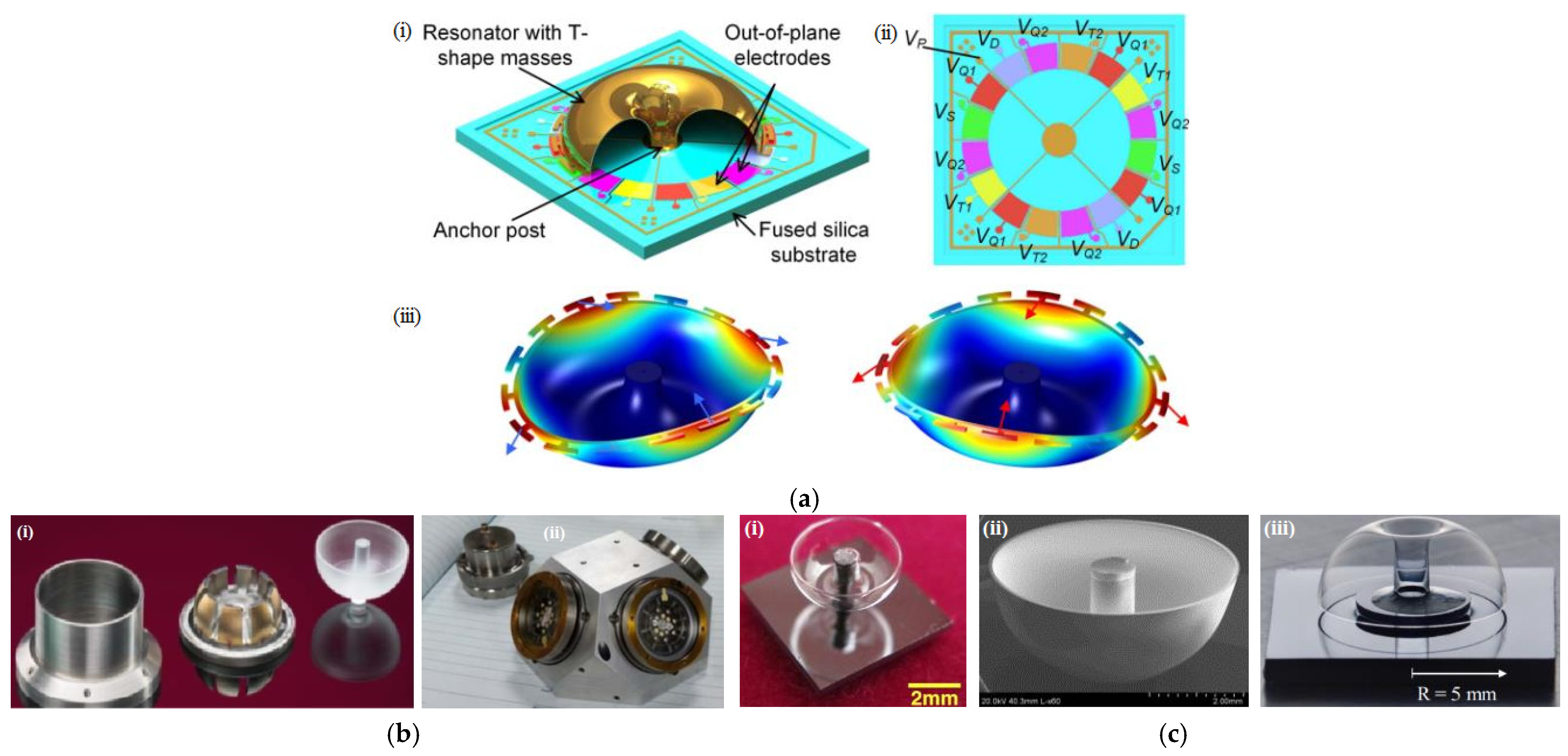
3.2.5. Hemisphere Structure
4. Impacts of Design, Fabrication and Factors on Performance
4.1. Performacne Impacts from Pespective of Design Types
4.2. Performacne Impacts Caused by Certain Factors
4.2.1. Environmental Sensitivity
4.2.2. Sock Resistance
4.2.3. Thermal Stress and Temperature Drift
4.2.4. Other Optimization Technologies
4.3. Fabrication Processes on the Impact of Permormance
4.4. Brief Summary
5. Features and Challenges of Gyroscope Technology
5.1. Typical Characteristics of Gyroscope Research
5.1.1. Multidisciplinary Integration
5.1.2. Statistical Properties of Results
5.1.3. Error and Corresponding Compensation
5.2. Challenges of Gyroscopes Technology
5.2.1. Challenge in Error Reduction Methods
5.2.2. Challenge from the Enhancement of Mechanical Sensitivity
5.2.3. Challenge in Mathematical Modelling of a System
5.2.4. Challenge in Machine, Levelling and Excitation Technologies
5.3. Suggestions for Future Research Directions
6. Conclusions and Perspective
- (i)
- An overview of the modelling principles and processes of gyroscopes based on the Coriolis force and resonance mechanisms lays a theoretical foundation for the research and development of microelectromechanical system (MEMS) gyroscopes. Moreover, the core performance indices of gyroscopes are systematically sorted, providing a standardized evaluation basis for measuring the performance of different gyroscopes and guiding their design and application.
- (ii)
- An in-depth analysis of the evolutionary process of gyroscope designs and the distinctive features of each development stage is performed. On this basis, typical structural forms of various MEMS gyroscopes (such as single-mass-block, dual-mass-block, quadruple-mass-block, ring/disc, and hemispherical structures) are discussed, along with their corresponding processing technologies. The correlations among different structures, processing methods, and gyroscope performance indices are also clarified, revealing how structural innovation and processing progress drive performance optimization.
- (iii)
- From the perspectives of design, fabrication, and other typical factors, analyses are provided to illustrate their impacts on performance, emphasizing the significance and challenges associated with compensation and optimization arising from internal and external influences such as design variations, process deviations, mechanical shock, thermal stress, and temperature drift.
- (iv)
- A summary of the prominent characteristic challenges in gyroscope technologies is as follows:
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Söderkvist, J. Micromachined gyroscopes. Sens. Actuators A Phys. 1994, 43, 65–71. [Google Scholar] [CrossRef]
- Lawrence, A. Modern Inertial Technology: Navigation, Guidance, and Control; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Pansiot, J.; Zhang, Z.Q.; Lo, B.; Yang, G. WISDOM: Wheelchair inertial sensors for displacement and orientation monitoring. Meas. Sci. Technol. 2011, 22, 105801. [Google Scholar] [CrossRef]
- Xu, Y.; Chen, X.Y.; Wang, Y.M. Two-mode navigation method for low-cost inertial measurement unit-based indoor pedestrian navigation. Simulation 2016, 92, 839–848. [Google Scholar] [CrossRef]
- Fan, L.S.; Tai, Y.C.; Muller, R.S. Integrated movable micromechanical structures for sensors and actuators. IEEE Trans. Electron Devices 1988, 35, 724–730. [Google Scholar] [CrossRef]
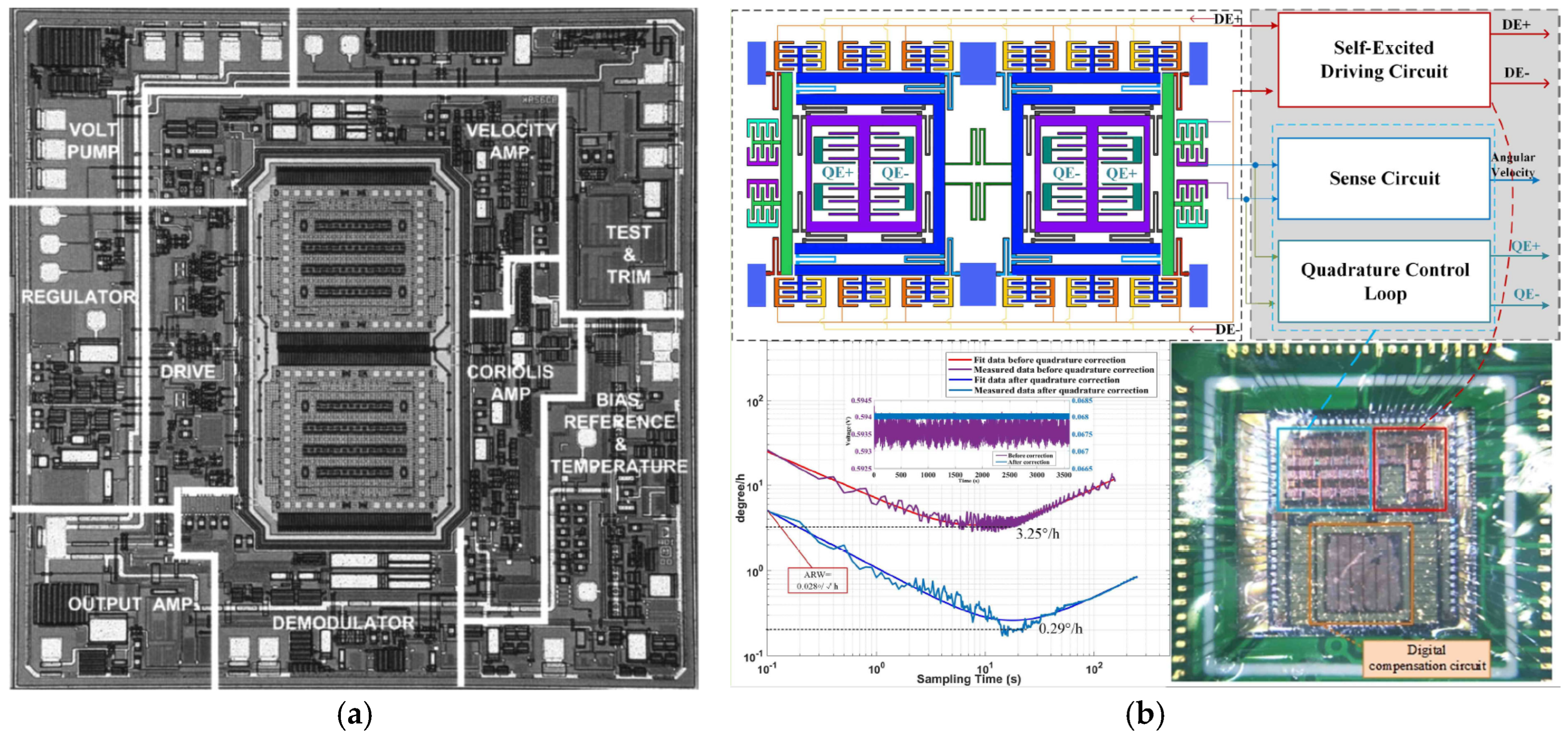
- Tatar, E.; Alper, S.E.; Akin, T. Quadrature-error compensation and corresponding effects on the performance of fully decoupled MEMS gyroscopes. J. Microelectromech. Syst. 2012, 21, 656–667. [Google Scholar] [CrossRef]
- Saukoski, M.; Aaltonen, L.; Halonen, K.A.I. Effects of synchronous demodulation in vibratory MEMS gyroscopes: A theoretical study. IEEE Sens. J. 2008, 8, 1722–1733. [Google Scholar] [CrossRef]
- Cui, J.; Chi, X.Z.; Ding, H.T.; Lin, L.T.; Yang, Z.C.; Yan, G.Z. Transient response and stability of the AGC-PI closed-loop controlled MEMS vibratory gyroscopes. J. Micromech. Microeng. 2009, 19, 125015. [Google Scholar] [CrossRef]
- Hou, Z.Q.; Xiao, D.B.; Wu, X.Z.; Dong, P.T.; Chen, Z.H.; Niu, Z.Y.; Zhang, X. Effect of axial force on the performance of micromachined vibratory rate gyroscopes. Sensors 2011, 11, 296–309. [Google Scholar] [CrossRef] [PubMed]
- Xiao, D.B.; Su, J.B.; Chen, Z.H.; Hou, Z.Q.; Wang, X.H.; Wu, X.Z. Improvement of mechanical performance for vibratory microgyroscope based on sense mode closed-loop control. J. Micro/Nanolith. MEMS MOEMS 2013, 12, 023001. [Google Scholar] [CrossRef][Green Version]
- Feng, R.; Qiu, A.P.; Shi, Q.; Su, Y. A theoretical and experimental study on temperature dependent characteristics of silicon MEMS gyroscope drive mode. Adv. Mater. Res. 2011, 403–408, 4237–4243. [Google Scholar] [CrossRef]
- Bernstein, J.; Cho, S.; King, A.T.; Kourepenis, A.; Maciel, P.; Weinberg, M. A micromachined comb-drive tuning fork rate gyroscope. In Proceedings of the IEEE Micro Electro Mechanical Systems, Fort Lauderdale, FL, USA, 10 February 1993; IEEE: New York, NY, USA, 1993; pp. 143–148. [Google Scholar] [CrossRef]
- Johnson, B.R.; Cabuz, E.; French, H.B.; Supino, R. Development of a MEMS gyroscope for northfinding applications. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium, Indian Wells, CA, USA, 4–6 May 2010; IEEE: New York, NY, USA, 2010; pp. 168–170. [Google Scholar] [CrossRef]
- Geiger, W.; Folkmer, B.; Sobe, U.; Sandmaier, H.; Lang, W. New designs of micromachined vibrating rate gyroscopes with decoupled oscillation modes. Sens. Actuators A Phys. 1998, 66, 118–124. [Google Scholar] [CrossRef]
- Antonello, R.; Oboe, R.; Prandi, L.; Biganzoli, F. Automatic Mode Matching in MEMS Vibrating Gyroscopes Using Extremum-Seeking Control. IEEE Trans. Ind. Electron. 2009, 56, 3880–3891. [Google Scholar] [CrossRef]
- Riaz, K.; Bazaz, S.A.; Saleem, M.M.; Shakoor, R.I. Design, damping estimation and experimental characterization of decoupled 3-DoF robust MEMS gyroscope. Sens. Actuators A Phys. 2011, 172, 523–532. [Google Scholar] [CrossRef]
- Shen, Q.; Li, H.; Hao, Y.C.; Yuan, W.Z.; Chang, H.L. Bias contribution modeling for a symmetrical micromachined Coriolis vibratory gyroscope. IEEE Sens. J. 2016, 16, 723–733. [Google Scholar] [CrossRef]
- Cetin, H.; Yaralioglu, G.G. Analysis of vibratory gyroscopes: Drive and sense mode resonance shift by coriolis force. IEEE Sens. J. 2017, 17, 347–358. [Google Scholar] [CrossRef]
- Tu, Y.H.; Peng, C.C. An ARMA-based digital twin for MEMS gyroscope drift dynamics modeling and real-time compensation. IEEE Sens. J. 2021, 21, 2712–2724. [Google Scholar] [CrossRef]
- Georgy, J.; Noureldin, A.; Korenberg, M.J.; Bayoumi, M.M. Modeling the stochastic drift of a MEMS-based gyroscope in gyro/odometer/GPS integrated navigation. IEEE Trans. Intell. Transp. Syst. 2010, 11, 856–872. [Google Scholar] [CrossRef]
- Li, X.; Li, Z. Vector-aided in-field calibration method for low-end MEMS gyros in attitude and heading reference systems. IEEE Trans. Instrum. Meas. 2014, 63, 2675–2681. [Google Scholar] [CrossRef]
- Shkel, A.M. Type I and type II micromachined vibratory gyroscopes. In Proceedings of the 2006 IEEE/ION Position, Location, And Navigation Symposium, San Diego, CA, USA, 25–27 April 2006; IEEE: New York, NY, USA, 2006; pp. 586–593. [Google Scholar] [CrossRef]
- Wang, S.H.; Al Farisi, M.S.; Tsukamoto, T.; Tanaka, S. Roll/pitch rate integrating mems gyroscope using dynamically balanced dual-mass resonator. In Proceedings of the 2020 IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Hiroshima, Japan, 23–26 March 2020; IEEE: New York, NY, USA, 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Fan, B.; Guo, S.W.; Cheng, M.M.; Yu, L.; Zhou, M.; Hu, W.Y.; Chen, Z.A.; Xu, D.C. A novel high-symmetry cobweb-like disk resonator gyroscope. IEEE Sens. J. 2019, 19, 10289–10297. [Google Scholar] [CrossRef]
- Yang, J.; Hamelin, B.; Ayazi, F. Investigating elastic anisotropy of 4H-SiC Using Ultra-High Q bulk acoustic wave resonators. J. Microelectromech. Syst. 2020, 29, 1473–1482. [Google Scholar] [CrossRef]
- Cao, H.L.; Xue, R.H.; Cai, Q.; Gao, J.Y.; Zhao, R.; Shi, Y.B.; Huang, K.; Shao, X.L.; Shen, C. Design and experiment for dual-mass MEMS gyroscope sensing closed-loop system. IEEE Access 2020, 8, 48074–48087. [Google Scholar] [CrossRef]
- Shao, X.L.; Shi, Y.; Zhang, W.D.; Cao, H.L. Neurodynamic approximation-based quantized control with improved transient performances for microelectromechanical system gyroscopes: Theory and experimental results. IEEE Trans. Ind. Electron. 2021, 68, 9972–9983. [Google Scholar] [CrossRef]
- Sung, S.; Sung, W.T.; Kim, C.; Yun, S.; Lee, Y.J. On the mode-matched control of MEMS vibratory gyroscope via phase-domain analysis and design. IEEE/ASME Trans. Mechatron. 2009, 14, 446–455. [Google Scholar] [CrossRef]
- Trusov, A.A.; Schofield, A.R.; Shkel, A.M. Micromachined rate gyroscope architecture with ultra-high quality factor and improved mode ordering. Sens. Actuators A Phys. 2011, 165, 26–34. [Google Scholar] [CrossRef]
- Yoon, S.; Lee, S.; Perkins, N.; Najafi, K. Analysis and wafer-level design of a high-order silicon vibration isolator for resonating MEMS devices. J. Micromech. Microeng. 2010, 21, 015017. [Google Scholar] [CrossRef]
- Xie, H.K.; Fedder, G.K. Fabrication, characterization, and analysis of a DRIE CMOS-MEMS gyroscope. IEEE Sens. J. 2003, 3, 622–631. [Google Scholar] [CrossRef]
- Sharma, A.; Zaman, M.F.; Ayazi, F. A sub-0.2°/hr bias drift micromechanical silicon gyroscope with automatic CMOS mode-matching. IEEE J. Solid-State Circuits 2009, 44, 1593–1608. [Google Scholar] [CrossRef]
- Sharma, M.; Sarraf, E.H.; Baskaran, R.; Cretu, E. Parametric resonance: Amplification and damping in MEMS gyroscopes. Sens. Actuators A Phys. 2012, 177, 79–86. [Google Scholar] [CrossRef]
- Dion, F.; Martel, S.; Denatale, J. 200mm High performance inertial sensor manufacturing process. In Proceedings of the 2018 IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Lake Como, Italy, 26–29 March 2018; IEEE: New York, NY, USA, 2018; pp. 1–2. [Google Scholar] [CrossRef]
- Denatale, J.; Martel, S.; Dion, F.; Lachance, J. Manufacturing transition of high-performance MEMS gyroscopes. In Proceedings of the 2020 IEEE/ION Position, Location and Navigation Symposium (PLANS), Portland, OR, USA, 20–23 April 2020; IEEE: New York, NY, USA, 2020; pp. 24–26. [Google Scholar] [CrossRef]
- Asadian, M.H.; Wang, Y.S.; Shkel, A.M. Development of 3D fused quartz hemi-toroidal shells for high-Q resonators and gyroscopes. J. Microelectromech. Syst. 2019, 28, 954–964. [Google Scholar] [CrossRef]
- Chen, J.L.; Tsukamoto, T.; Tanaka, S. Quad mass gyroscope with 16 ppm frequency mismatch trimmed by focus ion beam. In Proceedings of the 2019 IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Naples, FL, USA, 1–5 April 2019; IEEE: New York, NY, USA, 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Feng, H.Z.; Lou, W.Z.; Wang, D.K.; Zheng, F.Q.; Liao, M.H. System reliability analysis of MEMS gyroscope with multiple failure modes. In Proceedings of the 2018 10th International Conference on Modelling, Identification and Control (ICMIC), Guiyang, China, 2–4 July 2018; IEEE: New York, NY, USA, 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Li, J.; Broas, M.; Makkonen, J.; Mattila, T.T.; Hokka, J.; Paulasto-Kröckel, M. Shock impact reliability and failure analysis of a three-axis MEMS gyroscope. J. Microelectromech. Syst. 2014, 23, 347–355. [Google Scholar] [CrossRef]
- Patel, C.; Mccluskey, P.; Lemus, D. Performance and reliability of mems gyroscopes at high temperatures. In Proceedings of the 2010 12th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems, Las Vegas, NV, USA, 2–5 June 2010; IEEE: New York, NY, USA, 2010; pp. 1–5. [Google Scholar] [CrossRef]
- Betta, G.; Capriglione, D.; Carratù, M.; Catelani, M.; Ciani, L.; Patrizi, G.; Pietrosanto, A.; Sommella, P. Stress testing for performance analysis of orientation estimation algorithms. IEEE Trans. Instrum. Meas. 2022, 71, 1–12. [Google Scholar] [CrossRef]
- Cao, H.L. Dual-Mass Linear Vibration Silicon Based MEMS Gyroscope; Springer: Singapore, 2023; pp. 3–4. [Google Scholar] [CrossRef]
- Cao, H.L.; Li, H.S. Investigation of a vacuum packaged MEMS gyroscope architecture’s temperature robustness. Int. J. Appl. Electromagn. Mech. 2013, 41, 495–506. [Google Scholar] [CrossRef]
- Yang, B.; Wang, S.R.; Li, H.S.; Zhou, B.L. Mechanical-thermal noise in drive-mode of a silicon micro-gyroscope. Sensors 2009, 9, 3357–3375. [Google Scholar] [CrossRef]
- Yazdi, N.; Ayazi, F.; Najafi, K. Micromachined inertial sensors. Proc. IEEE 1998, 86, 1640–1659. [Google Scholar] [CrossRef]
- Gu, H.Y.; Su, W.; Zhao, B.L.; Zhou, H.; Liu, X.X. A design methodology of digital control system for MEMS gyroscope based on multi-objective parameter optimization. Micromachines 2020, 11, 75. [Google Scholar] [CrossRef]
- Cao, H.L.; Li, H.; Wang, S.R.; Yang, B.; Huang, L.B. Structure model and system simulation of MEMS gyroscope. J. Chin. Inert. Technol. 2013, 21, 524–529. [Google Scholar] [CrossRef]
- Wang, X.T.; Zheng, X.D.; Shen, Y.J.; Xia, C.H.; Liu, G.W.; Jin, Z.H.; Ma, Z.P. A digital control structure for Lissajous frequency-modulated mode MEMS gyroscope. IEEE Sens. J. 2022, 22, 19207–19219. [Google Scholar] [CrossRef]
- Ma, W.; Lin, Y.Y.; Liu, S.Q.; Zheng, X.D.; Jin, Z.H. A novel oscillation control for MEMS vibratory gyroscopes using a modified electromechanical amplitude modulation technique. J. Micromech. Microeng. 2016, 27, 025005. [Google Scholar] [CrossRef]
- Xu, P.F.; Wei, Z.Y.; Guo, Z.Y.; Jia, L.; Han, G.W.; Si, C.W.; Ning, J.; Yang, F.H. A real-time circuit phase delay correction system for MEMS vibratory gyroscopes. Micromachines 2021, 12, 506. [Google Scholar] [CrossRef] [PubMed]
- Yang, K.; Li, J.H.; Yang, J.J.; Xu, L.X. Research on adaptive closed-loop control of microelectromechanical system gyroscopes under temperature disturbance. Micromachines 2024, 15, 1102. [Google Scholar] [CrossRef]
- Yan, X.; Huang, W.Y.; Li, Z.; Chen, K.; Deng, G.W.; Wen, G.J.; Huang, Y.J. Novel high-precision micro-gyroscope based on cavity optomechanical system. Sci. Sin. Phys. Mech. Astron. 2023, 53, 114209. [Google Scholar] [CrossRef]
- Rui, G.; He, C.H.; Liu, D.C.; Zhao, Q.C.; Yang, Z.C.; Yan, G.Z. A temperature control system used for improving resonant frequency drift of MEMS gyroscopes. In Proceedings of the 10th IEEE International Conference on Nano/Micro Engineered and Molecular Systems, Xi’an, China, 7–11 April 2015; IEEE: New York, NY, USA, 2015; pp. 397–400. [Google Scholar] [CrossRef]
- Naumenko, D.; Tkachenko, A.; Lysenko, I.; Kovalev, A. Development and research of the sensitive element of the MEMS gyroscope manufactured using SOI technology. Micromachines 2023, 14, 895. [Google Scholar] [CrossRef]
- Kim, C.; Park, J.; Kim, T.; Kim, J.S.; Seong, J.; Shim, H.; Ko, H.; Cho, D.I. Development and evaluation of haltere-mimicking gyroscope for three-axis angular velocity sensing using a haltere-mimicking structure pair. Bioinspir. Biomim. 2022, 18, 016003. [Google Scholar] [CrossRef]
- Gao, Y.; Huang, L.B.; Ding, X.K.; Li, H.S. Design and implementation of a dual-mass MEMS gyroscope with high shock resistance. Sensors 2018, 18, 1037. [Google Scholar] [CrossRef]
- Kuang, Y.B.; Huo, X.Y.; Guo, W.T.; Li, X.X.; He, J.Y.; Mao, Q.; Ma, X.L.; Liu, J. Research on the method of optimizing the stress and improving the performance for MEMS gyroscope based on the cantilever-plate structure. Micromachines 2025, 16, 372. [Google Scholar] [CrossRef]
- Greiff, P.; Boxenhorn, B.; King, T.; Niles, L. Silicon monolithic micromechanical gyroscope. In Proceedings of the TRANSDUCERS ‘91: 1991 International Conference on Solid-State Sensors and Actuators. Digest of Technical Papers, San Francisco, CA, USA, 24–27 June 1991; IEEE: New York, NY, USA, 1991; pp. 966–968. [Google Scholar] [CrossRef]
- Tanaka, K.; Mochida, Y.; Sugimoto, S.; Moriya, K.; Hasegawa, T.; Atsuchi, K.; Ohwada, K. A micromachined vibrating gyroscope. In Proceedings of the IEEE Micro Electro Mechanical Systems, Amsterdam, The Netherlands, 29 January–2 February 1995; IEEE: New York, NY, USA, 1995; pp. 278–281. [Google Scholar] [CrossRef]
- Mochida, Y.; Tamura, M.; Ohwada, K. A micromachined vibrating rate gyroscope with independent beams for the drive and detection modes. In Proceedings of the Technical Digest. IEEE International MEMS 99 Conference. Twelfth IEEE International Conference on Micro Electro Mechanical Systems (Cat. No.99CH36291), Orlando, FL, USA, 21 January 1999; IEEE: New York, NY, USA, 1999; pp. 618–623. [Google Scholar] [CrossRef]
- Geiger, W.; Butt, W.U.; Gaißer, A.; Frech, J.; Braxmaier, M.; Link, T.; Kohne, A.; Nommensen, P.; Sandmaier, H.; Lang, W.; et al. Decoupled microgyros and the design principle DAVED. Sens. Actuators A Phys. 2002, 95, 239–249. [Google Scholar] [CrossRef]
- Alper, S.E.; Akin, T. A symmetric surface micromachined gyroscope with decoupled oscillation modes. Sens. Actuators A Phys. 2002, 97–98, 347–358. [Google Scholar] [CrossRef]
- Alper, S.E.; Silay, K.M.; Akin, T. A low-cost rate-grade nickel microgyroscope. Sens. Actuators A Phys. 2006, 132, 171–181. [Google Scholar] [CrossRef]
- Xiong, B.; Che, L.F.; Wang, Y.L. A novel bulk micromachined gyroscope with slots structure working at atmosphere. Sens. Actuators A Phys. 2003, 107, 137–145. [Google Scholar] [CrossRef]
- Sung, W.T.; Sung, S.; Lee, J.G.; Kang, T. Design and performance test of a MEMS vibratory gyroscope with a novel AGC force rebalance control. J. Micromech. Microeng. 2007, 17, 1939–1948. [Google Scholar] [CrossRef]
- Alper, S.E.; Temiz, Y.; Akin, T. A compact angular rate sensor system using a fully decoupled silicon-on-glass MEMS gyroscope. J. Microelectromech. Syst. 2008, 17, 1418–1429. [Google Scholar] [CrossRef]
- Cui, J.; Guo, Z.Y.; Zhao, Q.C.; Yang, Z.C.; Hao, Y.L.; Yan, G.Z. Force rebalance controller synthesis for a micromachined vibratory gyroscope based on sensitivity margin specifications. J. Microelectromech. Syst. 2011, 20, 1382–1394. [Google Scholar] [CrossRef]
- He, C.H.; Zhao, Q.C.; Liu, Y.X.; Yang, Z.C.; Yan, G.Z. Closed loop control design for the sense mode of micromachined vibratory gyroscopes. Sci. China Technol. Sci. 2013, 56, 1112–1118. [Google Scholar] [CrossRef]
- Li, Z.H.; Yang, Z.C.; Xiao, Z.X.; Hao, Y.L.; Li, T.; Wu, G.Y.; Wang, Y.Y. A bulk micromachined vibratory lateral gyroscope fabricated with wafer bonding and deep trench etching. Sens. Actuators A Phys. 2000, 83, 24–29. [Google Scholar] [CrossRef]
- Liu, X.S.; Yang, Z.C.; Chi, X.Z.; Cui, J.; Ding, H.T.; Guo, Z.Y.; Lv, B.; Lin, L.T.; Zhao, Q.C.; Yan, G.Z. A doubly decoupled lateral axis micromachined gyroscope. Sens. Actuators A Phys. 2009, 154, 218–223. [Google Scholar] [CrossRef]
- Xie, J.B.; Shen, Q.; Hao, Y.C.; Chang, H.L.; Yuan, W.Z. Design, fabrication and characterization of a low-noise Z-axis micromachined gyroscope. Microsyst. Technol. 2015, 21, 625–630. [Google Scholar] [CrossRef]
- Li, X.X.; Bao, M.H.; Yang, H.; Shen, S.Q.; Lu, D.R. A micromachined piezoresistive angular rate sensor with a composite beam structure. Sens. Actuators A Phys. 1999, 72, 217–223. [Google Scholar] [CrossRef]
- Yang, H.; Bao, M.H.; Yin, H.; Shen, S.Q. A novel bulk micromachined gyroscope based on a rectangular beam-mass structure. Sens. Actuators A Phys. 2002, 96, 145–151. [Google Scholar] [CrossRef]
- Acar, C.; Shkel, A. MEMS Vibratory Gyroscopes: Structural Approaches to Improve Robustness; Springer: Boston, MA, USA, 2009; pp. 243–247. [Google Scholar]
- Geen, J.A.; Sherman, S.J.; Chang, J.F.; Lewis, S.R. Single-chip surface micromachined integrated gyroscope with 50/spl deg//h Allan deviation. IEEE J. Solid-State Circuits 2002, 37, 1860–1866. [Google Scholar] [CrossRef]
- Zhang, H.; Yin, L.; Chen, W.P.; Fu, Q.; Zhang, W.B. Monolithic integrated interface ASIC with quadrature error correction for MEMS dual-mass vibration gyroscope. IEEE Sens. J. 2024, 24, 17486–17499. [Google Scholar] [CrossRef]
- Hanse, J.G. Honeywell MEMS inertial technology & product status. In Proceedings of the PLANS 2004. Position Location and Navigation Symposium (IEEE Cat. No. 04CH37556), Monterey, CA, USA, 26–29 April 2004; IEEE: New York, NY, USA, 2004; pp. 43–48. [Google Scholar] [CrossRef]
- Zaman, M.F.; Sharma, A.; Ayazi, F. High performance matched-mode tuning fork gyroscope. In Proceedings of the 19th IEEE International Conference on Micro Electro Mechanical Systems, Istanbul, Turkey, 22–26 January 2006; IEEE: New York, NY, USA, 2006; pp. 66–69. [Google Scholar] [CrossRef]
- Sharma, A.; Zaman, M.F.; Ayazi, F. A 0.2/hr micro-gyroscope with automatic CMOS mode matching. In Proceedings of the 2007 IEEE International Solid-State Circuits Conference. Digest of Technical Papers, San Francisco, CA, USA, 11–15 February 2007; IEEE: New York, NY, USA, 2007; pp. 386–610. [Google Scholar] [CrossRef]
- Wang, D.M.; Efimovskaya, A.; Shkel, A.M. Amplitude amplified dual-mass gyroscope: Design architecture and noise mitigation strategies. In Proceedings of the 2019 IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Naples, FL, USA, 1–5 April 2019; IEEE: New York, NY, USA, 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Wu, G.Q.; Chua, G.L.; Gu, Y.D. A dual-mass fully decoupled MEMS gyroscope with wide bandwidth and high linearity. Sens. Actuators A Phys. 2017, 259, 50–56. [Google Scholar] [CrossRef]
- Koumela, A.; Poulain, C.; Le Goc, C.; Verdot, T.; Joet, L.; Rey, P.; Berthelot, A.; Jourdan, G. Resilience to vibration of a tuning fork MEMS gyroscope. Procedia Eng. 2016, 168, 1725–1730. [Google Scholar] [CrossRef]
- Efimovskaya, A.; Wang, D.M.; Shkel, A.M. Mechanical trimming with focused ion beam for permanent tuning of MEMS dual-mass gyroscope. Sens. Actuators A Phys. 2020, 313, 112189. [Google Scholar] [CrossRef]
- Chen, J.L.; Tsukamoto, T.; Tanaka, S. Triple mass resonator for electrostatic quality factor tuning. J. Microelectromech. Syst. 2022, 31, 194–203. [Google Scholar] [CrossRef]
- Wang, S.H.; Chen, J.L.; Tsukamoto, T.; Langfelder, G.; Tanaka, S. Challenges in implementing pitch/roll rate integrating gyroscopes: A case study on a new dynamically balanced dual-mass resonator. IEEE Sens. J. 2023, 23, 27068–27075. [Google Scholar] [CrossRef]
- Vercier, N.; Chaumet, B.; Leverrier, B.; Bouyat, S. A new silicon axisymmetric gyroscope for aerospace applications. In Proceedings of the 2020 DGON Inertial Sensors and Systems (ISS), Braunschweig, Germany, 15–16 September 2020; IEEE: New York, NY, USA, 2020; pp. 1–18. [Google Scholar] [CrossRef]
- Prikhodko, I.P.; Zotov, S.A.; Trusov, A.A.; Shkel, A.M. Foucault pendulum on a chip: Rate integrating silicon MEMS gyroscope. Sens. Actuators A Phys. 2012, 177, 67–78. [Google Scholar] [CrossRef]
- Cho, J.Y. High-Performance Micromachined Vibratory Rate- and Rate-Integrating Gyroscopes. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2012. [Google Scholar]
- Zhou, B.; Zhang, T.; Yin, P.; Chen, Z.Y.; Song, M.L.; Zhang, R. Innovation of flat gyro: Center support quadruple mass gyroscope. In Proceedings of the 2016 IEEE International Symposium on Inertial Sensors and Systems, Laguna Beach, CA, USA, 22–25 February 2016; IEEE: New York, NY, USA, 2016; pp. 42–45. [Google Scholar] [CrossRef]
- Taheri-Tehrani, P.; Kline, M.; Izyumin, I.; Eminoglu, B.; Yeh, Y.C.; Yang, Y.S.; Chen, Y.H.; Flader, I.; Ng, E.J.; Kenny, T.W.; et al. Epitaxially-encapsulated quad mass gyroscope with nonlinearity compensation. In Proceedings of the 2016 IEEE 29th International Conference on Micro Electro Mechanical Systems (MEMS), Shanghai, China, 24–28 January 2016; IEEE: New York, NY, USA, 2016; pp. 966–969. [Google Scholar] [CrossRef]
- Wu, G.Q.; Chua, G.L.; Singh, N.; Gu, Y.D. A quadruple mass vibrating MEMS gyroscope with symmetric design. IEEE Sens. Lett. 2018, 2, 2541404. [Google Scholar] [CrossRef]
- Gianollo, M.; Mastri, V.; Zega, V.; Bestetti, M.; Falorni, L.; Langfelder, G. Miniaturized quadruple mass gyroscopes: Challenges and implementation. In Proceedings of the 2021 IEEE Sensors, Sydney, Australia, 31 October–3 November 2021; IEEE: New York, NY, USA, 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Knight, R.R.; Rudy, R.Q.; Pulskamp, J.S.; Benoit, R.R.; Devoe, D.L.; Lau, E. Quadruple mass gyroscope angle random walk reduction through linearized transduction. J. Microelectromech. Syst. 2024, 33, 308–321. [Google Scholar] [CrossRef]
- Putty, M.W. A Micromachined Vibrating Ring Gyroscope. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 1995. [Google Scholar]
- Juneau, T.; Pisano, A.P.; Smith, J.H. Dual axis operation of a micromachined rate gyroscope. In Proceedings of the International Solid State Sensors and Actuators Conference (Transducers ‘97), Chicago, IL, USA, 19 June 1997; IEEE: New York, NY, USA, 1997; pp. 883–886. [Google Scholar] [CrossRef]
- He, G.H.; Najafi, K. A single-crystal silicon vibrating ring gyroscope. In Proceedings of the Technical Digest. MEMS 2002 IEEE International Conference. Fifteenth IEEE International Conference on Micro Electro Mechanical Systems (Cat. No.02CH37266), Las Vegas, NV, USA, 24 January 2002; IEEE: New York, NY, USA, 2002; pp. 718–721. [Google Scholar] [CrossRef]
- Zhao, Q.C.; Liu, X.S.; Lin, L.T.; Guo, Z.Y.; Cui, J.; Chi, X.Z.; Yang, Z.C.; Yan, G.Z. A doubly decoupled micromachined vibrating wheel gyroscope. In Proceedings of the TRANSDUCERS 2009—2009 International Solid-State Sensors, Actuators and Microsystems Conference, Denver, CO, USA, 21–25 June 2009; IEEE: New York, NY, USA, 2009; pp. 296–299. [Google Scholar] [CrossRef]
- Cho, J.; Gregory, J.A.; Najafi, K. Single-crystal-silicon vibratory cylinderical rate integrating gyroscope (CING). In Proceedings of the 2011 16th International Solid-State Sensors, Actuators and Microsystems Conference, Beijing, China, 5–9 June 2011; IEEE: New York, NY, USA, 2011; pp. 2813–2816. [Google Scholar] [CrossRef]
- Han, F.T.; Liu, Y.F.; Wang, L.; Ma, G.Y. Micromachined electrostatically suspended gyroscope with a spinning ring-shaped rotor. J. Micromech. Microeng. 2012, 22, 105032. [Google Scholar] [CrossRef]
- Nitzan, S.; Ahn, C.H.; Su, T.H.; Li, M.; Ng, E.J.; Wang, S.; Yang, Z.M.; O’brien, G.; Boser, B.E.; Kenny, T.W.; et al. Epitaxially-encapsulated polysilicon disk resonator gyroscope. In Proceedings of the 2013 IEEE 26th International Conference on Micro Electro Mechanical Systems (MEMS), Taipei, Taiwan, 20–24 January; IEEE: New York, NY, USA, 2013; pp. 625–628. [Google Scholar] [CrossRef]
- Su, T.H.; Nitzan, S.H.; Taheri-Tehrani, P.; Kline, M.H.; Boser, B.E.; Horsley, D.A. Silicon MEMS disk resonator gyroscope with an integrated CMOS analog front-end. IEEE Sens. J. 2014, 14, 3426–3432. [Google Scholar] [CrossRef]
- Challoner, A.D.; Ge, H.H.; Liu, J.Y. Boeing disc resonator gyroscope. In Proceedings of the 2014 IEEE/ION Position, Location and Navigation Symposium—PLANS 2014, Monterey, CA, USA, 5–8 May 2014; IEEE: New York, NY, USA, 2014; pp. 504–514. [Google Scholar] [CrossRef]
- Zhou, X.; Xiao, D.B.; Wu, X.Z.; Wu, Y.L.; Hou, Z.Q.; He, K.X.; Li, Q.S. Stiffness-mass decoupled silicon disk resonator for high resolution gyroscopic application with long decay time constant (8.695s). Appl. Phys. Lett. 2016, 109, 263501. [Google Scholar] [CrossRef]
- Zhou, X.; Xiao, D.B.; Li, Q.S.; Hou, Z.Q.; He, K.X.; Chen, Z.H.; Wu, Y.L.; Wu, X.Z. Decaying time constant enhanced MEMS disk resonator for high precision gyroscopic application. IEEE/ASME Trans. Mechatron. 2018, 23, 452–458. [Google Scholar] [CrossRef]
- Li, Q.S.; Xiao, D.B.; Zhou, X.; Ou, F.; Hou, Z.Q.; Wu, X.Z. A novel honeycomb-like disk resonant gyroscope. In Proceedings of the 2017 19th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS), Kaohsiung, Taiwan, 18–22 June 2017; IEEE: New York, NY, USA, 2017; pp. 532–535. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Q.S.; Zhou, X.; Gao, K.; Wang, P.; Zhang, Y.M.; Hou, Z.Q.; Wu, X.Z.; Xiao, D.B. Stiffness-mass decoupled honeycomb-like disk resonator gyroscope. In Proceedings of the 2019 IEEE 32nd International Conference on Micro Electro Mechanical Systems (MEMS), Seoul, Republic of Korea, 27–31 January 2019; IEEE: New York, NY, USA, 2019; pp. 656–659. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Q.S.; Wang, P.; Zhang, Y.M.; Zhou, X.; Yu, L.; Wu, X.Z.; Xiao, D.B. 0.015 degree-per-hour honeycomb disk resonator gyroscope. IEEE Sens. J. 2021, 21, 7326–7338. [Google Scholar] [CrossRef]
- Kaji, S.; Gando, R.; Masunishi, K.; Ogawa, E.; Miyazaki, F.; Hiraga, H.; Tomizawa, Y.; Shibata, H. A <100 PPB/K frequency-matching temperature stability MEMS rate integrating gyroscope enabled by donut-mass structure. In Proceedings of the 2020 IEEE 33rd International Conference on Micro Electro Mechanical Systems (MEMS), Vancouver, BC, Canada, 18–22 January 2020; IEEE: New York, NY, USA, 2020; pp. 263–266. [Google Scholar] [CrossRef]
- Lin, D.; Macdonald, R.; Calbaza, D.; Scherer, B.; Johnson, T.; Toepfer, T.; Shaddock, D.; Andarawis, E. Sub-Degree-per-hour mems gyroscope for measurement while drilling at 300 °C. In Proceedings of the 2020 IEEE/ION Position, Location and Navigation Symposium (PLANS), Portland, OR, USA, 18–22 January 2020; IEEE: New York, NY, USA, 2020; pp. 1425–1431. [Google Scholar] [CrossRef]
- Wang, J.B.; Chen, L.; Zhang, M.; Chen, D.Y. A micro-machined vibrating ring gyroscope with highly symmetric structure for harsh environment. In Proceedings of the 2010 IEEE 5th International Conference on Nano/Micro Engineered and Molecular Systems, Xiamen, China, 20–23 January 2010; IEEE: New York, NY, USA, 2010; pp. 1180–1183. [Google Scholar] [CrossRef]
- Liu, J.L.; Chen, D.Y.; Wang, J.B. Regulating parameters of electromagnetic micromachined vibrating ring gyroscope by feedback control. Micro Nano Lett. 2012, 7, 1234–1236. [Google Scholar] [CrossRef]
- Wang, H.; Quan, H.Y.; Zhou, J.Q.; Zhang, L.; Xie, J.B.; Chang, H.L. A wafer-level vacuum packaged MEMS disk resonator gyroscope with 0.42°/h bias instability within±300°/s full scale. IEEE Trans. Ind. Electron. 2022, 69, 5304–5313. [Google Scholar] [CrossRef]
- Wen, H.R.; Daruwalla, A.; Liu, C.S.; Ayazi, F. A hermetically-sealed 2.9MHz N = 3 disk BAW gyroscope with sub-degree-per-hour bias instability. In Proceedings of the 2020 IEEE 33rd International Conference on Micro Electro Mechanical Systems (MEMS), Vancouver, BC, Canada, 18–22 January 2020; IEEE: New York, NY, USA, 2020; pp. 741–744. [Google Scholar] [CrossRef]
- Ren, X.J.; Zhou, X.; Tao, Y.; Li, Q.S.; Wu, X.Z.; Xiao, D.B. Radially pleated disk resonator for gyroscopic application. J. Microelectromech. Syst. 2021, 30, 825–835. [Google Scholar] [CrossRef]
- Gu, L.T.; Zhang, W.P.; Lu, H.L.; Wu, Y.T.; Fan, C.Y. Flower-like disk resonator for gyroscopic application. Rev. Sci. Instrum. 2022, 93, 115006. [Google Scholar] [CrossRef]
- Obitani, K.; Araya, K.; Yachi, M.; Tsuchiya, T. Piezoelectric disk gyroscope fabricated with single-crystal lithium niobate. J. Microelectromech. Syst. 2021, 30, 384–391. [Google Scholar] [CrossRef]
- Wei, W.Q.; Tian, H.M.; Chen, K.; Wang, F.E.; Lu, Z.H.; Chen, F.; Cao, H.L.; Xie, H.K. Triaxial MEMS gyroscopes: A review. IEEE Sens. J. 2025, 25, 35687–35707. [Google Scholar] [CrossRef]
- Meyer, A.D.; Rozelle, D.M. Milli-HRG inertial navigation system. In Proceedings of the 2012 IEEE/ION Position, Location and Navi-gation Symposium, Myrtle Beach, SC, USA, 23–26 April 2012. [Google Scholar] [CrossRef]
- Rozelle, D.M. The hemispherical resonator gyro: From wineglass to the planets. Spaceflight Mech. 2009, 134, 1157–1178. [Google Scholar]
- Li, W.; Xi, X.; Lu, K.; Shi, Y.; Hou, Z.Q.; Wu, Y.L.; Wu, X.Z.; Xiao, D.B. A novel high transduction efficiency micro shell resonator gyroscope with 16 t-shape masses using out-of-plane electrodes. IEEE Sens. J. 2019, 19, 4820–4828. [Google Scholar] [CrossRef]
- Cho, J.Y.; Singh, S.; Woo, J.K.; He, G.H.; Najafi, K. 0.00016 deg/√hr angle random walk (ARW) and 0.0014 deg/hr bias instability (BI) from a 5.2M-Q and 1-cm precision shell integrating (PSI) gyroscope. In Proceedings of the 2020 IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Hiroshima, Japan, 23–26 March 2020; IEEE: New York, NY, USA, 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Meyer, A.D.; Rozelle, D.M.; Trusov, A.A.; Sakaida, D.K. milli-HRG inertial sensor assembly—A reality. In Proceedings of the 2018 IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 23–26 April 2018; IEEE: New York, NY, USA, 2018; pp. 20–23. [Google Scholar] [CrossRef]
- Foloppe, Y.; Lenoir, Y. HRG Crystal™ DUAL CORE: Rebooting the INS revolution. In Proceedings of the 2019 DGON Inertial Sensors and Systems (ISS), Braunschweig, Germany, 10–11 September 2019; IEEE: New York, NY, USA, 2019; pp. 1–24. [Google Scholar] [CrossRef]
- Senkal, D. Micro-Glassblowing Paradigm for Realization of Rate Integrating Gyroscopes. Ph.D. Thesis, University of California, Irvine, CA, USA, 2015. [Google Scholar]
- Shao, P.; Tavassoli, V.; Mayberry, C.L.; Ayazi, F. A 3D-HARPSS polysilicon microhemispherical shell resonating gyroscope: Design, fabrication, and characterization. IEEE Sens. J. 2015, 15, 4974–4985. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Zhang, W.P.; Cui, F.; Tang, J. Three-dimensional micromachined diamond birdbath shell resonator on silicon substrate. Microsyst. Technol. 2020, 26, 1293–1299. [Google Scholar] [CrossRef]
- Gray, J.M.; Houlton, J.P.; Gertsch, J.C.; Brown, J.J.; Rogers, C.T.; George, S.M.; Bright, V.M. Hemispherical micro-resonators from atomic layer deposition. J. Micromech. Microeng. 2014, 24, 125028. [Google Scholar] [CrossRef]
- Tavassoli, V.; Hamelin, B.; Ayazi, F. Substrate-decoupled 3D micro-shell resonators. In Proceedings of the 2016 IEEE SENSORS, Orlando, FL, USA, 30 October–3 November 2016; IEEE: New York, NY, USA, 2016; pp. 1–3. [Google Scholar] [CrossRef]
- Hassan, J.N.A.; Huang, W.Y.; Wang, M.Y.; Zhang, S.Y.; Wen, G.J.; Huang, Y.J. Optomechanical gyroscope based on micro-hemispherical shell and optical ring resonators. IEEE Photonics J. 2024, 16, 5800617. [Google Scholar] [CrossRef]
- Eklund, E.J.; Shkel, A.M. Glass blowing on a wafer level. J. Microelectromech. Syst. 2007, 16, 232–239. [Google Scholar] [CrossRef]
- Cho, J.Y.; Yan, J.L.; Gregory, J.A.; Eberhart, H.W.; Peterson, R.L.; Najafi, K. 3-dimensional blow torch-molding of fused silica microstructures. J. Microelectromech. Syst. 2013, 22, 1276–1284. [Google Scholar] [CrossRef]
- Cho, J.Y.; Najafi, K. A high-q all-fused silica solid-stem wineglass hemispherical resonator formed using micro blow torching and welding. In Proceedings of the 2015 28th IEEE International Conference on Micro Electro Mechanical Systems (MEMS), Estoril, Portugal, 18–22 January 2015; IEEE: New York, NY, USA, 2015; pp. 821–824. [Google Scholar] [CrossRef]
- Nagourney, T.; Cho, J.Y.; Shiari, B.; Darvishian, A.; Najafi, K. 259 Second ring-down time and 4.45 million quality factor in 5.5 kHz fused silica birdbath shell resonator. In Proceedings of the 2017 19th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS), Kaohsiung, Taiwan, 18–22 June 2017; IEEE: New York, NY, USA, 2017; pp. 790–793. [Google Scholar] [CrossRef]
- Shi, Y.; Xi, X.; Li, B.; Chen, Y.M.; Wu, Y.L.; Xiao, D.B.; Wu, X.Z.; Lu, K. Micro hemispherical resonator gyroscope with teeth-like tines. IEEE Sens. J. 2021, 21, 13098–13106. [Google Scholar] [CrossRef]
- Cho, J.Y.; Woo, J.K.; He, G.H.; Yang, D.; Boyd, C.; Singh, S.; Darvishian, A.; Shiari, B.; Najafi, K. 1.5-million Q-factor vacuum-packaged birdbath resonator gyroscope (BRG). In Proceedings of the 2019 IEEE 32nd International Conference on Micro Electro Mechanical Systems (MEMS), Seoul, Republic of Korea, 27–31 January 2019; IEEE: New York, NY, USA, 2019; pp. 210–213. [Google Scholar] [CrossRef]
- Luo, B.; Shang, J.T.; Zhang, Y.Z. Hemispherical glass shell resonators fabricated using chemical foaming process. In Proceedings of the 2015 IEEE 65th Electronic Components and Technology Conference (ECTC), San Diego, CA, USA, 26–29 May 2015; IEEE: New York, NY, USA, 2015; pp. 2217–2221. [Google Scholar] [CrossRef]
- Crescenzi, R.; Castellito, G.V.; Quaranta, S.; Balucani, M. Design of a tri-axial surface micromachined MEMS vibrating gyroscope. Sensors 2020, 20, 2822. [Google Scholar] [CrossRef]
- Hu, H.T.; Calusi, B.; Bagolini, A.; Pantano, M.F. Design, analysis, and simulation of a MEMS tuning fork gyroscope with a mechanical amplification structure. Micromachines 2025, 16, 195. [Google Scholar] [CrossRef] [PubMed]
- Xu, P.F.; Si, C.W.; He, Y.R.; Wei, Z.Y.; Jia, L.; Han, G.W.; Ning, J.; Yang, F.H. A novel high-Q dual-mass MEMS tuning fork gyroscope based on 3D wafer-level packaging. Sensors 2021, 21, 6428. [Google Scholar] [CrossRef] [PubMed]
- Tian, H.M.; Zhang, Z.H.; Liu, L.; Wei, W.Q.; Cao, H.L. Design and implementation of a CMOS-MEMS out-of-plane detection gyroscope. Micromachines 2024, 15, 1484. [Google Scholar] [CrossRef]
- Suvorkin, V.; Garcia-Fernandez, M.; González-Casado, G.; Li, M.W.; Rovira-Garcia, A. Assessment of noise of MEMS IMU sensors of different grades for GNSS/IMU navigation. Sensors 2024, 24, 1953. [Google Scholar] [CrossRef]
- Xue, L.; Yang, B.; Wang, X.G.; Shan, B.; Gao, J.A.; Chang, H.L.; Yao, Y.F. Design of optimal estimation algorithm for multi-sensor fusion of a redundant MEMS gyro system. IEEE Sens. J. 2023, 23, 4577–4588. [Google Scholar] [CrossRef]
- De Alteriis, G.; Accardo, D.; Conte, C.; Schiano Lo Moriello, R. Performance enhancement of consumer-grade MEMS sensors through geometrical redundancy. Sensors 2021, 21, 4851. [Google Scholar] [CrossRef]
- Cheng, J.H.; Dong, J.L.; Landry, R.J.; Chen, D.D. A novel optimal configuration form redundant MEMS inertial sensors based on the orthogonal rotation method. Sensors 2014, 14, 13661–13678. [Google Scholar] [CrossRef]
- Lin, Z.R.; Xiong, Y.S.; Dai, H.D.; Xia, X.K. An experimental performance evaluation of the orientation accuracy of four nine-axis MEMS motion sensors. In Proceedings of the 2017 5th International Conference on Enterprise Systems (ES), Beijing, China, 22–24 September 2017; IEEE: New York, NY, USA, 2017; pp. 185–189. [Google Scholar] [CrossRef]
- Ma, Z.B.; Wang, Y.N.; Shen, Q.; Zhang, H.; Guo, X.T. Key processes of silicon-on-glass MEMS fabrication technology for gyroscope application. Sensors 2018, 18, 1240. [Google Scholar] [CrossRef]
- Diao, Z.L.; Quan, H.Y.; Lan, L.D.; Han, Y.F. Analysis and compensation of MEMS gyroscope drift. In Proceedings of the 2013 Seventh International Conference on Sensing Technology (ICST), Wellington, New Zealand, 3–5 December 2013; IEEE: New York, NY, USA, 2013; pp. 592–596. [Google Scholar] [CrossRef]
- Saqib, M.; Mubasher Saleem, M.; Mazhar, N.; Awan, S.U.; Shahbaz Khan, U. Design and analysis of a high-gain and robust multi-DOF electro-thermally actuated MEMS gyroscope. Micromachines 2018, 9, 577. [Google Scholar] [CrossRef]
- Xu, Y.Y.; Lin, J.; He, C.H.; Wu, H.; Huang, Q.W.; Yan, G.Z. Design of a shock-protected structure for MEMS gyroscopes over a full temperature range. Micromachines 2024, 15, 206. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Pan, Y.H.; Li, K.; He, L.L.; Wang, Q.Y.; Wang, W.D. Modeling and reliability analysis of MEMS gyroscope rotor parameters under vibrational stress. Micromachines 2024, 15, 648. [Google Scholar] [CrossRef]
- Chen, L.Q.; Miao, T.Q.; Li, Q.S.; Wang, P.; Wu, X.Z.; Xi, X.; Xiao, D.B. A temperature drift suppression method of mode-matched MEMS gyroscope based on a combination of mode reversal and multiple regression. Micromachines 2022, 13, 1557. [Google Scholar] [CrossRef]
- Liu, J.L.; Fu, M.R.; Meng, C.; Li, J.P.; Li, K.; Hu, J.; Chen, X.J. Consideration of thermo-vacuum stability of a MEMS gyroscope for space applications. Sensors 2020, 20, 7172. [Google Scholar] [CrossRef]
- Chen, C.; Zhou, J.Q.; Wang, H.Y.; Fan, Y.Y.; Song, X.Y.; Xie, J.B.; Bäck, T.; Wang, H. Machine learning-driven discovery of high-performance MEMS disk resonator gyroscope structural topologies. Microsyst. Nanoeng. 2024, 10, 161. [Google Scholar] [CrossRef]
- Chang, H.L.; Xue, L.; Qin, W.; Yuan, G.M.; Yuan, W.Z. An integrated MEMS gyroscope array with higher accuracy output. Sensors 2008, 8, 2886–2899. [Google Scholar] [CrossRef]
- Huang, F.R.; Wang, Z.; Xing, L.R.; Gao, C. A MEMS IMU Gyroscope Calibration Method Based on Deep Learning. IEEE Trans. Instrum. Meas. 2022, 71, 1003009. [Google Scholar] [CrossRef]
- Fan, Q.; Lin, C.; Liu, M.X.; Su, Y.; Zhao, W.L.; Zheng, D.W. High performance MEMS disk gyroscope with force-to-rebalance operation mode. In Proceedings of the 2018 IEEE SENSORS, New Delhi, India, 28–31 October 2018; IEEE: New York, NY, USA, 2018; pp. 1–3. [Google Scholar] [CrossRef]
- Wang, C.X.; Wu, K.; Wang, X.Y.; Li, Q.S.; Zhang, Y.M.; Wu, Y.L.; Wu, X.Z.; Xiao, D.B. A MEMS disk gyroscope with high fabrication precision, high quality factor (>810k) and high overload characteristic (>15000 g). J. Phys. Conf. Ser. 2024, 2740, 012062. [Google Scholar] [CrossRef]
- Liu, J.H.; Qu, T.L.; Xiong, C.X. Precision machining technology of high quality factor hemispherical resonator. In Proceedings of the 2nd International Forum of Young Scientists on Advanced Optical Manufacturing, Changchun, China, 29–31 July 2022; SPIE: San Francisco, CA, USA, 2023; p. 125071L. [Google Scholar] [CrossRef]
- Cui, J.; Zhao, Q.C. Thermal stabilization of quality factor for dual-axis MEMS gyroscope based on joule effect In Situ dynamic tuning. IEEE Trans. Ind. Electron. 2024, 71, 1060–1068. [Google Scholar] [CrossRef]
- Gill, W.A.; Howard, I.; Mazhar, I.; Mckee, K. A review of MEMS vibrating gyroscopes and their reliability issues in harsh environments. Sensors 2022, 22, 7405. [Google Scholar] [CrossRef]
- Goto, K.; Harada, S.; Hata, Y.; Ito, K.; Wado, H.; Cho, J.Y.; Najafi, K. High Q-factor mode-matched silicon gyroscope with a ladder structure. In Proceedings of the 2020 IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Hiroshima, Japan, 23–26 March 2020; IEEE: New York, NY, USA, 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Bu, F.; Xu, D.C.; Zhao, H.M.; Fan, B.; Cheng, M.M. MEMS gyroscope automatic real-time mode-matching method based on phase-shifted 45° additional force demodulation. Sensors 2018, 18, 3001. [Google Scholar] [CrossRef] [PubMed]
- Marx, M.; Cuignet, X.; Nessler, S.; De Dorigo, D.; Manoli, Y. An automatic MEMS gyroscope mode matching circuit based on noise observation. IEEE Trans. Circuits Syst. II Exp. Briefs 2019, 66, 743–747. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, C.; Chen, J.; Li, A. A review of symmetric silicon MEMS gyroscope mode-matching technologies. Micromachines 2022, 13, 1255. [Google Scholar] [CrossRef]
- Koenig, S.; Rombach, S.; Gutmann, W.; Jaeckle, A.; Weber, C.; Ruf, M.; Grolle, D.; Rende, J. Towards a navigation grade Si-MEMS gyroscope. In Proceedings of the 2019 DGON Inertial Sensors and Systems (ISS), Braunschweig, Germany, 10–11 September 2019; IEEE: New York, NY, USA, 2019; pp. 1–18. [Google Scholar] [CrossRef]
- Xu, Z.Y.; Xi, B.Q.; Yi, G.X.; Wang, D.W. A novel model for fully closed-loop system of hemispherical resonator gyroscope under force-to-rebalance mode. IEEE Trans. Instrum. Meas. 2020, 69, 9918–9930. [Google Scholar] [CrossRef]
- Wu, Y.X.; Pei, L. Gyroscope calibration via magnetometer. IEEE Sens. J. 2017, 17, 5269–5275. [Google Scholar] [CrossRef]
- Yang, H.T.; Zhou, B.; Wang, L.X.; Xing, H.F.; Zhang, R. A novel tri-axial MEMS gyroscope calibration method over a full temperature range. Sensors 2018, 18, 3004. [Google Scholar] [CrossRef]
- Zhou, J.; Jiang, T.; Jiao, J.W.; Wu, M. Design and fabrication of a micromachined gyroscope with high shock resistance. Microsyst. Technol. 2014, 20, 137–144. [Google Scholar] [CrossRef]
- Cameron, C.P.; Imamura, T.; Devmalya, C.; Vukasin, G.; Alter, A.; Kenny, T. Design comparison and survivability of epitaxially encapsulated MEMS disc resonating gyroscopes at high shock (>27,000g). In Proceedings of the 2020 IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Hiroshima, Japan, 23–26 March 2020; IEEE: New York, NY, USA, 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Miao, T.Q.; Li, Q.S.; Hu, X.P.; Wu, X.Z.; Wu, W.Q.; Xiao, D.B. Virtual rotating MEMS gyrocompassing with honeycomb disk resonator gyroscope. IEEE Electron. Device Lett. 2022, 43, 1331–1334. [Google Scholar] [CrossRef]
- Guan, Y.W. Research on the Dynamic Coupling Characteristics and Vibration Sensitivity of MEMS Tuning Fork Gyroscopes. Ph.D. Thesis, Beijing Institute of Technology, Beijing, China, 2017. (In Chinese). [Google Scholar] [CrossRef]
- Liu, M.X.; Fan, Q.; Zhao, J.; Su, Y. A phase compensation method for MEMS quadruple mass gyroscope in zero bias drift. IEEE Sens. J. 2021, 21, 3087–3096. [Google Scholar] [CrossRef]
- Wang, P.; Li, Q.S.; Zhang, Y.M.; Wu, Y.L.; Wu, X.Z.; Xiao, D.B. Bias thermal stability improvement of mode-matching MEMS gyroscope using mode deflection. J. Microelectromech. Syst. 2023, 32, 1–3. [Google Scholar] [CrossRef]
- Ren, J.B.; Zhou, T.; Zhou, Y.; Li, Y.X.; Su, Y. A real-time automatic mode-matching method based on phase-shifted virtual Coriolis force for MEMS disk resonator gyroscope. IEEE Sens. J. 2023, 23, 28673–28683. [Google Scholar] [CrossRef]
- Wang, P.; Li, Q.S.; Xu, Y.; Zhang, Y.M.; Xi, X.; Wu, Y.L.; Wu, X.Z.; Xiao, D.B. Calibration of coupling errors for scale factor nonlinearity improvement in navigation-grade honeycomb disk resonator gyroscope. IEEE Trans. Ind. Electron. 2023, 70, 5347–5355. [Google Scholar] [CrossRef]
- Sun, J.K.; Liu, K.; Yu, S.; Zhang, Y.M.; Xi, X.; Lu, K.; Shi, Y.; Wu, X.Z.; Xiao, D.B. Identification and correction of phase error for whole-angle micro-shell resonator gyroscope. IEEE Sens. J. 2022, 22, 19228–19236. [Google Scholar] [CrossRef]
- Cao, H.L.; Wei, W.Q.; Liu, L.; Ma, T.C.; Zhang, Z.K.; Zhang, W.J.; Shen, C.; Duan, X.M. A temperature compensation approach for dual-mass MEMS gyroscope based on PE-LCD and ANFIS. IEEE Access 2021, 9, 95180–95193. [Google Scholar] [CrossRef]
- Ren, C.H.; Guo, D.N.; Zhang, L.; Wang, T.H. Research on nonlinear compensation of the MEMS gyroscope under tiny angular velocity. Sensors 2022, 22, 6577. [Google Scholar] [CrossRef] [PubMed]
- Din, H.; Iqbal, F.; Lee, B. Design approach for reducing cross-axis sensitivity in a single-drive multi-axis MEMS gyroscope. Micromachines 2021, 12, 902. [Google Scholar] [CrossRef] [PubMed]

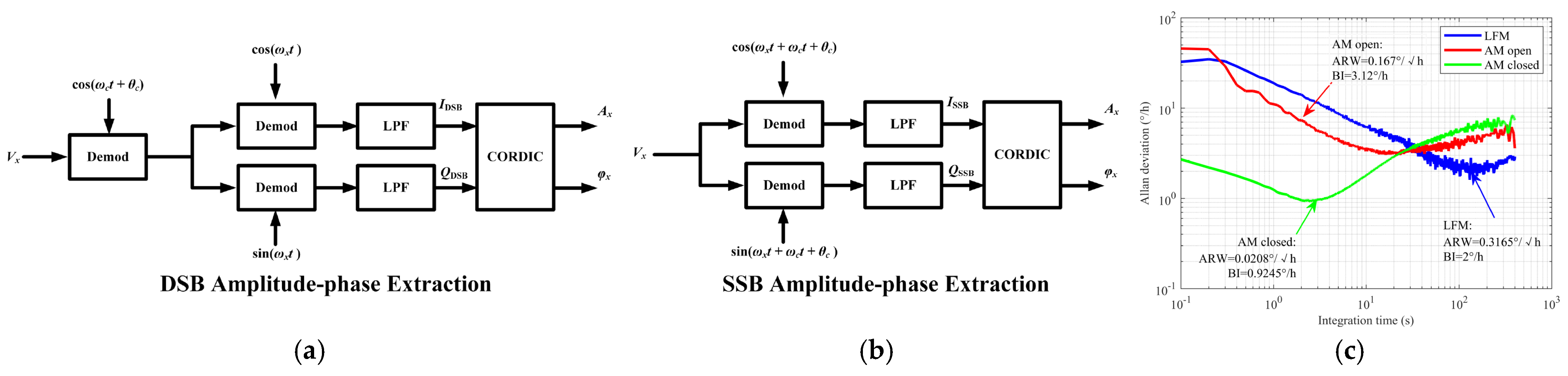
| Structure Type | Sensitivity (mV/°/s) | Noise Density (°/√h) | Stability Metrics | References |
|---|---|---|---|---|
| z-axis tuning fork MEMS gyroscope | 21.76 | —— | ZRO: 0.002 (°/s) | [46] |
| Dual-Mass System | —— | 0.0414 | Bias stability: 0.415°/h; Bandwidth: 104 Hz | [26] |
| Vibratory, doubly decoupled, bulk micromachined | 27.6 (scale factor) | 0.06 | Nonlinearity: <120 ppm; Settling time < 200 ms | [8] |
| Doubly decoupled, silicon-glass bonded | —— | 0.316 | Bias instability: 2°/h; ZRO drift: 0.1248°/s | [47] |
| Capacitive vibratory, mode-split | —— | 0.068 | Bias instability: 0.9°/h; Phase standard deviation: 0.0004° | [48] |
| Tuning fork, comb-driven, silicon-on-insulator (SOI) process | 23 (optimal) | —— | Bias stability: 7.52 × 10−4°/s; Nonlinearity: 0.0062% | [49] |
| Vibratory, non-decoupled, dual-mode, custom metal lid | 1.345 | 0.978 | Bias instability: 9.458°/h; ZRO: 0.095°/s | [50] |
| Linear vibrating tuning fork MEMS gyroscope | —— | —— | Overshoot: −96%; Settling time: 0.036 s | [51] |
| Cavity optomechanical architecture | 122.2 | 0.95 | —— | [52] |
| doubly decoupled tuning fork gyroscope | —— | —— | Frequency drift: 0.3 Hz/°C; Standard deviation: 0.027 | [53] |
| Control Type | Performance Improvement | Stability Enhancement | Implementation Complexity | References |
|---|---|---|---|---|
| Self-resonant, AGC, quadrature correction | Coupling force amplitude reduced 105×; ZRO reduced | Improved precision; ZRO: 0.002 (°/s) | GA+Monte Carlo: Medium-high; Adam-LMSD: Medium | [46] |
| Closed-loop (no further details) | Bias stability: 2.168–0.415°/h; ARW: 0.155–0.0414°/√h | Bandwidth: 13–104 Hz; Nonlinearity: 660–59.3 ppm | Moderate | [26] |
| AGC-PI | Setting time < 200 ms; Amplitude fluctuation < 16 ppm | Nonlinearity < 120 ppm; Threshold: 0.005°/s | Moderate | [8] |
| Digital PLLs, PI (LFM vs. AM) | LFM: ZRO drift 0.1248°/s vs. AM: 10.7139°/s | LFM: Nonlinearity 329 ppm vs. AM: 1902 ppm | Moderate | [47] |
| MEAM (vs. CEAM), AGC+PLL | Settling time: 45.2 ms; Bias instability improved 2.4× | ARW improved 1.4×; Phase standard deviation: 0.0004° | Moderate-high | [48] |
| PI (GA-optimized), Adam-LMS demodulator | Sensitivity: 17.7–23 mV/(°/s); Nonlinearity: 0.0085–0.0062% | Bias stability: 0.0015–7.52 × 10−4°/s | High | [49] |
| FTR, PLL, AGC, phase delay correction | ZRO reduced by 755% to 0.095°/s | Bias instability: 9.458°/h; ARW: 0.978°/√h | Moderate-high | [50] |
| Adaptive PID vs. classical PID | Overshoot reduced 96%; Settling time: 0.036 s vs. 0.06 s | Similar rise time; faster stabilization | Low | [51] |
| Cavity optomechanical detection-based control | Sensitivity up to 122.2 mV/(°/s) | Dual-decoupled structure reduces mode coupling | Low | [52] |
| Incremental PID (temperature control) | Frequency drift: 0.3 Hz/°C-stable | Improved frequency stability | Combination of hardware and software, relatively complex | [53] |
| Phase Error/Delay (°) | Phase Correction Mechanism | Impact on Performance Metrics | Temperature Range for Correction | References |
|---|---|---|---|---|
| —— | Quadrature error correction | Coupling force amplitude reduced 105×; ZRO reduced | —— | [46] |
| —— | Digital PLLs; phase tracking | LFM mode: ZRO drift 0.1248°/s vs. AM: 10.7139°/s | 10–50 °C | [47] |
| 0.0004 (phase standard deviation) | Phase-locked loop | Bias instability, ARW improved; phase standard deviation: 0.0004° | —— | [48] |
| Phase standard deviation: 0.0004° | PLL, Adam-LMS demodulator | Bias instability improved 2.4×; ARW improved 1.4× | tested under room temperature with 2 °C fluctuation | [49] |
| 19.419 ± 0.004 | Real-time PLL phase reference adjustment | ZRO reduced by 755% to 0.095°/s; ARW: 0.978°/√h; Bias instability: 9.458°/h | −20 to 70 °C | [50] |
| Structure Type | Typical Performance Metrics | Advantages | Limitations | Applications | References |
|---|---|---|---|---|---|
| Dual-mass gyroscope | Scale factor: 12.5 mV/(°/s); ARW: 3°/h, 0.047°/√h, 0.18°/(h·√Hz), 0.096°/√h, 0.45°/√h, 0.021°/√h, 0.028°/√h, 0.006°/√h; Bias instability: 12°/h, 1.6°/h, 0.2°/h, 0.09°/h, 9.6°/h, 0.29°/h, <0.012°/h; Q-factor: up to 36,000; Bandwidth: 1–100 Hz; Shock resistance: >33,000 g | Vibration decoupling, high Q-factor, reduced environmental sensitivity, differential detection suppresses noise | Requires tuning, trimming, frequency matching; performance optimization still challenging | Automotive and aerospace navigation | [75,76,77,78,79,80,81,82,83,84,85,86,117] |
| Quadruple-mass gyroscope (QMG) | Resonant frequency: ~2 kHz; Q-factor: up to 1.2 million; ARW: 26.4°/√h, 0.72°/(h·√Hz), 0.0264°/√h, 0.28°/√h, 0.006°/√h, 0.0005°/√h; Bias instability: 0.12°/h, 5.9°/h, 0.08°/h; Measurement range: ±150°/s | Fully symmetric structure, suitable for FM detection | Requires large sensor area to ensure suspension and mode decoupling | Consumer electronics, tactical-grade sensors | [87,88,89,90,91,92,93,117] |
| Ring/disc resonator gyroscope (DRG) | ARW: 6°/√h, 14.4°/√h, 10.4°/(h·√Hz), 27°/√h, 3.6°/(h·√Hz), 0.015°/(h·√Hz), 0.36°/√h, 0.048°/√h, 0.138°/√h, 0.0009°/√h, 0.012°/√h, 0.083°/√h, 0.015°/√h, 0.004°/√h, 0.004°/√h, 0.026°/√h, 0.05°/√h; Bias instability: 10°/s, 0.16°/s, 20°/h, 0.01°/h, 0.08°/h, 0.11°/h, 0.015°/h, 0.87°/h, 0.85°/h, 0.42°/h; Q-factor: up to 650,000; Scale factor: 0.286 mV/(°/s), 39.8 mV/(°/s), 132 mV/(°/s), 98.1 mV/(°/s) | High precision, high Q-factor, stiffness–mass decoupling design, suitable for mass production | Complex design | High-end navigation, aerospace, UAVs | [24,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117] |
| Architecture Type | Bias Stability | Angle Random Walk | Notable Performance Advantages | Notable Limitations | References |
|---|---|---|---|---|---|
| Single-mass, triaxial | —— | —— | Improved navigation with noise modelling | No redundancy | [141] |
| Mult-sensor, redundant (orthogonal/cubic/optimal) | >25% reduction | >25% reduction, 3.2×/3.7× reduction | High reliability, error reduction | Hardware complexity, missing data | [142,143,144] |
| Dual-mass | 0.09°/h | 0.0096°/√h | High stability, sensitivity | Not Multi-sensor, specialized design | [80] |
| 9-axis | —— | —— | Static error (0.05°); dynamic error (0.5°) | No architecture detail | [145] |
| Design Type | Bias Stability | Angle Random Walk | Environmental Sensitivity | References |
|---|---|---|---|---|
| Triaxial inertial measurement unit | —— | —— | Field (auto/bike), Global navigation satellite system/inertial measurement unit | [141] |
| 9-gyroscope, orthogonal | —— | —— | Simulation, fault detection and isolation test | [144] |
| 6-gyroscope, cubic | >25% reduction | >25% reduction | Field, Global navigation satellite system, stationary/dynamic | [143] |
| 4/5/6-gyroscope, redundant | —— | Angle random walk 3.2×, rate random walk 3.7× reduction | Swing test, simulation | [142] |
| Dual-mass | 0.09 degrees per hour | 0.0096 degrees per root hour | Vacuum, 10 h, temperature/vacuum stabilized | [80] |
| —— | —— | Kalman filter output variance ≤ 30% | —— | [147] |
| 9-axis | —— | —— | static/dynamic, orientation | [145] |
| Process Type | Key Parameters | Quality Metrics | Limitations | References |
|---|---|---|---|---|
| SOG: patterning, anodic bonding, DRIE, CMP | Silicon thickness: 50 μm, roughness: 1.13 nm | Q~12,000, frequency~4 kHz | Lag effect, notching, etch endpoint control | [146] |
| SOI, single crystal silicon, digital control | —— | Q~100,000, bias stability 0.18°/h | —— | [156] |
| Process Type | Key Parameters | Quality Metrics | Limitations | References |
|---|---|---|---|---|
| Laser-induced etching (LIE) on fused silica | Etch width 11 μm, temperature 20–70 °C, 10–30 min | Q > 810,000, overload > 15,000 g, 45 MPa | Subsurface cracks, etch control, vacuum requirement | [157] |
| Precision machining, polishing, etching | Roundness 0.17 μm, roughness 15.2 nm | Q = 3.11 × 107 | Surface loss, stress, geometry limits | [158] |
| Fused silica, hemispherical resonator | Shell radius 10–15 mm, damage layer 0–100 μm | QTED reduction up to 92.5% | Wall thickness nonuniformity | Geometric parameters |
| Process Type | Key Parameters | Quality Metrics | Limitations | References |
|---|---|---|---|---|
| Anodic bonding (silicon to Pyrex) | Bonding after wet etch, pre-DRIE | Well-defined structures, no footing | Wafer misalignment, lapping damage | [146] |
| Direct bonding (fused silica) | Resonator to substrate | High process precision | Bonding error, stress | [157] |
| Performance Metric | Process Influence | Achieved Results | Limiting Factors | References |
|---|---|---|---|---|
| Surface roughness | Chemical Mechanical Polishing (CMP), cerium oxide polish | 1.13 nm | Lapping damage, misalignment | [146] |
| Subsurface cracks, etch width | Laser-Induced Etching (LIE), ultrasonic, annealing | Etch width 11 μm, crack width 4 μm | Subsurface cracks, etch control | [157] |
| Surface roughness | Precision polishing/etching | 15.2 nm | Surface loss, stress | [158] |
| Performance Metric | Process Influence | Achieved Results | Limiting Factors | References |
|---|---|---|---|---|
| Overload, strength | Laser-induced etching (LIE), structure compensation | >15,000 g, 45 MPa | Crack formation, etch uniformity | [157] |
| Mechanical performance | DRIE optimization | No notching /footing | Lag effect, endpoint control | [146] |
| Performance Metric | Process Influence | Achieved Results | Limiting Factors | References |
|---|---|---|---|---|
| Q-factor | DRIE/CMP optimization | 10,437–12,058 | Lag effect, etch uniformity | [146] |
| Q-factor | Laser-induced etching (LIE), structure compensation | 817,000–819,000 | Subsurface cracks, vacuum | [157] |
| Q-factor | Precision machining /polishing | 3.11 × 107 | Surface loss, stress, geometry | [158] |
| Q-factor | SOI, digital compensation | ~100,000 | —— | [156] |
| Q-factor stability | In situ Joule tuning | ΔQ~150 ppm | Not fabrication- limited | [159] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, H.; Su, H.; Tang, Q.; Nisa, F.u.; He, L.; Zhang, T.; Liu, X.; Liu, Z. Review of Research Advances in Gyroscopes’ Structural Forms and Processing Technologies Viewed from Performance Indices. Sensors 2025, 25, 6193. https://doi.org/10.3390/s25196193
Luo H, Su H, Tang Q, Nisa Fu, He L, Zhang T, Liu X, Liu Z. Review of Research Advances in Gyroscopes’ Structural Forms and Processing Technologies Viewed from Performance Indices. Sensors. 2025; 25(19):6193. https://doi.org/10.3390/s25196193
Chicago/Turabian StyleLuo, Hang, Hongbin Su, Qiwen Tang, Fazal ul Nisa, Liang He, Tao Zhang, Xiaoyu Liu, and Zhen Liu. 2025. "Review of Research Advances in Gyroscopes’ Structural Forms and Processing Technologies Viewed from Performance Indices" Sensors 25, no. 19: 6193. https://doi.org/10.3390/s25196193
APA StyleLuo, H., Su, H., Tang, Q., Nisa, F. u., He, L., Zhang, T., Liu, X., & Liu, Z. (2025). Review of Research Advances in Gyroscopes’ Structural Forms and Processing Technologies Viewed from Performance Indices. Sensors, 25(19), 6193. https://doi.org/10.3390/s25196193








