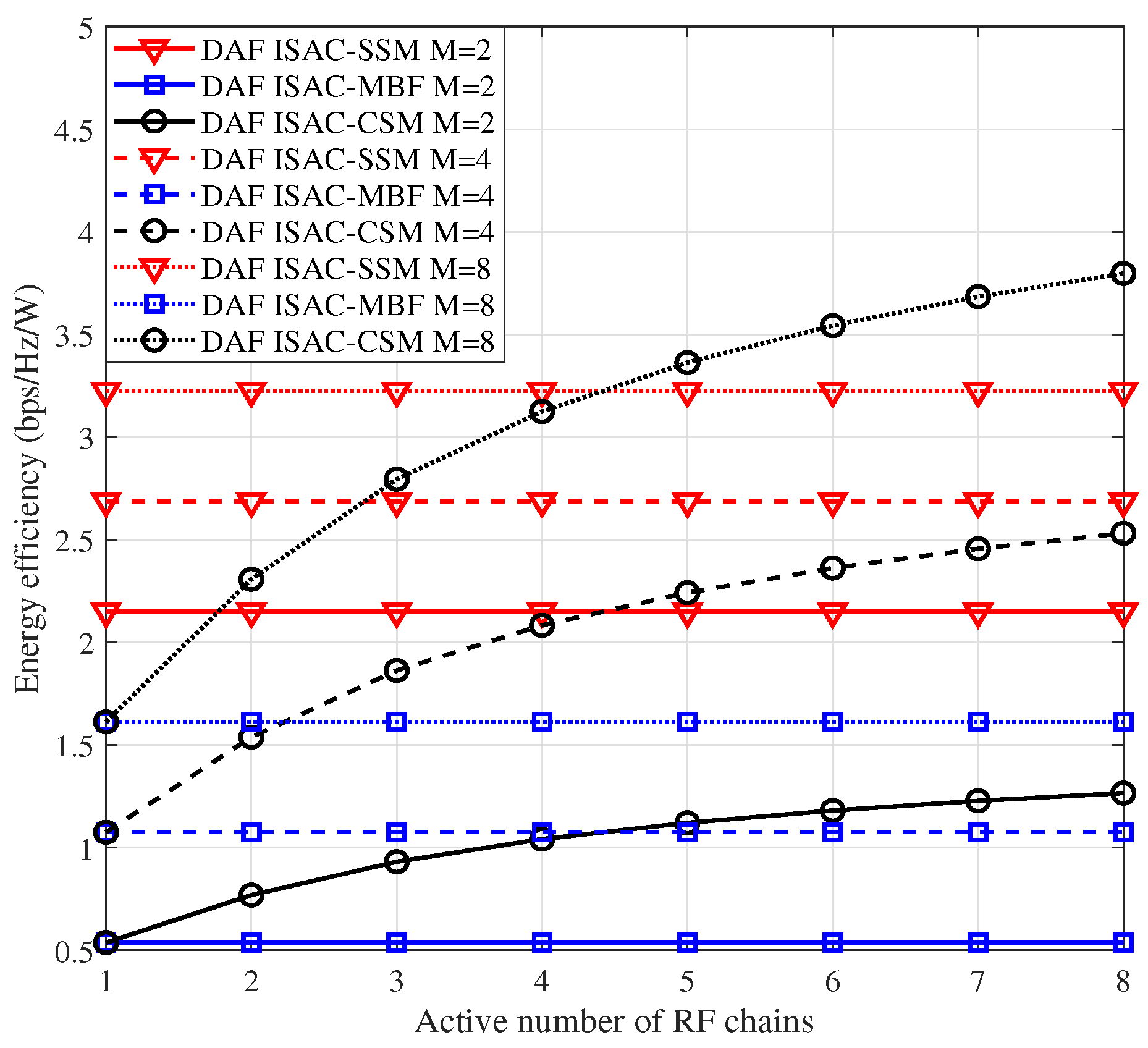
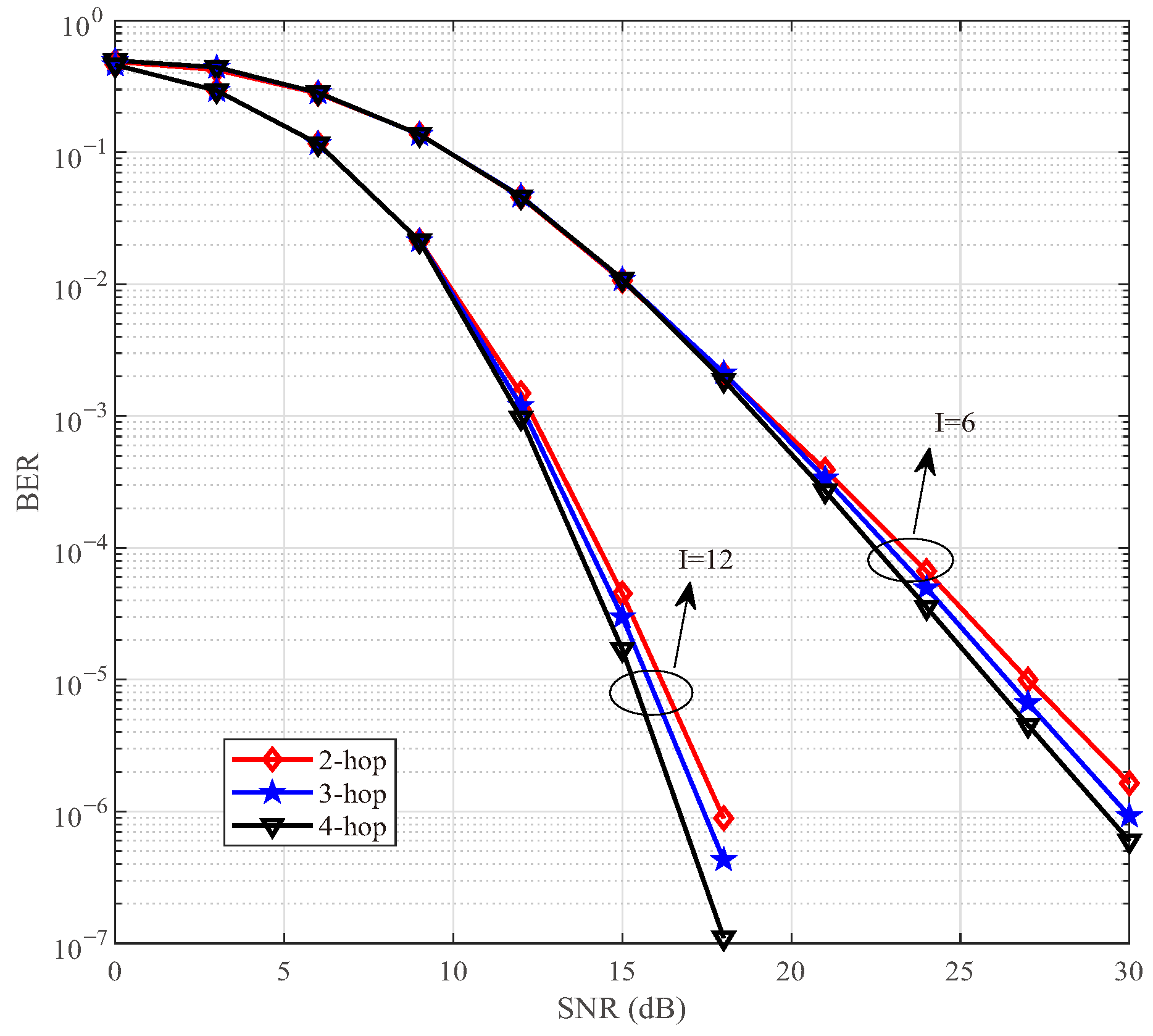
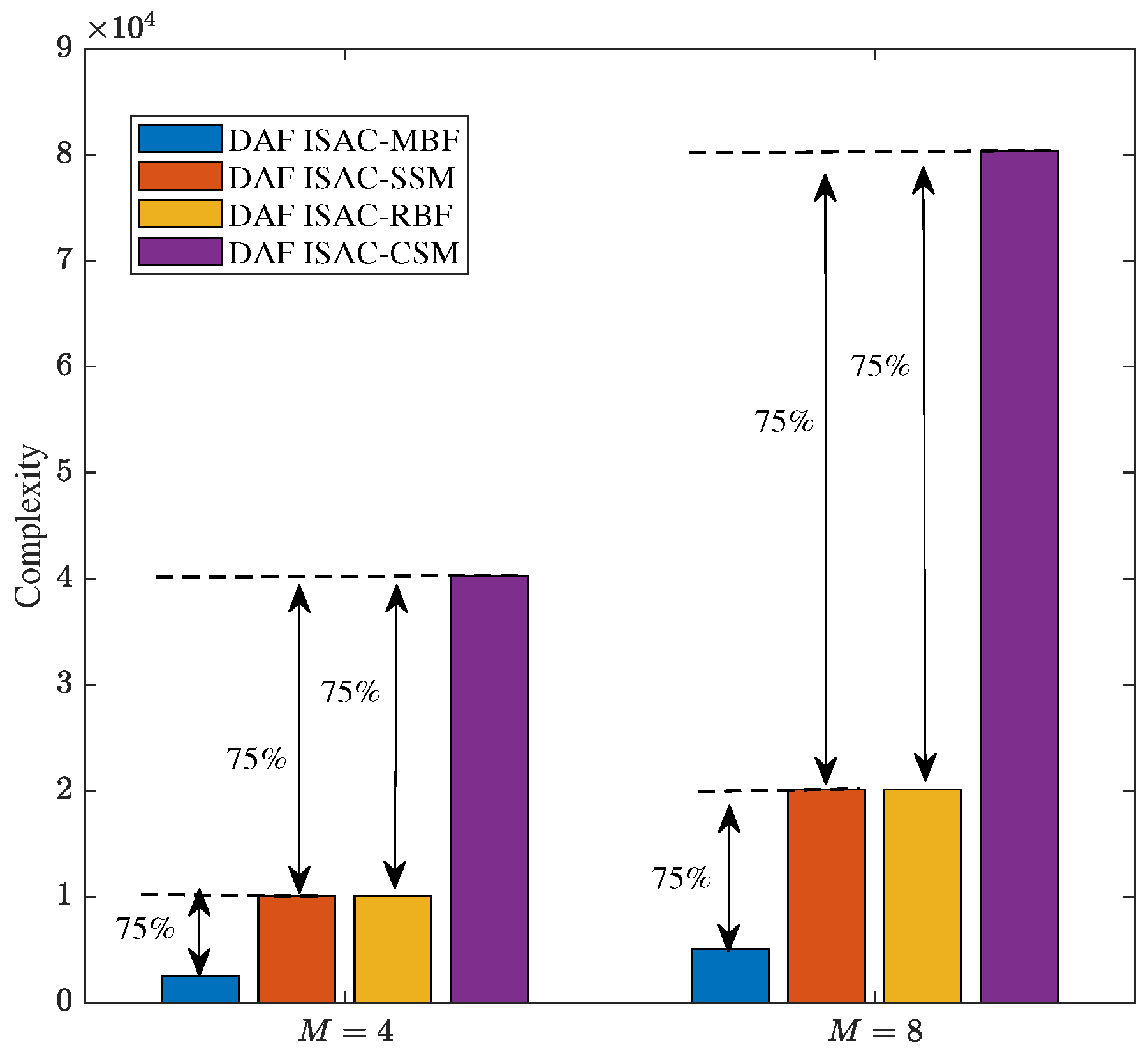
2.1. Channel Model
Each vehicle is equipped with
transmit antennas and
receiver antennas for information exchange. In this paper, to characterize the finite scattering characteristics of mmWave propagation, we adopt the geometric Saleh–Valenzuela channel model [
27]. Specifically, we utilize a simplified channel model, assuming that each scattering cluster contributes a single path to the channel [
17]. Under this assumption, we define
n as a certain hop and
l as a specific link within that hop. Without loss of generality, each path has only one scattering cluster, and
I is the total scattering clusters. According to [
17], the channel matrix at (hop
n, link
l, and time instance
m) can be expressed as
where
is the gain of the
i-th scattering cluster. The normalized Doppler frequency shift is defined as
, with
v being the relative velocity between two vehicles,
being sampling time,
being the speed of light, and
being the carrier frequency. By defining the angle of arrival as
and the angle of departure as
, the
- and
-dimensional array responses at the transmitter and receiver under the half-wavelength uniform linear arrays, namely
, and
, are given by
where
and
represent the phase difference for transmitter and receiver, respectively. Also,
is the carrier wavelength, and
and
denote the antenna spacing for transmitter and receiver, respectively.
Specifically, when
and
are sufficiently large, the beamwidth between the transmitter and receiver becomes narrower. Thus the interference between scattering clusters is restricted [
17]. Taking
and
as examples to denote the transmit beams pointing to two different scattering clusters, and using the transmitted array response as an example, the inner product of the two array responses can be expressed as
Without loss of generality, it is assumed that all scatterers in DAF ISAC-SSM V2V communication are distributed between the transmitter and receiver channel, i.e.,
is satisfied. Therefore, we can get
when
tends to infinity, Equation (
5) can be simplified to
Note that when the number of transmit and receive antennas are large, the resulting beam is very narrow. At this point, we consider that there is interference between the beams; the inner product of the array responses is expressed as [
17]
The mentioned Equation (
8) further implies that the interference among scattering clusters is constrained. Hence, within the context of this paper, we assume an exact orthogonality among all angles of arrival and angles of departure. Similar to [
17], This assumption is utilized to simplify the theoretical computations in this paper.
2.2. Radar Model
The radar transmission power and the distance between the two vehicles at (link
l and hop
n) are denoted by
and
, respectively. Similar to [
28], the SNR is calculated as
where
represents the target’s cross-section of the radar detected target, and
is the carrier wavelength of the radar. The gains of the radar transmission antenna and reception antenna are denoted by
and
, respectively. Additionally, consider a more realistic scenario that includes three types of noise: receiver noise
, cluster interference
C, and interference from adjacent vehicles
J. Particularly, the receiver noise can be represented as
, where
k is the Boltzmann’s constant,
is the noise temperature,
is the reception bandwidth, and
F is the noise figure of the radar receiver, respectively. According to [
29], the interference from adjacent vehicles can be represented as
, where
z is the interference to the target vehicle from the transmission power of surrounding vehicles, satisfying
, and
(in meters) represents the distance from the
j-th neighboring vehicle. Similar to [
28], the values used in the simulations are as follows:
,
,
,
, and
.
The threshold SNR at the radar receiver is set to be a certain value . To ensure effective radar detection, the threshold SNR must satisfy .
2.3. Communications Model
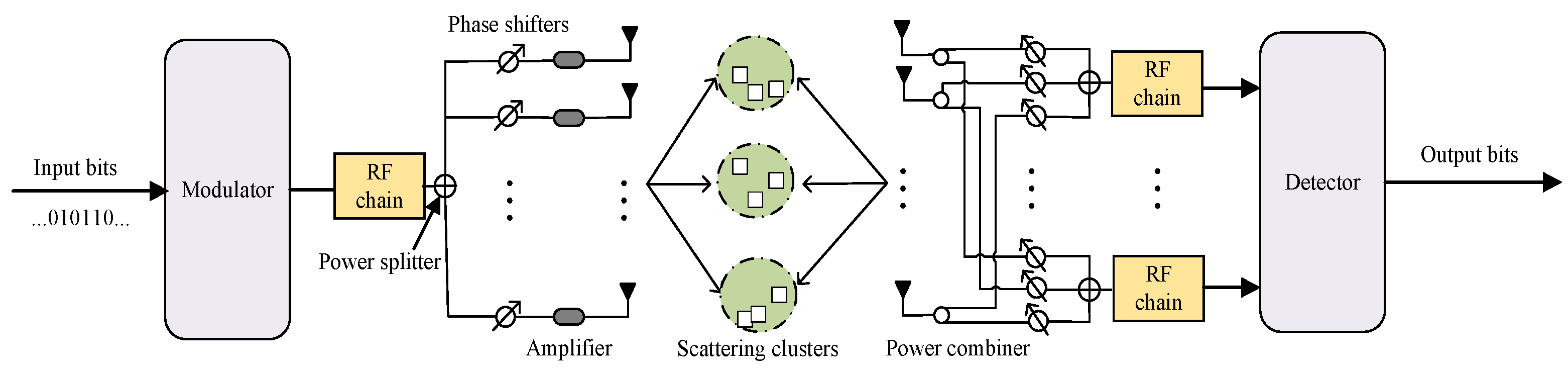
The detail system model of the DAF ISAC-SSM system is shown in the
Figure 2, encompassing the transmission and the detection parts.
(1) DAF ISAC-SSM Transmission: The transmitter indexes and activates the corresponding scattering clusters. The information bits are divided into two parts for transmission. The first part, comprising bits, are modulated into symbols through the use of an M-ary quadrature amplitude modulation (QAM) constellation, with representing the set of modulation symbols.
To transmit the symbols of the first part,
bits of the information bits are utilized to form a beam directed towards the receiver. We sort the gains
of the scattering paths constituting the channel in descending order. Without loss of generality,
. In each time slot, the top
scattering paths having the highest path gains are chosen as candidate scattering paths [
17]. One of the
(
) candidate scattering clusters is selected as the transmission direction. Therefore, the achievable SE of the proposed DAF ISAC-SSM system is
Let
x be the transmitted symbol to the desired relay vehicle. For transmit information, beamforming at (hop
n; link
l) is carried out on the antennas as follows
where
is the phase difference of the top
scattering paths for transmitter, i.e.,
.
During the first hop, the source vehicle transmits the signal to the relay vehicle. Notably, the source vehicle does not engage in signal-forwarding activities. Consequently, the received signal at the relay vehicle during the first hop (at hop
n, link
l, and time instant
m) can be derived as
where
represents the communication transmit power, and
is an additive white Gaussian noise vector.
When the number of hops satisfies
[
17,
30], DAF is utilized to relay the signal to the subsequent hop. Specially, the relay first detects (demodulates and decodes) the received signal. Then, the relay then re-modulates the decoded bits into a new, clean signal and amplifies it for transmission to the next hop. Under these circumstances, the received signal can be expressed as
where
is the amplification factor when adopting the DAF strategy, which is capable of eliminating noise accumulation while amplifying the amplitude of the useful signal. It can be specifically expressed as
where
is the path loss factor. For the convenience of research, in the subsequent introduction, let
.
It is worth noting that the implementation of the DAF protocol in multi-hop V2V networks presents three key challenges: (1) error propagation, where incorrect detection at relay nodes amplifies errors across hops, particularly detrimental in low-SNR regimes; (2) latency and processing overhead, as demodulation–remodulation operations at each relay introduce delays that may hinder ultra-low-latency safety applications; and (3) synchronization and channel dynamics, since accurate channel state information acquisition becomes challenging in high-mobility scenarios. To mitigate these issues, our proposed scheme leverages ISAC-derived side information (e.g., angle/Doppler estimates) to enable sensing-aided relay selection (optimizing SNR) and enhance synchronization robustness. While DAF inherently trades off latency for reliability, its core advantage lies in preventing noise accumulation across hops—making it superior to amplify-and-forward in long-range multi-hop scenarios. The integration of ISAC thus serves as a critical step toward practical DAF deployment in dynamic V2V environments.
The following example illustrates the DAF ISAC-SSM with four selected scattering clusters in a multi-hop V2V network. For the input data stream
, a subset of bits whose length corresponds to a length of
is extracted. The initial
bits are utilized for QAM modulation with a modulation order of
. In contrast, the subsequent
bits are employed to index the
= 4 scattering clusters. The
Table 3 depicts the transmission scheme in detail. Thus, for
, Equation (
13) becomes
(2) ISAC-SSM Detection: The receiver (Rx) signal
is subjected to phase manipulation through shifters, combined by each RF chain, and subsequently down-converted. When the weights of the Rx phase shifters are specified
, with
corresponding to the transmission direction, the maximum SNR can be attained. Given the Rx’s inability to accurately anticipate the beamforming direction of the transmitter (Tx), multiple RF chains are employed at the Rx to generate beams that are oriented towards the candidate scattering clusters. Denoting
as the phase shifter weights for steering towards the scattering cluster, we have
The signal after the RF chain can be represented as
To recover the transmitted bit information, the maximum likelihood (ML) detector can be expressed as
where
is the detected transmission direction, and
is the detected transmission symbol.
Owing to the existence of radar, we utilize the perceived angle information for Doppler shift compensation. The received signal following compensation is expressed as
where
represents the angle error resulting from imperfect radar detection. It is further modeled as a Gaussian distribution with a mean of zero and a variance of
.
More specifically, the Doppler compensation scheme is fundamentally enabled by the tight integration of sensing and communication, where the normalized Doppler frequency shift directly couples the vehicle’s motion to the sensed angle of departure (). This relationship underscores that accurate angle estimation is critical for quantifying and mitigating Doppler effects. The first-order compensator operates as a phase derotator, applying a conjugate phase shift to the received signal symbol-by-symbol, thereby counteracting the linear phase drift induced by mobility. The compensation process forms a closed-loop cycle: (1) radar sensing extracts real-time angle information from echo signals, (2) the Doppler shift is computed from the sensed angle, and (3) the derived phase correction is applied to the data stream. To address practical imperfections, the model explicitly incorporates an angle error term , allowing rigorous quantification of the compensator’s robustness to sensing inaccuracies. The reliability of angular data in dynamic environments stems from its direct acquisition via the radar’s signal processing chain, which provides high refresh rates (millisecond-scale) and sub-degree spatial precision, ensuring timely adaptation to vehicular dynamics. This seamless fusion of sensing and communication is pivotal for enhancing reliability in high-mobility V2V scenarios.
When the hop count exceeds two, we denote the static version of
as
(where
). By substituting Equation (
17) into Equation (
19), we are able to derive that the signal power is
, while the noise power is
. The instantaneous SNR of the compensated received signal, which is defined as the ratio of the signal power to the noise power, can be explicitly expressed as follows:
The threshold SNR at the communication receiver is set to be a certain value
. To ensure effective communication, the threshold SNR must satisfy
.