Pre-Dog-Leg: A Feature Optimization Method for Visual Inertial SLAM Based on Adaptive Preconditions
Abstract
1. Introduction
- We model feature-point information as Multi-State Constraint Kalman Filter (MSCKF) [33] features and propose a robust multi-candidate initializer. In addition, we introduce an adaptive SPAI-Jacobi preconditioning mechanism tailored to feature-point information: it automatically activates when the Hessian becomes ill-conditioned (large condition number) while incurring no extra overhead for well-conditioned problems.
- To address the real-time bottleneck of Dog-Leg [34] in high-dimensional nonlinear SLAM—namely excessive iterations and poor convergence—we integrate Dog-Leg into feature-point estimation and enhance it with preconditioning: Dog-Leg updates are performed in the preconditioned parameter space, and the increments are pulled back via the inverse preconditioning operator to the original state space, suppressing pathological behavior, accelerating convergence, and improving accuracy and robustness.
- Experiments show that the feature-point-driven preconditioner effectively reduces the Hessian condition number and markedly speeds up Dog-Leg convergence, improving overall efficiency in high-dimensional nonlinear SLAM. On the EuRoC dataset, our method achieves lower absolute trajectory error than RVIO2, VINS-Mono, and OpenVINS, demonstrating higher positioning accuracy and robustness and confirming its practical effectiveness in complex environments.
2. Pre-Conditioned Construction Principle
2.1. Analysis of the Characteristic Point Parameter Pathology Problem
2.2. Methods of Constructing Preconditioned Matrices
3. Pre-Dog-Leg Based Feature Point Optimization Approach
3.1. Multi-Candidate Initialization Strategy
3.2. Combination Preconditioner Design
| Algorithm 1: Build Inverse DepthPreconditioner |
| Input: Hessian matrix Output: P_combined # 1. Initialization Set preconditioner_ready = false Set P_combined = Identity # 2. Check Conditioning If : return where # 3. Build SPAI Preconditioner Diagonal: Off-diagonal: and i ≠ j where α , # 4. Construct Jacobi Preconditioner For row = 0 to 2: End for # 5. Combine Preconditioners P_combined = P_spai × N Return P_combined |
3.3. Pre-Dog-Leg Algorithm
| Algorithm 2: Pre-Dog-Leg algorithm based on preconditions |
, convergence flag converged #1. Multi-candidate initialization: #2. Trust region initialization and main optimization loop: radius = 0.05 (initial trust region radius) iteration = 0 while iteration < 80 and converged #3. Preconditioned space transformation: # Preconditioned gradient # Preconditioned Hessian #4. Dog-Leg step calculation: Else: Dog-Leg combination step calculation #5. Transform back to original parameter space: # Transform back from preconditioned space # Keep original space step #6. Model prediction reduction #7. Status update: if a > 0.05: x = x_new # Accept update Hessian = J(x)ᵀ × J(x) # Update Hessian #8. Radius Updates if a > 0.9 radius = min(2.0, radius × 1.8) else if a < 0.05 radius = max(10−6 radius × 0.3) |
4. Experiment
4.1. Pre-Dog-Leg Algorithm Condition Number Verification
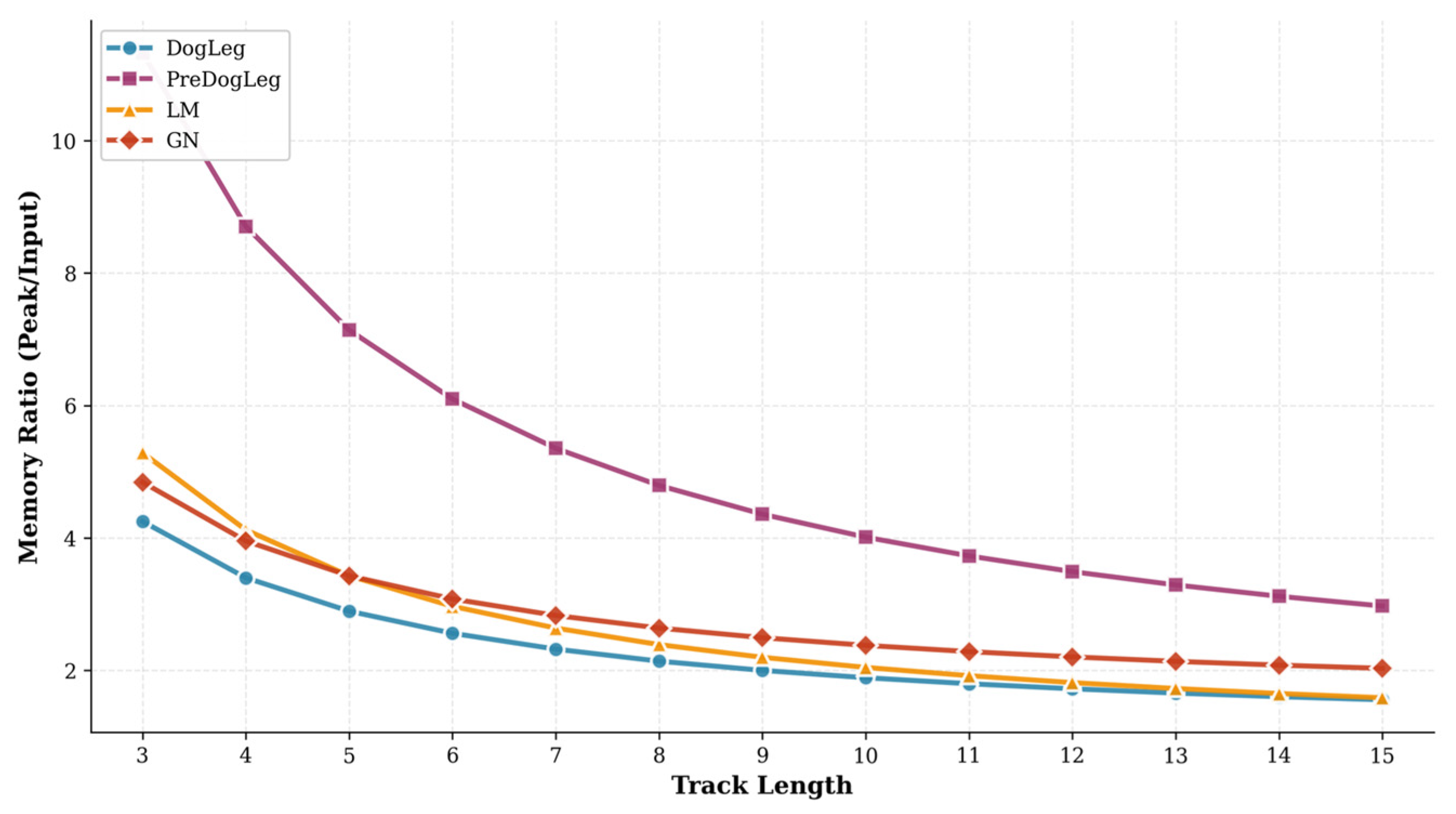
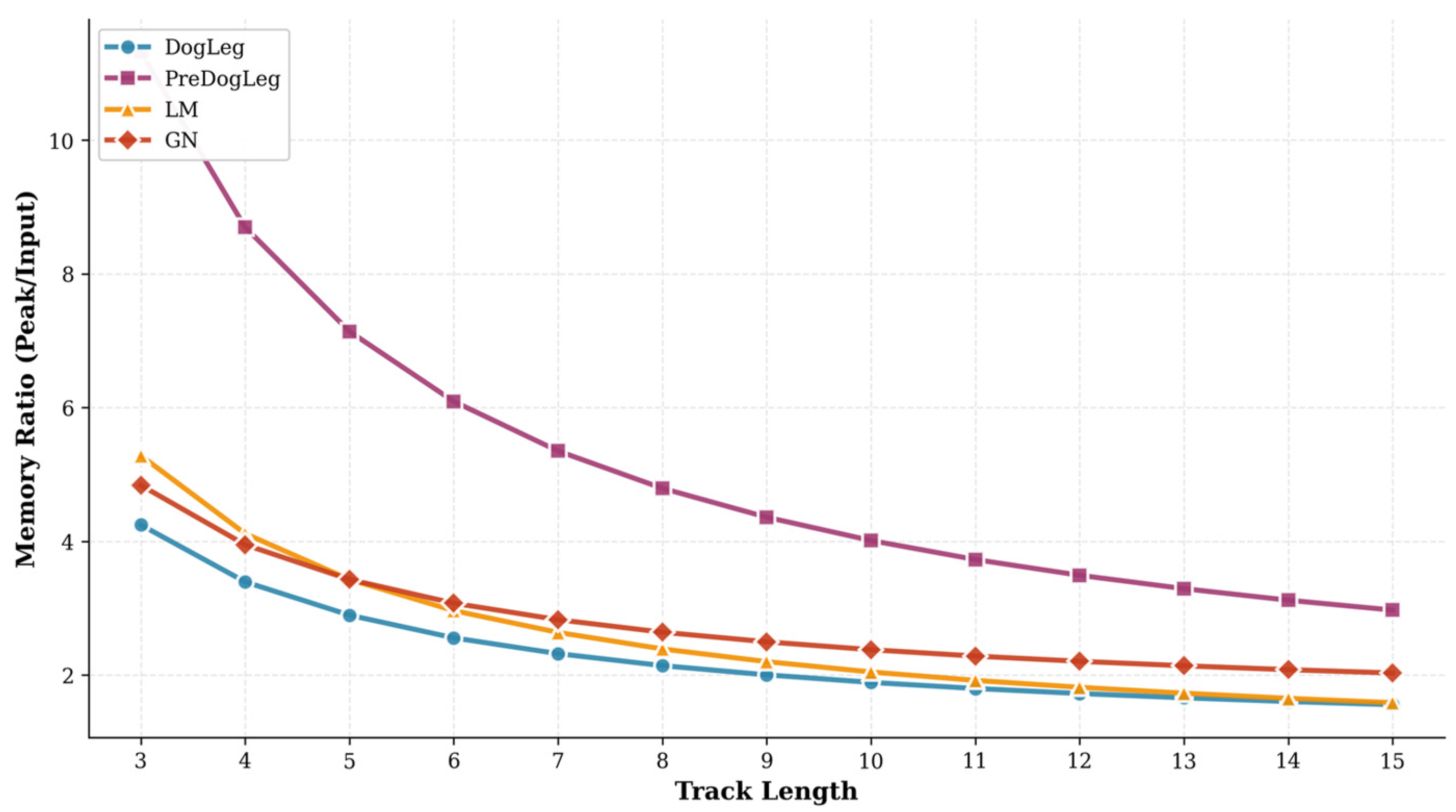
4.2. Pre-Dog-Leg Convergence Performance Experiment
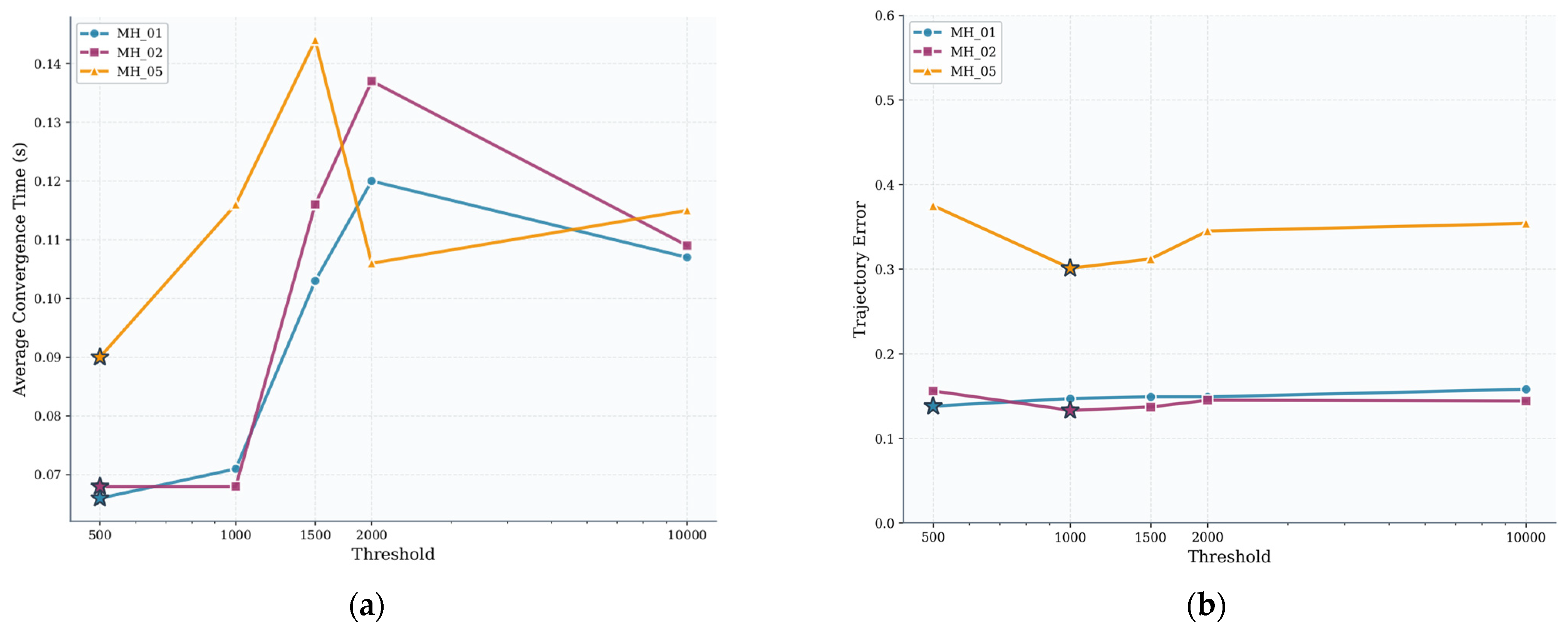
4.3. Pre-Dog-Leg Sensitivity Test Experiment
4.4. Pre-Dog-Leg Localization Accuracy Experiment
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gao, G.; Yi, Y.; Zhong, Y.; Liang, S.; Hu, G.; Gao, B. A robust Kalman filter based on kernel density estimation for system state estimation against measurement outliers. IEEE Trans. Instrum. Meas. 2025, 74, 1003812. [Google Scholar] [CrossRef]
- Li, J.; Wang, S.; Hao, J.; Ma, B.; Chu, H.K. UVIO: Adaptive Kalman filtering UWB-aided visual-inertial SLAM system for complex indoor environments. Remote Sens. 2024, 16, 3245. [Google Scholar] [CrossRef]
- Van Goor, P.; Mahony, R. An equivariant filter for visual-inertial odometry. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 14432–14438. [Google Scholar]
- Yang, Y.; Chen, C.; Lee, W.; Huang, G. Decoupled right invariant error states for consistent visual-inertial navigation. IEEE Robot. Autom. Lett. 2022, 7, 1627–1634. [Google Scholar] [CrossRef]
- Chen, C.; Yang, Y.; Geneva, P.; Huang, G. FEJ2: A consistent visual-inertial state estimator design. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022. [Google Scholar]
- Fu, S.; Yao, Z.; Guo, J.; Wang, H. Online and Graph-Based Temporal Alignment for Monocular-Inertial SLAM Applied on Android Smart Phones. In Proceedings of the IEEE International Conference on Mechatronics and Automation (ICMA), Guilin, China, 7–9 August 2022; pp. 1116–1122. [Google Scholar]
- Memon, Z.W.; Chen, Y.; Zhang, H. An adaptive threshold-based pixel point tracking algorithm using reference features leveraging the multi-state constrained Kalman filter feature point triangulation technique for depth mapping the environment. Sensors 2025, 25, 2849. [Google Scholar] [CrossRef]
- Qin, T.; Li, P.; Shen, S. VINS-mono: A robust and versatile monocular visual-inertial state estimator. IEEE Trans. Robot. 2018, 34, 1004–1020. [Google Scholar] [CrossRef]
- Bai, X.; Hsu, L.T. GNSS/visual/IMU/map integration via sliding window factor graph optimization for vehicular positioning in urban areas. IEEE Trans. Intell. Veh. 2025, 10, 296–305. [Google Scholar] [CrossRef]
- Xiao, J.; Xiong, D.; Yu, Q.; Huang, K.; Lu, H.; Zeng, Z. A real-time sliding-window-based visual-inertial odometry for MAVs. IEEE Trans. Ind. Inform. 2020, 16, 4049–4058. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Z.; Liu, A.; Sun, Y.; Jing, S. Fusion of binocular vision, 2D lidar and IMU for outdoor localization and indoor planar mapping. Meas. Sci. Technol. 2022, 34, 025203. [Google Scholar] [CrossRef]
- Demmel, N.; Sommer, C.; Cremers, D.; Niessner, M. Square root bundle adjustment for large-scale reconstruction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 11723–11732. [Google Scholar]
- Lee, J.; Park, S.Y. PLF-VINS: Real-time monocular visual-inertial SLAM with point-line fusion and parallel-line fusion. IEEE Robot. Autom. Lett. 2021, 6, 7033–7040. [Google Scholar] [CrossRef]
- Xu, W.; Chen, Y.; Liu, S.; Nie, A.; Chen, R. Multi-Robot Cooperative Simultaneous Localization and Mapping Algorithm Based on Sub-Graph Partitioning. Sensors 2025, 25, 2953. [Google Scholar] [CrossRef]
- Xiong, J.; Xiong, Z.; Zhuang, Y.; Cheong, J.W.; Dempster, A.G. Fault-tolerant cooperative positioning based on hybrid robust Gaussian belief propagation. IEEE Trans. Intell. Transp. Syst. 2023, 24, 6425–6431. [Google Scholar] [CrossRef]
- Yan, S.; Lu, S.; Liu, G.; Zhan, Y.; Lou, J.; Zhang, R. Real-time kinematic positioning algorithm in graphical state space. In Proceedings of the 2023 International Technical Meeting of The Institute of Navigation, Long Beach, CA, USA, 23–26 January 2023; pp. 637–648. [Google Scholar]
- Dutt, R.; Acharyya, A. Low-complexity square-root unscented Kalman filter design methodology. Circuits Syst. Signal Process. 2023, 42, 6900–6928. [Google Scholar] [CrossRef]
- Sun, M.; Guo, C.; Jiang, P.; Mao, S.; Chen, Y.; Huang, R. SRIF: Semantic shape registration empowered by diffusion-based image morphing and flow estimation. In Proceedings of the SIGGRAPH Asia 2024 Conference Papers, Tokyo, Japan, 3–6 December 2024; pp. 1–11. [Google Scholar]
- Sandoval, K.E.; Witt, K.A. Somatostatin: Linking cognition and Alzheimer disease to therapeutic targeting. Pharmacol. Rev. 2024, 76, 1291–1325. [Google Scholar] [CrossRef] [PubMed]
- Peng, Y.; Chen, C.; Huang, G. Technical report: Ultrafast square-root filter-based VINS. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024. [Google Scholar]
- Huai, Z.; Huang, G. Square-root robocentric visual-inertial odometry with online spatiotemporal calibration. IEEE Robot. Autom. Lett. 2022, 7, 9961–9968. [Google Scholar] [CrossRef]
- Zheng, Y. Rank-deficient square-root information filter for unified GNSS precise point positioning model. Meas. Sci. Technol. 2025, 36, 026313. [Google Scholar] [CrossRef]
- Dillon, G.; Kalantzis, V.; Xi, Y.; Saad, Y. A hierarchical low-rank Schur complement preconditioner for indefinite linear systems. SIAM J. Sci. Comput. 2018, 40, A2234–A2252. [Google Scholar] [CrossRef]
- Xu, T.; Kalantzis, V.; Li, R.; Xi, Y.; Dillon, G.; Saad, Y. parGeMSLR: A parallel multilevel Schur complement low-rank preconditioning and solution package for general sparse matrices. Parallel Comput. 2022, 113, 102956. [Google Scholar] [CrossRef]
- Zheng, Q.; Xi, Y.; Saad, Y. A power Schur complement low-rank correction preconditioner for general sparse linear systems. SIAM J. Matrix Anal. Appl. 2021, 42, 659–682. [Google Scholar] [CrossRef]
- Ke, T.; Agrawal, P.; Zhang, Y.; Zhen, W.; Guo, C.X.; Sharp, T.; Dutoit, R.C. PC-SRIF: Preconditioned Cholesky-based square root information filter for vision-aided inertial navigation. arXiv 2024, arXiv:2409.11372. [Google Scholar]
- Chen, C.; Geneva, P.; Peng, Y.; Lee, W.; Huang, G. Optimization-based VINS: Consistency, marginalization, and FEJ. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Detroit, MI, USA, 1–5 October 2023. [Google Scholar]
- Chen, C.; Peng, Y.; Huang, G. Fast and consistent covariance recovery for sliding-window optimization-based VINS. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024. [Google Scholar]
- Campos, C.; Elvira, R.; Rodríguez, J.J.G.; Montiel, J.M.; Tardós, J.D. ORB-SLAM3: An accurate open-source library for visual, visual-inertial, and multimap SLAM. IEEE Trans. Robot. 2021, 37, 1874–1890. [Google Scholar] [CrossRef]
- Merrill, N.; Huang, G. Visual-inertial SLAM as simple as A, B, VINS. arXiv 2024, arXiv:2406.05969. [Google Scholar] [CrossRef]
- Zhai, S.; Wang, N.; Wang, X.; Chen, D.; Xie, W.; Bao, H.; Zhang, G. XR-VIO: High-precision visual-inertial odometry with fast initialization for XR applications. arXiv 2025, arXiv:2502.01297. [Google Scholar]
- Li, J.; Pan, X.; Huang, G.; Zhang, Z.; Wang, N.; Bao, H.; Zhang, G. RD-VIO: Robust visual-inertial odometry for mobile augmented reality in dynamic environments. IEEE Trans. Vis. Comput. Graph. 2024, 30, 6941–6955. [Google Scholar] [CrossRef]
- Mourikis, A.I.; Roumeliotis, S.I. A multi-state constraint Kalman filter for vision-aided inertial navigation. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Rome, Italy, 10–14 April 2007; pp. 3565–3572. [Google Scholar]
- Powell, M.J.D. A new algorithm for unconstrained optimization. In Nonlinear Programming; Rosen, J.B., Mangasarian, O.L., Ritter, K., Eds.; Academic Press: New York, NY, USA, 1970; pp. 31–65. [Google Scholar]
- Grote, M.J.; Huckle, T. Parallel preconditioning with sparse approximate inverses. SIAM J. Sci. Comput. 1997, 18, 838–853. [Google Scholar] [CrossRef]
- Benzi, M. Preconditioning techniques for large linear systems: A survey. J. Comput. Phys. 2002, 182, 418–477. [Google Scholar] [CrossRef]
- Björck, Å. Numerical Methods for Least Squares Problems; SIAM: Philadelphia, PA, USA, 1996. [Google Scholar]
- Zhang, Z.; Scaramuzza, D. A tutorial on quantitative trajectory evaluation for visual(-inertial) odometry. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 7244–7251. [Google Scholar]
- Geneva, P.; Eckenhoff, K.; Lee, W.; Huang, G.; Scaramuzza, D.; Kelly, A.; Dellaert, F. OpenVINS: A research platform for visual-inertial estimation. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 4666–4672. [Google Scholar]

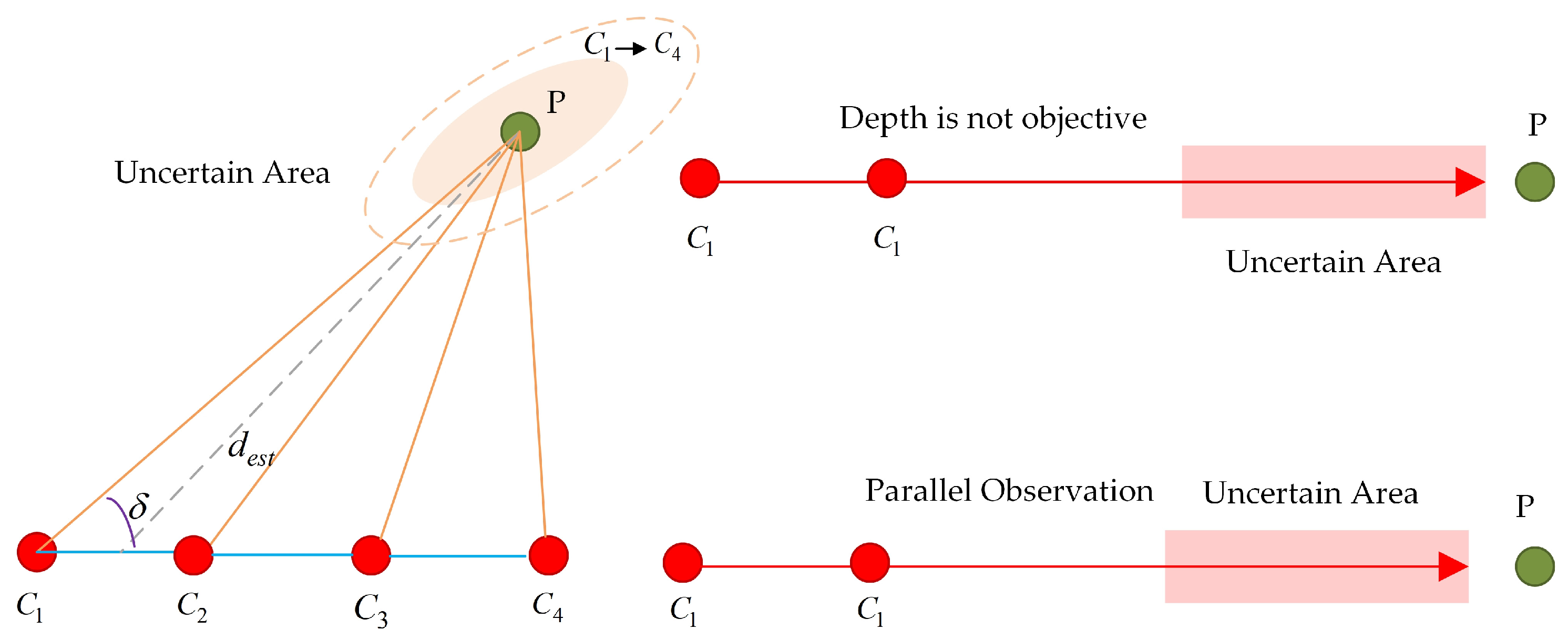

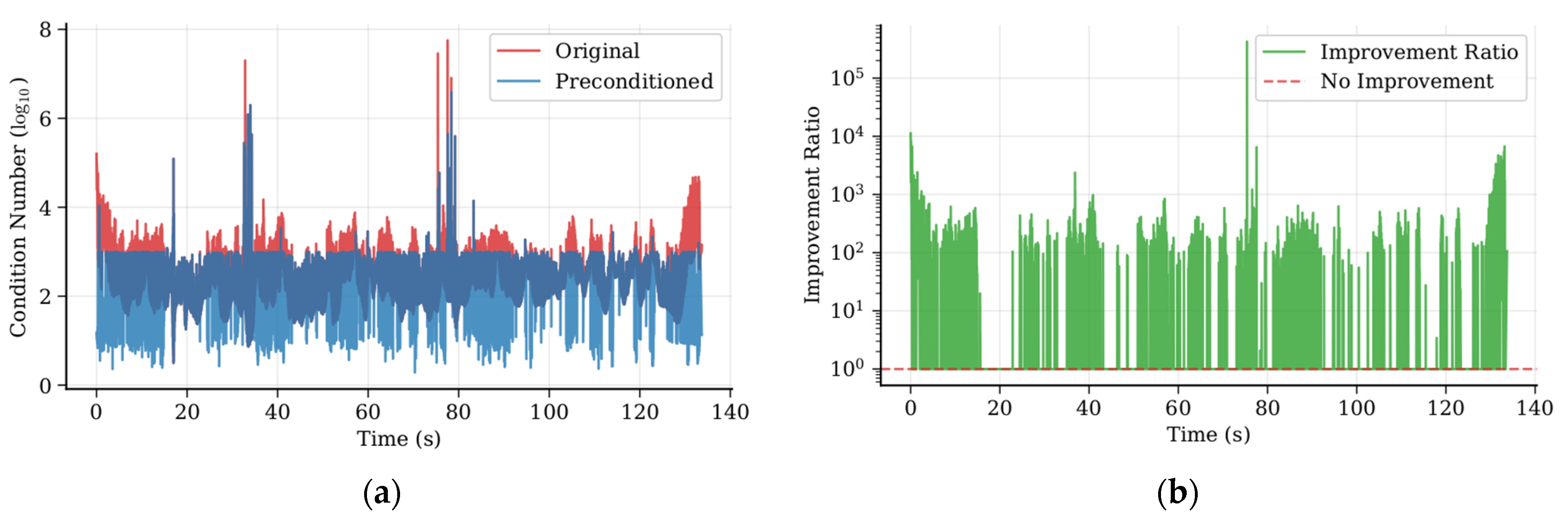
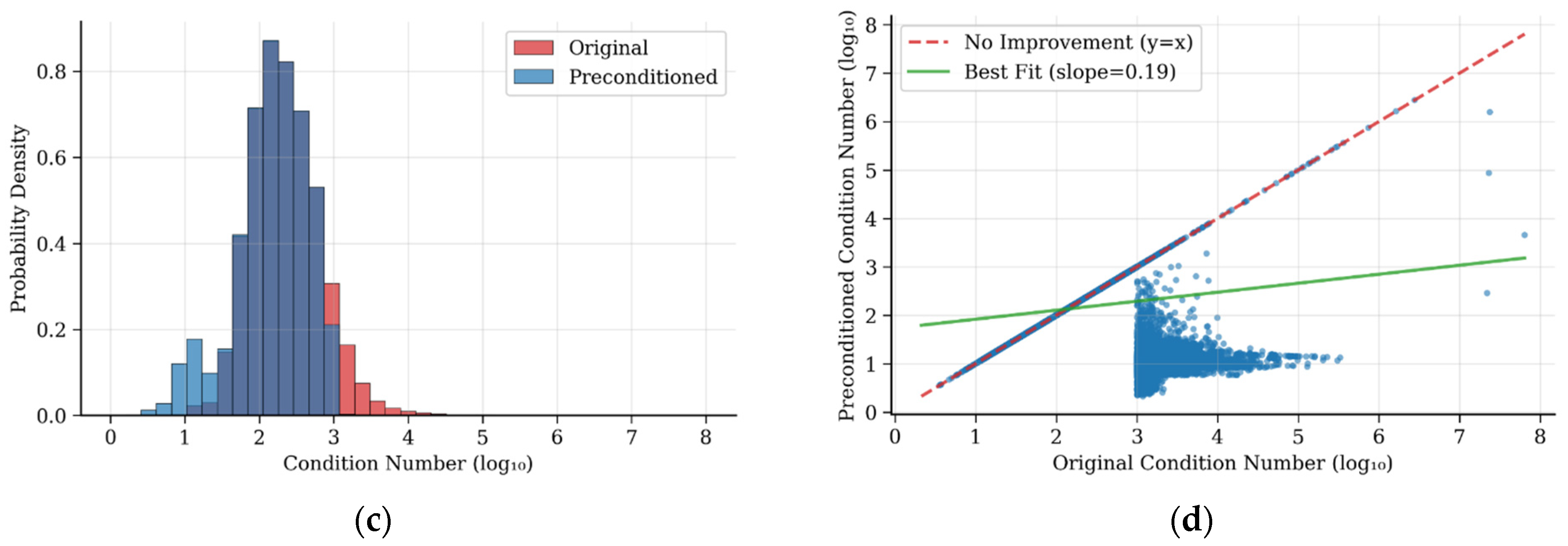
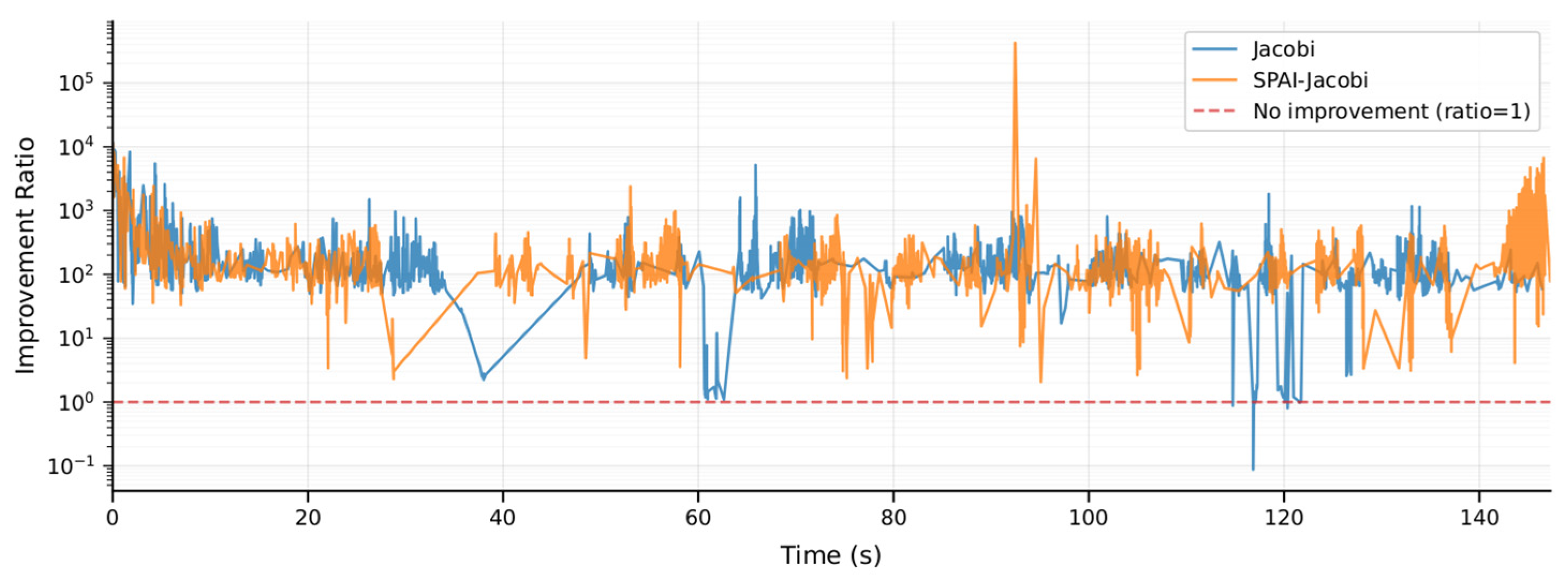
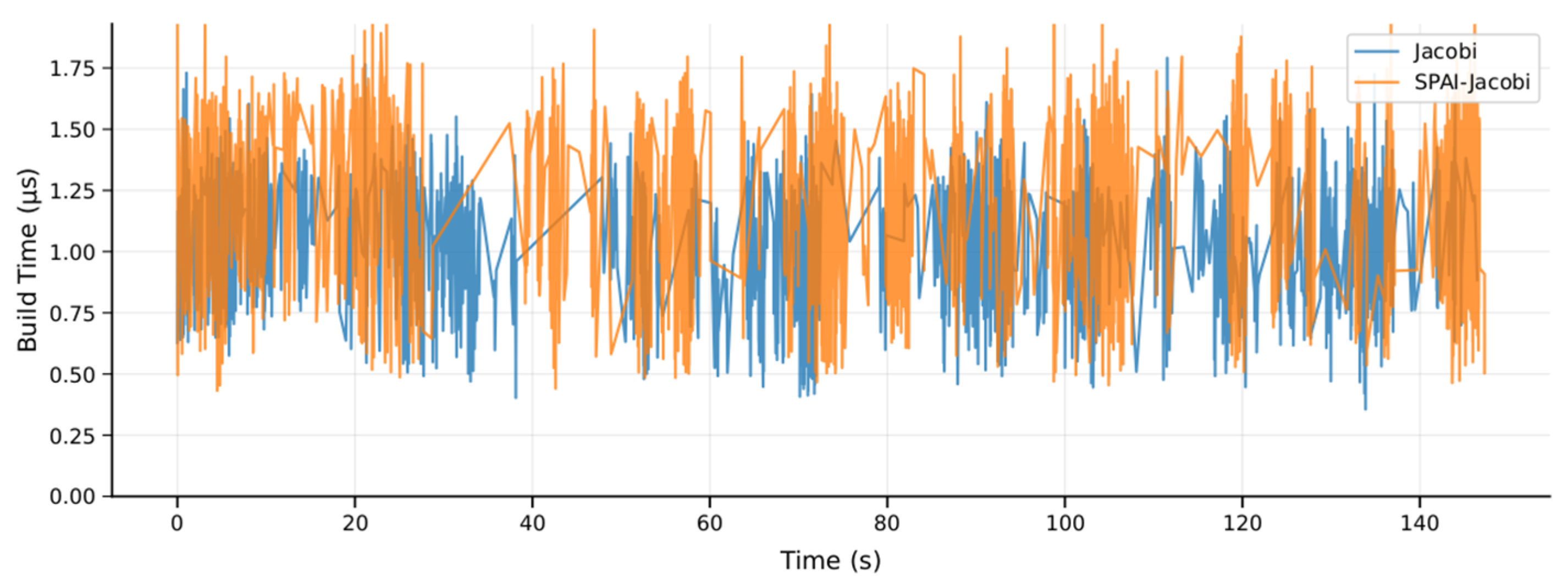
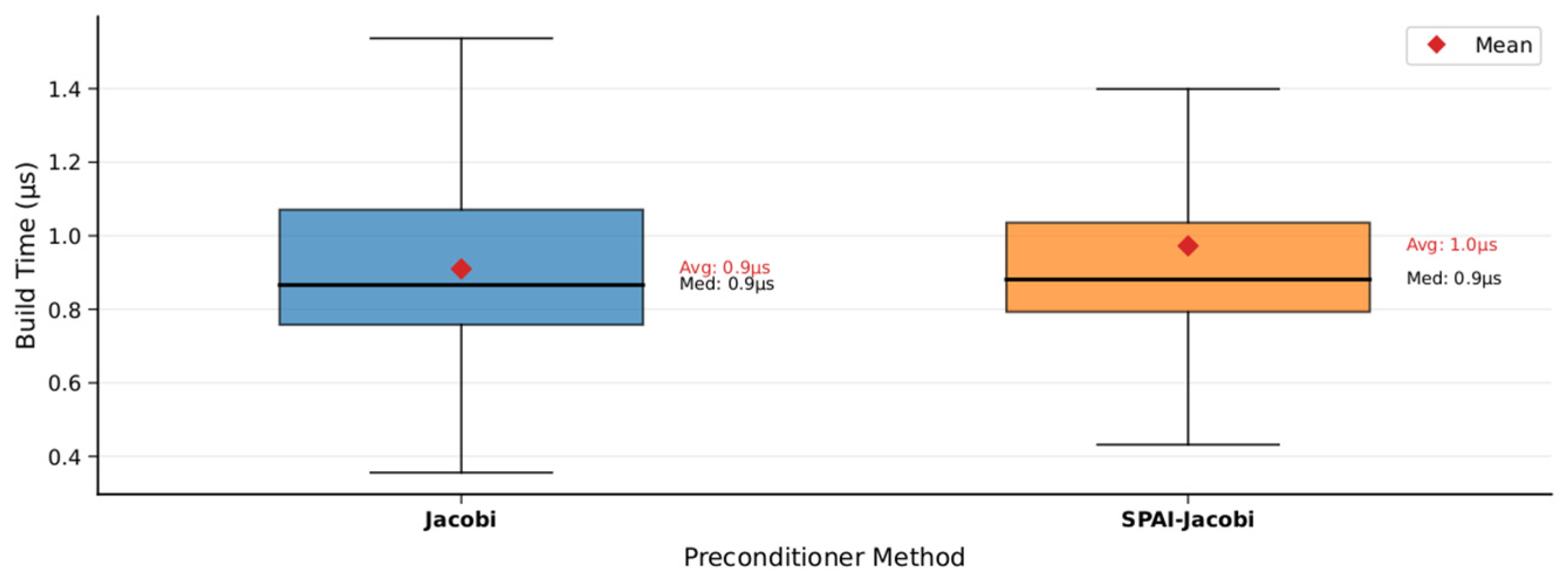
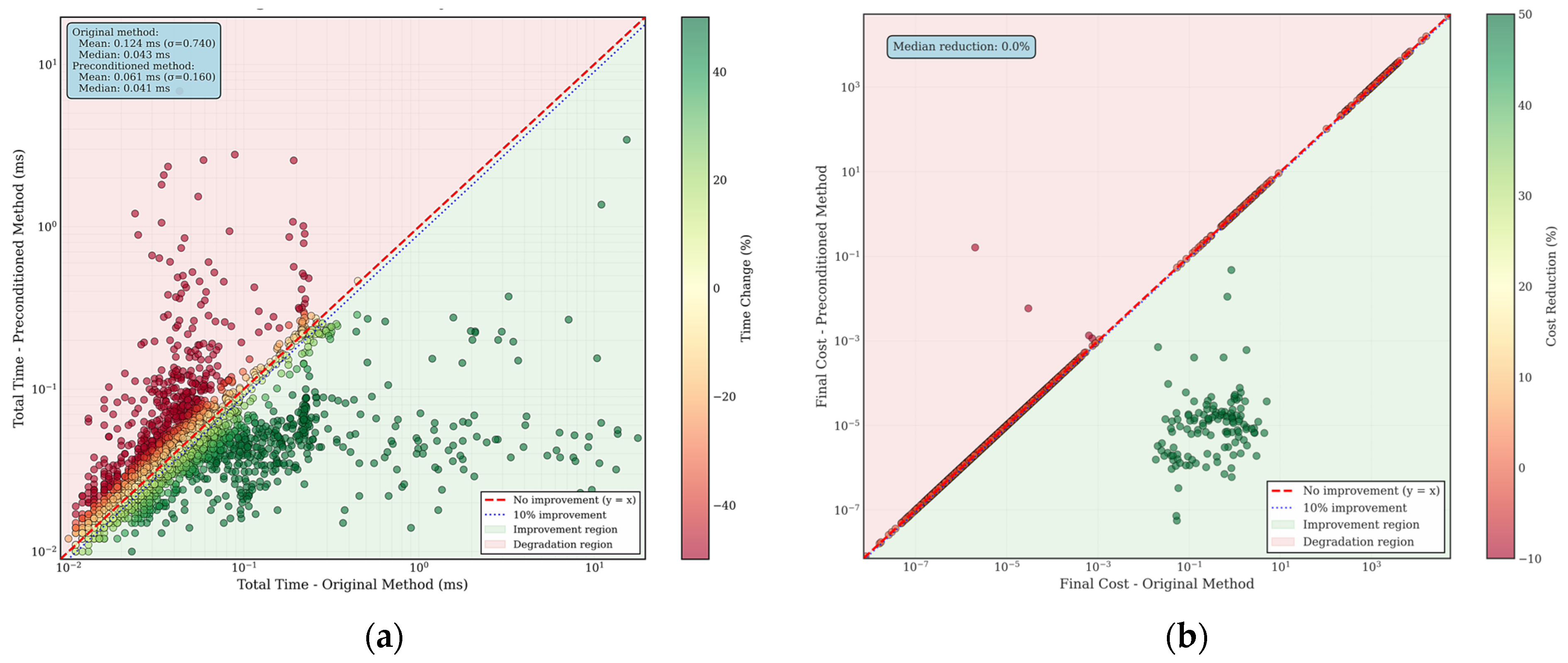
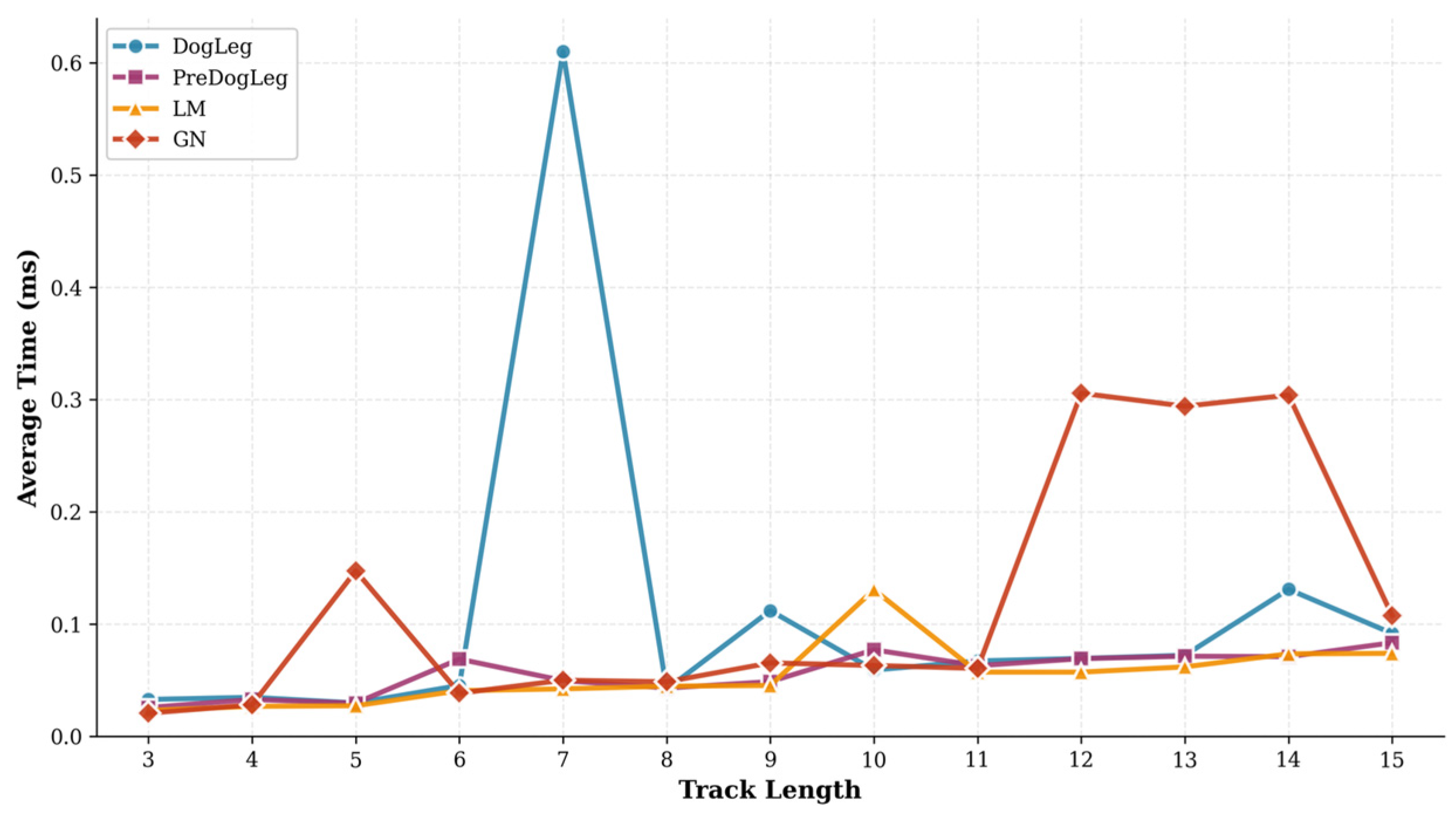





| Aspect | The Global State Is Unobservable | Feature Point Information Is Not Observable | ||||
|---|---|---|---|---|---|---|
| FEJ | PC-SRIF | RVIO2 | SRIF | [30] | [32] | |
| Issue | Information matrix null space | Single-precision Cholesky stability issues | Global frame changes lead to instability | Sliding-window BA Hessian ill-conditioned | Pure rotation (no parallax) + feature mismatches | Pure rotation/static motion yields Hessian singularity |
| Target Block | Global State and Linearization | Sliding Window Optimization | State Estimation Framework | Nonlinear Solve | Deep learning + priors | Front-end feature matching |
| Limitations | No extra observations; unobservable issues persist | Depends on initial guess; poor initialization causes linearization errors | Inherent unobservability persists | Inherent unobservability persists | Relies on deep learning for scale estimation | Relies on IMU for scale estimation |
| Dataset | Distance (m) | Average Linear Velocity (m/s) | Average Angular Velocity (Rad/s) | Duration (s) | Difficulty/Characteristics |
|---|---|---|---|---|---|
| 0.44 | 182 | 0.22 | good texture, bright | ||
| 0.49 | 150 | 0.21 | good texture, bright | ||
| 0.99 | 132 | 0.29 | fast motion, bright | ||
| 0.88 | 111 | 0.21 | fast motion, dark |
| Method | Convergence Rate (ms) | Memory Ratio | RMSE (m) | ||||
|---|---|---|---|---|---|---|---|
| Max | Min | std | Median | Mean | |||
| LM | 9.422 | 0.009 | 0.266 | 0.050 | 0.071 | 1.7309 | 0.176 |
| GN | 28.370 | 0.009 | 0.633 | 0.063 | 0.109 | 2.1405 | 0.175 |
| Dog-Leg | 25.369 | 0.014 | 0.515 | 0.066 | 0.093 | 1.6619 | 0.193 |
| Pre-Dog-Leg | 10.336 | 0.013 | 0.251 | 0.064 | 0.071 | 3.2962 | 0.147 |
| Method | Convergence Rate (ms) | Memory Ratio | RMSE | ||||
|---|---|---|---|---|---|---|---|
| Max | Min | std | Median | Mean | |||
| LM | 36.10 | 0.010 | 1.241 | 0.053 | 0.183 | 1.836 | 0.329 |
| GN | 25.13 | 0.012 | 0.992 | 0.066 | 0.175 | 2.145 | 0.317 |
| Dog-Leg | 30.67 | 0.017 | 1.120 | 0.069 | 0.197 | 1.667 | 0.353 |
| Pre-Dog-Leg | 19.53 | 0.014 | 0.651 | 0.068 | 0.116 | 3.316 | 0.301 |
| Threshold | MH_01 | MH_02 | MH_05 | |||
|---|---|---|---|---|---|---|
| Avg. Convergence Time (ms) | ATE (m) | Avg. Convergence Time (ms) | ATE (m) | Convergence Time (ms) | ATE (m) | |
| 500 | 0.066 | 0.138 | 0.068 | 0.156 | 0.090 | 0.375 |
| 1000 | 0.071 | 0.147 | 0.068 | 0.133 | 0.116 | 0.301 |
| 1500 | 0.103 | 0.149 | 0.116 | 0.137 | 0.144 | 0.312 |
| 2000 | 0.120 | 0.149 | 0.137 | 0.145 | 0.106 | 0.345 |
| 10,000 | 0.107 | 0.158 | 0.109 | 0.144 | 0.115 | 0.354 |
| Method | Dates | Max | Mean | Median | Min | RMSE | SSE | std |
|---|---|---|---|---|---|---|---|---|
| RVIO2 | MH_01 | 0.417 | 0.159 | 0.151 | 0.008 | 0.176 | 86.27 | 0.084 |
| MH_02 | 0.324 | 0.122 | 0.104 | 0.020 | 0.138 | 42.90 | 0.064 | |
| MH_03 | 0.597 | 0.174 | 0.162 | 0.014 | 0.199 | 93.27 | 0.097 | |
| MH_05 | 0.638 | 0.310 | 0.286 | 0.007 | 0.329 | 198.7 | 0.113 | |
| Vins-mono | MH_01 | 0.316 | 0.143 | 0.118 | 0.032 | 0.161 | 36.01 | 0.075 |
| MH_02 | 0.517 | 0.127 | 0.086 | 0.033 | 0.168 | 42.08 | 0.110 | |
| MH_03 | 0.420 | 0.162 | 0.157 | 0.010 | 0.182 | 43.41 | 0.082 | |
| MH_05 | 0.570 | 0.347 | 0.335 | 0.205 | 0.353 | 132.2 | 0.067 | |
| OpenVINS | MH_01 | 0.522 | 0.175 | 0.146 | 0.028 | 0.205 | 116.07 | 0.107 |
| MH_02 | 0.693 | 0.247 | 0.191 | 0.013 | 0.291 | 190.17 | 0.154 | |
| MH_03 | 0.635 | 0.259 | 0.244 | 0.045 | 0.284 | 184.73 | 0.116 | |
| MH_05 | 0.857 | 0.412 | 0.368 | 0.146 | 0.456 | 381.05 | 0.196 | |
| Pre-Dog-Leg | MH_01 | 0.312 | 0.132 | 0.124 | 0.011 | 0.147 | 59.98 | 0.065 |
| MH_02 | 0.294 | 0.119 | 0.111 | 0.002 | 0.133 | 40.29 | 0.061 | |
| MH_03 | 0.581 | 0.192 | 0.157 | 0.046 | 0.220 | 113.33 | 0.105 | |
| MH_05 | 0.585 | 0.028 | 0.026 | 0.010 | 0.301 | 168.8 | 0.106 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Lv, S.; Zhu, H.; Li, Y.; Yu, H.; Wang, Y.; Zhang, K. Pre-Dog-Leg: A Feature Optimization Method for Visual Inertial SLAM Based on Adaptive Preconditions. Sensors 2025, 25, 6161. https://doi.org/10.3390/s25196161
Zhao J, Lv S, Zhu H, Li Y, Yu H, Wang Y, Zhang K. Pre-Dog-Leg: A Feature Optimization Method for Visual Inertial SLAM Based on Adaptive Preconditions. Sensors. 2025; 25(19):6161. https://doi.org/10.3390/s25196161
Chicago/Turabian StyleZhao, Junyang, Shenhua Lv, Huixin Zhu, Yaru Li, Han Yu, Yutie Wang, and Kefan Zhang. 2025. "Pre-Dog-Leg: A Feature Optimization Method for Visual Inertial SLAM Based on Adaptive Preconditions" Sensors 25, no. 19: 6161. https://doi.org/10.3390/s25196161
APA StyleZhao, J., Lv, S., Zhu, H., Li, Y., Yu, H., Wang, Y., & Zhang, K. (2025). Pre-Dog-Leg: A Feature Optimization Method for Visual Inertial SLAM Based on Adaptive Preconditions. Sensors, 25(19), 6161. https://doi.org/10.3390/s25196161







