The AMEE-PPI Method to Extract Typical Outcrop Endmembers from GF-5 Hyperspectral Images
Abstract
Highlights
- A hybrid algorithm named AMEE-PPI was proposed by integrating Automated Morphological Endmember Extraction (AMEE) and Pure Pixel Index (PPI), effectively overcoming limitations of each method and enhancing the precision and stability of endmember extraction from GF-5 hyperspectral images. The algorithm dynamically calculates pixel purity by running PPI within morphological structural elements, thus incorporating both spectral and spatial information.
- Experimental results on GF-5 hyperspectral images in a geologically complex outcrop region demonstrated that AMEE-PPI achieved superior performance compared to four classical algorithms (PPI, OSP, VCA, and AMEE), with the lowest Spectral Angle Distance (SAD) and Spectral Information Divergence (SID) values across all outcrop types. The extracted endmembers more closely matched ground-truth spectra, significantly improving hyperspectral representation of pure land-cover classes.
- The AMEE-PPI algorithm offers a more robust and accurate approach for endmember extraction in hyperspectral imagery, which is crucial for improving the quality of spectral unmixing, material classification, and object detection in remote sensing applications.
- By accurately identifying typical outcrop endmembers, the proposed method provides valuable spectral references for geological mapping, mineral exploration, and environmental monitoring, particularly in regions with complex surface compositions.
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Dataset Description and Data Processing
2.2.1. GF-5 Outcrop Data and Preprocessing
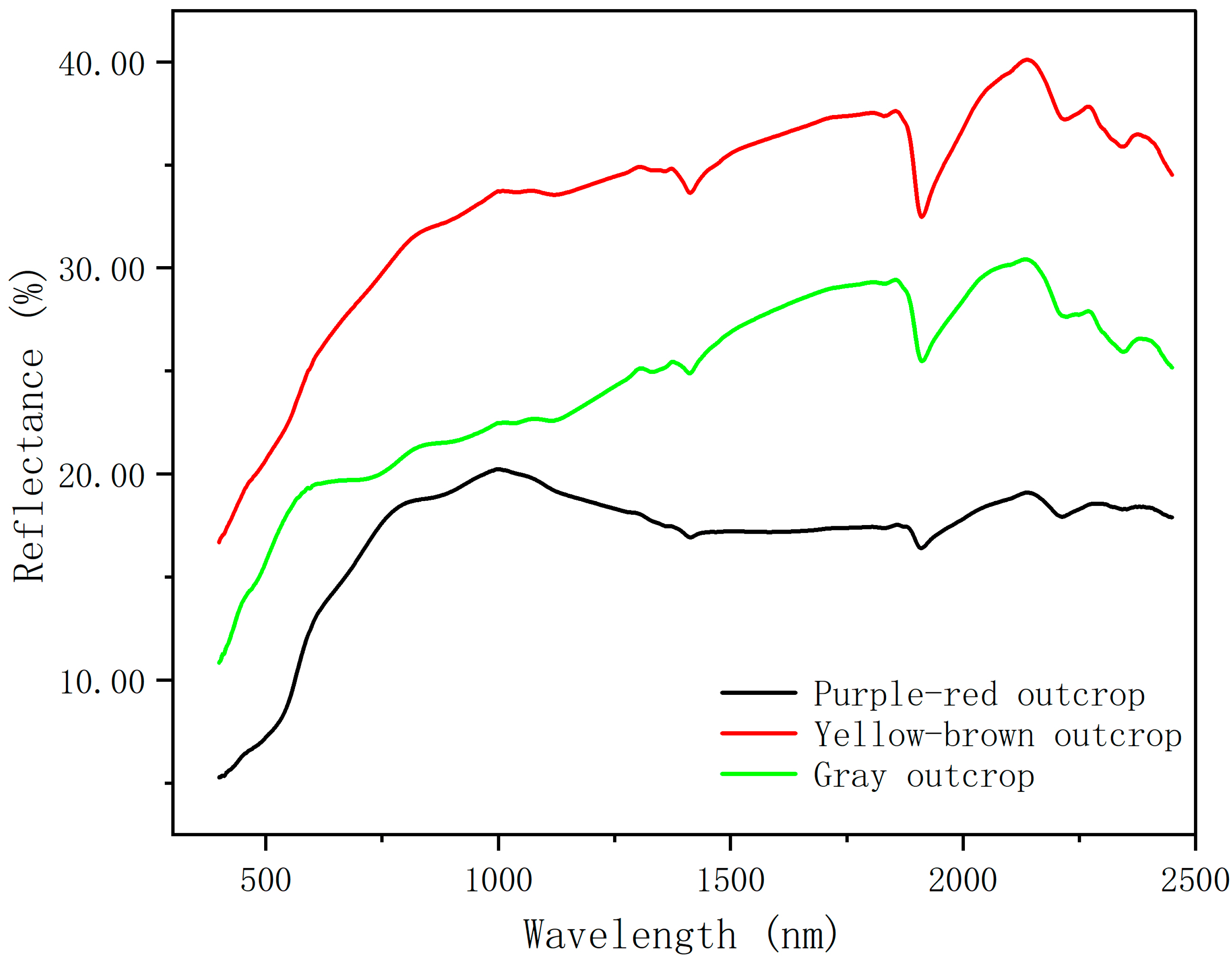
2.2.2. Standard Spectral Data of Ground Measurement
2.3. Methodology
2.3.1. Endmember Extraction Comparison Algorithms
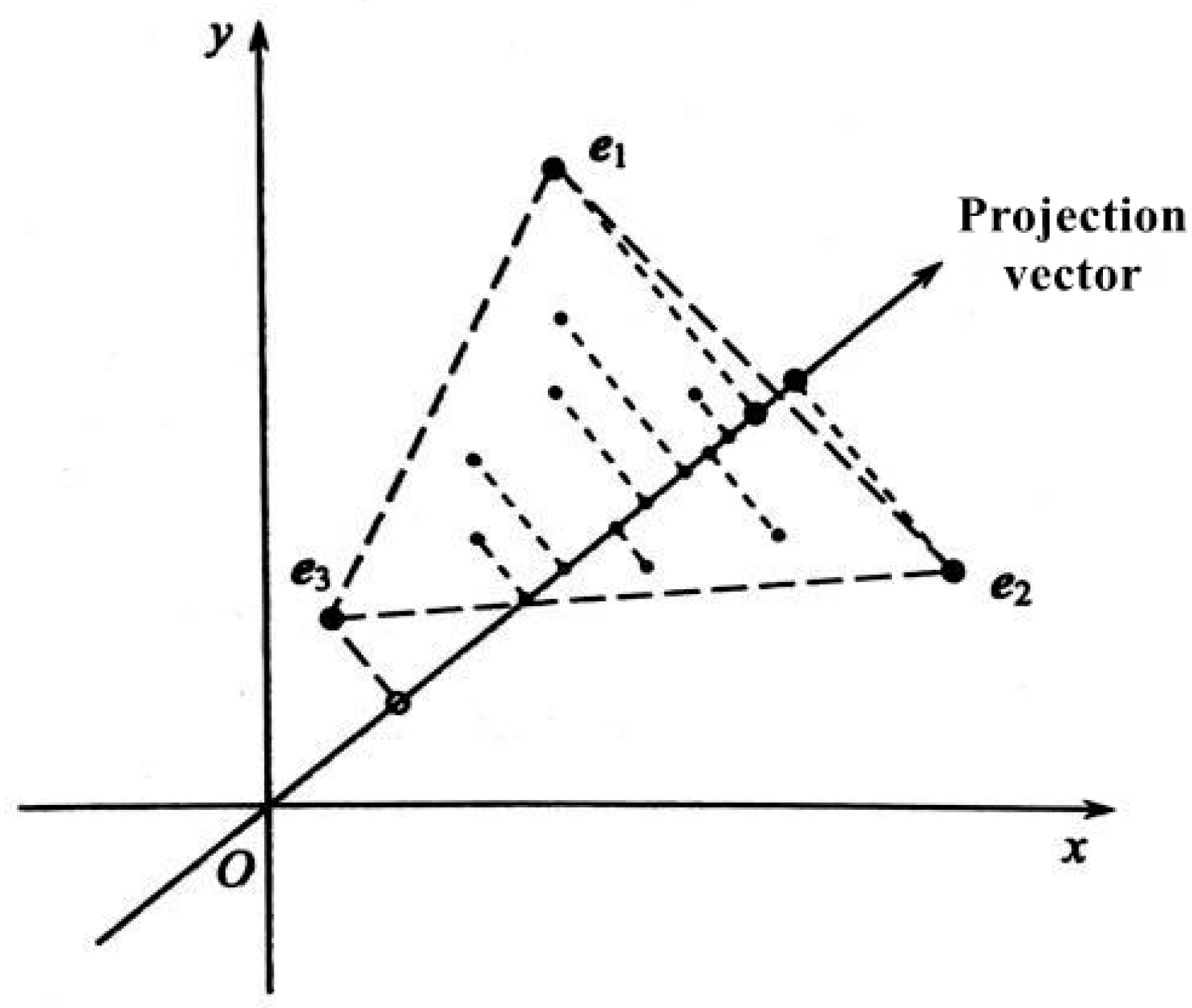
PPI
OSP
VCA
AMEE
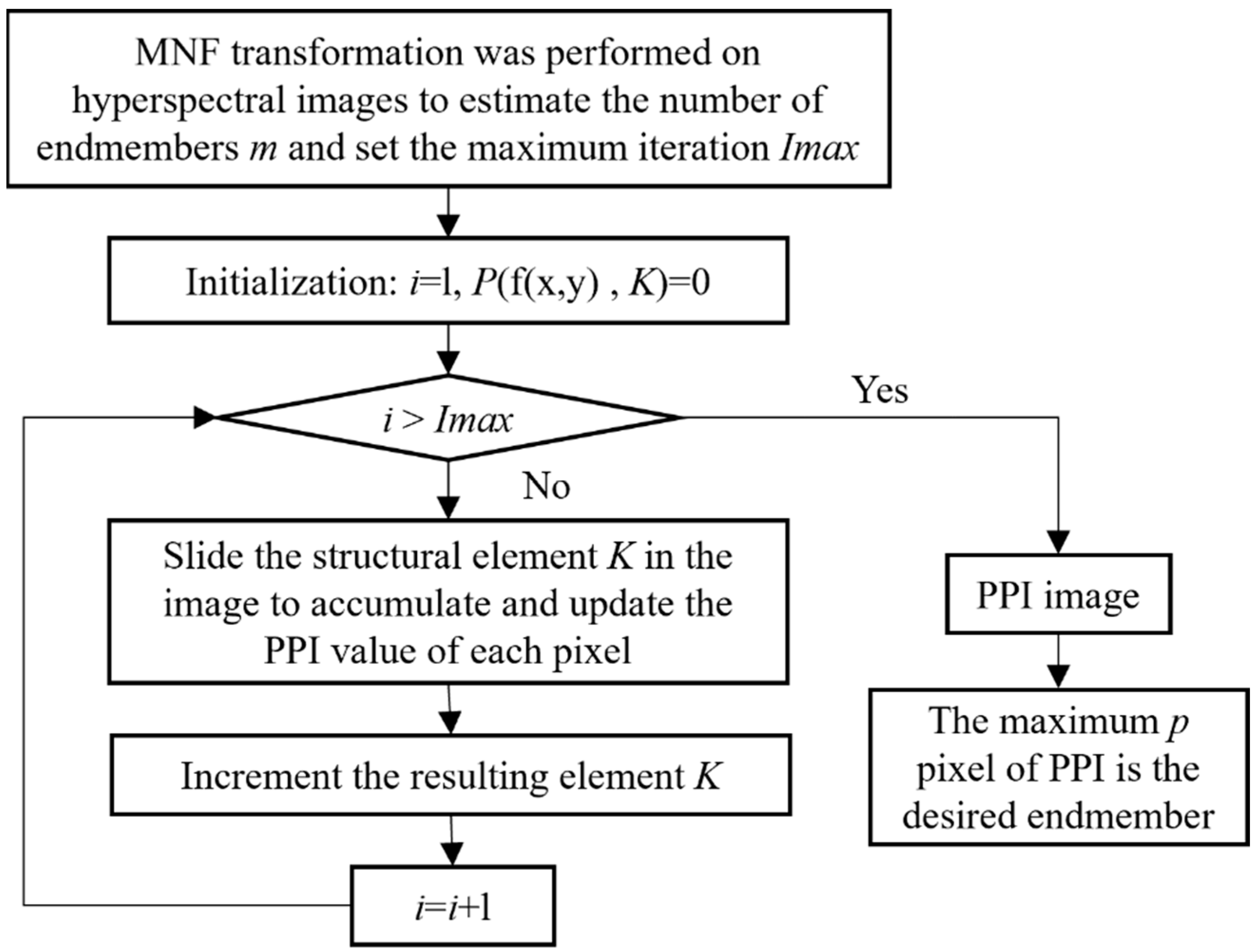
AMEE-PPI Algorithm
- (1)
- The image reduction and denoising process is realized by applying the minimum noise separation transformation to the whole image and estimating the number of end elements m.
- (2)
- The minimum size K_min and maximum size K_max of the structural elements are set to derive the maximum number of iterations I_max.
- (3)
- Make i = 1, the initial PPI value for all image elements P(f(x,y), K) = 0, and start the execution from the smallest structure element K_min.
- (4)
- Expansion according to the morphological structure operator defined by the PPI algorithm expansion to obtain the purity index of each image element within the structure element.
- (5)
- i = i + 1. If i = I_max, sequentially execute step (6); otherwise, increase the structure element K and return to step (4).
- (6)
- The PPI image is output concerning m image elements with larger PPI values identified as end elements.
2.4. Evaluation Index of Experimental Results
3. Results
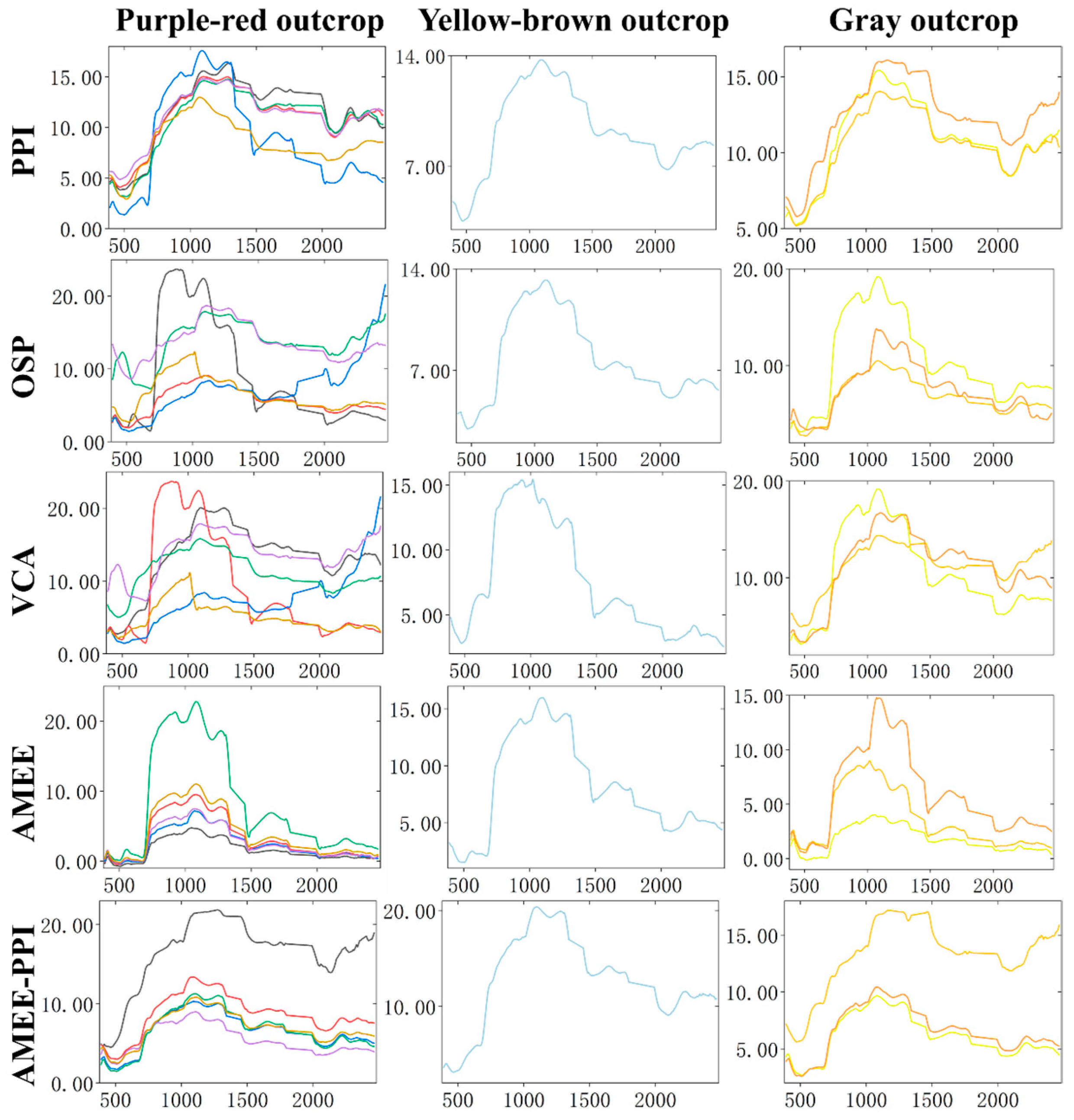
3.1. Evaluation of Endmember Extraction Algorithms for Hyperspectral Images
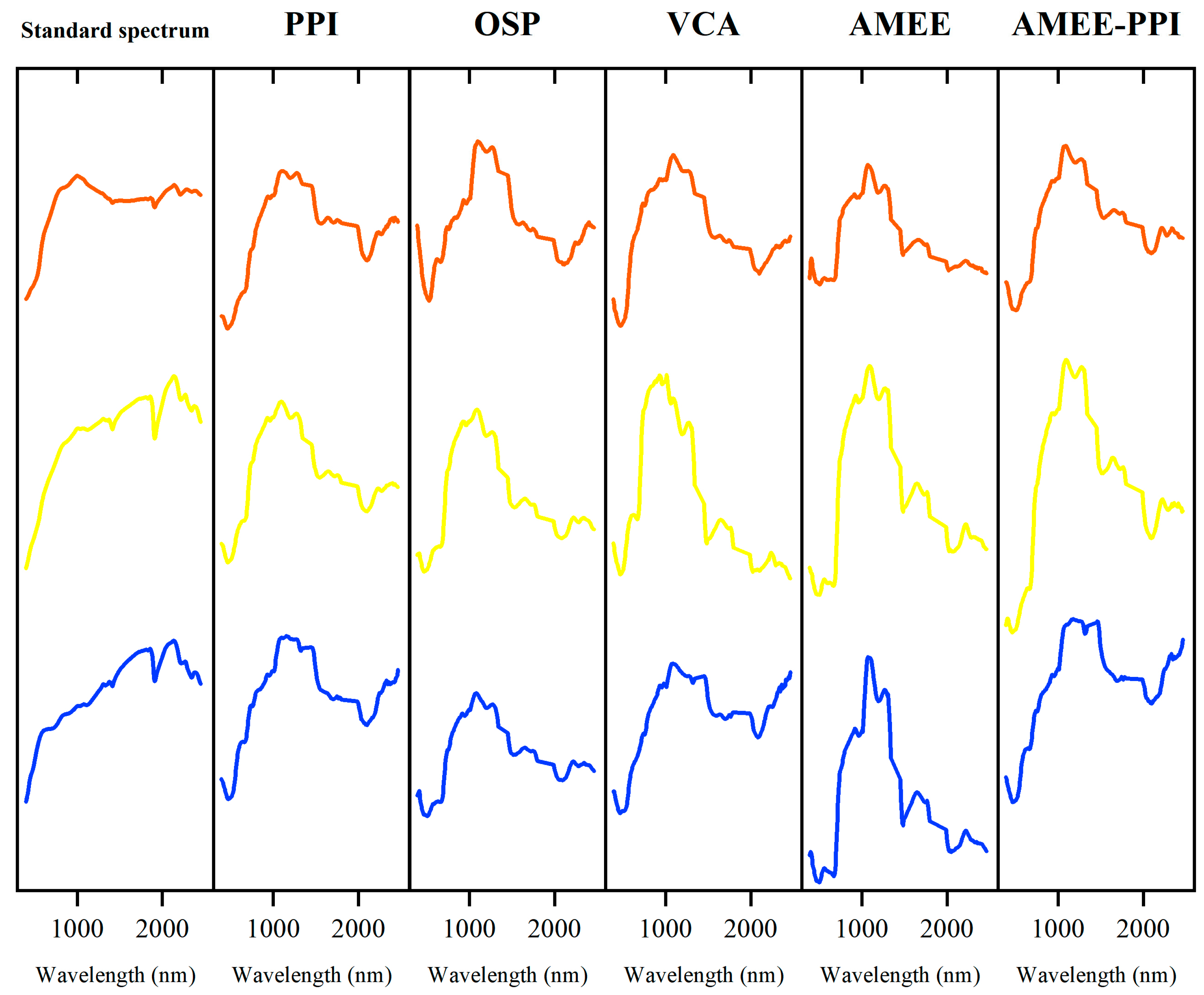
3.2. Comparative Analysis of Outcrop Endmember and Original Hyperspectral
4. Discussion
4.1. Comparison with Classical Algorithms and Method Characteristics
4.2. Robustness Analysis and Future Work
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khan, M.J.; Khan, H.S.; Yousaf, A.; Khurshid, K.; Abbas, A. Modern Trends in Hyperspectral Image Analysis: A Review. IEEE Access 2018, 6, 14118–14129. [Google Scholar] [CrossRef]
- Ye, C.; Liu, S.; Xu, M.; Du, B.; Wan, J.; Sheng, H. An endmember bundle extraction method based on multiscale sampling to address spectral variability for hyperspectral unmixing. Remote Sens. 2021, 13, 3941. [Google Scholar] [CrossRef]
- Ma, Y.; Wu, H.; Wang, L.; Huang, B.; Ranjan, R.; Zomaya, A.; Jie, W. Remote sensing big data computing: Challenges and opportunities. Future Gener. Comput. Syst. 2015, 51, 47–60. [Google Scholar] [CrossRef]
- Chen, Q.; Ding, W.; Huang, X.; Wang, H. Generalized interval type-II fuzzy rough model-based feature discretization for mixed pixels. IEEE Trans. Fuzzy Syst. 2022, 31, 845–859. [Google Scholar] [CrossRef]
- Zhang, B.; Sun, X.; Gao, L.; Yang, L. Endmember extraction of hyperspectral remote sensing images based on the ant colony optimization (ACO) algorithm. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2635–2646. [Google Scholar] [CrossRef]
- Wang, J.; Wang, D.; Huang, T.; Huang, J.; Zhao, X.; Deng, L. Endmember independence constrained hyperspectral unmixing via nonnegative tensor factorization. Knowl.-Based Syst. 2021, 216, 106657. [Google Scholar] [CrossRef]
- Beibei, N. Research on Endmember Extraction Algorithm and Application of Hyperspectral Remote Sensing Image. Master’s Thesis, Dept. Geomatics Engineering, Central South University, Changsha, China, 2014. (In Chinese). [Google Scholar]
- Bowles, J.H.; Palmadesso, P.J.; Antoniades, J.A.; Baumback, M.M.; Rickard, L.J. Use of filter vectors in hyperspectral data analysis. In Infrared Spaceborne Remote Sensing III; SPIE: Bellingham, WA, USA, 1995; pp. 148–157. [Google Scholar]
- Theiler, J.P.; Lavenier, D.D.; Harvey, N.R.; Perkins, S.J.; Szymanski, J.J. Using blocks of skewers for faster computation of pixel purity index. In Imaging Spectrometry VI; SPIE: Bellingham, WA, USA, 2000; pp. 61–71. [Google Scholar]
- Winter, M.E. N-FINDR: An algorithm for fast autonomous spectral end-member determination in hyperspectral data. In Imaging Spectrometry V; SPIE: Bellingham, WA, USA, 1999; pp. 266–275. [Google Scholar]
- Nascimento, J.M.; Dias, J.M. Vertex component analysis: A fast algorithm to unmix hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 898–910. [Google Scholar] [CrossRef]
- Gruninger, J.H.; Ratkowski, A.J.; Hoke, M.L. The sequential maximum angle convex cone (SMACC) endmember model. In Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery X; SPIE: Bellingham, WA, USA, 2004; pp. 1–14. [Google Scholar]
- Plaza, A.; Martinez, P.; Pιrez, R.; Plaza, J. Spatial/spectral endmember extraction by multidimensional morphological operations. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2025–2041. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, J. A new maximum simplex volume method based on householder transformation for endmember extraction. IEEE Trans. Geosci. Remote Sens. 2011, 50, 104–118. [Google Scholar] [CrossRef]
- Nouri, T.; Oskouei, M.M.; Zekri, H. A comparison study of ORASIS and VCA for mineralogical unmixing of hyperspectral data. J. Indian Soc. Remote Sens. 2016, 44, 723–733. [Google Scholar] [CrossRef]
- Liu, H.; Lu, Y.; Wu, Z.; Du, Q.; Chanussot, J.; Wei, Z. Bayesian unmixing of hyperspectral image sequence with composite priors for abundance and endmember variability. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–15. [Google Scholar] [CrossRef]
- Ozkan, S.; Kaya, B.; Akar, G.B. EndNet: Sparse AutoEncoder Network for Endmember Extraction and Hyperspectral Unmixing. IEEE Trans. Geosci. Remote Sens. 2019, 57, 482–496. [Google Scholar] [CrossRef]
- Shah, D.; Zaveri, T. A Novel Geo-Stat Endmember Extraction Algorithm. In Proceedings of the 2019 IEEE Region 10 Conference (TENCON), Kochi, India, 17–20 October 2019; pp. 2685–2689. [Google Scholar]
- Hong, D.; Gao, L.; Yao, J.; Yokoya, N.; Chanussot, J.; Heiden, U.; Zhang, B. Endmember-Guided Unmixing Network (EGU-Net): A General Deep Learning Framework for Self-Supervised Hyperspectral Unmixing. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 6518–6531. [Google Scholar] [CrossRef]
- Li, C.; Zhang, B.; Hong, D.; Jia, X.; Plaza, A.; Chanussot, J. Learning Disentangled Priors for Hyperspectral Anomaly Detection: A Coupling Model-Driven and Data-Driven Paradigm. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 6883–6896. [Google Scholar] [CrossRef] [PubMed]
- Wenli, Z.; Shengqiang, L. Ore Recognition and Mining Technology at Chengui Mine in Hunan in the Qing Dynasty. J. Guangxi Univ. Natl. (Nat. Sci. Ed.) 2021, 27, 3–05. (In Chinese) [Google Scholar]
- Jie, C.; Lei, D.U.; Jing, L.I.; Yachao, H.; Zihong, G. Improved algorithm for hyperspectral data dimension determination. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2017; p. 012044. [Google Scholar]
- Gonzalez, C.; Lopez, S.; Mozos, D.; Sarmiento, R. FPGA implementation of the HySime algorithm for the determination of the number of endmembers in hyperspectral data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2870–2883. [Google Scholar] [CrossRef]
- Wang, R.L. Study on Geoheritage Investigation and Development Model of Lufeng Dinosaur National Geopark, Yunan. Master’s Thesis, China University of Geosciences, Beijing, China, 2015. [Google Scholar]
- Ren, K.; Sun, W.; Meng, X.; Yang, G.; Du, Q. Fusing china gf-5 hyperspectral data with gf-1, gf-2 and sentinel-2a multispectral data: Which methods should be used? Remote Sens. 2020, 12, 882. [Google Scholar] [CrossRef]
- Wan, L.; Lin, Y.; Zhang, H.; Wang, F.; Liu, M.; Lin, H. GF-5 hyperspectral data for species mapping of mangrove in Mai Po, Hong Kong. Remote Sens. 2020, 12, 656. [Google Scholar] [CrossRef]
- Shen, X.; Bao, W.; Qu, K. Spatial-Spectral Hyperspectral Endmember Extraction Using a Spatial Energy Prior Constrained Maximum Simplex Volume Approach. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1347–1361. [Google Scholar] [CrossRef]
- Lin, H. Hyperspectral Detection and Spatial Inversion of Surface Outcrop Features in the Dinosaur Valley Ring Structure. Doctoral Thesis, Kunming University of Science and Technology, Kunming, China, 2023. (In Chinese). [Google Scholar]
- Jun, X.U.; Cailing, W.; Li, W. An improved endmember extraction method of mathematical morphology based on PPI algorithm. Acta Geod. et Cartogr. Sin. 2019, 48, 996. [Google Scholar]
- Li, Y.; Ye, C.; Ge, Y.; Junior, J.M.; Gonηalvese, W.N.; Li, J. Identifying building rooftops in hyperspectral imagery using CNN with pure pixel index. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 12022–12034. [Google Scholar] [CrossRef]
- Liang, Y.J.; Jian, J. Classification of Hyperspectral Images Based on Segmented Principal Components and PPI. Remote Sens. Inf. 2020, 35, 129–134. (In Chinese) [Google Scholar]
- Song, M.P.; Xu, X.W.; Chang, C.I.; An, J.B.; Yao, L. Orthogonal Vector Projection Algorithm for Spectral Unmixing. Spectrosc. Spectr. Anal. 2015, 35, 3465–3470. [Google Scholar]
- Li, H.; Chang, C.; Song, M. Recursive band processing of orthogonal subspace projection for hyperspectral imagery. IEEE Geosci. Remote Sens. Lett. 2015, 13, 3–7. [Google Scholar] [CrossRef]
- Chang, C.; Chen, S.; Li, H.; Chen, H.; Wen, C. Comparative study and analysis among ATGP, VCA, and SGA for finding endmembers in hyperspectral imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4280–4306. [Google Scholar] [CrossRef]
- Lu, X.; Wu, H.; Yuan, Y.; Yan, P.; Li, X. Manifold regularized sparse NMF for hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 2012, 51, 2815–2826. [Google Scholar] [CrossRef]
- Heylen, R.; Parente, M.; Gader, P. A review of nonlinear hyperspectral unmixing methods. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1844–1868. [Google Scholar] [CrossRef]
- Zortea, M.; Plaza, A. Spatial preprocessing for endmember extraction. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2679–2693. [Google Scholar] [CrossRef]
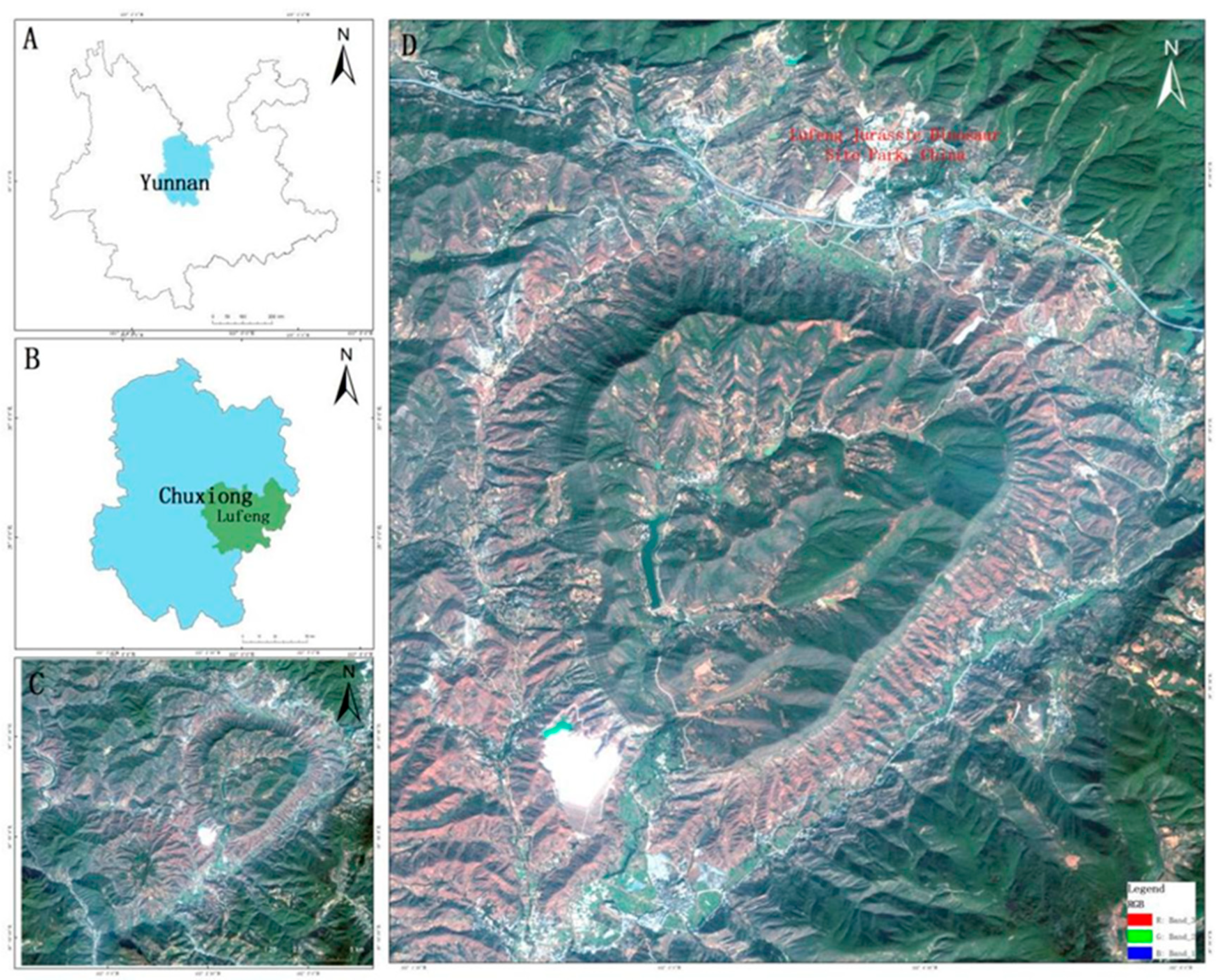
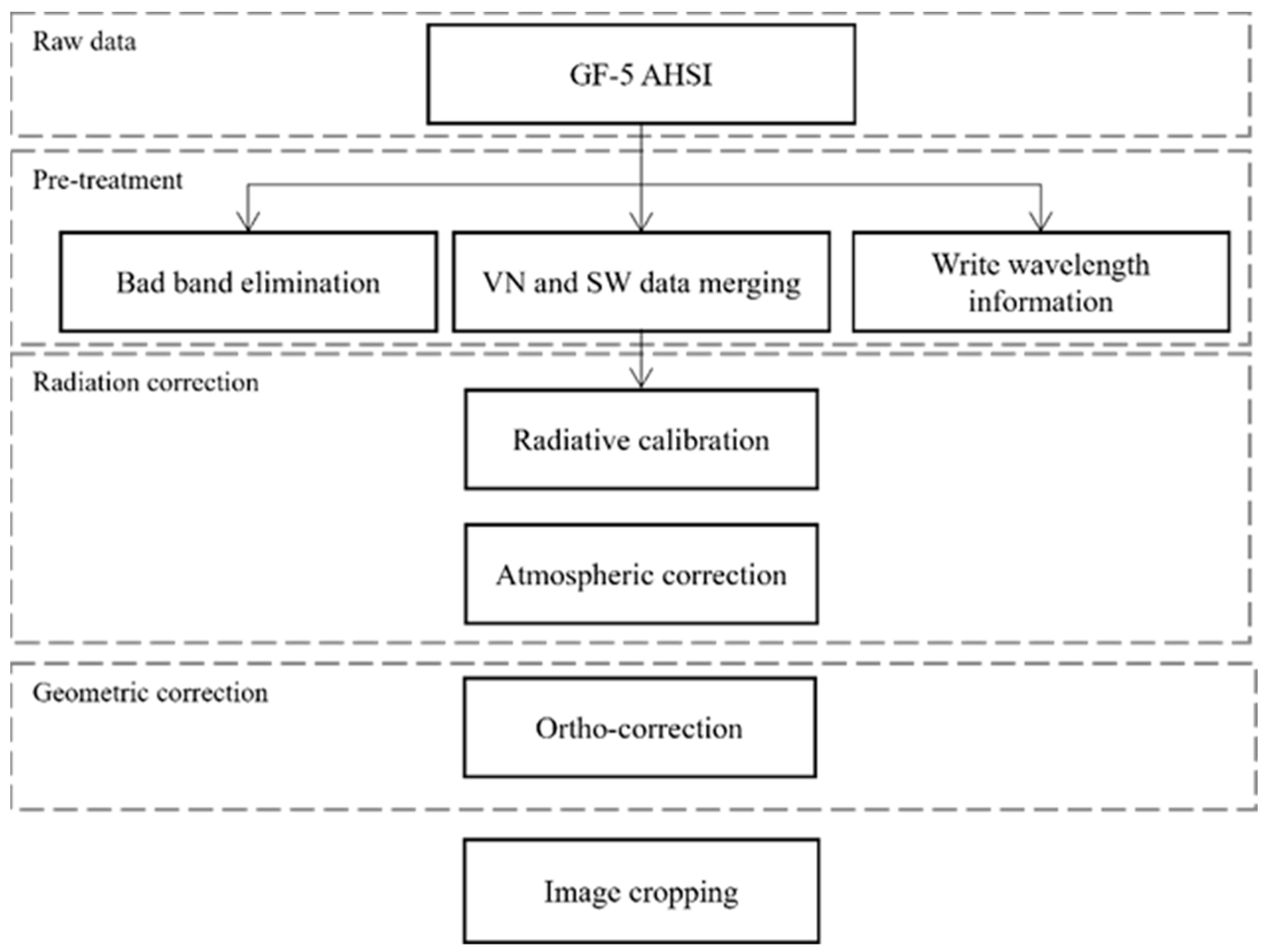

| Spectral Range/nm | Spatial Resolution/m | Width/km | Spectral Resolution/nm | Number of Bands | Average Orbital Height/km |
| 400~2500 | 30 | 60 | VNIR:5; SWIR:10 | 330 | 705 |
| Outcrop | PPI | OSP | VCA | AMEE | AMEE-PPI |
|---|---|---|---|---|---|
| Purple–red outcrop | 0.136 | 0.188 | 0.158 | 0.608 | 0.135 |
| Yellow–brown outcrop | 0.366 | 0.356 | 0.520 | 0.482 | 0.316 |
| Gray outcrop | 0.204 | 0.330 | 0.202 | 0.610 | 0.191 |
| Outcrop | PPI | OSP | VCA | AMEE | AMEE-PPI |
|---|---|---|---|---|---|
| Purple–red outcrop | 0.030 | 0.066 | 0.040 | 1.002 | 0.028 |
| Yellow–brown outcrop | 0.195 | 0.197 | 0.486 | 0.461 | 0.184 |
| Gray outcrop | 0.060 | 0.168 | 0.062 | 0.788 | 0.055 |
| Original Hyperspectral | Outcrop Endmember | |||
|---|---|---|---|---|
| SAD/Rad | SID/Bit | SAD/Rad | SID/Bit | |
| Purple–red outcrop | 0.211 | 0.096 | 0.135 | 0.028 |
| Yellow–brown outcrop | 0.355 | 0.199 | 0.316 | 0.184 |
| Gray outcrop | 0.257 | 0.095 | 0.191 | 0.055 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, L.; Hu, J.; Gan, S.; Yuan, X.; Lu, Y.; Zhao, H.; Han, G. The AMEE-PPI Method to Extract Typical Outcrop Endmembers from GF-5 Hyperspectral Images. Sensors 2025, 25, 6143. https://doi.org/10.3390/s25196143
Hu L, Hu J, Gan S, Yuan X, Lu Y, Zhao H, Han G. The AMEE-PPI Method to Extract Typical Outcrop Endmembers from GF-5 Hyperspectral Images. Sensors. 2025; 25(19):6143. https://doi.org/10.3390/s25196143
Chicago/Turabian StyleHu, Lin, Jiankai Hu, Shu Gan, Xiping Yuan, Yu Lu, Hailong Zhao, and Guang Han. 2025. "The AMEE-PPI Method to Extract Typical Outcrop Endmembers from GF-5 Hyperspectral Images" Sensors 25, no. 19: 6143. https://doi.org/10.3390/s25196143
APA StyleHu, L., Hu, J., Gan, S., Yuan, X., Lu, Y., Zhao, H., & Han, G. (2025). The AMEE-PPI Method to Extract Typical Outcrop Endmembers from GF-5 Hyperspectral Images. Sensors, 25(19), 6143. https://doi.org/10.3390/s25196143








