Deep Learning-Based Approach for Automatic Defect Detection in Complex Structures Using PAUT Data
Abstract
1. Introduction
- The development and validation of an automated, parameter-free SNR algorithm for rapid defect indication.
- A comparative analysis of three distinct deep learning architectures (FCN, CNN, and CATT-S) on a diverse PAUT dataset.
- The proposal of a novel CATT-S model that effectively combines local feature extraction with global context modeling through self-attention, achieving state-of-the-art performance in complex PAUT data analysis.
- The use of a combined simulated and large-scale experimental dataset to demonstrate the practical viability and generalizability of the proposed methods.
2. Materials and Methods
2.1. Dataset Collection and Processing
2.2. Enhanced SNR-Based Method
- Constructing depth scans (D-scans), which involves applying max-projection across the beams.
- Collapsing the D-scan into a single depth-accumulated signal by averaging along the scanning axis.
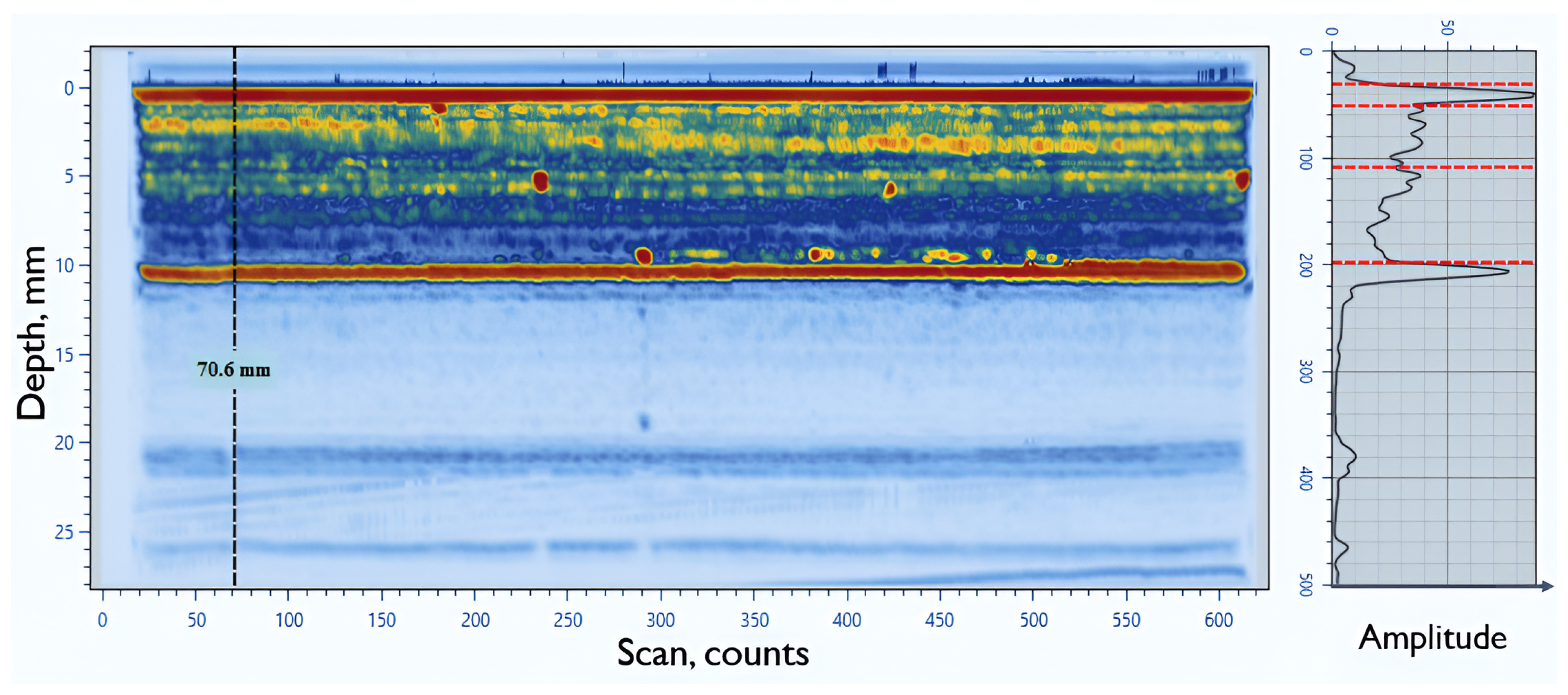
- Performing derivative analysis to automatically locate acoustic interfaces.
2.3. Deep Learning Models
3. SNR-Based Automatic Defect Detection
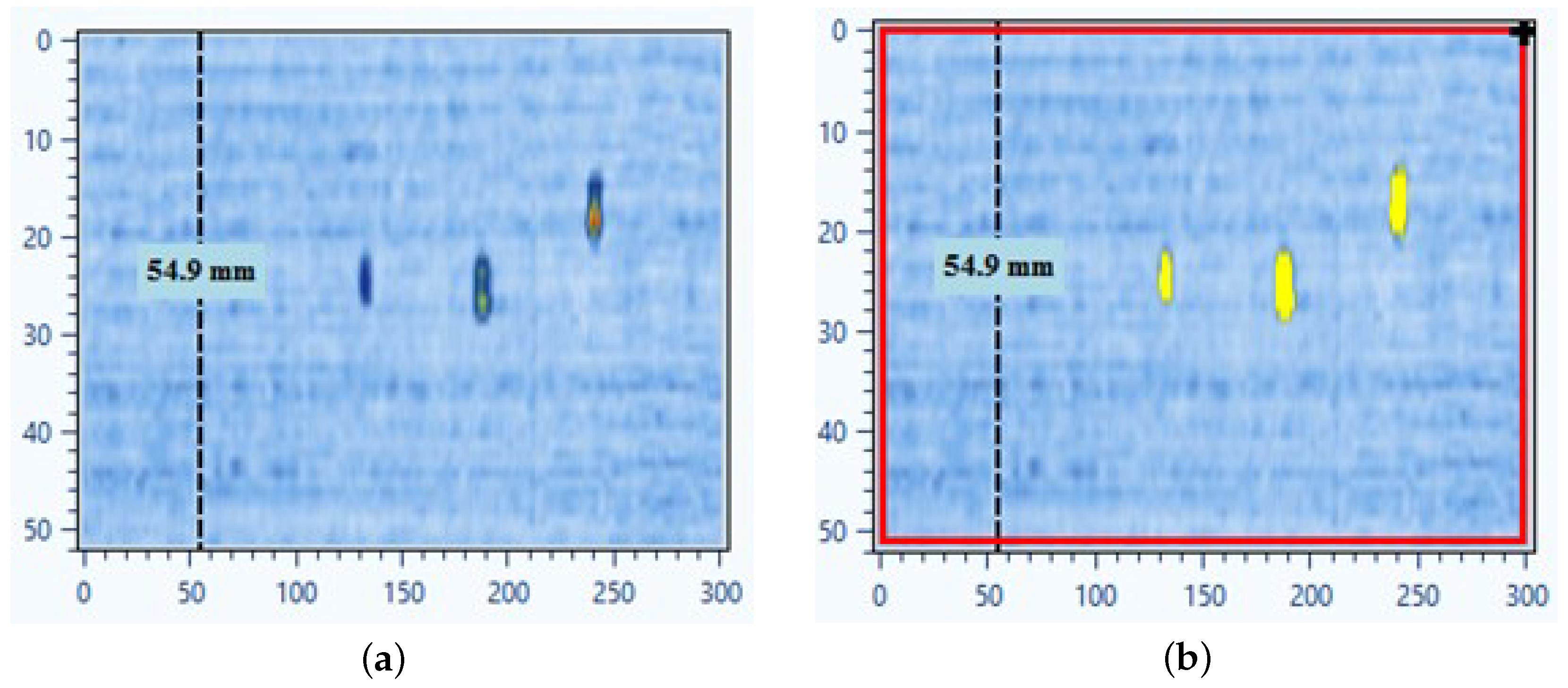
3.1. Automatic Depth-Gate Detection
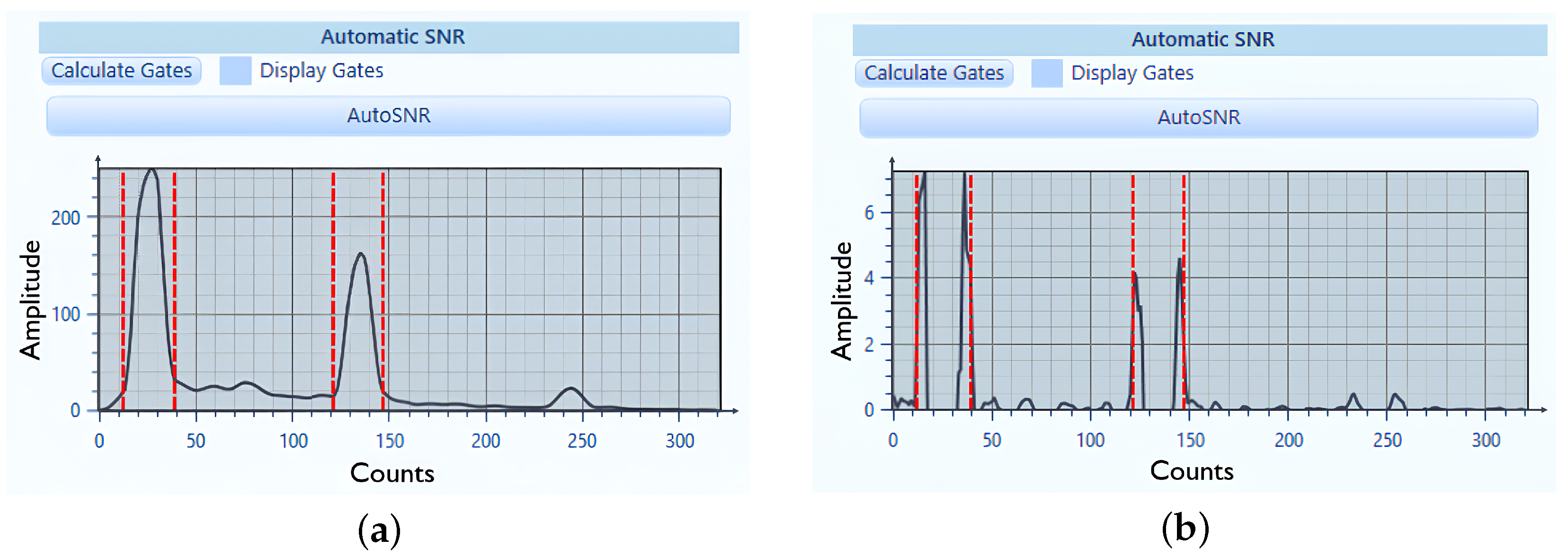
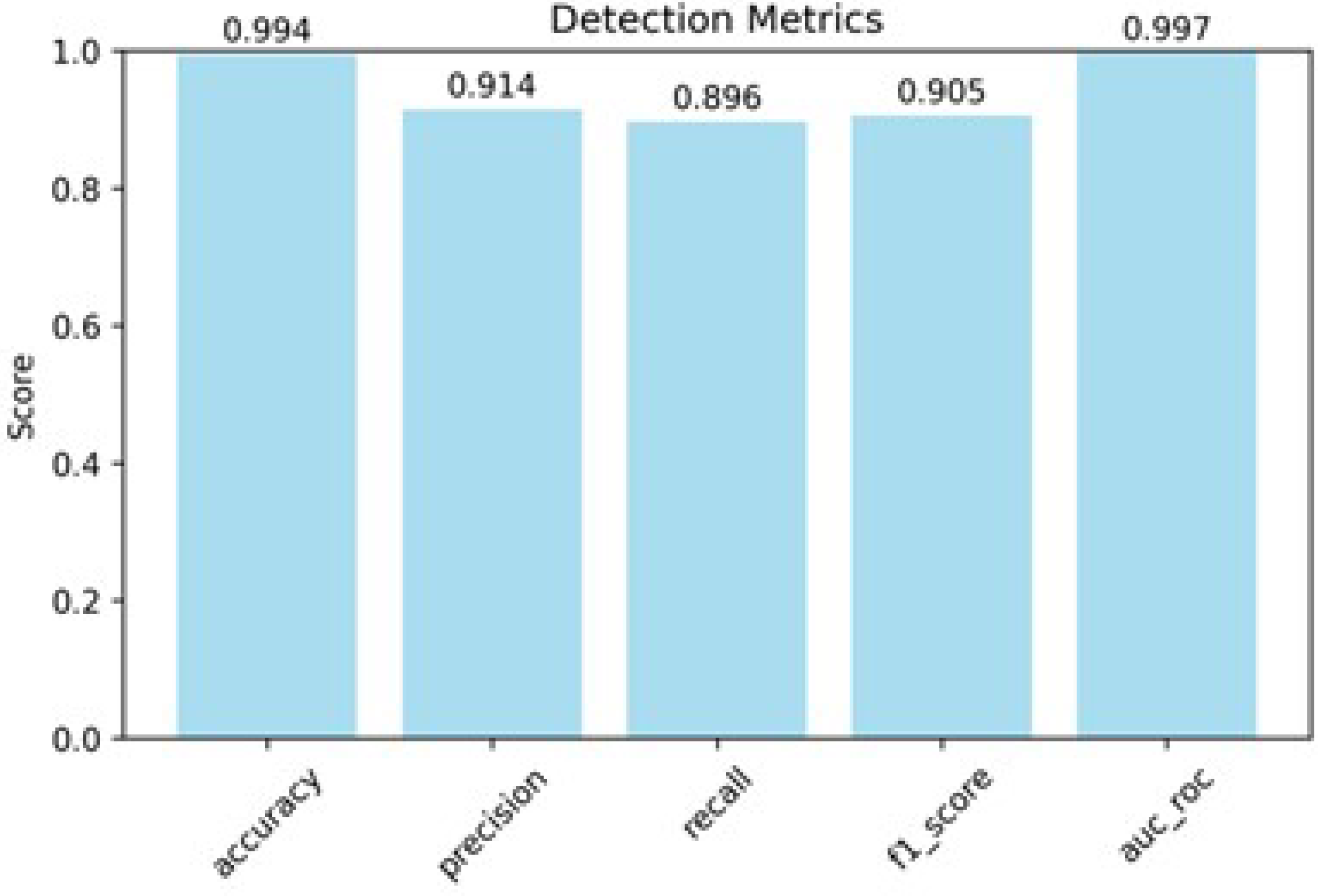
3.2. Signal-to-Noise–Based Defect Characterization
4. Deep Learning Architectures for Defect Detection
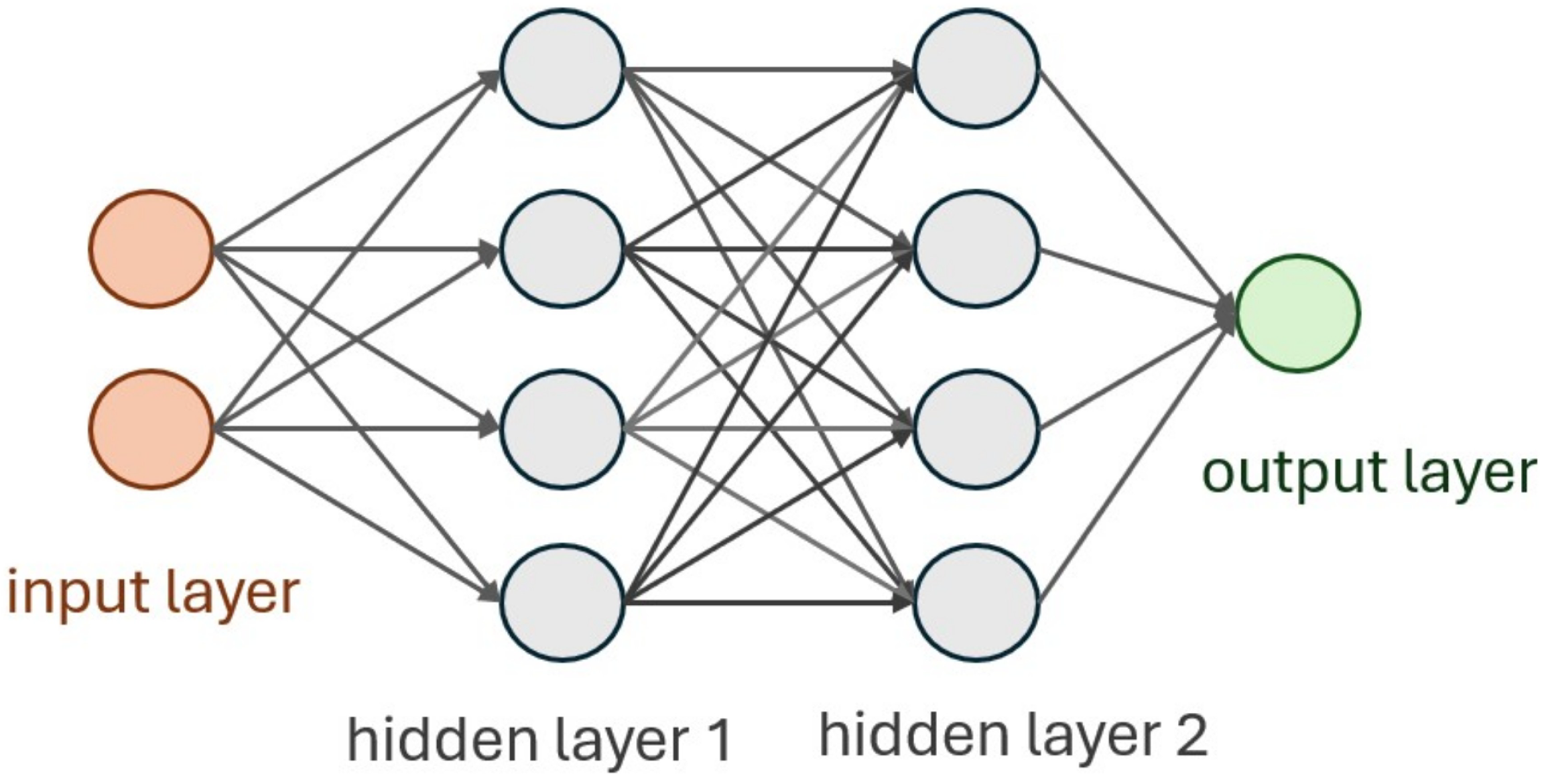
4.1. Fully Connected Neural Network
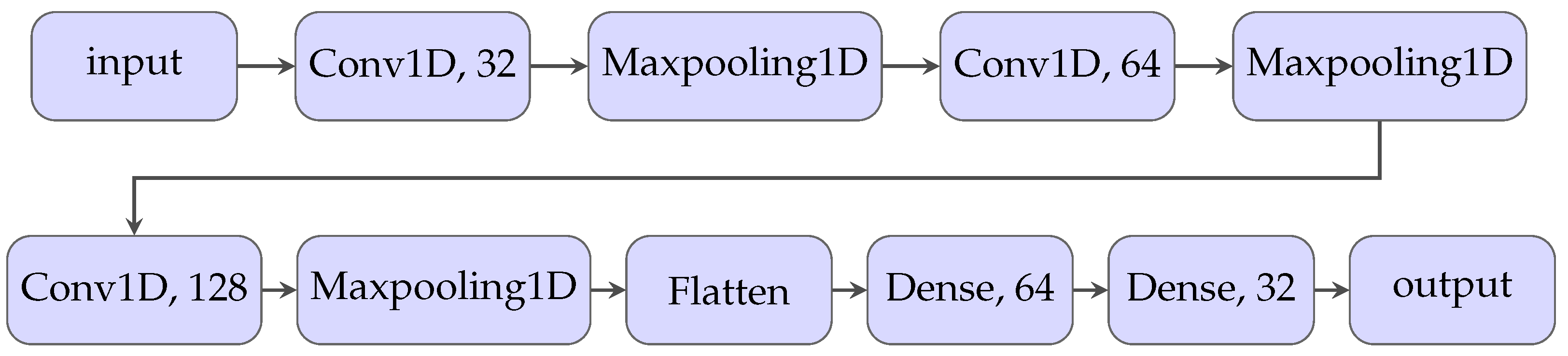
4.2. Convolutional 1D Neural Network
4.3. Transformer-Based Neural Network
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Raj, B.; Jayakumar, T.; Rao, B.P.C. Non-destructive testing and evaluation for structural integrity. Sadhana 1995, 20, 5–38. [Google Scholar] [CrossRef]
- Ondrejka, V.; Gergeľ, T.; Bucha, T.; Pástor, M. Innovative methods of non-destructive evaluation of log quality. Cent. Eur. For. J. 2021, 67, 3–13. [Google Scholar] [CrossRef]
- Boccardi, S.; Boffa, N.D.; Carlomagno, G.M.; Maio, L.; Meola, C.; Ricci, F. Infrared thermography and ultrasonics to evaluate composite materials for aeronautical applications. J. Phys. Conf. Ser. 2015, 658, 012007. [Google Scholar] [CrossRef]
- Garnier, C.; Pastor, M.L.; Eyma, F.; Lorrain, B. The detection of aeronautical defects in situ on composite structures using Non Destructive Testing. Compos. Struct. 2011, 93, 1328–1336. [Google Scholar] [CrossRef]
- Katnam, K.B.; Da Silva, L.F.M.; Young, T.M. Bonded repair of composite aircraft structures: A review of scientific challenges and opportunities. Prog. Aerosp. Sci. 2013, 61, 26–42. [Google Scholar] [CrossRef]
- Drewry, M.A.; Georgiou, G.A. A review of NDT techniques for wind turbines. Insight-Non Test. Cond. Monit. 2007, 49, 137–141. [Google Scholar] [CrossRef]
- Ciang, C.C.; Lee, J.R.; Bang, H.J. Structural health monitoring for a wind turbine system: A review of damage detection methods. Meas. Sci. Technol. 2008, 19, 122001. [Google Scholar] [CrossRef]
- Raišutis, R.; Jasiūnienė, E.; Šliteris, R.; Vladišauskas, A. The review of non-destructive testing techniques suitable for inspection of the wind turbine blades. Ultragarsas-Ultrasound 2008, 63, 26–30. [Google Scholar]
- Galappaththi, U.I.K.; De Silva, A.K.M.; Macdonald, M.; Adewale, O.R. Review of inspection and quality control techniques for composite wind turbine blades. Insight-Non Test. Cond. Monit. 2012, 54, 82–85. [Google Scholar] [CrossRef]
- Greene, E. Marine composites non-destructive evaluation. Ship Struct. 2014, 1, 416–427. [Google Scholar]
- Soutis, C. Fibre reinforced composites in aircraft construction. Prog. Aerosp. Sci. 2005, 41, 143–151. [Google Scholar] [CrossRef]
- Dwivedi, S.K.; Vishwakarma, M.; Soni, A. Advances and researches on non destructive testing: A review. Mater. Today Proc. 2018, 5, 3690–3698. [Google Scholar] [CrossRef]
- Li, W.; Zhou, Z.; Li, Y. Inspection of butt welds for complex surface parts using ultrasonic phased array. Ultrasonics 2019, 96, 75–82. [Google Scholar] [CrossRef] [PubMed]
- Bai, Z.; Chen, S.; Jia, L.; Zeng, Z. Phased array ultrasonic signal compressive detection in low-pressure turbine disc. NDT E Int. 2017, 89, 1–13. [Google Scholar] [CrossRef]
- Yang, S.; Yoon, B.; Kim, Y. Using phased array ultrasonic technique for the inspection of straddle mount-type low-pressure turbine disc. NDT E Int. 2009, 42, 128–132. [Google Scholar] [CrossRef]
- Aulin, A.; Shahzad, K.; MacKenzie, R.; Bott, S. Comparison of non-destructive examination techniques for crack inspection. In Proceedings of the International Pipeline Conference, Calgary, AB, Canada, 28 September–2 October 2020; American Society of Mechanical Engineers: New York, NY, USA, 2020; Volume 84447, p. V001T03A044. [Google Scholar]
- Xu, Q.; Wang, H. Sound field modeling method and key imaging technology of an ultrasonic phased array: A review. Appl. Sci. 2022, 12, 7962. [Google Scholar] [CrossRef]
- Shi, H.; Ebrahimi, M.; Zhou, P.; Shao, K.; Li, J. Ultrasonic and phased-array inspection in titanium-based alloys: A review. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2023, 237, 511–530. [Google Scholar] [CrossRef]
- Liu, W.; Wen, Z.; Wang, J.; Wang, S.; Wang, H.; Zhang, W.; Hong, J. Experimental Study on Lateral Resolution of Phased Array Ultrasonic Testing of Irregular Structure Weld Defects. Shock Vib. 2022, 2022, 1427417. [Google Scholar] [CrossRef]
- Szávai, S.; Bézi, Z.; Dudra, J.; Méhész, I. Modelling of phased array ultrasonic inspection of a steam generator dissimilar metal weld. Procedia Struct. Integr. 2016, 2, 1015–1022. [Google Scholar] [CrossRef]
- Kumar, S.; Menaka, M.; Venkatraman, B. Phased array ultrasonic inspection of dissimilar weld joints in nuclear facility by experiment and simulation. In Proceedings of the NDE India Conference, Bengaluru, India, 5–7 December 2019. [Google Scholar]
- Si, J.; Wei, D.; Yang, Y.; Tang, X. CIVA Simulation and Experiment Verification for Thin-Walled Small-Diameter Pipes by Using Phased Array Ultrasonic Testing. In Proceedings of the ASME Pressure Vessels and Piping Conference, Minneapolis, MN, USA, 19–24 July 2020; American Society of Mechanical Engineers: New York, NY, USA, 2020; Volume 83815, p. V001T01A080. [Google Scholar]
- Zhang, X.; Feng, N.; Wang, Y.; Shen, Y. Acoustic emission detection of rail defect based on wavelet transform and Shannon entropy. J. Sound Vib. 2015, 339, 419–432. [Google Scholar] [CrossRef]
- Hao, Q.; Zhang, X.; Wang, Y.; Shen, Y.; Makis, V. A novel rail defect detection method based on undecimated lifting wavelet packet transform and Shannon entropy-improved adaptive line enhancer. J. Sound Vib. 2018, 425, 208–220. [Google Scholar] [CrossRef]
- Yaacoubi, S.; Montresor, S.; Bentahar, M. A model-based approach for in-situ automatic defect detection in welds using ultrasonic phased array. Expert Syst. Appl. 2022, 206, 117747. [Google Scholar]
- Kadhim, S.J.; Al-Sabur, R.K.; Ali, A.B.K. Application of Different Median Filter Algorithms for Welding Defects Clarification in Radiographic Images. Univ. Thi-Qar J. Eng. Sci. 2020, 11, 56–61. [Google Scholar] [CrossRef]
- Mineo, C.; MacLeod, C.; Morozov, M.; Pierce, S.G.; Summan, R.; Rodden, T.; Kahani, D.; Powell, J.; McCubbin, P.; McCubbin, C.; et al. Flexible integration of robotics, ultrasonics and metrology for the inspection of aerospace components. AIP Conf. Proc. 2017, 1806, 020008. [Google Scholar]
- Bertovic, M.; Virkkunen, I. NDE 4.0: New paradigm for the NDE inspection personnel. In Handbook of Nondestructive Evaluation 4.0; Springer: Cham, Switzerland, 2022; pp. 239–269. [Google Scholar]
- Virkkunen, I.; Koskinen, T.; Jessen-Juhler, O.; Rinta-Aho, J. Augmented ultrasonic data for machine learning. J. Nondestruct. Eval. 2021, 40, 4. [Google Scholar] [CrossRef]
- Siljama, O.; Koskinen, T.; Jessen-Juhler, O.; Virkkunen, I. Automated flaw detection in multi-channel phased array ultrasonic data using machine learning. J. Nondestruct. Eval. 2021, 40, 67. [Google Scholar] [CrossRef]
- Kim, Y.H.; Lee, J.R. Automated data evaluation in phased-array ultrasonic testing based on A-scan and feature training. NDT E Int. 2024, 141, 102974. [Google Scholar] [CrossRef]
- Plastropoulos, A.; Torbali, M.E.; Avdelidis, N.P.; Ibarra-Castanedo, C.; Klein, M.; Maldague, X.P. Advanced NDT inspection approach for aircraft composite panels. In Proceedings of the Thermosense: Thermal Infrared Applications XLVI, Orlando, FL, USA, 15–19 April 2024; SPIE: Bellingham, WA, USA, 2024; Volume 13047, pp. 115–124. [Google Scholar]
- Sudharsan, P.L.; Gantala, T.; Balasubramaniam, K. Multi modal data fusion of PAUT with thermography assisted by Automatic Defect Recognition System (M-ADR) for NDE Applications. NDT E Int. 2024, 143, 103062. [Google Scholar] [CrossRef]
- Tunukovic, V.; McKnight, S.; Mohseni, E.; Pierce, S.G.; Pyle, R.; Duernberger, E.; O’Hare, T. A study of machine learning object detection performance for phased array ultrasonic testing of carbon fibre reinforced plastics. NDT E Int. 2024, 144, 103094. [Google Scholar] [CrossRef]
- Scabini, L.F.; Bruno, O.M. Structure and performance of fully connected neural networks: Emerging complex network properties. Physica A 2023, 615, 128585. [Google Scholar] [CrossRef]
- Salman, S.; Liu, X. Overfitting mechanism and avoidance in deep neural networks. arXiv 2019, arXiv:1901.06566. [Google Scholar] [CrossRef]
- Lin, T.; Horne, B.G.; Giles, C.L. How embedded memory in recurrent neural network architectures helps learning long-term temporal dependencies. Neural Netw. 1998, 11, 861–868. [Google Scholar] [CrossRef]
- Medak, D.; Posilović, L.; Subašić, M.; Budimir, M.; Lončarić, S. Deep learning-based defect detection from sequences of ultrasonic B-scans. IEEE Sens. J. 2021, 22, 2456–2463. [Google Scholar] [CrossRef]
- Sendra, T.; Belanger, P. On the use of a Transformer Neural Network to deconvolve ultrasonic signals. Ultrasonics 2025, 152, 107639. [Google Scholar] [CrossRef] [PubMed]
- Na, Y.; He, Y.; Deng, B.; Lu, X.; Wang, H.; Wang, L.; Cao, Y. Advances of Machine Learning in Phased Array Ultrasonic Non-Destructive Testing: A Review. Artif. Intell. 2025, 6, 124. [Google Scholar] [CrossRef]
- Zhang, Q.; Peng, J.; Tian, K.; Wang, A.; Li, J.; Gao, X. Advancing ultrasonic defect detection in high-speed wheels via UT-YOLO. Sensors 2024, 24, 1555. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, Y. Weld Defect Downscaling Recognition for Phased Array Ultrasonic Data Based on Semantic Segmentation. E-J. Nondestruct. Test. 2024, 29, 29918. [Google Scholar] [CrossRef]
- I, B.; Barashok, K.; Choi, Y.; Choi, Y.; Aslam, M.; Lee, J. Machine learning techniques in ultrasonics-based defect detection and material characterization: A comprehensive review. Adv. Mech. Eng. 2025, 17, 1–41. [Google Scholar] [CrossRef]
- Krautkrämer, J.; Krautkrämer, H. Ultrasonic Testing of Materials, 4th ed.; Springer: Berlin/Heidelberg, Germany, 1990. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. In Advances in Neural Information Processing Systems 30; Curran Associates, Inc.: Red Hook, NY, USA, 2017; pp. 5998–6008. [Google Scholar]

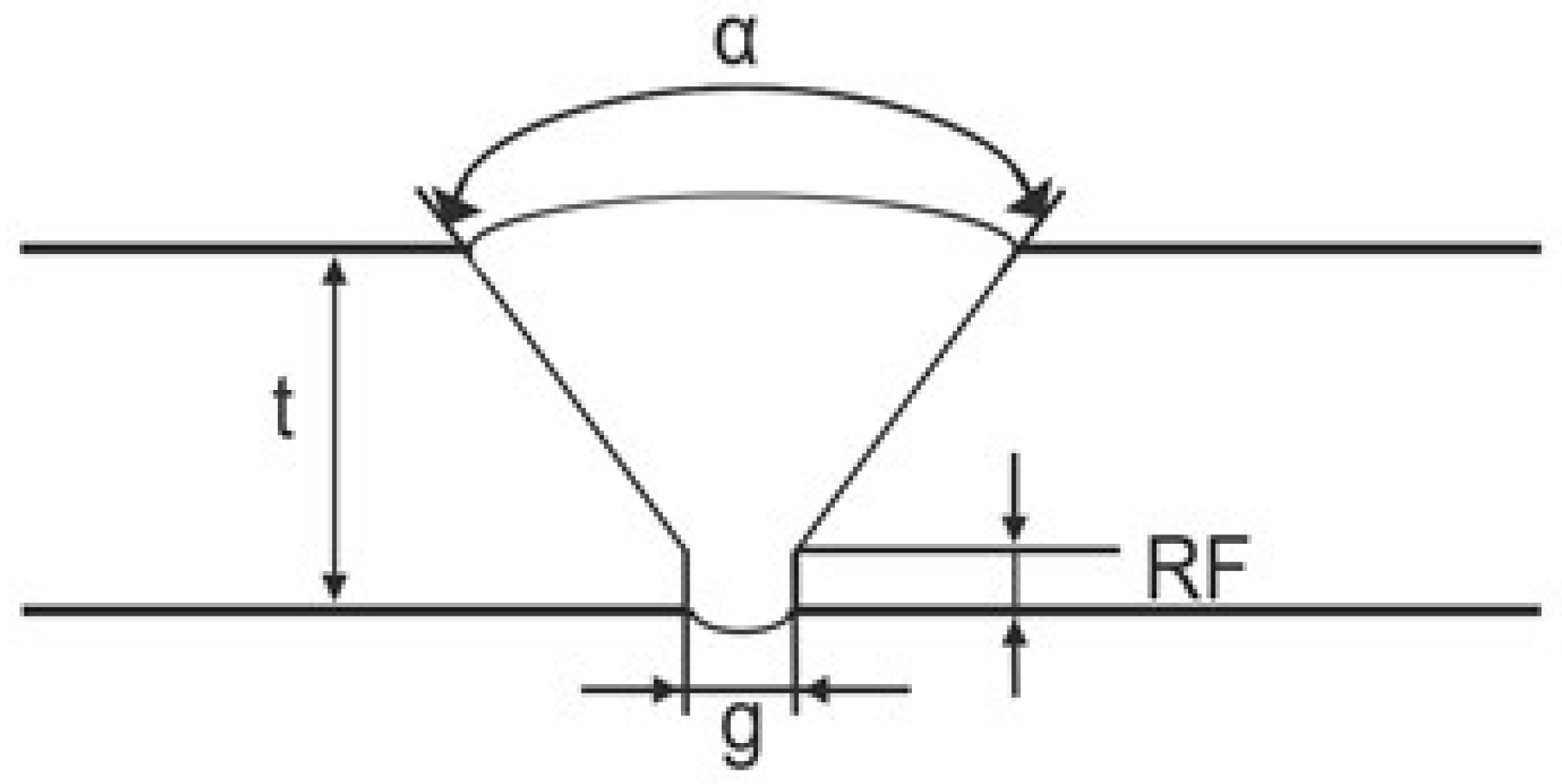





| Parameter Varied | Range/Values | Notes |
|---|---|---|
| Root face () | 0–3 mm | Variation in root face thickness |
| Gap () | 1–4 mm | Joint gap between plates |
| Thickness (t) | 5.6–18 mm | Variation in plate thickness |
| Angle () | 70°, 75° | Weld V-groove angle |
| Defect types | Cracks, Porosity, Inclusions | Defects variation placed in weld root and weld toe |
| Non-defective samples | Included | Various geometrical profiles without flaws |
| Structural noise | Varied amplitude & density | Simulated inspection conditions |
| Dataset size | ∼200 S-scan samples | Each S-scan consists of 39 A-scan signals |
| Augmentation | ×2.5 | Variations in noise maps and signal recombination |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barshok, K.; Choi, J.-I.; Lee, J. Deep Learning-Based Approach for Automatic Defect Detection in Complex Structures Using PAUT Data. Sensors 2025, 25, 6128. https://doi.org/10.3390/s25196128
Barshok K, Choi J-I, Lee J. Deep Learning-Based Approach for Automatic Defect Detection in Complex Structures Using PAUT Data. Sensors. 2025; 25(19):6128. https://doi.org/10.3390/s25196128
Chicago/Turabian StyleBarshok, Kseniia, Jung-In Choi, and Jaesun Lee. 2025. "Deep Learning-Based Approach for Automatic Defect Detection in Complex Structures Using PAUT Data" Sensors 25, no. 19: 6128. https://doi.org/10.3390/s25196128
APA StyleBarshok, K., Choi, J.-I., & Lee, J. (2025). Deep Learning-Based Approach for Automatic Defect Detection in Complex Structures Using PAUT Data. Sensors, 25(19), 6128. https://doi.org/10.3390/s25196128







