A Trinocular System for Pedestrian Localization by Combining Template Matching with Geometric Constraint Optimization
Abstract
1. Introduction
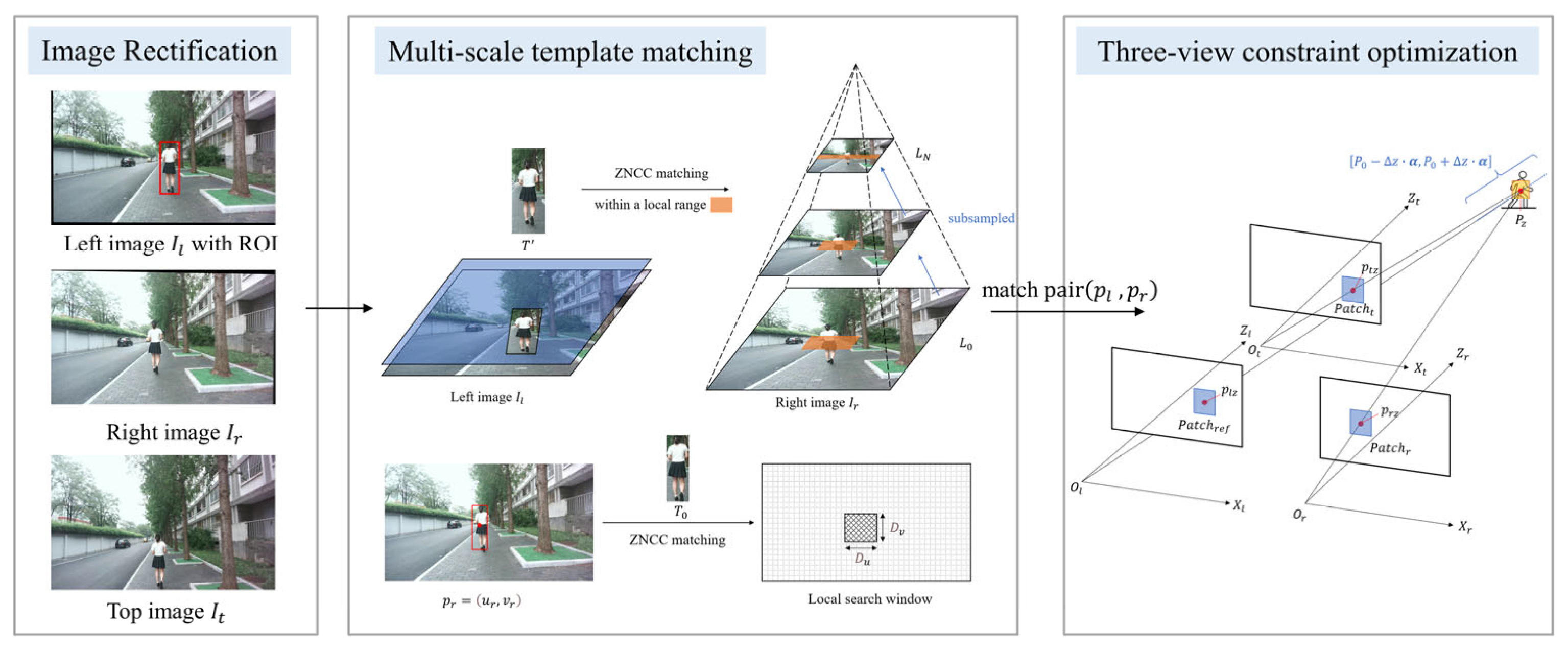
2. Methodology
2.1. Camera Settings and Symbols
- Intrinsic calibration: Each camera (, , ) was calibrated independently to obtain its intrinsic parameters. These parameters include the intrinsic matrix (which encodes the focal lengths , principal point coordinates and the vector of distortion coefficients . The distortion vector accounts for primary radial and tangential lens distortions. The intrinsic parameters are denoted as , and .
- Extrinsic calibration: The spatial relationship between the cameras was determined by performing extrinsic calibration. With serving as the reference coordinate frame, we computed the rotation matrix () and translation vector () for the - and - pairs, denoted as and .
- Image Rectification: The stereo image pair was rectified using the extrinsic parameters to align epipolar lines, yielding the reprojection matrix , the relative rotation , the relative translation , and the rotation matrices and . Specifically, and represent the transformation from the original camera coordinate systems into their rectified counterparts. The top image was undistorted using its intrinsic parameters .
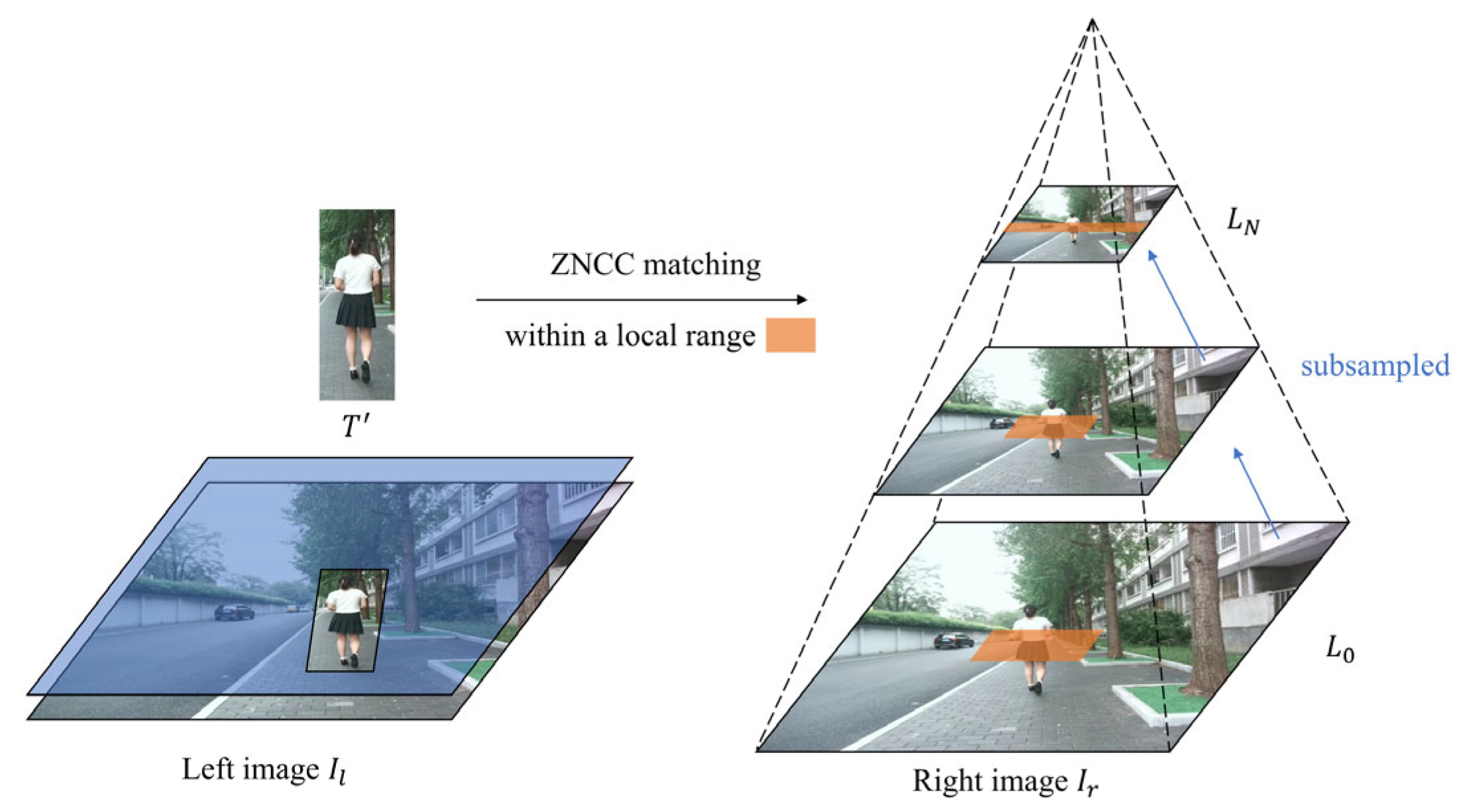
2.2. Multi-Scale Template Matching for Initialization
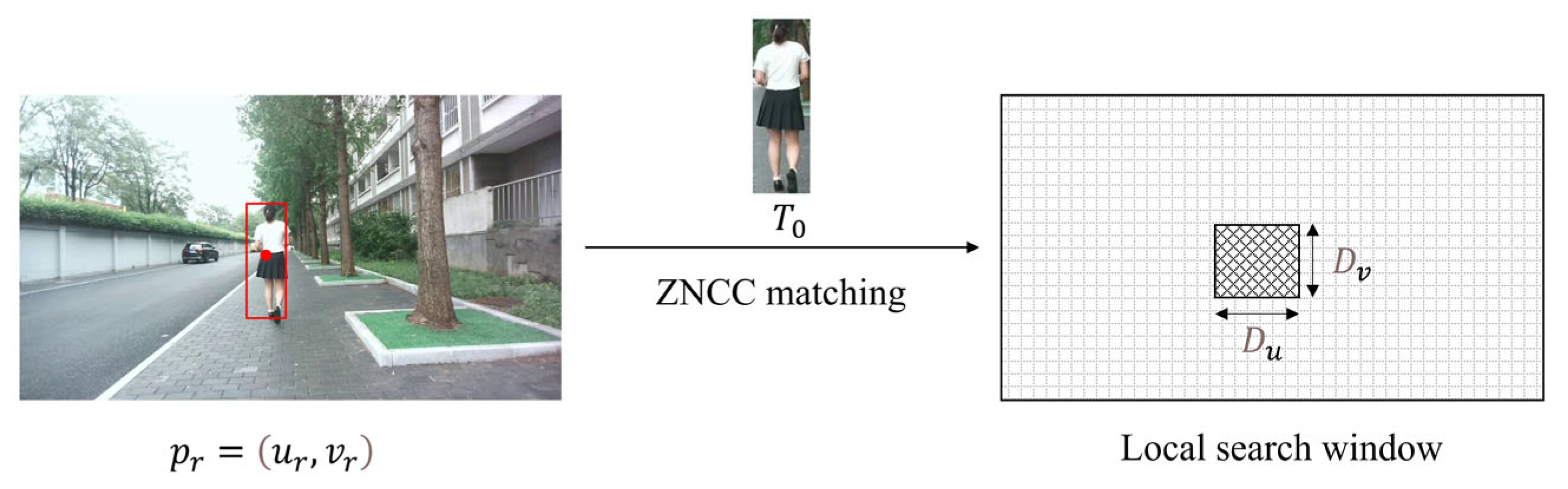
2.2.1. Template Preprocessing
- If , the template is expanded by a factor to incorporate richer contextual information from the surrounding region. The resulting dimensions are defined as .
- If , the template is cropped by a factor to remove redundant information, which could degrade matching stability. The resulting dimensions are defined as .
- If , the template is considered adequate. The resulting dimensions are defined as .
2.2.2. Matching Strategy
2.3. Three-View Constraint Optimization
2.3.1. Initial Point Triangulation and Search Space Construction
2.3.2. Depth Optimization
- The reference patch, , of size pixels, is extracted from the left view , centered at the point . The patch size is determined by the equation , where and are the width and height of the initial ROI, respectively. The term is a scaling factor that relates the patch size to the size of the ROI.
- For each candidate point , we extract corresponding patches, and , from the right view and the top view , centered on their respective projected coordinates, and .
- The similarity scores are then calculated between and the patches from the right and top views ( and , defined as:
- The total similarity score for a candidate point is defined as the weighted sum of the individual scores:where and are the weighting coefficients for the right and top views, respectively.
- By iterating through all candidate points , the point that yields the maximum total score is selected as the optimal estimate, .
3. Experimental Results
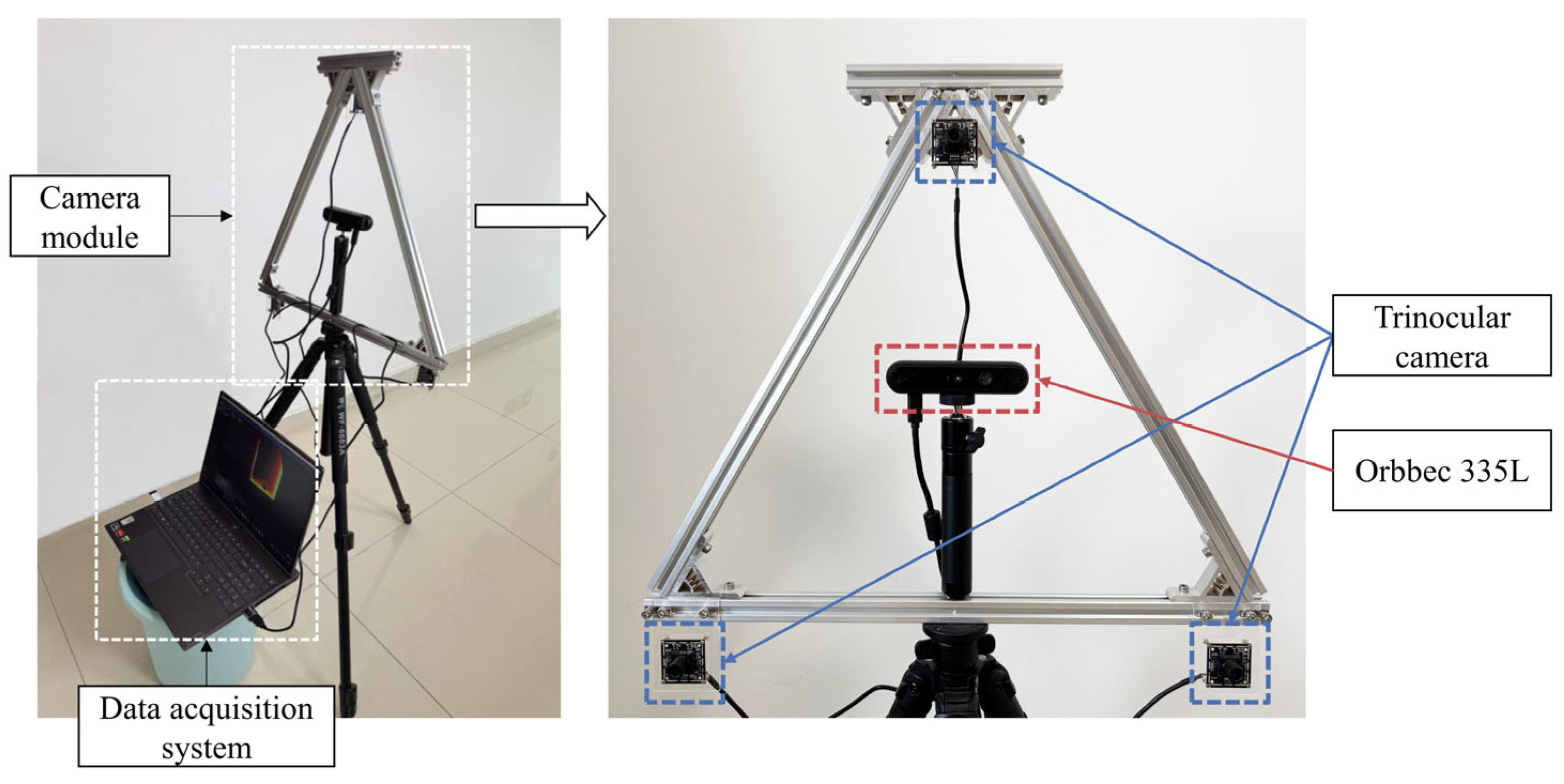
3.1. Dataset Collection and Parameters
3.1.1. Dataset Collection
3.1.2. Parameters
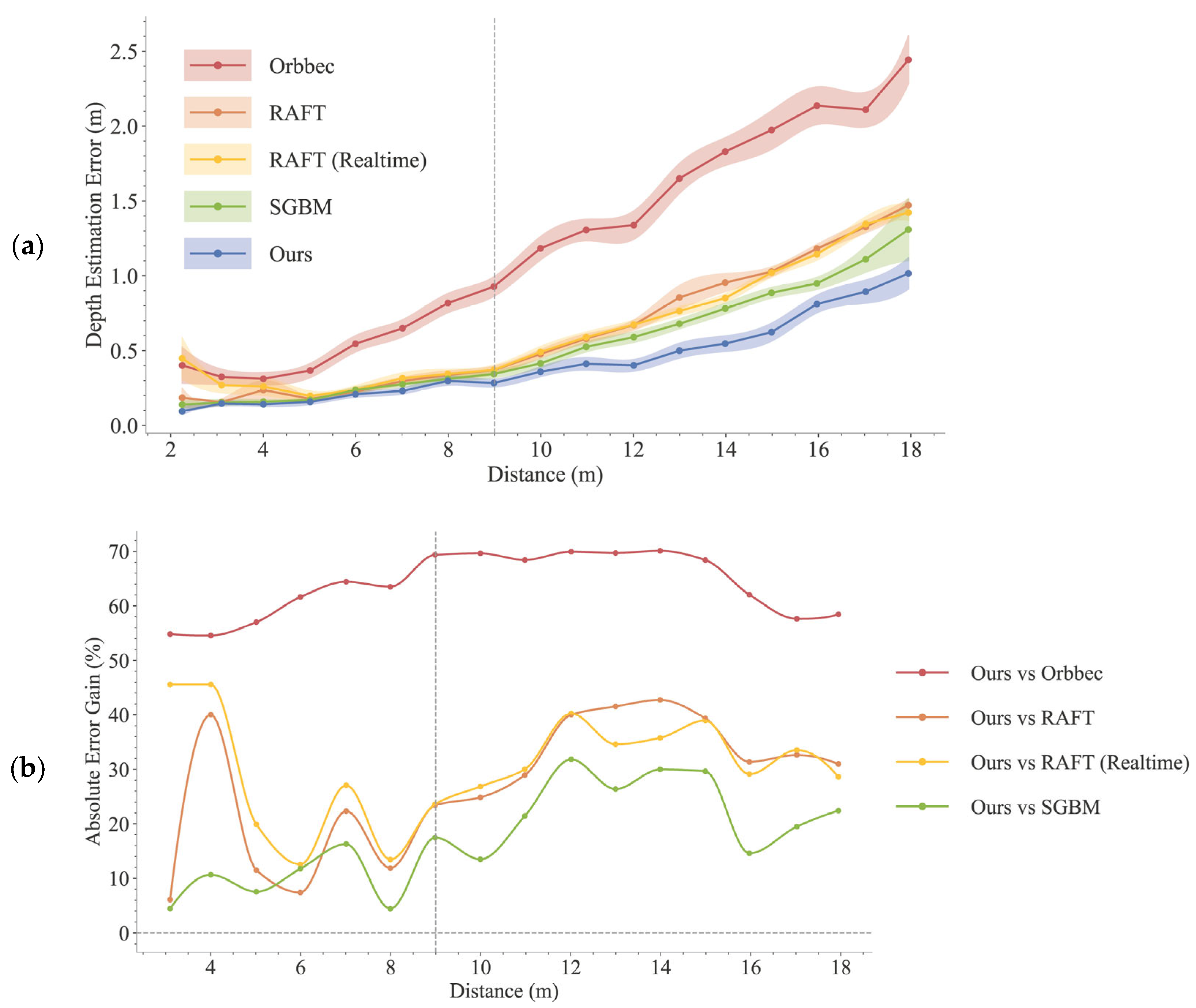
3.2. Accuracy Evaluation
3.2.1. Comparison of Accuracy
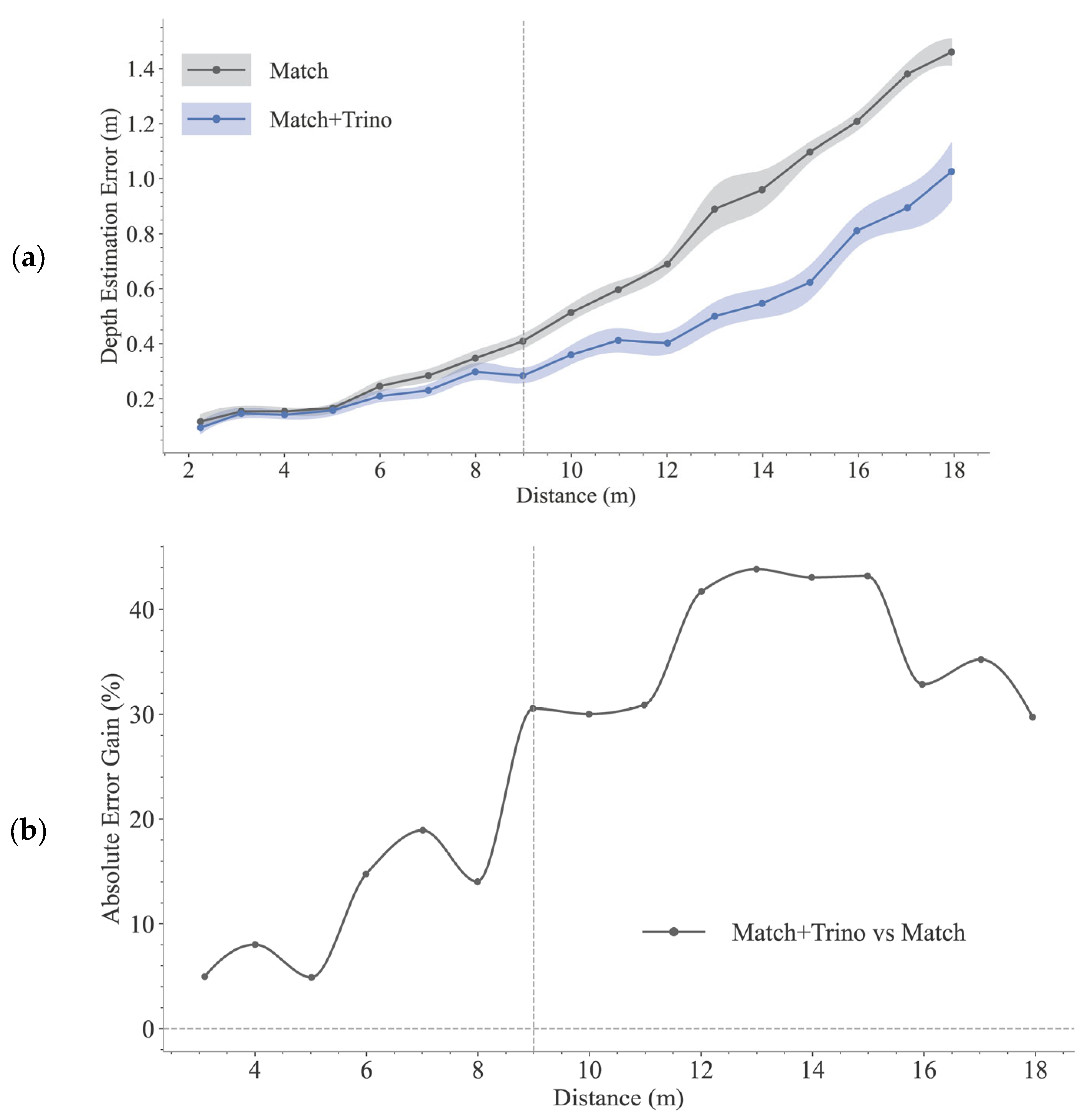
3.2.2. Ablation Study
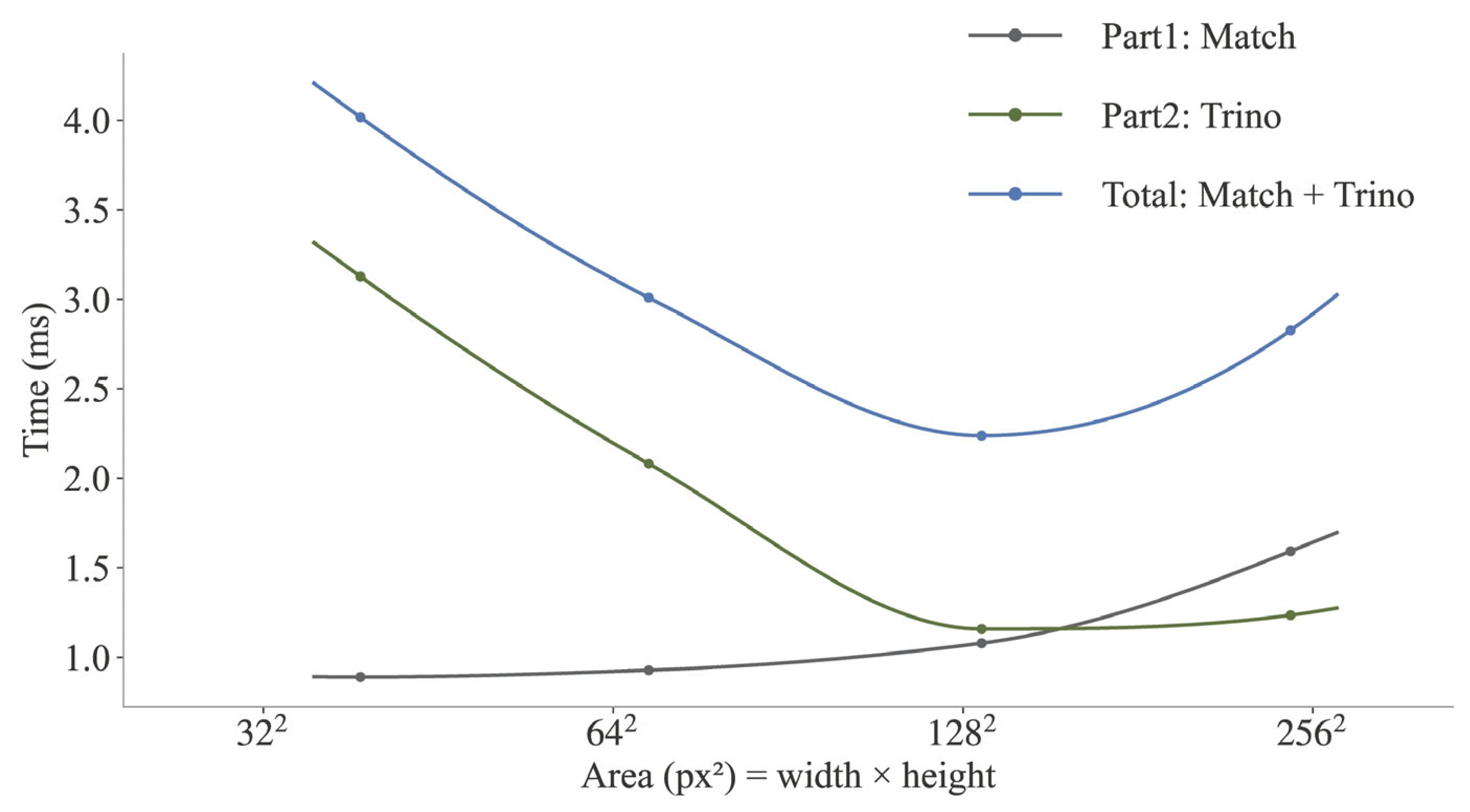
3.3. Computational Performance
3.3.1. Comparison of Computational Efficiency
3.3.2. Time Breakdown
3.4. Qualitative Analysis of Matching and Detection Inaccuracies
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Algorithm A1 The proposed trinocular stereo vision localization algorithm |
| Input: Left image , right image , top image , original target template (from left image) , camera parameter set . Output: The target (in the left camera coordinate system). 1: ImageRectification “Obtaining initial matching from ” 2: = Preprocessing 3: Build image pyramids for and . 4: for from down to 0 do 5: if is then 6: Initial 7: Search 8: else 9: Initial 10: Search 11: end if 12: end for 13: Use for search: 14: 15: Find the best matching point for “Optimization based on ” 16: = Triangulation 17: for in with do 18: Candidate points 19: Extract corresponding to the projection point: 20: Projection 21: Calculate 22: end for 23: 24: return |
Appendix B
Appendix B.1
| Parameter | Value |
|---|---|
| minDisparity | 0 |
| numDisparities | 256 |
| blockSize | 5 |
| P1 | 1176 |
| P2 | 4704 |
| disp12MaxDiff | 1 |
| uniquenessRatio | 10 |
| speckleWindowSize | 100 |
| speckleRange | 32 |
Appendix B.2
| Component | Parameter | Value |
|---|---|---|
| Match | N | 3 |
| 4096 | ||
| 65,536 | ||
| 1.5 | ||
| 0.5 | ||
| 10 | ||
| 2 | ||
| 20 | ||
| 20 | ||
| Trino | 0.15 | |
| 0.1 | ||
| 0.5 | ||
| 0.5 | ||
| 0.5 |
References
- Choi, J.; Chun, D.; Kim, H.; Lee, H.-J. Gaussian yolov3: An accurate and fast object detector using localization uncertainty for autonomous driving. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October 2019; pp. 502–511. [Google Scholar]
- Trulls, E.; Corominas Murtra, A.; Pérez-Ibarz, J.; Ferrer, G.; Vasquez, D.; Mirats-Tur, J.M.; Sanfeliu, A. Autonomous navigation for mobile service robots in urban pedestrian environments. J. Field Robot. 2011, 28, 329–354. [Google Scholar] [CrossRef]
- Ahmed, D.B.; Díez, L.E.; Diaz, E.M.; Domínguez, J.J.G. A survey on test and evaluation methodologies of pedestrian localization systems. IEEE Sens. J. 2019, 20, 479–491. [Google Scholar] [CrossRef]
- Patel, I.; Kulkarni, M.; Mehendale, N. Review of sensor-driven assistive device technologies for enhancing navigation for the visually impaired. Multimed. Tools Appl. 2024, 83, 52171–52195. [Google Scholar] [CrossRef]
- Hsu, Y.; Wang, J.; Chang, C. A wearable inertial pedestrian navigation system with quaternion-based extended Kalman filter for pedestrian localization. IEEE Sens. J. 2017, 17, 3193–3206. [Google Scholar] [CrossRef]
- Charroud, A.; El Moutaouakil, K.; Palade, V.; Yahyaouy, A.; Onyekpe, U.; Eyo, E.U. Localization and mapping for self-driving vehicles: A survey. Machines 2024, 12, 118. [Google Scholar] [CrossRef]
- Li, G.; Xu, J.; Li, Z.; Chen, C.; Kan, Z. Sensing and navigation of wearable assistance cognitive systems for the visually impaired. IEEE Trans. Cogn. Dev. Syst. 2022, 15, 122–133. [Google Scholar] [CrossRef]
- Rai, A.; Mounier, E.; de Araujo, P.R.M.; Noureldin, A.; Jain, K. Investigation and Implementation of Multi-Stereo Camera System Integration for Robust Localization in Urban Environments. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2025, 48, 1255–1262. [Google Scholar] [CrossRef]
- Llorca, D.F.; Sotelo, M.A.; Parra, I.; Ocaña, M.; Bergasa, L.M. Error analysis in a stereo vision-based pedestrian detection sensor for collision avoidance applications. Sensors 2010, 10, 3741–3758. [Google Scholar] [CrossRef]
- Keller, C.G.; Enzweiler, M.; Rohrbach, M.; Llorca, D.F.; Schnorr, C.; Gavrila, D.M. The benefits of dense stereo for pedestrian detection. IEEE Trans. Intell. Transp. Syst. 2011, 12, 1096–1106. [Google Scholar] [CrossRef]
- Wang, J.; Meng, X.; Xu, H.; Pei, Y. Neural Modeling and Real-Time Environment Training of Human Binocular Stereo Visual Tracking. Cogn. Comput. 2023, 15, 710–730. [Google Scholar] [CrossRef]
- Zhang, Z.; Tao, W. Pedestrian detection in binocular stereo sequence based on appearance consistency. IEEE Trans. Circuits Syst. Video Technol. 2015, 26, 1772–1785. [Google Scholar] [CrossRef]
- Xie, Q.; Long, Q.; Li, J.; Zhang, L.; Hu, X. Application of intelligence binocular vision sensor: Mobility solutions for automotive perception system. IEEE Sens. J. 2023, 24, 5578–5592. [Google Scholar] [CrossRef]
- Yang, L.; Wang, B.; Zhang, R.; Zhou, H.; Wang, R. Analysis on location accuracy for the binocular stereo vision system. IEEE Photonics J. 2017, 10, 1–16. [Google Scholar] [CrossRef]
- Poggi, M.; Tosi, F.; Batsos, K.; Mordohai, P.; Mattoccia, S. On the synergies between machine learning and binocular stereo for depth estimation from images: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 5314–5334. [Google Scholar] [CrossRef] [PubMed]
- Brown, M.Z.; Burschka, D.; Hager, G.D. Advances in computational stereo. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 993–1008. [Google Scholar] [CrossRef]
- Hirschmuller, H. Stereo processing by semiglobal matching and mutual information. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 30, 328–341. [Google Scholar] [CrossRef]
- Kendall, A.; Martirosyan, H.; Dasgupta, S.; Henry, P.; Kennedy, R.; Bachrach, A.; Bry, A. End-to-end learning of geometry and context for deep stereo regression. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 66–75. [Google Scholar]
- Chang, J.-R.; Chen, Y.-S. Pyramid stereo matching network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 5410–5418. [Google Scholar]
- Lipson, L.; Teed, Z.; Deng, J. Raft-stereo: Multilevel recurrent field transforms for stereo matching. In Proceedings of the 2021 International Conference on 3D Vision (3DV), London, UK, 1–3 December 2021; pp. 218–227. [Google Scholar]
- Li, J.; Wang, P.; Xiong, P.; Cai, T.; Yan, Z.; Yang, L.; Liu, J.; Fan, H.; Liu, S. Practical stereo matching via cascaded recurrent network with adaptive correlation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 16263–16272. [Google Scholar]
- Xu, G.; Wang, X.; Ding, X.; Yang, X. Iterative geometry encoding volume for stereo matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 21919–21928. [Google Scholar]
- Szeliski, R. Computer Vision: Algorithms and Applications, 2nd ed.; Springer Nature: Cham, Switzerland, 2022; pp. 595–612. [Google Scholar]
- Scharstein, D.; Szeliski, R. A taxonomy and evaluation of dense two-frame stereo correspondence algorithms. Int. J. Comput. Vis. 2002, 47, 7–42. [Google Scholar] [CrossRef]
- Teed, Z.; Deng, J. Raft: Recurrent all-pairs field transforms for optical flow. In Proceedings of the 16th European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 402–419. [Google Scholar]
- Shamsafar, F.; Woerz, S.; Rahim, R.; Zell, A. Mobilestereonet: Towards lightweight deep networks for stereo matching. In Proceedings of the 2022 IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2022; pp. 2417–2426. [Google Scholar]
- Yang, L.; Tang, W. A lightweight stereo depth estimation network based on mobile devices. In Proceedings of the Seventh International Conference on Computer Graphics and Virtuality, Hangzhou, China, 23–25 February 2024; pp. 41–52. [Google Scholar]
- Qian, W.; Hu, C.; Wang, H.; Lu, L.; Shi, Z. A novel target detection and localization method in indoor environment for mobile robot based on improved YOLOv5. Multimed. Tools Appl. 2023, 82, 28643–28668. [Google Scholar] [CrossRef]
- Wang, L.; Li, L.; Wang, H.; Zhu, S.; Zhai, Z.; Zhu, Z. Real-time vehicle identification and tracking during agricultural master-slave follow-up operation using improved YOLO v4 and binocular positioning. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2023, 237, 1393–1404. [Google Scholar] [CrossRef]
- Zuo, J.; Wang, Y.; Wang, R. Method for Acquiring Passenger Standing Positions on Subway Platforms Based on Binocular Vision. IEEE Access 2025, 13, 32971–32980. [Google Scholar] [CrossRef]
- Ding, J.; Yan, Z.; We, X. High-accuracy recognition and localization of moving targets in an indoor environment using binocular stereo vision. ISPRS Int. J. Geo-Inf. 2021, 10, 234. [Google Scholar] [CrossRef]
- Wei, B.; Liu, J.; Li, A.; Cao, H.; Wang, C.; Shen, C.; Tang, J. Remote distance binocular vision ranging method based on improved YOLOv5. IEEE Sens. J. 2024, 24, 11328–11341. [Google Scholar] [CrossRef]
- Guo, J.; Chen, H.; Liu, B.; Xu, F. A system and method for person identification and positioning incorporating object edge detection and scale-invariant feature transformation. Measurement 2023, 223, 113759. [Google Scholar] [CrossRef]
- Nguyen, U.; Heipke, C. 3d pedestrian tracking using local structure constraints. ISPRS J. Photogramm. Remote Sens. 2020, 166, 347–358. [Google Scholar] [CrossRef]
- Sarlin, P.-E.; DeTone, D.; Malisiewicz, T.; Rabinovich, A. Superglue: Learning feature matching with graph neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 4938–4947. [Google Scholar]
- Hayat, M.; Gupta, M.; Suanpang, P.; Nanthaamornphong, A. Super-resolution methods for endoscopic imaging: A review. In Proceedings of the 2024 12th International Conference on Internet of Everything, Microwave, Embedded, Communication and Networks (IEMECON), Jaipur, India, 24–26 October 2024; pp. 1–6. [Google Scholar]
- Tosi, F.; Bartolomei, L.; Poggi, M. A survey on deep stereo matching in the twenties. Int. J. Comput. Vis. 2025, 133, 4245–4276. [Google Scholar] [CrossRef]
- Chuang, K.; Lin, W. Improve the Applicability of Trinocular Stereo Camera in Navigation and Obstacle Avoidance. In Proceedings of the 2025 1st International Conference on Consumer Technology, Matsue, Japan, 29–31 March 2025; pp. 1–4. [Google Scholar]
- Bi, S.; Gu, Y.; Zou, J.; Wang, L.; Zhai, C.; Gong, M. High precision optical tracking system based on near infrared trinocular stereo vision. Sensors 2021, 21, 2528. [Google Scholar] [CrossRef]
- Liu, C.; Lin, W. A Novel Stereo Vision Universality Algorithm Model Suitable for Tri-PSMNet and InvTri-PSMNet. In Proceedings of the 2025 1st International Conference on Consumer Technology, Matsue, Japan, 29–31 March 2025; pp. 1–4. [Google Scholar]
- Zhang, Y. Multi-ocular Stereovision. In 3D Computer Vision: Foundations and Advanced Methodologies; Springer: Singapore, 2024; pp. 203–235. [Google Scholar]
- Wang, J.; Peng, C.; Li, M.; Li, Y.; Du, S. The study of stereo matching optimization based on multi-baseline trinocular model. Multimed. Tools Appl. 2022, 81, 12961–12972. [Google Scholar] [CrossRef]
- Wang, H.; Li, M.; Wang, J.; Li, Y.; Du, S. A Discussion of Optimization about Stereo Image Depth Estimation Based on Multi-baseline Trinocular Camera Model. In Proceedings of the 2021 International Conference on Computational Science and Computational Intelligence, Las Vegas, NV, USA, 15–17 December 2021; pp. 1716–1720. [Google Scholar]
- Roghani, S.E.S.; Koyuncu, E. Canonical Trinocular Camera Setups and Fisheye View for Enhanced Feature-Based Visual Aerial Odometry. IEEE Access 2024, 12, 134888–134901. [Google Scholar] [CrossRef]
- Pathak, S.; Hamada, T.; Umeda, K. Trinocular 360-degree stereo for accurate all-round 3D reconstruction considering uncertainty. Adv. Robot. 2024, 38, 1038–1051. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, Q.; Wu, Y.; Ma, Y.; Wang, C. Trinocular vision and spatial prior based method for ground clearance measurement of transmission lines. Appl. Opt. 2021, 60, 2422–2433. [Google Scholar] [CrossRef]
- Isa, M.A.; Leach, R.; Branson, D.; Piano, S. Vision-based detection and coordinate metrology of a spatially encoded multi-sphere artefact. Opt. Lasers Eng. 2024, 172, 107885. [Google Scholar] [CrossRef]
- Ma, Y.; Li, Q.; Xing, J.; Huo, G.; Liu, Y. An intelligent object detection and measurement system based on trinocular vision. IEEE Trans. Circuits Syst. Video Technol. 2019, 30, 711–724. [Google Scholar] [CrossRef]
- Oh, S.; Hoogs, A.; Perera, A.; Cuntoor, N.; Chen, C.-C.; Lee, J.T.; Mukherjee, S.; Aggarwal, J.K.; Lee, H.; Davis, L. A large-scale benchmark dataset for event recognition in surveillance video. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Colorado Springs, CO, USA, 20–25 June 2011; pp. 3153–3160. [Google Scholar]
- Jocher, G.; Chaurasia, A.; Qiu, J. Ultralytics YOLOv8. Available online: https://github.com/ultralytics/ultralytics (accessed on 21 August 2025).





| Camera | ||||
|---|---|---|---|---|
| 711.9746 | 710.7513 | 656.8128 | 370.2462 | |
| 709.7325 | 708.6549 | 639.3270 | 338.5957 | |
| 720.5992 | 721.1380 | 626.4810 | 372.2269 |
| Pair | (mm) | |
|---|---|---|
| Method | MAE (m) | RMSE (m) | STD (m) |
|---|---|---|---|
| Orbbec 335L | 1.221 | 1.549 | 0.953 |
| SGBM | 0.536 | 0.734 | 0.501 |
| RAFT-Stereo | 0.623 | 0.800 | 0.501 |
| RAFT-Stereo (Realtime) | 0.621 | 0.781 | 0.473 |
| Match (Ours, w/o Opt.) | 0.638 | 0.815 | 0.508 |
| Match + Trino (Ours) | 0.435 | 0.615 | 0.434 |
| Parameter: | MAE (2–6 m) | MAE (6–12 m) | MAE (12–18 m) |
|---|---|---|---|
| (0.25, 0.75) | 0.161 ± 0.009 | 0.309 ± 0.012 | 0.695 ± 0.026 |
| (0.5, 0.5) (default) | 0.154 ± 0.009 | 0.313 ± 0.013 | 0.702 ± 0.026 |
| (0.75, 0.25) | 0.167 ± 0.011 | 0.330 ± 0.014 | 0.735 ± 0.027 |
| Parameter: | MAE (2–6 m) | MAE (6–12 m) | MAE (12–18 m) |
|---|---|---|---|
| 0.3 | 0.208 ± 0.011 | 0.521 ± 0.021 | 1.169 ± 0.045 |
| 0.5 (default) | 0.154 ± 0.009 | 0.313 ± 0.013 | 0.702 ± 0.026 |
| 0.7 | 0.150 ± 0.008 | 0.290 ± 0.011 | 0.699 ± 0.023 |
| Parameter: | MAE (2–6 m) | MAE (6–12 m) | MAE (12–18 m) |
|---|---|---|---|
| 0.05 | 0.155 ± 0.009 | 0.315 ± 0.013 | 0.709 ± 0.026 |
| 0.1 (default) | 0.154 ± 0.009 | 0.313 ± 0.013 | 0.702 ± 0.026 |
| 0.2 | 0.160 ± 0.009 | 0.314 ± 0.013 | 0.695 ± 0.026 |
| Parameter: | MAE (2–6 m) | MAE (6–12 m) | MAE (12–18 m) |
|---|---|---|---|
| 0.1 | 0.156 ± 0.009 | 0.311 ± 0.013 | 0.712 ± 0.029 |
| 0.15 (default) | 0.154 ± 0.009 | 0.313 ± 0.013 | 0.702 ± 0.026 |
| 0.2 | 0.157 ± 0.009 | 0.312 ± 0.013 | 0.709 ± 0.026 |
| Algorithms/Components | Average Time (ms) | Throughput (FPS) @ N = 1 * |
|---|---|---|
| SGBM | 51.02 | 19.60 |
| RAFT-Stereo | 739.43 | 1.35 |
| RAFT-Stereo (Realtime) | 21.26 | 47.04 |
| Part 1: Match (Ours) | 0.98 | - |
| Part 2: Trino (Ours) | 2.15 | - |
| Total: Match+Trino (Ours) | 3.13 | 319.49 |
| * | Mean Area (px2) | SGBM (ms) | RAFT-Stereo (ms) | RAFT-Stereo (Realtime) (ms) | Ours (ms) |
|---|---|---|---|---|---|
| 1875.85 | 51.59 | 739.04 | 21.30 | 4.02 | |
| 5342.40 | 50.87 | 740.13 | 21.26 | 3.01 | |
| 18,990.66 | 50.73 | 738.74 | 21.20 | 2.24 | |
| 62,398.28 | 50.21 | 738.53 | 21.25 | 2.83 |
| * | (m) | Match GFLOPs | Match Latency (ms) | Trino GFLOPs | Trino Latency (ms) | |
|---|---|---|---|---|---|---|
| 13.5 | 2.71 | 0.034 | 0.890 | 0.0058 | 3.126 | |
| 22.1 | 1.82 | 0.096 | 0.928 | 0.0041 | 2.081 | |
| 40.9 | 1.00 | 0.342 | 1.079 | 0.0027 | 1.158 | |
| 69.5 | 0.57 | 1.12 | 1.591 | 0.0023 | 1.235 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Huang, S.; Li, Y.; Xu, J.; Xu, S. A Trinocular System for Pedestrian Localization by Combining Template Matching with Geometric Constraint Optimization. Sensors 2025, 25, 5970. https://doi.org/10.3390/s25195970
Zhao J, Huang S, Li Y, Xu J, Xu S. A Trinocular System for Pedestrian Localization by Combining Template Matching with Geometric Constraint Optimization. Sensors. 2025; 25(19):5970. https://doi.org/10.3390/s25195970
Chicago/Turabian StyleZhao, Jinjing, Sen Huang, Yancheng Li, Jingjing Xu, and Shengyong Xu. 2025. "A Trinocular System for Pedestrian Localization by Combining Template Matching with Geometric Constraint Optimization" Sensors 25, no. 19: 5970. https://doi.org/10.3390/s25195970
APA StyleZhao, J., Huang, S., Li, Y., Xu, J., & Xu, S. (2025). A Trinocular System for Pedestrian Localization by Combining Template Matching with Geometric Constraint Optimization. Sensors, 25(19), 5970. https://doi.org/10.3390/s25195970








