1. Introduction
In the context of global climate governance and energy decarbonization transition, the green change in transportation has become a key initiative to achieve “dual-carbon” goal [
1]. Leveraging significant technical and economic advantages such as high energy density, long cycle life, and a wide operating temperature range, lithium-ion batteries have emerged as the core driving force for the development of electric vehicles (EVs) [
2]. However, with their widespread adoption in EVs, safety hazards arising from performance degradation have become increasingly prominent, representing a key bottleneck hindering industry progress. Consequently, developing high-precision and practical state of health (SOH) estimation algorithms stands as a key technological challenge for ensuring safe and reliable operation of EVs and promoting sustainable development of the industry [
3]. The performance of these algorithms is critically dependent on the quality of data from onboard sensors, such as voltage and current sensors within the battery management system (BMS), making sensor data reliability a decisive factor for accurate and robust estimation.
Extensive research has been conducted on battery SOH assessment, with approaches that can be summarized as direct measurement methods, model-driven methods and data-driven methods [
4,
5]. Direct measurement methods determine SOH by measuring capacity or internal resistance, including ampere-hour counting method and electrochemical impedance spectroscopy. While these techniques are simple and easy to implement, they must be carried out in specific environments and are difficult to apply online [
6]. Model-driven methods enable SOH estimation by describing and characterizing the internal electrochemical mechanisms or external behavioral features of the battery [
7]. They mainly include electrochemical models and equivalent circuit models [
8]. Model-based methods are interpretable and logical, enabling the estimation of battery capacity from the intrinsic causes of aging. However, such methods require periodic updating of parameters and have limited generalization capabilities, making them difficult to apply to different battery types and operating conditions.
In recent years, the integration of artificial intelligence and machine learning has become an indispensable approach for addressing the complex challenges of battery reliability and health management [
9,
10]. A comprehensive review by Bello et al. [
11] provides a holistic analysis of this evolution, meticulously detailing various battery degradation mechanisms and highlighting the critical role of machine learning in enabling advanced prognostics and health management. Their work particularly emphasizes the application of intelligent algorithms for SOH estimation. These data-driven methods do not require an understanding of the complex internal mechanisms of the battery, instead, they utilize historical data extracted from the charging and discharging processes or adopt an end-to-end approach to achieve SOH estimation [
12]. Typically, traditional machine learning algorithms, such as support vector machines [
13,
14], Gaussian process regression [
15,
16,
17,
18], and random forests [
19,
20,
21], implement SOH estimation by constructing models and using manually extracted features and correlation analysis. However, these methods rely on manually extracted health indicators and are insensitive to data variations, resulting in limited generalization [
22]. In contrast, deep learning methods such as long short-term memory network (LSTM) and gated recurrent unit (GRU) can automatically extract features and perform end-to-end learning, avoiding complexity of manual feature extraction and significantly improving accuracy of SOH estimation [
23]. Recent breakthroughs are being driven by the adoption of more sophisticated architectures. For instance, temporal convolutional networks, often enhanced with optimization algorithms or attention mechanisms, prove effective in capturing complex temporal patterns within battery operational data [
24,
25]. These approaches demonstrate the power of advanced neural networks in modeling the long-term dependencies inherent in battery signals. Although data-driven approaches show great potential in the field of battery condition estimation, their inherent “black-box” nature poses significant limitations. This opacity means that key features extracted from complex models often lack intuitive physical meaning, making it difficult to effectively integrate chemical and physical degradation processes into the estimation model. Incremental capacity (IC) analysis, as an important tool for extracting features, converts voltage plateau of charging curve into a differential capacity curve with significant peaks, enabling a coupled analysis of the battery’s health degradation process and its internal electrochemical mechanisms [
26]. Li et al. [
27] proposed an improved IC curve acquisition method based on reference voltage, from which characteristic variables were extracted, and SOH estimation was realized using gaussian process regression, which verified that the proposed method could provide accurate SOH estimation. Xu et al. [
28] implemented SOH estimation based on peak features of IC curves using Transformer model with multi-head attention mechanism and verified that the proposed method provided higher accuracy than machine learning methods.
In real-world scenarios, batteries are often charged and discharged from various states of charge, making it difficult to obtain complete charging and discharging curves [
29]. This uncertainty directly affects reliability of SOH estimation methods based on feature extraction [
30,
31]. Therefore, the complexity and stochasticity of actual charging and discharging process must be taken into account when developing SOH estimation methods. To address this, Gao et al. [
32] proposed a new method for SOH estimation based on a novel state-space model using IC curves which utilized partial charging data. Lin et al. [
26] proposed an advanced integrated learning framework technique to estimate SOH using arbitrary charging voltage information.
In addition, most existing estimation methods consider only the temporal information of sequences while ignoring their spatial information. In recent years, the graph neural network (GNN), which can effectively process spatial data and extract spatial features, has attracted attention of scholars in field of battery SOH estimation [
33]. Yao et al. [
34] first used GNN for battery capacity prediction problem, but it requires complete charging data to extract features, which is not suitable for practical applications. He et al. [
35] proposed an approach based on graph convolution and LSTM to realize SOH estimation for batteries with multi-stage constant current–constant voltage fast charging strategy. Xu et al. [
36] proposed a feature extractor that combines a residual (Res) structure with an attention mechanism. This extractor is designed to automatically capture temporal and spatial information from aging features. These features were then used to estimate battery capacity with an LSTM model enhanced by a graph attention network (GAT). However, a significant drawback was that the segmented data used in their study lacked physical interpretability. Despite such limitations, these studies show that fusing temporal and spatial features can significantly improve SOH estimation accuracy and provide a new direction for future performance optimization of battery management system.
Although impressive progress has been made in current research, most existing data-driven SOH estimation methods tend to ignore physical interpretability of feature sequence extraction and its spatial correlation. Therefore, there is a pressing need for a method that not only achieves high accuracy but also provides physical interpretability by leveraging both spatial and temporal degradation information. To address these issues, this paper proposes a novel method for SOH estimation in lithium-ion batteries, which combines a physically interpretable feature extraction technique based on IC analysis with a hybrid model that integrates GAT and bi-directional gated recurrent unit (BiGRU). The main contributions of this paper include:
A novel physically interpretable feature extraction method is proposed. By dynamically selecting an optimal voltage window centered on IC peaks, the method ensures that the extracted feature fragments are directly linked to key electrochemical degradation mechanisms, enhancing the model’s interpretability.
A hybrid GAT-BiGRU architecture is developed for synergistic spatial–temporal feature learning. To capture the complex relationships within the data, the framework first converts the time-series input into a graph structure and then GAT is employed to model the dependencies between these interconnected data segments while BiGRU captures their long-term temporal dependencies, offering a more comprehensive representation of the battery’s degradation processes.
The proposed method’s superiority is rigorously validated on two public benchmark datasets, highlighting its strong generalization and robustness in handling diverse operational conditions. Furthermore, a detailed analysis of its computational footprint confirms its low operational complexity and rapid inference speed, demonstrating its suitability for deployment in resource-constrained embedded platforms.
The rest of the paper is organized as follows:
Section 2 describes the methodology presented in this paper.
Section 3 describes experimental setup.
Section 4 describes experimental results and discusses them in detail.
Section 5 summarizes work of this paper.
2. Methodology
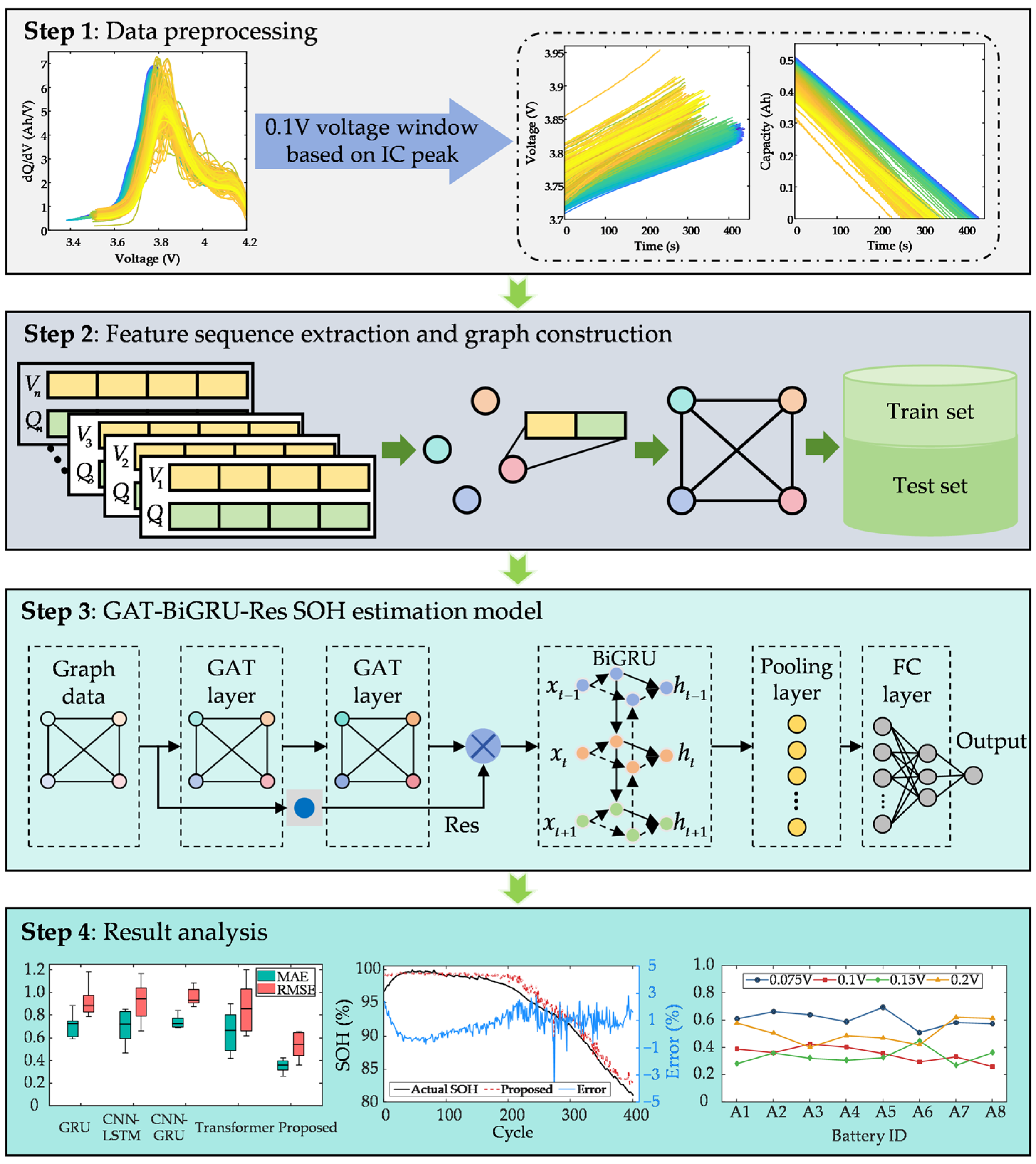
To address the challenges of incomplete data acquisition during real-world charging operations and the limited interpretability in feature sequences, this paper proposes a lithium-ion battery SOH estimation method based on explainable feature segments using a GAT-BiGRU-Res model, with its framework illustrated in
Figure 1. The specific process is as follows. Firstly, IC analysis is employed to dynamically track the temporal evolution patterns of IC curve peaks, adaptively determining a 0.1 V optimal voltage window for extracting voltage/capacity segment pairs. Next, interpolation aligns the voltage and capacity sequences, each of which is divided into four parts to capture local degradation features. Temporal data are then transformed into graph-structured data through graph modeling, with each sub-segment’s voltage–capacity feature vector serving as a graph node. Finally, the graph data are processed by the proposed model, where the GAT extracts spatial correlations among nodes, the BiGRU models temporal dependencies, and residual connections optimize gradient propagation. A fully connected layer outputs the discharge capacity estimate, thus enabling precise SOH estimation.
2.1. Data Preprocessing
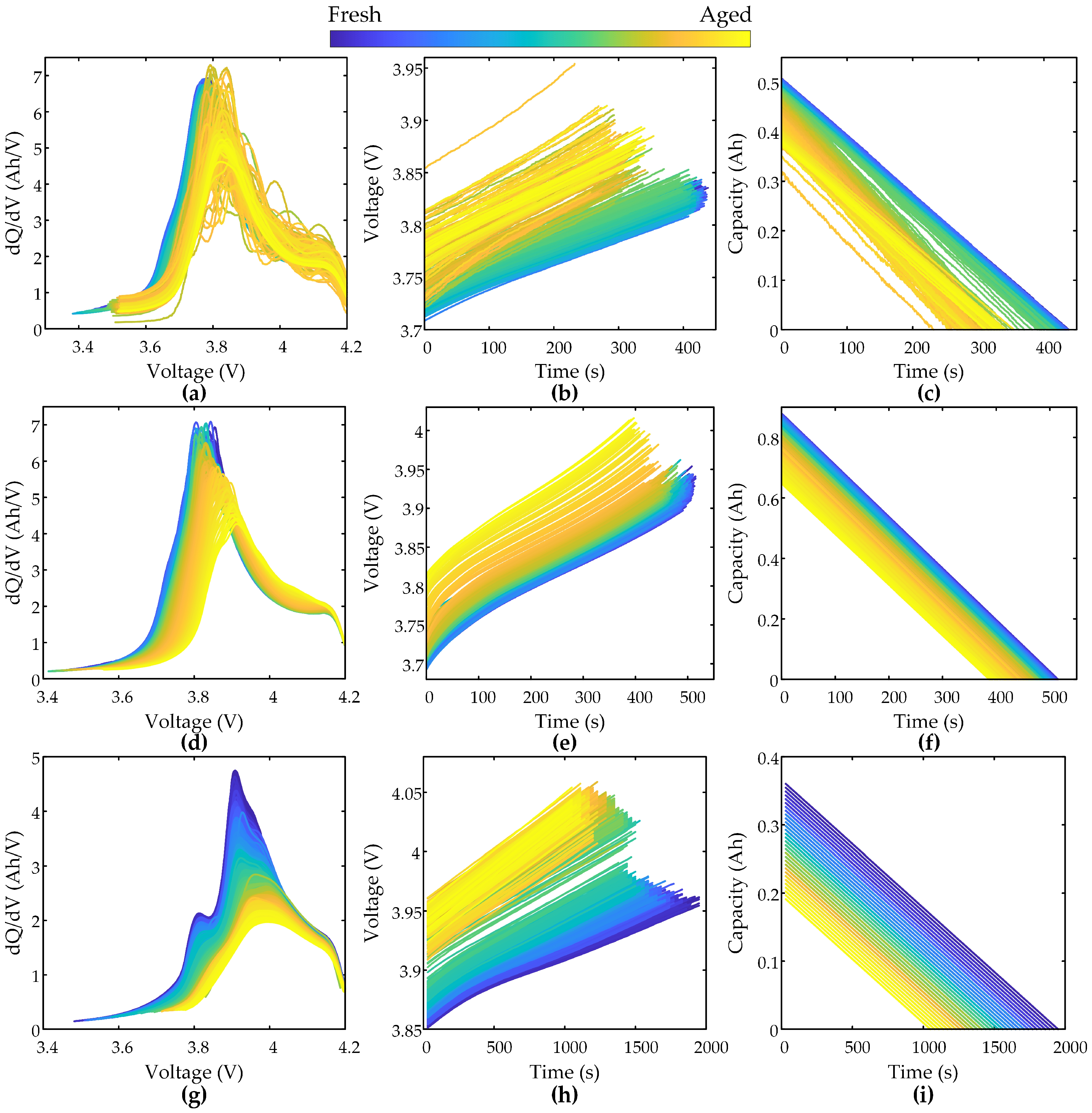
The entire process of SOH estimation begins with the acquisition of operational data from the battery. Specifically, the voltage and current data used as the foundation for our analysis are captured in real-time by dedicated sensors integrated within the BMS during the charging process. Lin et al. [
37] extracted feature sequences by selecting a fixed voltage range. However, this approach lacks a certain degree of flexibility and is prone to omit key aging information in view of the variability and complexity of the battery usage process. In addition, while various data-driven adaptive windowing techniques can identify statistically salient regions, they often fail to capture features with clear physical meaning, which hinders model interpretability. To overcome this limitation, this paper adopts a voltage segment from a dynamically selected voltage range based on the IC peak, along with the corresponding capacity data. This strategy significantly enhances the physical interpretability of the extracted features. Specifically, the peaks on an IC curve are direct manifestations of electrochemical phase transitions during lithium embedding and de-embedding, and their evolution is highly sensitive to degradation mechanisms. For example, reduced peak amplitudes correlate with decreased lithium-ion diffusion coefficients from cathode material cracking or electrolyte decomposition, while peak displacement reflects increased interfacial impedance due to solid electrolyte interphase film thickening at the anode. By dynamically centering the voltage window on the IC peak, this method ensures that the feature fragments are anchored to these physically meaningful events. This process guarantees that the same underlying aging phenomena are consistently captured, even as the peak’s position shifts due to degradation, thereby making the feature selection process transparent and scientifically grounded. The IC curve is defined as the rate of change in capacity with respect to voltage, and can be approximated by the following formula:
where
k is sampling interval,
and
denote the capacity and voltage at the
k-th sampling point.
In order to eliminate the effect of data noise, this paper adopts Gaussian filtering method, which has been proven to effectively smooth battery charging data [
38]. The formula of Gaussian function is as follows:
where
represents an individual data point from the input signal that is being smoothed,
represents Gaussian function, which outputs the weight for a given input
, and
and
denote the mean and standard deviation of the data distribution, respectively. Then, the filtered value of each point is calculated by taking a weighted average of its neighboring points, using weights determined by the Gaussian function.
Then, the voltage fragment
and capacity fragment
can be defined as:
where
,
,
is the voltage at the IC peak position,
is the capacity at voltage
,
is the capacity at voltage
. Then, data standardization is carried out to eliminate effect of differences in data units.
2.2. Construction of Graph-Structured Data
To ensure consistency of the feature sequences across different cycles, cubic spline interpolation method is used to keep data aligned, and in this paper, the length of the feature sequences in each cycle is set to 80. In order to capture localized aging information in the feature sequence, feature fragments are further subdivided into four equal sub-segments for finer analysis of battery aging, which enhances the ability to characterize local changes and helps to gain insight into battery aging process. Each sub-segment represents a node in graph, then the node feature
can be represented as:
where
denotes vector concatenation,
represents the
r-th node,
and
denote the
r-th sub-segment of voltage fragment and capacity fragment.
Then, the node identity matrix can be expressed as:
The edges between these nodes are dynamically constructed based on the similarity of their feature vectors, for which cosine similarity is chosen. This selection is critical for capturing the essential attributes of battery degradation. The aging process often induces distinct morphological changes in the voltage and capacity profiles. Cosine similarity is adept at quantifying such morphological similarities by measuring the cosine of the angle between two vectors. This contrasts with Euclidean distance, which is sensitive to amplitude variations. Furthermore, while dynamic time warping (DTW) is a powerful tool for comparing sequences, its primary advantage lies in aligning series of different lengths. Our preprocessing step, which uses cubic spline interpolation to standardize segment lengths, obviates the need for DTW. Thus, cosine similarity provides a computationally efficient and physically meaningful measure of affinity between feature segments. The similarity matrices of voltage and capacity are first computed separately:
where
and
,
denotes the 2-norm.
Subsequently, normalize the matrices and perform weighted fusion to generate the joint similarity matrix:
where
denotes the joint weight.
Finally, we extract Top-
K edges while excluding self-loops to construct adjacency matrix
:
where
denotes the top
maximum values in the
m-th row of
,
denotes predefined maximum degree, which is 3, enabling the construction of a fully connected graph.
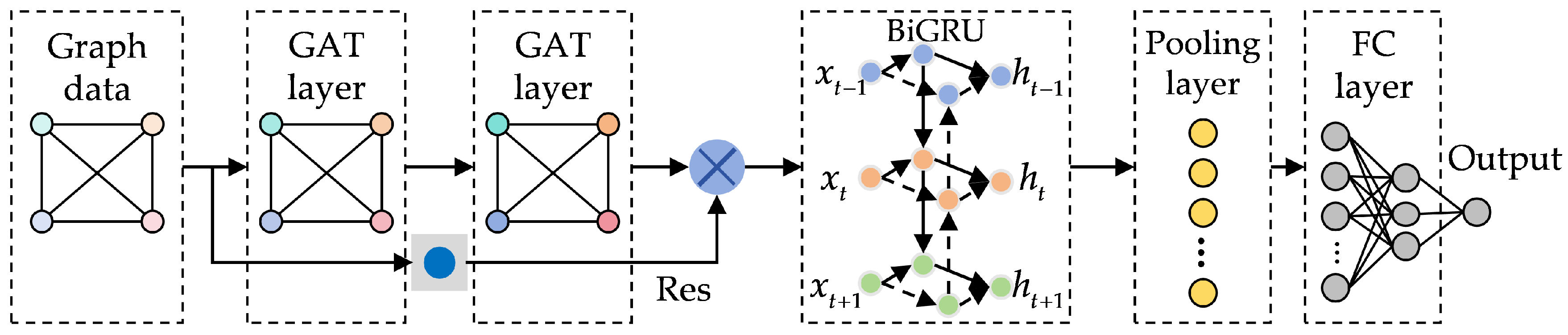
2.3. SOH Estimation Model
GAT is an advanced graph neural network architecture evolved from graph convolutional networks. It dynamically computes attention coefficients between target nodes and their neighbors through learnable mechanisms, rather than using predefined connection weights. This enables GAT to adaptively capture correlations and relative importance between nodes and their neighbors, leading to more accurate information aggregation from neighboring nodes and generating enriched node representations. Unlike conventional convolutional neural network (CNN), which is constrained to Euclidean data and uses static kernels, GAT is more adept at processing graph-structured data with non-Euclidean relationships. Its attention mechanism can dynamically learn the complex dependencies between different feature fragments, providing a more flexible and powerful approach for capturing non-local correlations. During battery aging, sub-segments exhibit heterogeneous degradation rates with inherent correlations. Therefore, employing GAT to extract latent dependencies between voltage sequences and capacity sequences from graph-structured data enables precise SOH estimation.
First, the nodes consisting of voltage and capacity sequences are linearly transformed using learnable weight matrix
in graph attention layer:
where
and
denote the feature vectors of node
i before and after transformation, respectively.
To capture dynamic correlation between nodes, attention coefficients of target node and its neighboring nodes are calculated:
where
denotes the learnable parameter vector.
In order to eliminate effect of node degree differences, a function is used to normalize the attention coefficients to obtain final attention weights:
where
denotes neighbor set of node
.
To enhance the model representation, multi-head attention mechanism is used to learn node relationships in parallel. Each attention head independently calculates different inter-node weights to generate differentiated node representations from multiple perspectives:
where
denotes index of an attention head in the multi-head attention mechanism,
denotes a nonlinear activation function.
Then, node information in the whole graph structure is summarized by averaging outputs of multiple attention heads in an operation. Meanwhile, in order to prevent loss of information caused by the GAT layers, Res is employed. By creating a skip connection that allows the gradient to flow directly, Res effectively mitigates the gradient vanishing phenomenon, which in turn enhances the model’s ability to portray nonlinear degradation trajectory of battery, ultimately yielding the final spatial feature vector. Critically, this is achieved via a computationally inexpensive element-wise addition, representing a highly favorable trade-off for the significant improvement in training stability.
To comprehensively capture bi-directional temporal dependencies in the spatial feature vectors extracted by the GAT layers, this work employs a specifically designed BiGRU architecture for temporal modeling. This architecture is selected for its effective balance of performance and computational efficiency, as it offers a comparable ability to capture long-range dependencies as more complex recurrent structures but with fewer parameters. The framework explicitly couples forward and backward GRU to dynamically integrate historical states and future evolution trends. This capability is particularly critical for battery degradation modeling because there exists an inherent causal relationship between past performance and future deterioration patterns. The bi-directional architecture enables the hidden state at each time step to be informed by the context of the entire sequence, resulting in a more robust and context-aware representation of the battery’s condition. This architecture consists of a single BiGRU layer, which is adept at capturing complex temporal patterns without excessive computational overhead. The hidden size for the forward and backward GRU is set to 80. Among them, the forward and backward process hidden layer is calculated as:
The output calculation formula is as follows:
where
is the input at time
t,
denotes the hidden layer weights of the forward process,
represents the hidden layer weights of the backward process, and
is the output bias. The feature vectors processed by BiGRU layer are fed into fully connected layers, which transforms the hidden states into estimated discharge capacity.
4. Results and Discussion
4.1. Results of the Proposed Method
To validate effectiveness of the proposed method, each battery’s data in the dataset is randomly divided into training and test sets in ratio of 6:4 to ensure generalization ability of the model under different data distributions. By reserving a substantial 40% of the data for the test set, we ensure a more robust assessment of the model’s performance on unseen data. The experiments are implemented using Python 3.9 on a device powered by a 12th-generation Intel iCore i7−12700 CPU, 32 GB RAM, and a single GeForce RTX 3050 GPU. To provide insight into the model’s computational demand during the training stage, we measured the time required to process individual battery data. The average per epoch training time for a single battery is 1.7 s on the XJTU-Batch1 dataset, 1.1 s on XJTU-Batch2, and 4.5 s on CALCE-CX2.
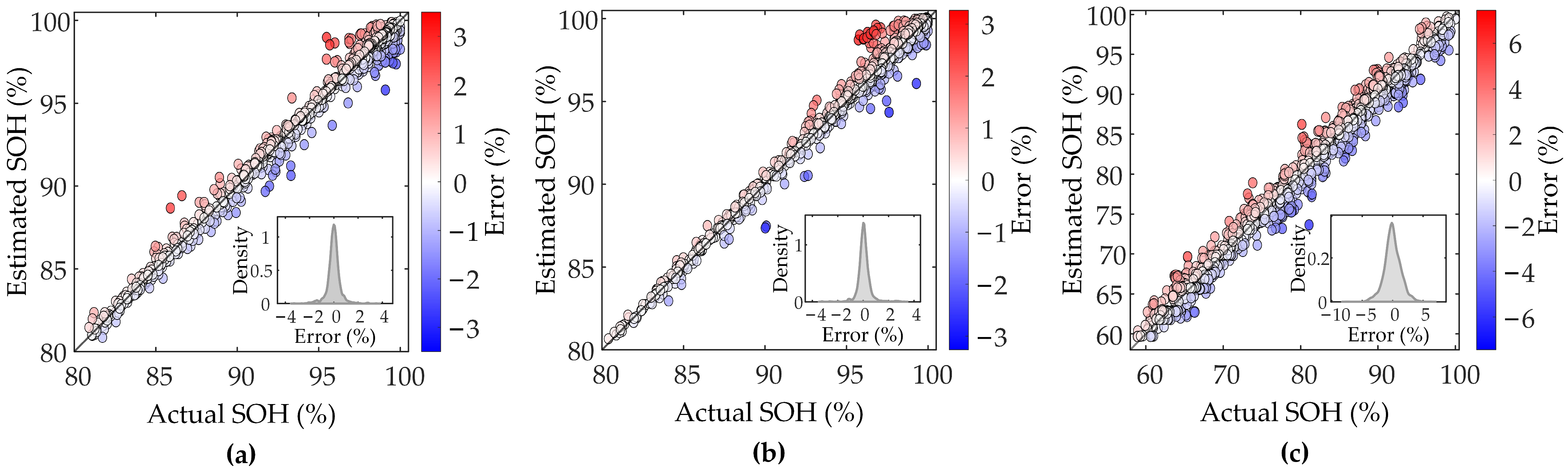
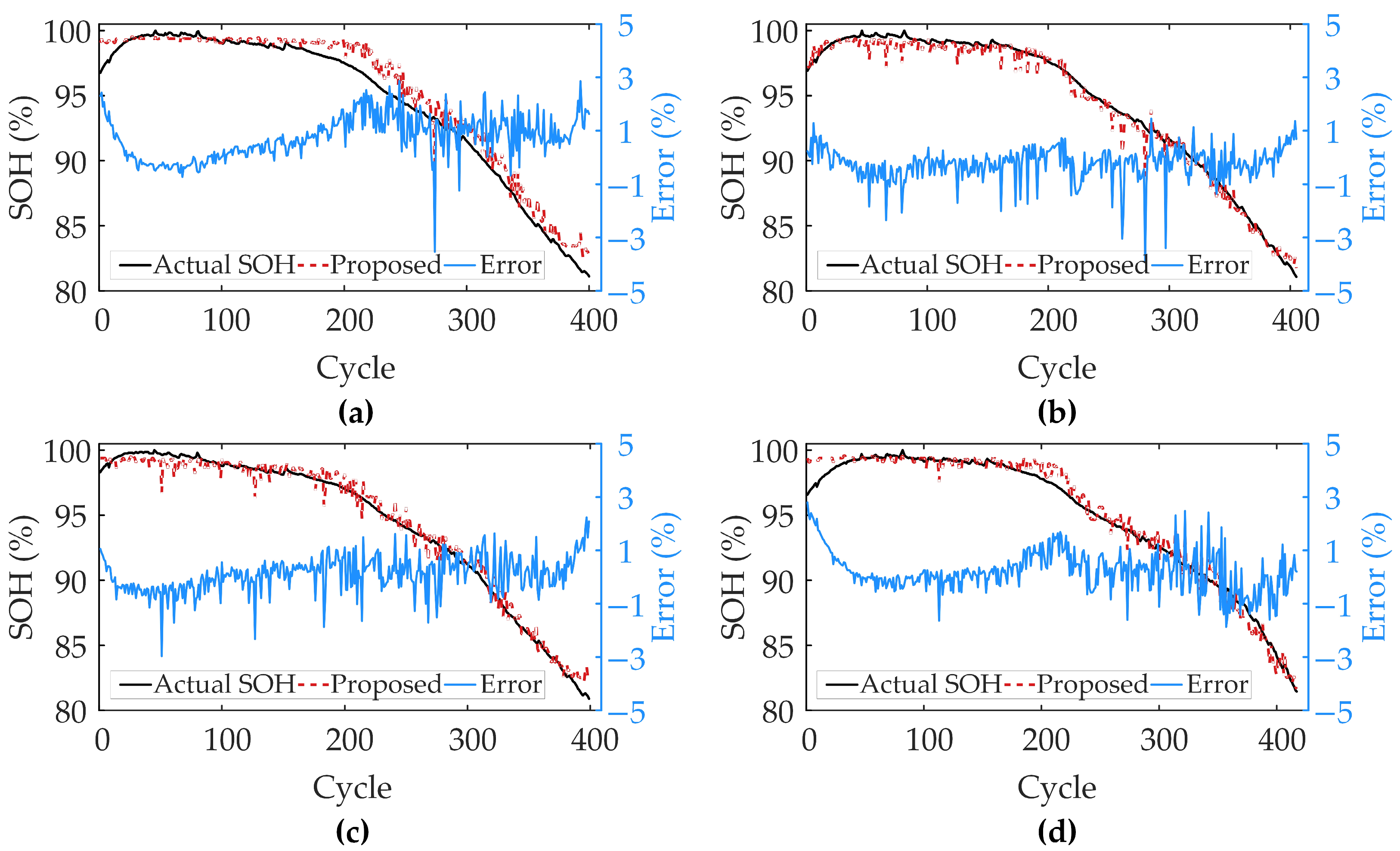
Figure 5 demonstrates SOH estimation results of the proposed method.
The proposed method shows excellent SOH estimation performance under different charging conditions and material scenarios, indicating that the selected voltage and capacity series can effectively reflect the evolution of the batteries’ degradation trajectories. In XJTU and CALCE datasets, the estimation curves of the proposed method consistently and closely match actual capacity degradation curves, showing excellent tracking accuracy and stability. Even in the early and mid-late cycles, the proposed method can still accurately capture nonlinear changes in aging rate of the batteries and complex local capacity regeneration phenomena in the CALCE dataset, with less error volatility. This verifies high accuracy and wide applicability of the proposed method in SOH estimation, both in simple degradation trends and complex operating conditions. Based on the error results, it can be seen that the error distributions are close to normal, with peaks all close to zero, indicating that most of the estimation errors are close to zero. Specifically, the error ranges are between −3% and 3% for Batch1, between −4% and 4% for Batch2, and between −6% and 6% for CX2, where most of the data points are centered around ±1%, ±1%, and ±4%, respectively. These results verify validity and reliability of the proposed method on different datasets to accurately estimate SOH.
Table 2 shows average of the results of the proposed method for evaluation metrics in the three datasets. The results verify that the proposed method has advantages of high accuracy and stability, and the estimation results are highly consistent with the actual capacity degradation trajectory. Compared with the estimation accuracies of Batch1 and Batch2, the accuracy of CX2 decreases, which may be attributed to the more obvious capacity regeneration phenomenon in the whole process of the batteries in this dataset, and the degradation process is more complicated, leading to a slight decrease in accuracy. However, the model still maintains a high level of estimation accuracy, verifying its effectiveness in complex degradation scenarios.
The strong performance documented in
Figure 5 and
Table 2 is a direct consequence of the physically informed feature engineering strategy. As established in
Section 2.1, the feature fragments are dynamically extracted from a voltage window anchored to the IC peak. The IC peak serves as a reliable proxy for internal electrochemical phase transitions, and its evolutionary characteristics, such as the reduction in peak amplitude and shifts in peak position, are highly correlated with key degradation mechanisms. Therefore, the high accuracy of the model stems from its ability to process inputs that directly quantify the progression of these critical aging modes. This linkage between the model’s inputs and the battery’s underlying electrochemistry provides a clear mechanistic explanation for its robust quantitative performance.
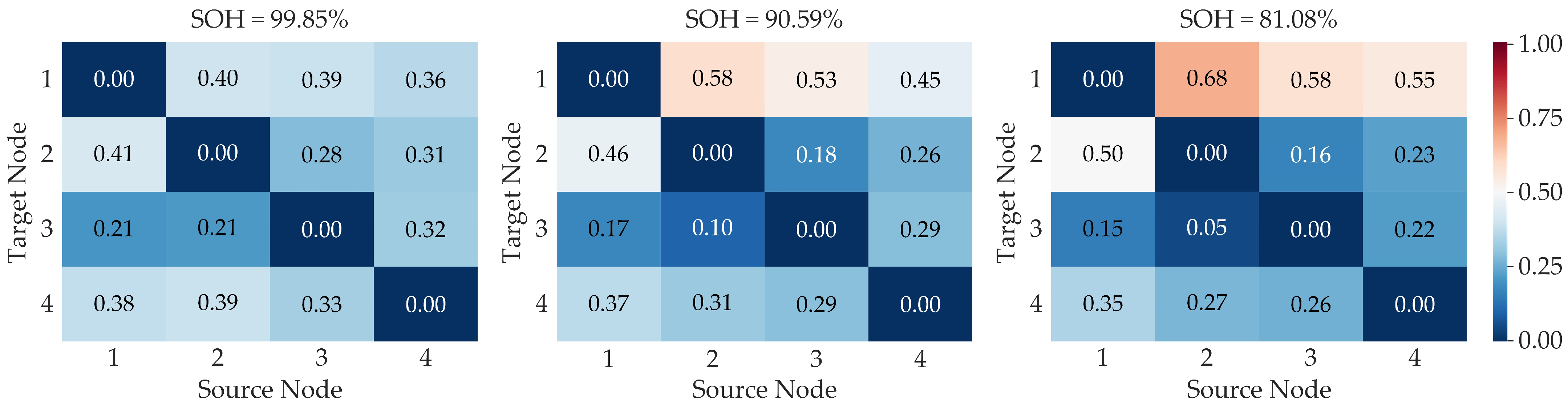
To provide insight into the model’s internal decision-making process, the attention mechanism of the GAT is visualized.
Figure 6 displays the attention heatmaps for a representative battery at different aging stages selected based on SOH values. The results reveal a clear evolution in the model’s analytical priorities as the battery degrades.
In the early stage when aging characteristics are subtle, the model’s attention is relatively distributed across multiple feature relationships. As the battery enters the mid stage, a clear trend of prioritization emerges. The model assigns heightened importance to the information that target node 1 receives, particularly from source nodes 2 and 3. This indicates the model begins to identify the initial segment of the voltage window as a critical area for information integration. Finally, in the late stage, the analytical priority becomes highly specific. The attention that target node 1 pays to source node 2 becomes the single most dominant relationship in the matrix. This demonstrates that the model has successfully distilled the most critical indicator for severe degradation. This evolution from a broad analysis to a specific one showcases the model’s ability to dynamically learn and adapt its strategy, providing strong evidence for the interpretability of our proposed model.
4.2. Comparision of Methods
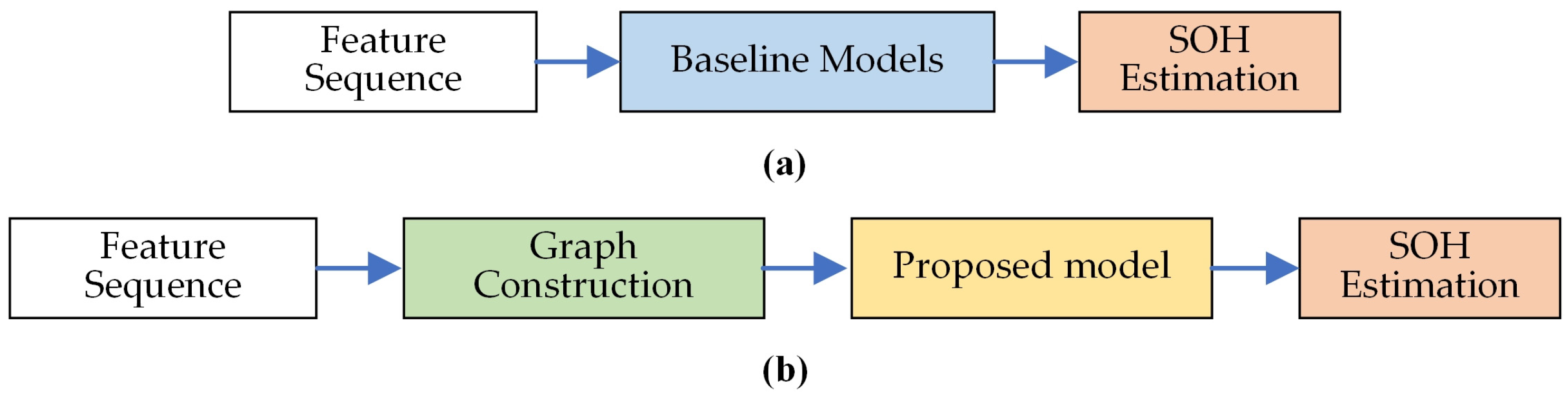
In this paper, the benchmark deep learning methods GRU, CNN-LSTM, CNN-GRU and Transformer are utilized to compare with the proposed method, where the inputs of the comparison method are feature sequences created by concatenating the voltage and capacity sequences. The baseline models and the proposed method take fundamentally different architectural approaches to processing the input features.
Figure 7 provides a schematic comparison of the data processing pipelines to visually illustrate these differences. The baseline models directly input the feature sequence into their respective architectures to learn temporal patterns. In contrast, the proposed method first transforms this sequence into a graph structure, enabling the explicit capture of spatial correlations between feature fragments before temporal modeling. The SOH estimation results are shown in
Figure 8 and
Table 3.
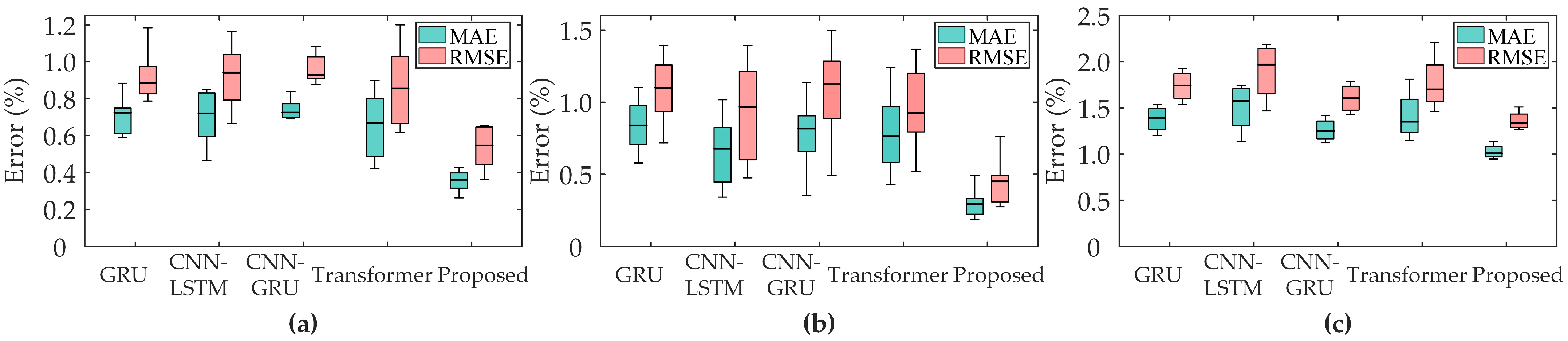
Figure 8 shows SOH estimation results of Batch1, Batch2 and CX2 in different methods, respectively.
Table 3 presents the error metrics of different methods across datasets, with the best results for each dataset highlighted in bold. Our proposed method has the lowest MAE and RMSE, indicating its superior accuracy. As can be seen from the boxplots, the GRU method exhibits relatively high MAE and RMSE values, indicating substantial estimation errors. Although CNN-LSTM, CNN-GRU, and Transformer reduce average errors compared to GRU, they still underperform the proposed method. This suggests inherent limitations in conventional deep learning approaches for SOH estimation, particularly in effectively leveraging spatial feature information. Moreover, the proposed method maintains low errors across datasets, demonstrating strong stability and generalization. This indicates that the proposed method is highly adaptable to different types of battery data and can be applied to a variety of battery SOH estimation scenarios.
The preceding comparison demonstrates the superiority of the proposed method over conventional sequence-based models. However, a pertinent question arises as to whether this advantage stems primarily from the model’s architecture or from the graph-based data representation itself. To decouple these factors and facilitate a more direct comparison, a further experiment is conducted. In this experiment, the benchmark models are adapted to accept graph-structured inputs by integrating a GAT layer, thereby ensuring an identical input format across all models. The results of this augmented comparison are presented in
Table 4.
A comparison between
Table 3 and
Table 4 reveals that the integration of a GAT layer and graph-structured inputs leads to a general improvement in the estimation accuracy of the benchmark models. For instance, the MAE of the GRU model on the XJTU-Batch1 dataset improved from 0.706% to 0.395%. This finding underscores the value of explicitly modeling the spatial correlations between feature fragments via the proposed graph construction strategy. Crucially, even under these modified conditions, the proposed GAT-BiGRU-Res model consistently exhibits the lowest error and highest R
2 values across most datasets. This indicates that while the graph representation provides a significant benefit, the unique architectural combination of GAT for spatial feature extraction and BiGRU for capturing bi-directional temporal dependencies offers a distinct and synergistic advantage. The results suggest that this specific architecture is more effective at learning a comprehensive representation of the battery degradation process than simply applying a GAT layer to conventional sequence models.
4.3. Data Sensitivity Analysis
4.3.1. Sensitivity to Voltage Ranges
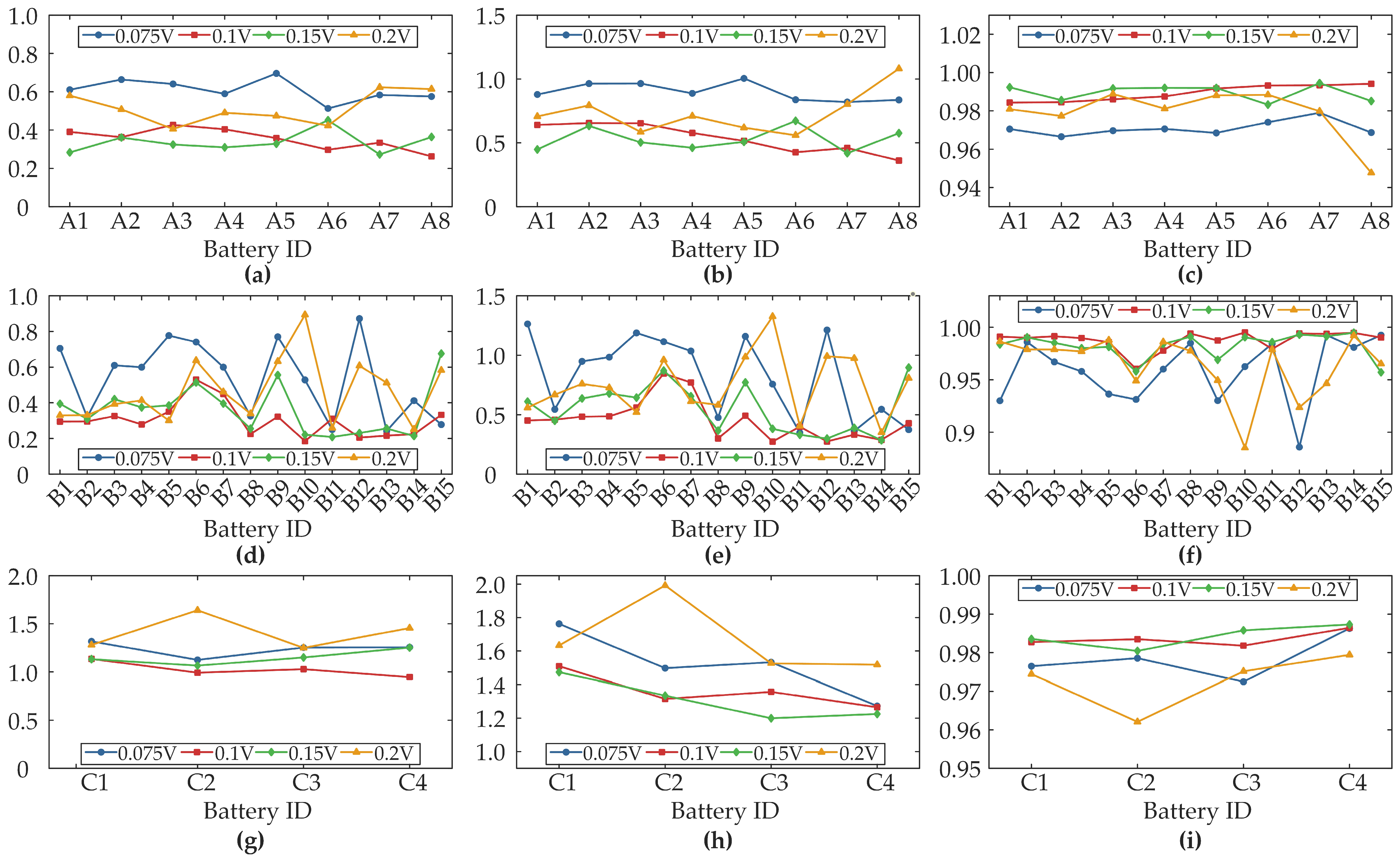
In order to investigate the effect of different voltage ranges on model performance, SOH estimation is validated for different voltage ranges. Specifically, four voltage window sizes were selected for comparative analysis: 0.075 V, 0.1 V, 0.15 V, and 0.2 V.
Figure 9 demonstrates the impact of voltage window selection on SOH estimation performance for the proposed method.
Table 5 presents the error results for different voltage ranges across datasets, where the best result for each dataset within each voltage range is highlighted in bold.
The results show that the 0.1 V range achieves optimal balance between accuracy and computational efficiency, capturing critical polarization features while avoiding noise sensitivity in shorter segments (0.075 V) and feature redundancy in longer segments (0.2 V). Although a 0.15 V range delivers comparable accuracy to the 0.1 V benchmark, the optimal choice is determined by factors related to practical implementation and robustness, as neither setting demonstrates a consistent performance advantage across all datasets. The primary differentiating factor is the data requirement. The 0.15 V window is substantially wider, which demands a larger, uninterrupted segment of charging data. This increased requirement can limit the algorithm’s applicability in real-world scenarios where charging sessions are often fragmented. Thus, employing the 0.1 V voltage window enables accurate SOH estimation across complex degradation scenarios, simultaneously ensuring model efficiency and enhancing deployment feasibility for practical battery management systems.
4.3.2. Sensitivity to Graph Connectivity
To empirically validate the principled selection of
as justified in
Section 2.2, we performed a sensitivity analysis by varying
from 1 to 3. This experiment aims to confirm that modeling the complete relational structure of the feature segments leads to optimal performance. The results are presented in
Table 6.
The results in
Table 6 provide strong empirical support for our selection. It demonstrates a monotonic improvement in model performance across all metrics as
increases from 1 to 3. This trend confirms that a fully connected graph enables the GAT to capture the most comprehensive set of spatial dependencies, thereby achieving the highest estimation accuracy. It also confirms the importance of graph density for the model’s ability to capture the intricate relationships between feature fragments. When
, each node aggregates information from only its single most similar neighbor, resulting in limited information flow and potentially preventing the model from perceiving global dependencies. As
increases, the graph becomes denser, allowing the GAT to aggregate features from a wider neighborhood when updating each node’s representation. Finally, at
, the graph is fully connected, enabling each node to consider the influence of all other nodes, thus forming the most comprehensive and holistic representation of the battery’s internal state. Therefore, a fully connected graph empowers the GAT to capture the most complete set of spatial dependencies, which yields the highest estimation accuracy.
4.3.3. Sensitivity to the Number of Nodes
The number of feature sub-segments, which corresponds to the number of nodes in the constructed graph, is a critical hyperparameter that defines the model’s analytical granularity. This study proposes a 4-node configuration, a choice that represents a deliberate trade-off between model resolution and complexity. A coarser segmentation (e.g., 2 nodes) may oversimplify the representation of the battery’s degradation process and fail to capture important localized features. Conversely, an overly fine segmentation (e.g., 8 or 16 nodes) can increase model complexity and introduce data redundancy, potentially amplifying the effect of noise without yielding proportional gains in accuracy. To empirically validate the selection of four nodes, a sensitivity analysis is conducted to compare its performance against configurations with coarser and finer granularities. The results of this analysis are summarized in
Table 7.
The results presented in
Table 7 provide strong validation for the proposed 4-node configuration. For the XJTU_Batch1 and CALCE_CX2 datasets, the 4-node model achieves optimal performance, demonstrating the lowest MAE and RMSE values. While the 8-node configuration shows a marginally lower MAE for the XJTU_Batch2 dataset, the proposed 4-node model exhibits a superior RMSE and R
2 value, indicating a more balanced and robust performance overall.
A consistent pattern emerges across all datasets: increasing the number of nodes from 2 to 4 yields a significant improvement in estimation accuracy. However, further increasing the granularity to 8 or 16 nodes provides no consistent or substantial benefits and, in several instances, leads to a minor degradation in performance. This trend suggests that the 4-node configuration effectively captures the essential characteristics of the aging process. Finer segmentations appear to offer diminishing returns, introducing complexity without enhancing the model’s ability to generalize. Therefore, this analysis confirms that the choice of four nodes is a well-justified selection, establishing an effective balance between feature resolution and model complexity.
4.4. Model Generalization Performance Analysis
The generalization of the proposed method is further verified in this section by training the model on data from the first four batteries in Batch1 and testing it on the remaining batteries from the same batch. According to
Figure 10, the proposed model performs well in tracking the dynamic changes in health state and is highly consistent with trend of the actual values, which verifies effectiveness of the proposed model in capturing the batteries degradation trend. The error analysis shows that the model maintains a high estimation accuracy during most of the cycles, despite large prediction bias in some cycles. In addition, consistency of the model’s performance on different batteries proves its good generalization ability to adapt to differences between different battery individuals.
Table 8 shows that the proposed model provides reliable SOH estimation results on different batteries. The average MAE, RMSE, and R
2 values for all batteries are 0.608, 0.802, and 0.977, respectively, which indicates that the proposed model achieves high accuracy across different batteries and effectively handles battery-to-battery variations, demonstrating good generalization capability.
4.5. Analysis of Model Deployment Feasibility
The practical utility of an SOH estimation algorithm is contingent not only on its accuracy but also on its feasibility for deployment on resource-constrained hardware. Therefore, we conducted an analysis of the proposed model’s deployment readiness, and metrics including network parameters, size, floating point operations (FLOPs), multiply–accumulate operations (MACs), inference memory, and inference time are evaluated, with the results summarized in
Table 9. The results show that model’s architecture is relatively lightweight, comprising approximately 0.45 million parameters, requiring 1.68 MFLOPs per inference, and exhibiting a memory footprint increase of only 0.46 MB during execution. To test its real-world performance on an edge device, the model is executed on a Raspberry Pi 4 B (Raspberry Pi Ltd., Cambridge, UK), with a 1.5 GHz 64-bit quad-core Arm Cortex-A72 CPU and 8 GB of RAM. The test results show an average inference time of just 17.55 ms. In addition, the methodology utilizes charging data are standard outputs from the sensors universally equipped in commercial BMS hardware. The model’s requirement for low-frequency sampling is well within the typical operational parameters of these sensors. This confirms that the input data requirements do not pose a significant implementation challenge.
Collectively, these metrics provide strong evidence for the model’s deployment feasibility. The modest parameter count, low operational complexity, and fast inference speed on a representative embedded system strongly support its suitability for real-time SOH estimation on modern BMS platforms. This performance profile suggests the model is well-suited for contemporary hardware environments, while its application in systems with more severe resource constraints may warrant specific consideration.
4.6. Performance Evaluation with Noisy and Incomplete Data
To evaluate the model’s suitability for real-world BMS applications, where data can be imperfect, two experiments are conducted to assess the model’s robustness against sensor noise and data loss. The input feature sequences of the test set are modified for this purpose, and the results are summarized in
Table 10 and
Table 11.
First, to simulate the effect of sensor noise, additive white gaussian noise is added to the input features. The intensity of the noise is quantified using the signal-to-noise ratio (SNR) in decibels (dB). Three levels are tested: a low-noise condition (30 dB), a medium-noise condition (25 dB), and a high-noise condition (20 dB). As shown in
Table 10, the model’s performance degrades gracefully as the noise level increases, demonstrating its resilience to measurement noise. To simulate intermittent data loss, a portion of the data points are randomly removed from the input sequences and subsequently filled using interpolation. The results in
Table 11 show a similar trend of graceful degradation. The estimation error increases with the rate of missing data, but the model avoids catastrophic failure, underscoring its ability to extract stable features from incomplete data. This analysis confirms the model’s robustness, a critical attribute for practical deployment. However, the results also underscore that more reliable input data are crucial for optimal model performance. While the model demonstrates resilience by avoiding catastrophic failure, its estimation precision noticeably decreases under severe noise and high data loss rates. This reveals a practical limitation: the model’s reduced accuracy in these extreme scenarios might be insufficient for applications that require high-precision performance.
5. Conclusions
In this paper, a novel GAT-BiGRU-Res model for SOH estimation of Li-ion batteries based on feature fragment data are proposed and validated. The study successfully demonstrates an interpretable feature engineering approach where an aging-sensitive 0.1 V voltage window, dynamically selected via IC peak analysis, effectively extracts physically meaningful feature fragments. The proposed synergistic architecture, leveraging a graph attention network for spatial correlations and a bi-directional gated recurrent unit for temporal dependencies, is then shown to adeptly leverage these high-quality inputs. This integrated methodology achieves excellent accuracy with MAEs of 0.355%, 0.303%, and 1.025% on the XJTU-Batch1, XJTU-Batch2, and CALCE-CX2 datasets, respectively. From an industrial perspective, the significance of this work lies in its excellent balance between high accuracy and computational efficiency. With only 0.45 million parameters and requiring just 1.68 MFLOPs per inference, the model achieves a rapid average inference time of 17.55 ms on a representative embedded device. This quantified efficiency confirms its strong potential for deployment in real-time, resource-constrained embedded platforms, thereby enhancing the safety and reliability of energy storage systems.
While the current findings are promising, acknowledging the study’s scope is crucial for charting future research pathways. The model’s efficacy is established using widely recognized public benchmark datasets with standardized testing protocols. However, these protocols do not encompass all dynamic scenarios in real-world applications. Future work should therefore focus on three key areas: (1) expanding validation to a wider range of datasets that incorporate diverse operational scenarios, (2) investigating the influence of temperature on the degradation mechanisms reflected in the IC curve to develop temperature-adaptive models, and (3) exploring transfer learning techniques to facilitate rapid adaptation to new battery chemistries. By addressing these aspects, the proposed framework can be evolved into a more universally applicable and trustworthy solution for advanced battery diagnostics.