Multi-Sensor Heterogeneous Signal Fusion Transformer for Tool Wear Prediction
Abstract
1. Introduction
- Multi-domain feature fusion strategy for multi-sensor heterogeneous signals: Effectively integrates multi-source industrial sensor signals through collaborative modeling of time-domain, frequency-domain, and time–frequency-domain features, providing feature-re-engineering-free extensibility to diverse sensor types while leveraging complementary signal characteristics.
- Position-embedding-free MSMDT network design: Enables parallel processing and real-time collaborative prediction of cross-sensor information, enhancing effective feature fusion for heterogeneous temporal signals.
- Breakthrough in single-sensor and single-feature dependency limitations: The proposed method can adaptively extract deep-level features that characterize tool wear and automatically predict its progression, achieving promising results.
2. Related Work
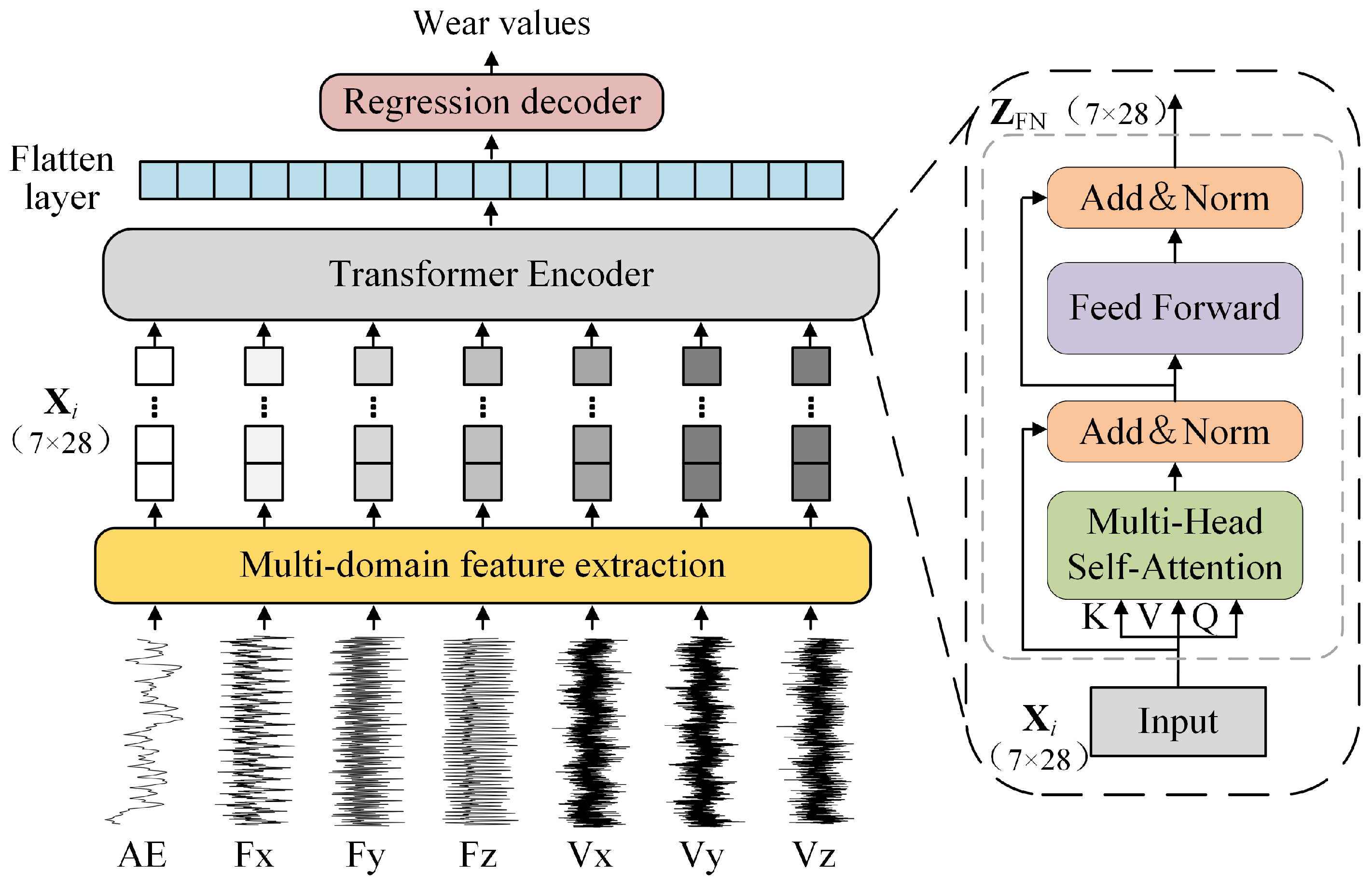
3. MSMDT
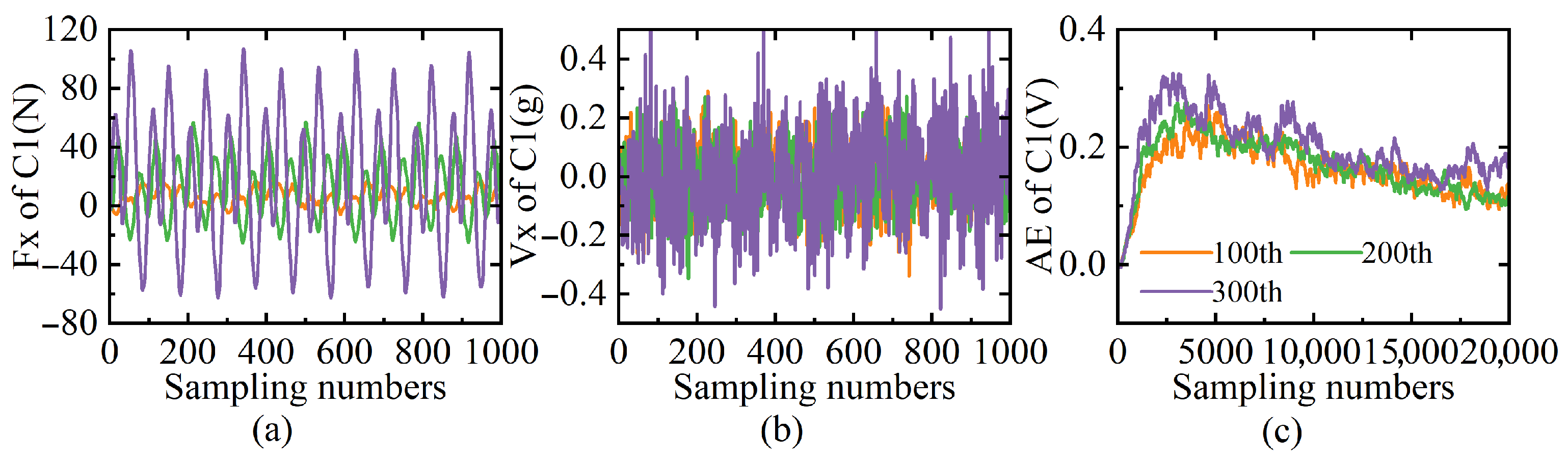
3.1. Multi-Sensor Signal Input
- Acoustic emission sensors are cost-effective and readily available, but they are prone to mechanical noise and require complex signal analysis.
- Cutting force sensors are highly sensitive to tool wear signals and provide accurate monitoring, albeit at a higher cost.
- Vibration sensors offer easy installation, low cost, and abundant information, but they are susceptible to environmental interference.
3.2. Multi-Domain Feature Extraction
- Time domain (9 features): Statistical descriptors of signal amplitudes, including standard deviation, variance, peak-to-peak, RMS value, skewness coefficient, kurtosis coefficient, crest factor, margin factor, and waveform factor.
- Frequency domain (3 features): Spectral characteristics including center gravity frequency, frequency variance, and mean square frequency.
- Time–frequency domain (16 features): Wavelet packet decomposition energies across 16 sub-bands.
| Domain | Feature | Expression | Explanation |
|---|---|---|---|
| Time domain (9 features) | Standard deviation | Sample standard deviation | |
| Variance | Sample variance | ||
| Peak-to-peak | Difference between extrema | ||
| RMS value | Root mean square | ||
| Skewness coefficient | 3rd standardized moment | ||
| Kurtosis coefficient | Excess kurtosis | ||
| Crest factor | Peak-to-RMS ratio | ||
| Margin factor | Peak-to-average ratio | ||
| Waveform factor | RMS-to-average ratio | ||
| Frequency domain (3 features) | Center gravity frequency | Spectral centroid | |
| Frequency variance | Spectral spread | ||
| Mean square frequency | Spectral RMS | ||
| Time–frequency domain (16 features) | Wavelet packet energy | Decomposition energy |
3.3. Backbone Structure
3.3.1. Input Representation and Tokenization
3.3.2. Position-Embedding-Free Inter-Sensor Interaction
3.3.3. Encoder Computational Architecture
- (1)
- Multi-Head Self-Attention Mechanism
- (2)
- Layer-wise Processing
3.4. Regression Decoder
4. Experimentation and Validation
4.1. Experimental Setup
4.1.1. Datasets and Preprocessing
4.1.2. Model Configuration and Hyperparameters
4.1.3. Evaluation Metrics
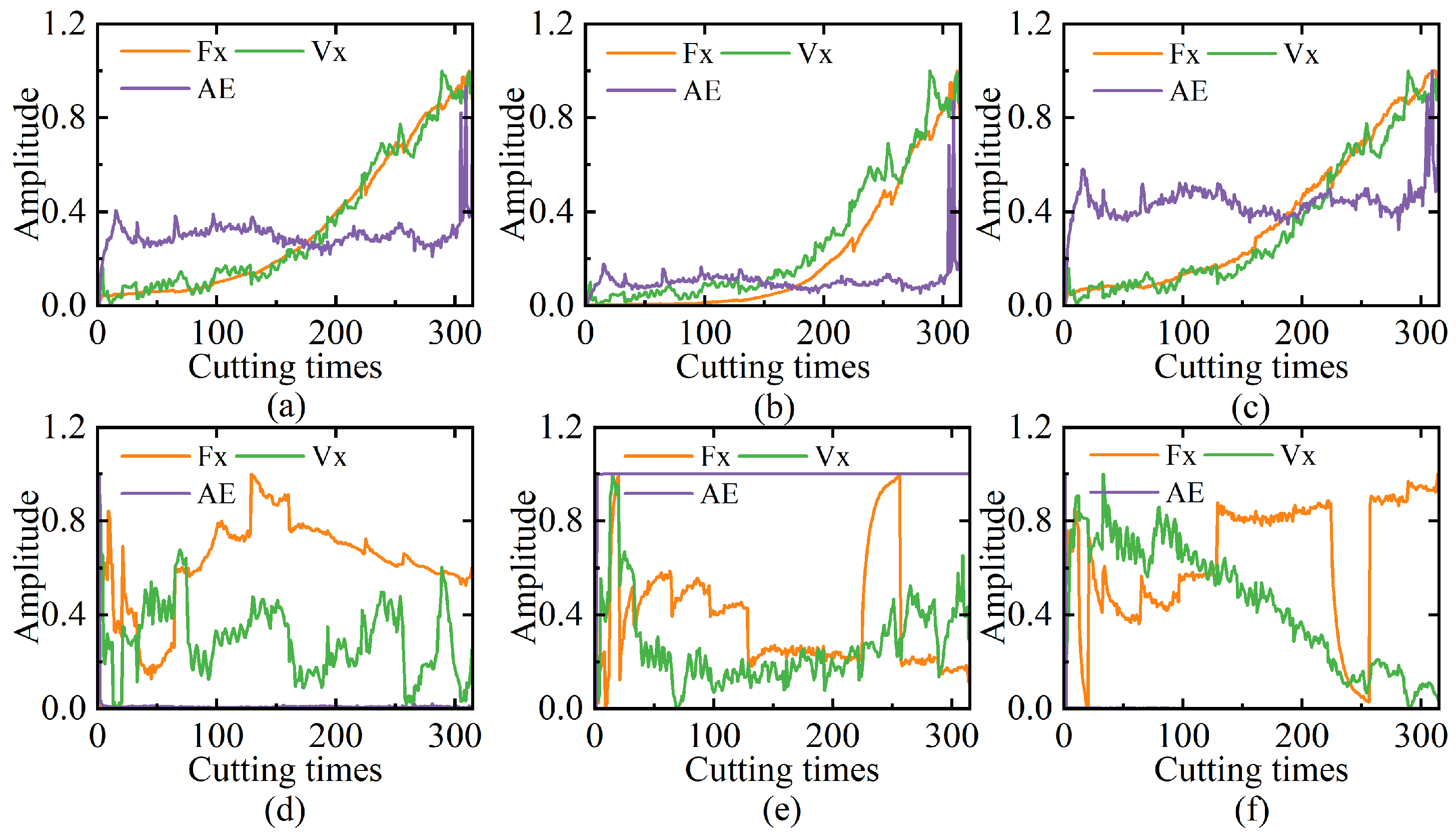
4.2. Visualization and Analysis of Multi-Sensor Features
4.3. Ablation Experiment
4.3.1. Ablation Experiment on Multi-Sensor Signal Input
4.3.2. Ablation Experiment on Multi-Domain Feature Selection
4.3.3. Ablation Experiment on Position Embedding
4.3.4. Ablation Experiment on Multi-Head Attention
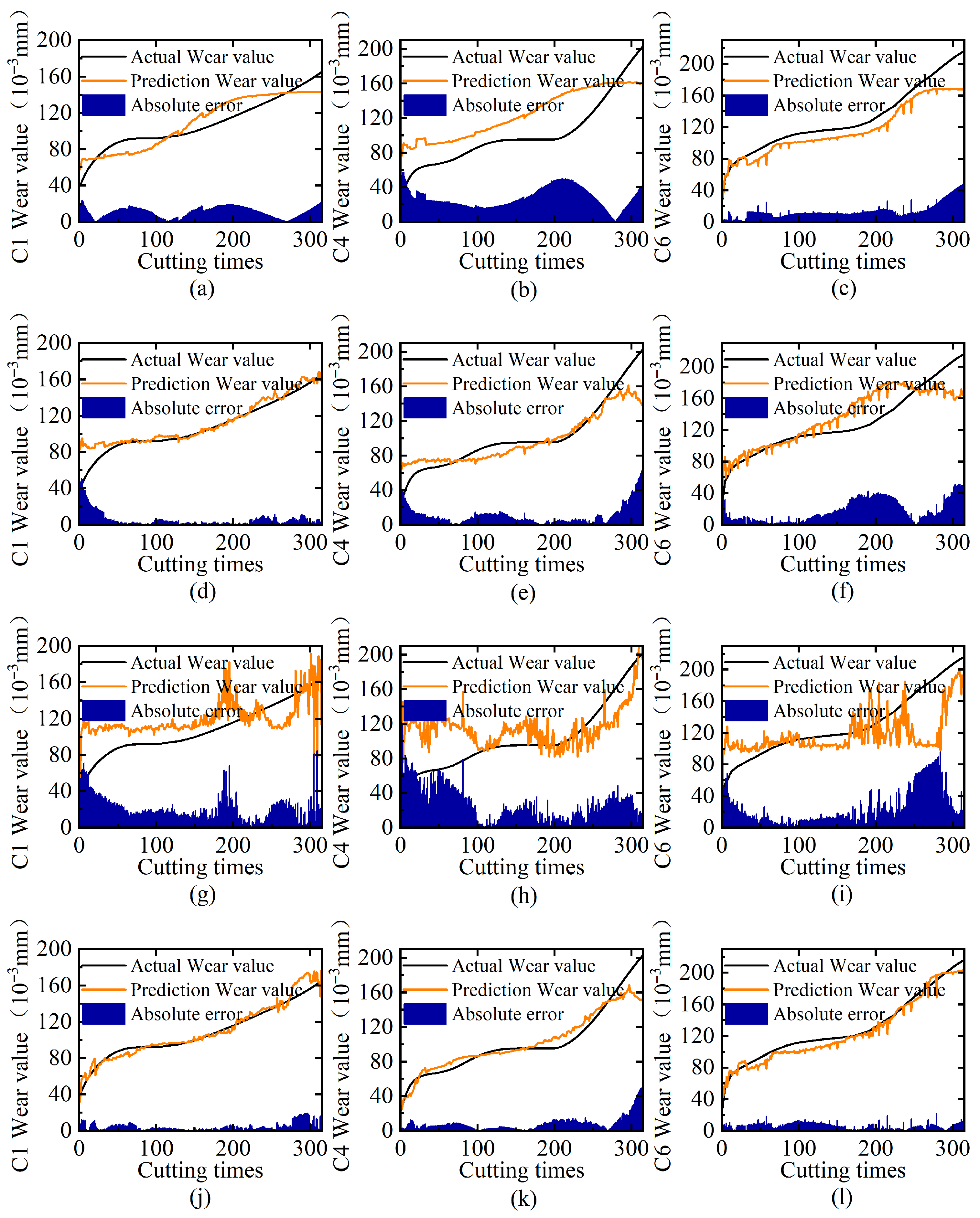
4.4. Comparison with Other Methods
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Banda, T.; Farid, A.A.; Li, C.; Jauw, V.L.; Lim, C.S. Application of machine vision for tool condition monitoring and tool performance optimization–A review. Int. J. Adv. Manuf. Technol. 2022, 121, 7057–7086. [Google Scholar] [CrossRef]
- Zhang, X.; Lu, X.; Wang, S.; Wang, W.; Li, W. A multi-sensor based online tool condition monitoring system for milling process. Procedia CIRP 2018, 72, 1136–1141. [Google Scholar] [CrossRef]
- Munaro, R.; Attanasio, A.; Del Prete, A. Tool Wear Monitoring with Artificial Intelligence Methods: A Review. J. Manuf. Mater. Process. 2023, 7, 129. [Google Scholar] [CrossRef]
- Zhu, K.; Yu, X. The monitoring of micro milling tool wear conditions by wear area estimation. Mech. Syst. Signal Process. 2017, 93, 80–91. [Google Scholar] [CrossRef]
- Čerče, L.; Pušavec, F.; Kopač, J. 3D cutting tool-wear monitoring in the process. J. Mech. Sci. Technol. 2015, 29, 3885–3895. [Google Scholar] [CrossRef]
- Caesarendra, W.; Triwiyanto, T.; Pandiyan, V.; Glowacz, A.; Permana, S.D.H.; Tjahjowidodo, T. A CNN prediction method for belt grinding tool wear in a polishing process utilizing 3-axes force and vibration data. Electronics 2021, 10, 1429. [Google Scholar] [CrossRef]
- Huang, Z.; Zhu, J.; Lei, J.; Li, X.; Tian, F. Tool wear monitoring with vibration signals based on short-time Fourier transform and deep convolutional neural network in milling. Math. Probl. Eng. 2021, 2021, 9976939. [Google Scholar] [CrossRef]
- Bhaskaran, J. On-line monitoring the hard turning using distribution parameters of acoustic emission signal. Appl. Mech. Mater. 2015, 787, 907–911. [Google Scholar] [CrossRef]
- de Farias, A.; de Almeida, S.L.R.; Delijaicov, S.; Seriacopi, V.; Bordinassi, E.C. Simple machine learning allied with data-driven methods for monitoring tool wear in machining processes. Int. J. Adv. Manuf. Technol. 2020, 109, 2491–2501. [Google Scholar] [CrossRef]
- Jantunen, E. A summary of methods applied to tool condition monitoring in drilling. Int. J. Mach. Tools Manuf. 2002, 42, 997–1010. [Google Scholar] [CrossRef]
- Zhu, G.; Hu, S.; Tang, H. Prediction of tool wear in CFRP drilling based on neural network with multicharacteristics and multisignal sources. Compos. Adv. Mater. 2021, 30, 1–15. [Google Scholar] [CrossRef]
- Rodrigo Henriques Lopes da Silva, M.B.d.S.; Hassui, A. A probabilistic neural network applied in monitoring tool wear in the end milling operation via acoustic emission and cutting power signals. Mach. Sci. Technol. 2016, 20, 386–405. [Google Scholar] [CrossRef]
- Shah, M.; Borade, H.; Dave, V.; Agrawal, H.; Nair, P.; Vakharia, V. Utilizing TGAN and ConSinGAN for improved tool wear prediction: A comparative study with ED-LSTM, GRU, and CNN models. Electronics 2024, 13, 3484. [Google Scholar] [CrossRef]
- Rmili, W.; Ouahabi, A.; Serra, R.; Leroy, R. An automatic system based on vibratory analysis for cutting tool wear monitoring. Measurement 2016, 77, 117–123. [Google Scholar] [CrossRef]
- Elangovan, M.; Devasenapati, S.B.; Sakthivel, N.; Ramachandran, K. Evaluation of expert system for condition monitoring of a single point cutting tool using principle component analysis and decision tree algorithm. Expert Syst. Appl. 2011, 38, 4450–4459. [Google Scholar] [CrossRef]
- Lin, Y.R.; Lee, C.H.; Lu, M.C. Robust tool wear monitoring system development by sensors and feature fusion. Asian J. Control 2022, 24, 1005–1021. [Google Scholar] [CrossRef]
- Rafezi, H.; Akbari, J.; Behzad, M. Tool Condition Monitoring based on sound and vibration analysis and wavelet packet decomposition. In Proceedings of the 2012 8th International Symposium on Mechatronics and its Applications, Sharjah, United Arab Emirates, 10–12 April 2012; pp. 1–4. [Google Scholar] [CrossRef]
- Fu, Y.; Zhang, Y.; Gao, Y.; Gao, H.; Mao, T.; Zhou, H.; Li, D. Machining vibration states monitoring based on image representation using convolutional neural networks. Eng. Appl. Artif. Intell. 2017, 65, 240–251. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, J.; Mo, R.; Zhang, X. In-process tool condition forecasting based on a deep learning method. Robot. Comput.-Integr. Manuf. 2020, 64, 101924. [Google Scholar] [CrossRef]
- Wang, C.; Wang, G.; Wang, T.; Xiong, X.; Ouyang, Z.; Gong, T. Exploring the Processing Paradigm of Input Data for End-to-End Deep Learning in Tool Condition Monitoring. Sensors 2024, 24, 5300. [Google Scholar] [CrossRef]
- Gao, D.; Liao, Z.; Lv, Z.; Lu, Y. Multi-scale statistical signal processing of cutting force in cutting tool condition monitoring. Int. J. Adv. Manuf. Technol. 2015, 80, 1843–1853. [Google Scholar] [CrossRef]
- Zhang, P.; Gao, D.; Lu, Y.; Ma, Z.; Wang, X.; Song, X. Cutting tool wear monitoring based on a smart toolholder with embedded force and vibration sensors and an improved residual network. Measurement 2022, 199, 111520. [Google Scholar] [CrossRef]
- Morgan, J.; O’Donnell, G.E. Cyber physical process monitoring systems. J. Intell. Manuf. 2018, 29, 1317–1328. [Google Scholar] [CrossRef]
- Alonso, F.; Salgado, D. Analysis of the structure of vibration signals for tool wear detection. Mech. Syst. Signal Process. 2008, 22, 735–748. [Google Scholar] [CrossRef]
- Sorgato, M.; Bertolini, R.; Ghiotti, A.; Bruschi, S. Tool wear analysis in high-frequency vibration-assisted drilling of additive manufactured Ti6Al4V alloy. Wear 2021, 477, 203814. [Google Scholar] [CrossRef]
- Danielak, M.; Witaszek, K.; Ekielski, A.; Żelaziński, T.; Dudnyk, A.; Durczak, K. Wear Detection of Extruder Elements Based on Current Signature by Means of a Continuous Wavelet Transform. Processes 2023, 11, 3240. [Google Scholar] [CrossRef]
- Wang, K.; Wang, A.; Wu, L.; Xie, G. Machine tool wear prediction technology based on multi-sensor information fusion. Sensors 2024, 24, 2652. [Google Scholar] [CrossRef] [PubMed]
- Cai, W.; Zhang, W.; Hu, X.; Liu, Y. A hybrid information model based on long short-term memory network for tool condition monitoring. J. Intell. Manuf. 2020, 31, 1497–1510. [Google Scholar] [CrossRef]
- Marani, M.; Zeinali, M.; Songmene, V.; Mechefske, C.K. Tool wear prediction in high-speed turning of a steel alloy using long short-term memory modelling. Measurement 2021, 177, 109329. [Google Scholar] [CrossRef]
- He, X.; Zhong, M.; He, C.; Wu, J.; Yang, H.; Zhao, Z.; Yang, W.; Jing, C.; Li, Y.; Chen, G. A Novel Tool Wear Identification Method Based on a Semi-Supervised LSTM. Lubricants 2025, 13, 72. [Google Scholar] [CrossRef]
- Cheng, M.; Jiao, L.; Yan, P.; Jiang, H.; Wang, R.; Qiu, T.; Wang, X. Intelligent tool wear monitoring and multi-step prediction based on deep learning model. J. Manuf. Syst. 2022, 62, 286–300. [Google Scholar] [CrossRef]
- Chan, Y.W.; Kang, T.C.; Yang, C.T.; Chang, C.H.; Huang, S.M.; Tsai, Y.T. Tool wear prediction using convolutional bidirectional LSTM networks. J. Supercomput. 2022, 78, 810–832. [Google Scholar] [CrossRef]
- Li, X.; Qin, X.; Wu, J.; Yang, J.; Huang, Z. Tool wear prediction based on convolutional bidirectional LSTM model with improved particle swarm optimization. Int. J. Adv. Manuf. Technol. 2022, 123, 4025–4039. [Google Scholar] [CrossRef]
- Bazi, R.; Benkedjouh, T.; Habbouche, H.; Rechak, S.; Zerhouni, N. A hybrid CNN-BiLSTM approach-based variational mode decomposition for tool wear monitoring. Int. J. Adv. Manuf. Technol. 2022, 119, 3803–3817. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Red Hook, NY, USA, 4–9 December 2017; pp. 6000–6010. [Google Scholar] [CrossRef]
- Nath, A.G.; Udmale, S.S.; Raghuwanshi, D.; Singh, S.K. Structural Rotor Fault Diagnosis Using Attention-Based Sensor Fusion and Transformers. IEEE Sens. J. 2022, 22, 707–719. [Google Scholar] [CrossRef]
- Hou, Y.; Wang, J.; Chen, Z.; Ma, J.; Li, T. Diagnosisformer: An efficient rolling bearing fault diagnosis method based on improved Transformer. Eng. Appl. Artif. Intell. 2023, 124, 106507. [Google Scholar] [CrossRef]
- Zhong, S.; Ali, R. Joint Self-Attention Mechanism and Residual Network for Automated Monitoring of Intelligent Sensor in Consumer Electronics. IEEE Trans. Consum. Electron. 2024, 70, 1302–1309. [Google Scholar] [CrossRef]
- PHM Society. 2010 PHM Society Conference Data Challenge. 2010. Available online: https://phmsociety.org/2010-phm-data-challenge-comes-to-a-close/ (accessed on 18 May 2010).
- Zhao, R.; Wang, J.; Yan, R.; Mao, K. Machine health monitoring with LSTM networks. In Proceedings of the 2016 10th International Conference on Sensing Technology (ICST), Nanjing, China, 11–13 November 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Qiao, H.; Wang, T.; Wang, P.; Qiao, S.; Zhang, L. A Time-Distributed Spatiotemporal Feature Learning Method for Machine Health Monitoring with Multi-Sensor Time Series. Sensors 2018, 18, 2932. [Google Scholar] [CrossRef]
- Nie, L.; Zhang, L.; Xu, S.; Cai, W.; Yang, H. Remaining Useful Life Prediction of Milling Cutters Based on CNN-BiLSTM and Attention Mechanism. Symmetry 2022, 14, 2243. [Google Scholar] [CrossRef]
- He, Z.; Shi, T.; Chen, X. An Innovative Study for Tool Wear Prediction Based on Stacked Sparse Autoencoder and Ensemble Learning Strategy. Sensors 2025, 25, 2391. [Google Scholar] [CrossRef]

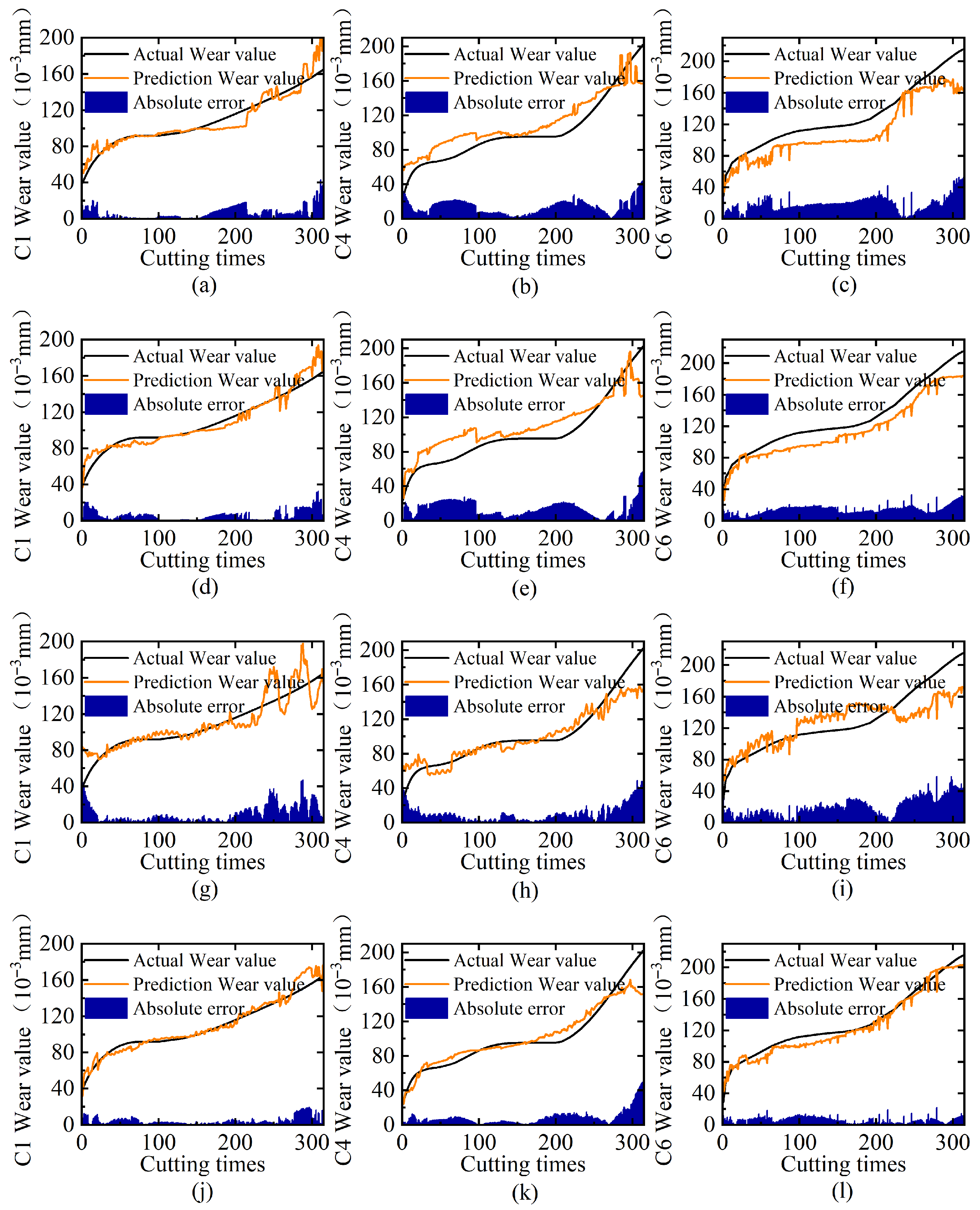
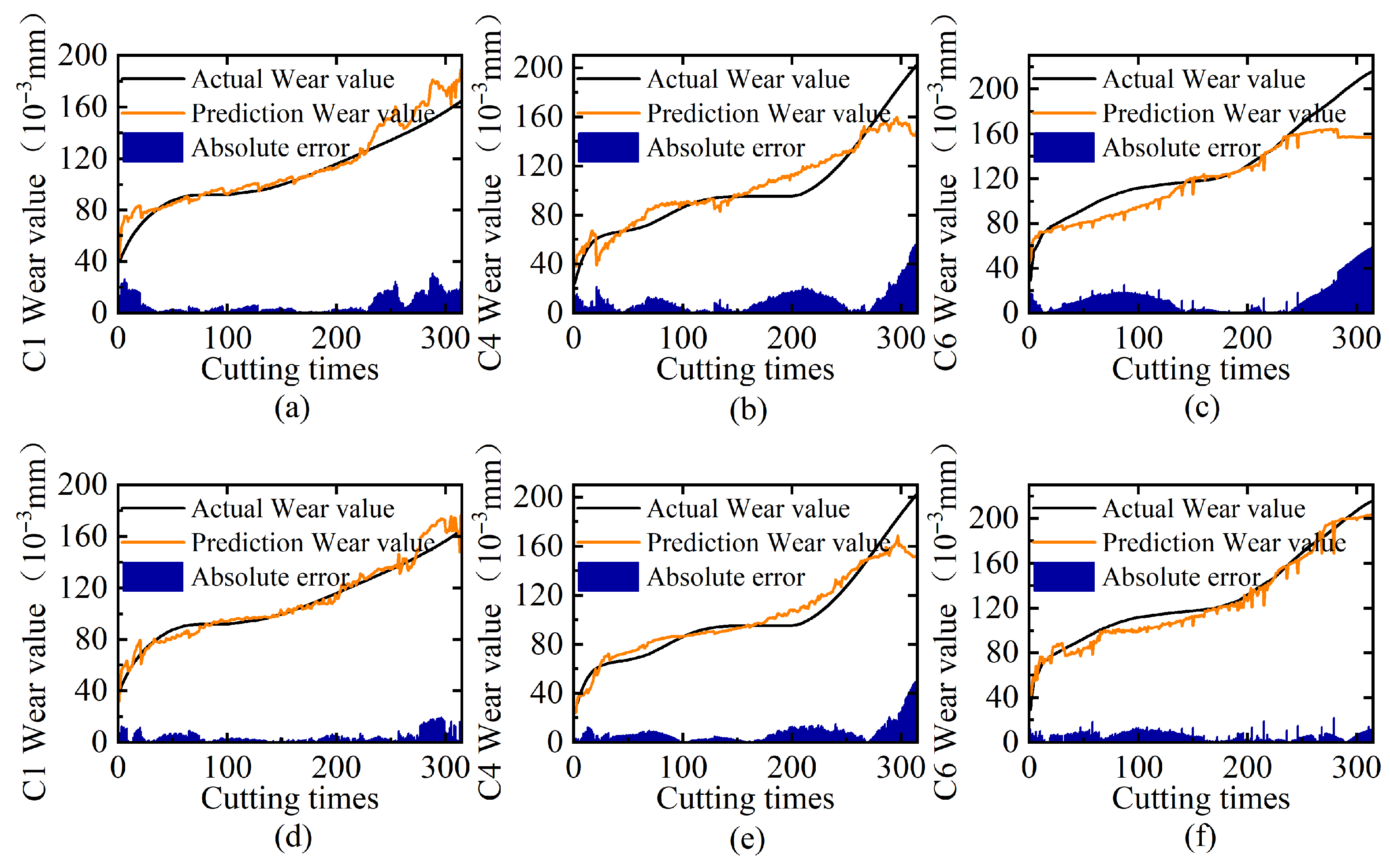
| Group | Train Set | Test Set |
|---|---|---|
| 1 | C4, C6 | C1 |
| 2 | C1, C6 | C4 |
| 3 | C1, C4 | C6 |
| Sensor Type | C1 | C4 | C6 | |||
|---|---|---|---|---|---|---|
| MAE | RMSE | MAE | RMSE | MAE | RMSE | |
| Cutting force sensor | 17.43 | 22.62 | 27.74 | 30.27 | 13.80 | 16.82 |
| Vibration sensor | 10.81 | 12.30 | 10.75 | 15.79 | 12.36 | 15.04 |
| AE sensor | 20.77 | 25.26 | 26.90 | 34.14 | 24.77 | 33.52 |
| Multi-sensor | 4.47 | 6.35 | 8.27 | 12.06 | 6.06 | 7.19 |
| Feature Domain | C1 | C4 | C6 | |||
|---|---|---|---|---|---|---|
| MAE | RMSE | MAE | RMSE | MAE | RMSE | |
| Time domain | 6.30 | 9.34 | 13.75 | 16.24 | 18.88 | 21.37 |
| Frequency domain | 5.60 | 8.13 | 14.34 | 17.45 | 14.29 | 15.38 |
| Time–frequency domain | 9.45 | 13.60 | 10.29 | 14.40 | 10.87 | 15.26 |
| Multi-domain | 4.47 | 6.35 | 8.27 | 12.06 | 6.06 | 7.19 |
| C1 | C4 | C6 | ||||
|---|---|---|---|---|---|---|
| MAE | RMSE | MAE | RMSE | MAE | RMSE | |
| With position embedding | 7.39 | 10.21 | 10.46 | 14.61 | 13.33 | 19.46 |
| Without position embedding | 4.47 | 6.35 | 8.47 | 12.06 | 6.06 | 7.19 |
| Heads | C1 | C4 | C6 | |||
|---|---|---|---|---|---|---|
| MAE | RMSE | MAE | RMSE | MAE | RMSE | |
| 1 | 5.17 | 6.49 | 8.19 | 12.34 | 14.80 | 17.92 |
| 4 | 7.20 | 9.26 | 11.50 | 13.19 | 7.81 | 9.43 |
| 7 | 4.73 | 5.97 | 11.70 | 14.22 | 13.13 | 15.61 |
| 14 | 4.47 | 6.35 | 8.27 | 12.06 | 6.06 | 7.19 |
| 28 | 5.82 | 9.37 | 7.90 | 12.11 | 6.05 | 8.44 |
| Method | C1 | C4 | C6 | |||
|---|---|---|---|---|---|---|
| MAE | RMSE | MAE | RMSE | MAE | RMSE | |
| LR | 24.4 | 31.1 | 16.3 | 19.3 | 24.4 | 30.9 |
| SVR | 15.6 | 18.5 | 17.0 | 19.6 | 24.9 | 31.5 |
| MLP | 24.5 | 31.2 | 18.0 | 20.0 | 24.8 | 31.4 |
| CNN | 9.31 | 12.19 | 11.29 | 14.59 | 34.69 | 40.48 |
| RNN | 13.1 | 15.6 | 16.7 | 19.7 | 25.5 | 32.9 |
| LSTM | 19.6 | 23.9 | 15.6 | 20.8 | 25.3 | 32.4 |
| Deep LSTMs [40] | 8.3 | 12.1 | 8.7 | 10.2 | 15.2 | 18.9 |
| CNN-LSTM [41] | 11.18 | 13.77 | 9.39 | 11.85 | 11.34 | 14.33 |
| CABLSTM [42] | 7.47 | 8.17 | - | - | - | - |
| BiLSTM [32] | 12.8 | 14.6 | 10.9 | 14.2 | 14.7 | 17.7 |
| CNN-BiLSTM [20] | 5.53 | 6.93 | 7.70 | 10.10 | 8.66 | 11.84 |
| SSAE [43] | - | 6.66 | - | 11.59 | - | 8.49 |
| MSMDT (Ours) | 4.47 | 6.35 | 8.27 | 12.06 | 6.06 | 7.19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, J.; Liu, X.; Liao, Q.; Wang, T.; Wang, L.; Yang, P. Multi-Sensor Heterogeneous Signal Fusion Transformer for Tool Wear Prediction. Sensors 2025, 25, 4847. https://doi.org/10.3390/s25154847
Zhou J, Liu X, Liao Q, Wang T, Wang L, Yang P. Multi-Sensor Heterogeneous Signal Fusion Transformer for Tool Wear Prediction. Sensors. 2025; 25(15):4847. https://doi.org/10.3390/s25154847
Chicago/Turabian StyleZhou, Ju, Xinyu Liu, Qianghua Liao, Tao Wang, Lin Wang, and Pin Yang. 2025. "Multi-Sensor Heterogeneous Signal Fusion Transformer for Tool Wear Prediction" Sensors 25, no. 15: 4847. https://doi.org/10.3390/s25154847
APA StyleZhou, J., Liu, X., Liao, Q., Wang, T., Wang, L., & Yang, P. (2025). Multi-Sensor Heterogeneous Signal Fusion Transformer for Tool Wear Prediction. Sensors, 25(15), 4847. https://doi.org/10.3390/s25154847






