Dual-Branch Deep Learning with Dynamic Stage Detection for CT Tube Life Prediction
Abstract
1. Introduction
2. Experiment Dataset and Preprocessing Step
2.1. Data Description
2.2. Preprocessing Step
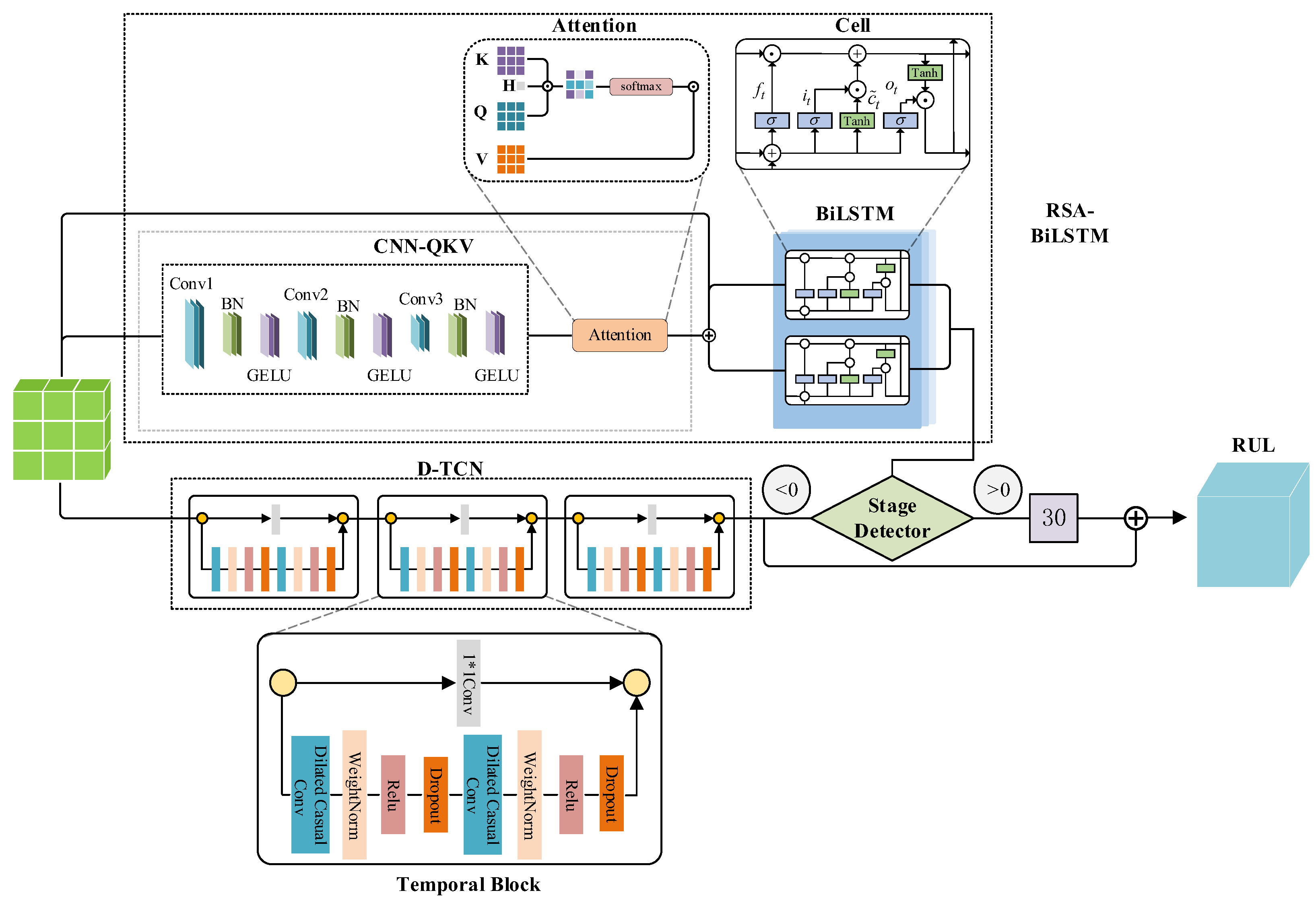
3. The Proposed Method
3.1. Method Overview
3.2. RSA-LSTM Branch
3.3. TCN Branch
3.4. Model Loss Function
3.5. Phase Detector Design and Phased Training Strategy
4. Case Study
4.1. Evaluation Metrics
- 1.
- Mean Squared Error (MSE): MSE is particularly suitable for RUL prediction as it heavily penalizes large prediction errors, which are critical in maintenance planning. In CT tube maintenance, a significant prediction error (e.g., predicting 20 days when actual RUL is 5 days) could lead to equipment failure and patient care disruption. MSE is calculated as Equation (45):where is the actual value, is the predicted value, and is the sample size. MSE evaluates the performance of prediction models through squared errors, which is sensitive to large errors.
- 2.
- Mean Absolute Error (MAE): MAE provides an intuitive understanding of average prediction accuracy in the same units as the target variable (days). This is directly interpretable by maintenance personnel who need to understand the typical prediction uncertainty when planning maintenance schedules. Unlike MSE, MAE is less sensitive to outliers, providing a robust measure of typical model performance. MAE calculated as
- 3.
- Coefficient of Determination (R2): R2 indicates how well the model explains the variance in RUL values, which is crucial for assessing model reliability across different CT tubes and operating conditions. In medical equipment maintenance, understanding the proportion of RUL variance that can be explained by the model helps in risk assessment and decision-making confidence. R2 is calculated aswhere is the mean of the actual values. The R2 value typically ranges between 0 and 1, with values closer to 1 indicating better model fit, meaning the model can explain more variance in the dependent variable. These three metrics provide complementary perspectives: MSE emphasizes accuracy in critical situations, MAE provides practical interpretability, and R2 assesses overall model reliability.
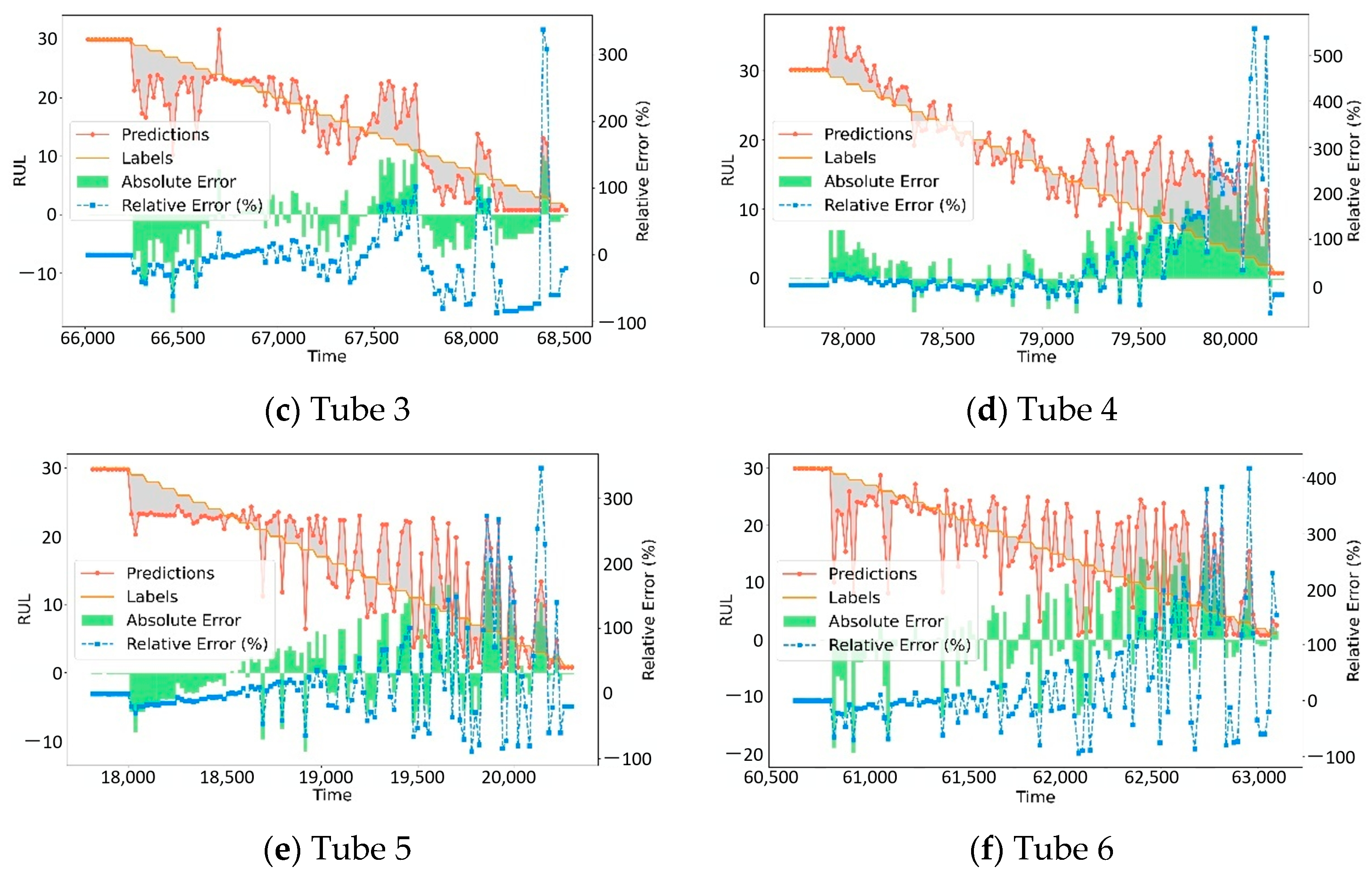
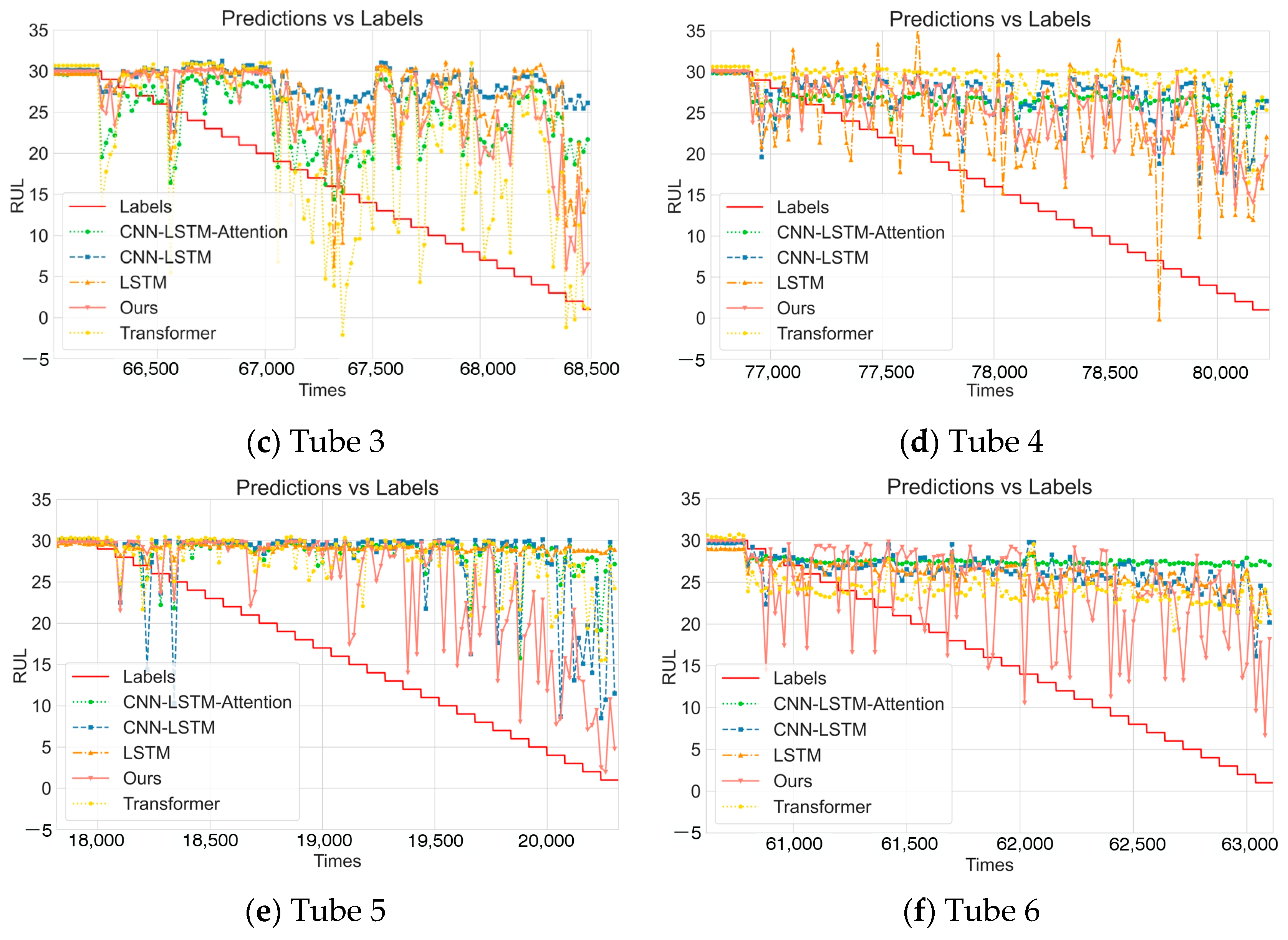
4.2. Comparative Experiments
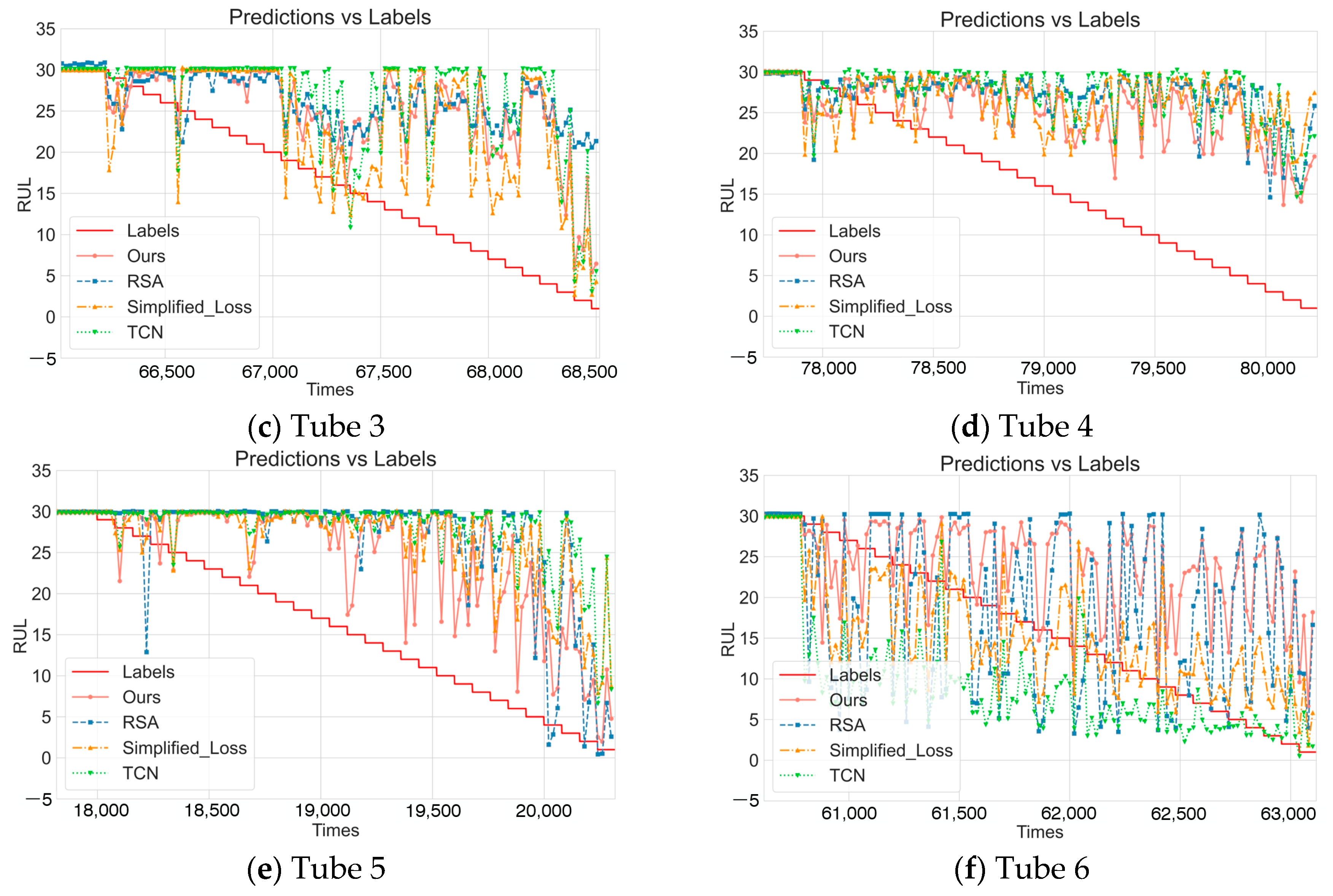
4.3. Ablation Study
- No pre-training model (No_Pretraining): Removed the pre-training phase, directly training with randomly initialized model parameters to verify the impact of the pre-training strategy on model performance.
- Residual self-attention model (RSA): Only retained the RSA-BiLSTM branch of DDLNet to evaluate the effectiveness of the RSA-BiLSTM branch acting alone.
- Simplified loss function model (Simplified_Loss): Used standard mean squared error (MSE) to replace the composite loss function proposed in this paper, removing the relative error term to verify the impact of loss function design on prediction accuracy.
- Temporal convolutional network model (TCN): Only retained the TCN branch to evaluate the effectiveness of the TCN branch acting alone.
4.4. Discussion
- (1)
- Domain Adaptation and Transferability
- (2)
- Practical System Integration and Deployment
- (3)
- Model Interpretability and Clinical Trust
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| RUL | Remaining Useful Life |
| CT | Computed Tomography |
| PdM | Predictive Maintenance |
| PvM | Preventive Maintenance |
| IoMT | Internet of Medical Things |
| DDLNet | Dual-branch Deep Learning Network |
| RSA-BiLSTM | Residual self-attention Bidirectional Long Short-Term Memory |
| D-TCN | Dilation-Temporal Convolutional Network |
| CNN | Convolutional Neural Network |
| LSTM | Long Short-Term Memory |
| QKV | Query-Key-Value |
| MSE | Mean Squared Error |
| MAE | Mean Absolute Error |
| R2 | Coefficient of Determination |
| EMA | Exponential Moving Average |
| SVR | Support Vector Regression |
| CLSTM | Convolutional Long Short-Term Memory |
| AEC | Automatic Exposure Control |
| ZEC | Z-direction Exposure Control |
| LOOCV | Leave-One-Out Cross-Validation |
References
- Kassavin, M.; Chang, K.J. Computed Tomography Colonography: 2025 Update. Radiol. Clin. 2025, 63, 405–417. [Google Scholar] [CrossRef]
- Tamizuddin, F.; Stojanovska, J.; Toussie, D.; Shmukler, A.; Axel, L.; Srinivasan, R.; Fujikura, K.; Broncano, J.; Frank, L.; Villasana-Gomez, G. Advanced Computed Tomography and Magnetic Resonance Imaging in Ischemic and Nonischemic Cardiomyopathies. Echocardiography 2025, 42, e70106. [Google Scholar] [CrossRef] [PubMed]
- Erbay, M.I.; Manubolu, V.S.; Stein-Merlob, A.F.; Ferencik, M.; Mamas, M.A.; Lopez-Mattei, J.; Baldassarre, L.A.; Budoff, M.J.; Yang, E.H. Integration and Potential Applications of Cardiovascular Computed Tomography in Cardio-Oncology. Curr. Cardiol. Rep. 2025, 27, 51. [Google Scholar] [CrossRef]
- Tabakov, S. X-Ray Tube Arcing: Manifestation and Detection during Quality Controol. Med. Phys. Int. J. 2018, 6, 157–161. [Google Scholar]
- Zhang, W.; Yang, D.; Wang, H. Data-driven methods for predictive maintenance of industrial equipment: A survey. IEEE Syst. J. 2019, 13, 2213–2227. [Google Scholar] [CrossRef]
- Zhao, R.; Yan, R.; Chen, Z.; Mao, K.; Wang, P.; Gao, R.X. Deep learning and its applications to machine health monitoring. Mech. Syst. Signal Process. 2019, 115, 213–237. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, W.; Miao, Q. Adaptive diagnosis and prognosis for Lithium-ion batteries via Lebesgue time model with multiple hidden state variables. Appl. Energy 2025, 392, 125986. [Google Scholar] [CrossRef]
- Cardona Ortegón, A.F.; Guerrero, W.J. Optimizing maintenance policies of computed tomography scanners with stochastic failures. In Service Oriented, Holonic and Multi-Agent Manufacturing Systems for Industry of the Future: Proceedings of SOHOMA Latin America 2021, Bogota, Colombia, 27–28 January 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 331–342. [Google Scholar]
- Li, J.; Deng, W.; Dang, X.; Zhao, H. Cross-domain adaptation fault diagnosis with maximum classifier discrepancy and deep feature alignment under variable working conditions. IEEE Trans. Reliab. 2025, 1–10. [Google Scholar] [CrossRef]
- Khider, M.O.; Hamza, A.O. Medical equipment maintenance management system: Review and analysis. J. Clin. Eng. 2022, 47, 151–159. [Google Scholar] [CrossRef]
- Zhong, J.; Zhang, H.; Miao, Q. Enhancing aircraft reliability with information redundancy: A sensor-modal fusion approach leveraging deep learning. Reliab. Eng. Syst. Saf. 2025, 261, 111068. [Google Scholar] [CrossRef]
- Wang, D.; Tsui, K.-L.; Miao, Q. Prognostics and health management: A review of vibration based bearing and gear health indicators. IEEE Access 2017, 6, 665–676. [Google Scholar] [CrossRef]
- Chen, H.; Sun, Y.; Li, X.; Zheng, B.; Chen, T. Dual-Scale Complementary Spatial-Spectral Joint Model for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 6772–6789. [Google Scholar] [CrossRef]
- Zonta, T.; Da Costa, C.A.; da Rosa Righi, R.; de Lima, M.J.; Da Trindade, E.S.; Li, G.P. Predictive maintenance in the Industry 4.0: A systematic literature review. Comput. Ind. Eng. 2020, 150, 106889. [Google Scholar] [CrossRef]
- Zhong, J.; Zhang, H.; Miao, Q. Flight anomaly detection and localization based on flight data fusion and random channel masking. Appl. Soft Comput. 2025, 174, 113023. [Google Scholar] [CrossRef]
- Khalaf, A.; Hamam, Y.; Alayli, Y.; Djouani, K. The effect of maintenance on the survival of medical equipment. J. Eng. Des. Technol. 2013, 11, 142–157. [Google Scholar] [CrossRef]
- Sabah, S.; Moussa, M.; Shamayleh, A. Predictive maintenance application in healthcare. In Proceedings of the 2022 Annual Reliability and Maintainability Symposium (RAMS), Tucson, AZ, USA, 24–27 January 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–9. [Google Scholar]
- Lyu, G.; Zhang, H.; Miao, Q. Parallel state fusion LSTM-based early-cycle stage lithium-ion battery RUL prediction under Lebesgue sampling framework. Reliab. Eng. Syst. Saf. 2023, 236, 109315. [Google Scholar] [CrossRef]
- Kelvin-Agwu, M.; Adelodun, M.O.; Igwama, G.T.; Anyanwu, E.C. The Impact of Regular Maintenance on the Longevity and Performance of Radiology Equipment. Int. J. Eng. Res. Dev. 2024, 20, 171–177. [Google Scholar]
- Azrul Shazril, M.H.S.E.M.; Mashohor, S.; Amran, M.E.; Hafiz, N.F.; Ali, A.M.; Bin Naseri, M.S.; Rasid, M.F.A. Assessment of IoT-Driven Predictive Maintenance Strategies for Computed Tomography Equipment: A Machine Learning Approach. IEEE Access 2024, 12, 195505–195515. [Google Scholar] [CrossRef]
- Zhou, H.; Liu, Q.; Liu, H.; Chen, Z.; Li, Z.; Zhuo, Y.; Li, K.; Wang, C.; Huang, J. Healthcare facilities management: A novel data-driven model for predictive maintenance of computed tomography equipment. Artif. Intell. Med. 2024, 149, 102807. [Google Scholar] [CrossRef]
- Fink, O.; Wang, Q.; Svensén, M.; Dersin, P.; Lee, W.-J.; Ducoffe, M. Potential, challenges and future directions for deep learning in prognostics and health management applications. Eng. Appl. Artif. Intell. 2020, 92, 103678. [Google Scholar] [CrossRef]
- Shahraki, A.F.; Yadav, O.P.; Liao, H. A review on degradation modelling and its engineering applications. Int. J. Perform. Eng. 2017, 13, 299. [Google Scholar] [CrossRef]
- Wang, H.; Liao, H.; Ma, X.; Bao, R. Remaining useful life prediction and optimal maintenance time determination for a single unit using isotonic regression and gamma process model. Reliab. Eng. Syst. Saf. 2021, 210, 107504. [Google Scholar] [CrossRef]
- Wen, Y.; Wu, J.; Das, D.; Tseng, T.-L. Degradation modeling and RUL prediction using Wiener process subject to multiple change points and unit heterogeneity. Reliab. Eng. Syst. Saf. 2018, 176, 113–124. [Google Scholar] [CrossRef]
- Ding, D.; Wang, Z.; Han, Q.-L. A set-membership approach to event-triggered filtering for general nonlinear systems over sensor networks. IEEE Trans. Autom. Control 2019, 65, 1792–1799. [Google Scholar] [CrossRef]
- Ge, X.; Han, Q.-L.; Wang, Z. A threshold-parameter-dependent approach to designing distributed event-triggered H∞ consensus filters over sensor networks. IEEE Trans. Cybern. 2018, 49, 1148–1159. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, C.; Gonçalves, G. Remaining Useful Life prediction and challenges: A literature review on the use of Machine Learning Methods. J. Manuf. Syst. 2022, 63, 550–562. [Google Scholar] [CrossRef]
- Wei, J.; Dong, G.; Chen, Z. Remaining useful life prediction and state of health diagnosis for lithium-ion batteries using particle filter and support vector regression. IEEE Trans. Ind. Electron. 2017, 65, 5634–5643. [Google Scholar] [CrossRef]
- Li, C.; Xie, W.; Zheng, B.; Yi, Q.; Yang, L.; Hu, B.; Deng, C. An enhanced CLKAN-RF framework for robust anomaly detection in unmanned aerial vehicle sensor data. Knowl.-Based Syst. 2025, 319, 113690. [Google Scholar] [CrossRef]
- Ren, L.; Jia, Z.; Laili, Y.; Huang, D. Deep learning for time-series prediction in IIoT: Progress, challenges, and prospects. IEEE Trans. Neural Netw. Learn. Syst. 2023, 35, 15072–15091. [Google Scholar] [CrossRef]
- Zhong, J.; Zhang, H.; Miao, Q. A Novel Altitude Measurement Channel Reconstruction Method Based on Symbolic Regression and Information Fusion. IEEE Trans. Instrum. Meas. 2024, 74, 3502212. [Google Scholar] [CrossRef]
- Wang, B.; Lei, Y.; Li, N.; Yan, T. Deep separable convolutional network for remaining useful life prediction of machinery. Mech. Syst. Signal Process. 2019, 134, 106330. [Google Scholar] [CrossRef]
- Zhong, J.; Zhang, H.; Liu, Q.; Miao, Q.; Huang, J. Prognosis for Filament Degradation of X-Ray Tubes Based on IoMT Time Series Data. IEEE Internet Things J. 2024, 12, 8084–8094. [Google Scholar] [CrossRef]
- Ma, M.; Mao, Z. Deep-convolution-based LSTM network for remaining useful life prediction. IEEE Trans. Ind. Informatics 2020, 17, 1658–1667. [Google Scholar] [CrossRef]
- Li, B.; Tang, B.; Deng, L.; Zhao, M. Self-attention ConvLSTM and its application in RUL prediction of rolling bearings. IEEE Trans. Instrum. Meas. 2021, 70, 3518811. [Google Scholar] [CrossRef]



| CT Number | Tube Number | Start Time | End Time | Data Volume |
|---|---|---|---|---|
| CT-1 | Tube-1 | 5 August 2021 | 8 April 2023 | 223,346 |
| CT-2 | Tube-2 | 26 July 2019 | 27 June 2023 | 368,026 |
| CT-3 | Tube-3 | 10 March 2021 | 23 September 2023 | 342,590 |
| CT-4 | Tube-4 | 19 July 2019 | 19 July 2022 | 401,173 |
| CT-5 | Tube-5 | 1 November 2022 | 21 July 2023 | 101,592 |
| CT-6 | Tube-6 | 16 March 2017 | 2 July 2018 | 315,587 |
| Tube 1 | Tube 2 | Tube 3 | Tube 4 | Tube 5 | Tube 6 | Average | Mean ± Std | ||
|---|---|---|---|---|---|---|---|---|---|
| LSTM | MSE | 7.0079 | 5.5311 | 7.2104 | 6.9019 | 30.6251 | 7.9749 | 10.8752 | 10.88 ± 9.42 |
| MAE | 1.0671 | 0.9354 | 0.8343 | 1.0600 | 2.0037 | 1.5975 | 1.2497 | 1.25 ± 0.42 | |
| R2 | 0.4904 | 0.4202 | 0.2181 | 0.1665 | 0.0018 | 0.2406 | 0.2563 | 0.26 ± 0.18 | |
| Transformer | MSE | 9.8224 | 6.7637 | 8.0440 | 7.9642 | 25.6668 | 8.8649 | 11.1877 | 11.19 ± 6.89 |
| MAE | 1.3350 | 1.0859 | 1.2381 | 1.0490 | 1.8629 | 1.6177 | 1.3648 | 1.36 ± 0.31 | |
| R2 | 0.2858 | 0.2910 | 0.1277 | 0.0383 | 0.2286 | 0.1558 | 0.1879 | 0.19 ± 0.09 | |
| CNN-BiLSTM-Attention | MSE | 7.9168 | 6.9328 | 7.2402 | 6.5597 | 28.7354 | 8.3603 | 10.9575 | 10.96 ± 8.44 |
| MAE | 1.3342 | 0.8737 | 1.0731 | 0.5802 | 2.1097 | 1.3533 | 1.2207 | 1.22 ± 0.51 | |
| R2 | 0.4243 | 0.2732 | 0.2148 | 0.2079 | 0.0643 | 0.2039 | 0.2314 | 0.23 ± 0.11 | |
| CNN-LSTM | MSE | 11.0675 | 7.1686 | 8.3275 | 6.5126 | 27.3177 | 7.5794 | 11.3289 | 11.33 ± 7.75 |
| MAE | 0.7506 | 0.7373 | 0.8901 | 0.5626 | 1.8493 | 1.1650 | 0.9925 | 0.99 ± 0.43 | |
| R2 | 0.1952 | 0.2485 | 0.0969 | 0.2132 | 0.1096 | 0.2782 | 0.1903 | 0.19 ± 0.07 | |
| CNN-LSTM-Attention | MSE | 10.1311 | 4.8093 | 8.1599 | 6.9712 | 28.0831 | 8.9272 | 11.1803 | 11.18 ± 8.35 |
| MAE | 0.8454 | 1.1660 | 1.4669 | 0.9929 | 1.8041 | 1.0507 | 1.221 | 1.22 ± 0.36 | |
| R2 | 0.2633 | 0.4958 | 0.1151 | 0.1582 | 0.0846 | 0.1499 | 0.2112 | 0.21 ± 0.14 | |
| DDLNet | MSE | 4.3101 | 1.4099 | 2.2568 | 1.2323 | 4.3685 | 3.9320 | 2.9183 | 2.92 ± 1.39 |
| MAE | 0.5401 | 0.2618 | 0.4395 | 0.2396 | 0.6989 | 0.6072 | 0.4645 | 0.46 ± 0.18 | |
| R2 | 0.6866 | 0.8522 | 0.7553 | 0.8512 | 0.8576 | 0.6256 | 0.7714 | 0.77 ± 0.10 | |
| Tube 1 | Tube 2 | Tube 3 | Tube 4 | Tube 5 | Tube 6 | Average | ||
|---|---|---|---|---|---|---|---|---|
| No_ Pretraining | MSE | 5.6894 | 3.0773 | 3.8784 | 3.6361 | 6.1974 | 4.2178 | 4.4494 |
| MAE | 0.7138 | 0.4869 | 0.5031 | 0.3441 | 0.7910 | 0.6226 | 0.5769 | |
| R2 | 0.5863 | 0.6774 | 0.5794 | 0.5609 | 0.7980 | 0.5983 | 0.6334 | |
| RSA | MSE | 8.1404 | 2.9982 | 5.0797 | 1.9206 | 14.9232 | 6.2074 | 6.5449 |
| MAE | 0.8099 | 0.4659 | 1.0019 | 0.3161 | 1.5266 | 0.9060 | 0.8377 | |
| R2 | 0.4081 | 0.6857 | 0.4491 | 0.7681 | 0.5136 | 0.4089 | 0.5389 | |
| Simplified_Loss | MSE | 8.0198 | 2.6110 | 5.6173 | 2.6930 | 7.2068 | 6.8265 | 5.4957 |
| MAE | 1.0629 | 0.4379 | 0.5650 | 0.4537 | 0.7515 | 0.8406 | 0.6853 | |
| R2 | 0.4168 | 0.7263 | 0.3908 | 0.6748 | 0.7651 | 0.3154 | 0.5482 | |
| TCN | MSE | 7.7832 | 2.6779 | 4.8627 | 2.3752 | 6.7110 | 6.2493 | 5.1099 |
| MAE | 1.0474 | 0.5253 | 0.6724 | 0.2997 | 0.7228 | 0.7227 | 0.6651 | |
| R2 | 0.4341 | 0.7193 | 0.4727 | 0.7132 | 0.7813 | 0.4049 | 0.5876 | |
| Ours | MSE | 4.3101 | 1.4099 | 2.2568 | 1.2323 | 4.3685 | 3.9320 | 2.9183 |
| MAE | 0.5401 | 0.2618 | 0.4395 | 0.2396 | 0.6989 | 0.6072 | 0.4645 | |
| R2 | 0.6866 | 0.8522 | 0.7553 | 0.8512 | 0.8576 | 0.6256 | 0.7714 | |
| α_Base | β_Base | γ_Base | Average MSE | Average MAE | Average R2 |
|---|---|---|---|---|---|
| 0.8 | 0.15 | 0.05 | 2.92 ± 1.39 | 0.46 ± 0.18 | 0.77 ± 0.10 |
| 0.6 | 0.15 | 0.05 | 3.45 ± 1.52 | 0.53 ± 0.19 | 0.70 ± 0.13 |
| 0.7 | 0.15 | 0.05 | 3.08 ± 1.42 | 0.48 ± 0.17 | 0.75 ± 0.11 |
| 0.9 | 0.15 | 0.05 | 3.15 ± 1.44 | 0.49 ± 0.17 | 0.74 ± 0.12 |
| 1.0 | 0.15 | 0.05 | 3.38 ± 1.50 | 0.52 ± 0.19 | 0.71 ± 0.12 |
| 0.8 | 0.10 | 0.05 | 3.28 ± 1.47 | 0.50 ± 0.18 | 0.73 ± 0.12 |
| 0.8 | 0.20 | 0.05 | 3.19 ± 1.45 | 0.49 ± 0.17 | 0.74 ± 0.11 |
| 0.8 | 0.15 | 0.03 | 3.12 ± 1.43 | 0.48 ± 0.17 | 0.75 ± 0.11 |
| 0.8 | 0.15 | 0.07 | 3.25 ± 1.48 | 0.51 ± 0.19 | 0.72 ± 0.12 |
| 0.7 | 0.10 | 0.05 | 3.42 ± 1.51 | 0.52 ± 0.19 | 0.71 ± 0.13 |
| 0.9 | 0.20 | 0.05 | 3.56 ± 1.54 | 0.54 ± 0.20 | 0.68 ± 0.14 |
| 0.6 | 0.20 | 0.07 | 3.89 ± 1.63 | 0.58 ± 0.22 | 0.64 ± 0.15 |
| 1.0 | 0.10 | 0.03 | 3.71 ± 1.59 | 0.56 ± 0.21 | 0.66 ± 0.14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Liu, Y.; Qin, Z.; Li, H.; Xie, S.; Fan, L.; Liu, Q.; Huang, J. Dual-Branch Deep Learning with Dynamic Stage Detection for CT Tube Life Prediction. Sensors 2025, 25, 4790. https://doi.org/10.3390/s25154790
Chen Z, Liu Y, Qin Z, Li H, Xie S, Fan L, Liu Q, Huang J. Dual-Branch Deep Learning with Dynamic Stage Detection for CT Tube Life Prediction. Sensors. 2025; 25(15):4790. https://doi.org/10.3390/s25154790
Chicago/Turabian StyleChen, Zhu, Yuedan Liu, Zhibin Qin, Haojie Li, Siyuan Xie, Litian Fan, Qilin Liu, and Jin Huang. 2025. "Dual-Branch Deep Learning with Dynamic Stage Detection for CT Tube Life Prediction" Sensors 25, no. 15: 4790. https://doi.org/10.3390/s25154790
APA StyleChen, Z., Liu, Y., Qin, Z., Li, H., Xie, S., Fan, L., Liu, Q., & Huang, J. (2025). Dual-Branch Deep Learning with Dynamic Stage Detection for CT Tube Life Prediction. Sensors, 25(15), 4790. https://doi.org/10.3390/s25154790





