Accurate Wideband RCS Estimation from Limited Field Data Using Infinitesimal Dipole Modeling with Compressive Sensing
Abstract
1. Introduction
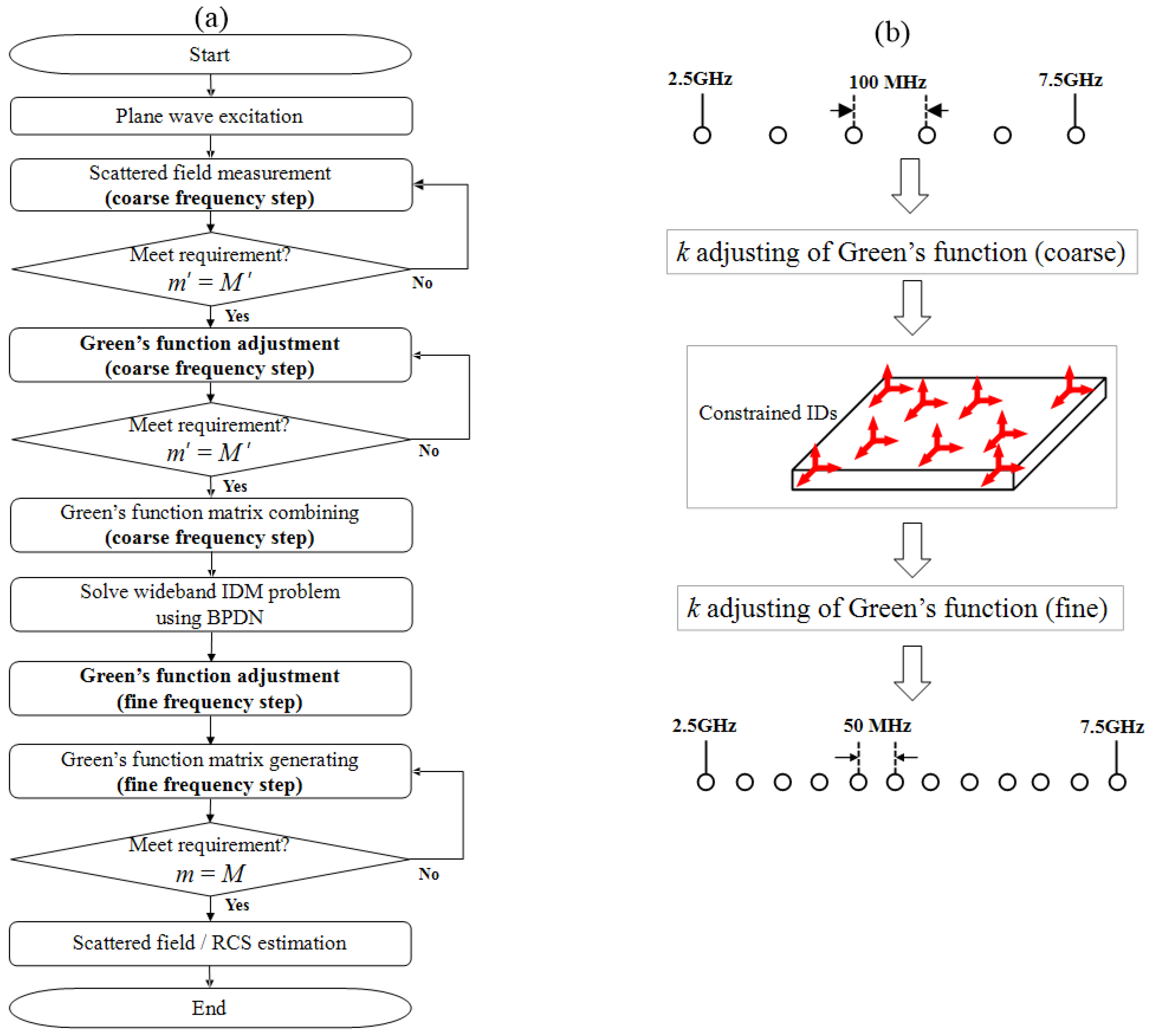
2. Wideband IDM Formula with Limited Scattered Field Data
2.1. Dyadic Green’s Function Expression and IDM Formula
2.2. Proposed Green’s Function Adjustment for Efficient Estimation of Wideband RCS Characteristics
2.3. Wideband IDM Formula with Green’s Function Adjustment and Compressive Sensing
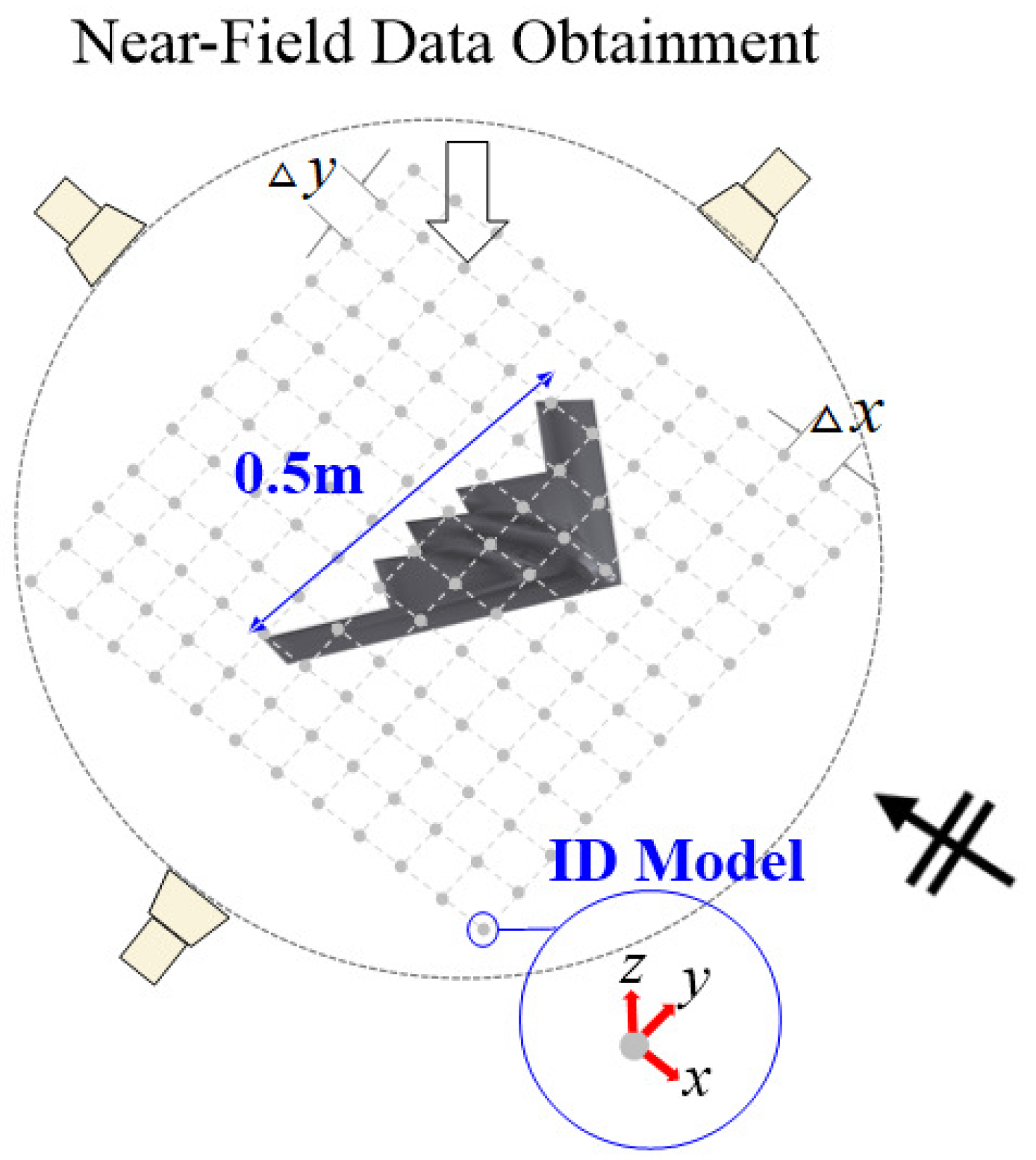
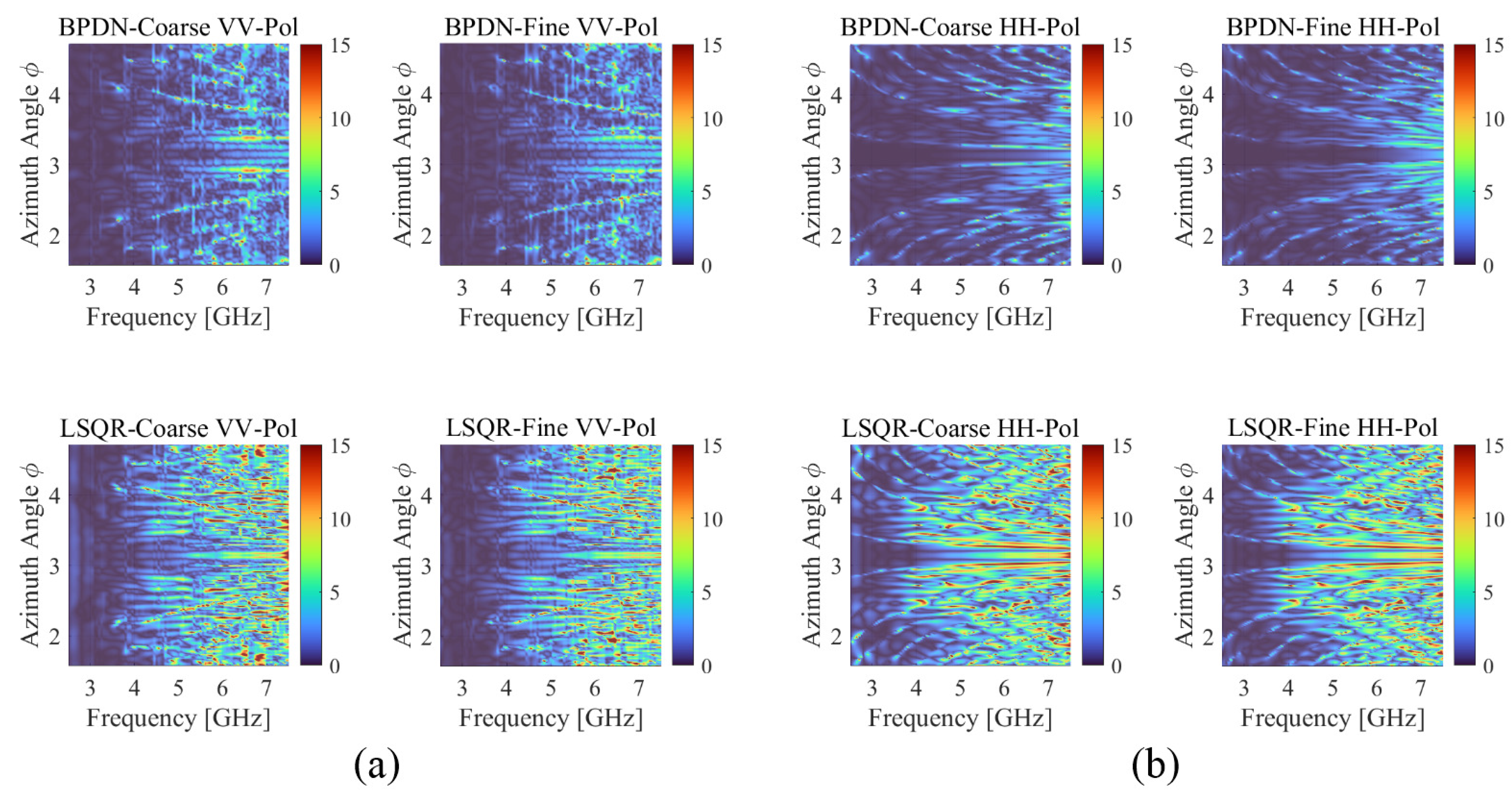
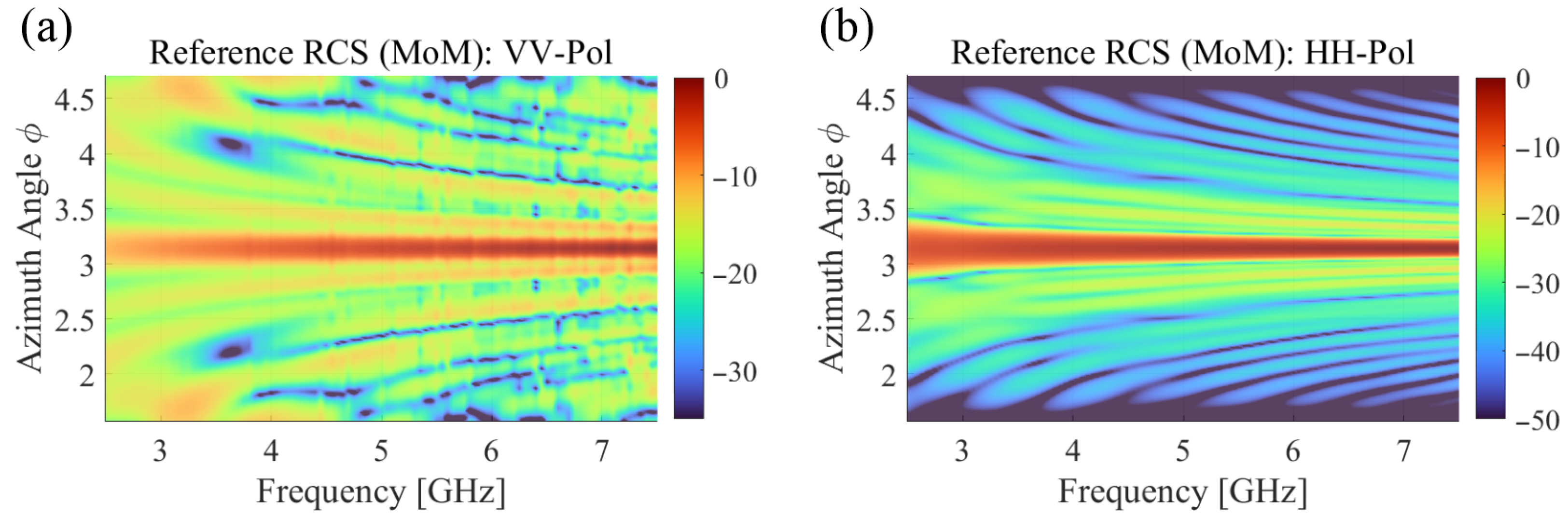
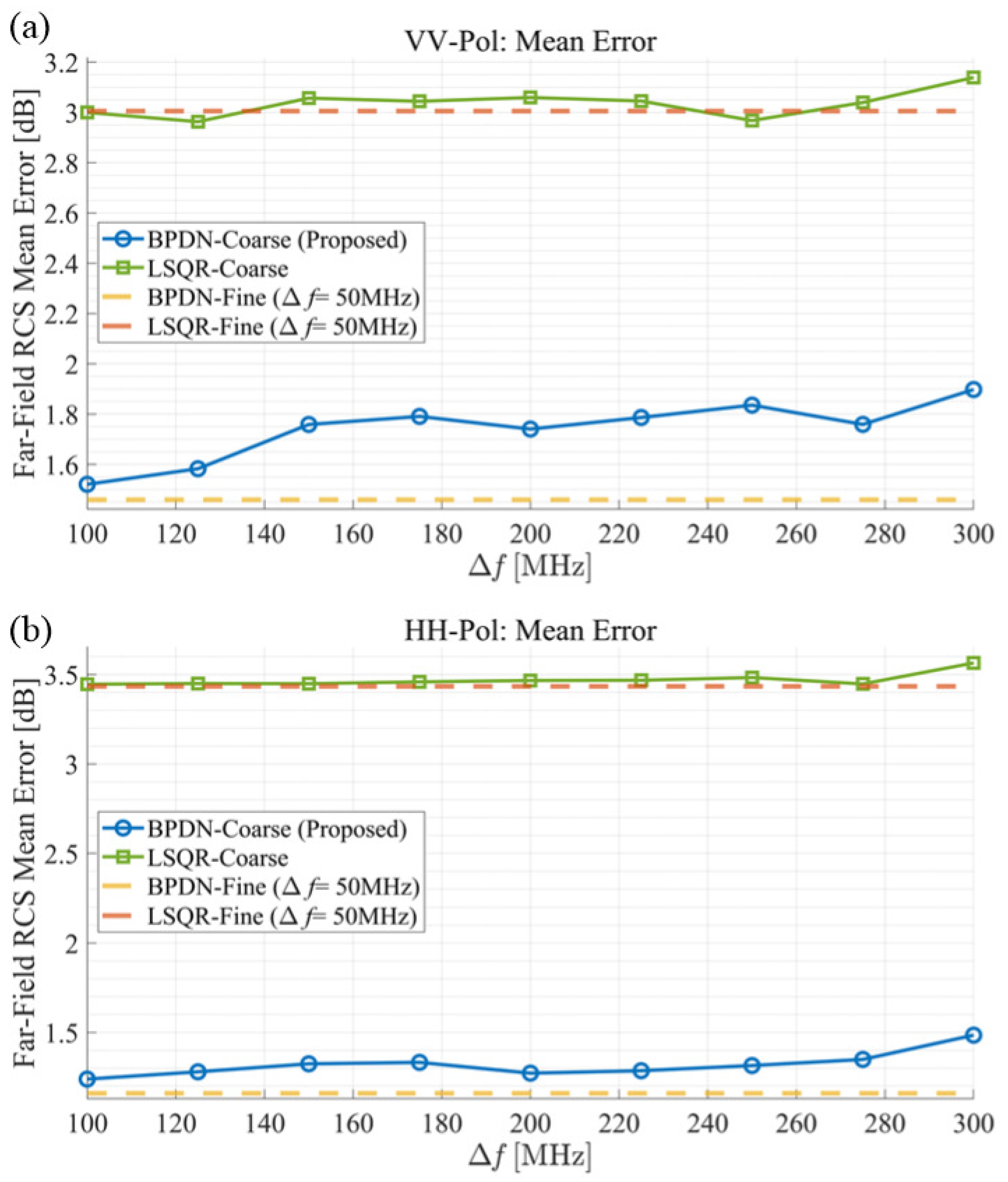
3. Numerical Results for Proposed Method
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, J.; Shi, Z.; Cheng, X.; Fu, Q. Automatic target recognition of SAR images based on global scattering center model. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3713–3729. [Google Scholar]
- Zhou, J.; Zhao, H.; Shi, Z.; Fu, Q. Global scattering center model extraction of radar targets based on wideband measurements. IEEE Trans. Antennas Propag. 2008, 56, 2051–2060. [Google Scholar] [CrossRef]
- Zhou, J.; Shi, Z.; Fu, Q. Three-dimensional scattering center extraction based on wide aperture data at a single elevation. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1638–1655. [Google Scholar] [CrossRef]
- Bhalla, R.; Ling, H. Three-dimensional scattering center extraction using the shooting and bouncing ray technique. IEEE Trans. Antennas Propag. 1996, 44, 1445–1453. [Google Scholar] [CrossRef]
- Lee, H.-J.; Noh, Y.-H.; Yook, J.-G. Using the CLEAN Method in Three-Dimensional Polarimetric ISAR Imaging Based on Volumetric Scattering Points. J. Electromagn. Eng. Sci. 2024, 24, 18–25. [Google Scholar] [CrossRef]
- Ozdemir, C. Inverse Synthetic Aperture Radar Imaging with MATLAB Algorithms; Wiley: Hoboken, NJ, USA, 2012; Volume 210. [Google Scholar]
- LaHaie, I.J. Overview of an image-based technique for predicting farfield radar cross section from near-field measurements. IEEE Antennas Propag. Mag. 2003, 45, 159–169. [Google Scholar] [CrossRef]
- Vaupel, T.; Eibert, T.F. Comparison and application of near-field ISAR imaging techniques for far-field radar cross section determination. IEEE Trans. Antennas Propag. 2006, 54, 144–151. [Google Scholar] [CrossRef]
- Kim, W.; Lm, H.; Noh, Y.; Hong, I.; Tae, H.; Kim, J.; Yook, J. Near-Field to Far-Field RCS Prediction on Arbitrary Scanning Surfaces Based on Spherical Wave Expansion. Sensors 2020, 20, 7199. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, W.; Zhang, W.; Sun, J.; Xing, B.; Ligthart, L. Radar Cross Section Near-Field to Far-Field Prediction for Isotropic-point Scattering Target Based on Regression Estimation. Sensors 2020, 20, 6023. [Google Scholar] [CrossRef] [PubMed]
- Ahn, S.; Koh, J. RCS Prediction Using Prony Method in High-Frequency Band for Military Aircraft Models. Aerospace 2022, 9, 734. [Google Scholar] [CrossRef]
- Noh, Y.-H.; Im, H.R.; Kim, W.; Hong, I.-P.; Yook, J.-G. Communication bistatic RCS estimation using monostatic scattering centers with compressive sensing. IEEE Trans. Antennas Propag. 2022, 70, 7350–7355. [Google Scholar] [CrossRef]
- Li, S.; Zhao, G.; Li, H.; Ren, B.; Hu, W.; Liu, Y.; Yu, W.; Sun, H. Near-field radar imaging via compressive sensing. IEEE Trans. Antennas Propag. 2015, 63, 828–833. [Google Scholar] [CrossRef]
- LaHaie, I.J.; Dester, G.D. Application of L1 minimization to imagebased near field-to-far field RCS transformations. In Proceedings of the 2019 13th European Conference on Antennas and Propagation (EuCAP), Krakow, Poland, 31 March–5 April 2019; pp. 1–5. [Google Scholar]
- Noh, Y.-H.; Kim, W.; Tae, H.-S.; Kim, J.-K.; Hong, I.-P.; Yook, J.-G. RCS feature extraction using discretized point scatterer with compressive sensing. IEEE Antennas Wirel. Propag. Lett. 2021, 20, 165–168. [Google Scholar] [CrossRef]
- Mikki, S.M.; Kishk, A.A. Theory and applications of infinitesimal dipole models for computational electromagnetics. IEEE Trans. Antennas Propag. 2007, 55, 1325–1337. [Google Scholar] [CrossRef]
- Yang, S.J.; Kim, Y.D.; Yun, D.J.; Yi, D.W.; Myung, N.H. Antenna modeling using sparse infinitesimal dipoles based on recursive convex optimization. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 662–665. [Google Scholar] [CrossRef]
- Han, J.-H.; Lee, W.; Kim, Y.D. Infinitesimal dipole modeling from sparse far-field patterns for predicting electromagnetic characteristics of unknown antennas. IEEE Trans. Antennas Propag. 2022, 70, 10245–10252. [Google Scholar] [CrossRef]
- Yang, S.J.; Kim, Y.D. An accurate near-field focusing of array antenna based on near-field active element pattern and infinitesimal dipole modeling. IEEE Access 2021, 9, 143771–143781. [Google Scholar] [CrossRef]
- Oh, J.-I.; Yang, S.-J.; Kim, S.; Yu, J.-W.; Kim, Y.-D. Antenna Diagnostics Based on Infinitesimal Dipole Modeling With Limited Measurement on Antenna Aperture. IEEE Antennas Wirel. Propag. Lett. 2022, 21, 923–927. [Google Scholar] [CrossRef]
- Han, S.-H.; Lim, S.-J.; Yu, J.-W.; Kim, Y.-D. Antenna Pattern Measurement for Mobile Terminals via Magnetic Infinitesimal Dipole Based Source Reconstruction. IEEE Access 2024, 12, 78982–78987. [Google Scholar] [CrossRef]
- Lian, S.; Wang, W.; Lou, S.; Li, P.; Xu, W.; Zhang, W. Analysis of scattering characteristics of the cylindrical conformal arrays with variable curvature based on infinitesimal dipole model. IEEE Antennas Wirel. Propag. Lett. 2025; early access. [Google Scholar]
- Lian, S.; Wang, W.; Lou, S.; Li, P.; Zhang, W. Analysis of Scattering Characteristics of Large Array Structures Based on Infinitesimal Dipole Model. IEEE Trans. Antennas Propag. 2025, 73, 341–350. [Google Scholar] [CrossRef]
- Lou, S.; Qian, S.; Lian, S.; Wang, W.; Bao, H.; Leng, G. Analysis of High-Order Mutual Coupling Effect of Antenna Arrays Based on Infinitesimal Dipole Model. IEEE Trans. Antennas Propag. 2025, 73, 3628–3638. [Google Scholar] [CrossRef]
- Kim, Y.-D.; Yang, S.-J.; Myung, N.-H.; Yu, J.-W. Improved Prediction of the Wideband Beam Pattern Shape of Antenna Array Based on Infinitesimal Dipole Modeling. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 2309–2313. [Google Scholar] [CrossRef]
- Zhang, Y.-X.; Jiao, Y.-C.; Zhu, M.-D.; Zhang, Y. Wideband near-field RCS measurement techniques with improved far-field RCS prediction accuracies. IEEE Trans. Instrum. Meas. 2023, 72, 8000404. [Google Scholar] [CrossRef]
- Potgieter, M.; Odendaal, J.W.; Blaauw, C.; Joubert, J. Bistatic RCS measurements of large targets in a compact range. IEEE Trans. Antennas Propag. 2019, 67, 2847–2852. [Google Scholar] [CrossRef]
- Gibson, W.C. The Method of Moments in Electromagnetics; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Harrington, R.F. Field Computation by Moment Methods; Macmillan: New York, NY, USA, 1968. [Google Scholar]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Beck, A.; Teboulle, M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imag. Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef]
- Candes, E.J.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]




| RCS Mean Error [dB] | Processing Time | ||
|---|---|---|---|
| VV-Pol | HH-Pol | for IDM [s] | |
| Proposed | 1.31 * | 0.85 * | 9.15 ** |
| BPDN-Fine | 1.22 | 0.88 | 51.50 |
| LSQR-Coarse | 2.88 | 3.48 | 0.54 |
| LSQR-Fine | 2.92 | 3.47 | 2.77 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.-W.; Jung, Y.C.; Yang, S.-J. Accurate Wideband RCS Estimation from Limited Field Data Using Infinitesimal Dipole Modeling with Compressive Sensing. Sensors 2025, 25, 4771. https://doi.org/10.3390/s25154771
Lee J-W, Jung YC, Yang S-J. Accurate Wideband RCS Estimation from Limited Field Data Using Infinitesimal Dipole Modeling with Compressive Sensing. Sensors. 2025; 25(15):4771. https://doi.org/10.3390/s25154771
Chicago/Turabian StyleLee, Jeong-Wan, Ye Chan Jung, and Sung-Jun Yang. 2025. "Accurate Wideband RCS Estimation from Limited Field Data Using Infinitesimal Dipole Modeling with Compressive Sensing" Sensors 25, no. 15: 4771. https://doi.org/10.3390/s25154771
APA StyleLee, J.-W., Jung, Y. C., & Yang, S.-J. (2025). Accurate Wideband RCS Estimation from Limited Field Data Using Infinitesimal Dipole Modeling with Compressive Sensing. Sensors, 25(15), 4771. https://doi.org/10.3390/s25154771





