Abstract
The endoscopic capsule is a miniaturized device used for medical diagnosis, which is less invasive compared to traditional gastrointestinal endoscopy and can reduce patient discomfort. However, it faces challenges in communication transmission, such as high power consumption, serious signal interference, and low data transmission rate. To address these issues, this paper proposes an optimized modulation scheme that is low-cost, low-power, and robust in harsh environments, aiming to improve its transmission rate. The scheme is analyzed in terms of the in-body channel. The analysis and discussion for the scheme in wireless body area networks (WBANs) are divided into three aspects: bit error rate (BER) performance, energy efficiency (EE), and spectrum efficiency (SE), and complexity. These correspond to the following issues: transmission rate, communication quality, and low power consumption. The results demonstrate that the optimized scheme is more suitable for improving the communication performance of endoscopic capsules.
1. Introduction
With the development of healthcare, people are no longer limited to traditional detection methods. For example, some tests that require patients’ internal examination are no longer confined to wired methods but focus more on user experience. A typical medical application is gastrointestinal endoscopy, where a patient swallows and excretes an endoscopic capsule that sends signals for detecting its internal conditions [1,2,3]. Gastrointestinal endoscopy is mainly used to help diagnose diseases such as gastritis, gastric ulcers, gastroesophageal reflux disease, intestinal inflammation, and digestive tract tumors. Through gastrointestinal endoscopy, doctors can directly observe the condition of the stomach, esophagus, small intestine, and large intestine, identifying lesions such as ulcers, tumors, and polyps for precise localization. This requires an investigation of the signal transmission quality in body area network environments [4,5,6]. An important aspect of smart healthcare is the development of communication technology for internal body channels, such as endoscopic capsules. The usage of an endoscopic capsule involves ingesting a capsule that contains communication functionality, allowing it to transmit real-time data while traveling through the gastrointestinal tract. The capsule can capture gastrointestinal images and send them to external devices for analysis and diagnosis, offering a less invasive alternative to traditional approaches like gastroscopy or colonoscopy [7]. A key challenge in this field is ensuring the communication system can effectively adapt to a patient’s internal body environment, including dealing with interference and maintaining a stable connection [8]. This is a critical area of focus in advanced smart healthcare technologies.
Wireless body area networks (WBANs) are emerging technologies that play a critical role in various fields, particularly in healthcare and medical monitoring applications. WBANs enable continuous monitoring of physiological parameters through wearable devices, providing real-time health data to clinicians for better decision-making and timely interventions [9]. These networks are composed of small, low-power devices embedded in or worn on the body, which communicate wirelessly with external devices such as smartphones or health monitoring systems. The IEEE 802.15.6 standard has been specifically designed to address the unique challenges of WBANs, including energy efficiency, low latency, and reliability in healthcare settings [3]. Recent research has focused on improving the performance of WBANs by optimizing medium access control (MAC) protocols and Physical (PHY) layer parameters. For instance, a modified IEEE 802.15.6 MAC scheme has been proposed to enhance performance in e-health applications by adjusting superframe structures and access mechanisms to better meet healthcare demands [10]. Considering a practical scenario, the channel model 2 (CM2) in the WBAN standard is a variable on-body channel model described in the IEEE. Additionally, a study by Siddik et al. investigates the effects of MAC and PHY layer parameters on the performance of IEEE 802.15.6 CSMA/CA, using a Markov chain-based model to assess network performance under various scenarios [11]. The integration of WBANs with advanced modulation schemes and energy-efficient technologies holds significant potential for improving healthcare delivery through continuous, real-time health monitoring. However, overcoming the challenges of signal interference, energy consumption, and scalability remains a critical area of research. Future developments in this field should focus on optimizing communication protocols, enhancing energy efficiency, and exploring more robust integration strategies with existing healthcare infrastructures [12,13]. Given the capsule’s compact size and the realities of patient use, what is needed is a low-cost, low-power modulation that delivers reliable communication without bulky or power-hungry filters and equalizers.
Differential chaos shift keying (DCSK) is a promising modulation technique known for its low cross-correlation, low power consumption, exceptional autocorrelation, and broadband spectral characteristics. Therefore, it can have strong robustness against non-stationary environments such as multipath interference without the need for filtering and equalization [14]. However, these advantages come at the cost of reduced system spectral efficiency (SE). To enhance the transmission rate, the implementation of the M-ary DCSK (M-DCSK) method becomes necessary. Several M-DCSK systems have been developed to achieve high data rates by combining index modulation (IM) with traditional binary DCSK [15,16,17,18,19]. Numerous methods are using the coded-shift DCSK (CS-DCSK) based on Walsh codes, introduced in [20]. Subsequent developments have led to the generalized CS-DCSK, high-data-rate CS-DCSK, and CS-DCSK with code index modulation, targeting high-speed systems, as presented in [21,22,23], respectively. These schemes offer a notable improvement in spectral efficiency by enabling the transmission of multiple bits per symbol period. Additionally, a MIMO M-ary DCSK scheme was proposed in [24]. Despite these advantages, the complexity of these schemes remains relatively high. Additionally, several schemes based on M-ary phase shift keying (MPSK) and M-ary quadrature amplitude modulation (MQAM) for DCSK have been proposed [25], with a focus on optimal constellation design. These schemes make use of a reference chaotic signal in the information-carrying part [26], which is modulated by MPSK and MQAM using M-ary symbols. Furthermore, an M-DCSK system employing an MPSK constellation [27], based on orthogonal chaotic frequency shift keying (QCSK) [28], has been proposed, demonstrating improved bit error rate (BER) performance.
In recent years, WBANs have become a crucial part of modern healthcare systems, particularly for applications such as health monitoring, wearable sensors, and medical implants. These systems typically need effective communication methods to transmit critical biomedical data. Among various modulation techniques, DCSK has emerged as a promising approach due to its robustness against noise, interference, and fading, which are common in the in-body communication channels. Ref. [29] demonstrated that chaotic secure communication systems, such as those using DCCK, offer robust security and low power consumption, making them ideal for WBAN applications. Furthermore, Li and Zhang provided an in-depth performance analysis of DCCK in WBANs, showing its potential in achieving high reliability while maintaining low energy consumption, even in complex wireless environments [30]. In addition to performance improvements, the security of transmitted data in WBANs is crucial due to the sensitive nature of health-related information. Ref. [31] proposed a secure communication framework based on DCCK modulation, emphasizing its ability to safeguard data transmission from potential eavesdropping. Their work highlights the key advantage of chaotic modulation in WBANs, offering both privacy and communication efficiency. Furthermore, Ref. [32] explored the design and performance of DCCK in WBANs, showing that it effectively reduces bit error rates and enhances the stability of data transmission in noisy environments.
Interbody (In-body) communication, where signals travel through or around the human body, presents several unique challenges such as high attenuation, multipath fading, and interference from the body itself. DCSK, which utilizes the chaotic dynamics of a signal for modulation, has demonstrated its potential to handle these challenges effectively. The chaotic nature of the signal offers high resilience to interference and provides enhanced security features, which are vital for medical and health-related applications where data integrity and privacy are crucial. Previous studies have shown that DCSK can significantly improve performance in highly dynamic and noisy environments, such as those found in in-body channels. Ref. [33] explored DCSK for body area networks (BANs) and demonstrated that this modulation scheme effectively mitigates the effects of fading and interference in in-body communication environments, ensuring reliable data transmission under adverse conditions. Furthermore, the challenges posed by highly dynamic channels are discussed, and a DCSK-based solution that performs well in fluctuating channel conditions is proposed, enhancing the communication quality and robustness [34].
In summary, DCSK offers several advantages for in-body communication systems, including resilience to channel impairments, low power consumption, and enhanced security features. These benefits make it a highly suitable candidate for the future of body-centric medical and healthcare networks.
The contributions of this paper are shown as follows:
(1) This paper first introduces the model of the in-body channel environment, as well as the channel environment model of WBANs, including the establishment of relevant models and the setting of parameters. Based on the characteristics of the in-body channel environment and the demand for transmission efficiency, a Multi-level Index Position M-ary Differential Chaos Shift Keying (MIP-MDCSK) scheme is designed. This scheme improves the transmission rate by combining index position with MDCSK, where part of the transmission bits are realized by index position and the other part is implemented by the MDCSK modulation itself. The principle of its implementation is discussed in detail.
(2) The energy efficiency (EE), spectral efficiency (SE), and complexity of the proposed scheme are derived and calculated. A comparison with other related schemes shows that the proposed approach achieves a significant improvement in both energy efficiency and spectral efficiency, albeit with a slight increase in complexity. Specifically, the trade-off between complexity and performance is carefully examined, and it is found that by sacrificing a small amount of computational complexity, the scheme offers considerable gains in both energy and spectral efficiency.
(3) Simulations were conducted to compare the performance of the proposed scheme in the in-body channel environment within WBANs. The results show that the scheme demonstrates excellent bit error rate (BER) performance in the in-body channel environment. This indicates that the proposed scheme is well-suited for in-body environments. Additionally, the varying BER performance in the environments can be used to infer information about the current channel conditions, such as the specific type of channel environment and the position of the body. This provides a potential method for adaptive communication systems to dynamically adjust to environmental changes.
Section 2 introduced the channel model and presents the principle of the MIP-MDCSK scheme for impulsive noise in a channel. Section 3 computes EE, SE, and the complexity of MIP-MDCSK and compares them with corresponding schemes. Analysis of performances, simulation, and results are presented in Section 4, respectively. Section 5 concludes the paper.
2. Principle of the MIP-MDCSK Scheme
2.1. Channel Model
The traditional endoscopic capsule communication transmission model is shown in Figure 1. In order to better address the issues of low cost and low power consumption, we have optimized the signal design scheme for the transmission module. For the pathway dissipation of the body’s surface and inner body, we can represent it using logarithmic functions. However, this is not applicable for intracellular signaling pathways. Nevertheless, the formula provided for pathway dissipation is essentially applicable to intracellular signaling pathways [35].
where mm represents the reference distance, d denotes the distance from the skin surface to the chest cavity, with units in mm, and represents the pathway dissipation, measured in dB. n is the exponent of pathway dissipation, while a represents the fitted constant. Equation (1) provides a good fit for the dissipation of pathways within the body with , , and dB.
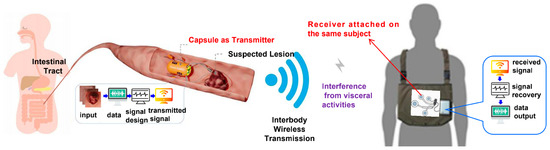
Figure 1.
Endoscopic capsule implementation scheme.
Based on the body surface profile of UWB and free space, the logarithmic distribution of narrowband channels is quite similar to the probability density function (PDF) of shadowing effects [36]. Computational results have demonstrated that the logarithmic distribution also accurately represents shadowing data for different distances in intracellular signaling pathways. Therefore, Equation (1) can be rewritten as
where N represents a random variable that follows a normal distribution, with a mean value of and a standard deviation of . The parameter N varies depending on the value of d.
In the channel model for in-body to on-body communication, Khalghi A proposed in reference [37] that the multipath gain and delay depth (d) follow linear Gaussian distributions with means and for the l-th multipath, and variances and , respectively. The Moreover, can be expressed as
where the is the peak average power, and is the exponential decay factor of peak power. For a given depth d, is always a constant. Similarly, can be expressed as
where the is the Peak average power, is the exponential decay factor of peak power.
2.2. IP-MDCSK and General MIP-MDCSK Sharing One Reference Signal over In-Body Channel
2.2.1. IP-MDCSK
The system based on IP-MDCSK with bits is achieved by index modulation, and the bits are achieved by MDCSK. Thus, the total number of transmitted bits is , and the symbol duration is , with . The chaotic generator generates the reference signal , with being its Hilbert transform. Thus, the transmitted signal is , where is the symbol in the signal space [27], and and are the orthogonal coordinates of the chaotic symbol . Assume that time slots are chosen from a total of P time slots to transmit the information-bearing signals, while the remaining time slots remain unused. takes values within the range from 1 to , where is less than P. As a result, the total is given by for indexes, and t is the number of indexes selected. Hence, the output of the transmitter is expressed as
where , which is used to carry the reference signal. , , . denotes an R-length chaotic signal sequence, and is the spreading factor. The overall number of possible transmitted information-bearing signals is . Assuming , the matrix for index position is expressed as
where is the active row selected from the M matrix, represented as , is the index position selected from the matrix M. The ⨂ is the Kronecker product.
Assuming the modulated symbols are transmitted over a PLC channel with multipath, and the x-th received signal is obtained as
where is the impulse function, and are the gain and delay of the lth path, respectively, and L is the number of paths. is the noise for in-body whose PDF follows Equation (2). When and L paths are one, the channel has only one path.
At the receiver, both MDCSK and index positions are detected. For the index part, position information-bearing signals . After obtaining the position of information-bearing signals, the reference signal on the receiver correlates with the received information-bearing signal , and then the is obtained. Moreover, can be obtained by correlating and , where is the Hilbert transform of . The received symbol is decided by . We assume that the delay is much shorter than the chaotic sequence duration, i.e., . Thus, the inter-symbol interference (ISI) present can be neglected [27]. After finding the indexed position, the decision variable of and can be written as
Similarly, when , the corresponding decision variable can be expressed as
can be detected using the maximum comparator as
where is caused by the reference signal and is caused by the Hilbert transform of .
2.2.2. A General MIP-MDCSK with Shared Reference Signal
The IP-MDCSK can improve the BER performance at the expense of bandwidth efficiency [38]. Considering the bandwidth utilization, MIP-MDCSK is proposed. The block of the scheme is shown in Figure 2, which has t information-bearing signals mapped to t different indexes that are sharing the same reference signal. The total transmitted bits are , where . Similarly, the output of the transmitter for MIP-MDCSK is
where , and consists of t independent components, given as , the and are also the index positions selected from the matrix M.
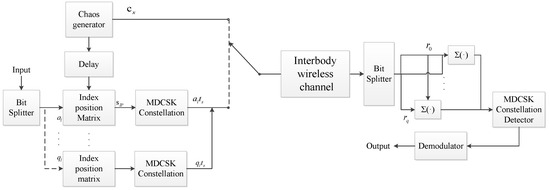
Figure 2.
Block diagram of the MIP-MDCSK scheme for data transmission module of Endoscopic Capsule.
Where the is also the position index modulation symbol. The total number of possible transmitted information-bearing signals is .
At the receiver, the detector detects the positions of multi-index with maximum comparator, where the and are obtained. Then, the remaining bits of information are obtained by demodulation of the MDCSK.
3. Performance Analysis
3.1. Energy Efficiency (EE), and Spectral Efficiency (SE)
We assume that all systems utilize the same chaotic signal with an R-length and unit energy as a reference. In the proposed scheme, the symbol energy is expressed as
where is the energy of the reference sequence. Thus, and . It is obvious that is used to transmit the reference signal while is used to transmit bits. Thus the energy required for transmitting one bit, which is compared with reference part , is:
Subsequently, the energy efficiency (EE), i.e., the number of bits per unit of data energy, can be written as
Table 1 presents the energy efficiency (EE) of various chaotic modulation schemes. As observed in the table, DCSK transmits only a single bit across two time slots, resulting in an EE of 1/2. In contrast, the traditional MDCSK transmits bits within the same time period. The table also highlights that 2IP-MDCSK achieves a significantly higher EE compared to IP-MDCSK, MCS-DCSK, and MDCSK. Furthermore, the EE values for these schemes improve as the value of M increases.

Table 1.
Comparisons of energy efficiency (EE).
A comparison of spectral efficiency (SE) between the proposed MIP-MDCSK and other relevant schemes is provided in Table 2. Let represent the bandwidth. The SE for MIP-MDCSK is given by equation [17]. Similar expressions for the SE of the other schemes are also included in the table. The results indicate that the proposed MIP-MDCSK consistently offers a higher SE than IP-MDCSK, and it outperforms MCS-DCSK when the parameters are appropriately chosen. However, it falls short of traditional MDCSK in terms of SE. In conclusion, the proposed system achieves a balanced trade-off between SE, EE, and BER performance.

Table 2.
Comparisons of spectral efficiency (SE).
3.2. Complexity Analysis Comparison with MDCSK
This section presents a comparison of the hardware computational complexity of MIP-MDCSK with that of the corresponding MDCSK schemes, all of which operate at the same modulation order (M). The details of the components involved in the transmission and reception processes for MIP-MDCSK, MCS-DCSK, and MDCSK are summarized in Table 3 and Table 4, respectively. To achieve M-ary modulation, all schemes require the use of filtration twice, both at the transmitter and receiver, in order to generate orthogonal signals. Additionally, the complexity of MIP-MDCSK and MCS-DCSK systems is increased due to the implementation of position and Walsh code selection techniques, making them more intricate than the MDCSK scheme. Furthermore, the delay units in the transmitter and multipliers in the receiver of MIP-MDCSK are more sophisticated compared to those in the other schemes. As a result, the increased computational complexity in MIP-MDCSK is a trade-off for its enhanced BER performance.

Table 3.
Comparisons of Transmitter Computational Complexity.

Table 4.
Comparisons of Receiver Computational Complexity.
4. Numerical Result
This section presents an analysis of the performance of systems utilizing the proposed constellation scheme under various system parameters. The distribution parameters corresponding to different distances are shown as Table 5.

Table 5.
The distribution parameters corresponding to depth [39].
To investigate the BER performance of the system in an in-body channel environment, we examine the effects of parameters such as , M, n, and the in-body channel parameter depth. Figure 3 demonstrates the performance of the 2IP-MDCSK system under in-body channel conditions with system parameters set as depth = 80 mm, M = 4, and n = 2. From the figure, it is evident that the overall BER performance deteriorates as increases. However, when = 32, the BER performance is significantly worse compared to other values. This can be attributed to the characteristics of the chaotic signal. At smaller values, the system struggles to effectively exhibit the correlation properties, leading to a higher likelihood of bit errors.
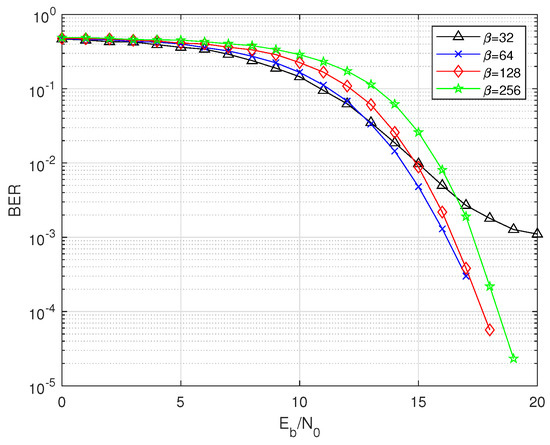
Figure 3.
BER comparison of 2IP-MDCSK for over in-body channel.
Figure 4 illustrates the impact of different values of M and on the performance of the MIP-MDCSK system under varying depth conditions within an in-body environment. Overall, as M increases, the BER performance deteriorates, while an increase in leads to improved system performance. Moreover, the influence of M on the BER performance is significantly more pronounced than that of . For instance, in Figure 4a, at a BER of , the gap between 2IP-4DCSK and 4IP-4DCSK is 1 dB, whereas the gap between 2IP-4DCSK and 2IP-8DCSK at the same BER is 2.5 dB. This clearly demonstrates that the constellation parameters have a much greater impact on the BER performance than the IP components. Regarding the effect of depth on the system, a comparison from Figure 4a,b shows that when depth = 80 mm, the overall BER performance is better than when depth = 20 mm. At a BER of , the 2IP-4DCSK system shows a gain of approximately 1 dB at depth = 80 mm compared to depth = 20 mm. This suggests that a greater depth brings the system closer to the in-body channel environment, indicating that the system is better suited for in-body channel conditions.
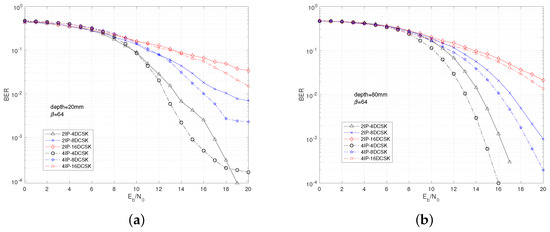
Figure 4.
BER comparison of MIP-MDCSK for in-body channel. (a) depth = 20 mm. (b) depth = 80 mm.
Further discussion on the impact of depth on the system is provided in Figure 5. As shown in the figure, the BER performance at depth = 80 mm is significantly better than at depth = 20 mm. At depth = 20 mm, when the increases to a certain level, the system gradually experiences an error floor. The SNR value at which the error floor begins to appear shifts to a lower value as M decreases. However, for the MIP-MDCSK system itself, its performance is optimal when M = 4, and the BER performance deteriorates as M increases, which is contrary to the behavior observed with the error floor. In contrast, at depth = 80 mm, the system does not exhibit a noticeable error floor, further supporting the suitability of this system model for channels that closely resemble in-body environments.
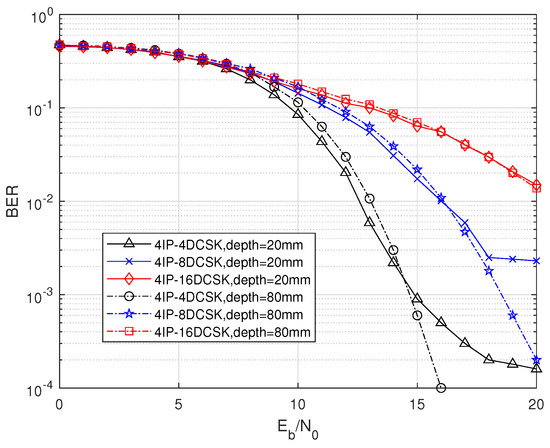
Figure 5.
BER comparison of MIP-MDCSK for depth in in-body channel, with .
To further discuss the proposed solution, it is compared with MCS-MDCSK and MDCSK, as shown in Figure 6. According to the graph, the proposed scheme has the best bit error rate performance under different depth parameters. From the other two schemes, it is known that at depth = 80 mm, their bit error rate performance is better at depth = 20 mm than when the is small and worse than at depth = 20 mm when the is large. The intersection points of the proposed MIP-MDCSK appear earlier.
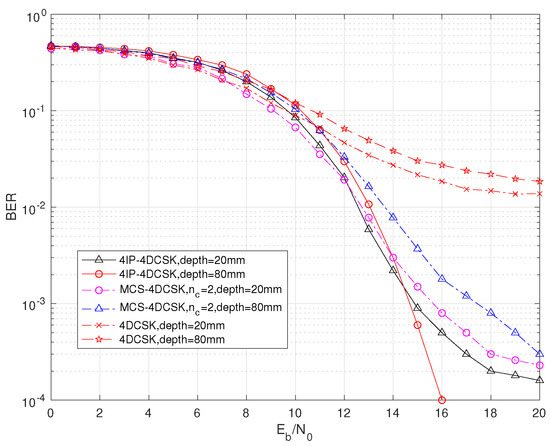
Figure 6.
BER comparison of 2IP-MDCSK among MDCSK and MCS-MDCSK, with = 64 over in-body channel.
5. Conclusions
This paper addresses issues such as high power consumption, significant signal interference, and low data transmission rates in capsule endoscopy communication. It proposes a modulation optimization scheme (MIP-MDCSK) aimed at improving performance through three main aspects: BER performance, EE, and SE. The performance of the proposed scheme is evaluated for WBANs.
Through Monte Carlo simulations, the BER is evaluated in the in-body channel. The results reveal that the in-body channel yields favorable BER performance, especially as the value increases, indicating better robustness against noise. The gap between 2IP-4DCSK and 4IP-4DCSK is 1 dB, whereas the gap between 2IP-4DCSK and 2IP-8DCSK at the same BER is 2.5 dB at a BER of . Moreover, the BER of the system can be significantly reduced to , indicating that it meets the BER performance requirements of in-body channel devices that need to be synchronized in medical image transmission environments.
Therefore, this optimized solution can address the low-cost and low-power communication transmission of endoscopic capsules while improving transmission performance, thus promoting the widespread adoption and development of endoscopic capsules.
Author Contributions
Conceptualization, M.M. and C.Y.; methodology, M.M.; software, M.M. and Z.X.; validation, Z.X.; formal analysis, M.M.; investigation, M.M.; resources, Z.X.; data curation, M.M.; writing—original draft preparation, M.M.; writing—review and editing, C.Y.; visualization, M.M.; supervision, M.M.; project administration, M.M., J.Y. and L.Z.; funding acquisition, M.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (No. 62301277, 62471244), the Natural Science Research Start-up Foundation of Recruiting Talents of Nanjing University of Posts and Telecommunications (No. NY223019, NY223134), the Jilun Medical Intelligent Technology (Nanjing) Co., Ltd. (No. 2024-298).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
See Liu, W. Performance Analysis of Differential Chaotic Shift Keying Ultra-Wideband Systems in In-Body Channels. Master’s Thesis, Xiamen University, Xiamen, China, 2022.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Liu, H.; Shi, J.; Song, L.; Liu, L.; Wang, Y.; Cheng, T.; Wang, J. Novel Multiband Antenna Design and Performance Evaluation for Wireless Electronic Capsule Systems. IEEE J. Electromagn. RF Microw. Med. Biol. 2024, 8, 332–343. [Google Scholar] [CrossRef]
- Alshammari, A.; Iqbal, A.; Basir, A.; Simorangkir, R.B.V.B.; Mabrouk, I.B. Ultra-Miniaturized Dual-Band Implantable Antenna for Wireless Capsule Endoscopy. IEEE Sens. J. 2024, 24, 15210–15218. [Google Scholar] [CrossRef]
- Song, M.; Liu, H.; Guo, Q. Deep-Learning-Based Channel Prediction for Wireless Capsule Endoscopy in PLC-Class-A Noise. IEEE J. Biomed. Health Inform. 2025, 29, 456–467. [Google Scholar]
- Hu, Z.; Han, C.; Deng, Y.; Wang, X. Multi-Task Deep Reinforcement Learning for Terahertz NOMA Resource Allocation with Hybrid Discrete and Continuous Actions. IEEE Trans. Veh. Technol. 2024, 73, 11647–11663. [Google Scholar] [CrossRef]
- Särestöniemi, M.; Pomalaza-Ráez, C.; Kissi, C.; Berg, M.; Hämäläinen, M.; Iinatti, J. WBAN Channel Characteristics Between Capsule Endoscope and Receiving Directive UWB On-Body Antennas. IEEE Access 2020, 8, 55953–55968. [Google Scholar] [CrossRef]
- Luo, C.; Tang, A.; Gao, F.; Liu, J.; Wang, X. Channel Modeling Framework for Both Communications and Bistatic Sensing Under 3GPP Standard. IEEE J. Sel. Areas Sens. 2024, 1, 166–176. [Google Scholar] [CrossRef]
- Dhali, A.; Kipkorir, V.; Maity, R. AI-Assisted Capsule Endoscopy vs. Conventional Capsule Endoscopy for Small Bowel Lesions. J. Gastroenterol. Hepatol. 2025, 40, 1105–1118. [Google Scholar] [CrossRef] [PubMed]
- Song, D.; Ren, J.; Wang, L.; Li, Y.; Zhang, X. Designing a Common DP-LDPC Code Pair for Variable On-Body Channels. IEEE Trans. Wireless Commun. 2022, 21, 9596–9609. [Google Scholar] [CrossRef]
- Mehedi, I.M.; Rao, K.P.; Alotaibi, F.M.; Alkanfery, H.M. Intelligent Wireless Capsule Endoscopy for the Diagnosis of Gastrointestinal Diseases. Diagnostics 2023, 13, 1445. [Google Scholar] [CrossRef]
- Siddik, A.; Hasi, M.A.A.; Nitu, J.A.; Sarker, S.; Sultana, N.; Ali, E. Modified IEEE 802.15.6 MAC scheme for e-health applications. J. E-Health Res. 2022, 12, 123–130. [Google Scholar]
- Siddik, A.; Hasi, M.A.A.; Islam, M.R.; Nitu, J.A. Effects of MAC and PHY layer parameters on IEEE 802.15.6 CSMA/CA performance. IEEE Trans. Wirel. Commun. 2024, 33, 2155–2163. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, L.; Xu, W. Integration of WBANs with advanced modulation schemes for healthcare applications. IEEE Trans. Wirel. Commun. 2019, 28, 200–210. [Google Scholar]
- Gupta, R.; Kumar, S.; Sharma, A. Energy-efficient communication protocols for WBANs in healthcare systems. IEEE Commun. Mag. 2018, 56, 42–49. [Google Scholar]
- Ding, W.; Zhang, Z.; Liu, F. Energy-efficient DCSK for body networks under power constraints. IEEE Trans. Ind. Inform. 2017, 14, 3445–3455. [Google Scholar]
- Chen, P.; Chen, H.; Shi, L.; Lin, Z.; Li, Y. Initial Chaotic Value-based Index Modulation for Wireless Communications. IEEE Trans. Commun. 2024, 72, 6014–6028. [Google Scholar] [CrossRef]
- Qian, M.; Cai, G.; Fang, Y.; Chen, P.; Han, G. Design of link-selection strategies for buffer-aided DCSK-SWIPT relay system. IEEE Trans. Commun. 2020, 68, 6023–6038. [Google Scholar] [CrossRef]
- Miao, M.; Wang, L.; Chen, G.; Xu, W. Design and analysis of replica piecewise M-ary DCSK scheme for power line communications with asynchronous impulsive noise. IEEE Trans. Circuits Syst. I Reg. Papers 2020, 67, 5443–5453. [Google Scholar] [CrossRef]
- Xie, K.; Cai, G.; Kaddoum, G. Design and Performance Analysis of RIS-Aided DCSK-WPC System With Energy Buffer. IEEE Trans. Commun. 2023, 71, 1726–1739. [Google Scholar] [CrossRef]
- Cai, G.; Fang, Y.; Wen, J.; Mumtaz, S.; Song, Y.; Frascolla, V. Multi-carrier M-ary DCSK system with code index modulation: An efficient solution for chaotic communications. IEEE J. Sel. Top. Signal Process. 2019, 13, 1375–1386. [Google Scholar] [CrossRef]
- Xu, W.; Wang, L.; Kaddoum, G. A novel differential chaos shift keying modulation. Int. J. Bifurc. Chaos 2011, 21, 799–814. [Google Scholar] [CrossRef]
- Xu, W.; Wang, L.; Kaddoum, G. A new data rate adaption communications scheme for code-shift differential chaos shift keying modulation. Int. J. Bifurc. Chaos 2012, 22, 1250201. [Google Scholar] [CrossRef]
- Kaddoum, G.; Gagnon, F. Design of a High-Data-Rate Differential Chaos-Shift Keying System. IEEE Trans. Circuits Syst. II 2012, 59, 448–452. [Google Scholar] [CrossRef]
- Xu, W.; Huang, T.; Wang, L. Code-Shifted Differential Chaos Shift Keying With Code Index Modulation for High Data Rate Transmission. IEEE Trans. Wireless Commun. 2017, 65, 4285–4294. [Google Scholar] [CrossRef]
- Wang, S.; Wang, X. M-DCSK-based chaotic communications in MIMO multipath channels with no channel state information. IEEE Trans. Circuits Syst. II Express Briefs 2010, 57, 1001–1005. [Google Scholar] [CrossRef]
- Cai, G.; Fang, Y.; Han, G.; Lau, F.C.M.; Wang, L. A square-constellation-based M-ary DCSK communication system. IEEE Access 2016, 9, 6295–6303. [Google Scholar] [CrossRef]
- Cai, G.; Song, Y. Closed-form BER expressions of M-ary DCSK systems over multipath Rayleigh fading channels. IEEE Commun. Lett. 2020, 24, 1192–1196. [Google Scholar] [CrossRef]
- Wang, L.; Cai, G.; Chen, G. Design and performance analysis of a new multiresolution M-ary differential chaos shift keying communication system. IEEE Trans. Wireless Commun. 2015, 14, 5197–5208. [Google Scholar] [CrossRef]
- Galias, Z.; Maggio, G.M. Quadrature chaos-shift keying: Theory and performance analysis. IEEE Trans. Circuits Syst. I Reg. Papers 2001, 48, 1510–1519. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, X. Chaotic secure communication system for wireless body area networks using differential chaos shift keying. IEEE Trans. Ind. Inform. 2018, 14, 3962–3971. [Google Scholar]
- Li, X.; Zhang, L. Differential chaos shift keying for wireless body area networks: A performance analysis. IEEE Trans. Wirel. Commun. 2017, 16, 3025–3036. [Google Scholar]
- Fang, Z.; Yang, X. A secure communication framework based on differential chaos shift keying modulation for WBAN. IEEE Access 2020, 8, 182642–182650. [Google Scholar]
- Wang, Y.; Wu, S. Design and performance analysis of differential chaos shift keying in wireless body area networks. IEEE Trans. Commun. 2016, 64, 3245–3255. [Google Scholar]
- Zhao, Z.; Yang, X. DCSK for Body Area Networks: Mitigating fading and interference in in-body communication environments. IEEE Trans. Commun. 2019, 67, 1234–1245. [Google Scholar]
- He, L.; Zhang, Y.; Wang, X. DCSK-based solution for highly dynamic channels in body area networks. IEEE Access 2020, 8, 192344–192355. [Google Scholar]
- Molisch, A.F. An ultra-wideband body area propagation channel model from statics to implementation. IEEE Trans. Microw. Theory Tech. 2006, 54, 1820–1826. [Google Scholar]
- Molisch, A.F. Ultra-wideband propagation channels. Proc. IEEE 2009, 97, 353–371. [Google Scholar] [CrossRef]
- Khaleghi, A.; Balasingham, I. On-body communication systems: Channel modeling and analysis. IEEE Trans. Antennas Propag. 2013, 61, 1053–1063. [Google Scholar]
- Miao, M.; Wang, L.; Katz, M.; Xu, W. Hybrid Modulation Scheme Combining PPM with Differential Chaos Shift Keying Modulation. IEEE Wireless Commun. Lett. 2018, 8, 340–343. [Google Scholar] [CrossRef]
- Liu, W. Performance Analysis of Differential Chaotic Shift Keying Ultra-Wideband Systems in In-Body Channels. Master’s Thesis, Xiamen University, Xiamen, China, 2022. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).