A Sensor Data Prediction and Early-Warning Method for Coal Mining Faces Based on the MTGNN-Bayesian-IF-DBSCAN Algorithm
Abstract
1. Introduction
2. Materials and Methods
2.1. Multi-Task Graph Neural Network Time-Series Prediction Method for Multi-Parameter Gas Sensors
2.1.1. Data Preprocessing
2.1.2. Model Structure
- Input Convolutional Layer
- 2.
- Initialization of Skip Connection
- 3.
- Temporal Convolutional Layer
- 4.
- Update of Skip Connection
- 5.
- Graph Convolutional Layer
- 6.
- Residual Connection
- 7.
- Layer Normalization
- 8.
- Final Output Layer
- 9.
- Loss Function and Optimization
2.2. Bayesian–Isolation Forest–Density-Based Spatial Clustering of Applications with the Noise Gas Anomaly Detection Model
2.2.1. Concatenation of Prediction Data and Residuals
2.2.2. Isolation Forest Anomaly Detection
- Anomaly Score Calculation
- 2.
- Anomaly Detection
2.2.3. Density-Based Spatial Clustering of Applications with the Noise Gas Anomaly Detection Model
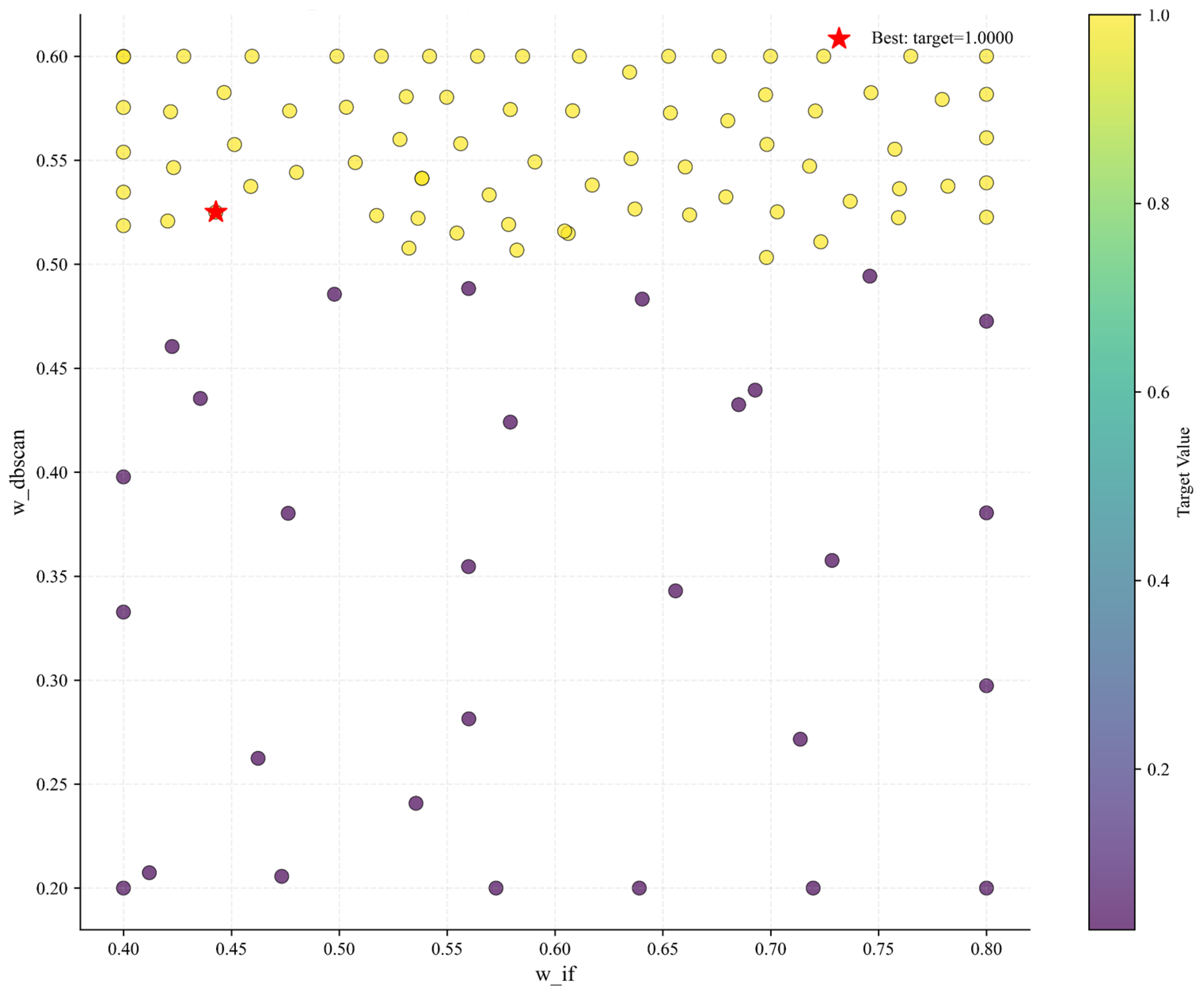
2.2.4. Bayesian Optimization
- Objective Function
- 2.
- Bayesian Optimization Process
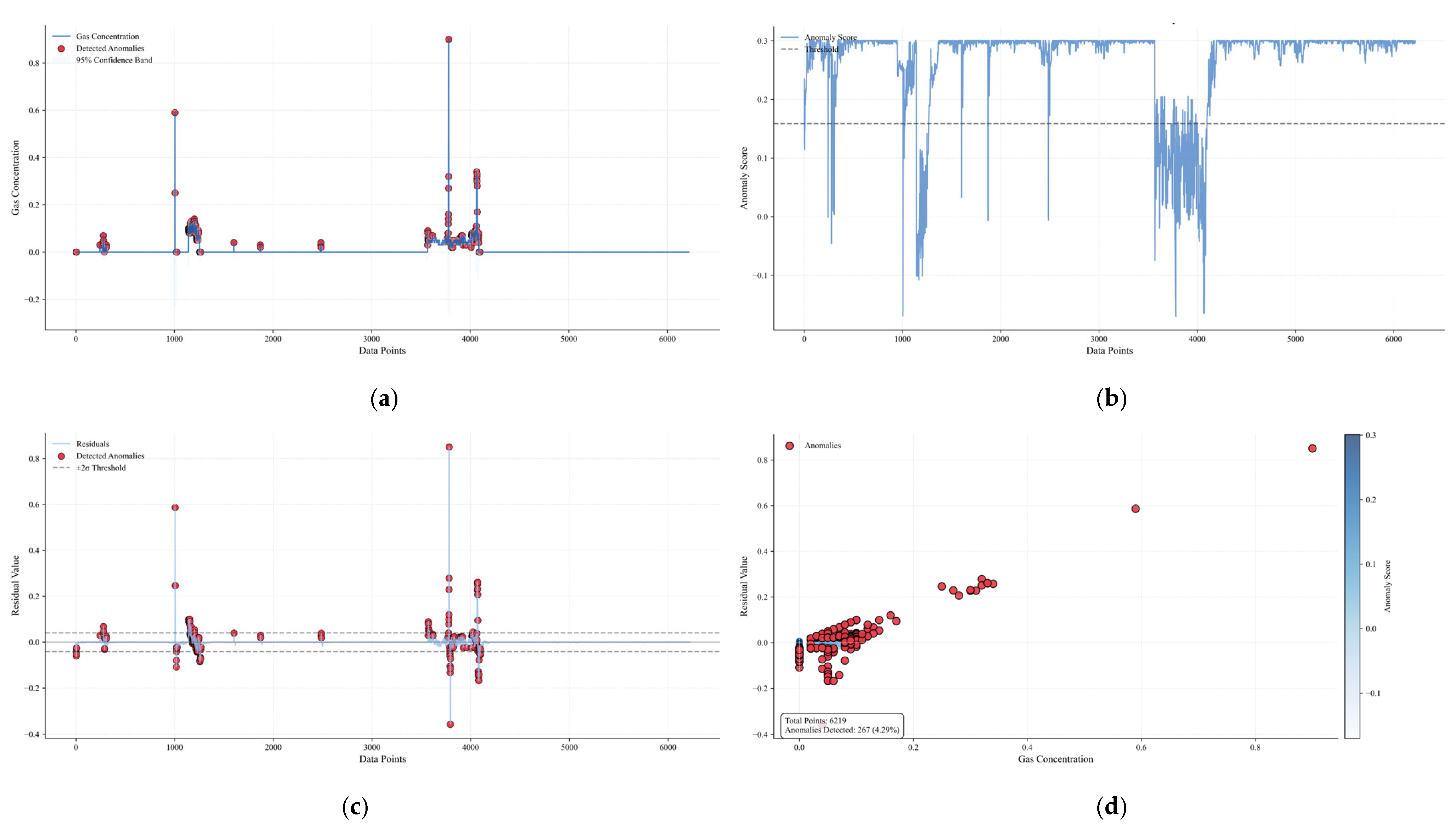
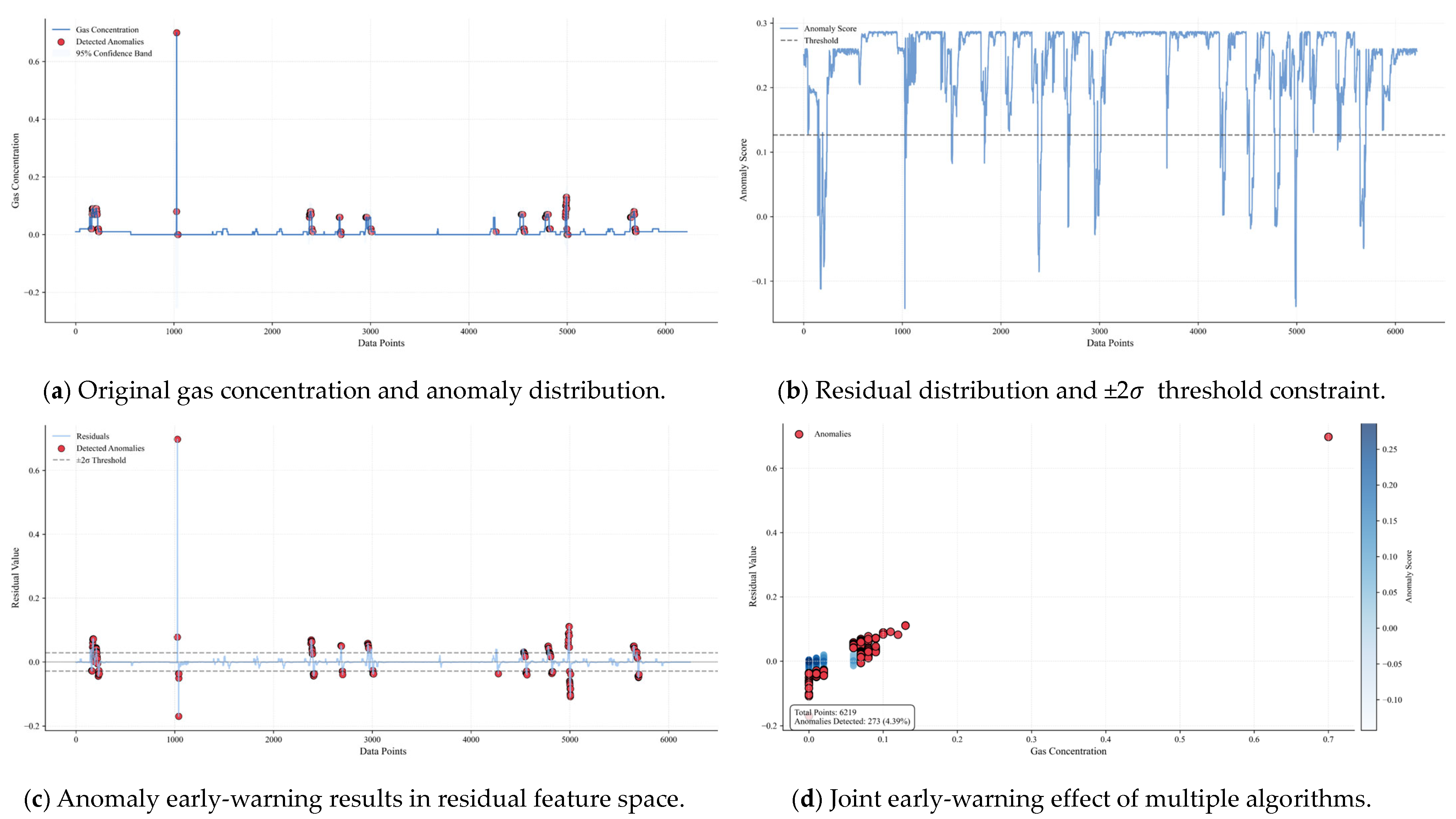
2.2.5. Joint Anomaly Detection
- Joint Score Calculation
- 2.
- Final Anomaly Detection
2.3. Sensor Layout Method
3. Results
3.1. Data Source and Algorithm Settings
3.2. Comparison of Algorithm Prediction Results
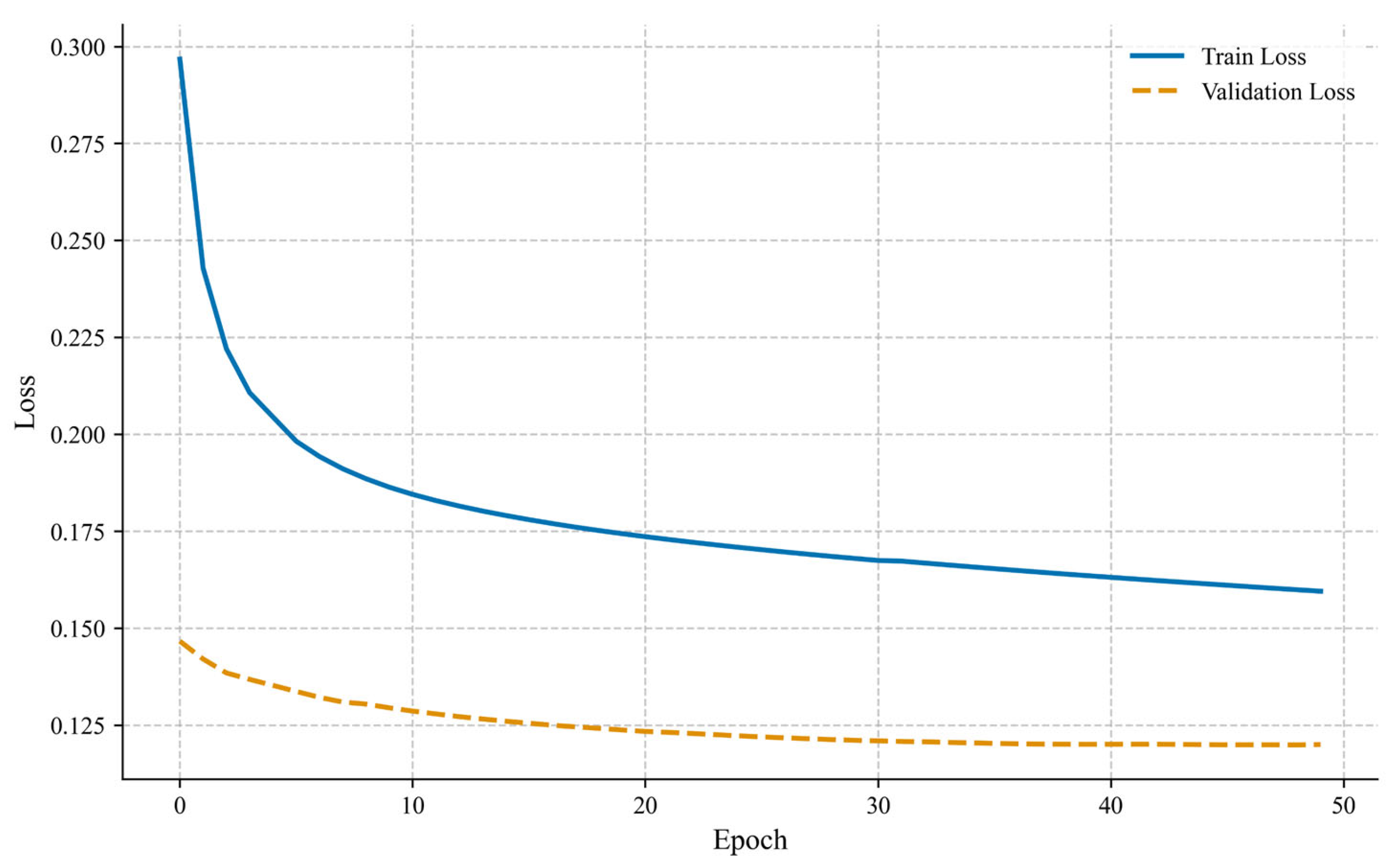
3.2.1. Training Process of the MTGNN Algorithm
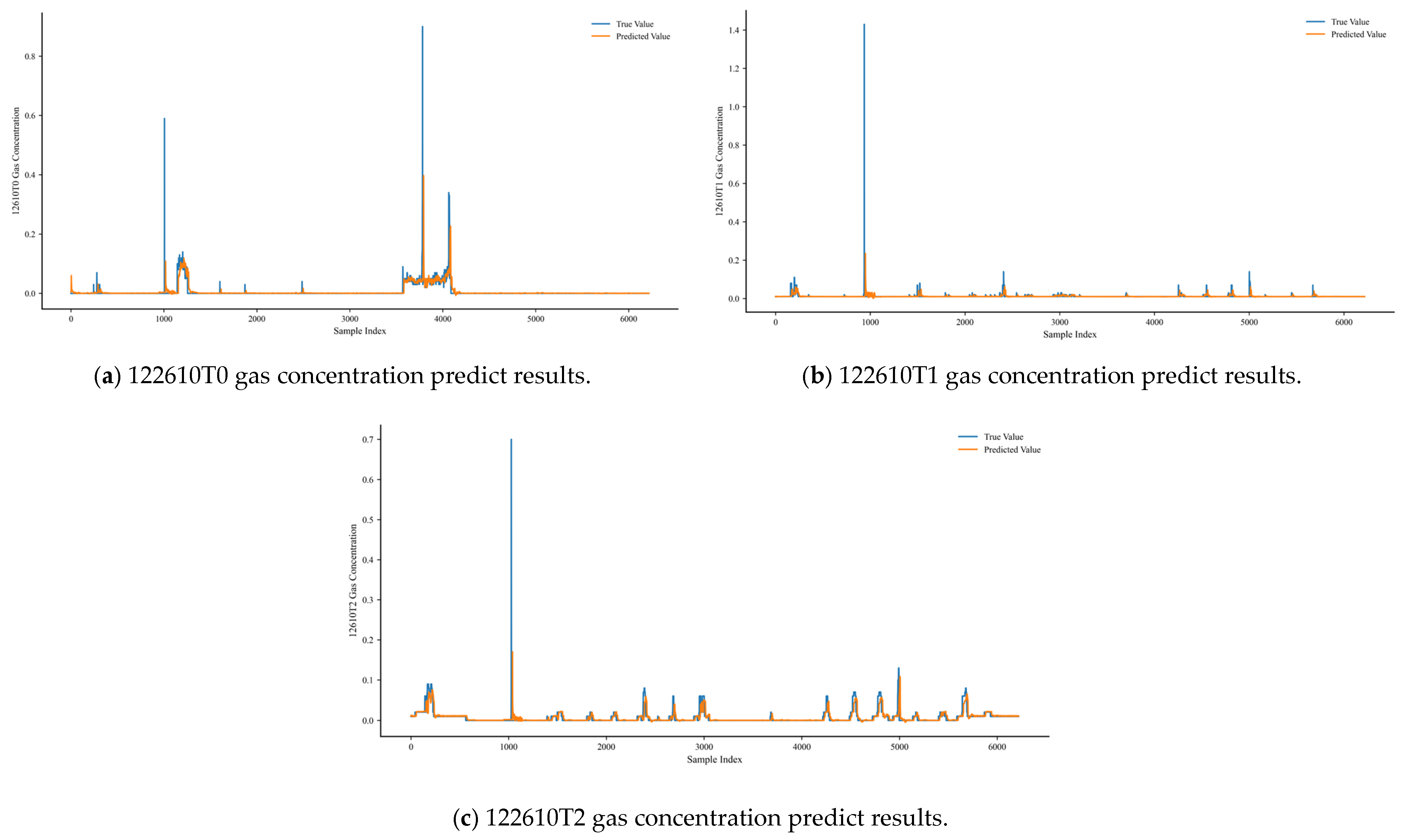
3.2.2. Prediction Results of the MTGNN Algorithm
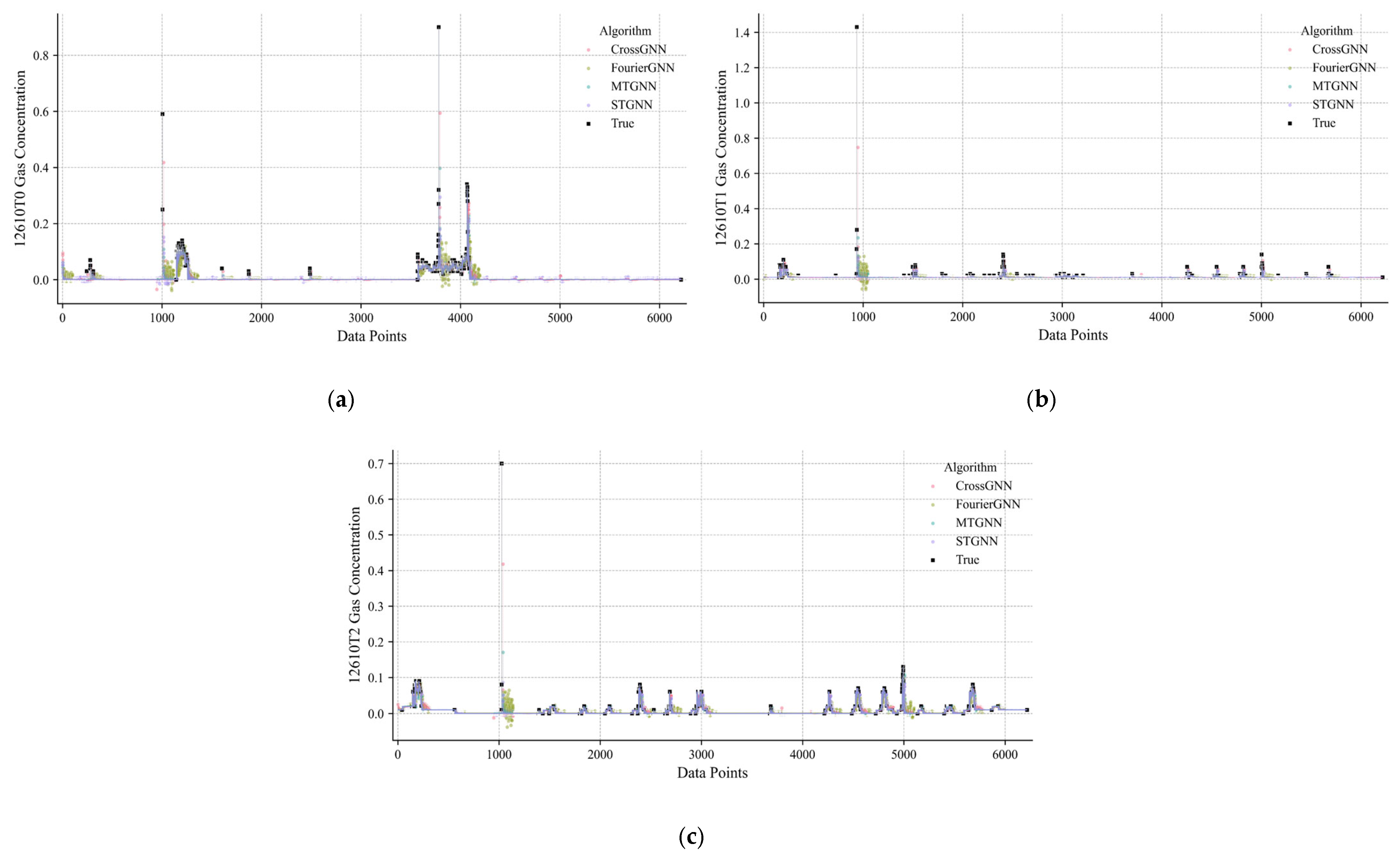
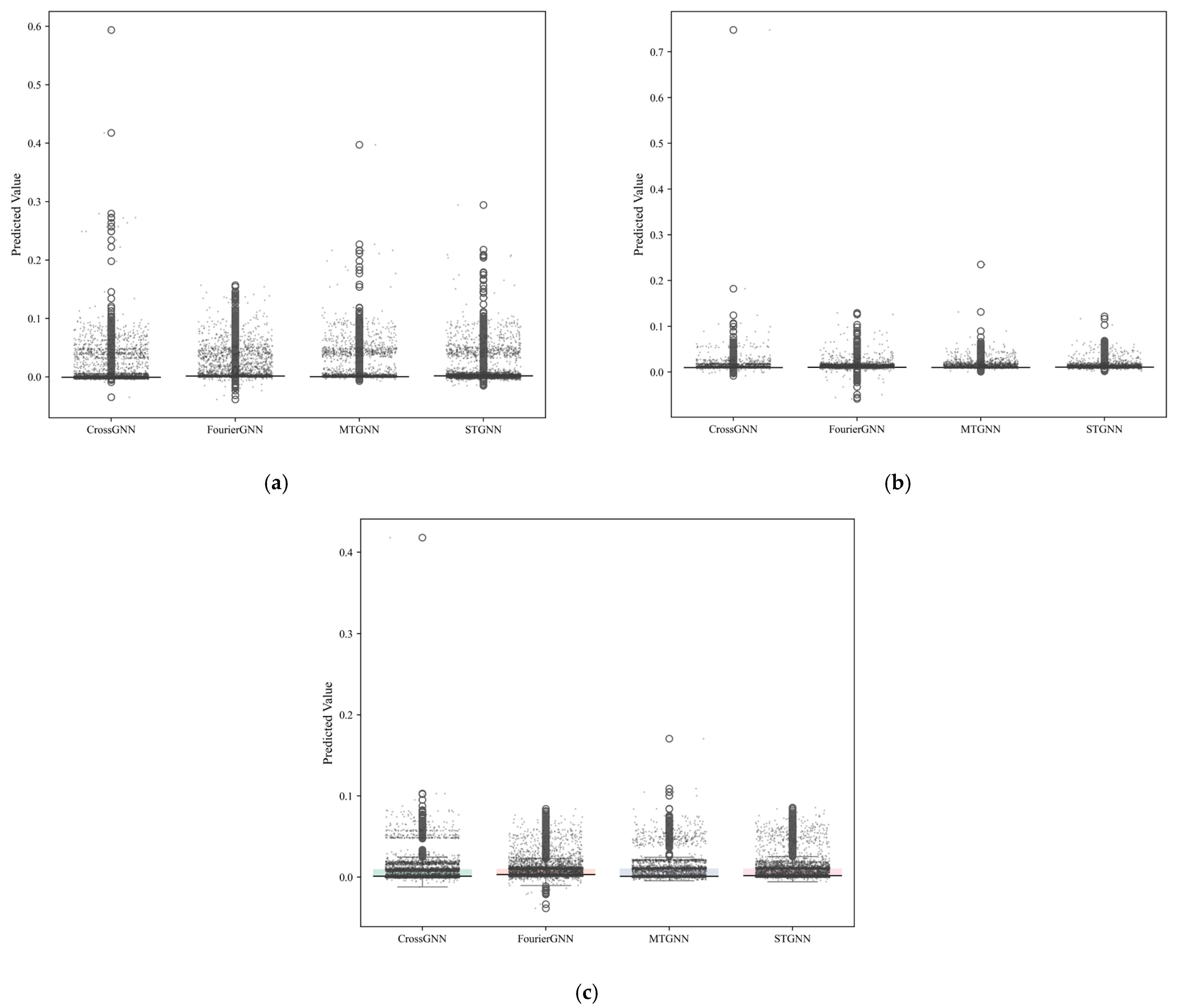
3.2.3. Comparison and Analysis of the Prediction Results of Multiple Algorithms
3.3. Early-Warning Method
3.3.1. Bayesian Algorithm Early-Warning Optimization Process
3.3.2. 122610T0 Gas Anomaly Detection Results
3.3.3. 122610T1 Gas Anomaly Detection Results
3.3.4. 122610T2 Gas Anomaly Detection Results
4. Conclusions
- Remarkable Advantages of Multi-Source Data-Fusion Prediction Performance
- 2.
- Bayesian Optimization Enhances Anomaly Detection Robustness
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hudson-Edwards, K.A.; Kemp, D.; Torres-Cruz, L.A.; Macklin, M.G.; Brewer, P.A.; Owen, J.R.; Franks, D.M.; Marquis, E.; Thomas, C.J. Tailings Storage Facilities, Failures and Disaster Risk. Nat. Rev. Earth Environ. 2024, 5, 612–630. [Google Scholar] [CrossRef]
- Alberto, D.; Izar, A.; Xabier, O.; Giuseppe, L.; Igor, G. Real-Time Identification of Borehole Rescue Environment Situation in Underground Disaster Areas Based on Multi-Source Heterogeneous Data Fusion. Saf. Sci. 2025, 181, 106690. [Google Scholar] [CrossRef]
- Chen, H.; Eldardiry, H. Graph Time-Series Modeling in Deep Learning: A Survey. ACM Trans. Knowl. Discov. Data 2024, 18, 1–35. [Google Scholar] [CrossRef]
- Jin, M.; Koh, H.Y.; Wen, Q.; Zambon, D.; Alippi, C.; Webb, G.I.; King, I.; Pan, S. A Survey on Graph Neural Networks for Time Series: Forecasting, Classification, Imputation, and Anomaly Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 10466–10485. [Google Scholar] [CrossRef]
- Guo, H.; Zhou, Z.; Zhao, D.; Gaaloul, W. EGNN: Energy-Efficient Anomaly Detection for IoT Multivariate Time Series Data Using Graph Neural Network. Future Gener. Comput. Syst. 2024, 151, 45–56. [Google Scholar] [CrossRef]
- Wang, D.; Zhu, J.; Yin, Y.; Ignatius, J.; Wei, X.; Kumar, A. Dynamic Travel Time Prediction with Spatiotemporal Features: Using a GNN-Based Deep Learning Method. Ann. Oper. Res. 2024, 340, 571–591. [Google Scholar] [CrossRef]
- Shi, J.; Li, J.; Zhang, H.; Xie, B.; Xie, Z.; Yu, Q.; Yan, J. Real-Time Gas Explosion Prediction at Urban Scale by GIS and Graph Neural Network. Appl. Energy 2025, 377, 124614. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Y.; Chen, W.; Li, L.; Hao, H. Machine Learning Prediction of BLEVE Loading with Graph Neural Networks. Reliab. Eng. Syst. Saf. 2024, 241, 109639. [Google Scholar] [CrossRef]
- Wang, Z.; Han, Z.; Zhao, J.; Wang, W. A Spatiotemporal Characteristics Based Multi-Nodes State Prediction Method for Byproduct Gas System and Its Application on Safety Assessment. Control Eng. Pract. 2025, 158, 106280. [Google Scholar] [CrossRef]
- Chen, S.; Du, W.; Wang, B.; Cao, C. Dynamic Prediction of Multisensor Gas Concentration in Semi-Closed Spaces: A Unified Spatiotemporal Inter-Dependencies Approach. J. Loss Prev. Process Ind. 2025, 94, 105569. [Google Scholar] [CrossRef]
- Wang, C.; Zhou, D.; Wang, X.; Liu, S.; Shao, T.; Shui, C.; Yan, J. Multiscale Graph Based Spatio-Temporal Graph Convolutional Network for Energy Consumption Prediction of Natural Gas Transmission Process. Energy 2024, 307, 132489. [Google Scholar] [CrossRef]
- Zhang, X.; Shi, J.; Li, J.; Huang, X.; Xiao, F.; Wang, Q.; Usmani, A.S.; Chen, G. Hydrogen Jet and Diffusion Modeling by Physics-Informed Graph Neural Network. Renew. Sustain. Energy Rev. 2025, 207, 114898. [Google Scholar] [CrossRef]
- Karasu, S.; Altan, A. Crude Oil Time Series Prediction Model Based on LSTM Network with Chaotic Henry Gas Solubility Optimization. Energy 2022, 242, 122964. [Google Scholar] [CrossRef]
- Song, S.; Chen, J.; Ma, L.; Zhang, L.; He, S.; Du, G.; Wang, J. Research on a Working Face Gas Concentration Prediction Model Based on LASSO-RNN Time Series Data. Heliyon 2023, 9, e14864. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Hu, Q.; Li, J.; Li, W.; Liu, T.; Xin, M.; Jin, Q. Decoupling Representation Contrastive Learning for Carbon Emission Prediction and Analysis Based on Time Series. Appl. Energy 2024, 367, 123368. [Google Scholar] [CrossRef]
- Zhou, W.; Li, X.; Qi, Z.; Zhao, H.; Yi, J. A Shale Gas Production Prediction Model Based on Masked Convolutional Neural Network. Appl. Energy 2024, 353, 122092. [Google Scholar] [CrossRef]
- Shi, J.; Li, J.; Tam, W.C.; Gardoni, P.; Usmani, A.S. Physics_GNN: Towards Physics-Informed Graph Neural Network for the Real-Time Simulation of Obstructed Gas Explosion. Reliab. Eng. Syst. Saf. 2025, 256, 110777. [Google Scholar] [CrossRef]
- Xu, J.; Zhu, W.; Xu, J.; Wu, J.; Li, Y. High-Intensity Longwall Mining-Induced Ground Subsidence in Shendong Coalfield, China. Int. J. Rock. Mech. Min. Sci. 2021, 141, 104730. [Google Scholar] [CrossRef]
- Xu, J.; Gao, M.; Wang, Y.; Yu, Z.; Zhao, J.; DeJong, M.J. Numerical Investigation of the Effects of Separated Footings on Tunnel-Soil-Structure Interaction. J. Geotech. Geoenviron. Eng. 2025, 151, 04025057. [Google Scholar] [CrossRef]
- Sun, M.; Qin, S. Research on Multi-Step Prediction of Pipeline Corrosion Rate Based on Adaptive MTGNN Spatio-Temporal Correlation Analysis. Appl. Sci. 2025, 15, 5686. [Google Scholar] [CrossRef]
- Ren, H.-T.; Cao, W.-B.; Qin, J.; Cai, C.-C.; Li, D.-S.; Li, T.-T.; Lou, C.-W.; Lin, J.-H. Enhanced Removal of Tetracycline by Sandwich Layer Composite Membrane Based on the Synergistic Effect of Photocatalysis and Adsorption. Sep. Purif. Technol. 2024, 341, 126910. [Google Scholar] [CrossRef]
- Cao, Y.; Xiang, H.; Zhang, H.; Zhu, Y.; Ting, K.M. Anomaly Detection Based on Isolation Mechanisms: A Survey. arXiv 2024. [Google Scholar] [CrossRef]
- Li, M.; Su, M.; Zhang, B.; Yue, Y.; Wang, J.; Deng, Y. Research on a DBSCAN-IForest Optimisation-Based Anomaly Detection Algorithm for Underwater Terrain Data. Water 2025, 17, 626. [Google Scholar] [CrossRef]
- Paulson, J.A.; Tsay, C. Bayesian Optimization as a Flexible and Efficient Design Framework for Sustainable Process Systems. Curr. Opin. Green Sustain. Chem. 2025, 51, 100983. [Google Scholar] [CrossRef]







| Location of Sensors | MAE | RMSE | MASE |
|---|---|---|---|
| 122610T0 | 0.003712888 | 0.020322414 | 2.975095 |
| 122610T1 | 0.002372786 | 0.020097299 | 2.221986 |
| 122610T2 | 0.004348235 | 0.014315962 | 7.90565 |
| Algorithm | MAE | RMSE | MASE |
|---|---|---|---|
| CrossGNN | 0.004625052 | 0.022911226 | 3.706002 |
| FourierGNN | 0.005878239 | 0.021198189 | 4.710166 |
| MTGNN (base) | 0.003712888 | 0.020322414 | 2.975095 |
| STGNN | 0.004896523 | 0.020451846 | 3.923529 |
| Algorithm | MAE | RMSE | MASE |
|---|---|---|---|
| CrossGNN | 0.002693928 | 0.022391291 | 2.522717 |
| FourierGNN | 0.003135901 | 0.020463146 | 2.936602 |
| MTGNN (base) | 0.002372786 | 0.020097299 | 2.221986 |
| STGNN | 0.002823277 | 0.019965895 | 2.643846 |
| Algorithm | MAE | RMSE | MASE |
|---|---|---|---|
| CrossGNN | 0.004625052 | 0.022911226 | 3.706002 |
| FourierGNN | 0.00609257 | 0.015168412 | 11.077077 |
| MTGNN (base) | 0.004348235 | 0.014315962 | 7.90565 |
| STGNN | 0.004979862 | 0.014472567 | 9.054029 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Wang, X.; Qiao, W.; Shang, H.; Yan, Z.; Qin, Z. A Sensor Data Prediction and Early-Warning Method for Coal Mining Faces Based on the MTGNN-Bayesian-IF-DBSCAN Algorithm. Sensors 2025, 25, 4717. https://doi.org/10.3390/s25154717
Liu M, Wang X, Qiao W, Shang H, Yan Z, Qin Z. A Sensor Data Prediction and Early-Warning Method for Coal Mining Faces Based on the MTGNN-Bayesian-IF-DBSCAN Algorithm. Sensors. 2025; 25(15):4717. https://doi.org/10.3390/s25154717
Chicago/Turabian StyleLiu, Mingyang, Xiaodong Wang, Wei Qiao, Hongbo Shang, Zhenguo Yan, and Zhixin Qin. 2025. "A Sensor Data Prediction and Early-Warning Method for Coal Mining Faces Based on the MTGNN-Bayesian-IF-DBSCAN Algorithm" Sensors 25, no. 15: 4717. https://doi.org/10.3390/s25154717
APA StyleLiu, M., Wang, X., Qiao, W., Shang, H., Yan, Z., & Qin, Z. (2025). A Sensor Data Prediction and Early-Warning Method for Coal Mining Faces Based on the MTGNN-Bayesian-IF-DBSCAN Algorithm. Sensors, 25(15), 4717. https://doi.org/10.3390/s25154717






