An Effective QoS-Aware Hybrid Optimization Approach for Workflow Scheduling in Cloud Computing
Abstract
1. Introduction
- (1)
- A novel hybrid architecture combining HEFT’s efficiency with WOA’s global search capability.
- (2)
- An improved WOA incorporating Lévy flight to avoid local optima.
- (3)
- An efficient fitness function balancing makespan and cost to meet the different QoS preferences.
- (4)
- Validation of better performance of HLWOA through simulation and comparison with other scheduling algorithms.
2. Related Works
3. Models and Problem Formulation
3.1. The Cloud Resource Model
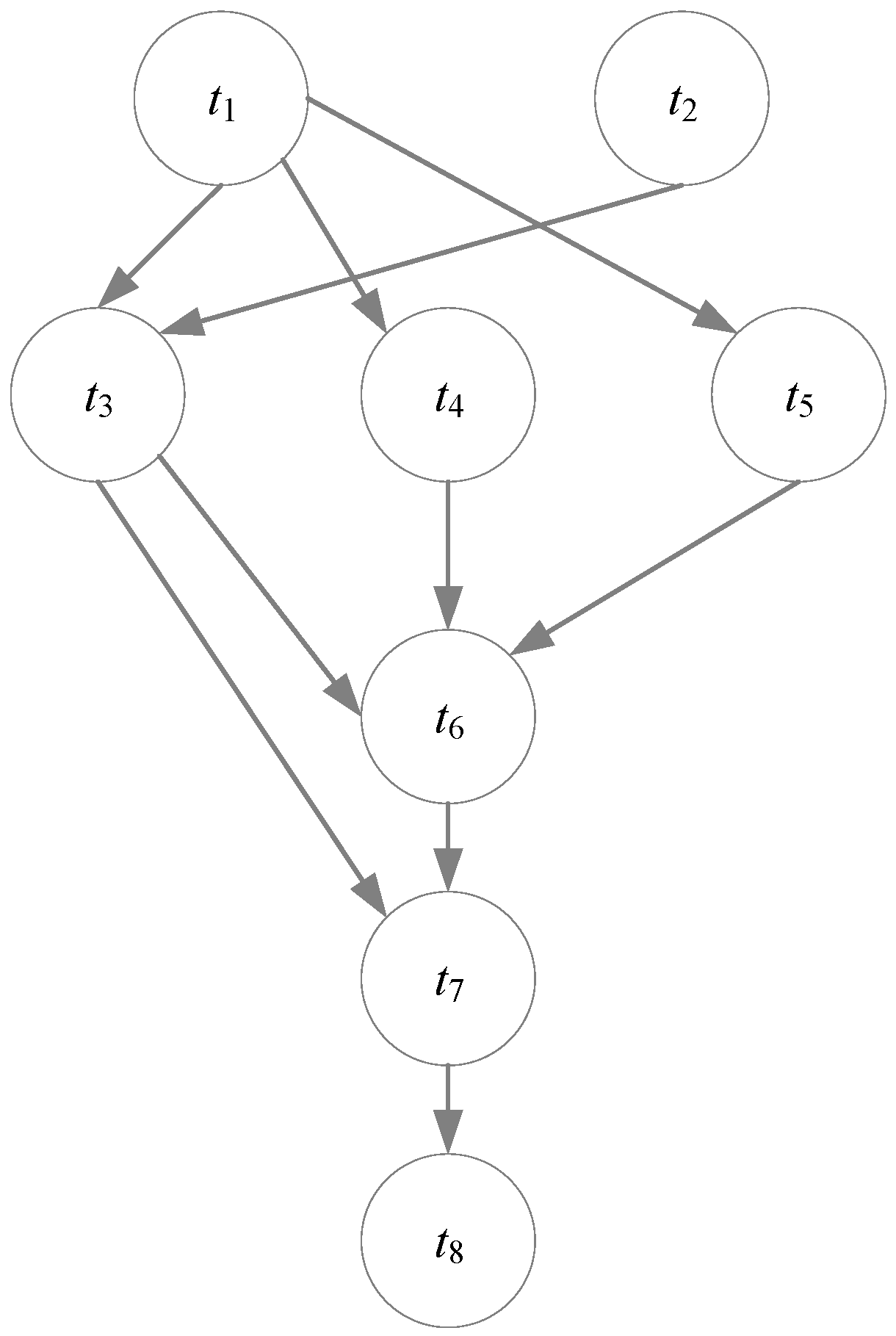
3.2. The Workflow Model
3.3. Problem Formulation
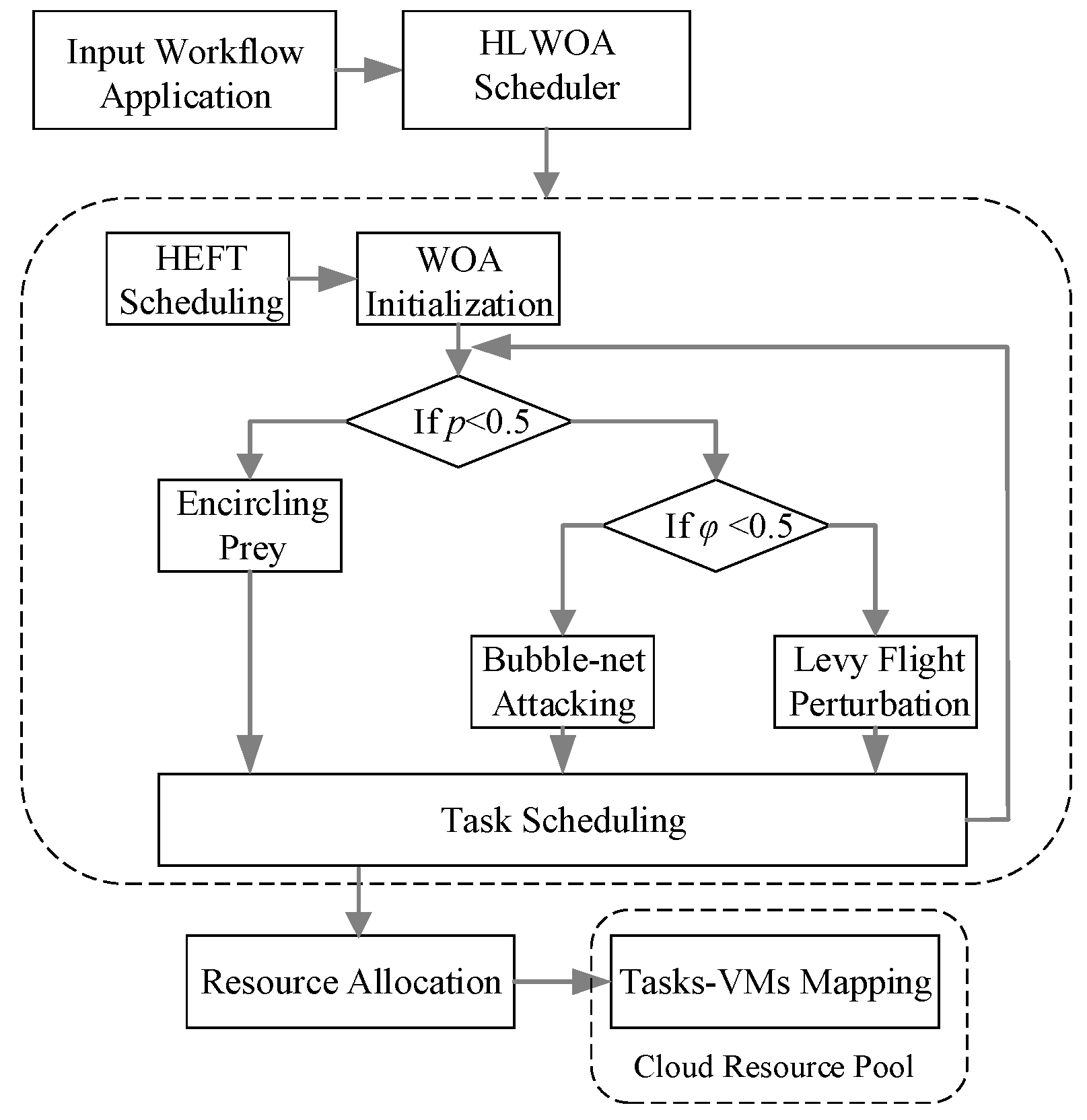
4. A QoS-Aware Workflow Scheduling Optimization Approach
4.1. HEFT Scheduling
- (1)
- Initialization phase
- (2)
- Reverse topology sorting traversal
- (3)
- Average computation time
- (4)
- Communication overhead for successor tasks
- (5)
- Update the upward ranking value
- (6)
- Generate task sequence
- (7)
- Assign VMs to the tasks
| Algorithm 1 Workflow scheduling Based on HEFT |
| Input: the workflow , W[i][k], B[k][l] Output: A task_list sorted in descending order of Upward rank, the allocation of task to VM for each task in do rank_u] ← 0 end for for each task in reverse topological order of Dag do Obtain the average computation time using Equation (17) if is empty then rank_u else Obtain the by Equations (18)–(20) Update the by Equation (21) end if end for task_list ← [] temp_list ← sort by in descending order while temp_list is not empty do for each task in temp_list do all_pred_scheduled ← true for each predecessor task of do if not in task_list then all_pred_scheduled ← false break end if end for if all_pred_scheduled then task_list.append) temp_list.remove) break end if end for end while return task_list allocation ← {} machine_ready_time ← [0, 0, …, 0] for each task in task_list do earliest_finish_time ← ∞ selected_machine ← −1 for each machine k in Machines do Calculate of on Calculate of on Update the selected_machine based on earliest completion time end for Assign to the selected_machine Add this assignment to the allocation update the ready time of end for return allocation |
4.2. Resource Allocation Optimization Based on Levy-WOA
- (1)
- Population Initialization
- (2)
- Fitness Evaluation
- (3)
- Encircling Prey
- (4)
- Bubble-Net Attacking
- (5)
- Levy Flight Perturbation
- (6)
- Update the Individual and Output the Global Optimal Solution
| Algorithm 2 Levy-WOA workflow scheduling optimization algorithm |
| Input: task_list, allocation obtained from HEFT, Dag = (T, E), VM_list, pre data_size bandwidth population_size = 50, max_iterations = 200, = 0.01, = 1.5, = 1, = 0.5, = 0.5 Output: the best solution best_schedule population = [] for i = 1 to population_size-1 do schedule = {} for task in task_list do vm = random_select(VM_list) Obtain the start time using Equation (7) Obtain end time of the current task and Equation (9) schedule[task] = (vm, start_time, end_time) end for population.append(schedule) end for population.append(allocation) For each schedule in population do Calculate makespan of the workflow by Equation (11) Calculate total cost by Equation (12) Calculate fitness value using Equation (23) end for Return Initial “best_schedule” with the highest fitness value among the population Return Initial “best_fitness” with the hightest fitness value among the population = 0 while do = rand(), = rand(). for each schedule in population do if < 0.5 then Obtain a new schedule by Encircling Prey of WOA using Equations (24)–(28) else if < 0.5 then l = rand (−1, 1) for task in task_list: Obtain a new schedule by the spiral update in Bubble-net Attacking using Equations (29) and (30) else for task in task_list: Obtain a new schedule by Levy Flight Perturbation using Equations (31)–(34) end if end if Calculate” current_fitness” the fitness value of the current new schedule using Equation (23) If current_fitness > best_fitness then best_schedule the current new schedule best_fitness the current_fitness end if end for = + 1 end while Return best_schedule |
- (1)
- Heavy-tailed distribution: As shown in Equations (31)–(33), the Lévy step length Lévy(β) follow a heavy-tailed distribution. This endows the algorithm with a high probability of performing short-range fine-grained searches while retaining a small probability of long-range jumps. This property precisely matches the practical needs of cloud scheduling, where most tasks keep their current VM assignments and only a few critical tasks require cross-VM adjustments.
- (2)
- Local Optimum Escape Mechanism: When the encircling or bubble-net attacking behavior of WOA causes the population to converge on a suboptimal solution (e.g., all individuals assign computationally intensive tasks to low-performance VMs), Lévy flight’s long step sizes can disrupt this uniformity. For instance, in a given iteration, a compute-heavy task may suddenly shift from its original low-performance VM to an entirely different high-performance VM. Even if the current best solution yields a makespan of 1200 s, Lévy perturbation could abruptly discover a new solution with a makespan of 1100 s while increasing the cost by only 2%.
4.3. Time Complexity Analysis
5. Experimental Evaluation
5.1. Experiment Setup
- (1)
- Experimental Setting:
- (2)
- Comparison Algorithms
- (3)
- Performance Metrics
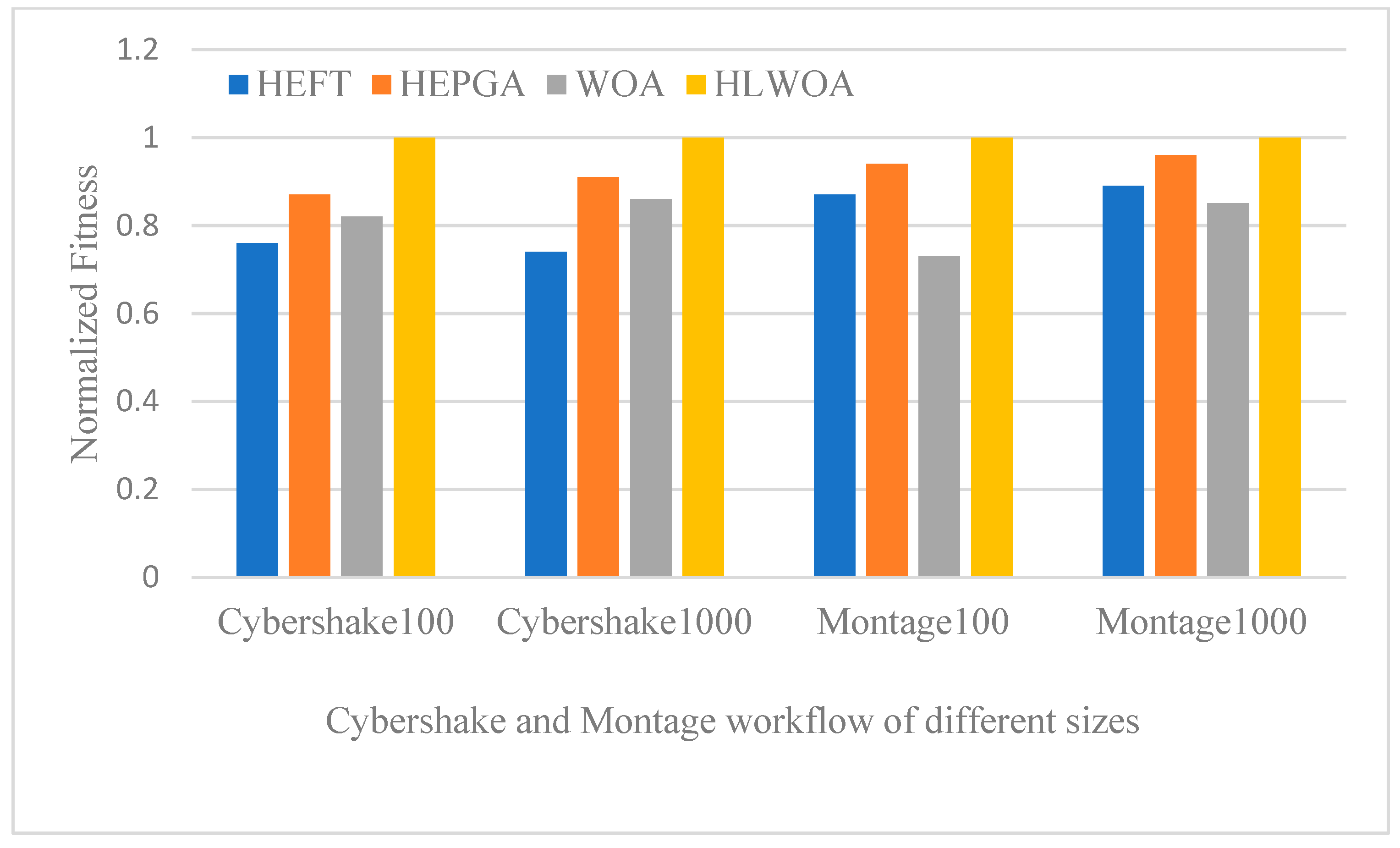
5.2. Experimental Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviations | Terms |
| IaaS | Infrastructure as a Service |
| PaaS | Platform as a Service |
| SaaS | Software as a Service |
| VM | Virtual Machine |
| QoS | Quality of Service |
| HEFT | Heterogeneous Earliest Finish Time |
| DAG | Directed Acyclic Graph |
| WOA | Whale Optimization Algorithm |
References
- Coleman, T.; Casanova, H.; Pottier, L.; Kaushik, M.; Deelman, E.; da Silva, R.F. WfCommons: A framework for enabling scientific workflow research and development. Future Gener. Comput. Syst. 2022, 128, 16–27. [Google Scholar] [CrossRef]
- Islam, R.; Patamsetti, V.; Gadhi, A.; Gondu, R.M.; Bandaru, C.M.; Kesani, S.C.; Abiona, O. The future of cloud computing: Benefits and challenges. Int. J. Commun. Netw. Syst. Sci. 2023, 16, 53–65. [Google Scholar] [CrossRef]
- Hawaou, K.S.; Kamla, V.C.; Yassa, S.; Romain, O.; Mboula, J.E.N.; Bitjoka, L. Industry 4.0 and industrial workflow scheduling: A survey. J. Ind. Inf. Integr. 2024, 38, 100546. [Google Scholar]
- Bouabdallah, R.; Fakhfakh, F. Workflow Scheduling in Cloud-Fog Computing Environments: A Systematic Literature Review. Concurr. Comput. Pract. Exp. 2024, 36, e8304. [Google Scholar] [CrossRef]
- Ahmad, W.; Alam, B. An efficient list scheduling algorithm with task duplication for scientific big data workflow in heterogeneous computing environments. Concurr. Comput. Pract. Exp. 2021, 33, e5987. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Mangalampalli, S.; Karri, G.R.; Kose, U. Multi objective trust aware task scheduling algorithm in cloud computing using whale optimization. J. King Saud Univ.-Comput. Inf. Sci. 2023, 35, 791–809. [Google Scholar] [CrossRef]
- Gupta, S.; Iyer, S.; Agarwal, G.; Manoharan, P.; Algarni, A.D.; Aldehim, G.; Raahemifar, K. Efficient prioritization and processor selection schemes for heft algorithm: A makespan optimizer for task scheduling in cloud environment. Electronics 2022, 11, 2557. [Google Scholar] [CrossRef]
- Choudhary, A.; Rajak, R. A novel strategy for deterministic workflow scheduling with load balancing using modified min-min heuristic in cloud computing environment. Clust. Comput. 2024, 27, 6985–7006. [Google Scholar] [CrossRef]
- Raeisi-Varzaneh, M.; Dakkak, O.; Fazea, Y.; Kaosar, M.G. Advanced cost-aware Max–Min workflow tasks allocation and scheduling in cloud computing systems. Clust. Comput. 2024, 27, 13407–13419. [Google Scholar] [CrossRef]
- Ahmed, S.; Omara, F.A. An Enhanced Workflow Scheduling Algorithm for Cloud Computing Environment. Int. J. Intell. Eng. Syst. 2022, 15I, 627–646. [Google Scholar] [CrossRef]
- Medara, R.; Singh, R.S.; Sompalli, M. Energy and cost aware workflow scheduling in clouds with deadline constraint. Concurr. Comput. Pract. Exp. 2022, 34, e6922. [Google Scholar] [CrossRef]
- NoorianTalouki, R.; Shirvani, M.H.; Motameni, H. A heuristic-based task scheduling algorithm for scientific workflows in heterogeneous cloud computing platforms. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 4902–4913. [Google Scholar] [CrossRef]
- Sun, Z.; Zhang, B.; Gu, C.; Xie, R.; Qian, B.; Huang, H. ET2FA: A hybrid heuristic algorithm for deadline-constrained workflow scheduling in cloud. IEEE Trans. Serv. Comput. 2022, 16, 1807–1821. [Google Scholar] [CrossRef]
- Konjaang, J.K.; Xu, L. Meta-heuristic approaches for effective scheduling in infrastructure as a service cloud: A systematic review. J. Netw. Syst. Manag. 2021, 29, 15. [Google Scholar] [CrossRef]
- Singh, R.M.; Awasthi, L.K.; Sikka, G. Towards Metaheuristic Scheduling Techniques in Cloud and Fog: An Extensive Taxonomic Review. ACM Comput. Surv. 2023, 55, 1–43. [Google Scholar] [CrossRef]
- Xia, X.; Qiu, H.; Xu, X.; Zhang, Y. Multi-objective workflow scheduling based on genetic algorithm in cloud environment. Inf. Sci. 2022, 606, 38–59. [Google Scholar] [CrossRef]
- Rizvi, N.; Ramesh, D.; Wang, L.; Basava, A. A workflow scheduling approach with modified fuzzy adaptive genetic algorithm in IaaS clouds. IEEE Trans. Serv. Comput. 2022, 16, 872–885. [Google Scholar] [CrossRef]
- Anbarkhan, S.H.; Rakrouki, M.A. An enhanced PSO algorithm for scheduling workflow tasks in cloud computing. Electronics 2023, 12, 2580. [Google Scholar] [CrossRef]
- Tao, S.; Xia, Y.; Ye, L.; Yan, C.; Gao, R. DB-ACO: A deadline-budget constrained ant colony optimization for workflow scheduling in clouds. IEEE Trans. Autom. Sci. Eng. 2023, 21, 1564–1579. [Google Scholar] [CrossRef]
- Chakravarthi, K.K.; Shyamala, L.; Vaidehi, V. Cost-effective workflow scheduling approach on cloud under deadline constraint using firefly algorithm. Appl. Intell. 2021, 51, 1629–1644. [Google Scholar] [CrossRef]
- Bacanin, N.; Zivkovic, M.; Bezdan, T.; Venkatachalam, K.; Abouhawwash, M. Modified firefly algorithm for workflow scheduling in cloud-edge environment. Neural Comput. Appl. 2022, 34, 9043–9068. [Google Scholar] [CrossRef]
- Sahu, B.; Swain, S.K.; Mangalampalli, S.; Mishra, S. Multiobjective Prioritized Workflow Scheduling in Cloud Computing Using Cuckoo Search Algorithm. Appl. Bionics Biomech. 2023, 2023, 4350615. [Google Scholar] [CrossRef]
- Singhal, S.; Sharma, A. Mutative BFO-based scheduling algorithm for cloud environment. In Proceedings of the International Conference on Communication and Artificial Intelligence: ICCAI 2020, Mathura, India, 17–18 September 2020; pp. 589–599. [Google Scholar]
- Gu, Y.; Budati, C. Energy-aware workflow scheduling and optimization in clouds using bat algorithm. Future Gener. Comput. Syst. 2020, 113, 106–112. [Google Scholar] [CrossRef]
- Singh, G.; Chaturvedi, A.K. Hybrid modified particle swarm optimization with genetic algorithm (GA) based workflow scheduling in cloud-fog environment for multi-objective optimization. Clust. Comput. 2024, 27, 1947–1964. [Google Scholar] [CrossRef]
- Shobeiri, P.; Akbarian Rastaghi, M.; Abrishami, S.; Shobiri, B. PCP–ACO: A hybrid deadline-constrained workflow scheduling algorithm for cloud environment. J. Supercomput. 2024, 80, 7750–7780. [Google Scholar] [CrossRef]
- Mangalampalli, S.; Pokkuluri, K.S.; Kocherla, R.; Rapaka, A.; Kota, N.R. An efficient workflow scheduling algorithm in cloud computing using cuckoo search and PSO algorithms. In Innovations in Computer Science and Engineering, Proceedings of the Ninth ICICSE, Hyderabad, India, 3–4 September 2021; Springer: Berlin/Heidelberg, Germany, 2022; pp. 137–145. [Google Scholar]
- Yin, C.; Fang, Q.; Li, H.; Peng, Y.; Xu, X.; Tang, D. An optimized resource scheduling algorithm based on GA and ACO algorithm in fog computing. J. Supercomput. 2024, 80, 4248–4285. [Google Scholar] [CrossRef]
- Mohammadzadeh, A.; Masdari, M. Scientific workflow scheduling in multi-cloud computing using a hybrid multi-objective optimization algorithm. J. Ambient. Intell. Humaniz. Comput. 2023, 14, 3509–3529. [Google Scholar] [CrossRef]
- Pirozmand, P.; Javadpour, A.; Nazarian, H.; Pinto, P.; Mirkamali, S.; Ja’fari, F. GSAGA: A hybrid algorithm for task scheduling in cloud infrastructure. J. Supercomput. 2022, 78, 17423–17449. [Google Scholar] [CrossRef]
- Mikram, H.; El Kafhali, S.; Saadi, Y. HEPGA: A new effective hybrid algorithm for scientific workflow scheduling in cloud computing environment. Simul. Model. Pract. Theory 2024, 130, 102864. [Google Scholar] [CrossRef]
- Sudhakar, R.V.; Dastagiraiah, C.; Pattem, S.; Bhukya, S. Multi-Objective Reinforcement Learning Based Algorithm for Dynamic Workflow Scheduling in Cloud Computing. Indones. J. Electr. Eng. Inform. (IJEEI) 2024, 12, 640–649. [Google Scholar] [CrossRef]
- Wang, Z.; Zhan, W.; Duan, H.; Min, G.; Huang, H. Deep-Reinforcement-Learning-Based Continuous Workflows Scheduling in Heterogeneous Environments. IEEE Internet Things J. 2025, 12, 14036–14050. [Google Scholar] [CrossRef]
- Chandrasiri, S.; Meedeniya, D. Energy-Efficient Dynamic Workflow Scheduling in Cloud Environments Using Deep Learning. Sensors 2025, 25, 1428. [Google Scholar] [CrossRef]
- Pan, J.H.; Wei, Y. A deep reinforcement learning-based scheduling framework for real-time workflows in the cloud environment. Expert Syst. Appl. 2024, 255, 124845. [Google Scholar] [CrossRef]
- Luo, L.; Yan, X.; Wu, Q.; Sheng, V.S. Evolution Strategies-guided Deep Reinforcement Learning for Dynamic Hybrid Flow-shop Scheduling Problem. Tsinghua Sci. Technol. 2024. accepted. [Google Scholar]
- Ullah, I.; Singh, S.K.; Adhikari, D.; Khan, H.; Jiang, W.; Bai, X. Multi-Agent Reinforcement Learning for task allocation in the Internet of Vehicles: Exploring benefits and paving the future. Swarm Evol. Comput. 2025, 94, 101878. [Google Scholar] [CrossRef]
- Juve, G.; Chervenak, A.; Deelman, E.; Bharathi, S.; Mehta, G.; Vahi, K. Characterizing and profiling scientific workflows. Future Gener. Comput. Syst. 2013, 29, 682–692. [Google Scholar] [CrossRef]
| Type | vCPU | RAM (GB) | Bandwidth (Mbps) | (MB/s) | ($/h) | Number |
|---|---|---|---|---|---|---|
| 1 | 2 | 4 | 100 | 1.5 | 0.195 | 10 |
| 2 | 4 | 8 | 200 | 3.0 | 0.48 | 8 |
| 3 | 8 | 16 | 500 | 4.5 | 0.855 | 12 |
| Workflow | Application Area | Number of Tasks | DAG Structure | Data Dependency | Task Type |
|---|---|---|---|---|---|
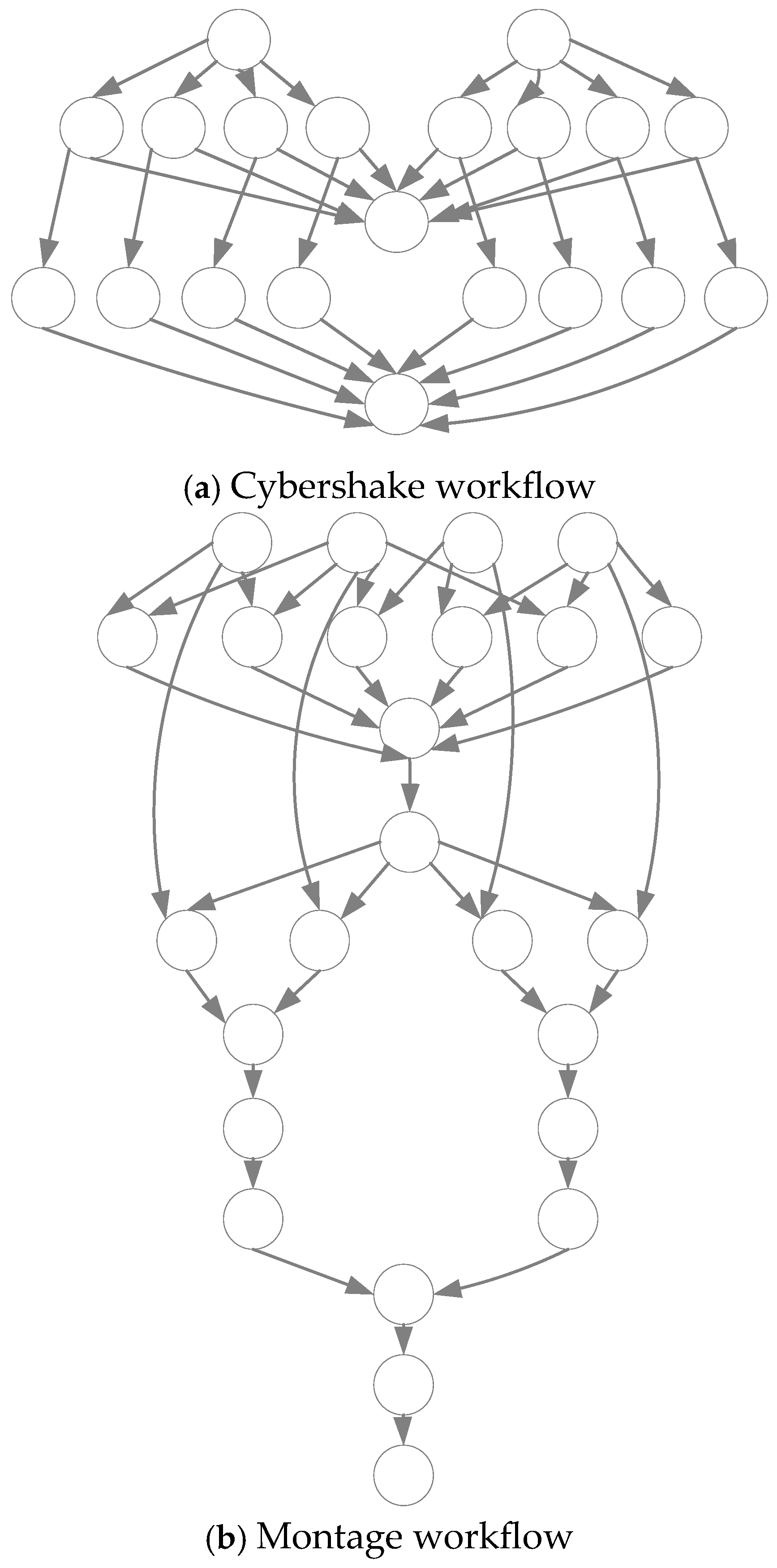
| Cybershake | Seismic risk analysis | 100/1000 | Relatively large depth | High | Computation intensive |
| Montage | Astronomical image stitching | 100/1000 | Moderate depth | Moderate | I/O intensive |
| Scheduling Algorithm | Makespan (Cybershake) | Cost (Cybershake) | ||
|---|---|---|---|---|
| 100 | 1000 | 100 | 1000 | |
| HEFT | 1422.91 | 11,335.32 | 4.75 | 25.51 |
| HEPGA | 1420.35 | 11,329.73 | 4.72 | 25.35 |
| WOA | 1417.02 | 11,333.68 | 4.71 | 24.96 |
| HLWOA | 1414.28 | 11,330.01 | 4.63 | 24.81 |
| Scheduling Algorithm | Makespan (Montage) | Cost (Montage) | ||
|---|---|---|---|---|
| 100 | 1000 | 100 | 1000 | |
| HEFT | 1205.01 | 11,219.02 | 2.65 | 17.81 |
| HEPGA | 1204.23 | 11,216.62 | 2.60 | 17.65 |
| WOA | 1206.02 | 11,217.58 | 2.62 | 17.79 |
| HLWOA | 1204.05 | 11,215.69 | 2.58 | 17.62 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, M.; Wang, Y. An Effective QoS-Aware Hybrid Optimization Approach for Workflow Scheduling in Cloud Computing. Sensors 2025, 25, 4705. https://doi.org/10.3390/s25154705
Cui M, Wang Y. An Effective QoS-Aware Hybrid Optimization Approach for Workflow Scheduling in Cloud Computing. Sensors. 2025; 25(15):4705. https://doi.org/10.3390/s25154705
Chicago/Turabian StyleCui, Min, and Yipeng Wang. 2025. "An Effective QoS-Aware Hybrid Optimization Approach for Workflow Scheduling in Cloud Computing" Sensors 25, no. 15: 4705. https://doi.org/10.3390/s25154705
APA StyleCui, M., & Wang, Y. (2025). An Effective QoS-Aware Hybrid Optimization Approach for Workflow Scheduling in Cloud Computing. Sensors, 25(15), 4705. https://doi.org/10.3390/s25154705




