BCINetV1: Integrating Temporal and Spectral Focus Through a Novel Convolutional Attention Architecture for MI EEG Decoding
Abstract
1. Introduction
- Challenge 1: The reliance on signal decomposition methods to address EEG signals non-stationarity. These methods often suffer from high parametric dependence and intrinsic flaws, including mode mixing, excessive decompositions, boundary issues, determining the appropriate number of modes, sensitivity to noise, and high computational costs.
- Challenge 2: Deep learning approaches, particularly those using CNN-based methods for end-to-end decoding, effectively capture local patterns but struggle to maintain the global time-varying features in non-stationary EEG signals.
- Challenge 3: Attention-based methods have recently made strides in detecting long-range patterns within signals, yet the precise localization of event time stamps and important spectral variations (ERS/ERD) has not been investigated. While some studies have focused on directly decoding features across EEG’s temporal, spectral, or spatial domains, they have not successfully localized the task-relevant neural signatures.
- First, we propose BCINetV1, an end-to-end framework featuring a simple yet effective parallel dual branch structure. It comprises three new modules: a temporal convolution-based attention block (T-CAB), a spectral convolution-based attention block (S-CAB), and a squeeze-and-excitation block (SEB). Together, these modules are designed to precisely identify, focus on, and fuse critical tempo-spectral patterns directly from raw EEG signals without manual preprocessing.
- Second, at the core of the T-CAB and S-CAB modules, we introduce Convolutional Self-Attention (ConvSAT), a novel attention mechanism. ConvSAT innovatively integrates 1D convolution operations into the self-attention framework to synergize the local feature extraction strengths of CNNs with the global contextual modeling of attention. This mechanism performs the heavy lifting, enabling the network to effectively capture both local details and long-range dependencies in non-stationary EEG signals.
- Third, we conduct a rigorous set of subject-specific experiments on four diverse public datasets, demonstrating that BCINetV1 consistently achieves state-of-the-art performance and stability. Furthermore, by visualizing the learned attention patterns, we show that the model’s decision-making is clinically interpretable and grounded in the identification of established neurophysiological markers like ERD/ERS.
- To address Challenge 1, BCINetV1 employs an end-to-end architecture where the convolutional layers within the T-CAB and S-CAB modules learn a task-relevant feature decomposition directly from the data, thereby eliminating the need for a separate, parameter-sensitive pre-processing pipeline like VMD or EMD.
- To overcome Challenge 2, BCINetV1 integrates a novel ConvSAT mechanism that explicitly models long-range temporal dependencies across the entire trial duration, allowing the model to capture the global, time-varying context of the EEG signal that standard, locality-biased CNNs inherently miss.
- To resolve Challenge 3, BCINetV1 provides direct, interpretable evidence of its decision-making. The attention masks generated by the T-CAB and S-CAB modules explicitly localize critical temporal and spectral events, successfully isolating well-established neurophysiological markers like event-related synchronization (ERS) and bridging the gap between deep learning and clinical interpretability.
2. Methodology—BCINetV1 Overview
2.1. Module 1: Temporal Convolution-Based Attention Block (T-CAB)
2.2. Module 2: Spectral Convolution-Based Attention Block (S-CAB)
2.3. Module 3: Squeeze and Excitation Block (SEB)
3. Materials and Experimental Protocols
3.1. Datasets
- Dataset 1: BCI Competition III dataset IVa [25] involved five healthy subjects performing two motor imagery tasks (right hand/right foot) across 280 trials each. EEG data was acquired using 118 electrodes (10/20 system) at 1000 Hz, subsequently down-sampled to 100 Hz.
- Dataset 2: the GigaDB dataset [25] expanded the participant pool significantly with 52 individuals performing binary class (right/left hand) motor imagery tasks. The data was recorded with 64 Ag/AgCl electrodes (10/10 system) over 100–120 trials per task at a 512 Hz sampling rate.
- Dataset 3: BCI Competition III dataset V [26] introduced more complex tasks with three-class mental imagery (left-hand, right-hand movements, and word association) from three participants. The EEG signals were accumulated using 32 electrodes (10/20 system) sampled at 512 Hz across three sessions.
- Dataset 4: BCI Competition IV dataset 2a [14] featured nine healthy subjects performing four types of motor imagery (left hand, right hand, feet, and tongue movements), with 288 trials per subject recorded from 22 Ag/AgCl electrodes at 250 Hz over two separate training and testing sessions.
3.2. Experimental Protocols
3.3. State-of-the-Art Comparison Models
4. Experimental Results and Discussions
4.1. Results and Discussions for Dataset 1
4.1.1. Five-Fold Classification Performance
4.1.2. Comparison of BCINetV1 with State-of-the-Art Methods
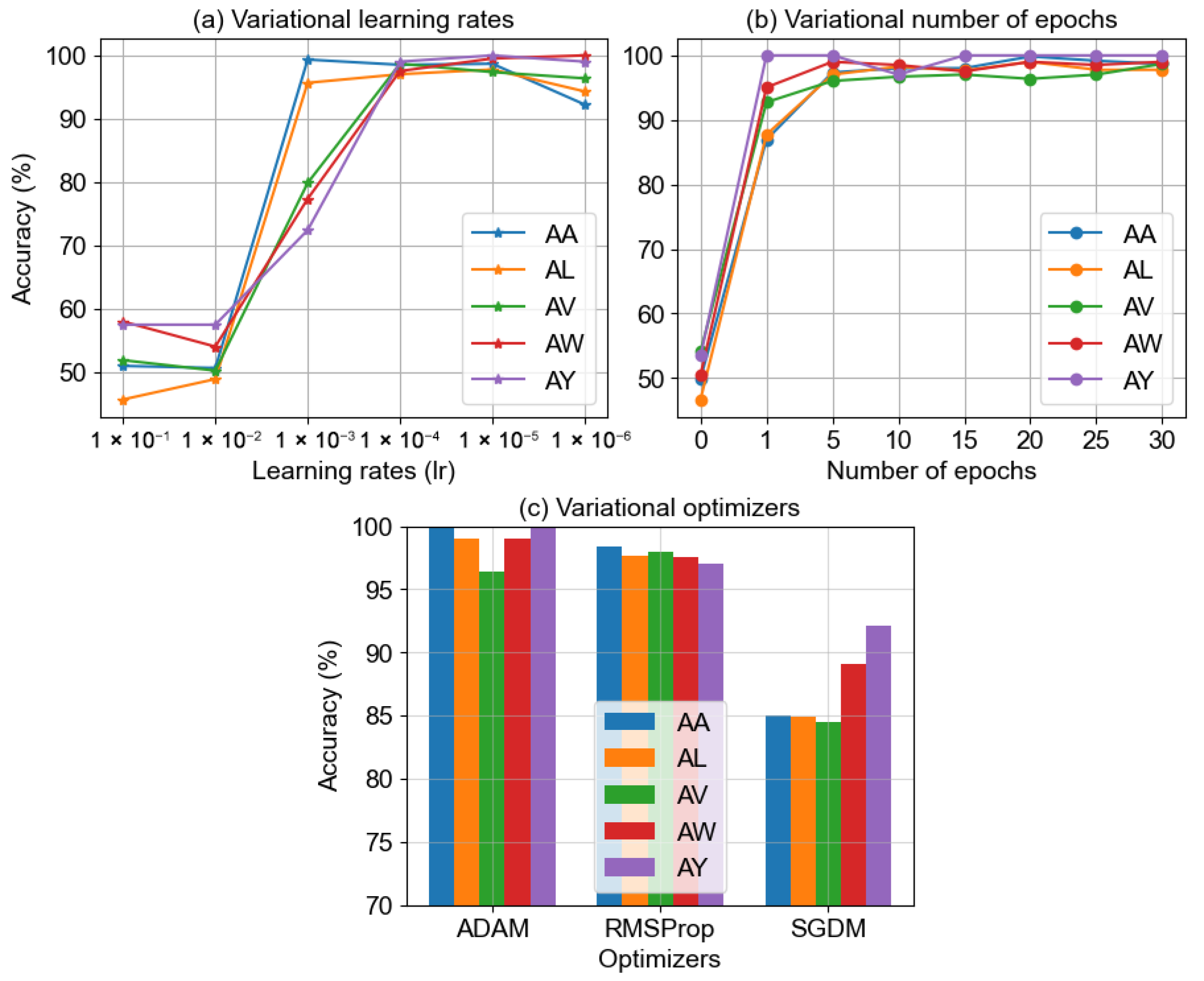
4.1.3. Effect of Variational Electrodes Combinations
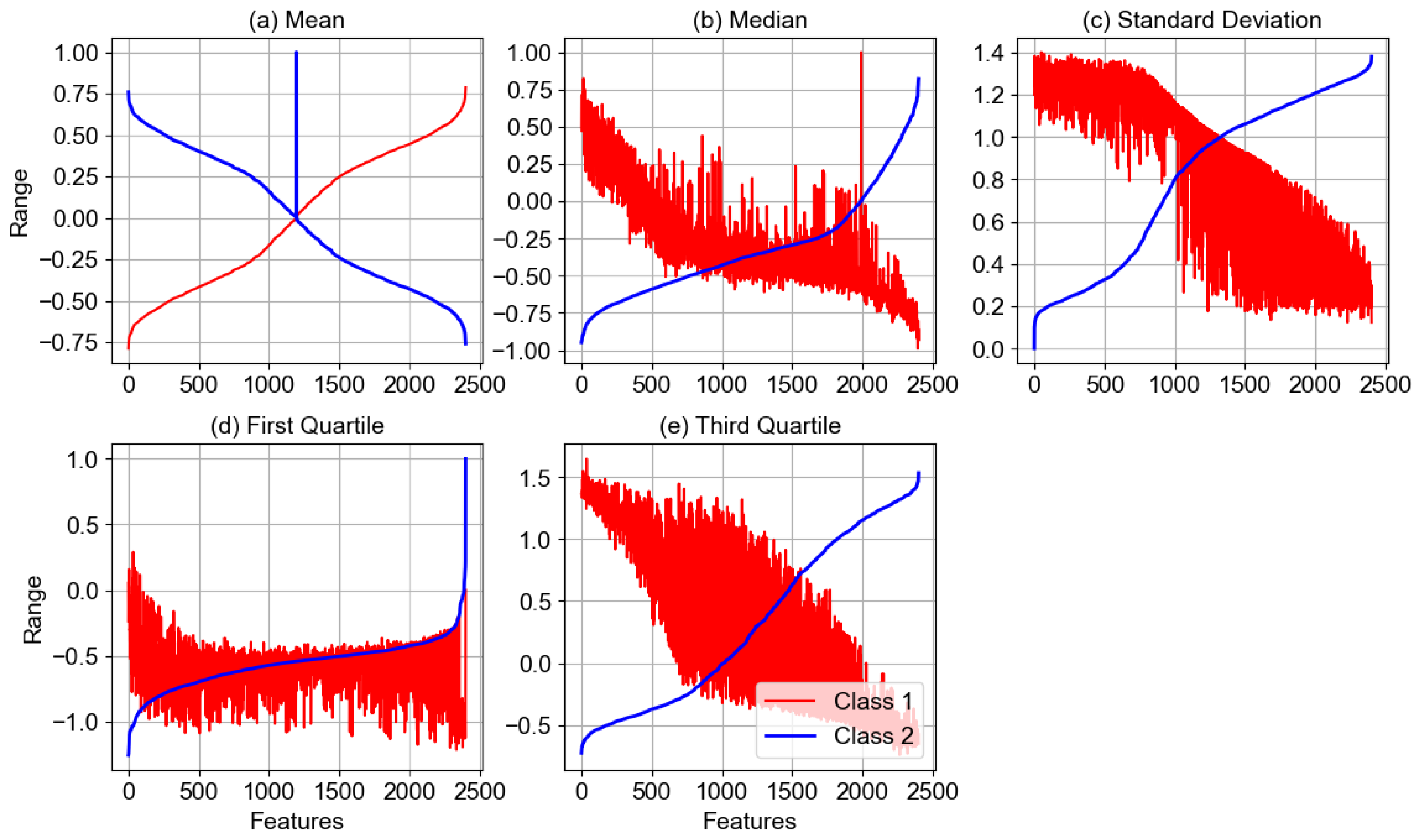
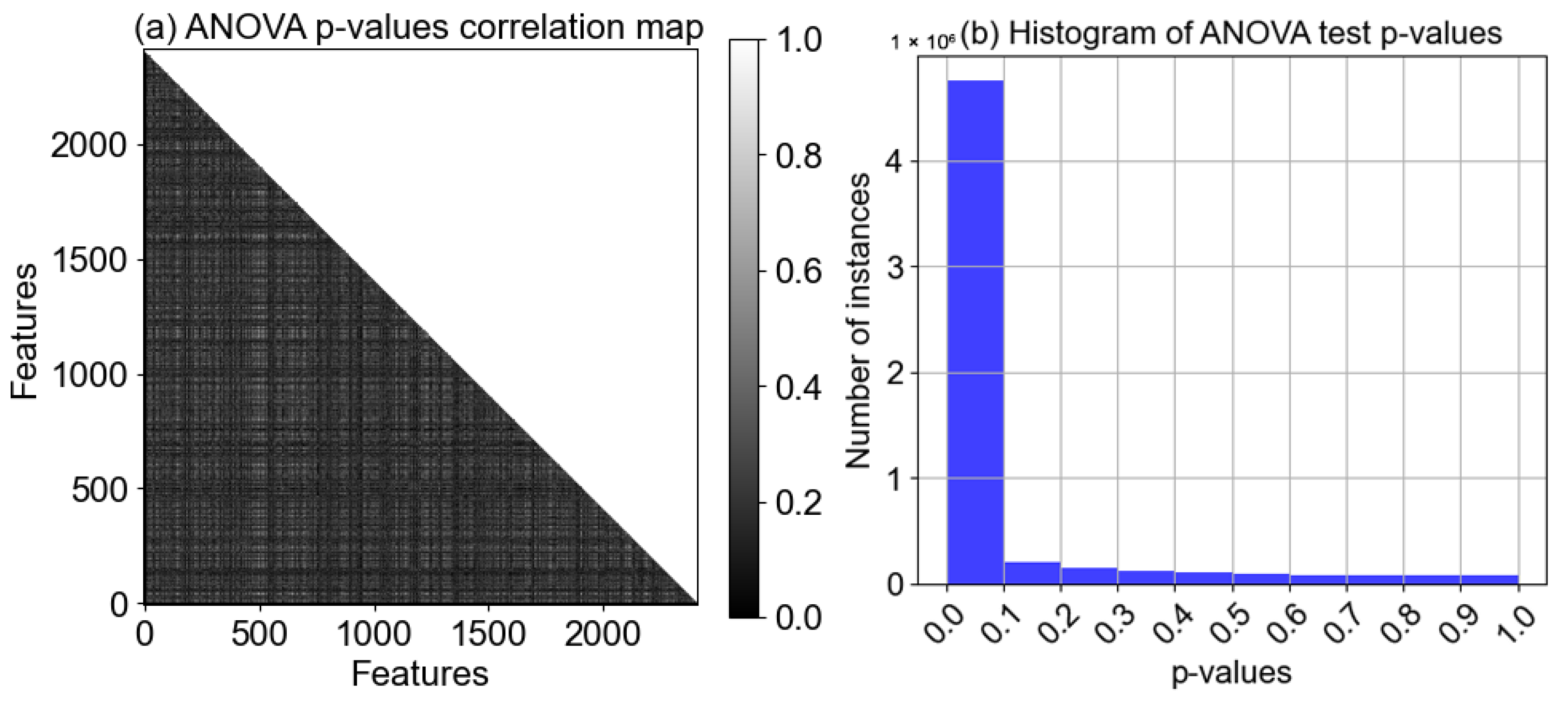
4.1.4. Statistical Analysis of Features
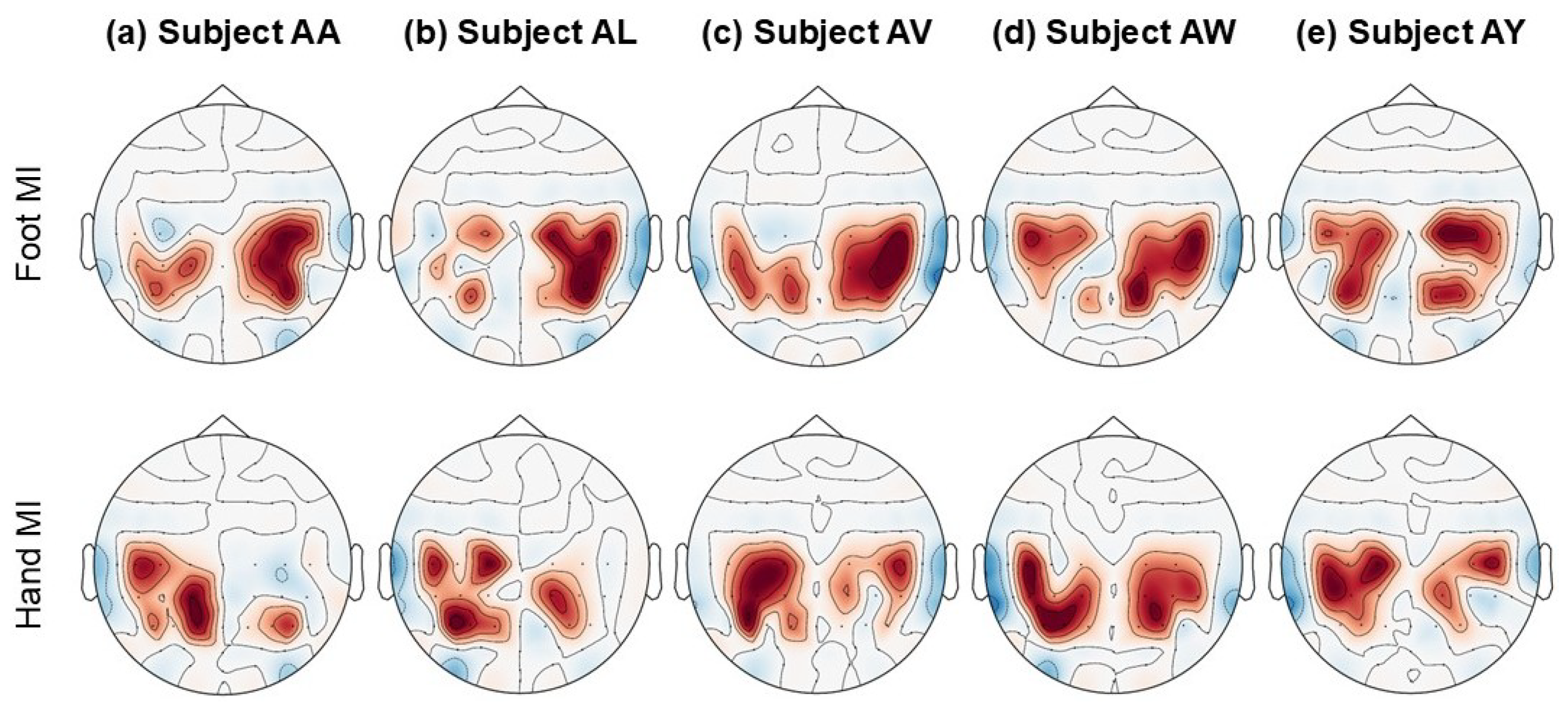
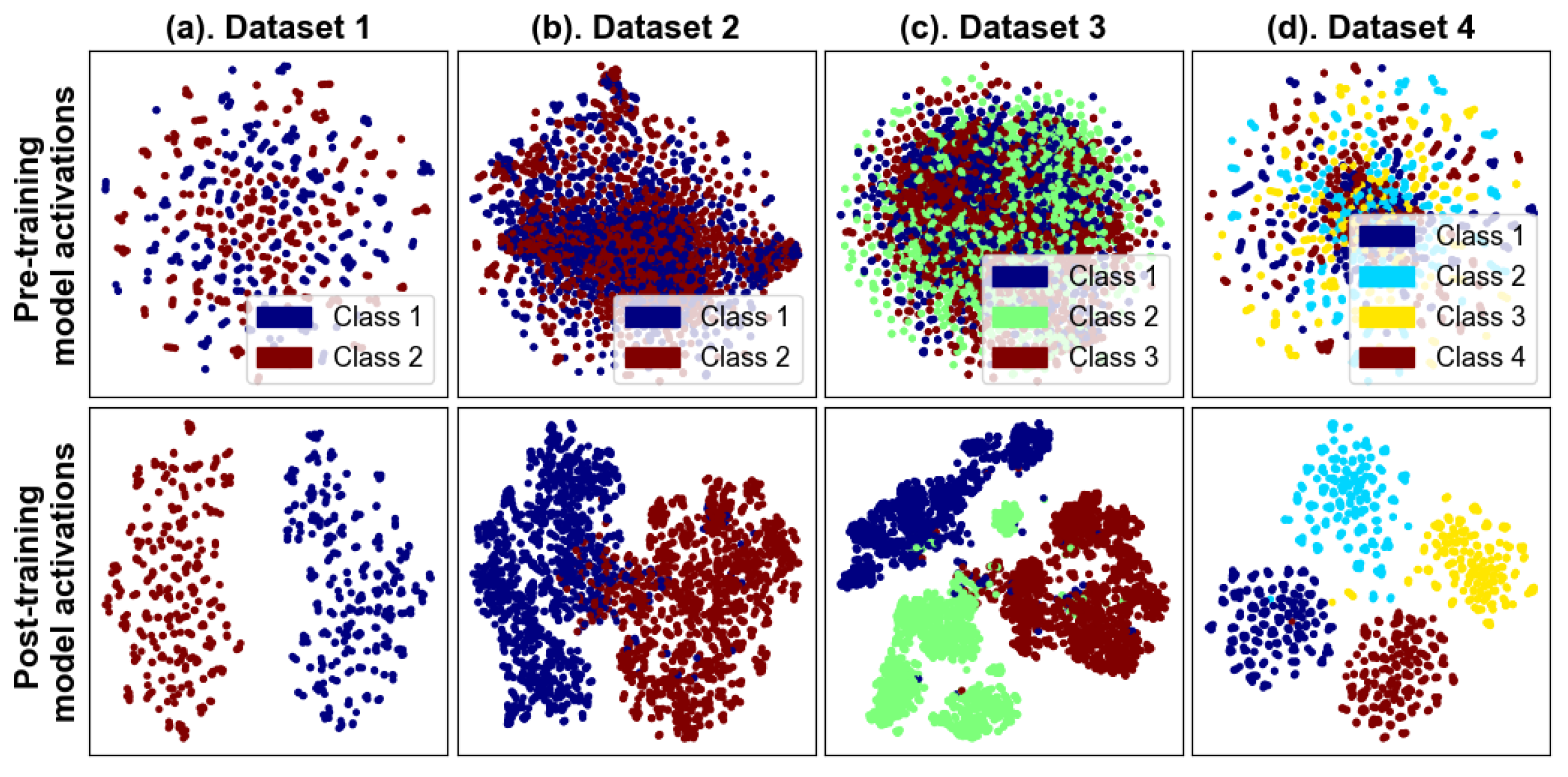
4.1.5. Topographical Maps and Features Representation
4.1.6. Ablation Study
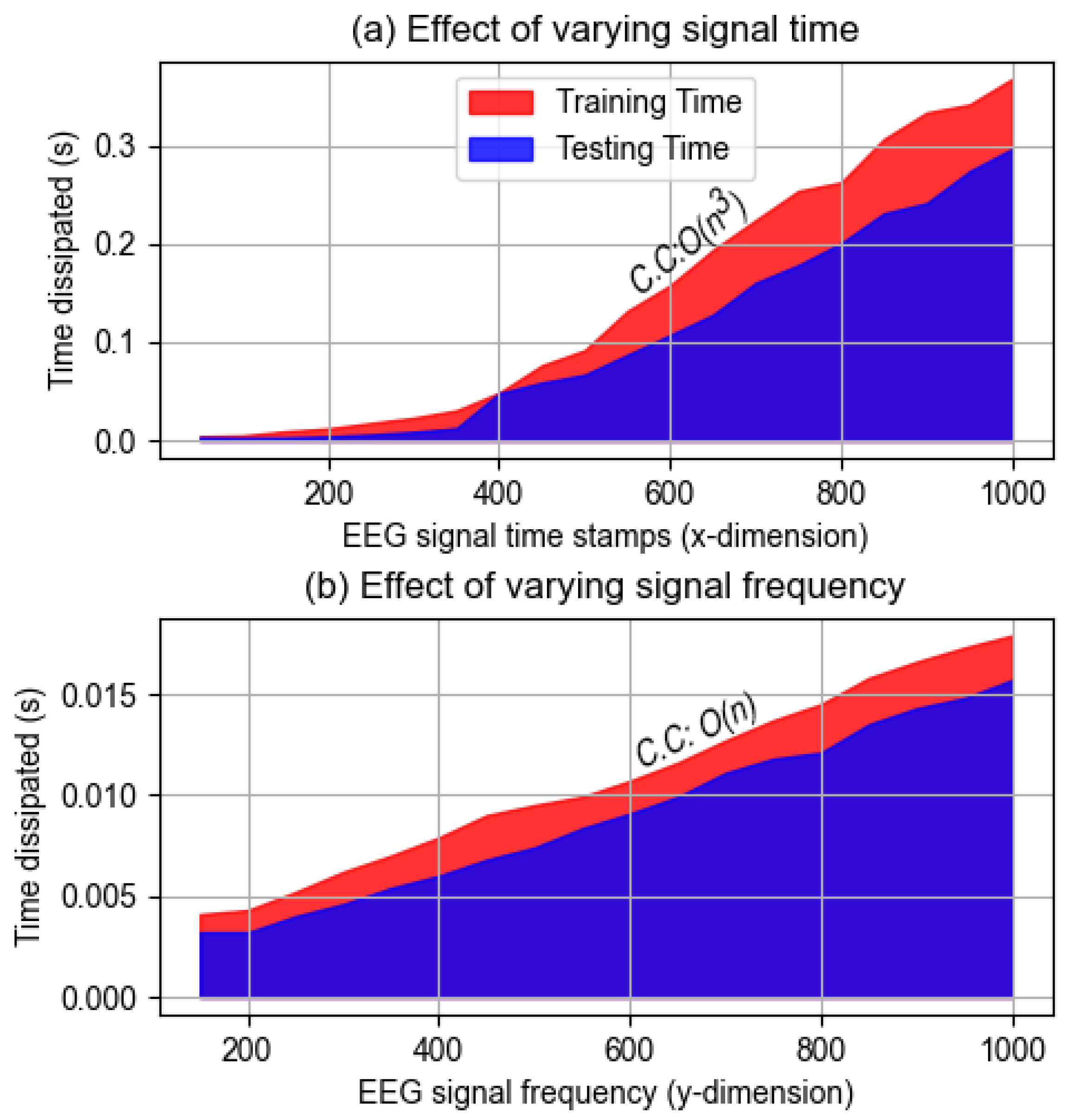
4.1.7. Computational Complexity Analysis
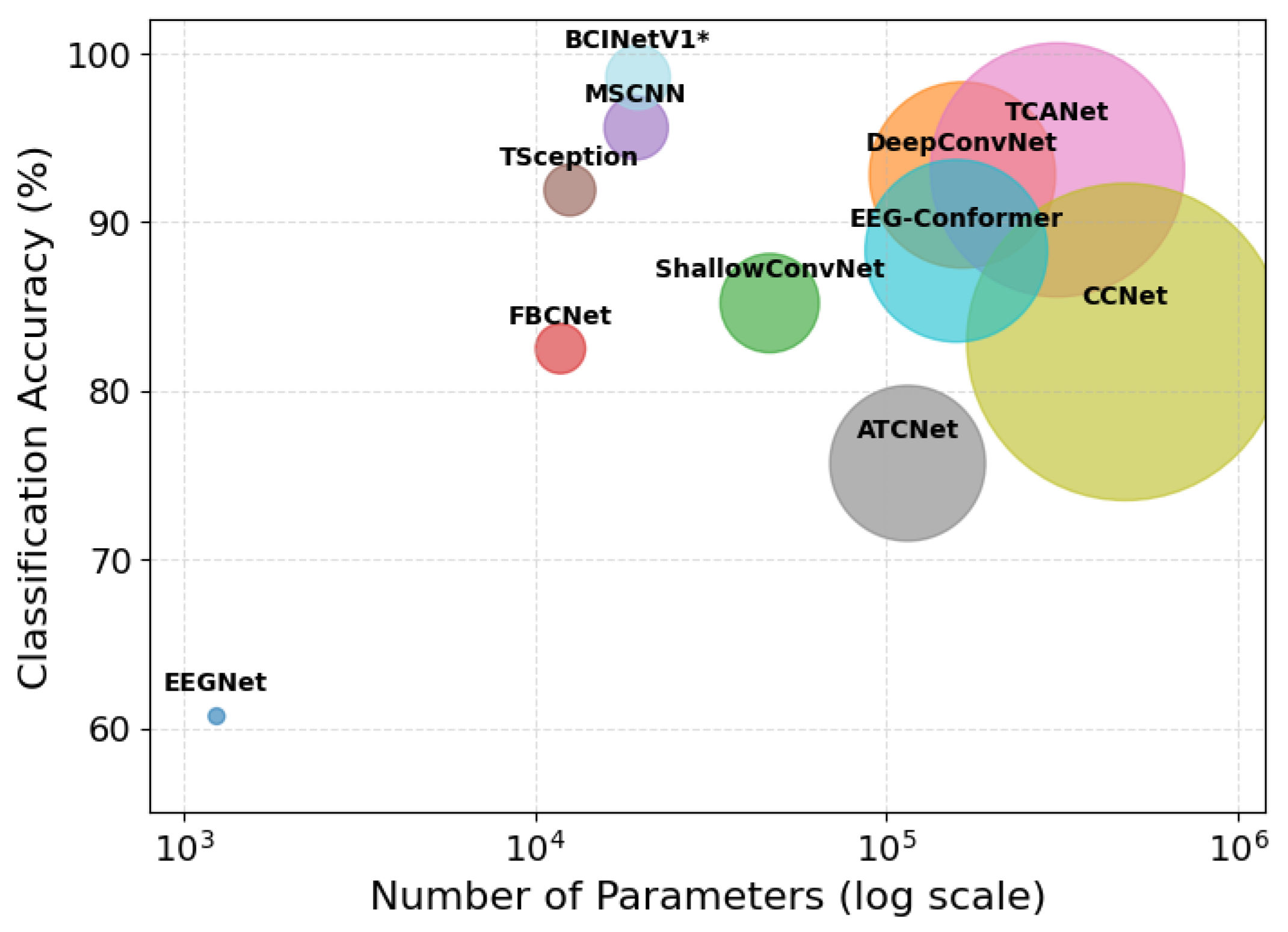
4.1.8. Analysis with Model Parameters
4.2. Analysis with Other BCI EEG Datasets
| Category | Authored By | Year | Method | Accuracy (%) | Recall (%) | F-score (%) | Kappa (%) |
|---|---|---|---|---|---|---|---|
| Hybird signal processing methods | Kumar et al. [52] | 2019 | CSP+LSTM | 68.1 ± 9.06 | 83.3 ± NA | - | 65.0 ± NA |
| Kumar et al. [53] | 2021 | OPTICAL+ | 69.5 ± NA | - | - | 39.8 ± NA | |
| Hossain et al. [54] | 2021 | SVM+LR+NB+KNNFFS | 71.1 ± 6.77 | 70.2 ± 5.60 | 79.0 ± 10.08 | - | |
| Park et al. [55] | 2023 | 3D-EEGNet | 81.3 ± 7.27 | - | - | - | |
| Yu et al. [25] | 2021 | EFD | 83.8 ± NA | - | 83.8 ± NA | - | |
| Binwen et al. [49] | 2022 | EFD-CNN | 89.9 ± NA | - | 89.9 ± NA | 79.8 ± NA | |
| Fan et al. [56] | 2023 | TFTP+3D-CNN | 91.9 ± NA | - | - | - | |
| Tyler et al. [48] | 2021 | DR+ICA+SVM | 92.0 ± NA | - | - | - | |
| Deep Learning methods | Simulated | 2025 | DeepConvNet | 67.7 ± 0.46 | 67.7 ± 0.46 | 67.7 ± 0.46 | 35.3 ± 0.91 |
| Simulated | 2025 | ShallowConvNet | 70.7 ± 4.54 | 70.6 ± 5.13 | 70.0 ± 4.40 | 41.3 ± 9.20 | |
| Simulated | 2025 | FBCNet | 75.9 ± 2.92 | 76.8 ± 3.01 | 76.1 ± 2.41 | 51.7 ± 5.86 | |
| Simulated | 2025 | CCNet | 78.8 ± 4.88 | 80.0 ± 5.84 | 79.7 ± 5.64 | 57.5 ± 9.78 | |
| Simulated | 2025 | EEG-Conformer | 84.9 ± 2.99 | 83.9 ± 2.45 | 85.6 ± 3.25 | 69.8 ± 5.98 | |
| Simulated | 2025 | TSception | 85.3 ± 4.76 | 84.5 ± 5.08 | 85.0 ± 5.16 | 69.9 ± 9.52 | |
| Simulated | 2025 | MSCNN | 90.6 ± 2.95 | 90.9 ± 3.52 | 90.3 ± 2.19 | 81.1 ± 5.92 | |
| Simulated | 2025 | ATCNet | 91.7 ± 1.07 | 90.9 ± 0.11 | 91.4 ± 0.25 | 83.3 ± 2.15 | |
| Simulated | 2025 | TCANet | 92.5 ± 3.00 | 92.7 ± 2.74 | 93.7 ± 3.59 | 84.9 ± 6.02 | |
| Simulated | 2025 | ST-Transformer | 93.7 ± 1.77 | 94.3 ± 1.83 | 93.3 ± 1.56 | 87.4 ± 3.54 | |
| This Study | 2025 | BCINetV1 | 96.6 ± 1.70 | 96.6 ± 1.73 | 96.5 ± 1.41 | 91.9 ± 2.51 |
5. Limitations and Future Work
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- World Health Organization. Over 1 in 3 People Affected by Neurological Conditions: The Leading Cause of Illness and Disability Worldwide. WHO News. 2024. Available online: https://www.who.int/news/item/14-03-2024-over-1-in-3-people-affected-by-neurological-conditions--the-leading-cause-of-illness-and-disability-worldwide (accessed on 9 May 2025).
- Daly, J.J.; Huggins, J.E. Brain-computer interface: Current and emerging rehabilitation applications. Arch. Phys. Med. Rehabil. 2015, 96, S1–S7. [Google Scholar] [CrossRef]
- Yu, X.; Aziz, M.Z.; Sadiq, M.T.; Jia, K.; Fan, Z.; Xiao, G. Computerized multidomain EEG classification system: A new paradigm. IEEE J. Biomed. Health Inform. 2022, 26, 3626–3637. [Google Scholar] [CrossRef]
- Lee, M.H.; Kwon, O.Y.; Kim, Y.J.; Kim, H.K.; Lee, Y.E.; Williamson, J.; Fazli, S.; Lee, S.W. EEG dataset and OpenBMI toolbox for three BCI paradigms: An investigation into BCI illiteracy. GigaScience 2019, 8, giz002. [Google Scholar] [CrossRef]
- Chaudhary, U.; Birbaumer, N.; Ramos-Murguialday, A. Brain–computer interfaces for communication and rehabilitation. Nat. Rev. Neurol. 2016, 12, 513–525. [Google Scholar] [CrossRef]
- Lotte, F.; Bougrain, L.; Cichocki, A.; Clerc, M.; Congedo, M.; Rakotomamonjy, A.; Yger, F. A review of classification algorithms for EEG-based brain–computer interfaces: A 10 year update. J. Neural Eng. 2018, 15, 031005. [Google Scholar] [CrossRef]
- Saeidi, M.; Karwowski, W.; Farahani, F.V.; Fiok, K.; Taiar, R.; Hancock, P.A.; Al-Juaid, A. Neural decoding of EEG signals with machine learning: A systematic review. Brain Sci. 2021, 11, 1525. [Google Scholar] [CrossRef]
- Li, D.; Wang, J.; Xu, J.; Fang, X.; Ji, Y. Cross-Channel Specific-Mutual Feature Transfer Learning for Motor Imagery EEG Signals Decoding. IEEE Trans. Neural Netw. Learn. Syst. 2023, 35, 13472–13482. [Google Scholar] [CrossRef]
- Moctezuma, L.A.; Molinas, M. Classification of low-density EEG for epileptic seizures by energy and fractal features based on EMD. J. Biomed. Res. 2020, 34, 180. [Google Scholar] [CrossRef]
- Akbari, H.; Sadiq, M.T.; Rehman, A.U. Classification of normal and depressed EEG signals based on centered correntropy of rhythms in empirical wavelet transform domain. Health Inf. Sci. Syst. 2021, 9, 9. [Google Scholar] [CrossRef]
- Pandey, P.; Seeja, K. Subject independent emotion recognition from EEG using VMD and deep learning. J. King Saud Univ.—Comput. Inf. Sci. 2022, 34, 1730–1738. [Google Scholar] [CrossRef]
- Thanigaivelu, P.; Sridhar, S.; Sulthana, S.F. OISVM: Optimal Incremental Support Vector Machine-based EEG Classification for Brain-computer Interface Model. Cogn. Comput. 2023, 15, 888–903. [Google Scholar] [CrossRef]
- Zhang, R.; Zong, Q.; Dou, L.; Zhao, X. A novel hybrid deep learning scheme for four-class motor imagery classification. J. Neural Eng. 2019, 16, 066004. [Google Scholar] [CrossRef]
- Brunner, C.; Leeb, R.; Müller-Putz, G.; Schlögl, A.; Pfurtscheller, G. BCI Competition 2008—Graz Data Set A; Institute for Knowledge Discovery (Laboratory of Brain-Computer Interfaces), Graz University of Technology: Graz, Austria, 2008; Volume 16, pp. 1–6. [Google Scholar]
- Dai, G.; Zhou, J.; Huang, J.; Wang, N. HS-CNN: A CNN with hybrid convolution scale for EEG motor imagery classification. J. Neural Eng. 2020, 17, 016025. [Google Scholar] [CrossRef]
- Lawhern, V.J.; Solon, A.J.; Waytowich, N.R.; Gordon, S.M.; Hung, C.P.; Lance, B.J. EEGNet: A compact convolutional neural network for EEG-based brain–computer interfaces. J. Neural Eng. 2018, 15, 056013. [Google Scholar] [CrossRef]
- Deng, X.; Zhang, B.; Yu, N.; Liu, K.; Sun, K. Advanced TSGL-EEGNet for motor imagery EEG-based brain-computer interfaces. IEEE Access 2021, 9, 25118–25130. [Google Scholar] [CrossRef]
- Ingolfsson, T.M.; Hersche, M.; Wang, X.; Kobayashi, N.; Cavigelli, L.; Benini, L. EEG-TCNet: An accurate temporal convolutional network for embedded motor-imagery brain–machine interfaces. In Proceedings of the 2020 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Toronto, ON, Canada,, 11–14 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 2958–2965. [Google Scholar]
- Musallam, Y.K.; AlFassam, N.I.; Muhammad, G.; Amin, S.U.; Alsulaiman, M.; Abdul, W.; Altaheri, H.; Bencherif, M.A.; Algabri, M. Electroencephalography-based motor imagery classification using temporal convolutional network fusion. Biomed. Signal Process. Control 2021, 69, 102826. [Google Scholar] [CrossRef]
- Schirrmeister, R.T.; Springenberg, J.T.; Fiederer, L.D.J.; Glasstetter, M.; Eggensperger, K.; Tangermann, M.; Hutter, F.; Burgard, W.; Ball, T. Deep learning with convolutional neural networks for EEG decoding and visualization. Hum. Brain Mapp. 2017, 38, 5391–5420. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Zhang, D.; Chen, K.; Jian, D.; Yao, L. Motor imagery classification via temporal attention cues of graph embedded EEG signals. IEEE J. Biomed. Health Inform. 2020, 24, 2570–2579. [Google Scholar] [CrossRef]
- Amin, S.U.; Altaheri, H.; Muhammad, G.; Abdul, W.; Alsulaiman, M. Attention-inception and long-short-term memory-based electroencephalography classification for motor imagery tasks in rehabilitation. IEEE Trans. Ind. Inform. 2021, 18, 5412–5421. [Google Scholar] [CrossRef]
- Huang, Y.C.; Chang, J.R.; Chen, L.F.; Chen, Y.S. Deep neural network with attention mechanism for classification of motor imagery EEG. In Proceedings of the 2019 9th International IEEE/EMBS Conference on Neural Engineering (NER), San Francisco, CA, USA, 20–23 March 2019; IEEE: Piscatway, NJ, USA, 2019; pp. 1130–1133. [Google Scholar]
- Yu, X.; Aziz, M.Z.; Hou, Y.; Li, H.; Lv, J.; Jamil, M. An extended computer aided diagnosis system for robust BCI applications. In Proceedings of the 2021 IEEE 9th International Conference on Information, Communication and Networks (ICICN), Xi’an, China, 25–28 November 2021; IEEE: Piscatway, NJ, USA, 2021; pp. 475–480. [Google Scholar]
- Blankertz, B.; Muller, K.R.; Krusienski, D.J.; Schalk, G.; Wolpaw, J.R.; Schlogl, A.; Pfurtscheller, G.; Millan, J.R.; Schroder, M.; Birbaumer, N. The BCI competition III: Validating alternative approaches to actual BCI problems. IEEE Trans. Neural Syst. Rehabil. Eng. 2006, 14, 153–159. [Google Scholar] [CrossRef]
- Kumar, S.; Sharma, A. A new parameter tuning approach for enhanced motor imagery EEG signal classification. Med. Biol. Eng. Comput. 2018, 56, 1861–1874. [Google Scholar] [CrossRef]
- Yang, G.; Liu, J. A novel multi-scale fusion convolutional neural network for EEG-based motor imagery classification. Biomed. Signal Process. Control 2024, 96, 106645. [Google Scholar] [CrossRef]
- Ding, Y.; Robinson, N.; Zhang, S.; Zeng, Q.; Guan, C. TSception: Capturing temporal dynamics and spatial asymmetry from EEG for emotion recognition. IEEE Trans. Affect. Comput. 2022, 14, 2238–2250. [Google Scholar] [CrossRef]
- Liu, X.; Shi, R.; Hui, Q.; Xu, S.; Wang, S.; Na, R.; Sun, Y.; Ding, W.; Zheng, D.; Chen, X. TCACNet: Temporal and channel attention convolutional network for motor imagery classification of EEG-based BCI. Inf. Process. Manag. 2022, 59, 103001. [Google Scholar] [CrossRef]
- Altaheri, H.; Muhammad, G.; Alsulaiman, M. Physics-informed attention temporal convolutional network for EEG-based motor imagery classification. IEEE Trans. Ind. Inform. 2022, 19, 2249–2258. [Google Scholar] [CrossRef]
- Fu, T.; Chen, L.; Fu, Z.; Yu, K.; Wang, Y. CCNet: CNN model with channel attention and convolutional pooling mechanism for spatial image steganalysis. J. Vis. Commun. Image Represent. 2022, 88, 103633. [Google Scholar] [CrossRef]
- Song, Y.; Zheng, Q.; Liu, B.; Gao, X. EEG conformer: Convolutional transformer for EEG decoding and visualization. IEEE Trans. Neural Syst. Rehabil. Eng. 2022, 31, 710–719. [Google Scholar] [CrossRef]
- Liu, S.; An, L.; Zhang, C.; Jia, Z. A spatial-temporal transformer based on domain generalization for motor imagery classification. In Proceedings of the 2023 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Honolulu, HI, USA, 1–4 October 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 3789–3794. [Google Scholar]
- Belwafi, K.; Gannouni, S.; Aboalsamh, H.; Mathkour, H.; Belghith, A. A dynamic and self-adaptive classification algorithm for motor imagery EEG signals. J. Neurosci. Methods 2019, 327, 108346. [Google Scholar] [CrossRef]
- Barmpas, K.; Panagakis, Y.; Adamos, D.A.; Laskaris, N.; Zafeiriou, S. BrainWave-Scattering Net: A lightweight network for EEG-based motor imagery recognition. J. Neural Eng. 2023, 20, 056014. [Google Scholar] [CrossRef]
- Singh, A.; Lal, S.; Guesgen, H.W. Reduce calibration time in motor imagery using spatially regularized symmetric positives-definite matrices based classification. Sensors 2019, 19, 379. [Google Scholar] [CrossRef]
- Singh, A.; Lal, S.; Guesgen, H.W. Small sample motor imagery classification using regularized Riemannian features. IEEE Access 2019, 7, 46858–46869. [Google Scholar] [CrossRef]
- Dai, M.; Wang, S.; Zheng, D.; Na, R.; Zhang, S. Domain transfer multiple kernel boosting for classification of EEG motor imagery signals. IEEE Access 2019, 7, 49951–49960. [Google Scholar] [CrossRef]
- Abougharbia, J.; Attallah, O.; Tamazin, M.; Nasser, A. A novel BCI system based on hybrid features for classifying motor imagery tasks. In Proceedings of the 2019 Ninth International Conference on Image Processing Theory, Tools and Applications (IPTA), Istanbul, Turkey, 6–9 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar]
- Hekmatmanesh, A.; Wu, H.; Jamaloo, F.; Li, M.; Handroos, H. A combination of CSP-based method with soft margin SVM classifier and generalized RBF kernel for imagery-based brain computer interface applications. Multimed. Tools Appl. 2020, 79, 17521–17549. [Google Scholar] [CrossRef]
- Wijaya, A.; Adji, T.B.; Setiawan, N.A. Logistic Regression based Feature Selection and Two-Stage Detection for EEG based Motor Imagery Classification. Int. J. Intell. Eng. Syst. 2021, 14, 134–146. [Google Scholar] [CrossRef]
- Sadiq, M.T.; Yu, X.; Yuan, Z.; Zeming, F.; Rehman, A.U.; Ullah, I.; Li, G.; Xiao, G. Motor imagery EEG signals decoding by multivariate empirical wavelet transform-based framework for robust brain–computer interfaces. IEEE Access 2019, 7, 171431–171451. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, J.; Wang, A.; Wu, H.; Zhao, Q.; Long, J. Subject adaptation convolutional neural network for EEG-based motor imagery classification. J. Neural Eng. 2022, 19, 066003. [Google Scholar] [CrossRef]
- Miao, M.; Hu, W.; Yin, H.; Zhang, K. Spatial-frequency feature learning and classification of motor imagery EEG based on deep convolution neural network. Comput. Math. Methods Med. 2020, 2020, 1981728. [Google Scholar] [CrossRef]
- Mehtiyev, A.; Al-Najjar, A.; Sadreazami, H.; Amini, M. Deepensemble: A novel brain wave classification in MI-BCI using ensemble of deep learners. In Proceedings of the 2023 IEEE International Conference on Consumer Electronics (ICCE), Las Vegas, NV, USA, 6–8 January 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–5. [Google Scholar]
- Sharma, N.; Upadhyay, A.; Sharma, M.; Singhal, A. Deep temporal networks for EEG-based motor imagery recognition. Sci. Rep. 2023, 13, 18813. [Google Scholar] [CrossRef]
- Grear, T.; Jacobs, D. Classifying EEG motor imagery signals using supervised projection pursuit for artefact removal. In Proceedings of the 2021 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Melbourne, Australia, 17–20 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 2952–2958. [Google Scholar]
- Huang, B.; Xu, H.; Yuan, M.; Aziz, M.Z.; Yu, X. Exploiting asymmetric EEG signals with EFD in deep learning domain for robust BCI. Symmetry 2022, 14, 2677. [Google Scholar] [CrossRef]
- Sadiq, M.T.; Yu, X.; Yuan, Z.; Aziz, M.Z. Identification of motor and mental imagery EEG in two and multiclass subject-dependent tasks using successive decomposition index. Sensors 2020, 20, 5283. [Google Scholar] [CrossRef]
- Siuly, S.; Zarei, R.; Wang, H.; Zhang, Y. A new data mining scheme for analysis of big brain signal data. In Proceedings of the Databases Theory and Applications: 28th Australasian Database Conference, ADC 2017, Brisbane, QLD, Australia, 25–28 September 2017; Proceedings 28. Springer: Berlin/Heidelberg, Germany, 2017; pp. 151–164. [Google Scholar]
- Kumar, S.; Sharma, A.; Tsunoda, T. Brain wave classification using long short-term memory network based OPTICAL predictor. Sci. Rep. 2019, 9, 9153. [Google Scholar] [CrossRef]
- Kumar, S.; Sharma, R.; Sharma, A. OPTICAL+: A frequency-based deep learning scheme for recognizing brain wave signals. Peerj Comput. Sci. 2021, 7, e375. [Google Scholar] [CrossRef]
- Hossain, M.Y.; Sayeed, A. A comparative study of motor imagery (mi) detection in electroencephalogram (eeg) signals using different classification algorithms. In Proceedings of the 2021 International Conference on Automation, Control and Mechatronics for Industry 4.0 (ACMI), Rajshahi, Bangladesh, 8–9 July 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Park, D.; Park, H.; Kim, S.; Choo, S.; Lee, S.; Nam, C.S.; Jung, J.Y. Spatio-temporal explanation of 3D-EEGNet for motor imagery EEG classification using permutation and saliency. IEEE Trans. Neural Syst. Rehabil. Eng. 2023, 31, 4504–4513. [Google Scholar] [CrossRef]
- Fan, C.; Yang, B.; Li, X.; Zan, P. Temporal-frequency-phase feature classification using 3D-convolutional neural networks for motor imagery and movement. Front. Neurosci. 2023, 17, 1250991. [Google Scholar] [CrossRef]
- Sadiq, M.T.; Yu, X.; Yuan, Z.; Aziz, M.Z.; Siuly, S.; Ding, W. A matrix determinant feature extraction approach for decoding motor and mental imagery EEG in subject-specific tasks. IEEE Trans. Cogn. Dev. Syst. 2020, 14, 375–387. [Google Scholar] [CrossRef]
- Luo, J.; Gao, X.; Zhu, X.; Wang, B.; Lu, N.; Wang, J. Motor imagery EEG classification based on ensemble support vector learning. Comput. Methods Programs Biomed. 2020, 193, 105464. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, P.; Cheng, L.; Li, M.; Li, H. Attention-Based Multiscale Spatial-Temporal Convolutional Network for Motor Imagery EEG Decoding. IEEE Trans. Consum. Electron. 2023, 70, 2423–2434. [Google Scholar] [CrossRef]
- Altaheri, H.; Muhammad, G.; Alsulaiman, M.; Amin, S.U.; Altuwaijri, G.A.; Abdul, W.; Bencherif, M.A.; Faisal, M. Deep learning techniques for classification of electroencephalogram (EEG) motor imagery (MI) signals: A review. Neural Comput. Appl. 2023, 35, 14681–14722. [Google Scholar] [CrossRef]
- Aghaei, A.S.; Mahanta, M.S.; Plataniotis, K.N. Separable common spatio-spectral patterns for motor imagery BCI systems. IEEE Trans. Biomed. Eng. 2015, 63, 15–29. [Google Scholar] [CrossRef]
- Zhao, D.; Tang, F.; Si, B.; Feng, X. Learning joint space–time–frequency features for EEG decoding on small labeled data. Neural Netw. 2019, 114, 67–77. [Google Scholar] [CrossRef]
- Sakhavi, S.; Guan, C.; Yan, S. Learning temporal information for brain-computer interface using convolutional neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 5619–5629. [Google Scholar] [CrossRef]
- Mahamune, R.; Laskar, S.H. An automatic channel selection method based on the standard deviation of wavelet coefficients for motor imagery based brain–computer interfacing. Int. J. Imaging Syst. Technol. 2023, 33, 714–728. [Google Scholar] [CrossRef]
- Mane, R.; Chew, E.; Chua, K.; Ang, K.K.; Robinson, N.; Vinod, A.P.; Lee, S.W.; Guan, C. FBCNet: A multi-view convolutional neural network for brain-computer interface. arXiv 2021, arXiv:2104.01233. [Google Scholar]
- Altuwaijri, G.A.; Muhammad, G. Electroencephalogram-based motor imagery signals classification using a multi-branch convolutional neural network model with attention blocks. Bioengineering 2022, 9, 323. [Google Scholar] [CrossRef]
- Ma, W.; Xue, H.; Sun, X.; Mao, S.; Wang, L.; Liu, Y.; Wang, Y.; Lin, X. A novel multi-branch hybrid neural network for motor imagery EEG signal classification. Biomed. Signal Process. Control. 2022, 77, 103718. [Google Scholar] [CrossRef]




| Sr. # | Model Name | Architecture/Working Mechanism | Significance | Relevance to BCINetV1 |
|---|---|---|---|---|
| CNN-based Models | ||||
| 1. | EEGNet [16] | Compact; temporal convolutions for frequency filters, followed by depthwise separable convolutions for efficient spatial filtering across EEG channels. Extracts time-domain dynamic features and their spatial distributions. | Highly efficient, generalizable benchmark for various EEG paradigms, good with limited data/resources. | BCINetV1 also employs convolutional layers; EEGNet serves as a foundational compact CNN baseline. |
| 2. | DeepConvNet [20] | Deeper architecture; standard convolutional and pooling layers for hierarchical feature learning from raw EEG. Extracts increasingly complex temporal and spatial features. | Early successful deep learning model for EEG, showed CNN capability for time-series brain data. | Represents a standard deep CNN approach; BCINetV1 builds upon and refines convolutional strategies. |
| 3. | ShallowConvNet [20] | Simpler, shallow architecture; temporal convolution followed by a spatial convolution. Extracts fundamental temporal patterns (e.g., band-power) and spatial distributions. | Strong, simpler baseline capturing basic EEG features with good interpretability. | Offers a contrast to deeper models and highlights efficiency; BCINetV1 aims for both depth and efficiency in its convolutional components. |
| 4. | FBCNet [27] | Integrates filter banks (frequency sub-bands) with CSP-like spatial filters learned within a CNN. Extracts frequency-specific spatial patterns. | Effectively combines traditional signal processing (filter banks, CSP) with deep learning. | BCINetV1 aims to learn spectral features directly; FBCNet provides a benchmark for hybrid spectral–spatial feature extraction. |
| 5. | MSCNN [28] | Parallel convolutional pathways with varying kernel sizes/receptive fields for multiscale processing. Extracts features from short/long duration events and localized/broader spatial activities. | Captures richer features by considering information from different resolutions, robust to signal variations. | BCINetV1 incorporates multiscale principles in its design; MSCNN is a direct benchmark for multiscale convolutional approaches. |
| 6. | TSception [29] | Multiscale temporal convolutions (inception-inspired) followed by spatial feature learning. Extracts diverse temporal features from various receptive fields for short/long-term dependencies. | Specialized for rich, multiscale temporal information extraction, crucial for dynamic brain states. | Aligns with BCINetV1’s focus on temporal feature extraction at multiple scales through its convolutional design. |
| Attention-based Models | ||||
| 7. | TCANet [30] | TCN backbone enhanced with temporal self-attention. Extracts long-range temporal dependencies and weights important time points. | Strong capability for sequential EEG modeling, highlights critical temporal segments. | BCINetV1 uses attention (ConvSAT); TCANet benchmarks attention specifically on temporal sequences learned by TCNs. |
| 8. | ATCNet [31] | Combines TCNs with attention across temporal, spatial, or feature dimensions. Extracts adaptively weighted temporal sequences and salient channel interactions. | Enhances TCN feature learning with dynamic, data-driven focus. | BCINetV1’s attention mechanism also aims for dynamic focus; ATCNet offers a comparison for TCNs augmented with attention. |
| 9. | CCNet [32] | Explicitly models inter-channel correlations using specialized convolutions/graphs with attention. Extracts spatial dependencies and connectivity patterns. | Focuses on complex spatial relationships in multi-channel EEG, vital for distributed brain activity. | While BCINetV1’s primary attention is tempo-spectral, CCNet provides context for attention on spatial/channel correlations. |
| 10. | EEG-Conformer [33] | Hybrid: CNNs for local feature extraction, then Conformer blocks (Transformer-style self-attention and convolution) for global dependencies. Extracts local, fine-grained features and global contextual relationships. | Effectively leverages CNN strengths for local patterns and Transformers for global interactions. | BCINetV1 combines convolution and attention; EEG-Conformer is a benchmark for hybrid CNN-Transformer (attention) architectures. |
| 11. | ST-Transformer or ST-DG [34] | Transformer-based; jointly models spatial (inter-channel) and temporal dependencies using factorized/specialized attention. Extracts integrated spatio-temporal dynamics. | Explicit, unified approach to capturing complex interplay between spatial and temporal aspects. | BCINetV1’s ConvSAT addresses tempo-spectral attention; ST-Transformer benchmarks pure Transformer-based spatio-temporal attention. |
| Category | Authored By | Year | Method | AA | AL | AV | AW | AY | Avg. | Std. |
|---|---|---|---|---|---|---|---|---|---|---|
| Hybird signal processing methods | Belwafi et al. [35] | 2019 | DSAA | 69.5 | 96.3 | 60.5 | 70.5 | 78.6 | 81.9 | 14.18 |
| Barmpas et al. [36] | 2023 | Brain-wave scattering Net | 78.9 | 92.2 | 60.3 | 86.7 | 85.7 | 80.7 | 11.07 | |
| Singh et al. [37] | 2019 | SR-MDRM | 79.4 | 100 | 73.4 | 89.2 | 88.4 | 86.1 | 10.15 | |
| Amardeep et al. [38] | 2019 | R-MDRM | 81.3 | 100 | 76.5 | 87.1 | 91.2 | 87.2 | 8.13 | |
| Dai et al. [39] | 2019 | DTMKB | 91.9 | 96.4 | 75.5 | 81.2 | 92.8 | 87.6 | 7.89 | |
| Jaidaa et al. [40] | 2019 | WPD+HOS+SVM | 89.6 | 99.3 | 77.9 | 97.5 | 94.3 | 91.7 | 7.66 | |
| Amin et al. [41] | 2020 | DFBCSP+DSLVQ+SSVM/GRBF | 93.5 | 98.5 | 81.8 | 93.6 | 96.1 | 92.7 | 5.77 | |
| Wijaya et al. [42] | 2021 | LRFS+TSD | 93.9 | 92.1 | 98.5 | 94.6 | 96.7 | 95.2 | 2.51 | |
| Sadiq et al. [43] | 2019 | MEWT+JIA+MLP | 95.0 | 95.0 | 95.0 | 100 | 100 | 97.0 | 2.70 | |
| Deep learning methods | Simulated | 2025 | EEGNet | 61.1 | 70.3 | 55.3 | 57.9 | 58.9 | 60.7 | 5.15 |
| Simulated | 2025 | ATCNet | 71.1 | 77.1 | 73.5 | 76.5 | 77.7 | 75.7 | 2.51 | |
| Simulated | 2025 | CCNet | 79.0 | 76.1 | 85.5 | 86.9 | 86.9 | 82.9 | 4.47 | |
| Liu et al. [44] | 2022 | SACNN | 91.0 | 92.0 | 77.0 | 77.0 | 79.0 | 83.2 | 6.82 | |
| Simulated | 2025 | ShallowConvNet | 77.5 | 81.8 | 88.3 | 89.8 | 89.9 | 85.2 | 4.80 | |
| Simulated | 2025 | EEG-Conformer | 89.7 | 86.1 | 86.7 | 87.9 | 90.9 | 88.3 | 1.80 | |
| Miao et al. [45] | 2020 | Spatial Frequency+CNN | 97.2 | 90.0 | 90.0 | 90.0 | 80.0 | 90.0 | 7.10 | |
| Simulated | 2025 | TSception | 93.6 | 89.3 | 93.6 | 89.4 | 93.6 | 91.9 | 2.07 | |
| Simulated | 2025 | DeepConvNet | 92.1 | 94.5 | 92.1 | 89.7 | 95.7 | 92.8 | 2.09 | |
| Simulated | 2025 | TCANet | 94.1 | 94.7 | 89.7 | 89.6 | 97.4 | 93.1 | 3.03 | |
| Mehtiyev et al. [46] | 2023 | DeepEnsembleNet | 96 | 96.6 | 88.7 | 90.6 | 96 | 93.6 | 3.26 | |
| Simulated | 2025 | MSCNN | 91.8 | 98.7 | 92.1 | 97.8 | 97.4 | 95.6 | 2.97 | |
| Sharma et al. [47] | 2023 | LSTM+multi-head Attention | 97.5 | 98.3 | 99.5 | 97.6 | 98.4 | 98.2 | 2.72 | |
| This study | 2025 | BCINetV1 | 98.2 | 98 | 98.7 | 99.0 | 99.4 | 98.6 | 0.50 |
| Experimental Blocks | Accuracy (%) | Extracted Features ANOVA Test p-Values |
|---|---|---|
| T-CAB w/o Temporal ConvSAT | 52.06 | * |
| SEB w/o channels reordering | 53.09 | * |
| S-CAB w/o Spectral ConvSAT | 55.08 | * |
| SEB | 72.45 | |
| T-CAB | 75.98 | |
| S-CAB | 85.09 | |
| T-CAB + SEB | 88.87 | |
| S-CAB + SEB | 90.67 | |
| T-CAB + S-CAB + SEB | 98.68 |
| Category | Authored By | Year | Method | Accuracy (%) | Recall (%) | F-Score (%) | Kappa (%) |
|---|---|---|---|---|---|---|---|
| Hybird signal processing methods | Siuly et al. [51] | 2017 | PCA based RF Model | 83.2 ± 8.33 | - | - | - |
| Sadiq et al. [57] | 2020 | 20-order Matrix Determinant+FFNN | 91.8 ± 2.58 | - | - | - | |
| Binwen et al. [49] | 2022 | EFD-CNN | 93.8 ± NA | - | 93.7 ± NA | 86.6 ± NA | |
| Sadiq et al. [50] | 2020 | CADMMI-SDI | 99.3 ± 2.60 | - | - | - | |
| Deep Learning methods | Simulated | 2025 | EEGNet | 83.1 ± 4.44 | 84.2 ± 4.83 | 83.5 ± 4.96 | 74.6 ± 6.69 |
| Simulated | 2025 | ShallowConvNet | 84.8 ± 1.82 | 85.0 ± 0.97 | 86.0 ± 1.96 | 77.1 ± 2.74 | |
| Simulated | 2025 | DeepConvNet | 84.9 ± 3.73 | 85.8 ± 4.16 | 84.8 ± 3.91 | 77.2 ± 5.60 | |
| Simulated | 2025 | CCNet | 86.5 ± 6.94 | 86.5 ± 6.81 | 87.0 ± 6.61 | 79.8 ± 10.43 | |
| Simulated | 2025 | FBCNet | 87.9 ± 1.55 | 87.4 ± 1.63 | 88.7 ± 2.14 | 81.7 ± 2.34 | |
| Simulated | 2025 | MSCNN | 88.9 ± 3.12 | 88.7 ± 3.77 | 88.3 ± 3.73 | 83.3 ± 4.68 | |
| Simulated | 2025 | TSception | 91.8 ± 1.79 | 91.3 ± 1.13 | 90.8 ± 1.38 | 87.6 ± 2.70 | |
| Simulated | 2025 | ATCNet | 93.4 ± 1.80 | 92.5 ± 1.64 | 92.2 ± 2.57 | 90.1 ± 2.71 | |
| Simulated | 2025 | ST-Transformer | 94.7 ± 2.55 | 93.6 ± 2.12 | 95.3 ± 1.95 | 92.1 ± 3.84 | |
| Simulated | 2025 | TCANet | 96.0 ± 1.93 | 95.6 ± 1.62 | 95.5 ± 1.57 | 94.0 ± 2.91 | |
| Simulated | 2025 | EEG-Comformer | 97.2 ± 1.95 | 98.3 ± 2.63 | 98.0 ± 1.07 | 95.7 ± 2.94 | |
| This Study | 2025 | BCINetV1 | 97.2 ± 0.30 | 96.9 ± 0.547 | 97.5 ± 0.52 | 95.3 ± 0.90 |
| Category | Authored By | Year | Method | Accuracy (%) | Recall (%) | F-score (%) | Kappa (%) |
|---|---|---|---|---|---|---|---|
| Hybird signal processing methods | Agha et al. [61] | 2016 | SCSSP | 63.8 ± 0.49 | - | - | - |
| Zhao et al. [62] | 2019 | WaSF+ConvNet | 69 ± NA | - | - | 58 ± NA | |
| Sakhavi et al. [63] | 2018 | C2CM | 74.4 ± NA | - | - | 65.9 ± NA | |
| Mahamune et al. [64] | 2022 | stdWC+CSP+CNN | 75.0 ± 0.67 | - | - | - | |
| Luo et al. [58] | 2020 | ESVL | 82.5 ± NA | - | - | 65 ± NA | |
| Deep Learning methods | Liu et al. [34] | 2023 | ST-Transformer | 57.7 ± 0.01 | - | - | - |
| Schirrmeister et al. [20] | 2017 | DeepConvNet | 70.9 ± NA | - | - | - | |
| Schirrmeister et al. [20] | 2017 | ShallowConvNet | 73.7 ± NA | - | - | - | |
| Simulated | 2025 | CCNet | 76.7 ± NA | 74.5 ± NA | 75.8 ± NA | 68.9 ± NA | |
| Simulated | 2025 | EEGNet | 76.4 ± 14.6 | - | - | 68.6 ± 19.5 | |
| Song et al. [33] | 2022 | EEG-Conformer | 78.6 ± 0.26 | - | - | 71.55 ± NA | |
| Mane et al. [65] | 2020 | FBCNet | 79.0 ± NA | - | - | - | |
| Altuwaijri et al. [66] | 2022 | MB-EEG-CBAM | 82.8 ± 11.3 | 83.2 ± 11.3 | 83 ± 0.15 | 77.1 ± 11.3 | |
| Ma et al. [67] | 2022 | MB-HNN | 83.9 ± 9.09 | 78 ± 12 | |||
| Altaheri et al. [31] | 2023 | ATCNet | 85.4 ± 9.1 | - | - | 81 ± 12 | |
| Liu et al. [30] | 2022 | TCANet | 86.8 ± 10.3 | - | - | - | |
| Yang et al. [28] | 2024 | MSFCNNnet | 87.1 ± 8.85 | - | 87 ± 9.01 | 82 ± 12 | |
| Zhang et al. [59] | 2023 | AMSTCNet | 87.5 ± 8.04 | 87.4±NA | 88 ± NA | 83 ± 0.11 | |
| Simulated | 2025 | TSception | 88.5 ± NA | 88.5 ± NA | 86.2 ± NA | 84.7 ± NA | |
| This Study | 2025 | BCINetV1 | 98.4 ± 0.60 | 98.4 ± 0.61 | 98.4 ± 0.60 | 97.8 ± 0.81 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aziz, M.Z.; Yu, X.; Guo, X.; He, X.; Huang, B.; Fan, Z. BCINetV1: Integrating Temporal and Spectral Focus Through a Novel Convolutional Attention Architecture for MI EEG Decoding. Sensors 2025, 25, 4657. https://doi.org/10.3390/s25154657
Aziz MZ, Yu X, Guo X, He X, Huang B, Fan Z. BCINetV1: Integrating Temporal and Spectral Focus Through a Novel Convolutional Attention Architecture for MI EEG Decoding. Sensors. 2025; 25(15):4657. https://doi.org/10.3390/s25154657
Chicago/Turabian StyleAziz, Muhammad Zulkifal, Xiaojun Yu, Xinran Guo, Xinming He, Binwen Huang, and Zeming Fan. 2025. "BCINetV1: Integrating Temporal and Spectral Focus Through a Novel Convolutional Attention Architecture for MI EEG Decoding" Sensors 25, no. 15: 4657. https://doi.org/10.3390/s25154657
APA StyleAziz, M. Z., Yu, X., Guo, X., He, X., Huang, B., & Fan, Z. (2025). BCINetV1: Integrating Temporal and Spectral Focus Through a Novel Convolutional Attention Architecture for MI EEG Decoding. Sensors, 25(15), 4657. https://doi.org/10.3390/s25154657








