A Kinodynamic Model for Dubins-Based Trajectory Planning in Precision Oyster Harvesting
Abstract
Highlights
- We developed a novel hybrid kinodynamic model combining the Dubins and Nomoto models to map steering input directly to spatial coordinates for underactuated boats.
- Field experiments in oyster aquaculture environments showed turning radius errors within 1.5% and trajectory following accuracy with sub-meter precision across various path complexities.
- Enable efficient and precise motion planning for autonomous oyster harvesting vessels under real-world constraints like starboard-turn-only paths.
- Provide a scalable foundation for integrating control systems and MIMO-compatible models in future aquaculture automation frameworks.
Abstract
1. Introduction
- Novel integration of the Nomoto and Dubins models, specifically designed for aquaculture applications and leveraging the strengths of both models—such as easy system identification and minimum turning radius calculation.
- Direct steering-to-coordinate mapping, unlike existing models that rely on indirect approximations, improving the precision in full-coverage path planning.
- Experimental validation in a real-world oyster harvesting environment, using gray-box system identification on a Carolina Skiff Model 21 DLX.
- Demonstration of practical feasibility for precision aquaculture, with motion primitives computed from identified model parameters and tested at the Horn Point Laboratory in Cambridge, MD.
2. Related Work
2.1. The Dubins Model
2.2. Kinodynamic Boat Models
2.2.1. The Nomoto Model
2.2.2. The Krasowski Model
2.2.3. The Davidson and Schiff Model and Asfihani Approach
2.3. Motion Primitives for Boats
3. Materials and Methods
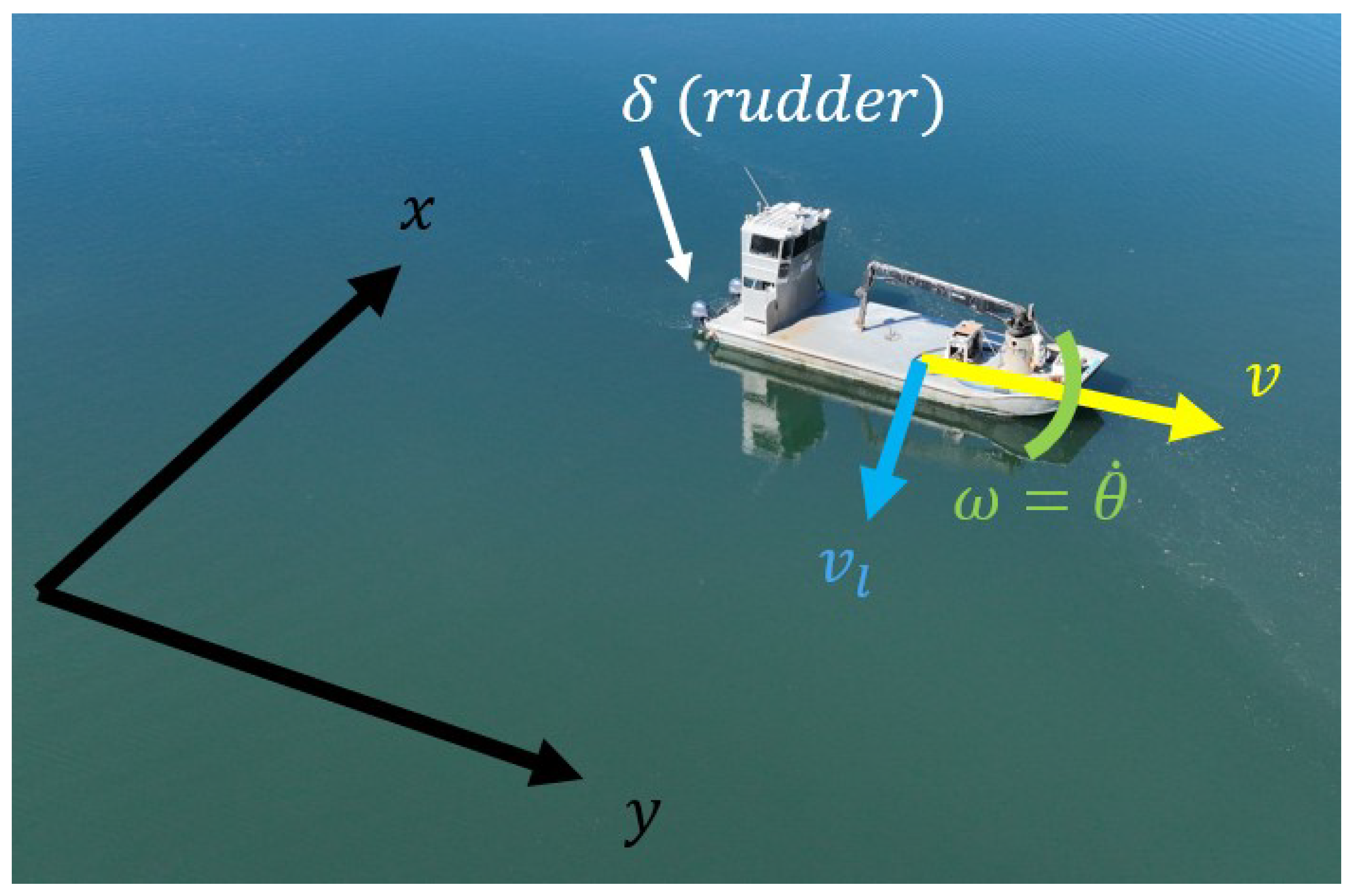
3.1. General Definitions and Assumptions
3.2. Model Derivation
3.2.1. Nonlinear Model
3.2.2. Linearized Model
3.3. Experimentation
3.3.1. Hardware and Setup
3.3.2. Experimental Process
4. Results
4.1. System Identification
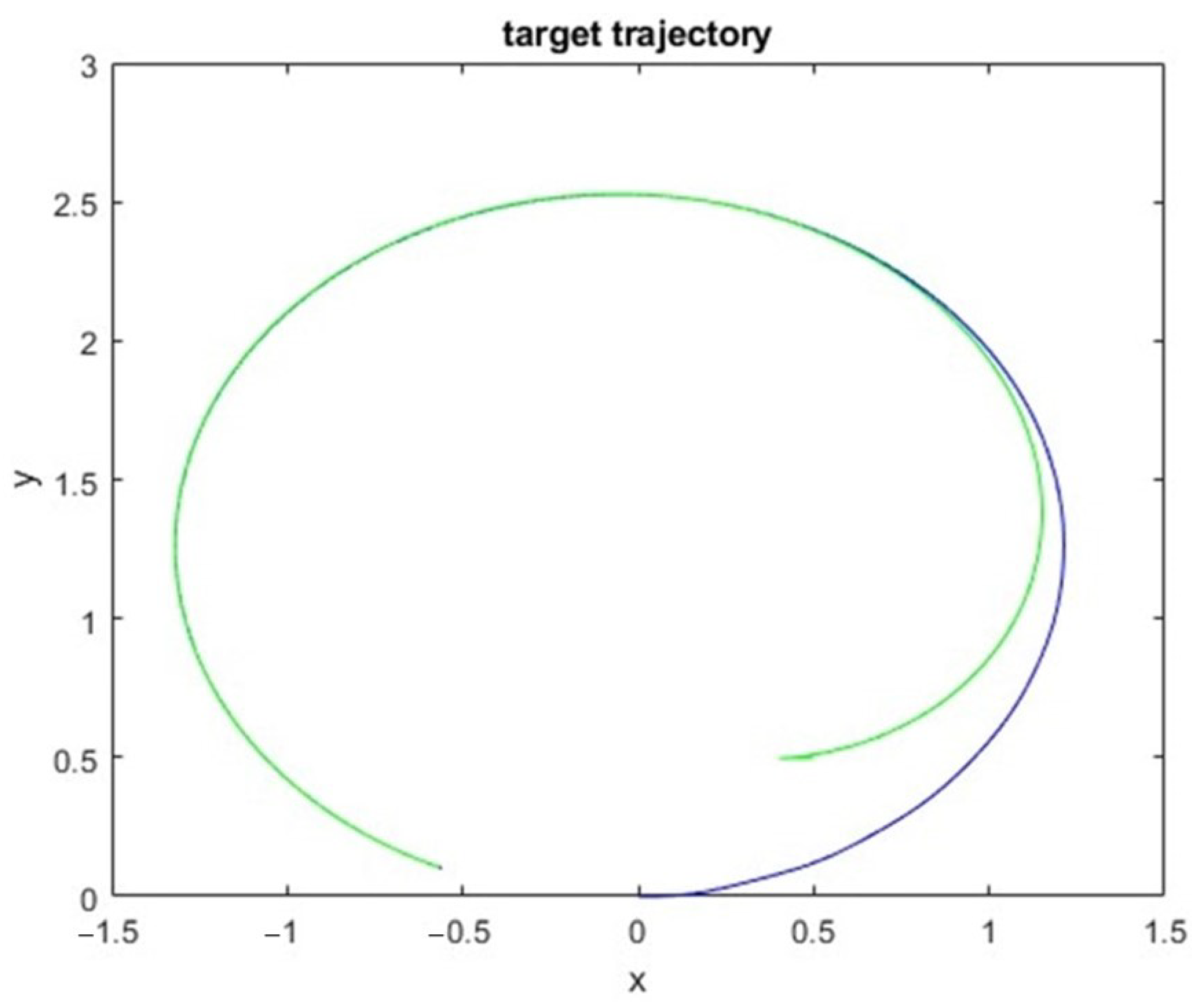
4.2. Trajectory Following
- 1.
- Starboard 5.5 s, straight 4.5 s, starboard 1 s;
- 2.
- Starboard 13 s, straight 2 s, starboard 21 s;
- 3.
- Starboard 19.5 s, straight 10 s, starboard 2 s.
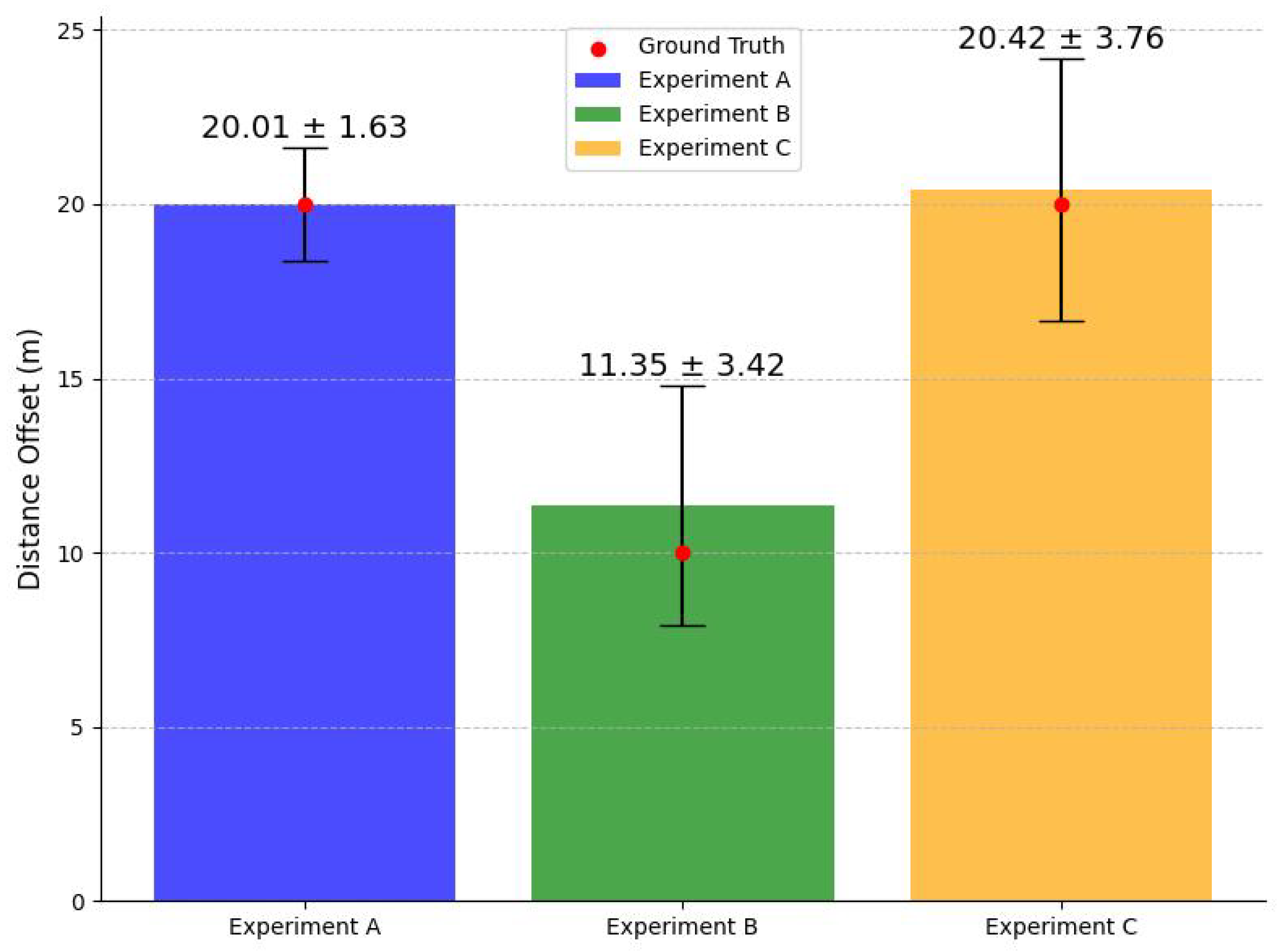
4.3. Analysis
5. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BCD | Boustrophedon Cellular Decomposition |
| CCF | Controllable Canonical Form |
| COLREG | International Regulations for Preventing Collisions at Sea |
| DOF | Degree-of-Freedom |
| FAO | United Nations Food and Agriculture Organization |
| GPS | Global Positioning System |
| GNSS | Global Navigation Satellite System |
| IMO | International Marine Organization |
| LOA | Length Overall |
| MSE | Mean Square Error |
| MIMO | Multi-input–Multi-output |
| RTK | Real-Time Kinematics |
| SE | Special Euclidean Group |
| SID | System Identification |
Appendix A. Preliminary Experiments
Appendix A.1. Preliminary Experiment on an RC Boat
Appendix A.1.1. Hardware, Setup, and Assumptions
Appendix A.1.2. Experimental Process and Results

Appendix A.2. Preliminary Simulation of a Linear Quadratic Regulator (LQR)
Appendix B. Generalized Controllable Canonical Form (CCF)
References
- Food and Agriculture Organization of the United Nations. The State of World Fisheries and Aquaculture 2022: Towards Blue Transformation; FAO: Rome, Italy, 2022. [Google Scholar] [CrossRef]
- Rothschild, B.J.; Ault, J.S.; Goulletquer, P.; Héral, M. Decline of the Chesapeake Bay oyster population: A century of habitat destruction and overfishing. Mar. Ecol. Prog. Ser. 1994, 111, 29–39. [Google Scholar] [CrossRef]
- Fossen, T.I.; Pettersen, K.Y. On uniform semiglobal exponential stability (USGES) of proportional line-of-sight guidance laws. Automatica 2014, 50, 2912–2917. [Google Scholar] [CrossRef]
- Øivind, K.K.; Coates, E.M. Enhancing Line-of-Sight Guidance to Improve Path Following for Marine Surface Vessels. IFAC-PapersOnLine 2024, 58, 1–8. [Google Scholar] [CrossRef]
- Tedrake, R.; Manchester, I.R.; Tobenkin, M.; Roberts, J.W. LQR-trees: Feedback Motion Planning via Sums-of-Squares Verification. Int. J. Robot. Res. 2010, 29, 1038–1052. [Google Scholar] [CrossRef]
- Majumdar, A.; Tedrake, R. Funnel libraries for real-time robust feedback motion planning. Int. J. Robot. Res. 2017, 36, 947–982. [Google Scholar] [CrossRef]
- Althoff, M.; Guernic, C.; Krogh, B. Reachable set computation for uncertain time-varying linear systems. In Proceedings of the HSCC’11-Proceedings of the 2011 ACM/SIGBED Hybrid Systems: Computation and Control, Chicago, IL, USA, 12–14 April 2011; pp. 93–102. [Google Scholar] [CrossRef]
- Dubins, L.E. On Curves of Minimal Length with a Constraint on Average Curvature, and with Prescribed Initial and Terminal Positions and Tangents. Am. J. Math. 1957, 79, 497–516. [Google Scholar] [CrossRef]
- LaValle, S.M. Planning Algorithms; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Hameed, I.A. Coverage Path Planning Software for Autonomous Robotic Lawn Mower using Dubins’ Curve. In Proceedings of the 2017 IEEE International Conference on Real-Time Computing and Robotics (RCAR), Okinawa, Japan, 14–18 July 2017; pp. 517–522. [Google Scholar]
- Pěnička, R.; Faigl, J.; Vana, P.; Saska, M. Dubins Orienteering Problem. IEEE Robot. Autom. Lett. 2017, 2, 1210–1217. [Google Scholar] [CrossRef]
- Lewis, J.S.; Edwards, W.; Benson, K.; Rekleitis, I.; O’Kane, J.M. Semi-Boustrophedon Coverage with a Dubins Vehicle. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 5630–5637. [Google Scholar] [CrossRef]
- Putri, D.K.R.; Subchan; Adzkiya, D.; Asfihani, T. Ship Heading Control for Dubins Path Tracking and Collision Avoidance using Model Predictive Control. In Proceedings of the 2019 International Conference on Information and Communications Technology (ICOIACT), Institut Teknologi Sepuluh Nopember, Surabaya, Indonesia, 24–25 July 2019. [Google Scholar]
- Parlangeli, G.; Palma, D.D.; Attanasi, R. A novel approach for 3PDP and real-time via point path planning of Dubins’ vehicles in marine applications. Control. Eng. Pract. 2024, 144, 105814. [Google Scholar] [CrossRef]
- Page, B.R.; Lambert, R.; Chavez-Galaviz, J.; Mahmoudian, N. Path Following Using Rendezvous Dubins Curves and Integral Line-of-Sight for Unmanned Marine Systems. Field Robot. 2022, 2, 1920–1942. [Google Scholar] [CrossRef]
- Fossen, T. Handbook of Marine Craft Hydrodynamics and Maneuvering; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Carrillo, S.; Contreras, J. Obtaining First and Second Order Nomoto Models of a Fluvial Support Patrol using Identification Techniques. Cienc. Tecnol. Buques 2018, 11, 19–28. [Google Scholar] [CrossRef]
- Krasowski, H.; Althoff, M. CommonOcean: Vessel Models. 2022. Available online: https://gitlab.lrz.de/tum-cps/commonocean-vessel-models/-/blob/main/documentation/vesselModels_commonOcean.pdf (accessed on 30 April 2024).
- Nomoto, K.; Taguchi, T.; Honda, K.; Hirano, S. On the steering qualities of ships. Int. Shipbuild. Prog. 1957, 4, 354–370. [Google Scholar] [CrossRef]
- Davidson, K.; Schiff, L. Turning and Course Keeping Qualities; Technical Report Report No. 98; TU Delft, Faculty of Marine Technology, Ship Hydromechanics Laboratory: Delft, The Netherlands, 1946. [Google Scholar]
- Otsubo, K. Parameter identification based on unity feedback responses for steering control in model experiments. J. Mar. Sci. Technol. 2023, 28, 551–567. [Google Scholar] [CrossRef]
- Mu, D.; Wang, G.; Fan, Y.; Bai, Y. Podded Propulsion Unmanned Surface Vehicle Model Identification Based on Field Experiments. In Proceedings of the 36th Chinese Control Conference, Dalian Maritime University, Dalian, China, 26–28 July 2017. [Google Scholar]
- International Maritime Organization. Standards for Ship Maneuverability; International Maritime Organization: London, UK, 2002; MSC.137(76). [Google Scholar]
- Liu, Z.; Chu, R. Robust adaptive heading control for a surface vessel with drift angles. Ocean. Eng. 2020, 205, 107310. [Google Scholar] [CrossRef]
- Li, J.H.; Lee, P.M.; Jun, B.H.; Lim, Y.K. Point-to-point navigation of underactuated ships. Automatica 2008, 44, 3201–3205. [Google Scholar] [CrossRef]
- Webster, D.; Meritt, D. Stabilizing Oyster Ground; Technical Report; Maryland Sea Grant Extension Program: College Park, MD, USA, 1988. [Google Scholar]
- Assani, N.; Pavic, I.; Vuksa, S.; Lausic, M. Analysis of the Nomoto Ship Model Response to Course Changes Using PID Controller in MATLAB/Simulink. In Proceedings of the ICTS 2020, Portorož, Slovenia, 4–5 June 2020. [Google Scholar]
- Arnaoot, H.M.; Abdin, H.; Gadalla, M. Design of Autonomous Ship Heading Controller considering Ship Movement Effects on Object(S) Detection. In Proceedings of the 2021 International Telecommunications Conference, ITC-Egypt, Alexandria Higher Institute of Engineering & Technology, Alexandria, Egypt, 13–15 July 2021. [Google Scholar]
- Zhang, Z.; Zhang, X.; Zhang, G. ANFIS-based course-keeping control for ships using nonlinear feedback technique. J. Mar. Sci. Technol. 2019, 24, 1326–1333. [Google Scholar] [CrossRef]
- Asfihani, T.; Subchan, S.; Rosyid, D.M.; Sulisetyono, A. Dubins Path Tracking Controller of USV using Model Predictive Control in Sea Field. J. Eng. Appl. Sci. 2019, 14, 7778–7787. [Google Scholar] [CrossRef]
- Jia, C.; Ma, J.; He, M.; Su, Y.; Zhang, Y.; Yu, Q. Motion primitives learning of ship-ship interaction patterns in encounter situations. Ocean. Eng. 2022, 247, 110708. [Google Scholar] [CrossRef]
- Stankiewicz, P.; Kobilarov, M. A Primitive-Based Approach to Good Seamanship Path Planning for Autonomous Surface Vessels. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 7767–7773. [Google Scholar] [CrossRef]
- United States Coast Guard. Navigation Rules: International-Inland; United States Department of Transportation: Washington, DC, USA, 1999.
- Johansen, T.A.; Perez, T.; Cristofaro, A. Ship Collision Avoidance and COLREGS Compliance Using Simulation-Based Control Behavior Selection with Predictive Hazard Assessment. IEEE Trans. Intell. Transp. Syst. 2016, 17, 3407–3422. [Google Scholar] [CrossRef]
- Lai, S.; Lan, M.; Chen, B.M. Control based motion primitives for quadrotor trajectory generation. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; pp. 8323–8329. [Google Scholar] [CrossRef]
- Mueller, M.W.; Hehn, M.; D’Andrea, R. A Computationally Efficient Motion Primitive for Quadrocopter Trajectory Generation. IEEE Trans. Robot. 2015, 31, 1294–1310. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear Control, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Chen, C.; Delefortrie, G.; Lataire, E. Effects of water depth and speed on ship motion control from medium deep to very shallow water. Ocean. Eng. 2021, 231, 109102. [Google Scholar] [CrossRef]
- Nise, N.S. Control Systems Engineering, 7th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]





| Model Comparison | Input → Output | Relative Simplicity | Main Usage |
|---|---|---|---|
| Nomoto | Steering → Yaw Velocity | High | Single-Rudder–Propeller Boats |
| Dubins | Yaw Velocity → Coordinates | High | Vehicles with Turning Radius |
| Davidson Schiff | Steering → Sway, Surge, Yaw Velocity | Low | Single-Rudder–Propeller Boats |
| Krasowski | Forces → Velocity and Acceleration | Moderate | Jet Propulsion Boats |
| Proposed Method | Steering → Coordinates | Moderate | Single-Rudder–Propeller Boats |
| Group | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| A | 3.882 | 1.618 | 1.204 | 1.253 | 1.664 | 1.333 | 0.828 | 1.383 | 2.559 | 1.168 |
| B | 0.1186 | 4.2825 | 1.6596 | 3.8799 | 6.2845 | 1.2872 | 3.4276 | 4.5934 | 2.4979 | 2.6499 |
| C | 7.8421 | 0.0148 | 6.3975 | 0.9592 | 3.8577 | 2.2120 | 2.2539 | 0.7595 | 0.0169 | 0.0317 |
| Group | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| A | 4.319 | 1.296 | 1.569 | 1.999 | 2.339 | 1.029 | 0.092 | ERR | 3.944 | 0.048 |
| B | ERR | ERR | ERR | ERR | ERR | ERR | ERR | ERR | ERR | ERR |
| C | ERR | 4.721 | 4.767 | ERR | 2.812 | ERR | ERR | ERR | ERR | ERR |
| Group | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| A | 5.054 | 5.055 | 5.062 | 5.137 | 5.069 | 5.137 | 5.107 | ERR | 5.091 | 5.049 |
| B | ERR | ERR | ERR | ERR | ERR | ERR | ERR | ERR | ERR | ERR |
| C | ERR | 4.651 | 8.191 | ERR | 3.968 | ERR | ERR | ERR | ERR | ERR |
| Group | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| A | 3.085 | 1.618 | 1.204 | 1.253 | 1.664 | 1.333 | 0.828 | ERR | 1.201 | 1.168 |
| B | ERR | ERR | ERR | ERR | ERR | ERR | ERR | ERR | ERR | ERR |
| C | ERR | 4.651 | 8.191 | ERR | 3.968 | ERR | ERR | ERR | ERR | ERR |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.; Wang, C.-Y.; Joshi, K.; Williams, A.; Hevaganinge, A.; Lin, X.; Kumar, S.S.S.; Pattillo, A.; Yu, M.; Chopra, N.; et al. A Kinodynamic Model for Dubins-Based Trajectory Planning in Precision Oyster Harvesting. Sensors 2025, 25, 4650. https://doi.org/10.3390/s25154650
Chen W, Wang C-Y, Joshi K, Williams A, Hevaganinge A, Lin X, Kumar SSS, Pattillo A, Yu M, Chopra N, et al. A Kinodynamic Model for Dubins-Based Trajectory Planning in Precision Oyster Harvesting. Sensors. 2025; 25(15):4650. https://doi.org/10.3390/s25154650
Chicago/Turabian StyleChen, Weiyu, Chiao-Yi Wang, Kaustubh Joshi, Alan Williams, Anjana Hevaganinge, Xiaomin Lin, Sandip Sharan Senthil Kumar, Allen Pattillo, Miao Yu, Nikhil Chopra, and et al. 2025. "A Kinodynamic Model for Dubins-Based Trajectory Planning in Precision Oyster Harvesting" Sensors 25, no. 15: 4650. https://doi.org/10.3390/s25154650
APA StyleChen, W., Wang, C.-Y., Joshi, K., Williams, A., Hevaganinge, A., Lin, X., Kumar, S. S. S., Pattillo, A., Yu, M., Chopra, N., Gray, M. W., & Tao, Y. (2025). A Kinodynamic Model for Dubins-Based Trajectory Planning in Precision Oyster Harvesting. Sensors, 25(15), 4650. https://doi.org/10.3390/s25154650









