An ALoGI PU Algorithm for Simulating Kelvin Wake on Sea Surface Based on Airborne Ku SAR
Abstract
1. Introduction
2. Simulation of Kelvin Wake on the Sea Surface
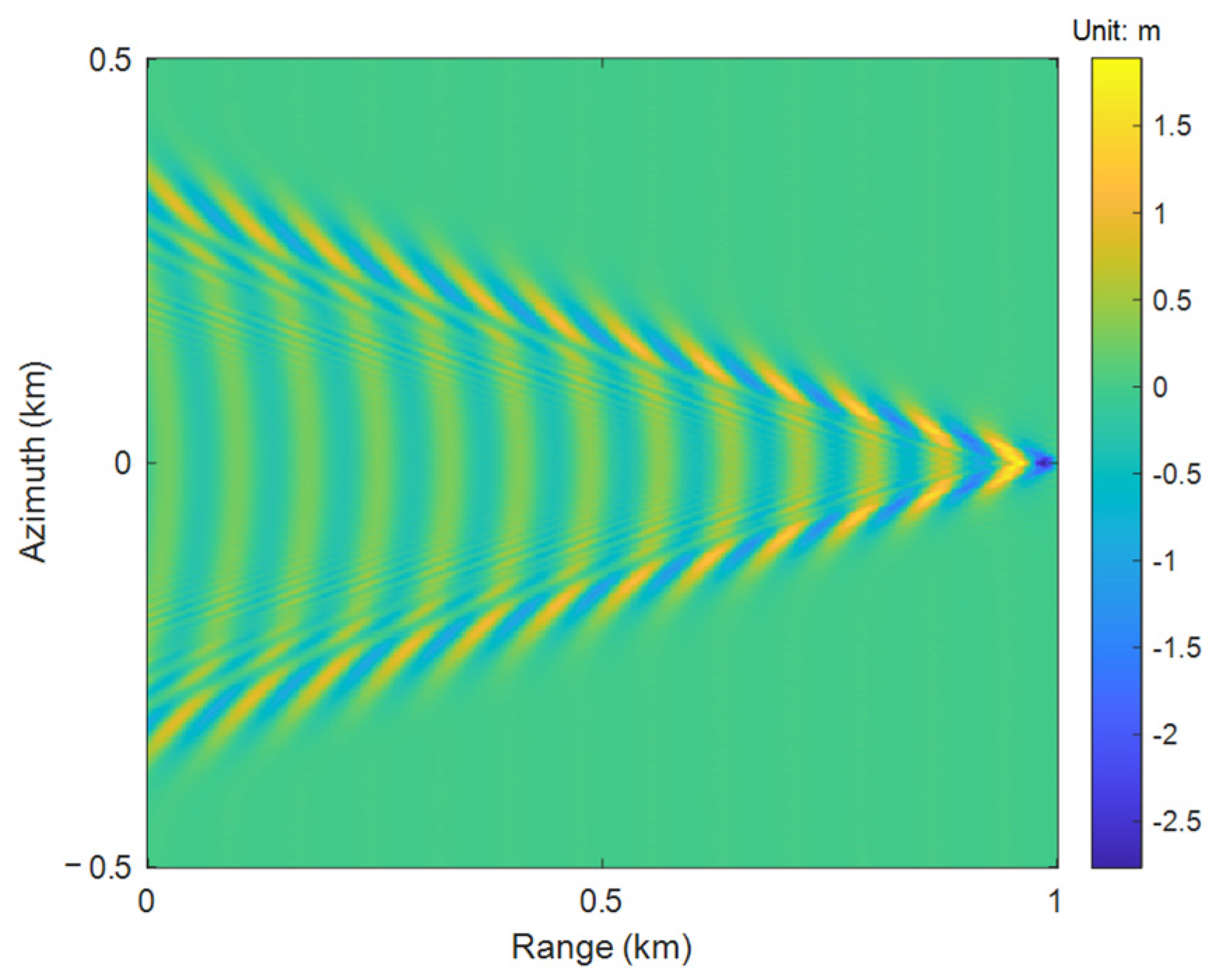
2.1. Kelvin Wake Wave Height
2.2. Model of Sea-Ship Surface Height
2.3. Model of Simulating Phase
3. Methods and Results of PU Algorithms
3.1. 4-FFT Algorithm
3.1.1. Principle of 4-FFT Algorithm
3.1.2. Results of 4-FFT Algorithm
3.2. Proposed ALoG Algorithm
3.2.1. Principle of Improved LoG Algorithm
3.2.2. Adaptive σ
3.2.3. Results of LoG and ALoG Algorithms
3.3. Principle and Method of Iteration
3.3.1. Principle of Iteration
3.3.2. Results of Iteration
4. Discussion
4.1. PCA
4.2. Profile Analysis
4.3. Sea Surface Background
5. Conclusions
- The proposed method improves the PU effect by introducing the Gaussian function into the Fourier expression of the 2D Laplacian.
- The adaptive variance of the Gaussian function has good performance and high stability under the tested noise levels of the simulation.
- The iterative algorithm plays a key role in the context of the tested noise levels of the simulation, significantly improving the performance of the algorithm and having good robustness. This highlights the superiority of the ALoGI algorithm.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tings, B.; Pleskachevsky, A.; Wiehle, S. Comparison of detectability of ship wake components between C-Band and X-Band synthetic aperture radar sensors operating under different slant ranges. ISPRS J. Photogramm. Remote Sens. 2023, 196, 306–324. [Google Scholar] [CrossRef]
- Graziano, M.D.; Grasso, M.; D’Errico, M. Performance analysis of ship wake detection on Sentinel-1 SAR images. Remote Sens. 2017, 9, 1107. [Google Scholar] [CrossRef]
- Hwang, P.A.; Sletten, M.A.; Toporkov, J.V. A note on Doppler processing of coherent radar backscatter from the water surface: With application to ocean surface wave measurements. J. Geophys. Res. Ocean. 2010, 115, C03026. [Google Scholar] [CrossRef]
- Carrasco, R.; Streßer, M.; Horstmann, J. A simple method for retrieving significant wave height from Dopplerized X-band radar. Ocean Sci. 2017, 13, 95–103. [Google Scholar] [CrossRef]
- Carrasco, R.; Horstmann, J.; Seemann, J. Significant wave height measured by coherent X-band radar. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5355–5365. [Google Scholar] [CrossRef]
- Liu, P.; Jin, Y.Q. Simulation of synthetic aperture radar imaging of dynamic wakes of submerged body. IET Radar Sonar Navig. 2017, 11, 481–489. [Google Scholar] [CrossRef]
- Tunaley, J.K.; Buller, E.H.; Wu, K.; Rey, M.T. The simulation of the SAR image of a ship wake. IEEE Trans. Geosci. Remote Sens. 1991, 29, 149–156. [Google Scholar] [CrossRef]
- Wang, J.-K.; Zhang, M.; Chen, J.-L.; Cai, Z. Application of facet scattering model in SAR imaging of sea surface waves with Kelvin wake. Prog. Electromagn. Res. B 2016, 67, 107–120. [Google Scholar] [CrossRef]
- Thomson, W. On ship waves. In Proceedings of the Institution of Mechanical Engineers; Institution of Mechanical Engineers: London, UK, 1887; Volume 38, pp. 409–434. [Google Scholar]
- Shemer, L.; Kagan, L.; Zilman, G. Simulation of ship wakes image by an along-track interferometric SAR. Int. J. Remote Sens. 1996, 17, 3577–3597. [Google Scholar] [CrossRef]
- Zilman, G.; Zapolski, A.; Marom, M. On detectability of a ship’s Kelvin wake in simulated SAR images of rough sea surface. IEEE Trans. Geosci. Remote Sens. 2014, 53, 609–619. [Google Scholar] [CrossRef]
- Jia, Y.; Liu, S.; Liu, Y.; Zhai, L.; Gong, Y.; Zhang, X. Echo-Level SAR Imaging Simulation of Wakes Excited by a Submerged Body. Sensors 2024, 24, 1094. [Google Scholar] [CrossRef] [PubMed]
- Hennings, I.; Romeiser, R.; Alpers, W.; Viola, A. Radar imaging of Kelvin arms of ship wakes. Int. J. Remote Sens. 1999, 20, 2519–2543. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, M.; Zhao, Y.-W.; Geng, X.-P. A bistatic SAR image intensity model for the composite ship–ocean scene. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4250–4258. [Google Scholar] [CrossRef]
- Bao, M.; Bruning, C.; Alpers, W. Simulation of ocean waves imaging by an along-track interferometric synthetic aperture radar. IEEE Trans. Geosci. Remote Sens. 1997, 35, 618–631. [Google Scholar]
- Wilson, M.B. A Michell Oseen-Flow Theory for Thin Ships. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 1971. [Google Scholar]
- Hasselmann, K.; Barnett, T.P.; Bouws, E.; Carlson, H.; Cartwright, D.E.; Enke, K.; Ewing, J.; Gienapp, A.; Hasselmann, D.; Kruseman, P. Measurements of wind-wave growth and swell decay during the Joint North Sea Wave Project (JONSWAP). Ergaenzungsheft Zur Dtsch. Hydrogr. Z. Reihe A 1973, 12, 1–95. [Google Scholar]
- Gao, Z.; Jia, Y.; Liu, S.; Zhang, X. A 2-D frequency-domain imaging algorithm for ground-based SFCW-ArcSAR. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5225514. [Google Scholar] [CrossRef]
- Eshbaugh, J.V.; Frasier, S.J. Measurement of sea surface displacement with interferometric radar. J. Atmos. Ocean. Technol. 2002, 19, 1087–1095. [Google Scholar] [CrossRef]
- Zeng, Y.; Song, C.; Xu, Z. Wave height estimation based on the phase time series of millimeter-wave radar. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1506905. [Google Scholar] [CrossRef]
- Sun, J.; Wang, Y.; Zhang, J.; Liang, Y.; Zhang, G.; Wan, A.; Zhang, S.; Ye, Z.; Zhou, Y.; Jing, Q. 2-D Phase Unwrapping in DAS Based on Transport-of-Intensity-Equation: Principle, Algorithm and Field Test. J. Light. Technol. 2024, 42, 6490–6500. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, H.; Ma, C.; Fan, C.; Zhao, H. Comparative study of phase unwrapping algorithms based on solving the Poisson equation. Meas. Sci. Technol. 2020, 31, 065004. [Google Scholar] [CrossRef]
- Wang, K.; Di, J.; Li, Y.; Ren, Z.; Kemao, Q.; Zhao, J. Transport of intensity equation from a single intensity image via deep learning. Opt. Lasers Eng. 2020, 134, 106233. [Google Scholar] [CrossRef]
- Zuo, C.; Huang, L.; Zhang, M.; Chen, Q.; Asundi, A. Temporal phase unwrapping algorithms for fringe projection profilometry: A comparative review. Opt. Lasers Eng. 2016, 85, 84–103. [Google Scholar] [CrossRef]
- Rizaev, I.G.; Karakuş, O.; Hogan, S.J.; Achim, A. Modeling and SAR imaging of the sea surface: A review of the state-of-the-art with simulations. ISPRS J. Photogramm. Remote Sens. 2022, 187, 120–140. [Google Scholar] [CrossRef]
- Rabaud, M.; Moisy, F. Ship wakes: Kelvin or Mach angle? Phys. Rev. Lett. 2013, 110, 214503. [Google Scholar] [CrossRef] [PubMed]
- Rizaev, I.; Karakuş, O.; Hogan, S.J.; Achim, A. The effect of sea state on ship wake detectability in simulated SAR imagery. In Proceedings of the 2020 IEEE International Conference on Image Processing (ICIP), Abu Dhabi, United Arab Emirates, 25–28 October 2020; pp. 3478–3482. [Google Scholar]
- Mitsuyasu, H.; Tasai, F.; Suhara, T.; Mizuno, S.; Ohkusu, M.; Honda, T.; Rikiishi, K. Observation of the power spectrum of ocean waves using a cloverleaf buoy. J. Phys. Oceanogr. 1980, 10, 286–296. [Google Scholar] [CrossRef]
- Holthuijsen, L.H. Waves in Oceanic and Coastal Waters; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Panico, A.; Graziano, M.D.; Renga, A. SAR-based vessel velocity estimation from partially imaged Kelvin pattern. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2067–2071. [Google Scholar] [CrossRef]
- Felguera-Martín, D.; González-Partida, J.-T.; Almorox-González, P.; Burgos-García, M.; Dorta-Naranjo, B.-P. Interferometric inverse synthetic aperture radar experiment using an interferometric linear frequency modulated continuous wave millimetre-wave radar. IET Radar Sonar Navig. 2011, 5, 39–47. [Google Scholar] [CrossRef]
- Rodriguez, E.; Martin, J. Theory and design of interferometric synthetic aperture radars. In Proceedings of the IEE Proceedings F (Radar and Signal Processing); The Institution of Engineering and Technology: Hong Kong, China, 1992; pp. 147–159. [Google Scholar]
- Schofield, M.A.; Zhu, Y. Fast phase unwrapping algorithm for interferometric applications. Opt. Lett. 2003, 28, 1194–1196. [Google Scholar] [CrossRef] [PubMed]
- Hÿtch, M.; Snoeck, E.; Kilaas, R. Quantitative measurement of displacement and strain fields from HREM micrographs. Ultramicroscopy 1998, 74, 131–146. [Google Scholar] [CrossRef]
- Zhai, L.; Zhang, X. InSAR Phase Unwrapping Algorithm Based on 4-FFT and Multi Grid Optimization. J. Microw. 2024, 40, 334–337. [Google Scholar]
- Duan, Y. Research on High-Accuracy InSAR Phase Unwrapping Technique via Iteration. Master’s Thesis, Electronic Science and Technology University, Chengdu, China, 2017. [Google Scholar]
- Zhang, Z. Phase Unwrapping Algorithm in Digital Holographic Microscopy. Master’s Thesis, Hebei University of Engineering, Handan, China, 2012. [Google Scholar]
- Fan, X.; Zhang, X.; Duan, Y.; Wei, S. An Multi-baseline High-Accuracy 4-FFT Phase Unwrapping Method via Iterative. In Proceedings of the 4th China High Resolution Earth Observation Conference, Wuhan, China, 17–18 September 2017; p. 17. [Google Scholar]
- Deng, X. Research on the Algorithm of Phase Unwrapping for Interferometric Synthetic Aperture Radar. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2013. [Google Scholar]
- Kurita, T. Principal component analysis (PCA). In Computer Vision: A Reference Guide; Springer: Cham, Switzerland, 2021; pp. 1013–1016. [Google Scholar]













| Parameters | Values | Parameters | Values |
|---|---|---|---|
| B | 50 m | D | 3.5 m |
| L | 6.5 m | Vs | 11 m/s (Fr = 0.5) |
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| S | 7 | θw | 45° |
| F | 80 km | t | 0 |
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| H | 3000 m | B | 2.5 m |
| f | 15 GHz | c | 108 m/s |
| Cor | RMSE (rad) | SNR (dB) | PSNR (dB) | Re-Cor | Re-RMSE (rad) | Re-SNR (dB) | Re-PSNR (dB) | ||
|---|---|---|---|---|---|---|---|---|---|
| U10 = 3 m/s | 4-FFT | 0.9976 | 0.0664 | 22.4673 | 71.6810 | 0.9447 | 0.2794 | 9.6002 | 59.2049 |
| LoG | 0.9975 | 0.0650 | 22.6559 | 71.8696 | 0.9450 | 0.2784 | 9.6339 | 59.2386 | |
| ALoG | 0.9977 | 0.0624 | 23.0089 | 72.2227 | 0.9476 | 0.2718 | 9.8407 | 59.4454 | |
| U10 = 8 m/s | 4-FFT | 0.9836 | 0.2211 | 14.4876 | 61.2401 | 0.8895 | 0.4707 | 6.6063 | 54.6760 |
| LoG | 0.9835 | 0.2211 | 14.4853 | 61.2378 | 0.8893 | 0.4713 | 6.5958 | 54.6655 | |
| ALoG | 0.9838 | 0.2195 | 14.5496 | 61.3021 | 0.8953 | 0.4584 | 6.8359 | 54.9057 | |
| U10 = 13 m/s | 4-FFT | 0.9288 | 0.5900 | 8.5571 | 52.7132 | 0.8007 | 0.7582 | 4.0002 | 50.5356 |
| LoG | 0.9286 | 0.5914 | 8.5376 | 52.6937 | 0.8013 | 0.7572 | 4.0117 | 50.5471 | |
| ALoG | 0.9296 | 0.5872 | 8.5990 | 52.7550 | 0.8118 | 0.7364 | 4.2533 | 50.7887 |
| Cor | RMSE (rad) | SNR (dB) | PSNR (dB) | Re-Cor | Re-RMSE (rad) | Re-SNR (dB) | Re-PSNR (dB) | ||
|---|---|---|---|---|---|---|---|---|---|
| U10 = 3 m/s | ALoG | 0.9977 | 0.0624 | 23.0089 | 72.2227 | 0.9476 | 0.2718 | 9.8407 | 59.4454 |
| Goldstein | 0.9988 | 0.0427 | 26.3067 | 75.5204 | 0.9973 | 0.0622 | 22.6547 | 72.2594 | |
| ALoGI | 0.9999 | 0.0015 | 55.2506 | 104.4643 | 0.9988 | 0.0414 | 26.1800 | 75.7846 | |
| U10 = 8 m/s | ALoG | 0.9838 | 0.2195 | 14.5496 | 61.3021 | 0.8953 | 0.4584 | 6.8359 | 54.9057 |
| Goldstein | 0.9756 | 0.2573 | 13.1689 | 59.9214 | 0.9943 | 0.1076 | 19.4268 | 67.4966 | |
| ALoGI | 0.9981 | 0.0719 | 24.2408 | 70.9933 | 0.9928 | 0.1210 | 18.4026 | 66.4723 | |
| U10 = 13 m/s | ALoG | 0.9296 | 0.5872 | 8.5990 | 52.7550 | 0.8118 | 0.7364 | 4.2533 | 50.7887 |
| Goldstein | 0.9181 | 0.6274 | 8.0232 | 52.1793 | 0.9894 | 0.1745 | 16.7601 | 63.2955 | |
| ALoGI | 0.9725 | 0.3674 | 12.6721 | 56.8281 | 0.9495 | 0.3819 | 9.9565 | 56.4919 |
| 4-FFT | LoG | ALoG | Goldstein | ALoGI | |
|---|---|---|---|---|---|
| U10 = 3 m/s | 0.8176 | 0.8326 | 0.8829 | 2.2274 | 4.1048 |
| U10 = 8 m/s | −0.5677 | −0.5705 | −0.5192 | 0.6578 | 1.6260 |
| U10 = 13 m/s | −2.6528 | −2.6543 | −2.5739 | −0.9892 | −0.6215 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhai, L.; Gong, Y.; Zhang, X. An ALoGI PU Algorithm for Simulating Kelvin Wake on Sea Surface Based on Airborne Ku SAR. Sensors 2025, 25, 4508. https://doi.org/10.3390/s25144508
Zhai L, Gong Y, Zhang X. An ALoGI PU Algorithm for Simulating Kelvin Wake on Sea Surface Based on Airborne Ku SAR. Sensors. 2025; 25(14):4508. https://doi.org/10.3390/s25144508
Chicago/Turabian StyleZhai, Limin, Yifan Gong, and Xiangkun Zhang. 2025. "An ALoGI PU Algorithm for Simulating Kelvin Wake on Sea Surface Based on Airborne Ku SAR" Sensors 25, no. 14: 4508. https://doi.org/10.3390/s25144508
APA StyleZhai, L., Gong, Y., & Zhang, X. (2025). An ALoGI PU Algorithm for Simulating Kelvin Wake on Sea Surface Based on Airborne Ku SAR. Sensors, 25(14), 4508. https://doi.org/10.3390/s25144508






