Alpine Meadow Fractional Vegetation Cover Estimation Using UAV-Aided Sentinel-2 Imagery
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
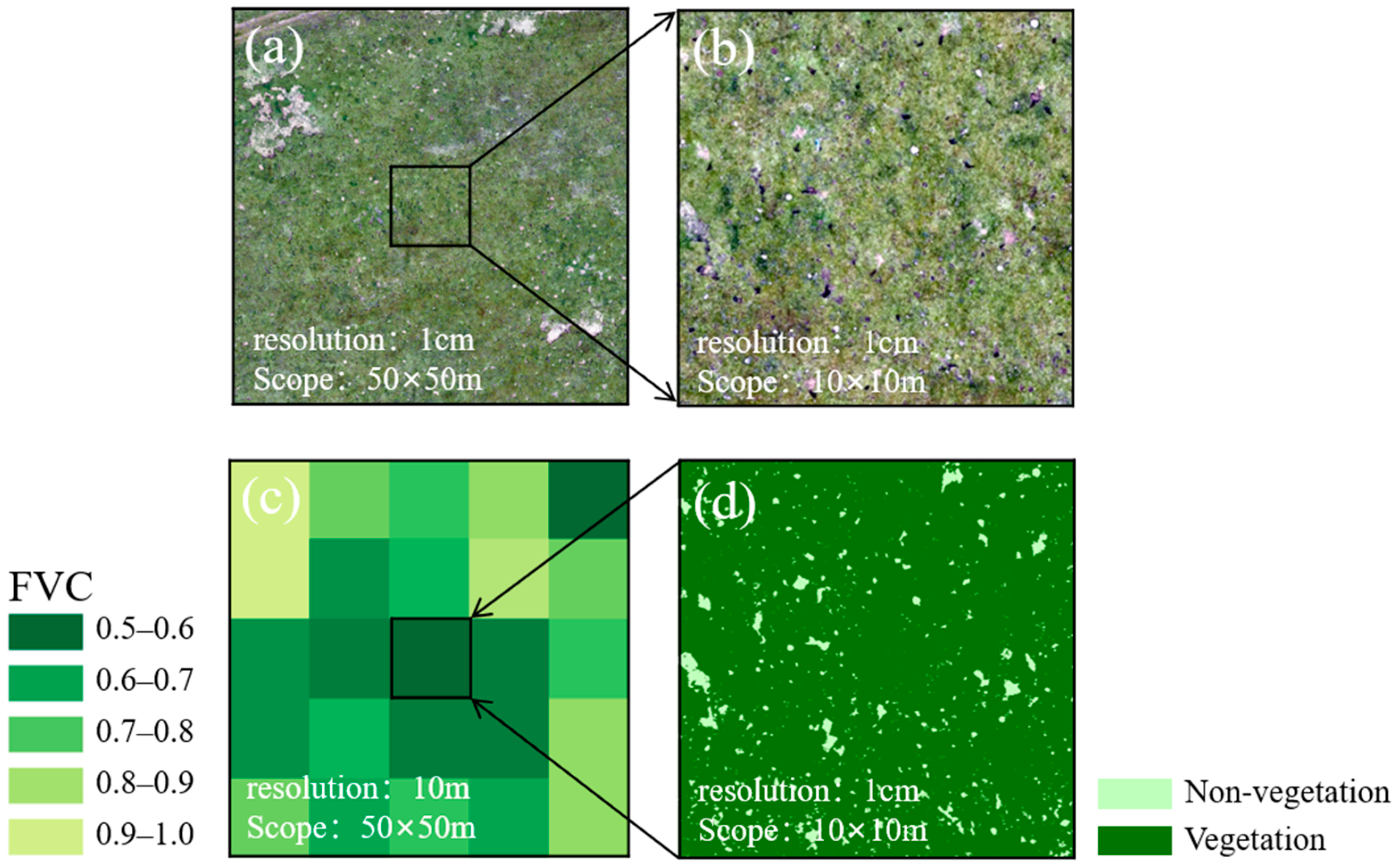
2.2. UAV Data Collection and Processing
2.3. Sentinel-2 Data Collection and Processing
2.4. The FVC Estimation by Integrating Sentinel-2 and UAV Data
2.4.1. Pixel Dichotomy Model-Based FVC Estimation
2.4.2. Machine Learning-Based FVC Estimation
2.5. Shapley Additive Explanations (SHAP) Method
2.6. Evaluation Metrics
3. Results
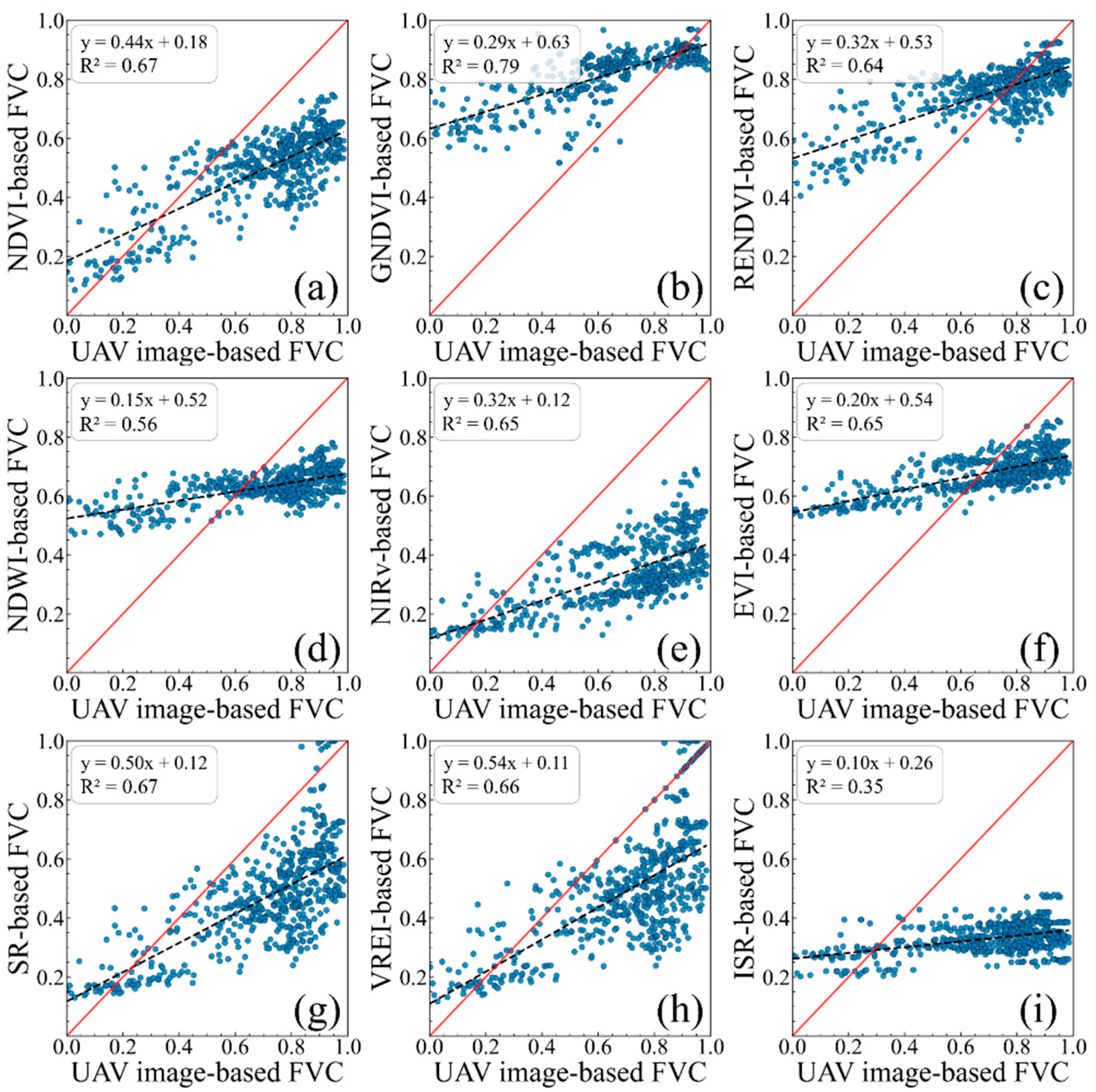
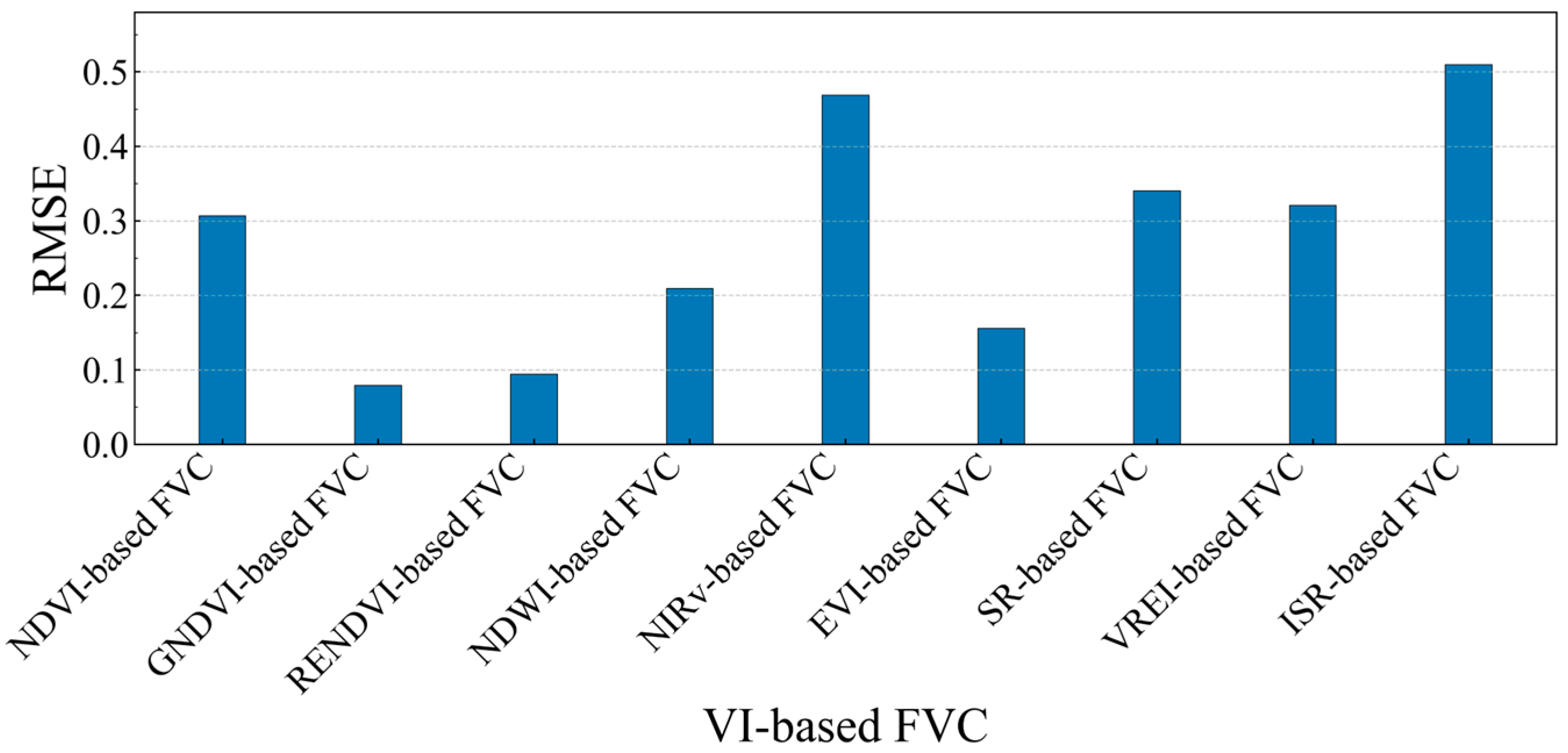
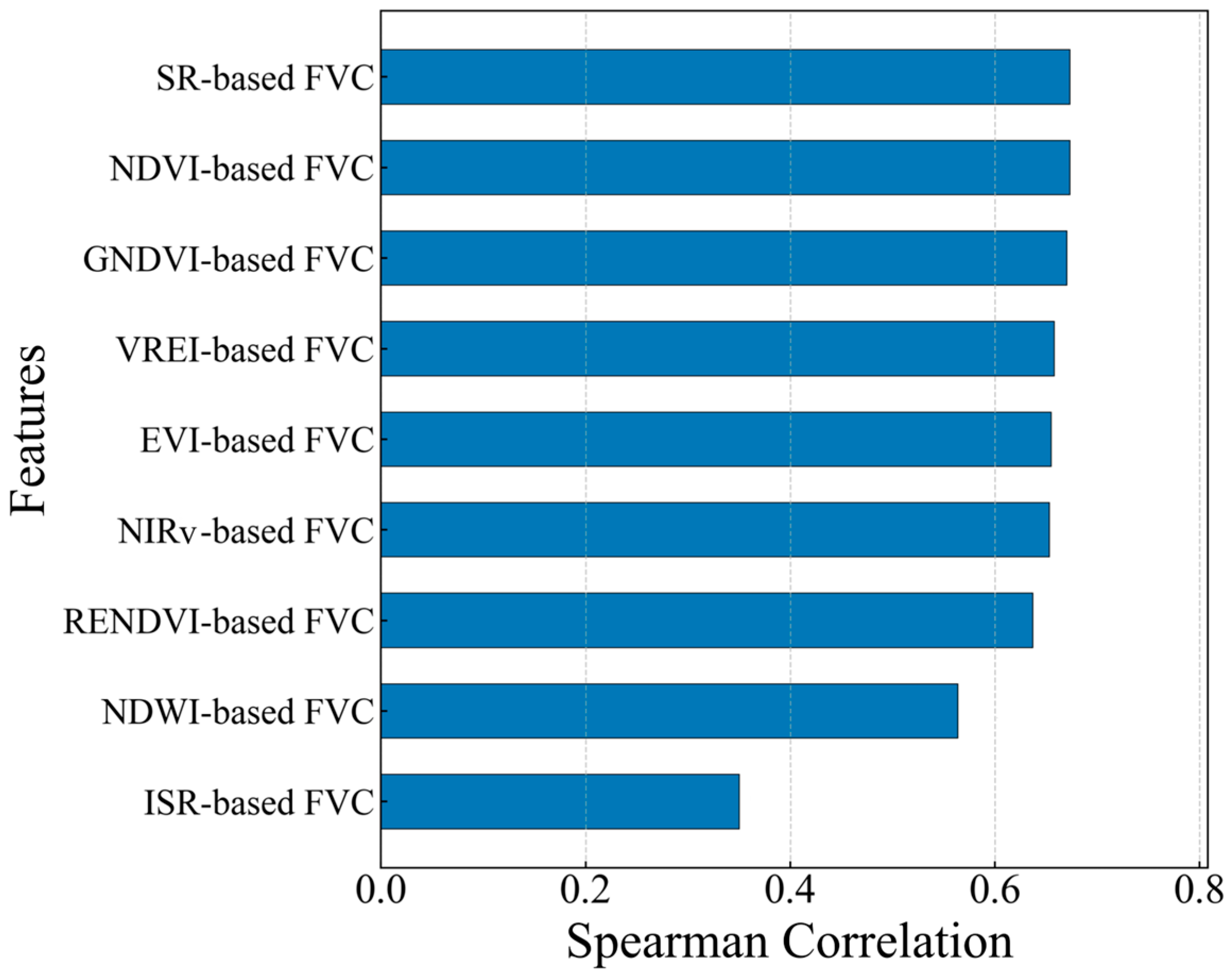
3.1. Pixel Dichotomy Model-Based FVC Estimation Analysis
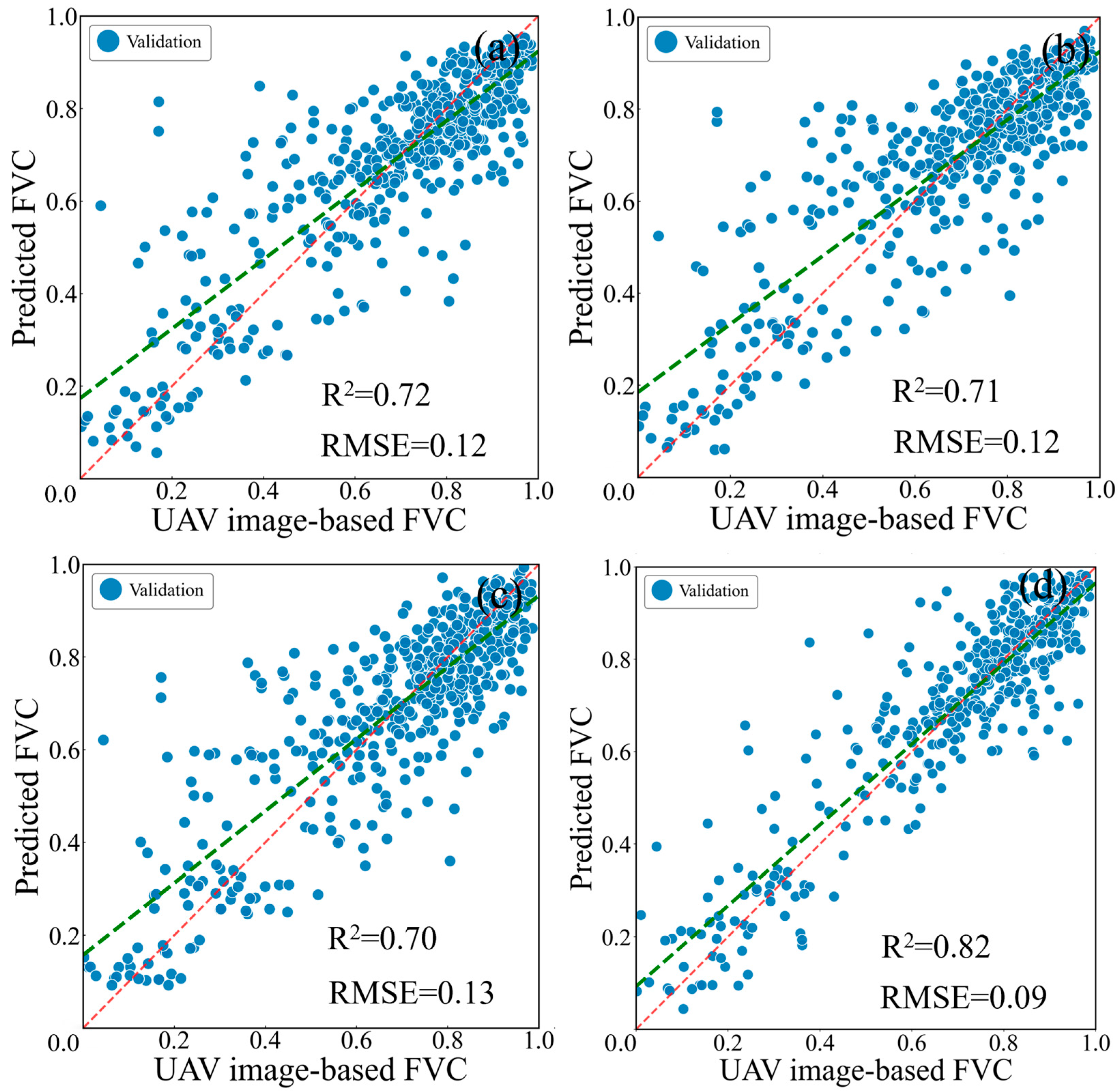
3.2. Machine Learning Model-Based FVC Estimation Analysis
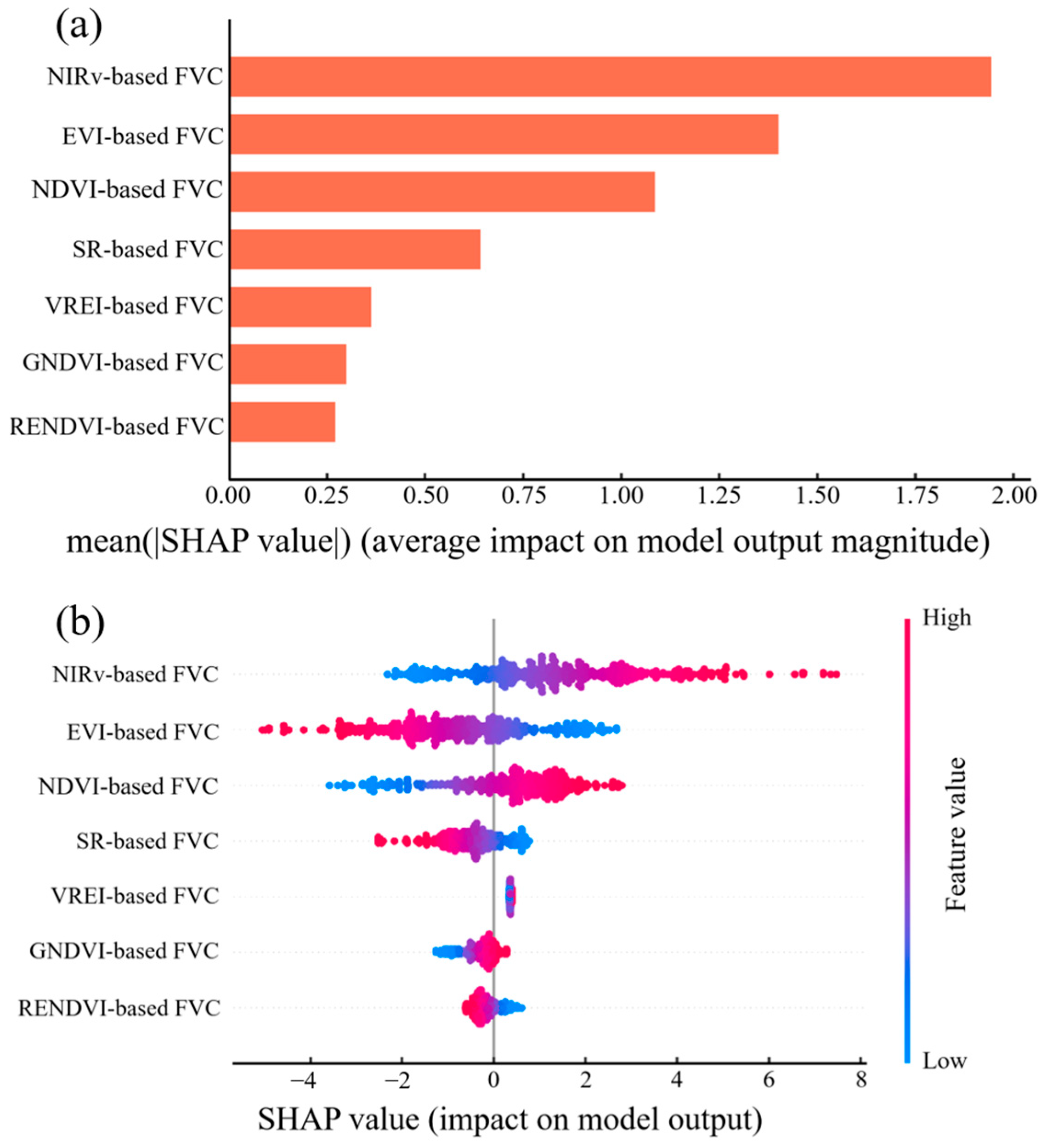
3.2.1. Feature Selection
3.2.2. Model Parameter Optimization
3.2.3. Comparison of FVC Estimation Accuracy
4. Discussion
4.1. Pixel Dichotomy-Based FVC Estimation Using Different Vegetation Indices
4.2. Feature Contribution Analysis of FVC Estimation Based on Machine Learning
4.3. Advantages and Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, H.; Gou, X.; Xue, B.; Ma, W.; Kuang, W.; Tu, Z.; Gao, L.; Yin, D.; Zhang, J. Research on the change of alpine ecosystem service value and its sustainable development path. Ecol. Indic. 2023, 146, 109893. [Google Scholar] [CrossRef]
- Dai, L.; Fu, R.; Guo, X.; Du, Y.; Zhang, F.; Cao, G. Variations in and factors controlling soil hydrological properties across different slope aspects in alpine meadows. J. Hydrol. 2023, 616, 128756. [Google Scholar] [CrossRef]
- Wang, S.; Duan, J.; Xu, G.; Wang, Y.; Zhang, Z.; Rui, Y.; Luo, C.; Xu, B.; Zhu, X.; Chang, X. Effects of warming and grazing on soil N availability, species composition, and ANPP in an alpine meadow. Ecology 2012, 93, 2365–2376. [Google Scholar] [CrossRef] [PubMed]
- Teng, Y.; Wang, C.; Wei, X.; Su, M.; Zhan, J.; Wen, L. Characteristics of Vegetation Change and Its Climatic and Anthropogenic Driven Pattern in the Qilian Mountains. Forests 2023, 14, 1951. [Google Scholar] [CrossRef]
- Wu, R.; Hu, G.; Ganjurjav, H.; Gao, Q. Sensitivity of grassland coverage to climate across environmental gradients on the Qinghai-Tibet Plateau. Remote Sens. 2023, 15, 3187. [Google Scholar] [CrossRef]
- Li, F.; Chen, W.; Zeng, Y.; Zhao, Q.; Wu, B. Improving estimates of grassland fractional vegetation cover based on a pixel dichotomy model: A case study in Inner Mongolia, China. Remote Sens. 2014, 6, 4705–4722. [Google Scholar] [CrossRef]
- Zhong, G.; Chen, J.; Huang, R.; Yi, S.; Qin, Y.; You, H.; Han, X.; Zhou, G. High spatial resolution fractional vegetation coverage inversion based on UAV and Sentinel-2 data: A case study of alpine grassland. Remote Sens. 2023, 15, 4266. [Google Scholar] [CrossRef]
- Jiang, Z.; Huete, A.R.; Chen, J.; Chen, Y.; Li, J.; Yan, G.; Zhang, X. Analysis of NDVI and scaled difference vegetation index retrievals of vegetation fraction. Remote Sens. Environ. 2006, 101, 366–378. [Google Scholar] [CrossRef]
- Jiapaer, G.; Chen, X.; Bao, A. A comparison of methods for estimating fractional vegetation cover in arid regions. Agric. Forest Meteorol. 2011, 151, 1698–1710. [Google Scholar] [CrossRef]
- Yan, K.; Gao, S.; Chi, H.; Qi, J.; Song, W.; Tong, Y.; Mu, X.; Yan, G. Evaluation of the Vegetation-Index-Based Dimidiate Pixel Model for Fractional Vegetation Cover Estimation. IEEE Trans. Geosci. Remote Sens. 2021, 60, 4400514. [Google Scholar] [CrossRef]
- Li, X.; Chen, J.; Chen, Z.; Lan, Y.; Ling, M.; Huang, Q.; Li, H.; Han, X.; Yi, S. Explainable machine learning-based fractional vegetation cover inversion and performance optimization—A case study of an alpine grassland on the Qinghai-Tibet Plateau. Ecol. Inform. 2024, 82, 102768. [Google Scholar] [CrossRef]
- Xu, Z.; Sun, B.; Zhang, W.; Gao, Z.; Yue, W.; Wang, H.; Wu, Z.; Teng, S. Is Spectral Unmixing Model or Nonlinear Statistical Model More Suitable for Shrub Coverage Estimation in Shrub-Encroached Grasslands Based on Earth Observation Data? A Case Study in Xilingol Grassland, China. Remote Sens. 2023, 15, 5488. [Google Scholar] [CrossRef]
- Derraz, R.; Muharam, F.M.; Nurulhuda, K.; Jaafar, N.A.; Yap, N.K. Ensemble and single algorithm models to handle multicollinearity of UAV vegetation indices for predicting rice biomass. Comput. Electron. Agric. 2023, 205, 107621. [Google Scholar] [CrossRef]
- Li, L.; Mu, X.; Jiang, H.; Chianucci, F.; Hu, R.; Song, W.; Qi, J.; Liu, S.; Zhou, J.; Chen, L.; et al. Review of ground and aerial methods for vegetation cover fraction (fCover) and related quantities estimation: Definitions, advances, challenges, and future perspectives. ISPRS J. Photogramm. 2023, 199, 133–156. [Google Scholar] [CrossRef]
- Weiss, M.; Jacob, F.; Duveiller, G. Remote sensing for agricultural applications: A meta-review. Remote Sens. Environ. 2020, 236, 111402. [Google Scholar] [CrossRef]
- Melville, B.; Fisher, A.; Lucieer, A. Ultra-high spatial resolution fractional vegetation cover from unmanned aerial multispectral imagery. Int. J. Appl. Earth Obs. 2019, 78, 14–24. [Google Scholar] [CrossRef]
- Yan, G.; Li, L.; Coy, A.; Mu, X.; Chen, S.; Xie, D.; Zhang, W.; Shen, Q.; Zhou, H. Improving the estimation of fractional vegetation cover from UAV RGB imagery by colour unmixing. ISPRS J. Photogramm. Remote Sens. 2019, 158, 23–34. [Google Scholar] [CrossRef]
- Gao, L.; Wang, X.; Johnson, B.A.; Tian, Q.; Wang, Y.; Verrelst, J.; Mu, X.; Gu, X. Remote sensing algorithms for estimation of fractional vegetation cover using pure vegetation index values: A review. ISPRS J. Photogramm. Remote Sens. 2020, 159, 364–377. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Zhang, J. Scaling effects on landscape metrics in alpine meadow on the central Qinghai-Tibetan Plateau. Glob. Ecol. Conserv. 2021, 29, e01742. [Google Scholar] [CrossRef]
- Riihimäki, H.; Luoto, M.; Heiskanen, J. Estimating fractional cover of tundra vegetation at multiple scales using unmanned aerial systems and optical satellite data. Remote Sens. Environ. 2019, 224, 119–132. [Google Scholar] [CrossRef]
- Chen, J.; Yi, S.; Qin, Y.; Wang, X. Improving estimates of fractional vegetation cover based on UAV in alpine grassland on the Qinghai–Tibetan Plateau. Int. J. Remote Sens. 2016, 37, 1922–1936. [Google Scholar] [CrossRef]
- Huang, R.; Chen, J.; Feng, Z.; Yang, Y.; You, H.; Han, X. Fitness for Purpose of Several Fractional Vegetation Cover Products on Monitoring Vegetation Cover Dynamic Change—A Case Study of an Alpine Grassland Ecosystem. Remote Sens. 2023, 15, 1312. [Google Scholar] [CrossRef]
- Gitelson, A.; Merzlyak, M.N. Spectral reflectance changes associated with autumn senescence of Aesculus hippocastanum L. and Acer platanoides L. leaves. Spectral features and relation to chlorophyll estimation. J. Plant Physiol. 1994, 143, 286–292. [Google Scholar] [CrossRef]
- Rouse, J.W.; Hass, R.H.; Shell, J.A.; Deering, D. Monitoring vegetation systems in the Great Plains with ERTS-1. In Proceedings of the Third Earth Resources Technology Satellite Symposium, Washington DC, USA, 10–14 December 1973; pp. 309–317. Available online: https://ntrs.nasa.gov/citations/19740022614 (accessed on 7 August 2013).
- Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a green channel in remote sensing of global vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Fernandes, R.; Butson, C.; Leblanc, S.; Latifovic, R. Landsat-5 TM and Landsat-7 ETM+ based accuracy assessment of leaf area index products for Canada derived from SPOT-4 VEGETATION data. Can. J. Remote Sens. 2003, 29, 241–258. [Google Scholar] [CrossRef]
- Tang, L.; Zhang, S.; Zhang, J.; Liu, Y.; Bai, Y. Estimating evapotranspiration based on the satellite-retrieved near-infrared reflectance of vegetation (NIRv) over croplands. Gisci. Remote Sens. 2021, 58, 889–913. [Google Scholar] [CrossRef]
- Birth, G.S.; McVey, G.R. Measuring the color of growing turf with a reflectance spectrophotometer. Agron. J. 1968, 60, 640–643. [Google Scholar] [CrossRef]
- Vogelmann, J.; Rock, B.; Moss, D. Red edge spectral measurements from sugar maple leaves. Int. J. Remote Sens. 1993, 14, 1563–1575. [Google Scholar] [CrossRef]
- Gao, B. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Gutman, G.; Ignatov, A. The derivation of the green vegetation fraction from NOAA/AVHRR data for use in numerical weather prediction models. Int. J. Remote Sens. 1998, 19, 1533–1543. [Google Scholar] [CrossRef]
- Li, X.; Zulkar, H.; Wang, D.; Zhao, T.; Xu, W. Changes in Vegetation Coverage and Migration Characteristics of Center of Gravity in the Arid Desert Region of Northwest China in 30 Recent Years. Land 2022, 11, 1688. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chen, X.; Sun, Y.; Qin, X.; Cai, J.; Cai, M.; Hou, X.; Yang, K.; Zhang, H. Assessing the Potential of UAV for Large-Scale Fractional Vegetation Cover Mapping with Satellite Data and Machine Learning. Remote Sens. 2024, 16, 3587. [Google Scholar] [CrossRef]
- Wen, X.; Xie, Y.; Wu, L.; Jiang, L. Quantifying and comparing the effects of key risk factors on various types of roadway segment crashes with LightGBM and SHAP. Accid. Anal. Prev. 2021, 159, 106261. [Google Scholar] [CrossRef] [PubMed]
- Shiferaw, H.; Bewket, W.; Eckert, S. Performances of machine learning algorithms for mapping fractional cover of an invasive plant species in a dryland ecosystem. Ecol. Evol. 2019, 9, 2562–2574. [Google Scholar] [CrossRef] [PubMed]
- Quast, R.; Albergel, C.; Calvet, J.; Wagner, W. A Generic First-Order Radiative Transfer Modelling Approach for the Inversion of Soil and Vegetation Parameters from Scatterometer Observations. Remote Sens. 2019, 11, 285. [Google Scholar] [CrossRef]
- Wang, X.; Jin, Y.; Schmitt, S.; Olhofer, M. Recent Advances in Bayesian Optimization. Acm. Comput. Surv. 2023, 55, 1–36. [Google Scholar] [CrossRef]
- Abdollahi, A.; Pradhan, B. Explainable artificial intelligence (XAI) for interpreting the contributing factors feed into the wildfire susceptibility prediction model. Sci. Total Environ. 2023, 879, 163004. [Google Scholar] [CrossRef] [PubMed]
- David, R.M.; Rosser, N.J.; Donoghue, D.N.M. Improving above ground biomass estimates of Southern Africa dryland forests by combining Sentinel-1 SAR and Sentinel-2 multispectral imagery. Remote Sens. Environ. 2022, 282, 113232. [Google Scholar] [CrossRef]
- Otsu, K.; Pla, M.; Duane, A.; Cardil, A.; Brotons, L. Estimating the threshold of detection on tree crown defoliation using vegetation indices from UAS multispectral imagery. Drones 2019, 3, 80. [Google Scholar] [CrossRef]
- Wang, F.; Huang, J.; Tang, Y.; Wang, X. New vegetation index and its application in estimating leaf area index of rice. Rice Sci. 2007, 14, 195–203. [Google Scholar] [CrossRef]
- Zeng, Y.; Hao, D.; Badgley, G.; Damm, A.; Rascher, U.; Ryu, Y.; Johnson, J.; Krieger, V.; Wu, S.; Qiu, H.; et al. Estimating near-infrared reflectance of vegetation from hyperspectral data. Remote Sens. Environ. 2021, 267, 112723. [Google Scholar] [CrossRef]
- Zhao, J.; Li, J.; Liu, Q.; Zhang, Z.; Dong, Y. Comparative Study of Fractional Vegetation Cover Estimation Methods Based on Fine Spatial Resolution Images for Three Vegetation Types. IEEE Geosci. Remote Sens. Lett. 2022, 19, 2508005. [Google Scholar] [CrossRef]
- Du, M.; Li, M.; Noguchi, N.; Ji, J.; Ye, M. Retrieval of fractional vegetation cover from remote sensing image of unmanned aerial vehicle based on mixed pixel decomposition method. Drones 2023, 7, 43. [Google Scholar] [CrossRef]

| Vegetation Indices | Calculation Formula | Reference |
|---|---|---|
| RENDVI | Gitelson and Merzlyak (1994) [23] | |
| NDVI | Rouse et al. (1973) [24] | |
| GNDVI | Gitelson et al. (1996) [25] | |
| EVI | Huete et al. (2002) [26] | |
| ISR | Fernandes et al. (2003) [27] | |
| NIRv | Tang L et al. (2021) [28] | |
| SR | Birth and McVey (1968) [29] | |
| VREI | Vogelmann et al. (1993) [30] | |
| NDWI | Gao (1996) [31] |
| Model | Parameters | Range | Optimal Value |
|---|---|---|---|
| RF | n_estimators | [50, 1000] | 959 |
| max_depth | [5, 30] | 22 | |
| min_samples_split | [2, 20] | 6 | |
| XGBoost | learning_rate | [0.01, 0.3] | 0.0108 |
| n_estimators | [50, 1000] | 717 | |
| max_depth | [3, 12] | 5 | |
| LightGBM | learning_rate | [0.01, 0.3] | 0.0204 |
| n_estimators | [50, 1000] | 612 | |
| max_depth | [3, 12] | 12 | |
| DNN | learning_rate | [0.0001, 0.01] | 0.0076 |
| layerDim | [2, 6] | 6 | |
| nodeDim | [32, 256] | 256 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, K.; Shao, Y.; Yao, N.; Yu, H.; Ma, S.; Mao, X.; Wang, L.; Wang, J. Alpine Meadow Fractional Vegetation Cover Estimation Using UAV-Aided Sentinel-2 Imagery. Sensors 2025, 25, 4506. https://doi.org/10.3390/s25144506
Du K, Shao Y, Yao N, Yu H, Ma S, Mao X, Wang L, Wang J. Alpine Meadow Fractional Vegetation Cover Estimation Using UAV-Aided Sentinel-2 Imagery. Sensors. 2025; 25(14):4506. https://doi.org/10.3390/s25144506
Chicago/Turabian StyleDu, Kai, Yi Shao, Naixin Yao, Hongyan Yu, Shaozhong Ma, Xufeng Mao, Litao Wang, and Jianjun Wang. 2025. "Alpine Meadow Fractional Vegetation Cover Estimation Using UAV-Aided Sentinel-2 Imagery" Sensors 25, no. 14: 4506. https://doi.org/10.3390/s25144506
APA StyleDu, K., Shao, Y., Yao, N., Yu, H., Ma, S., Mao, X., Wang, L., & Wang, J. (2025). Alpine Meadow Fractional Vegetation Cover Estimation Using UAV-Aided Sentinel-2 Imagery. Sensors, 25(14), 4506. https://doi.org/10.3390/s25144506







