Real-Time Wing Deformation Monitoring via Distributed Fiber Bragg Grating and Adaptive Federated Filtering
Abstract
1. Introduction
2. Materials and Methods
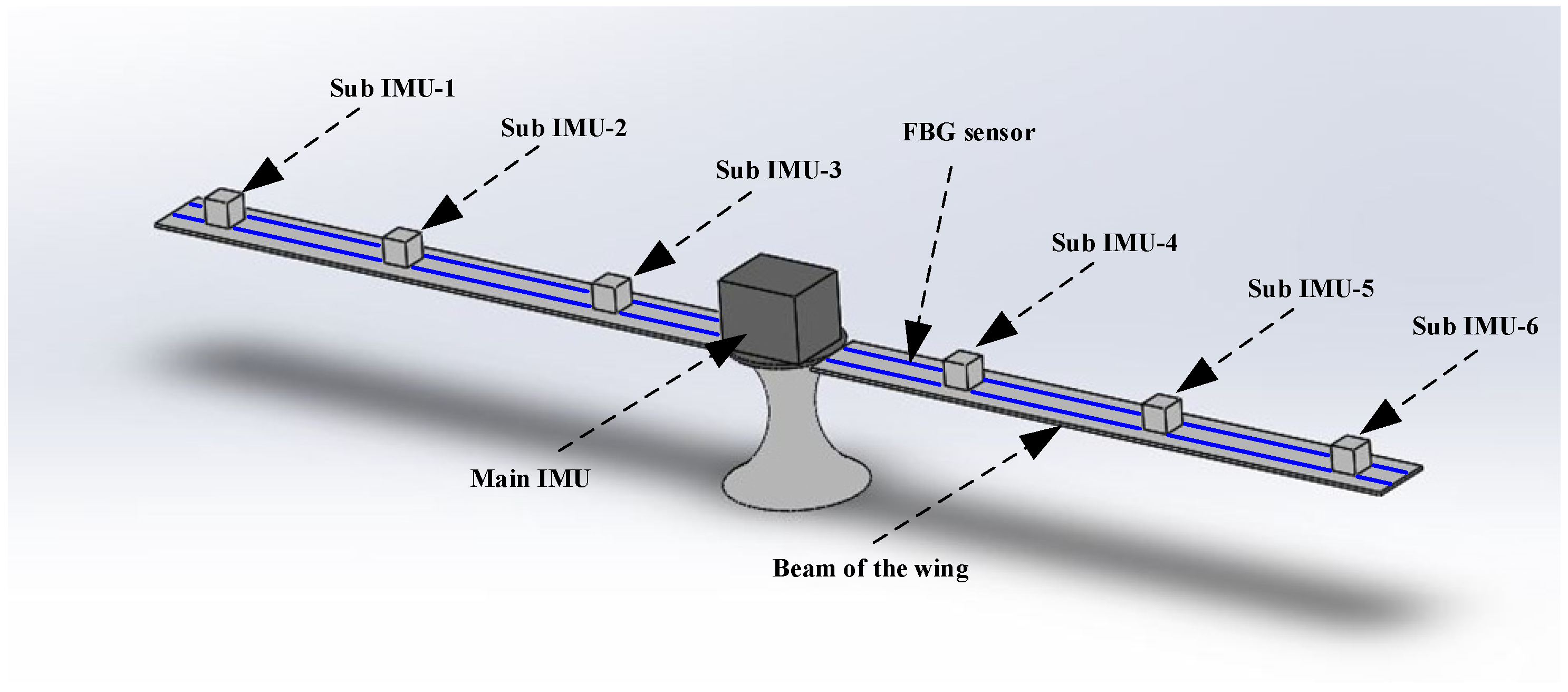
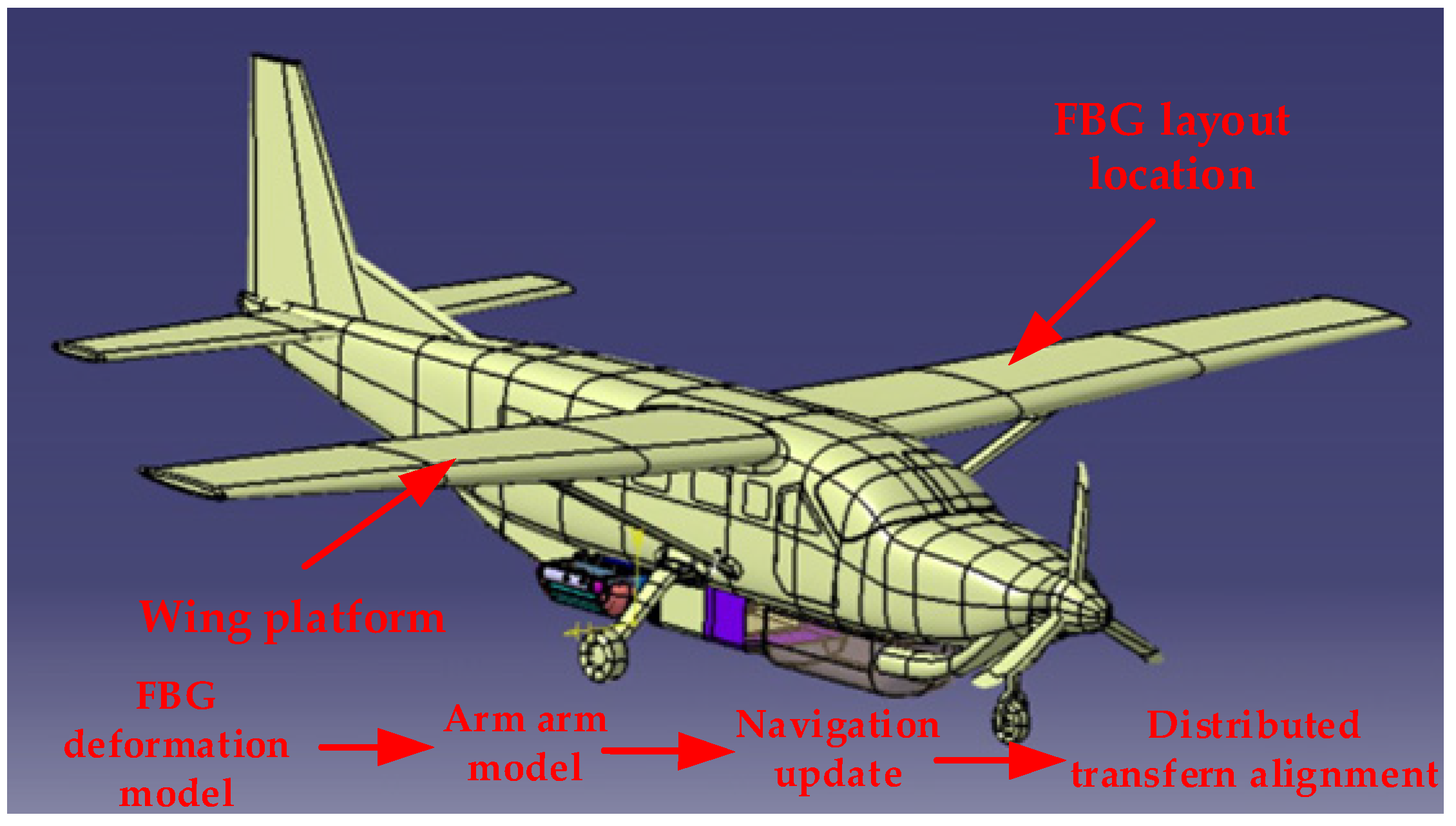
2.1. FBG Layout Packaging Design and Implementation
2.1.1. FBG Layout Design
2.1.2. FBG Packaging Design
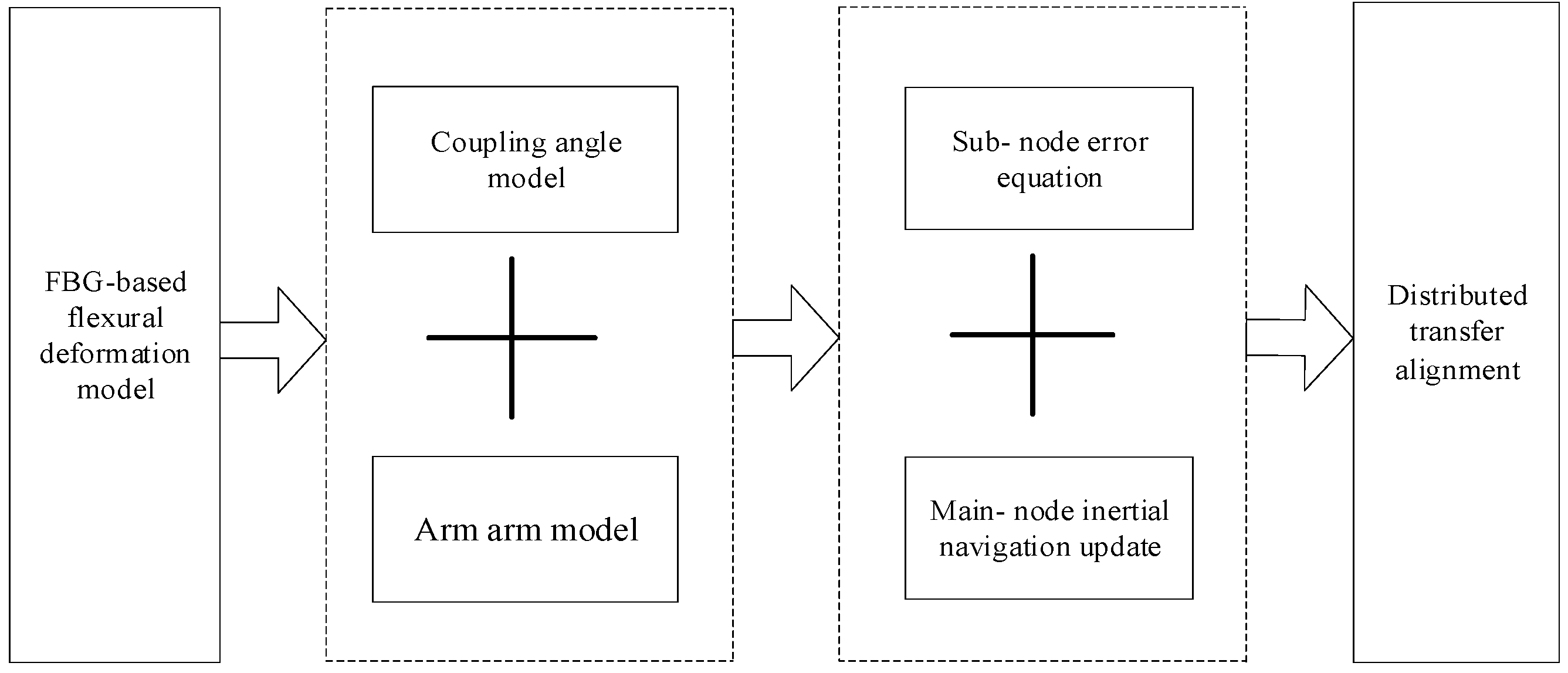
2.2. FBG Assisted Transfer Alignment
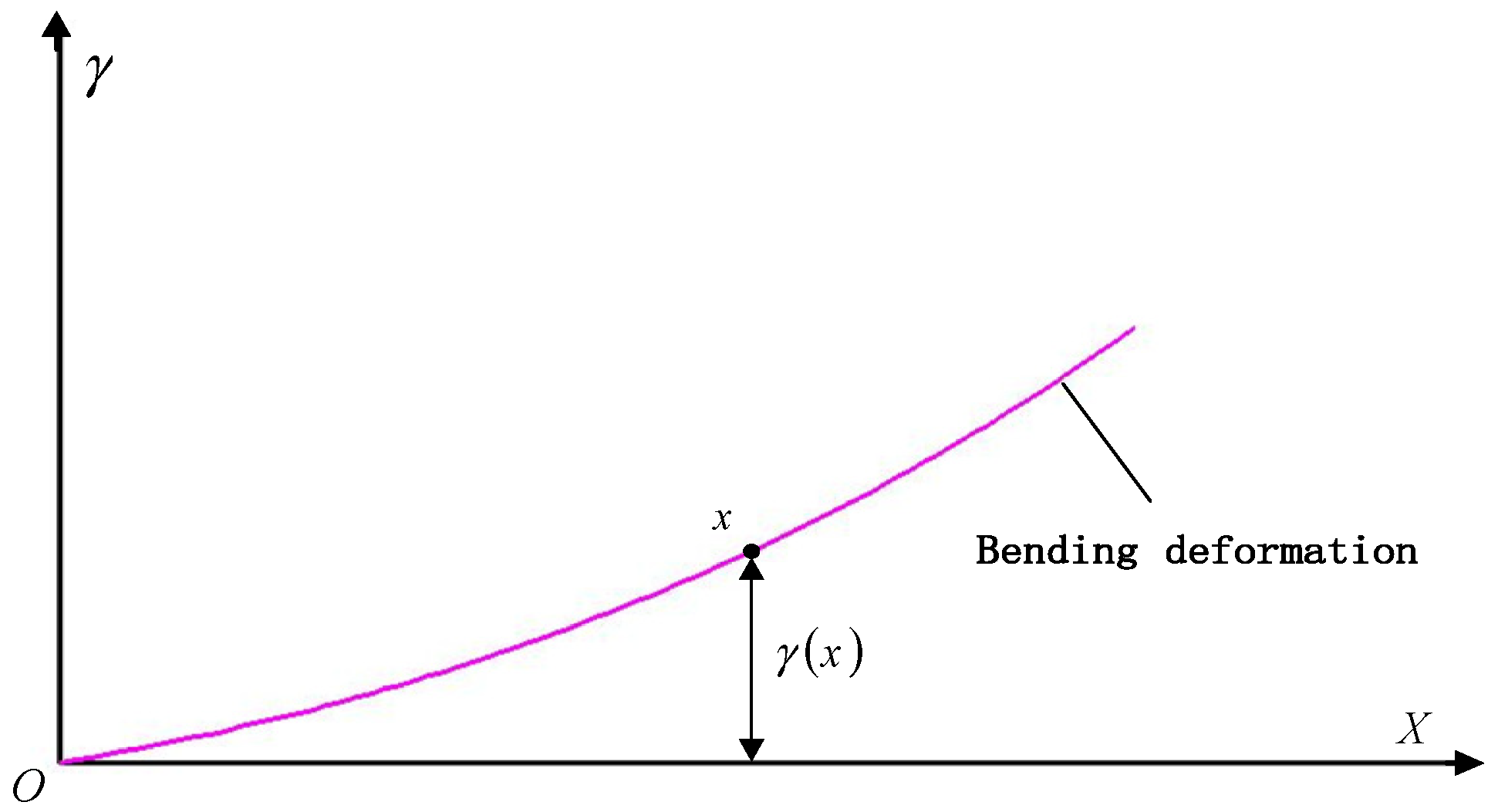
2.2.1. The Bending Deformation Angle Model Based on FBGs
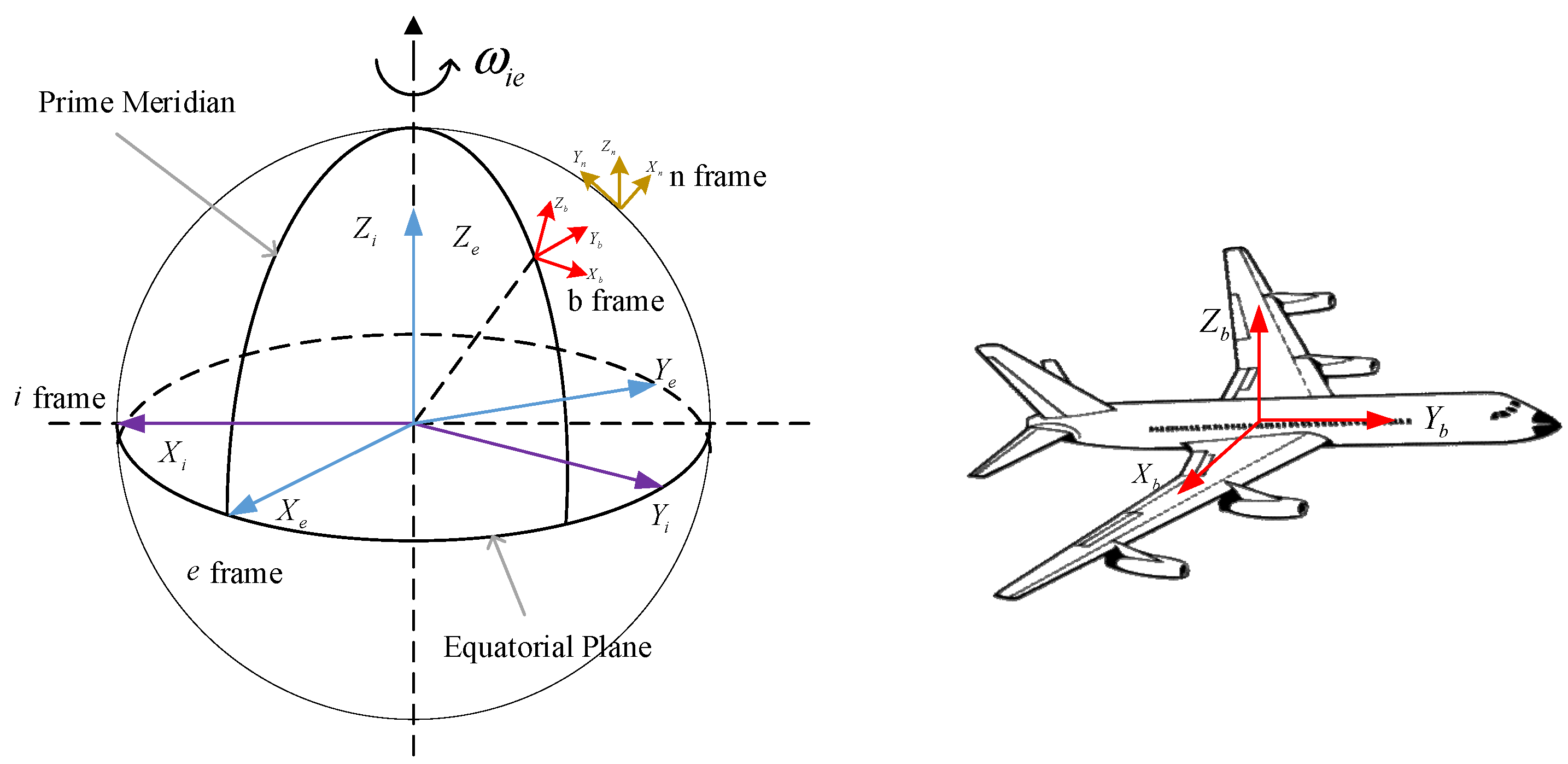
2.2.2. Coordinate System Description
- (1)
- Geocentric Inertial Coordinate System (, i-System)
- (2)
- Earth-Centered Earth-Fixed Coordinate System (, e system)
- (3)
- Navigation coordinate system (, n system)
- (4)
- Body Coordinate System (, b system)
2.2.3. Coupling Error Angle Model
2.2.4. Dynamic Lever Arm Model
2.2.5. Transfer Alignment Model
- (1)
- State equation
- (2)
- Measurement equation
- (1)
- Attitude measurements
- (2)
- Velocity measurement
- (3)
- Angular velocity measurement
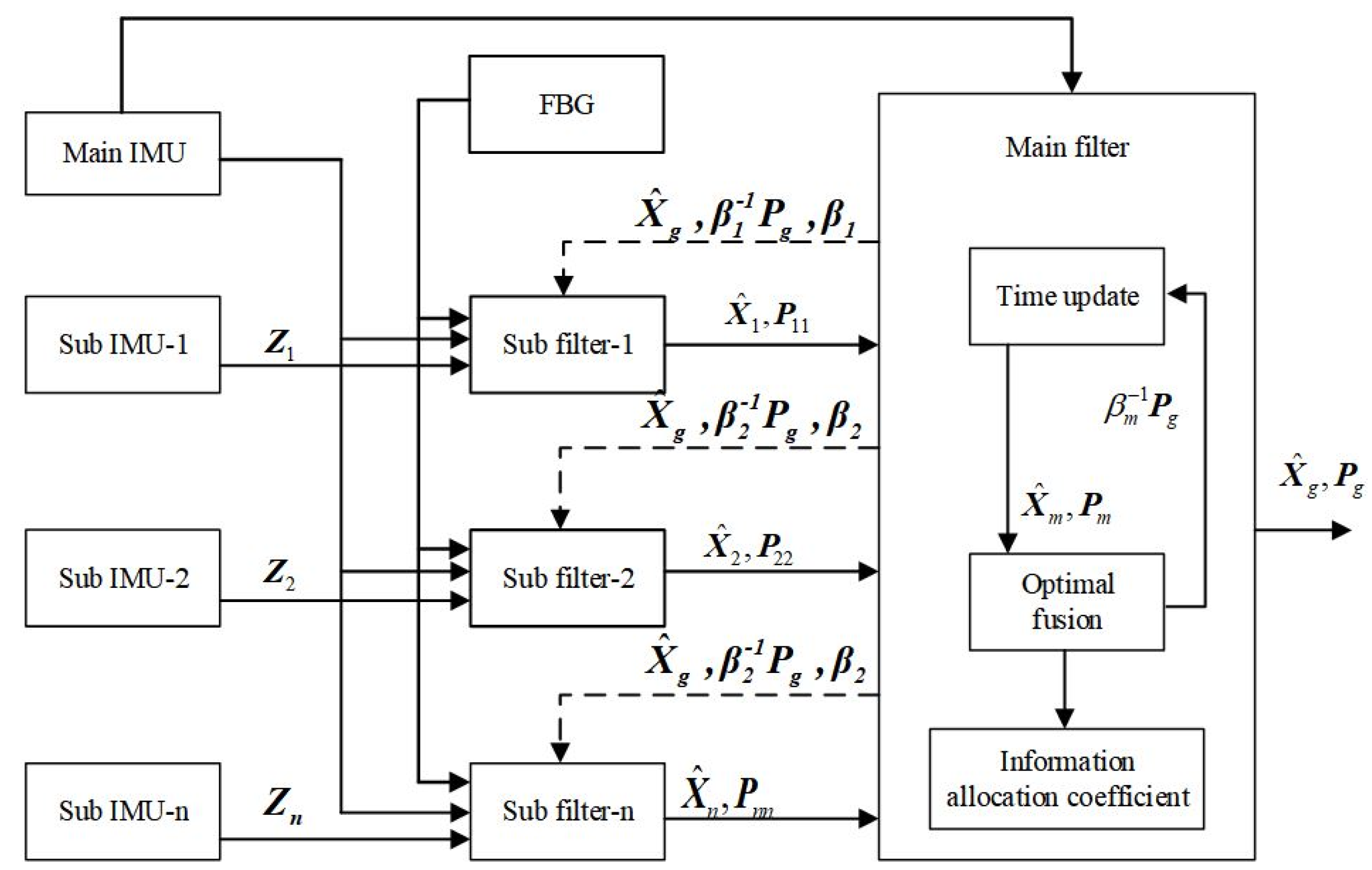
2.3. Multi-Sensor Filtering Method
2.3.1. Comparison of Distributed Multi-Sensor Filtering
2.3.2. Federated Filtering
- (1)
- Federal filtering formula
- (1)
- Information allocation
- (2)
- Time update
- (3)
- Measurement update
- (4)
- Information Fusion
- (2)
- Federal filtering mode classification
- (1)
- Zero reset mode
- (2)
- Variable proportion mode
- (3)
- No feedback mode
- (4)
- Fusion feedback mode
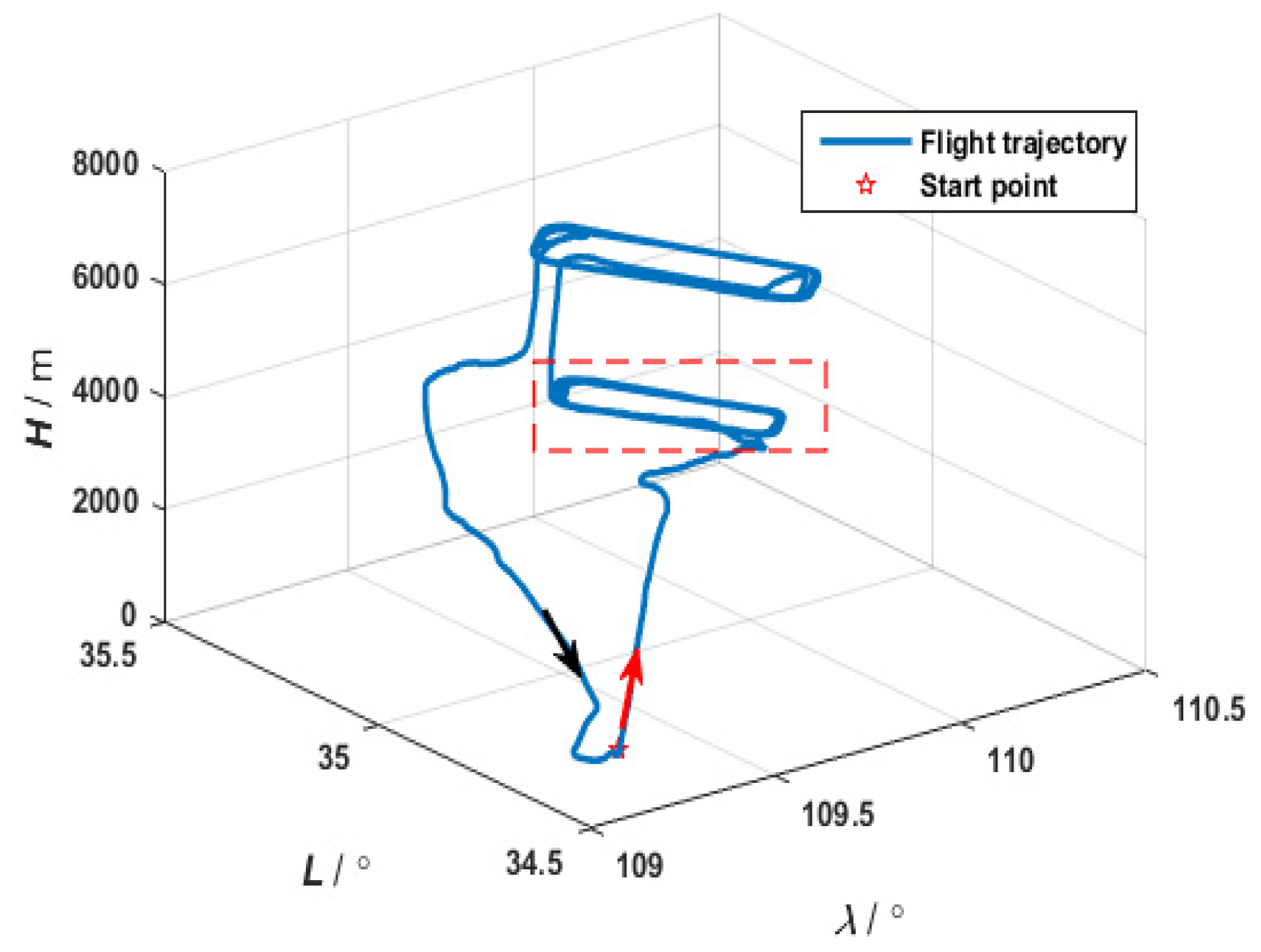
3. Results and Discussion
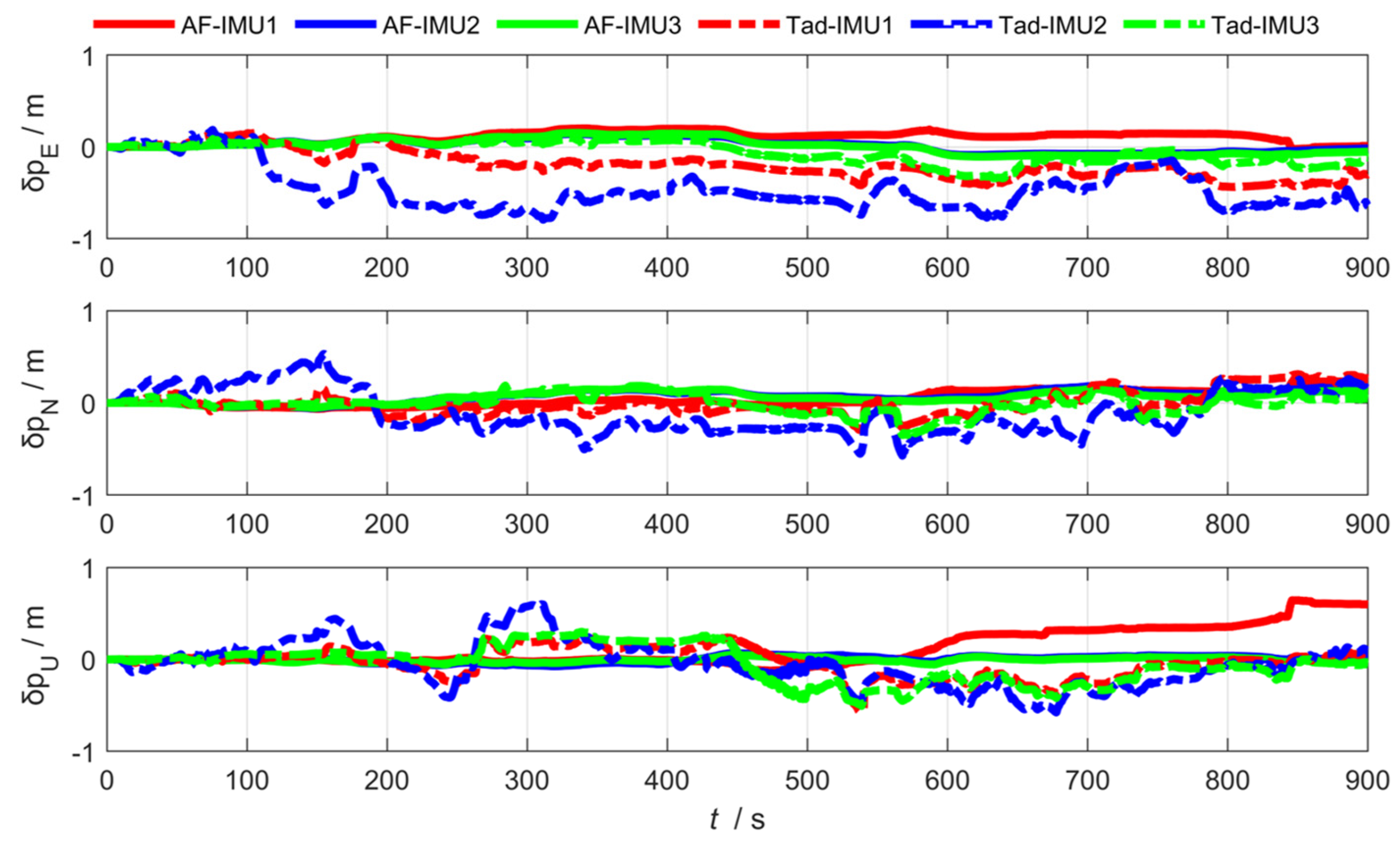
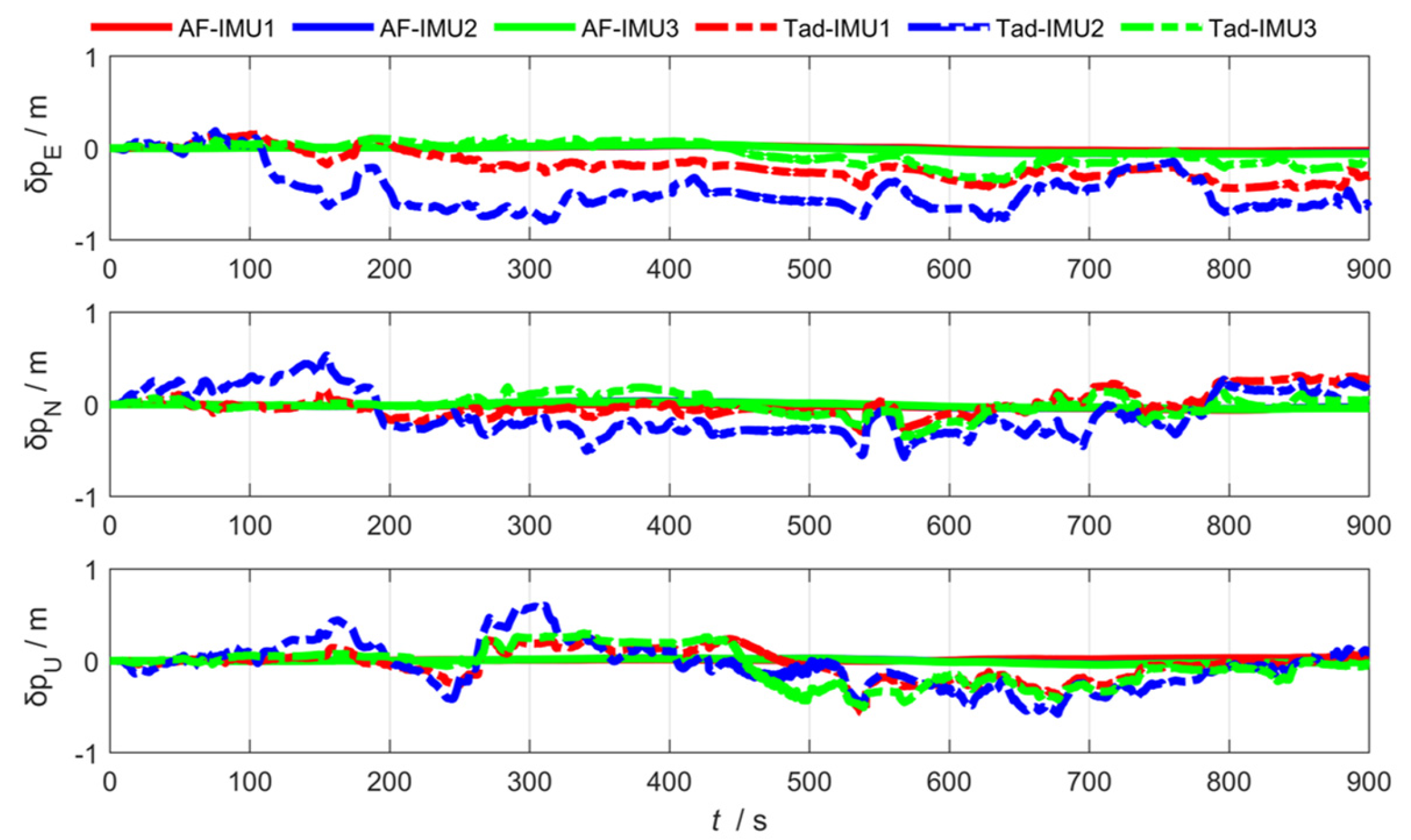
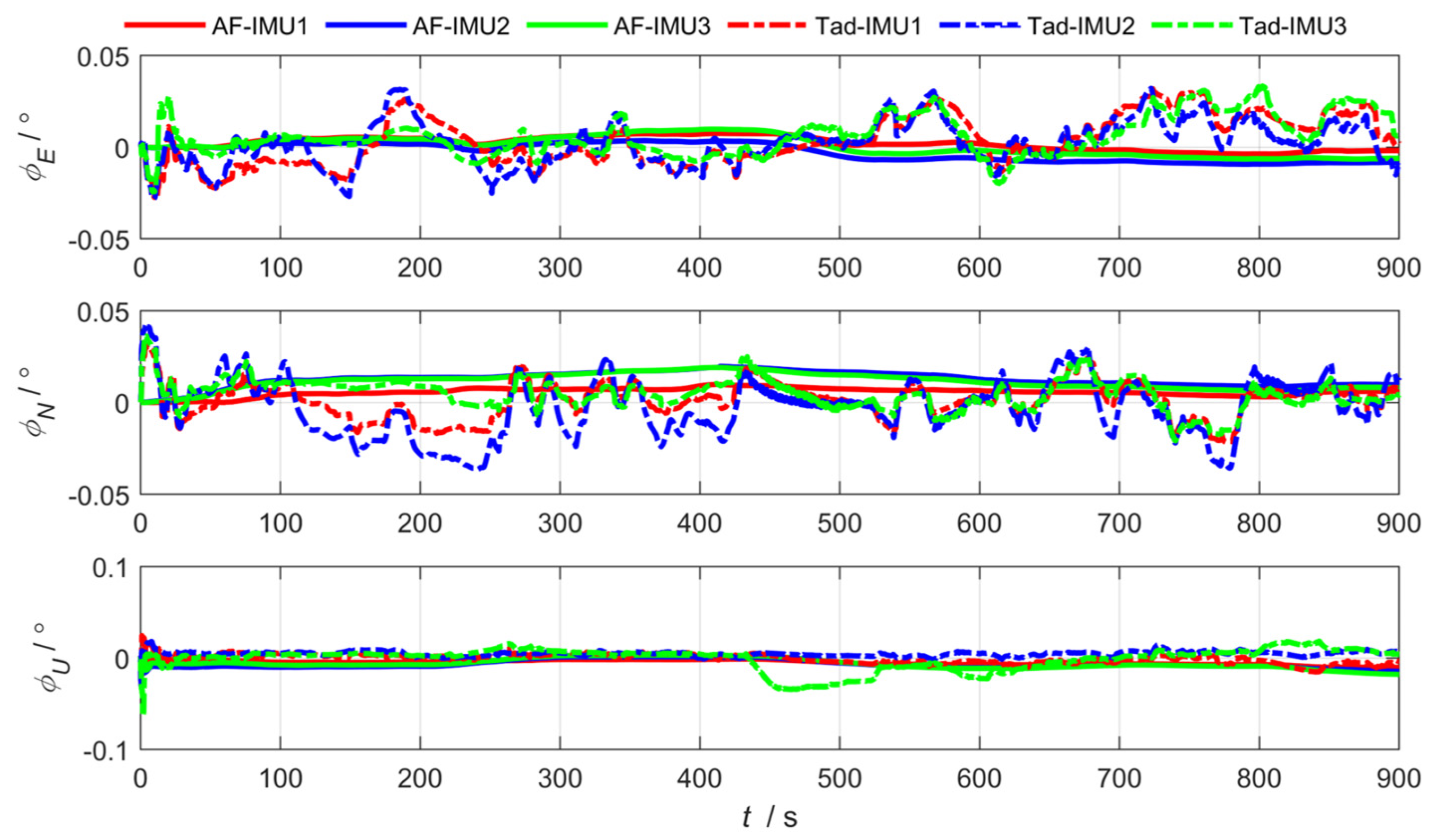
3.1. Federated Adaptive Filtering Method Based on Partition Coefficient
3.2. Federated Adaptive Filtering Method Based on the R Update
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, L.; Liu, Z.; Fang, J. An Accurate Motion Compensation for SAR Imagery based on INS/GPS with Dual-filter Correction. J. Navig. 2019, 72, 1399–1416. [Google Scholar] [CrossRef]
- Yang, Y.; Sun, S.; Huang, J. Large-Scale Aircraft Pose Estimation System Based on Depth Cameras. Appl. Sci. 2023, 13, 3736. [Google Scholar] [CrossRef]
- Talebi, S.P.; Werner, S.; Mandic, D.P. Quaternion-valued distributed filtering and control. IEEE Trans. Autom. Control 2020, 65, 4246–4257. [Google Scholar] [CrossRef]
- Li, G.; Liu, Z.; Zhang, J.; Zheng, L. Robust predictive control for anti-rolling path following of underactuated surface vessels using adaptive Kalman filter. Int. J. Adv. Robot. Syst. 2019, 16, 1729881419877269. [Google Scholar] [CrossRef]
- Khodarahmi, M.; Maihami, V. A review on Kalman filter models. Arch. Comput. Methods Eng. 2023, 30, 727–747. [Google Scholar] [CrossRef]
- Gardner, P.; Bull, L.A.; Gosliga, J.; Poole, J.; Dervilis, N.; Worden, K. A population-based SHM methodology for heterogeneous structures: Transferring damage localisation knowledge between different aircraft wings. Mech. Syst. Signal Process. 2022, 172, 108918. [Google Scholar] [CrossRef]
- Brooks, T.R.; Kenway, G.K.; Martins, J.R. Benchmark aerostructural models for the study of transonic aircraft wings. AIAA J. 2018, 56, 2840–2855. [Google Scholar] [CrossRef]
- Ye, W.; Gu, B.; Wang, Y. Airborne distributed position and orientation system transfer alignment method based on fiber bragg grating. Sensors 2020, 20, 2120. [Google Scholar] [CrossRef]
- Wang, B.; Ye, W.; Liu, Y. An Improved Real-time Transfer Alignment Algorithm based on Adaptive Noise Estimation for Distributed POS. IEEE Access 2020, 8, 102119–102127. [Google Scholar] [CrossRef]
- Wang, B.; Deng, Z.; Liu, C. Estimation of Information Sharing Error by Dynamic Deformation Between Inertial Navigation Systems. IEEE Trans. Ind. Electron. 2014, 61, 2015–2023. [Google Scholar] [CrossRef]
- Yang, J.; Wang, X.; Ding, X.; Wei, Q.; Shen, L. A fast and accurate transfer alignment method without relying on the empirical model of angular deformation. J. Navig. 2022, 75, 878–900. [Google Scholar] [CrossRef]
- Chen, W.; Yang, Z.; Gu, S. Adaptive transfer alignment method based on the observability analysis for airborne pod strapdown inertial navigation system. Sci. Rep. 2022, 12, 946. [Google Scholar]
- Qu, C.; Li, J. A novel relative motion measurement method based on distributed POS relative parameters matching transfer alignment. Measurement 2022, 202, 111890. [Google Scholar] [CrossRef]
- Vyazmin, V.S.; Golovan, A.A.; Govorov, A.D. Initial and final alignment of a strapdown airborne gravimeter and accelerometer bias determination. Gyroscopy Navig. 2023, 14, 48–55. [Google Scholar] [CrossRef]
- Soman, R.; Majewska, K.; Mieloszyk, M.; Malinowski, P.; Ostachowicz, W. Application of Kalman Filter based Neutral Axis tracking for damage detection in composites structures. Compos. Struct. 2018, 184, 66–77. [Google Scholar] [CrossRef]
- Wang, J.; Ma, Z.; Chen, X. Generalized Dynamic Fuzzy NN Model Based on Multiple Fading Factors SCKF and its Application in Integrated Navigation. IEEE Sens. J. 2020, 21, 3680–3693. [Google Scholar] [CrossRef]
- Li, H.; Jian, W.; Wang, S.; Liu, X. A method for SINS initial alignment of large misalignment angles based on simplified sage-husa filter with parameters resetting. In Proceedings of the 2017 Forum on Cooperative Positioning and Service (CPGPS), Harbin, China, 19–21 May 2017; pp. 3680–3693. [Google Scholar]
- Chen, J.; Song, J.; Guan, Z.; Lian, Y. Measurement of the distance from grain divider to harvesting boundary based on dynamic regions of interest. Int. J. Agric. Biol. Eng. 2021, 14, 226–232. [Google Scholar] [CrossRef]
- Kang, S. Design of Transfer Alignment Algorithm with Velocity and Azimuth Matching for the Aircraft Having Wing Flexibility. J. Korea Inst. Mil. Sci. Technol. 2023, 26, 214–226. [Google Scholar] [CrossRef]
- Cao, K.; Zhang, Y.; Feng, J. Application research of multi-source data fusion and multi-model ensemble methods in aircraft approach state prediction. IEEE Sens. J. 2024, 25, 8493–8505. [Google Scholar] [CrossRef]
- Geng, Y.; Wang, J. Adaptive estimation of multiple fading factors in Kalman filter for navigation applications. GPS Solut. 2008, 12, 273–279. [Google Scholar] [CrossRef]
- Hegde, G.; Asokan, S.; Hegde, G. Fiber Bragg grating sensors for aerospace applications: A review. ISSS J. Micro Smart Syst. 2022, 11, 257–275. [Google Scholar] [CrossRef]
- Liang, Y.; Hu, L.; Kong, L.; Li, H.; Dai, Z.; Chen, M. Thin-diameter photonic crystal fiber magnetic field sensor based on controlled hole collapse and infiltration. IEEE Sens. J. 2023, 23, 27337–27342. [Google Scholar] [CrossRef]
- Liang, Y.; Zhang, H.; Chen, T.; Lin, W.; Liu, B.; Liu, H. Design of a Mach-Zehnder Interferometric Fiber Sensing System Based on PCA-Assisted OAM Interrogation for Simultaneous Measurement of Refractive Index and Temperature. J. Light. Technol. 2022, 18, 6310–6316. [Google Scholar] [CrossRef]
- Giannakeas, I.N.; Khodaei, Z.S.; Aliabadi, M.H. Structural health monitoring cost estimation of a piezosensorized aircraft fuselage. Sensors 2022, 22, 1771. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Xu, Y.; Guo, J. Multi-parameter information detection of aircraft taxiing on an airport runway based on an ultra-weak FBG sensing array. Opt. Express 2024, 32, 25135–25146. [Google Scholar] [CrossRef]
- Yuan, L.; Wang, Q.; Zhao, Y. A wavelength-time division multiplexing sensor network with failure detection using fiber Bragg grating. Opt. Fiber Technol. 2024, 88, 103818. [Google Scholar] [CrossRef]
- Xu, W.; Bian, Q.; Liang, J. Recent advances in optical fiber high-temperature sensors and encapsulation technique. Chin. Opt. Lett. 2023, 21, 090007. [Google Scholar]
- Zeybek, M. Accuracy assessment of direct georeferencing UAV images with onboard global navigation satellite system and comparison of CORS/RTK surveying methods. Meas. Sci. Technol. 2021, 32, 065402. [Google Scholar] [CrossRef]
- Geng, H.; Liu, H.; Ma, L. Multi-sensor filtering fusion meets censored measurements under a constrained network environment: Advances, challenges and prospects. Int. J. Syst. Sci. 2021, 52, 3410–3436. [Google Scholar] [CrossRef]






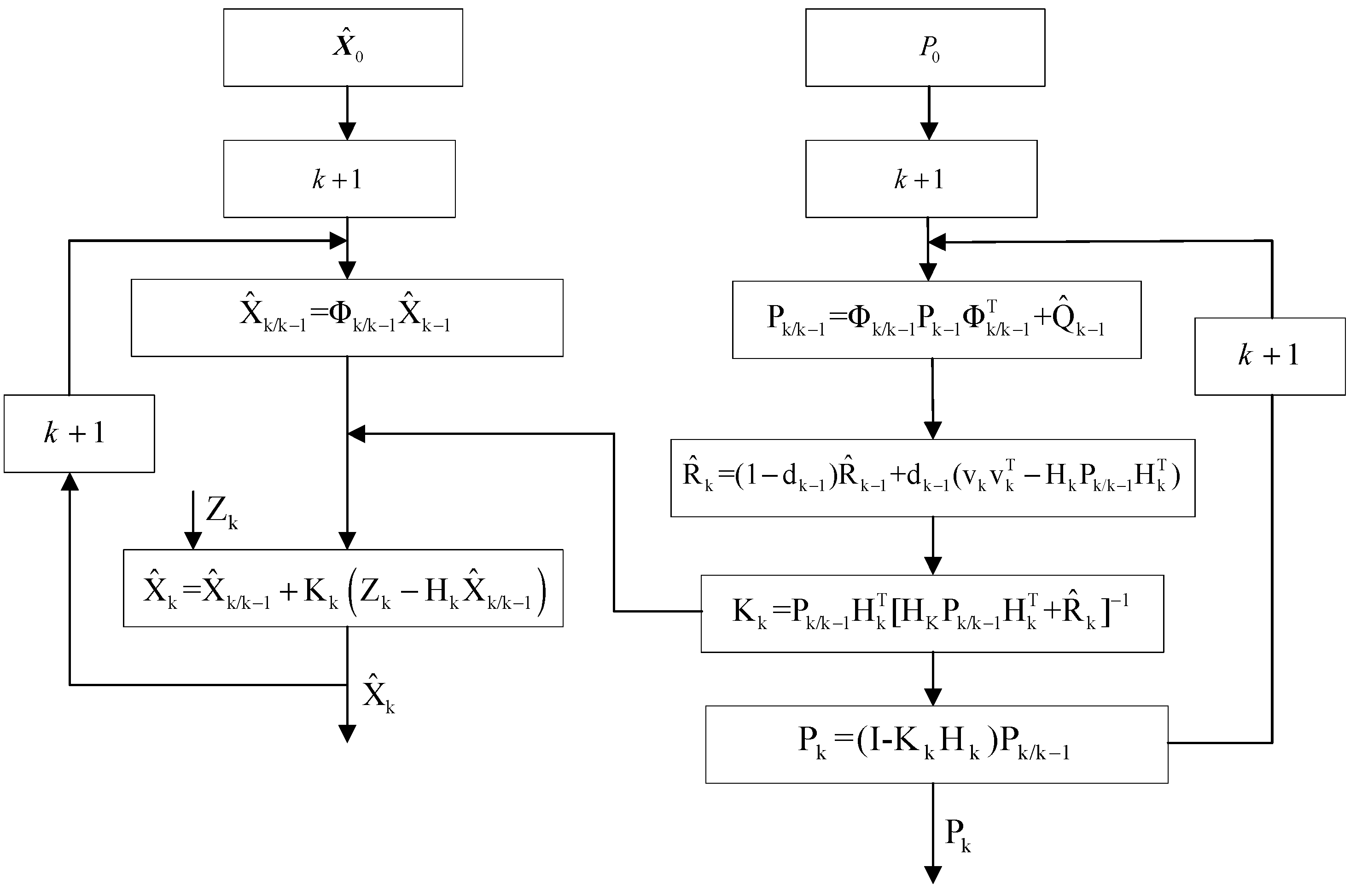

| IMU | Parameter | Method | RMSE | ||
|---|---|---|---|---|---|
| East | North | Up | |||
| IMU 1 | Position error (m) | Traditional Kalman Filter | 0.267 | 0.148 | 0.157 |
| Federated adaptive filtering based on partition coefficients | 0.013 | 0.023 | 0.016 | ||
| Arm error (m) | Traditional Kalman Filter | 0.018 | 0.012 | 0.005 | |
| Federated adaptive filtering based on partition coefficients | 0.002 | 0.006 | 0.001 | ||
| IMU 2 | Position error (m) | Traditional Kalman Filter | 0.543 | 0.262 | 0.246 |
| Federated adaptive filtering based on partition coefficients | 0.028 | 0.035 | 0.015 | ||
| Arm error (m) | Traditional Kalman Filter | 0.008 | 0.007 | 0.004 | |
| Federated adaptive filtering based on partition coefficients | 0.003 | 0.011 | 0.002 | ||
| IMU 3 | Position error (m) | Traditional Kalman Filter | 0.151 | 0.100 | 0.198 |
| Federated adaptive filtering based on partition coefficients | 0.022 | 0.024 | 0.015 | ||
| Arm error (m) | Traditional Kalman Filter | 0.004 | 0.007 | 0.003 | |
| Federated adaptive filtering based on partition coefficients | 0.003 | 0.012 | 0.002 | ||
| IMU | Parameter | Method | RMSE | ||
|---|---|---|---|---|---|
| Pitch | Roll | Yaw | |||
| IMU 1 | Attitude error (°) | Traditional Kalman Filter | 0.0131 | 0.0010 | 0.0050 |
| Federated adaptive filtering based on partition coefficients | 0.0028 | 0.0061 | 0.0063 | ||
| IMU 2 | Attitude error (°) | Traditional Kalman Filter | 0.0116 | 0.0150 | 0.0053 |
| Federated adaptive filtering based on partition coefficients | 0.0039 | 0.0096 | 0.0077 | ||
| IMU 3 | Attitude error (°) | Traditional Kalman Filter | 0.0125 | 0.0094 | 0.0116 |
| Federated adaptive filtering based on partition coefficients | 0.0032 | 0.0101 | 0.0080 | ||
| IMU | Parameter | Method | RMSE | ||
|---|---|---|---|---|---|
| East | North | Up | |||
| IMU 1 | Position error (m) | Traditional Kalman Filter | 0.267 | 0.148 | 0.157 |
| Federated adaptive filtering based on the R update | 0.012 | 0.027 | 0.014 | ||
| Arm error (m) | Traditional Kalman Filter | 0.018 | 0.012 | 0.005 | |
| Federated adaptive filtering based on the R update | 0.001 | 0.002 | 0.001 | ||
| IMU 2 | Position error (m) | Traditional Kalman Filter | 0.543 | 0.262 | 0.246 |
| Federated adaptive filtering based on the R update | 0.031 | 0.045 | 0.017 | ||
| Arm error (m) | Traditional Kalman Filter | 0.008 | 0.007 | 0.004 | |
| Federated adaptive filtering based on the R update | 0.003 | 0.006 | 0.001 | ||
| IMU 3 | Position error (m) | Traditional Kalman Filter | 0.151 | 0.100 | 0.198 |
| Federated adaptive filtering based on the R update | 0.025 | 0.037 | 0.015 | ||
| Arm error (m) | Traditional Kalman Filter | 0.004 | 0.007 | 0.003 | |
| Federated adaptive filtering based on the R update | 0.002 | 0.007 | 0.001 | ||
| IMU | Parameter | Method | RMSE | ||
|---|---|---|---|---|---|
| Pitch | Roll | Yaw | |||
| IMU 1 | Attitude error (°) | Traditional Kalman Filter | 0.0131 | 0.0010 | 0.0050 |
| Federated adaptive filtering based on the R update | 0.0025 | 0.0057 | 0.0063 | ||
| IMU 2 | Attitude error (°) | Traditional Kalman Filter | 0.0116 | 0.0150 | 0.0053 |
| Federated adaptive filtering based on the R update | 0.0027 | 0.0087 | 0.0075 | ||
| IMU 3 | Attitude error (°) | Traditional Kalman Filter | 0.0125 | 0.0094 | 0.0116 |
| Federated adaptive filtering based on the R update | 0.0023 | 0.0091 | 0.0076 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Z.; Chen, X.; Wang, C.; Cui, B. Real-Time Wing Deformation Monitoring via Distributed Fiber Bragg Grating and Adaptive Federated Filtering. Sensors 2025, 25, 4343. https://doi.org/10.3390/s25144343
Ma Z, Chen X, Wang C, Cui B. Real-Time Wing Deformation Monitoring via Distributed Fiber Bragg Grating and Adaptive Federated Filtering. Sensors. 2025; 25(14):4343. https://doi.org/10.3390/s25144343
Chicago/Turabian StyleMa, Zhen, Xiyuan Chen, Cundeng Wang, and Bingbo Cui. 2025. "Real-Time Wing Deformation Monitoring via Distributed Fiber Bragg Grating and Adaptive Federated Filtering" Sensors 25, no. 14: 4343. https://doi.org/10.3390/s25144343
APA StyleMa, Z., Chen, X., Wang, C., & Cui, B. (2025). Real-Time Wing Deformation Monitoring via Distributed Fiber Bragg Grating and Adaptive Federated Filtering. Sensors, 25(14), 4343. https://doi.org/10.3390/s25144343






