Improved Side-Channel Attack on CTR DRBG Using a Clustering Algorithm
Abstract
1. Introduction
1.1. Contribution
1.2. Organization
2. Preliminaries
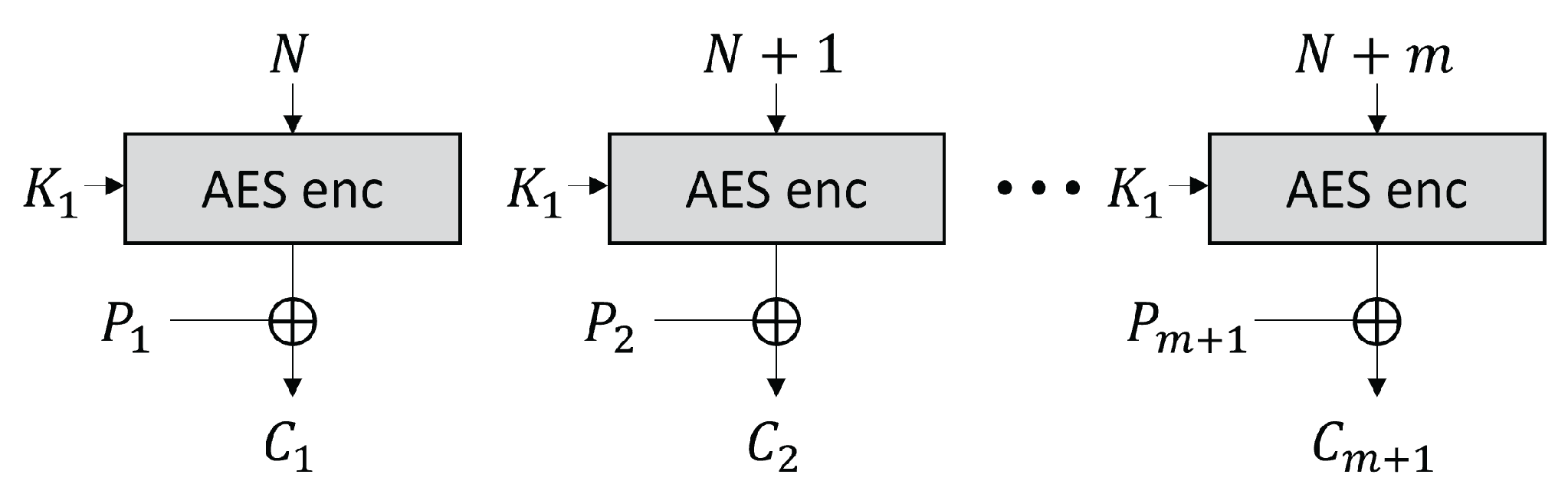
2.1. AES CTR Mode
2.2. Correlation Power Analysis
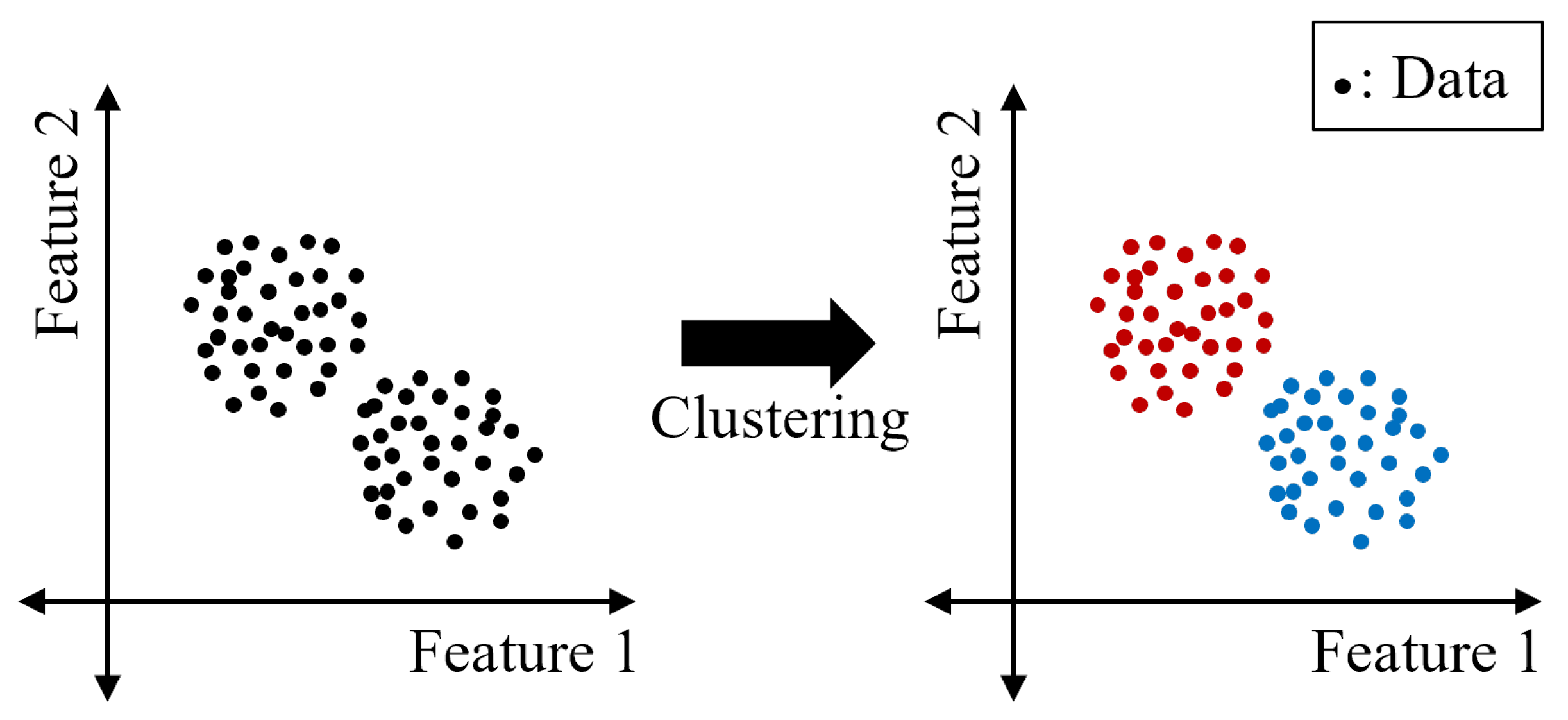
2.3. Clustering Algorithm
| Algorithm 1 k-means clustering algorithm |
| Input: data {}, number of clusters U, iteration I |
Output: centroid {}, cluster {}
|
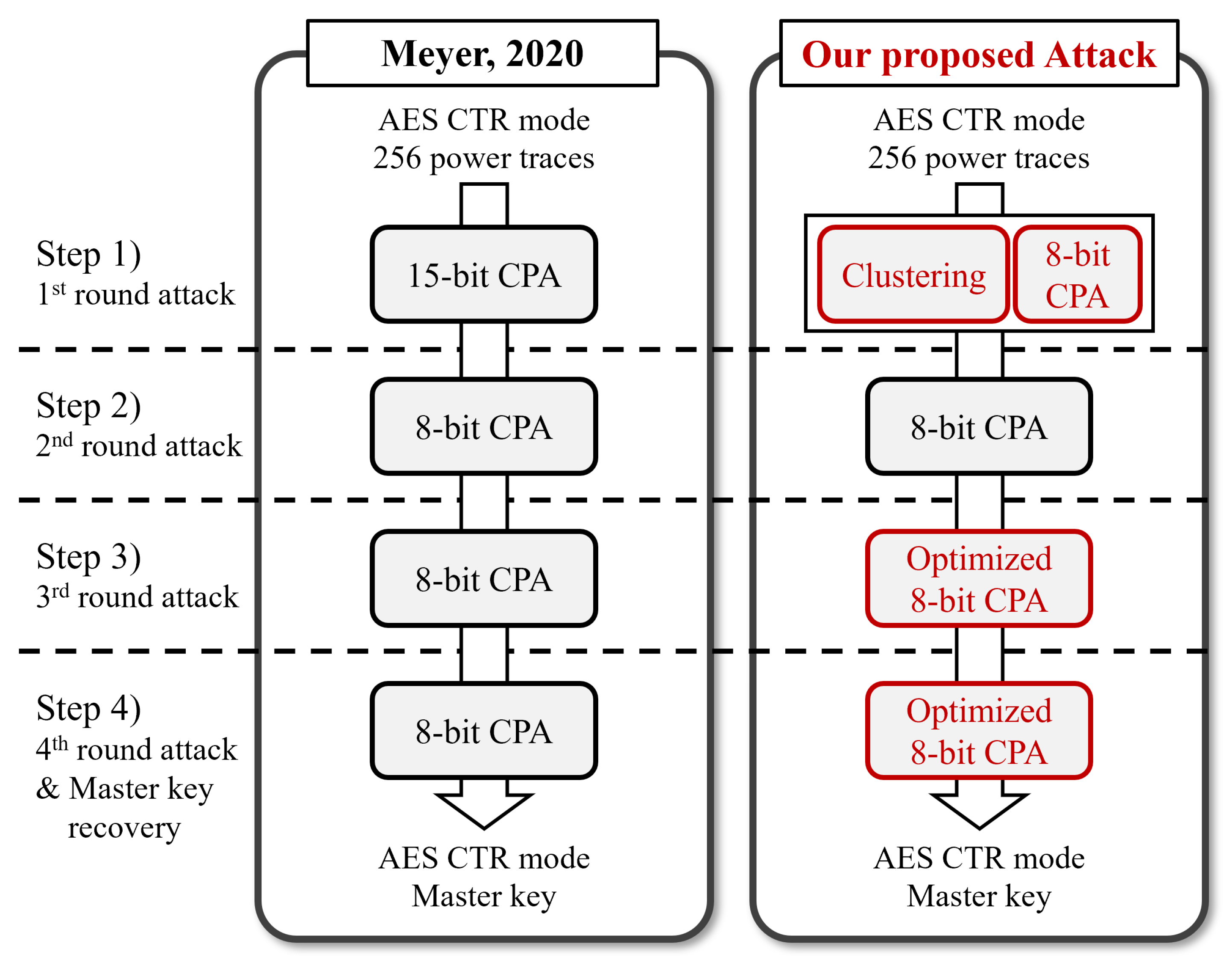
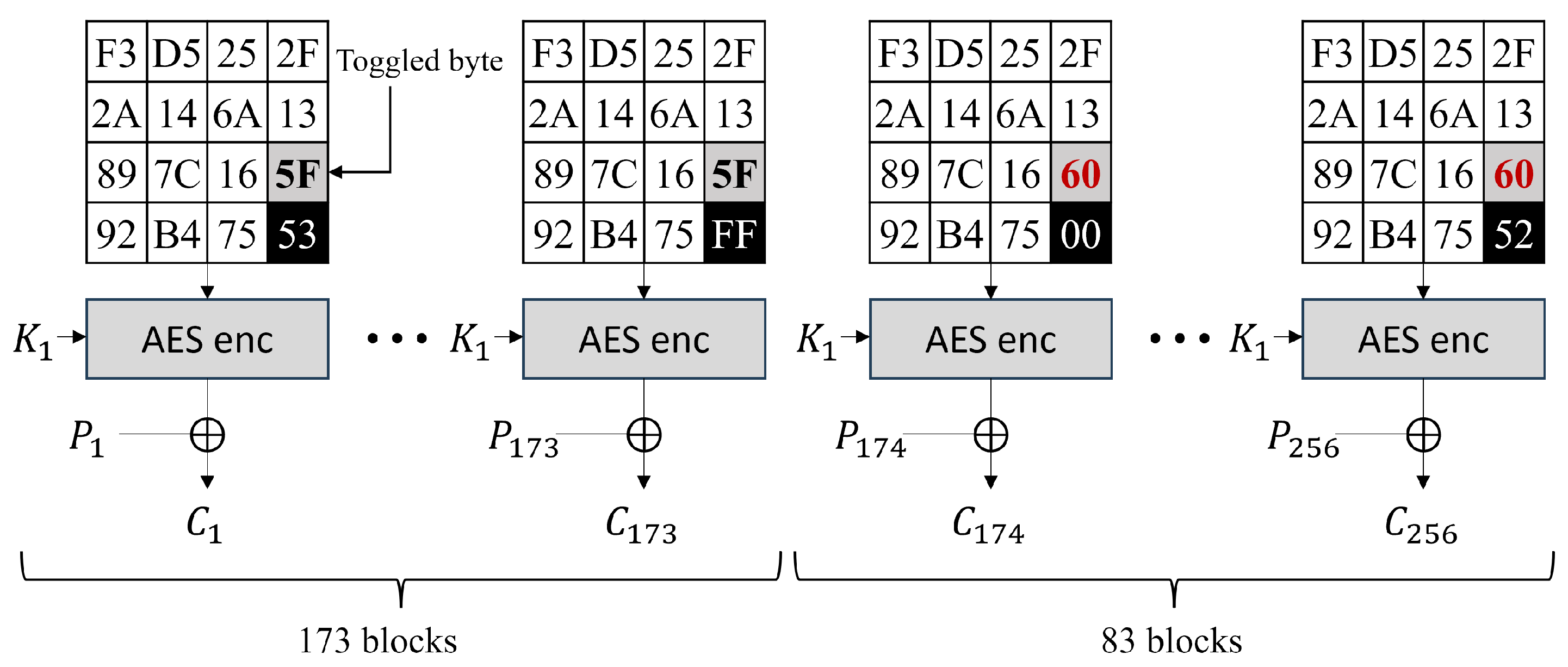
3. Previous Power Analysis on AES CTR Mode
3.1. Attack Step 1
3.2. Attack Step 2
3.3. Attack Step 3
3.4. Attack Step 4
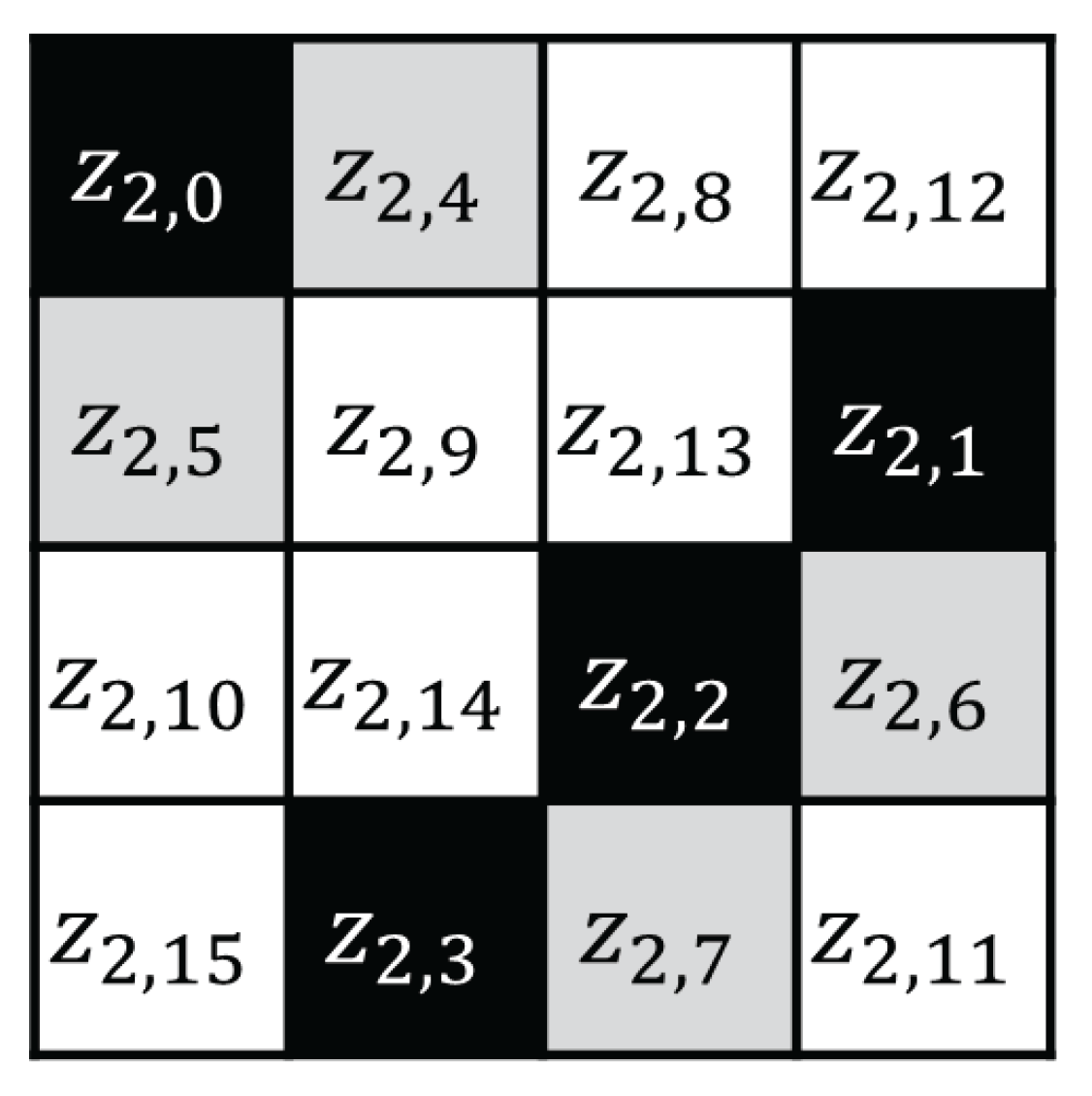
4. Our Proposed Power Analysis on AES CTR Mode
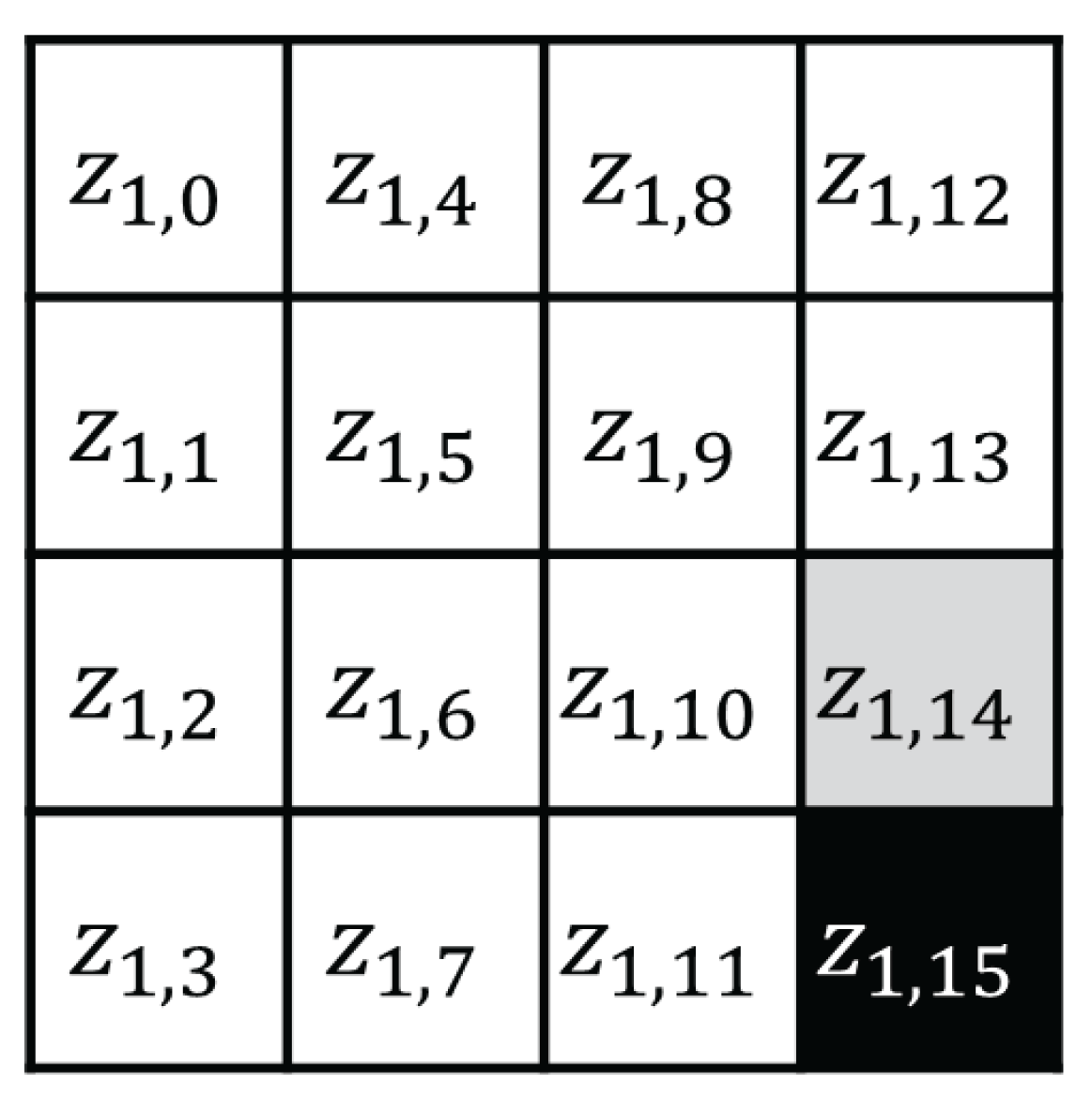
4.1. Attack Step 1
4.2. Attack Step 2
4.3. Attack Step 3
4.4. Attack Step 4
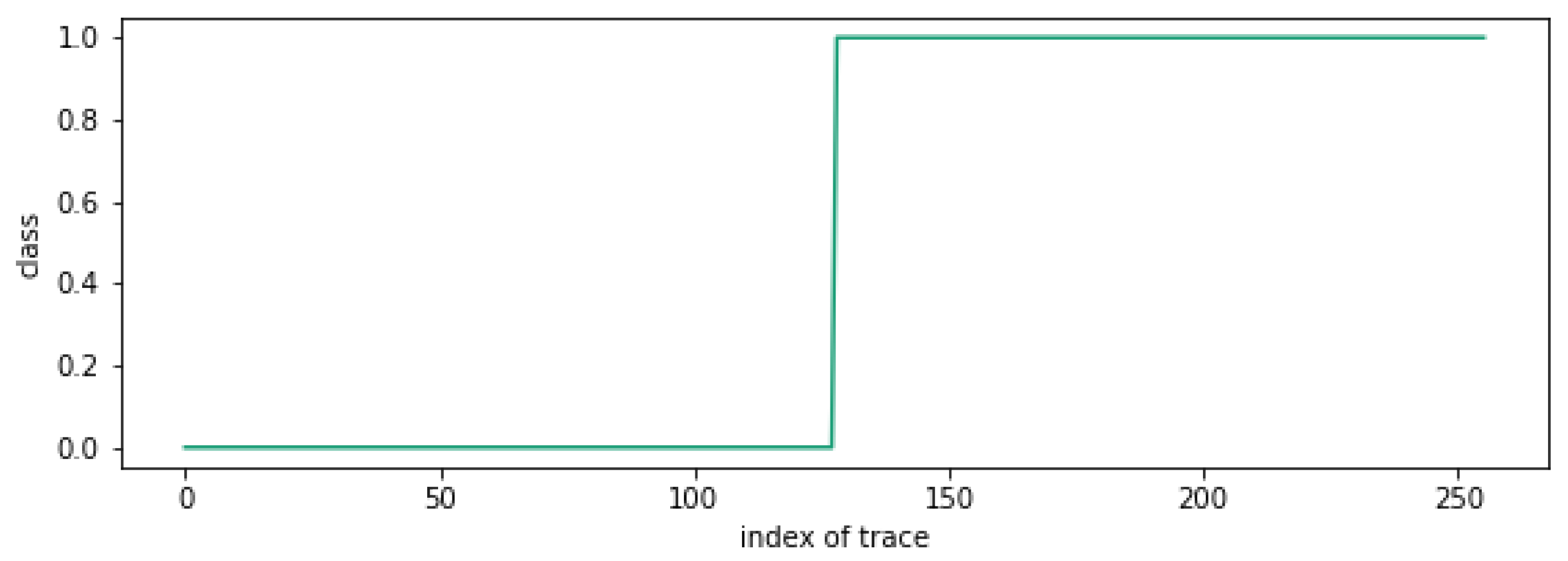
5. Experimental Results for the Proposed Clustering Attack
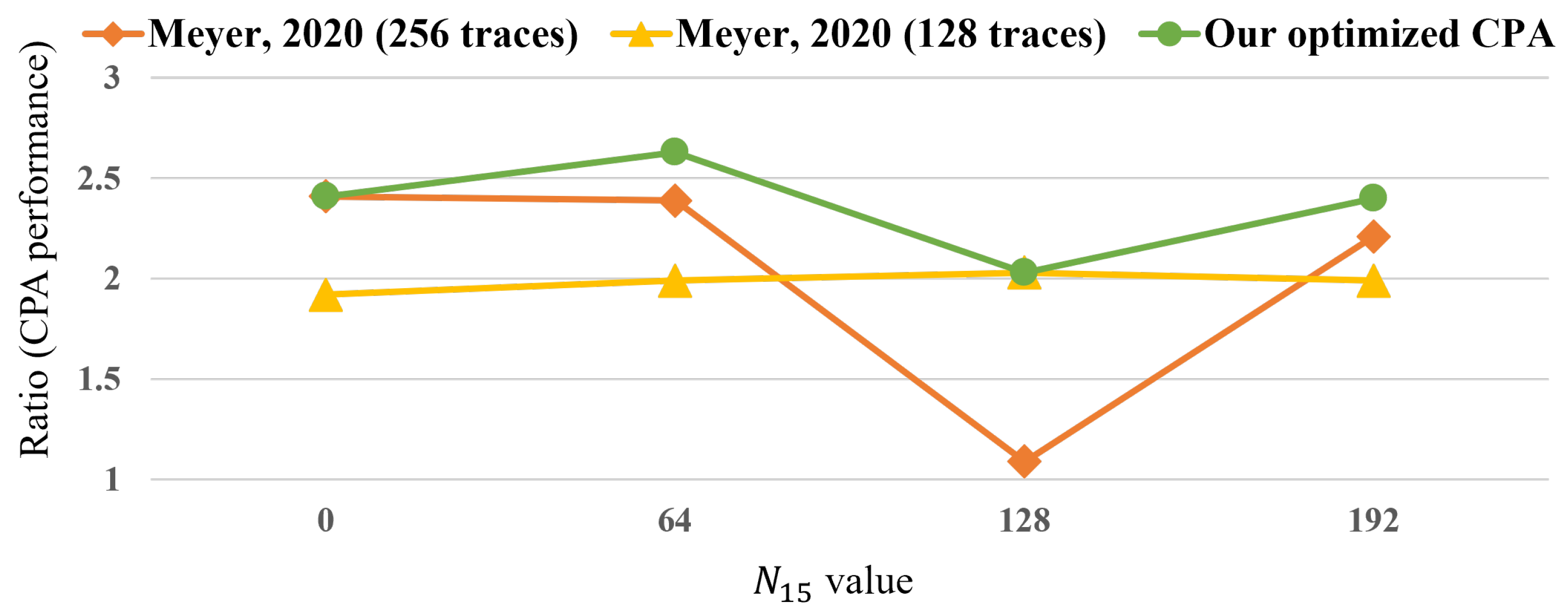
6. Comparison of Previous and Proposed Attacks
6.1. Comparison of Attack Step 1
6.1.1. Attack Success Rate
6.1.2. Attack Complexity
6.2. Comparison on Steps 3 and 4 of the Attack
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SCA | Side-Channel Attack |
| CPA | Correlation Power Analysis |
| CTR | Counter |
| DRBG | Deterministic Random Bit Generator |
Notations
| ⊕ | Exclusive OR operator |
| ≪ | Shift operator in 8-bit |
| · | AES field multiplication operator |
| AES S-Box function | |
| i | Round index |
| j | Byte index |
| i-th round input 16 bytes | |
| i-th round input j-th byte | |
| i-th round key 16 bytes | |
| i-th round key j-th byte | |
| i-th round SubBytes output 16 bytes | |
| i-th round SubBytes output j-th byte | |
| N | Nonce value 16 bytes of CTR mode |
| Nonce value j-th byte of CTR mode | |
| Counter value of CTR mode |
References
- Kocher, P.C.; Jaffe, J.; Jun, B. Differential Power Analysis. In Proceedings of the Advances in Cryptology—CRYPTO ’99, 19th Annual International Cryptology Conference, Santa Barbara, CA, USA, 15–19 August 1999; Wiener, M.J., Ed.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 1999; Volume 1666, pp. 388–397. [Google Scholar] [CrossRef]
- Moradi, A.; Mischke, O.; Paar, C. One Attack to Rule Them All: Collision Timing Attack versus 42 AES ASIC Cores. IEEE Trans. Comput. 2013, 62, 1786–1798. [Google Scholar] [CrossRef]
- Zhang, P.; Den, G.; Zhao, Q.; Chen, K. Em frequency domain correlation analysis on cipher chips. In Proceedings of the 2009 First International Conference on Information Science and Engineering, Nanjing, China, 26–28 December 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1729–1732. [Google Scholar]
- Krämer, J.; Nedospasov, D.; Schlösser, A.; Seifert, J. Differential Photonic Emission Analysis. In Proceedings of the Constructive Side-Channel Analysis and Secure Design—4th International Workshop, COSADE 2013, Paris, France, 6–8 March 2013; Revised Selected Papers. Prouff, E., Ed.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2013; Volume 7864, pp. 1–16. [Google Scholar] [CrossRef]
- Blömer, J.; Seifert, J. Fault Based Cryptanalysis of the Advanced Encryption Standard (AES). In Proceedings of the Financial Cryptography, 7th International Conference, FC 2003, Guadeloupe, French West Indies, 27–30 January 2003; Revised Papers. Wright, R.N., Ed.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2003; Volume 2742, pp. 162–181. [Google Scholar] [CrossRef]
- Moabalobelo, P.T. Differential Power Analysis of an AES Software Implementation. Master’s Thesis, University of Johannesburg, Johannesburg, South Africa, 2013. [Google Scholar]
- Aigner, M.; Oswald, E. Power Analysis Tutorial. Technical Report, TU Graz. 2000. Available online: https://cs.ru.nl/E.Poll/hw/dpa_tutorial.pdf (accessed on 27 May 2025).
- Mangard, S.; Oswald, E.; Popp, T. Power Analysis Attacks—Revealing the Secrets of Smart Cards; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Smith, K.J., Jr. Methodologies for Power Analysis Attacks on Hardware Implementations of AES; Rochester Institute of Technology: Rochester, NY, USA, 2009. [Google Scholar]
- Petrvalsky, M.; Drutarovsky, M.; Varchola, M. Differential power analysis of advanced encryption standard on accelerated 8051 processor. In Proceedings of the 2013 23rd International Conference Radioelektronika (RADIOELEKTRONIKA), Pardubice, Czech Republic, 16–17 April 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 334–339. [Google Scholar]
- Kocher, P.C. Timing Attacks on Implementations of Diffie-Hellman, RSA, DSS, and Other Systems. In Proceedings of the Advances in Cryptology—CRYPTO ’96, 16th Annual International Cryptology Conference, Santa Barbara, CA, USA, 18–22 August 1996; Koblitz, N., Ed.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 1996; Volume 1109, pp. 104–113. [Google Scholar] [CrossRef]
- Brier, E.; Clavier, C.; Olivier, F. Correlation Power Analysis with a Leakage Model. In Proceedings of the Cryptographic Hardware and Embedded Systems—CHES 2004: 6th International Workshop, Cambridge, MA, USA, 11–13 August 2004; Joye, M., Quisquater, J., Eds.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2004; Volume 3156, pp. 16–29. [Google Scholar] [CrossRef]
- Gierlichs, B.; Batina, L.; Tuyls, P.; Preneel, B. Mutual Information Analysis. In Proceedings of the Cryptographic Hardware and Embedded Systems—CHES 2008, 10th International Workshop, Washington, DC, USA, 10–13 August 2008; Oswald, E., Rohatgi, P., Eds.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2008; Volume 5154, pp. 426–442. [Google Scholar] [CrossRef]
- Timon, B. Non-Profiled Deep Learning-based Side-Channel attacks with Sensitivity Analysis. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2019, 2019, 107–131. [Google Scholar] [CrossRef]
- Chari, S.; Rao, J.R.; Rohatgi, P. Template Attacks. In Proceedings of the Cryptographic Hardware and Embedded Systems—CHES 2002, 4th International Workshop, Redwood Shores, CA, USA, 13–15 August 2002; Revised Papers. Kaliski, B.S., Koç, ç.K., Paar, C., Eds.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2002; Volume 2523, pp. 13–28. [Google Scholar] [CrossRef]
- Zeman, V.; Martinasek, Z. Innovative Method of the Power Analysis. Radioengineering 2013, 22, 586–594. [Google Scholar]
- Batina, L.; Gierlichs, B.; Lemke-Rust, K. Differential cluster analysis. In Proceedings of the International Workshop on Cryptographic Hardware and Embedded Systems, Lausanne, Switzerland, 6–9 September 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 112–127. [Google Scholar]
- Nascimento, E.; Chmielewski, Ł. Applying horizontal clustering side-channel attacks on embedded ECC implementations. In Proceedings of the International Conference on Smart Card Research and Advanced Applications, Lugano, Switzerland, 13–15 November 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 213–231. [Google Scholar]
- Sim, B.Y.; Park, A.; Han, D.G. Chosen-ciphertext clustering attack on CRYSTALS-KYBER using the side-channel leakage of Barrett reduction. IEEE Internet Things J. 2022, 9, 21382–21397. [Google Scholar] [CrossRef]
- Mangard, S. A Simple Power-Analysis (SPA) Attack on Implementations of the AES Key Expansion. In Proceedings of the Information Security and Cryptology—ICISC 2002, 5th International Conference, Seoul, Republic of Korea, 28–29 November 2002; Revised Papers. Lee, P.J., Lim, C.H., Eds.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2002; Volume 2587, pp. 343–358. [Google Scholar] [CrossRef]
- Kocher, P.C.; Jaffe, J.; Jun, B.; Rohatgi, P. Introduction to differential power analysis. J. Cryptogr. Eng. 2011, 1, 5–27. [Google Scholar] [CrossRef]
- Belaïd, S.; Fouque, P.A.; Gérard, B. Side-Channel Analysis of Multiplications in GF (2128) Application to AES-GCM. In Proceedings of the International Conference on the Theory and Application of Cryptology and Information Security, Kolkata, India, 10–14 December 2014; Springer: Berlin/Heidelberg, Germany, 2014; pp. 306–325. [Google Scholar]
- Jayasinghe, D.; Ragel, R.G.; Ambrose, J.A.; Ignjatovic, A.; Parameswaran, S. Advanced modes in AES: Are they safe from power analysis based side channel attacks? In Proceedings of the 32nd IEEE International Conference on Computer Design, ICCD 2014, Seoull, Republic of Korea, 19–22 October 2014; IEEE Computer Society: Piscataway, NJ, USA, 2014; pp. 173–180. [Google Scholar] [CrossRef]
- Fahd, S.; Afzal, M.; Abbas, H.; Iqbal, M.M.W.; Waheed, S. Correlation power analysis of modes of encryption in AES and its countermeasures. Future Gener. Comput. Syst. 2018, 83, 496–509. [Google Scholar] [CrossRef]
- Ebina, K.; Ueno, R.; Homma, N. Side-Channel Analysis Against SecOC-Compliant AES-CMAC. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 3772–3776. [Google Scholar] [CrossRef]
- Jaffe, J. A First-Order DPA Attack Against AES in Counter Mode with Unknown Initial Counter. In Proceedings of the Cryptographic Hardware and Embedded Systems—CHES 2007, 9th International Workshop, Vienna, Austria, 10–13 September 2007; Paillier, P., Verbauwhede, I., Eds.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2007; Volume 4727, pp. 1–13. [Google Scholar] [CrossRef]
- Meyer, L.D. Recovering the CTR_DRBG state in 256 traces. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2020, 2020, 37–65. [Google Scholar] [CrossRef]
- Tienteu, M.; Smith, E.; Santillan, E.M.; Kornegay, K.T.; Harvey, P.; Toutsop, O.; Yimer, T.; Morris, V.; Wandji, K. Template Attack Against AES in Counter Mode with Unknown Initial Counter. In Proceedings of the 13th IEEE Annual Computing and Communication Workshop and Conference, CCWC 2023, Las Vegas, NV, USA, 8–11 March 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 525–533. [Google Scholar] [CrossRef]
- Hayati, N.; Ramli, K.; Windarta, S.; Suryanegara, M. A Novel Secure Root Key Updating Scheme for LoRaWANs Based on CTR_AES DRBG 128. IEEE Access 2022, 10, 18807–18819. [Google Scholar] [CrossRef]
- Kim, Y.; Seo, S.C. Efficient Implementation of AES and CTR_DRBG on 8-Bit AVR-Based Sensor Nodes. IEEE Access 2021, 9, 30496–30510. [Google Scholar] [CrossRef]
- Kietzmann, P.; Schmidt, T.C.; Wählisch, M. A Guideline on Pseudorandom Number Generation (PRNG) in the IoT. ACM Comput. Surv. 2022, 54, 1–38. [Google Scholar] [CrossRef]
- Prada-Delgado, M.Á.; Baturone, I.; Dittmann, G.; Jelitto, J.; Kind, A. PUF-derived IoT identities in a zero-knowledge protocol for blockchain. Internet Things 2020, 9, 100057. [Google Scholar] [CrossRef]
- NIST FIPS PUB 197; Advanced Encryption Standard. NIST: Gaithersburg, MD, USA, 2001.
- Dworkin, M.J. Sp 800-38a 2001 Edition. Recommendation for Block Cipher Modes of Operation: Methods and Techniques; NIST: Gaithersburg, MD, USA, 2001. [Google Scholar]



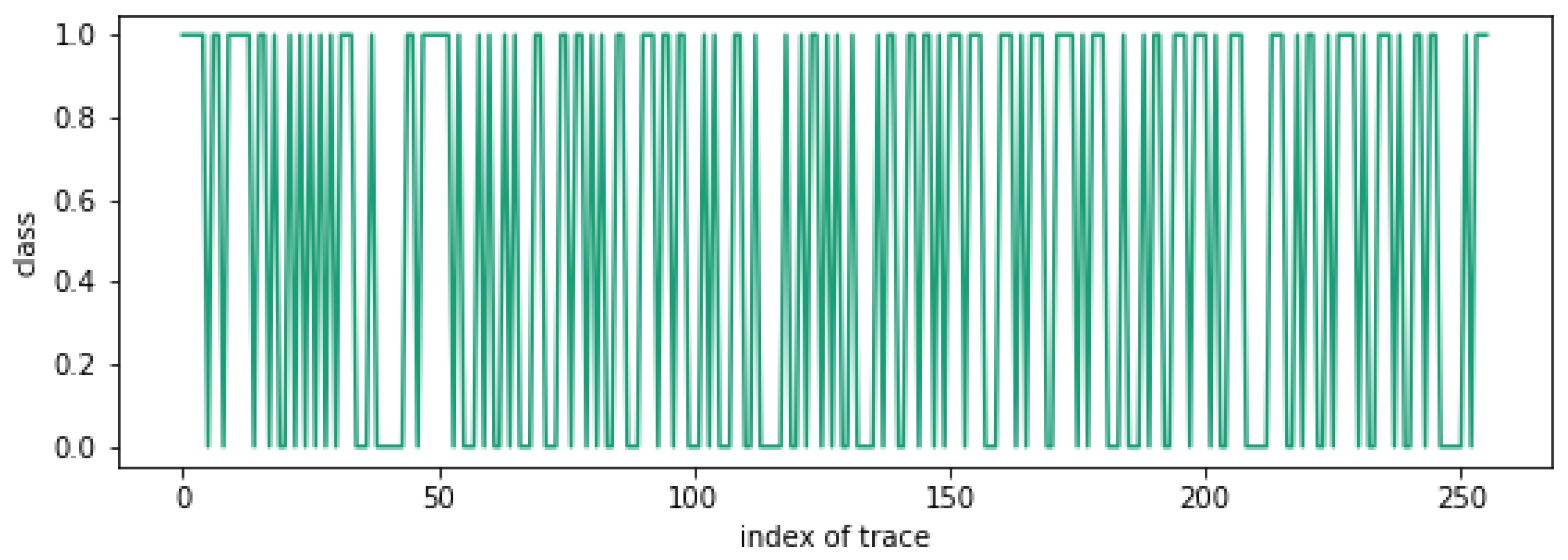
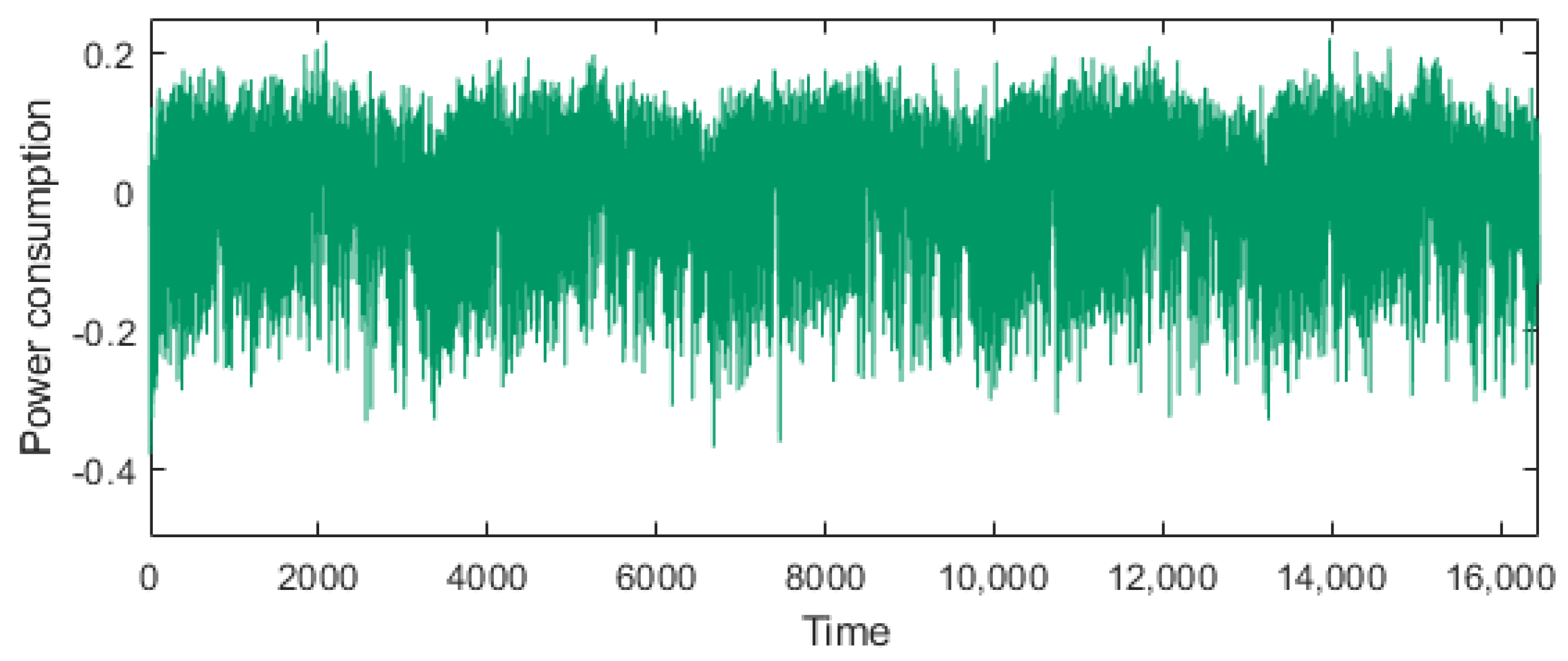

| Power Measurement Board | ChipWhisperer-Lite |
|---|---|
| Target chip | Atmel XMEGA128D4 |
| Number of AES traces | 256 |
| Sampling rate | 29.538 MS/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, J.; Han, D.-G. Improved Side-Channel Attack on CTR DRBG Using a Clustering Algorithm. Sensors 2025, 25, 4170. https://doi.org/10.3390/s25134170
Han J, Han D-G. Improved Side-Channel Attack on CTR DRBG Using a Clustering Algorithm. Sensors. 2025; 25(13):4170. https://doi.org/10.3390/s25134170
Chicago/Turabian StyleHan, Jaeseung, and Dong-Guk Han. 2025. "Improved Side-Channel Attack on CTR DRBG Using a Clustering Algorithm" Sensors 25, no. 13: 4170. https://doi.org/10.3390/s25134170
APA StyleHan, J., & Han, D.-G. (2025). Improved Side-Channel Attack on CTR DRBG Using a Clustering Algorithm. Sensors, 25(13), 4170. https://doi.org/10.3390/s25134170





