MLAD: A Multi-Task Learning Framework for Anomaly Detection
Abstract
1. Introduction
- We employ an unsupervised clustering strategy to group sensors into clusters and introduce a cluster-constrained GNN that enables the model to focus on sensor relationships within each cluster.
- We introduce a multi-task forecasting architecture to multivariate time-series anomaly detection that jointly learns global behaviors shared across all sensors and specialized patterns unique to each cluster of sensors, which finally benefits the performance of the downstream anomaly detection task.
- Extensive experiments on three public datasets show that MLAD outperforms state-of-the-art baselines, and ablation studies confirm the contribution of each module to its strong detection performance.
2. Related Work
2.1. Time-Series Anomaly Detection
2.2. Graph Neural Networks
2.3. Multi-Task Learning
3. Problem Statement
4. Methodology
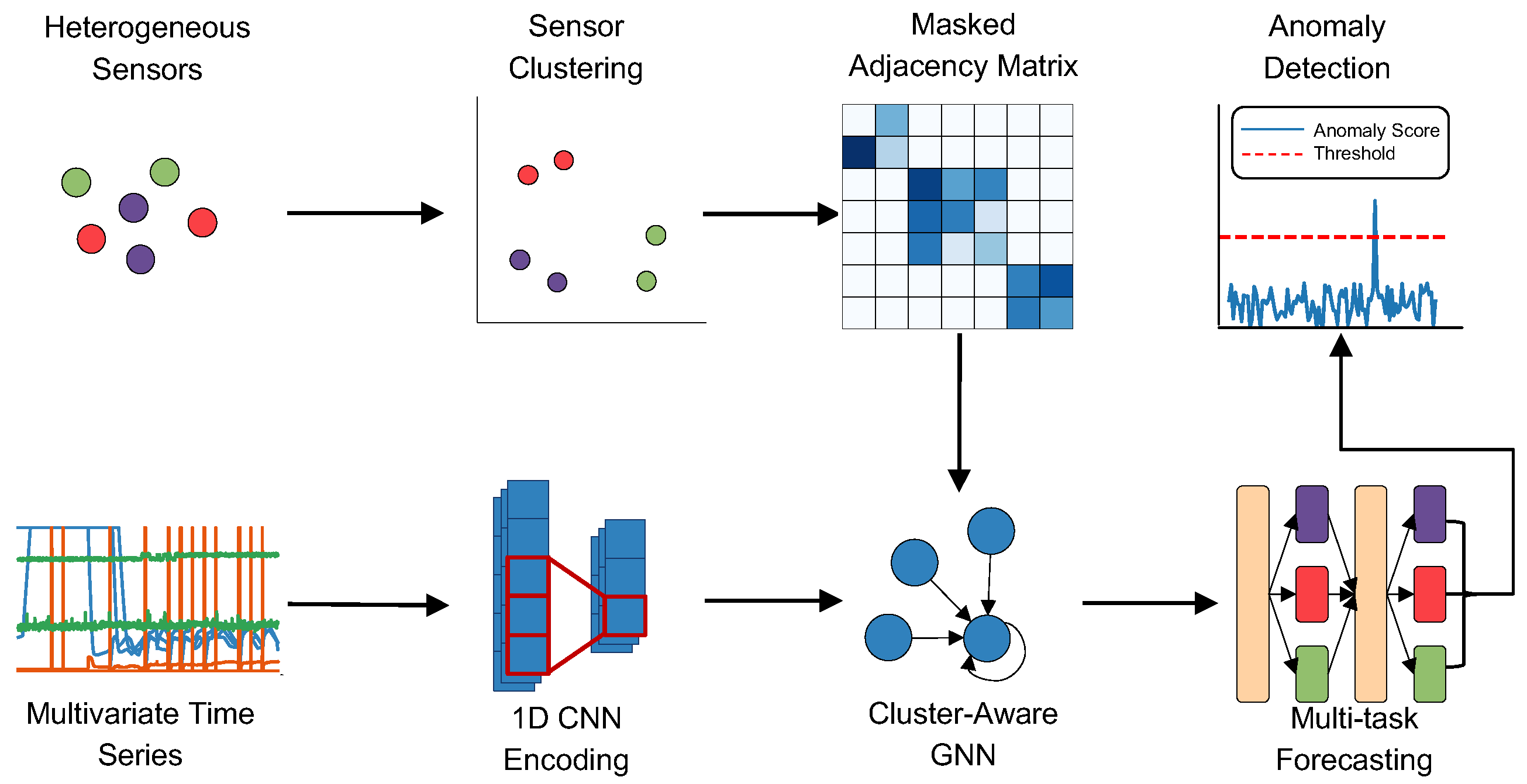
4.1. Overview of the Framework
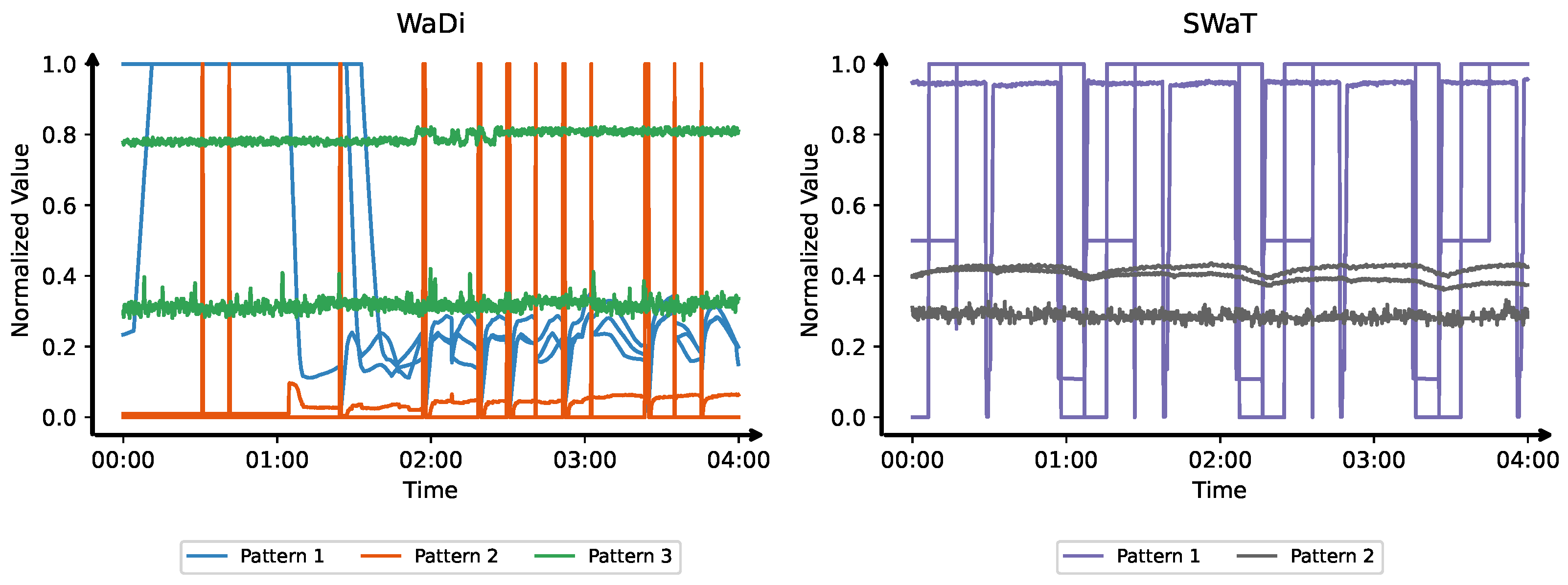
4.2. Sensor Clustering
4.3. GNN Learning with Cluster-Constrained Graph Construction
4.4. Multi-Task Forecasting
4.5. Anomaly Detection
5. Experiments
5.1. Experimental Settings
- SWaT [8] is collected from a scaled-down version of a real-world industrial water treatment testbed. The dataset comprises 11 days of multivariate sensor readings, divided into 7 days for training (normal data only) and 4 days for testing. During testing, anomalies are labeled based on a series of simulated attack scenarios. To ensure consistency with previous studies [10,11], we follow a common preprocessing approach: the first 21,600 samples are removed, and the data is downsampled by taking the median value over 10 s intervals.
- WaDi [7] is an extended version of the SWaT dataset, representing a more complex and larger-scale water distribution system. The training set includes 14 days of normal operation, while the test set contains 2 days of labeled attack data. As with SWaT, we remove the first 21,600 samples and apply 10-s median downsampling.
- SMD [29] (Server Machine Dataset) consists of time-series readings from 28 servers, each with 38 variables. However, prior studies have shown that 16 of these machines exhibit significant concept drift, which can confound anomaly detection performance [30]. Following [11], we focus only on the 12 machines with stable distributions and report averaged results across these selected subsets.
5.2. Overall Anomaly Detection Results
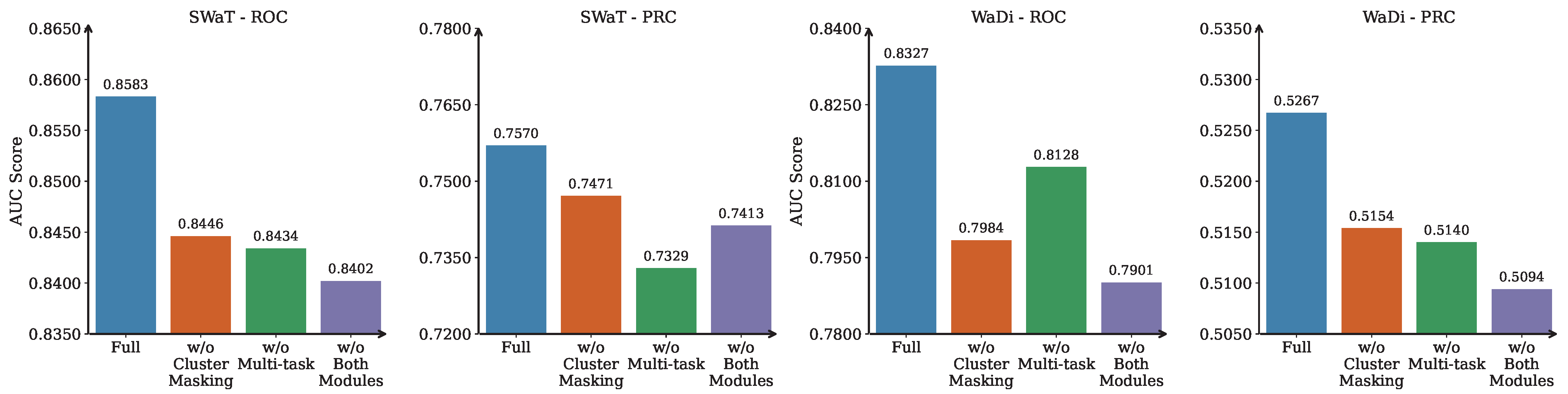
5.3. Ablation Study
6. Conclusions, Limitation, and Future Direction
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Blázquez-García, A.; Conde, A.; Mori, U.; Lozano, J.A. A Review on Outlier/Anomaly Detection in Time Series Data. ACM Comput. Surv. 2022, 54, 1–33. [Google Scholar] [CrossRef]
- Guato Burgos, M.F.; Morato, J.; Vizcaino Imacaña, F.P. A Review of Smart Grid Anomaly Detection Approaches Pertaining to Artificial Intelligence. Appl. Sci. 2024, 14, 1194. [Google Scholar] [CrossRef]
- Van Wyk, F.; Wang, Y.; Khojandi, A.; Masoud, N. Real-Time Sensor Anomaly Detection and Identification in Automated Vehicles. IEEE Trans. Intell. Transp. Syst. 2020, 21, 1264–1276. [Google Scholar] [CrossRef]
- Bałdyga, M.; Barański, K.; Belter, J.; Kalinowski, M.; Weichbroth, P. Anomaly Detection in Railway Sensor Data Environments: State-of-the-Art Methods and Empirical Performance Evaluation. Sensors 2024, 24, 2633. [Google Scholar] [CrossRef] [PubMed]
- Inoue, J.; Yamagata, Y.; Chen, Y.; Poskitt, C.M.; Sun, J. Anomaly Detection for a Water Treatment System Using Unsupervised Machine Learning. In Proceedings of the 2017 IEEE International Conference on Data Mining Workshops (ICDMW), New Orleans, LA, USA, 18–21 November 2017; pp. 1058–1065. [Google Scholar] [CrossRef]
- Ramotsoela, D.; Abu-Mahfouz, A.; Hancke, G. A Survey of Anomaly Detection in Industrial Wireless Sensor Networks with Critical Water System Infrastructure as a Case Study. Sensors 2018, 18, 2491. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, C.M.; Palleti, V.R.; Mathur, A.P. WADI: A Water Distribution Testbed for Research in the Design of Secure Cyber Physical Systems. In Proceedings of the 3rd International Workshop on Cyber-Physical Systems for Smart Water Networks, Pittsburgh, PA, USA, 21 April 2017; pp. 25–28. [Google Scholar] [CrossRef]
- Mathur, A.P.; Tippenhauer, N.O. SWaT: A Water Treatment Testbed for Research and Training on ICS Security. In Proceedings of the 2016 International Workshop on Cyber-physical Systems for Smart Water Networks (CySWater), Vienna, Austria, 11 April 2016; pp. 31–36. [Google Scholar] [CrossRef]
- Zamanzadeh Darban, Z.; Webb, G.I.; Pan, S.; Aggarwal, C.; Salehi, M. Deep Learning for Time Series Anomaly Detection: A Survey. ACM Comput. Surv. 2025, 57, 1–42. [Google Scholar] [CrossRef]
- Deng, A.; Hooi, B. Graph Neural Network-Based Anomaly Detection in Multivariate Time Series. Proc. AAAI Conf. Artif. Intell. 2021, 35, 4027–4035. [Google Scholar] [CrossRef]
- Zheng, Y.; Koh, H.Y.; Jin, M.; Chi, L.; Phan, K.T.; Pan, S.; Chen, Y.P.P.; Xiang, W. Correlation-Aware Spatial-Temporal Graph Learning for Multivariate Time-series Anomaly Detection. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 11802–11816. [Google Scholar] [CrossRef] [PubMed]
- Kozitsin, V.; Katser, I.; Lakontsev, D. Online Forecasting and Anomaly Detection Based on the ARIMA Model. Appl. Sci. 2021, 11, 3194. [Google Scholar] [CrossRef]
- Crépey, S.; Lehdili, N.; Madhar, N.; Thomas, M. Anomaly Detection in Financial Time Series by Principal Component Analysis and Neural Networks. Algorithms 2022, 15, 385. [Google Scholar] [CrossRef]
- Ma, J.; Perkins, S. Time-Series Novelty Detection Using One-Class Support Vector Machines. In Proceedings of the International Joint Conference on Neural Networks, Portland, OR, USA, 20–24 July 2003; Volume 3, pp. 1741–1745. [Google Scholar] [CrossRef]
- Sgueglia, A.; Di Sorbo, A.; Visaggio, C.A.; Canfora, G. A Systematic Literature Review of IoT Time Series Anomaly Detection Solutions. Future Gener. Comput. Syst. 2022, 134, 170–186. [Google Scholar] [CrossRef]
- Che, Z.; Purushotham, S.; Cho, K.; Sontag, D.; Liu, Y. Recurrent Neural Networks for Multivariate Time Series with Missing Values. Sci. Rep. 2018, 8, 6085. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Dong, Y. Temperature Forecasting via Convolutional Recurrent Neural Networks Based on Time-Series Data. Complexity 2020, 2020, 1–8. [Google Scholar] [CrossRef]
- Lin, S.; Clark, R.; Birke, R.; Schonborn, S.; Trigoni, N.; Roberts, S. Anomaly Detection for Time Series Using VAE-LSTM Hybrid Model. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 4322–4326. [Google Scholar] [CrossRef]
- Jin, M.; Koh, H.Y.; Wen, Q.; Zambon, D.; Alippi, C.; Webb, G.I.; King, I.; Pan, S. A Survey on Graph Neural Networks for Time Series: Forecasting, Classification, Imputation, and Anomaly Detection. arXiv 2024. [Google Scholar] [CrossRef] [PubMed]
- Ning, Z.; Jiang, Z.; Miao, H.; Wang, L. MST-GNN: A Multi-scale Temporal-Enhanced Graph Neural Network for Anomaly Detection in Multivariate Time Series. In Web and Big Data; Li, B., Yue, L., Tao, C., Han, X., Calvanese, D., Amagasa, T., Eds.; Springer Nature: Cham, Switzerland, 2023; Volume 13421, pp. 382–390. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, Q. A Survey on Multi-Task Learning. IEEE Trans. Knowl. Data Eng. 2022, 34, 5586–5609. [Google Scholar] [CrossRef]
- Yu, J.; Dai, Y.; Liu, X.; Huang, J.; Shen, Y.; Zhang, K.; Zhou, R.; Adhikarla, E.; Ye, W.; Liu, Y.; et al. Unleashing the Power of Multi-Task Learning: A Comprehensive Survey Spanning Traditional, Deep, and Pretrained Foundation Model Eras. arXiv 2024. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, Y.; Yang, Q. Multi-Task Learning in Natural Language Processing: An Overview. ACM Comput. Surv. 2024, 56, 1–32. [Google Scholar] [CrossRef]
- Kapidis, G.; Poppe, R.; Veltkamp, R.C. Multi-Dataset, Multitask Learning of Egocentric Vision Tasks. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 6618–6630. [Google Scholar] [CrossRef] [PubMed]
- Feng, X.; Liu, Z.; Wu, W.; Zuo, W. Social Recommendation via Deep Neural Network-Based Multi-Task Learning. Expert Syst. Appl. 2022, 206, 117755. [Google Scholar] [CrossRef]
- McInnes, L.; Healy, J.; Melville, J. UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction. arXiv 2018. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; KDD’96; pp. 226–231. [Google Scholar]
- Wu, Z.; Pan, S.; Long, G.; Jiang, J.; Chang, X.; Zhang, C. Connecting the Dots: Multivariate Time Series Forecasting with Graph Neural Networks. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual Event, 6–10 July 2020; pp. 753–763. [Google Scholar] [CrossRef]
- Su, Y.; Zhao, Y.; Niu, C.; Liu, R.; Sun, W.; Pei, D. Robust Anomaly Detection for Multivariate Time Series through Stochastic Recurrent Neural Network. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2828–2837. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, Y.; Han, J.; Su, Y.; Jiao, R.; Wen, X.; Pei, D. Multivariate Time Series Anomaly Detection and Interpretation Using Hierarchical Inter-Metric and Temporal Embedding. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Singapore, 14–18 August 2021; pp. 3220–3230. [Google Scholar] [CrossRef]
- Audibert, J.; Michiardi, P.; Guyard, F.; Marti, S.; Zuluaga, M.A. USAD: UnSupervised Anomaly Detection on Multivariate Time Series. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual Event, CA, USA, 6–10 July 2020; pp. 3395–3404. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, Y.; Duan, J.; Huang, C.; Cao, D.; Tong, Y.; Xu, B.; Bai, J.; Tong, J.; Zhang, Q. Multivariate Time-Series Anomaly Detection via Graph Attention Network. In Proceedings of the 2020 IEEE International Conference on Data Mining (ICDM), Sorrento, Italy, 17–20 November 2020; pp. 841–850. [Google Scholar] [CrossRef]
| SWaT | WADI | SMD | ||||
|---|---|---|---|---|---|---|
| AUC-ROC | AUC-PRC | AUC-ROC | AUC-PRC | AUC-ROC | AUC-PRC | |
| PCA | 0.8257 ± 0.0000 | 0.7298 ± 0.0000 | 0.5597 ± 0.0000 | † 0.2731 ± 0.0000 | 0.6742 ± 0.0000 | 0.2189 ± 0.0000 |
| Kmeans | 0.7391 ± 0.0000 | 0.2418 ± 0.0000 | † 0.6030 ± 0.0000 | 0.1158 ± 0.0000 | 0.5855 ± 0.0000 | 0.1308 ± 0.0000 |
| AutoEncoder | 0.8311 ± 0.0088 | 0.7224 ± 0.0094 | 0.5291 ± 0.0285 | 0.2210 ± 0.0205 | 0.8270 ± 0.0008 | 0.4388 ± 0.0046 |
| USAD | 0.8213 ± 0.0056 | 0.7087 ± 0.0055 | 0.5535 ± 0.0103 | 0.1945 ± 0.0008 | 0.7888 ± 0.0077 | 0.4686 ± 0.0011 |
| MTAD-GAT | 0.8261 ± 0.0040 | 0.7176 ± 0.0043 | 0.4119 ± 0.0295 | 0.0729 ± 0.0013 | † 0.8576 ± 0.0035 | † 0.5057 ± 0.0082 |
| THOC | † 0.8380 ± 0.0051 | † 0.7440 ± 0.0063 | 0.4840 ± 0.0112 | 0.1440 ± 0.0020 | 0.8512 ± 0.0045 | 0.4852 ± 0.0063 |
| GDN | 0.8124 ± 0.0177 | 0.7135 ± 0.0035 | 0.4725 ± 0.0056 | 0.0521 ± 0.0070 | 0.8443 ± 0.0150 | 0.4684 ± 0.0142 |
| CST-GL | * 0.8520 ± 0.0022 | 0.7628 ± 0.0032 | * 0.8283 ± 0.0179 | 0.5477 ± 0.0197 | * 0.8604 ± 0.0131 | * 0.5132 ± 0.0273 |
| MLAD (ours) | 0.8583 ± 0.0025 | * 0.7570 ± 0.0050 | 0.8327 ± 0.0040 | * 0.5267 ± 0.0034 | 0.8703 ± 0.0078 | 0.5204 ± 0.0031 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, K.; Tang, Z.; Liang, S.; Li, Z.; Liang, B. MLAD: A Multi-Task Learning Framework for Anomaly Detection. Sensors 2025, 25, 4115. https://doi.org/10.3390/s25134115
Li K, Tang Z, Liang S, Li Z, Liang B. MLAD: A Multi-Task Learning Framework for Anomaly Detection. Sensors. 2025; 25(13):4115. https://doi.org/10.3390/s25134115
Chicago/Turabian StyleLi, Kunqi, Zhiqin Tang, Shuming Liang, Zhidong Li, and Bin Liang. 2025. "MLAD: A Multi-Task Learning Framework for Anomaly Detection" Sensors 25, no. 13: 4115. https://doi.org/10.3390/s25134115
APA StyleLi, K., Tang, Z., Liang, S., Li, Z., & Liang, B. (2025). MLAD: A Multi-Task Learning Framework for Anomaly Detection. Sensors, 25(13), 4115. https://doi.org/10.3390/s25134115






