A Look-Up Table Assisted BiLSTM Neural Network Based Digital Predistorter for Wireless Communication Infrastructure
Abstract
1. Introduction
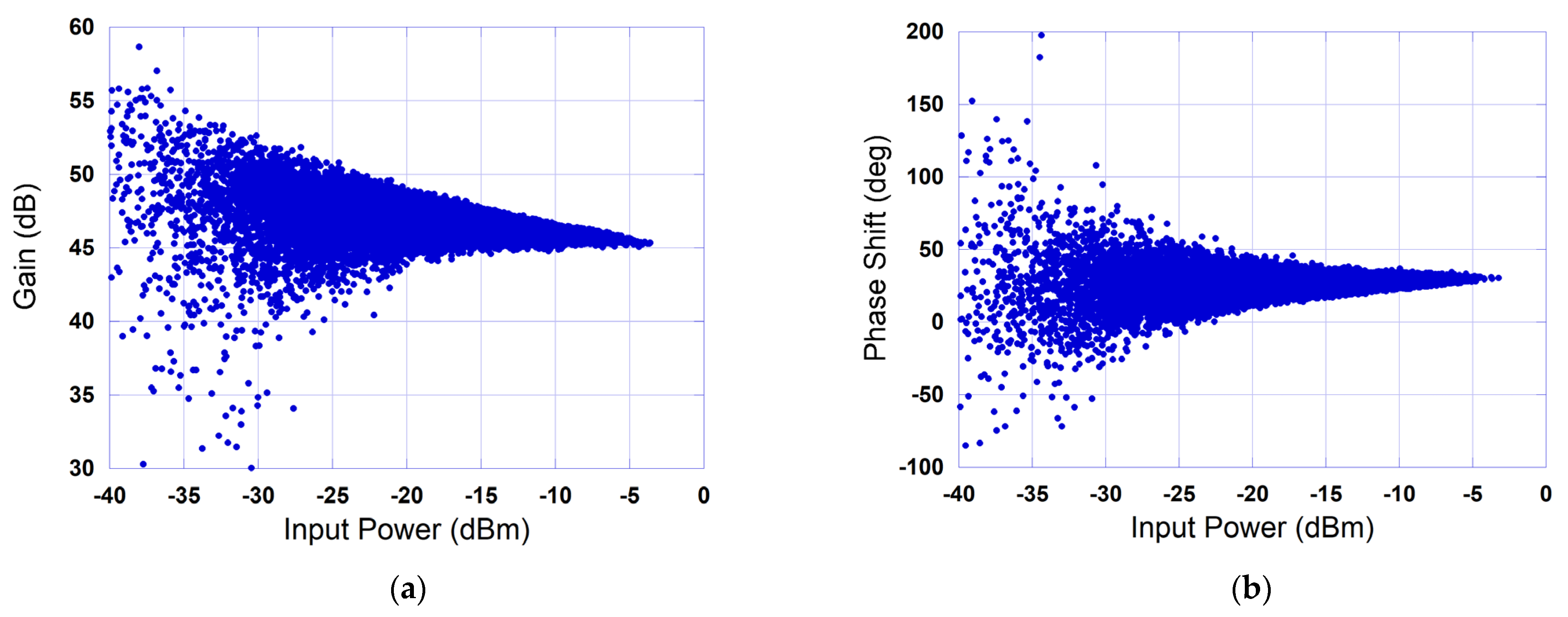
2. Limitation of Single Box Models
3. Proposed LUT-A-BiNN Predistorter Architecture
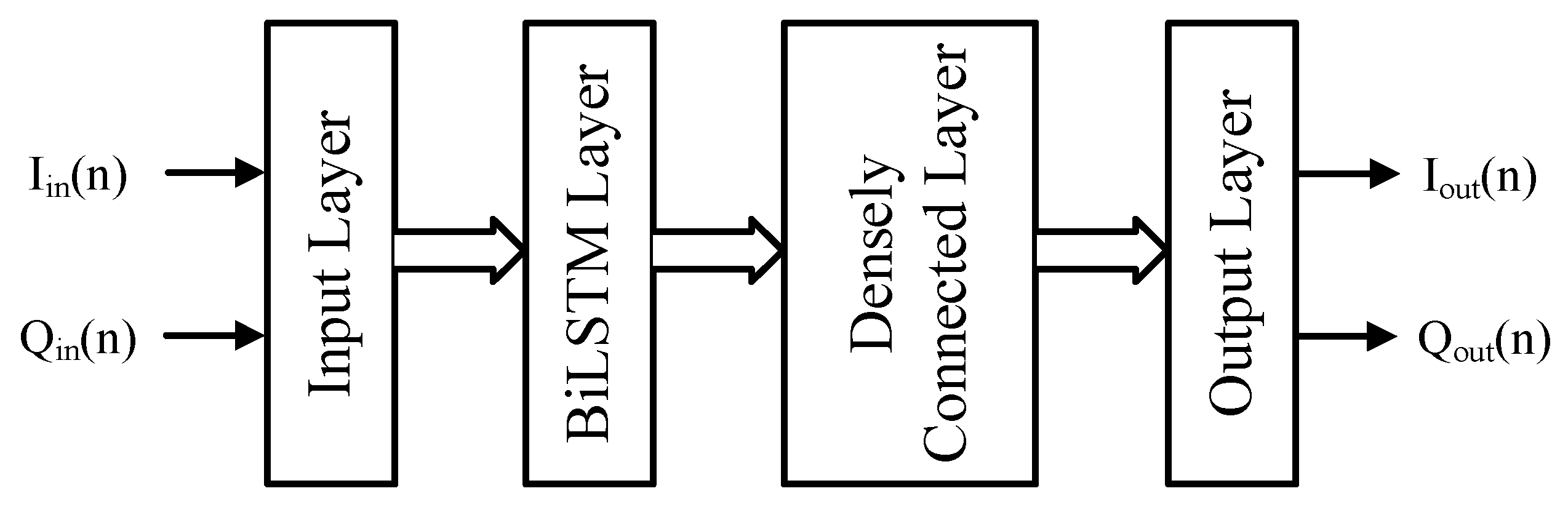
3.1. BiLSTM Neural Networks Architecture
3.2. LUT-Assisted BiLSTM Neural Network Architecture
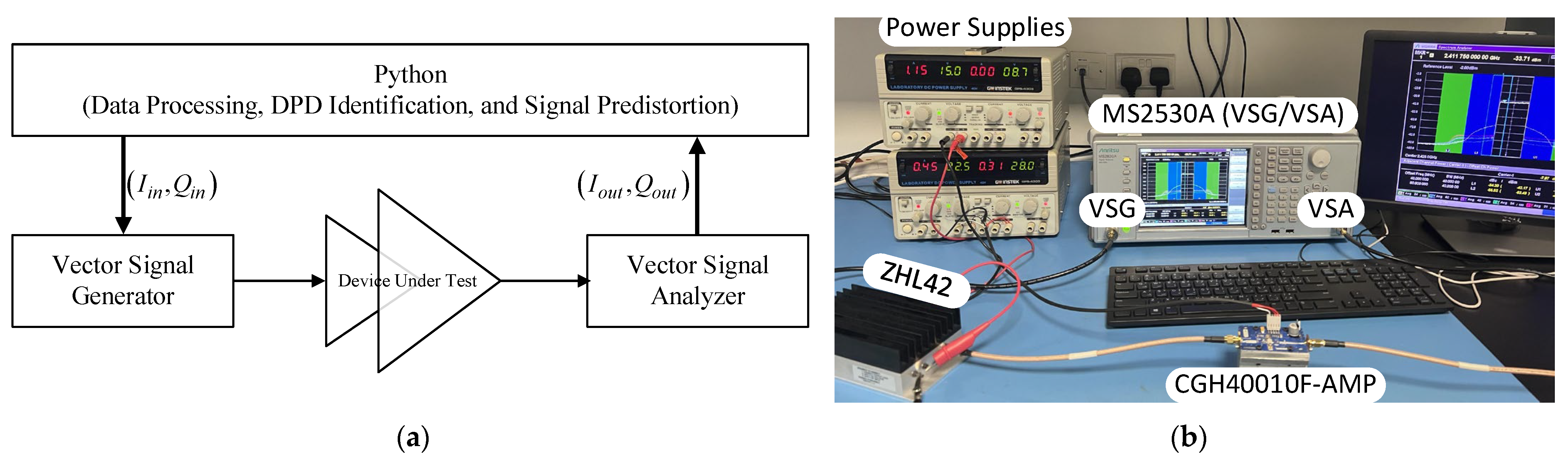
4. Experimental Validation and Performance Benchmarking
4.1. Experimental Setup
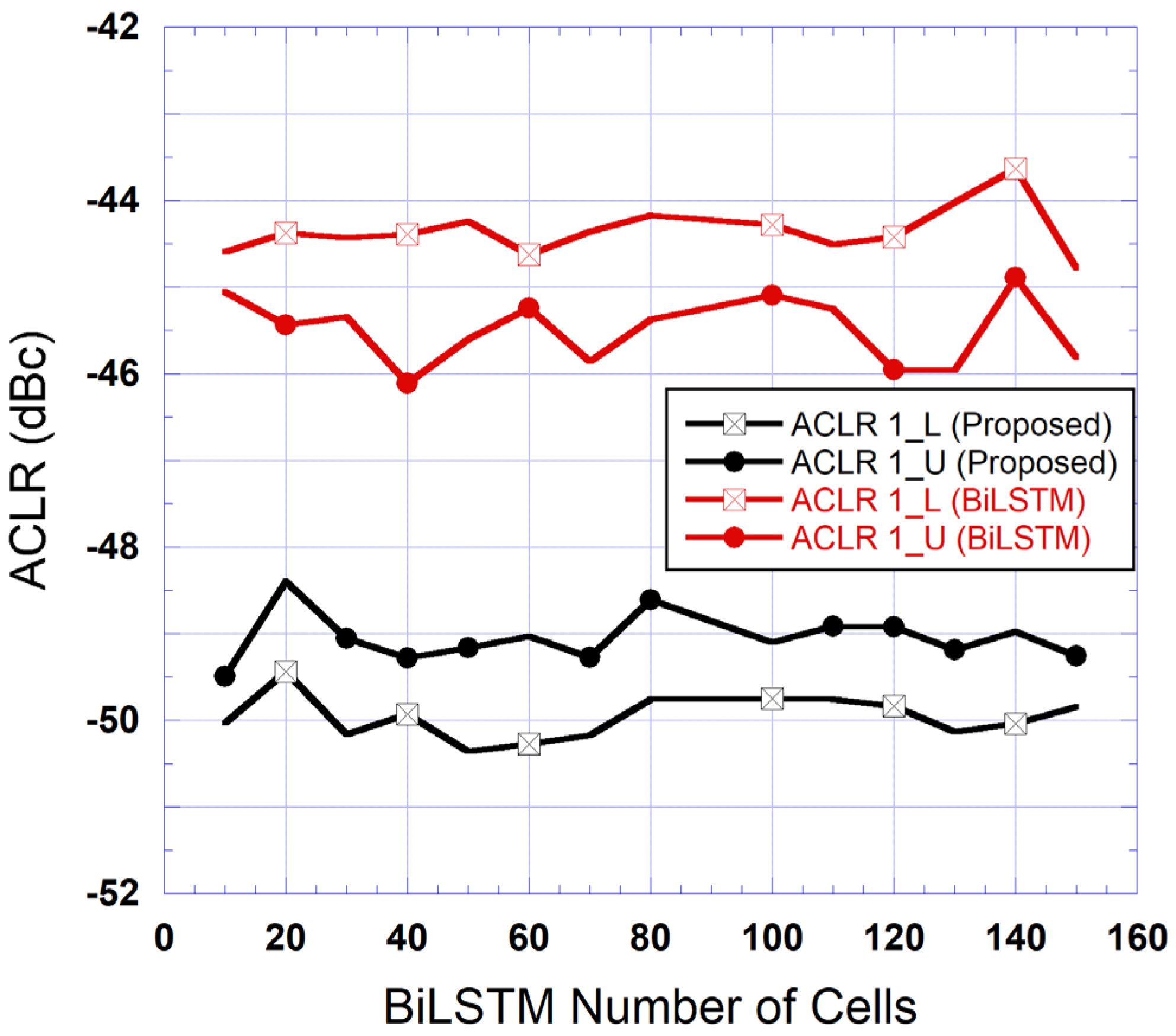
4.2. BiLSTM DPD
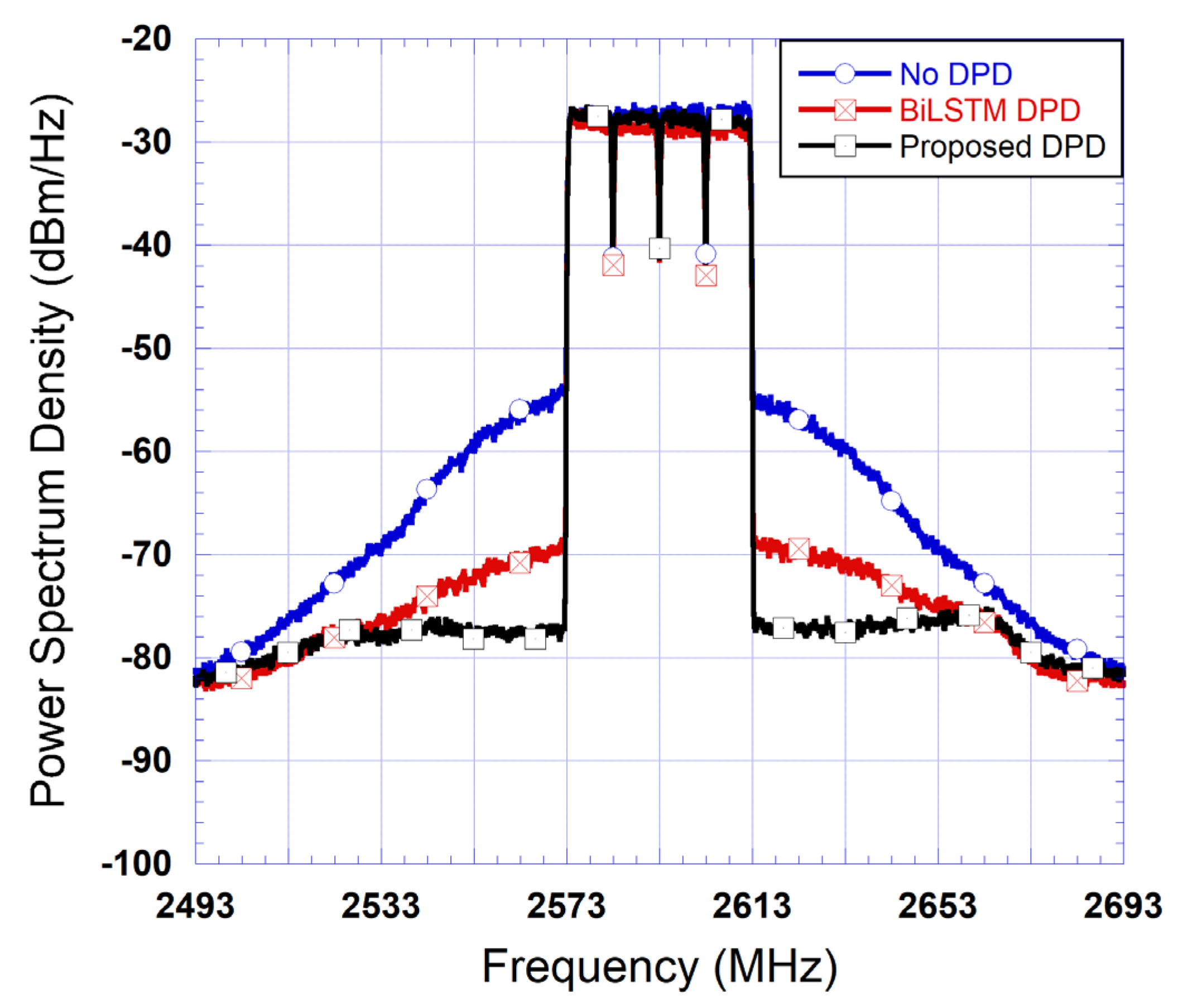
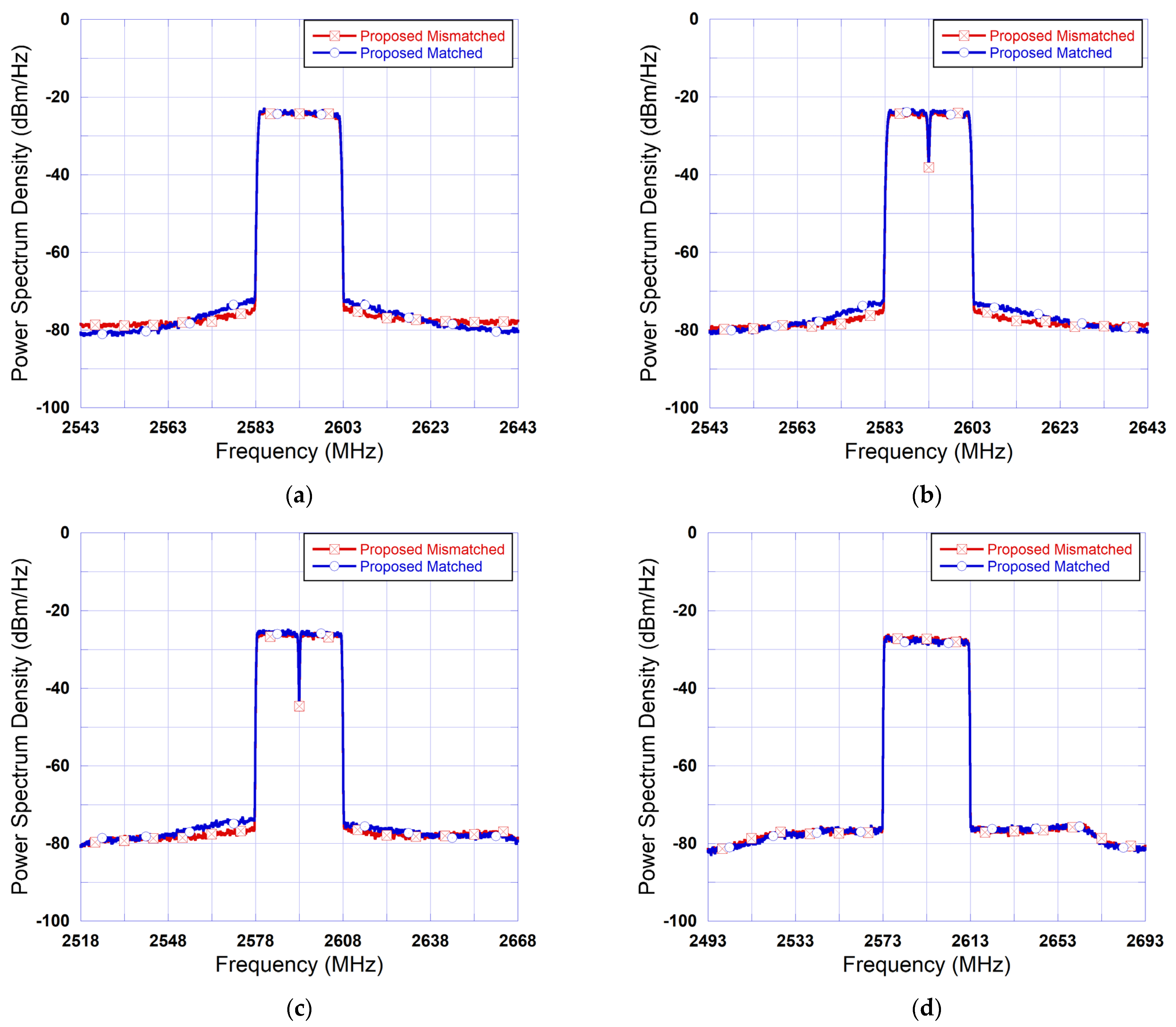
4.3. Performance Validation of the LUT-Assisted BiLSTM DPD
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ghannouchi, F.M.; Hammi, O.; Helaoui, M. Behavioral Modeling and Predistortion of Wideband Wireless Transmitters; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar] [CrossRef]
- Ghannouchi, F.M.; Hammi, O. Behavioral Modeling and Predistortion. IEEE Microw. Mag. 2009, 10, 52–64. [Google Scholar] [CrossRef]
- Guan, L.; Zhu, A. Green Communications: Digital Predistortion for Wideband RF Power Amplifiers. IEEE Microw. Mag. 2014, 15, 84–99. [Google Scholar] [CrossRef]
- Katz, A.; Wood, J.; Chokola, D. The Evolution of PA Linearization: From Classic Feedforward and Feedback Through Analog and Digital Predistortion. IEEE Microw. Mag. 2016, 17, 32–40. [Google Scholar] [CrossRef]
- Li, Y.; Wang, X.; Zhu, A. Complexity-reduced Model Adaptation for Digital Predistortion of RF Power Amplifiers with Pretraining-based Feature Extraction. IEEE Trans. Microw. Theory Technol. 2021, 69, 1780–1790. [Google Scholar] [CrossRef]
- Wang, X.; Li, Y.; Yin, H.; Yu, C.; Yu, Z.; Hong, W.; Zhu, A. Digital Predistortion of 5G Multiuser MIMO Transmitters using Low-Dimensional Feature-Based Model Generation. IEEE Trans. Microw. Theory Technol. 2022, 70, 1509–1520. [Google Scholar] [CrossRef]
- Jalili, F.; Tafuri, F.F.; Jensen, O.K.; Chen, Q.; Shen, M.; Pedersen, G.F. Bandwidth-Scalable Digital Predistortion of Active Phased Array using Transfer Learning Neural Network. IEEE Access 2023, 11, 13877–13888. [Google Scholar] [CrossRef]
- Rawat, M.; Rawat, K.; Ghannouchi, F.M. Adaptive Digital Predistortion of Wireless Power Amplifiers/Transmitters using Dynamic Real-Valued Focused Time-Delay Line Neural Networks. IEEE Trans. Microw. Theory Technol. 2010, 58, 95–104. [Google Scholar] [CrossRef]
- Rosołowski, D.W.; Jędrzejewski, K. Experimental Evaluation of PA Digital Predistortion Based on Simple Feedforward Neural Network. In Proceedings of the 2020 23rd International Microwave and Radar Conference, Warsaw, Poland, 5–8 October 2020. [Google Scholar] [CrossRef]
- Wang, D.; Aziz, M.; Helaoui, M.; Ghannouchi, F.M. Augmented Real-Valued Time-Delay Neural Network for Compensation of Distortions and Impairments in Wireless Transmitters. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 242–254. [Google Scholar] [CrossRef]
- Hu, X.; Liu, Z.; Yu, X.; Zhao, Y.; Chen, W.; Hu, B.; Du, X.; Li, X.; Helaoui, M.; Wang, W.; et al. Convolutional Neural Network for Behavioral Modeling and Predistortion of Wideband Power Amplifiers. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 3923–3937. [Google Scholar] [CrossRef]
- Jaraut, P.; Abdelhafiz, A.; Chenini, H.; Hu, X.; Helaoui, M.; Rawat, M.; Chen, W.; Boulejfen, N.; Ghannouchi, F.M. Augmented Convolutional Neural Network for Behavioral Modeling and Digital Predistortion of Concurrent Multiband Power Amplifiers. IEEE Trans. Microw. Theory Technol. 2021, 69, 4142–4156. [Google Scholar] [CrossRef]
- Jaraut, P.; Dhar, S.; Helaoui, M.; Boulejfen, N.; Rawat, M.; Chen, W.; Rawat, K.; Outaleb, N.; Ghannouchi, F.M. Behavioral Modeling and Digital Predistortion of Mismatched Wireless Transmitters using Convolution Neural Networks. IEEE Trans. Circuits Syst. II Exp. Briefs 2023, 70, 336–340. [Google Scholar] [CrossRef]
- Motaqi, A.; Helaoui, M.; Boulejfen, N.; Chen, W.; Ghannouchi, F.M. Artificial Intelligence-Based Power-Temperature Inclusive Digital Predistortion. IEEE Trans. Ind. Electron. 2022, 69, 13872–13880. [Google Scholar] [CrossRef]
- Ali, A.; Hammi, O. Bandwidth, Power and Carrier Configuration Resilient Neural Networks Digital Predistorter. IEEE Access 2023, 11, 63126–63135. [Google Scholar] [CrossRef]
- Sun, J.; Shi, W.; Yang, Z.; Yang, J.; Gui, G. Behavioral Modeling and Linearization of Wideband RF Power Amplifiers using BiLSTM Networks for 5G Wireless Systems. IEEE Trans. Veh. Technol. 2019, 68, 10348–10356. [Google Scholar] [CrossRef]
- Fischer-Buhner, A.; Anttila, L.; Dev Gomony, M.; Valkama, M. Recursive Neural Network with Phase-Normalization for Modeling and Linearization of RF Power Amplifiers. IEEE Microw. Wireless. Technol. Lett. 2024, 34, 809–812. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Y.; Liu, F.; Zhu, A. Vector Decomposition Based Time-Delay Neural Network Behavioral Model for Digital Predistortion of RF Power Amplifiers. IEEE Access 2019, 7, 91559–91568. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Y.; Li, G.; Liu, F. Vetor Decomposed Long Short-Term Memory Model for Behavioral Modeling and Digital Predistortion for Wideband Power Amplifiers. IEEE Access 2020, 8, 63780–63789. [Google Scholar] [CrossRef]
- Liu, T.; Boumaiza, S.; Ghannouchi, F.M. Deembedding Static Nonlinearities and Accurately Identifying and Modeling Memory Effects in Wide-band RF Transmitters. IEEE Trans. Microw. Theory Technol. 2005, 53, 3578–3587. [Google Scholar] [CrossRef]
- Morgan, D.R.; Ma, Z.; Kim, J.; Zierdt, M.G.; Pastalan, J. A Generalized Memory Polynomial Model for Digital Predistortion of RF Power Amplifiers. IEEE Trans. Signal Process. 2006, 54, 3852–3860. [Google Scholar] [CrossRef]
- Gilabert, P.; Montoro, G.; Bertran, E. On the Wiener and Hammerstein Models for Power Amplifier Predistortion. In Proceedings of the Asia Pacific Microwave Conference, Suzhou, China, 4–7 December 2005. [Google Scholar] [CrossRef]
- Liu, T.; Boumaiza, S.; Ghannouchi, F.M. Augmented Hammerstein Predistroter for Linearization of Broad-band Wireless Transmitters. IEEE Trans. Microw. Theory Technol. 2006, 54, 1340–1349. [Google Scholar] [CrossRef]
- Hammi, O.; Ghannouchi, F.M. Twin Nonlinear Twobox Models for Power Amplifiers and Transmitters Exhibiting Memory Effects with Application to Digital Predistortion. IEEE Microw. Wirel. Compon. Lett. 2009, 19, 530–532. [Google Scholar] [CrossRef]
- Wang, S.; Hussein, M.A.; Venard, O.; Baudoin, G. Identification of Low Order Cascaded Digital Predistortion with Different-Structure Stages for Linearization of Power Amplifiers. In Proceedings of the 2018 IEEE Topical Conference on RF/Microwave Power Amplifiers for Radio and Wireless Applications (PAWR), Anaheim, CA, USA, 14–17 January 2018. [Google Scholar] [CrossRef]
- Abdelnaby, M.; Alnajjar, R.; Bensmida, S.; Hammi, O. Reduced Complexity Sequential Digital Predistortion Technique for 5G Applications. Smart Cities 2024, 7, 772–785. [Google Scholar] [CrossRef]
- Hammi, O.; Kwan, A.; Bensmida, S.; Morris, K.A.; Ghannouchi, F.M. A Digital Predistortion System With Extended Correction Bandwidth With Application to LTE-A Nonlinear Power Amplifiers. IEEE Trans. Circuits Syst. I Reg. Pap. 2014, 61, 3487–3495. [Google Scholar] [CrossRef]
- Abdelhafiz, A.; Kwan, A.; Hammi, O.; Ghannouchi, F.M. Digital Predistortion of LTE-A Power Amplifiers using Compressed-Sampling-Based Unstructured Pruning of Volterra Series. IEEE Trans. Microw. Theory Technol. 2014, 62, 2583–2593. [Google Scholar] [CrossRef]
- Chang, H.; Han, R.; Jiang, C.; Yang, G.; Zhang, Q.; Wang, J. Dual Feature Indexed Quadratic Polynomial-Based Piecewise Behavioral Model for Digital Predistortion of RF Power Amplifiers. IEEE Trans. Broadcast. 2024, 70, 1302–1315. [Google Scholar] [CrossRef]
- Hemsi, C.S.; Panazio, C.M. Sparse Flexible Reduced-Volterra Model for Power Amplifier Digital Pre-Distortion. IEEE Access 2022, 10, 121970–121984. [Google Scholar] [CrossRef]
- Crespo-Cadenas, C.; Madero-Ayora, M.J.; Becerra, J.A.; Cruces, S. A Sparse-Bayesian Approach for the Design of Robust Digital Predistorters Under Power-Varying Operation. IEEE Trans. Microw. Theory Technol. 2022, 70, 4218–4230. [Google Scholar] [CrossRef]
- Sundermeyer, M.; Ney, H.; Schlüter, R. From feedforward to recurrent LSTM neural networks for language modeling. IEEE/ACM Trans. Audio Speech Lang. Process. 2015, 23, 517–529. [Google Scholar] [CrossRef]
- Jahangir, H.; Tayarani, H.; Gougheri, S.S.; Golkar, M.A.; Ahmadian, A.; Elkamel, A. Deep learning-based forecasting approach in smart grids with microclustering and bidirectional LSTM network. IEEE Trans. Ind. Electron. 2021, 68, 8298–8309. [Google Scholar] [CrossRef]

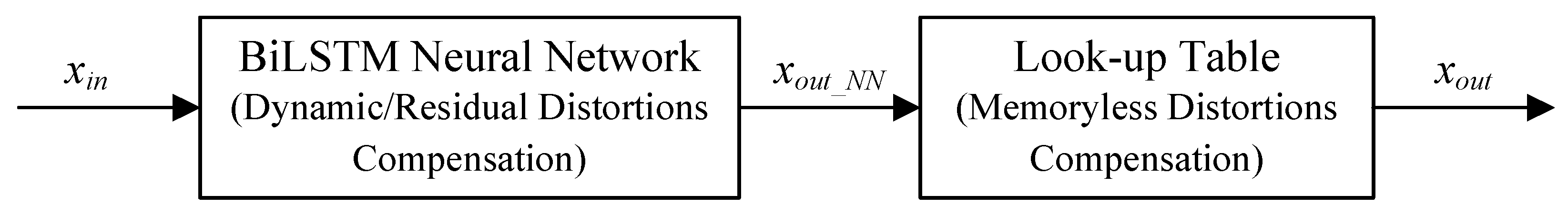

| Signal | Bandwidth | Number of Carriers | Sampling Rate | PAPR |
|---|---|---|---|---|
| 10 MHz (1C) | 10 MHz | 1 | 122.8 Msps | 10.4 dB |
| 20 MHz (1C) | 20 MHz | 1 | 122.8 Msps | 10.4 dB |
| 20 MHz (2C) | 20 MHz | 2 | 122.8 Msps | 10.5 dB |
| 30 MHz (2C) | 30 MHz | 2 | 153.6 Msps | 10.5 dB |
| 40 MHz (1C) | 40 MHz | 1 | 153.6 Msps | 10.5 dB |
| 40 MHz (4C) | 40 MHz | 4 | 153.6 Msps | 10.7 dB |
| Metric | RVTDNN | CNN | Vanilla LSMT | Stacked LSTM | BiLSTM |
|---|---|---|---|---|---|
| ACLR Upper | |||||
| ACLR Lower |
| DPD Type | ACLR1 [dBc] | ACLR2 [dBc] | ||
|---|---|---|---|---|
| Lower | Upper | Lower | Upper | |
| No DPD | ||||
| LUT DPD | ||||
| MP DPD | ||||
| BiLSTM DPD (NLSTM = 10) | ||||
| BiLSTM DPD (NLSTM = 150) | ||||
| Proposed DPD (NLSTM = 10) | ||||
| Signal | DPD | ACLR1 [dBc] | ACLR2 [dBc] | ||
|---|---|---|---|---|---|
| Lower | Upper | Lower | Upper | ||
| 10 MHz (1C) | Proposed Matched | ||||
| Proposed Mismatched | |||||
| BiLSTM Mismatched | |||||
| 20 MHz (1C) | Proposed Matched | ||||
| Proposed Mismatched | |||||
| BiLSTM Mismatched | |||||
| 20 MHz (2C) | Proposed Matched | ||||
| Proposed Mismatched | |||||
| BiLSTM Mismatched | |||||
| 30 MHz (2C) | Proposed Matched | ||||
| Proposed Mismatched | |||||
| BiLSTM Mismatched | |||||
| 40 MHz (1C) | Proposed Matched | ||||
| Proposed Mismatched | |||||
| BiLSTM Mismatched | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al Najjar, R.; Hammi, O. A Look-Up Table Assisted BiLSTM Neural Network Based Digital Predistorter for Wireless Communication Infrastructure. Sensors 2025, 25, 4099. https://doi.org/10.3390/s25134099
Al Najjar R, Hammi O. A Look-Up Table Assisted BiLSTM Neural Network Based Digital Predistorter for Wireless Communication Infrastructure. Sensors. 2025; 25(13):4099. https://doi.org/10.3390/s25134099
Chicago/Turabian StyleAl Najjar, Reem, and Oualid Hammi. 2025. "A Look-Up Table Assisted BiLSTM Neural Network Based Digital Predistorter for Wireless Communication Infrastructure" Sensors 25, no. 13: 4099. https://doi.org/10.3390/s25134099
APA StyleAl Najjar, R., & Hammi, O. (2025). A Look-Up Table Assisted BiLSTM Neural Network Based Digital Predistorter for Wireless Communication Infrastructure. Sensors, 25(13), 4099. https://doi.org/10.3390/s25134099







