1. Introduction
A coordinate measuring machine (CMM) is a measuring instrument that uses point acquisition to create geometric elements in order to verify the conformity of a manufactured part to its nominal definition in terms of both dimensions and shapes. More precisely, point acquisition means acquiring the three-dimensional coordinates of points in a reference frame linked to the part or machine itself. This ability to measure different types of characteristics with a single instrument makes these machines very interesting, though not perfect.
Whatever the acquisition technology is, every point coordinate is subject to measurement uncertainty, which is consequently propagated to the creation of the associated geometric elements, in terms of dimension, shape, orientation, and position.
Coordinate measuring machines (CMMs) are used for their accuracy, within an acceptance tolerance, and are verified using calibrated standards [
1]. However, the methods used to carry out the measurements do not allow us to assess the uncertainty of measurement on a conventional part [
2].
The study of the influence of CMM servo-control on measurements is rarely described in depth in the literature. A great deal of research has been carried out since the 1970s to improve the servo-control of machine tools [
3,
4], but the work on CMM servo-control has not been sufficiently developed. Coorevits [
5] addresses the problem of different probing errors, which are also presented by Bouaziz [
6]. They distinguish between the error on the approach vector and the tangential one on measurements of points, with the latter fault being described as a servo-control defect in [
6], which is negligible for large curvature and fine roughness. Servo influence on features other than points is not treated.
In a few cases, particularly when measuring circles on axisymmetrical skewed surfaces, servo-control errors lead to measurement faults that misinterpret the actual geometry of the part.
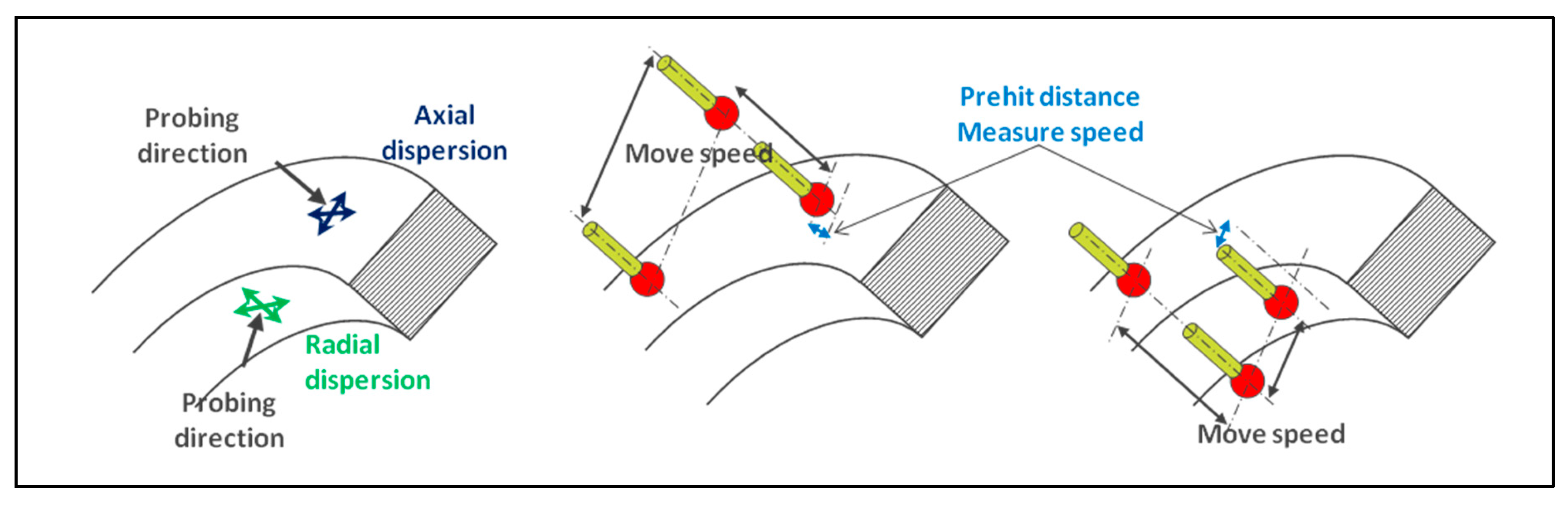
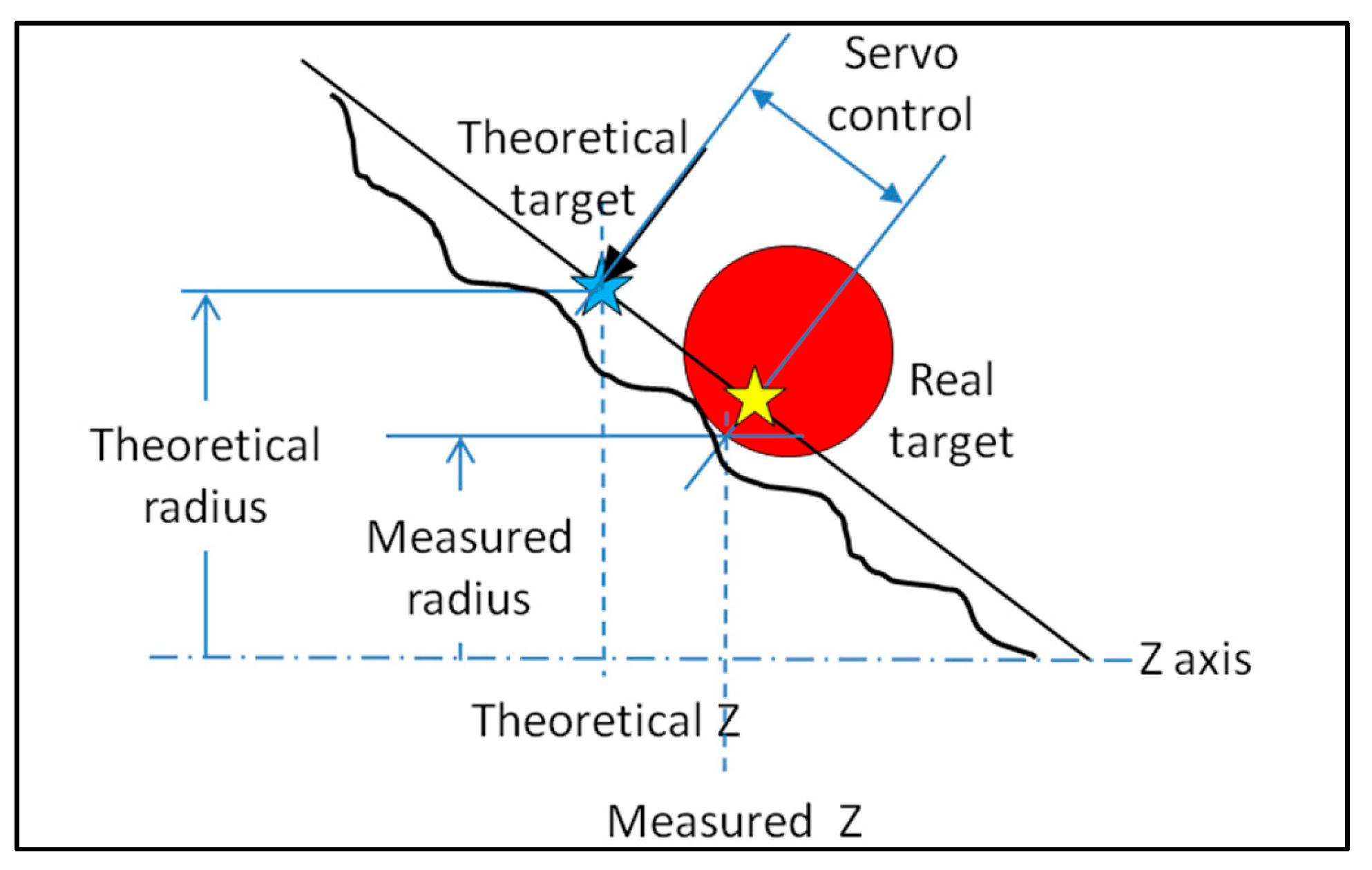
Servo-control defines the function between CMM movements and the actual position read on the measuring scales. Machine movements between two measured points can be broken down into three phases: retraction, displacement, and approach. These movements are generated at different speeds and accelerations depending on the distance between points. The speed decreases to measuring speed when the pre-hit distance is reached [
5]. In continuous scanning mode, speed and acceleration are set in the measurement parameters. This real-time adjustment is not as precise as the readout position, so there may be a difference of a few micrometers between the theoretical target and the actual target.
The servo-control neither affects the acceptance test nor the most conventional surface dimensions (planes, cylinders, etc.), especially when the associated element is constructed from center ball hits, before ball compensation. Despite being measured on a three-dimensional cylinder, a circle is a plane figure. The CMM servo-control does not permit the machine to move the probe in a perfect plane. Parasitic displacements parallel to the cylinder axis do not affect circle parameters in this case.
However, some dimensions cannot be accurately measured on a CMM without certain precautions being taken. This is the case for circularity and radial runout when they are located on conical or deformed surfaces, or any axisymmetric surface if it is not cylindrical. On these types of surfaces, the drive cannot control the probing system on a perfect plane [
7], so the measurement takes radial deviations due to axial discrepancy into account.
Section 3.2.2 provides a comprehensive overview of the impact of the servo-control fault between circles measured on cylinders or on cones.
Numerous research studies have been conducted on roundness and circularity, examining the effect of various parameters, except for servo-control. Nemedi [
8] compares the results obtained with different measuring systems, including CMMs and roundness measuring machines. Stepien [
9] shows the influence of scanning speed and probing direction on the roundness result. Drbùla [
10] also explains the effect of probing direction on conical measurements.
Gapinski [
11,
12] studies the evolution of results as a function of the angular sector measured by applying different algorithms. Gass [
13] presents the processing of the same measurements by different algorithms, such as least squares, Chebyshev, circumscribed minimum, or inscribed maximum. Samuel [
14] and Gadelmawla [
15] present different treatments of CMM data to assess circularity. Studies on runout are less numerous than those on circularity, and they are often in the field of gear measurements. In [
16], Guenther presents a method for measuring pitch. Lin [
17] studies the geometrical defects of the CMM on gear measurements, and Tao [
18] presents a method for measuring gear teeth. Without directly naming this as an effect of servo-control, Mazur [
19,
20] describes the differences in positioning between the target and the acquired points on different types of surfaces. He also describes the absence in the ISO 10 360 standards [
21] of parameters such as positioning accuracy and repeatability, which are found in robot standards [
22].
Examples of uncertainty evaluation are presented for circularity by Jalid [
23], and another for taper by Wang [
24]. Among all the publications relating to these studies, those presenting data sets allowing the servo-control error to be calculated are rare [
19,
20]. Some articles present results in two dimensions only [
11,
12,
14,
15], which does not allow the servo-control error to be identified. In these studies, its effect has no influence on the results, as the measured features are not distorted, except for certain gear or cone measurements. NIST (the National Institute of Standards and Technology of the United States) uses different data sets to test the algorithms [
25]. Sets that mimic CMM measurements can be used to highlight the servo-control fault, even if this is not the desired objective.
A servo-control error can be estimated by the distance between the theoretical target and the measured target. It results from the interpretation of real-time scale readings and the positioning command sent by the controller. This fault depends on various parameters, such as travel speed, probe offsets, electronic configuration, and the number of axes required for travel. It has no influence on most shape dimensions (flatness, cylindricity, surface profile, etc.), as the positioning deviation is not very significant compared to the distance between points. Nevertheless, it may affect measurement repeatability in the case of surfaces with high roughness measured with a small probe diameter, which is not recommended either [
26].
To identify servo-control faults, it is necessary to access the actual coordinates of the measured points via the software. However, access to these data is not always direct.
The use of a calibrated ring gauge makes it possible to pinpoint different aspects of a servo-control fault while retaining the diameter and circularity measurement references.
In this article, we suggest a way of characterizing the effect of servo-control on the measurement of the coordinates of a point, a circle, and a deformed surface, respectively. Two solutions are presented to avoid servo-control defects. The proposed method is demonstrated in the case of a calibration sphere and for the measurement of a torus. This study does not deal with probe triggering (TTP), which itself presents too many deviations in circularity measurements due to the lobing of the probe, even if some improvements have been described in [
27,
28]. Some TTP models are equipped with three spring-loaded contacts. Depending on the probing direction, one, two, or three contacts will open. The probing force is, therefore, linked to the force of one, two, or three springs, so the measurement of a circle may present a so-called “three-lobed” defect in the shape of a triangle. We limit the scope of our study to scanning heads, which avoid the three-lobed circles of the TTPs [
26].
Section 2 of this article describes the proposed innovative methodology. Before concluding,
Section 3 deals with the measurement results obtained from several geometric configurations.
The aim of this paper is to help metrologists characterize certain hidden parameters of their CMMs, especially the servo-control, and then reduce the uncertainties of their results.
2. Materials and Methods
In this section, a servo-control defect is assumed to exist, whatever its value or its cause. As described in the Introduction, the servo-control is unable to ensure the same precision in CMM moves as in the CMM readings. This results in a number of defects, which are presented in
Section 3. Warped surfaces represent features such as cones, spheres, toruses, or any axisymmetric surface other than a cylinder. These surfaces are supposed to be sensitive to servo-control.
All the equations presented below can be translated into certain CMM software, or used as post-processing.
Both of the methods presented necessarily begin by defining the datum system in order to create the right direction for measurements and basic dimensions.
2.1. Defining Servo-Control
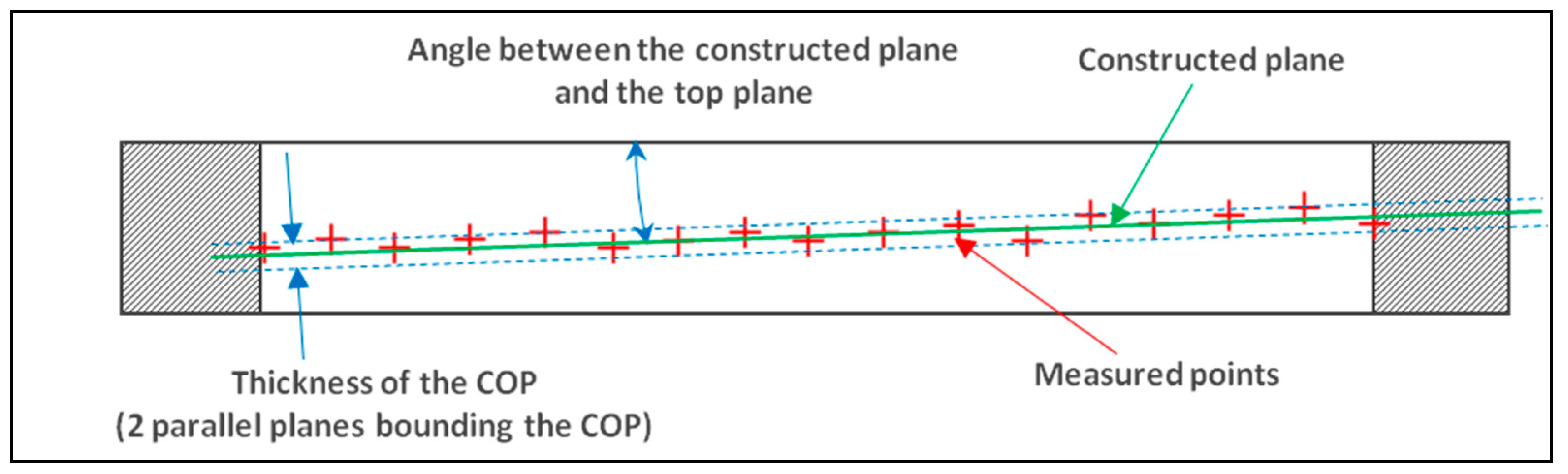
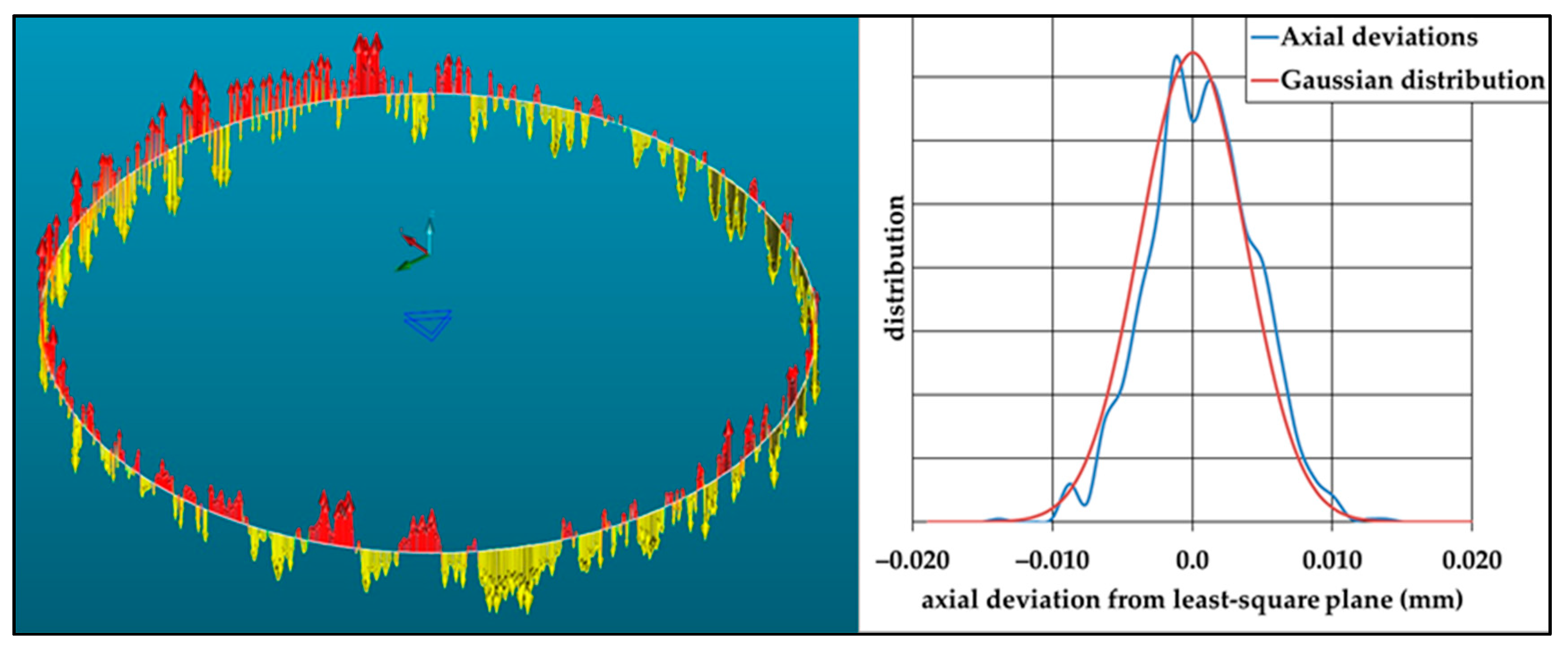
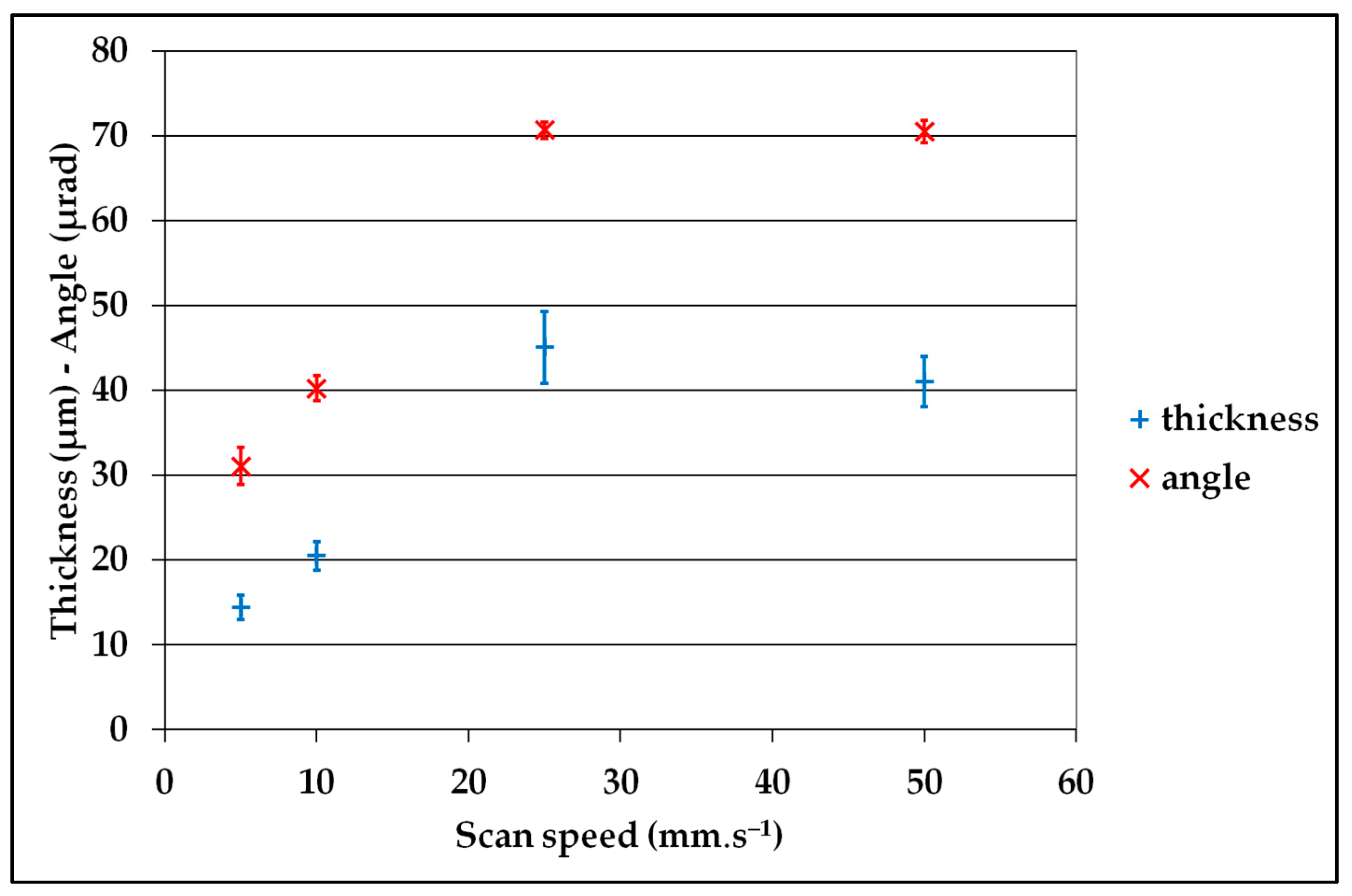
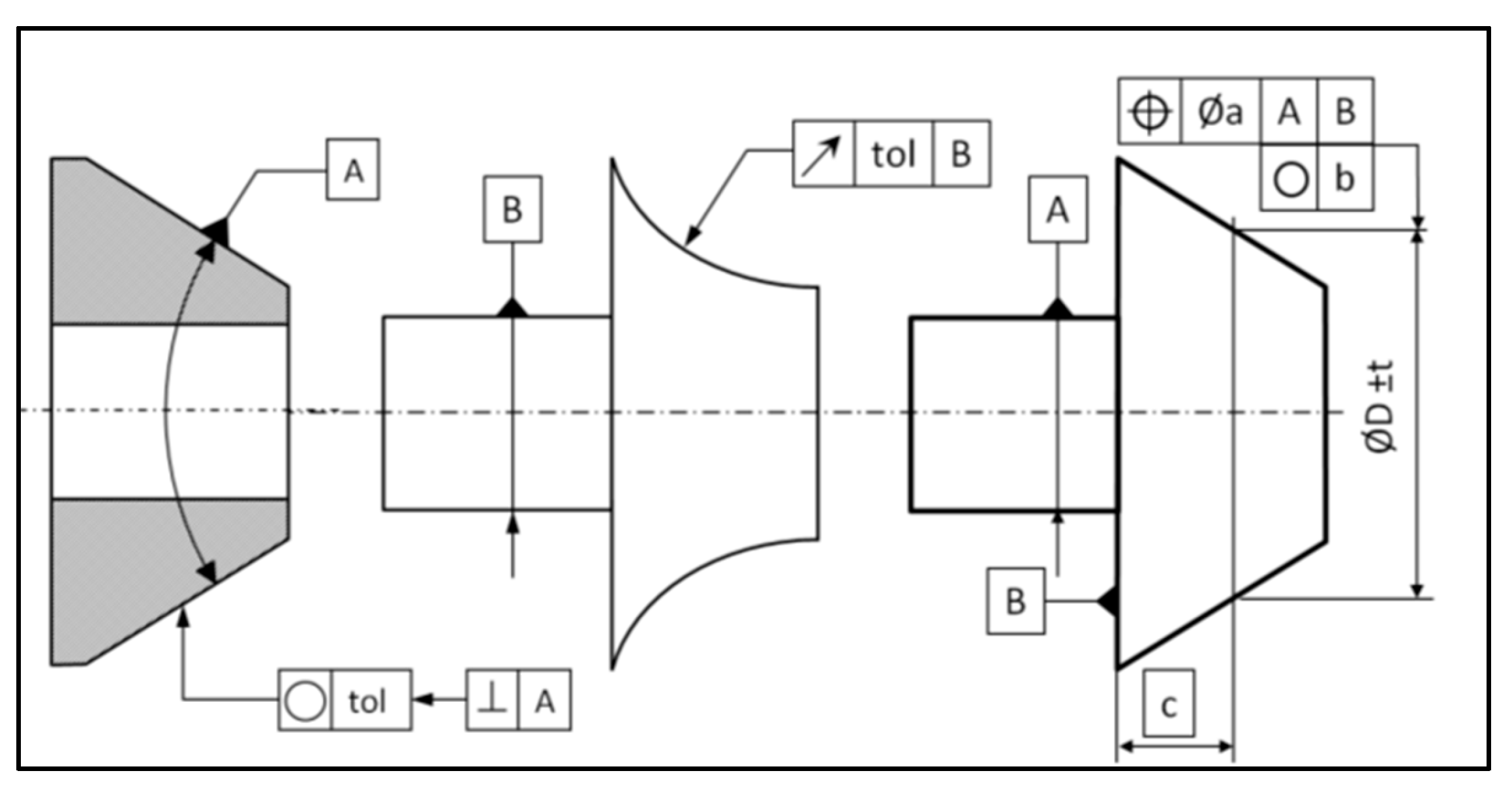
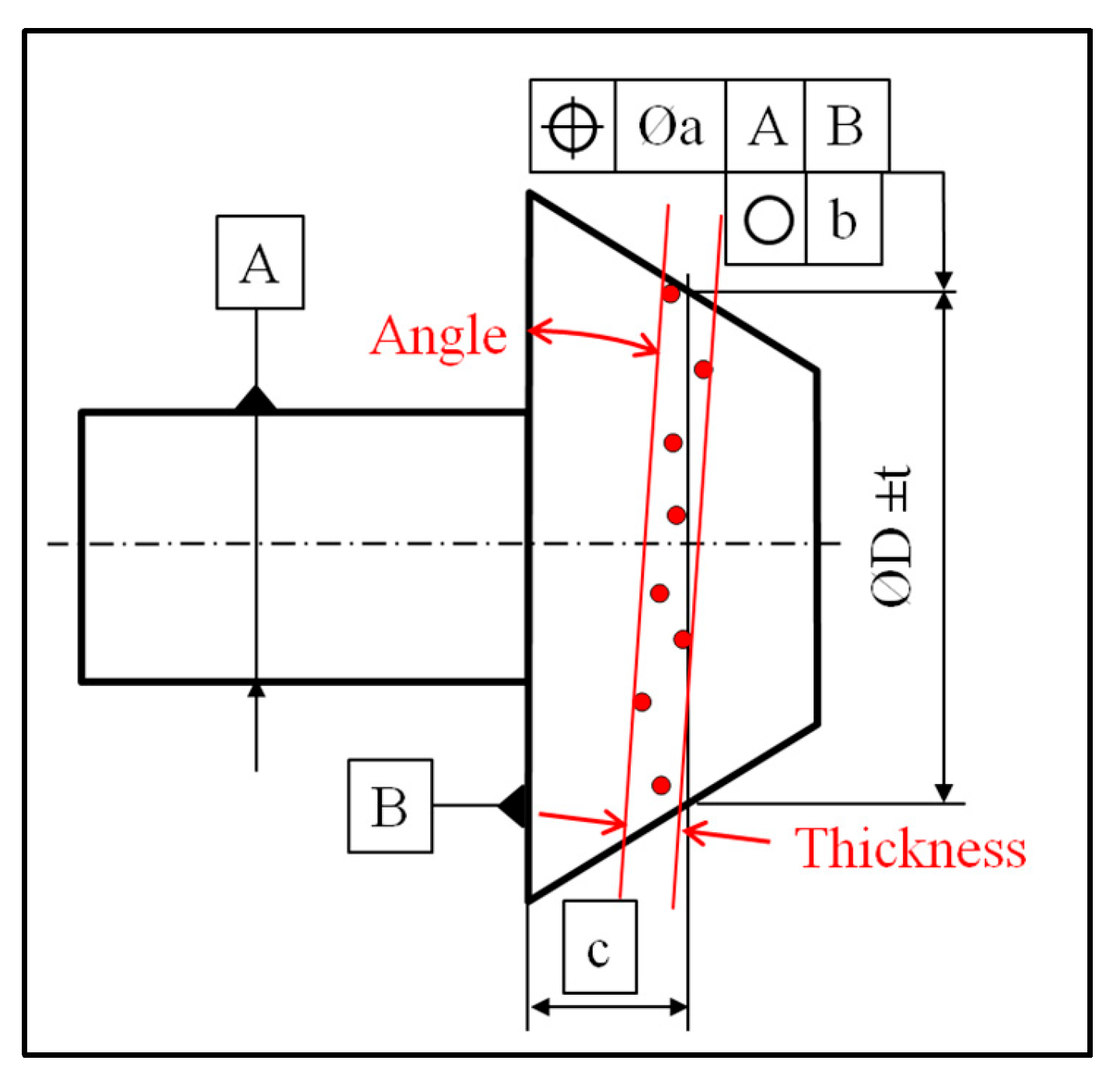
The servo-control of a CNC (CNC: Computer Numerical Control) machine describes the relationship between a movement command sent to the controller and the actual movement of the machine. The difference between the theoretical target and the actual coordinates should be small, but it is not zero. Most features are unaffected by this function, with the exception of point coordinates and circles measured on deformed surfaces. For example, on a conical surface, an axial deviation creates a radial deviation. In the case of a cylinder, an axial deviation does not affect the radius measurement. This axial dispersion can be observed while measuring a circle, without affecting the results. This measurement may be used to define two defects, such as the thickness of the point cloud and the angle between the actual plane displacement of the probe and its theoretical path. Those parameters are developed in
Section 3.
2.2. First Method
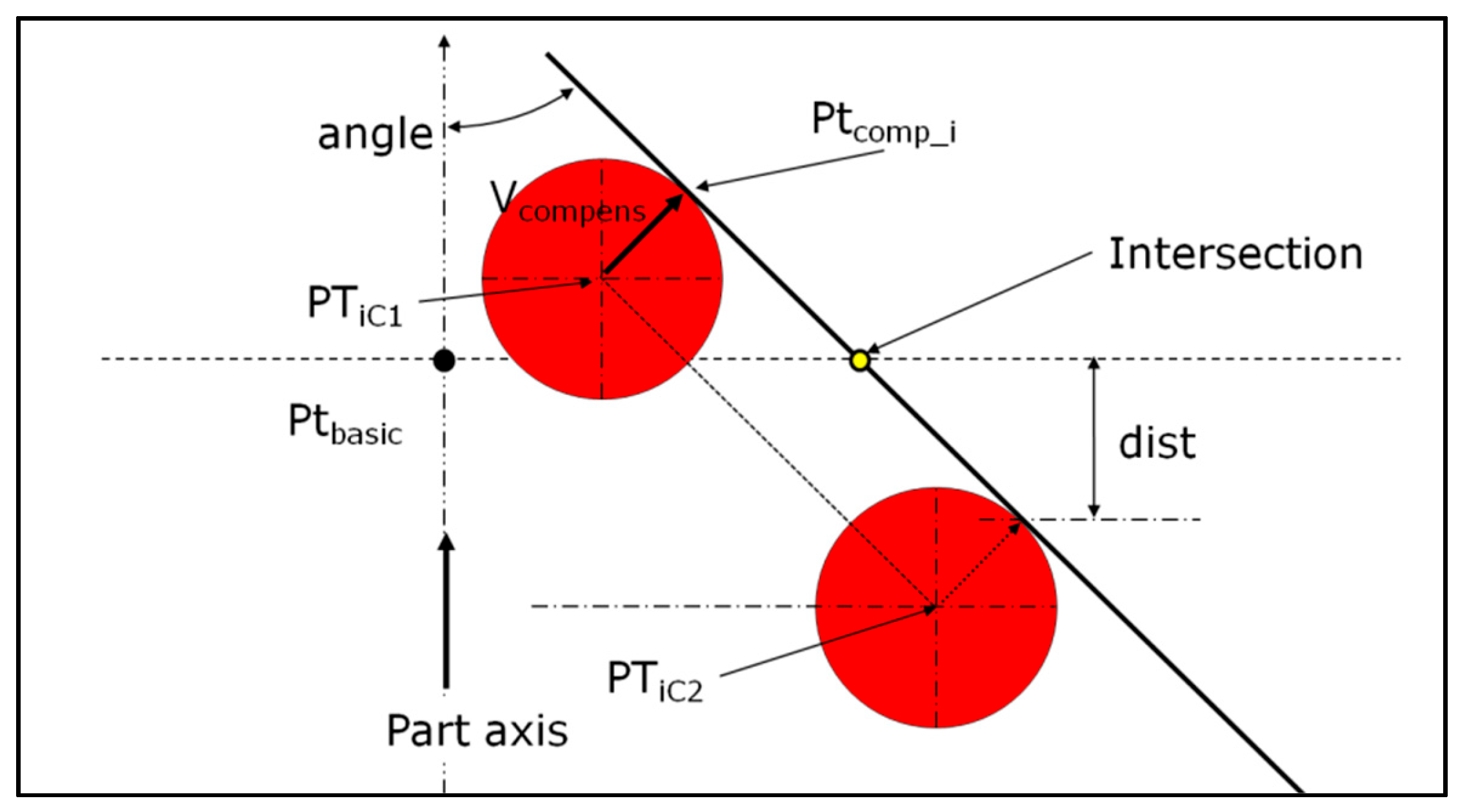
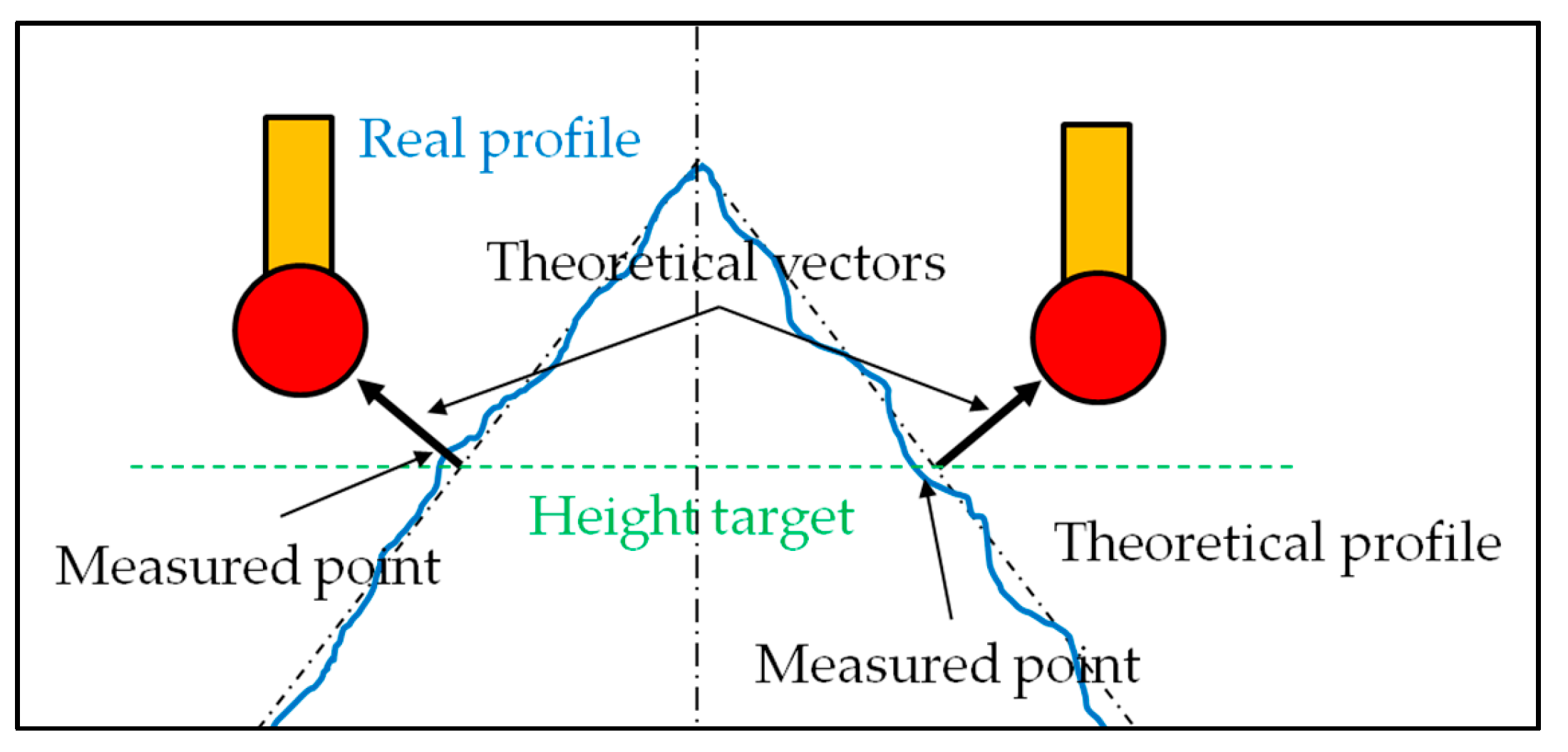
To avoid the servo-control fault, which affects the results of circles measured on warped surfaces, the first solution consists of constructing the circle from two measured circles instead of one (
Figure 1).
The method requires the measurement of circles with the same number of hits in the same direction, if possible. Both circles (
C1 and
C2) must be close together, from a few hundredths to a few tenths of a millimeter around the basic dimension, with the distance between them depending on the surface curvature (
Figure 2). The closer the circles, the greater the accuracy of the result. However, the defect characterization described in
Section 3 enables the shortest distance to be respected between circles to be defined. This ensures that all point-to-point vectors are pointing in the same direction.
The calculation uses center ball coordinates for each hit (
Figure 2) following these different steps:
Vcompens is a unit vector by definition of the cross product between two unit perpendicular vectors. The dot product between the compensation vector and the approach vector must be positive. This allows for the compensation of the ball radius on the right side.
In (7), cos(angle) can be replaced by because the dot product is calculated between unit vectors.
Then, the circle can be constructed from all the constructed points, which are coplanar to the basic plane. If the circles are measured using the normal vector of the feature, then the coordinates of the contact point can be used directly.
In the event of continuous scanning, the number of hits of both circles could vary if the software does not allow it to be set. Should the parameter setting be scan density, a straightforward solution would be to calculate the diameter ratio (larger/smaller). Multiplying the density of the scan conducted on the larger diameter by the ratio should provide an equal, or very close to equal, number of hits to the scan on the smaller diameter. The construction of intersected points can be time-consuming in online treatment, depending on the software, due to the large number of hits. It may be worthwhile to consider creating these points in the post-treatment phase.
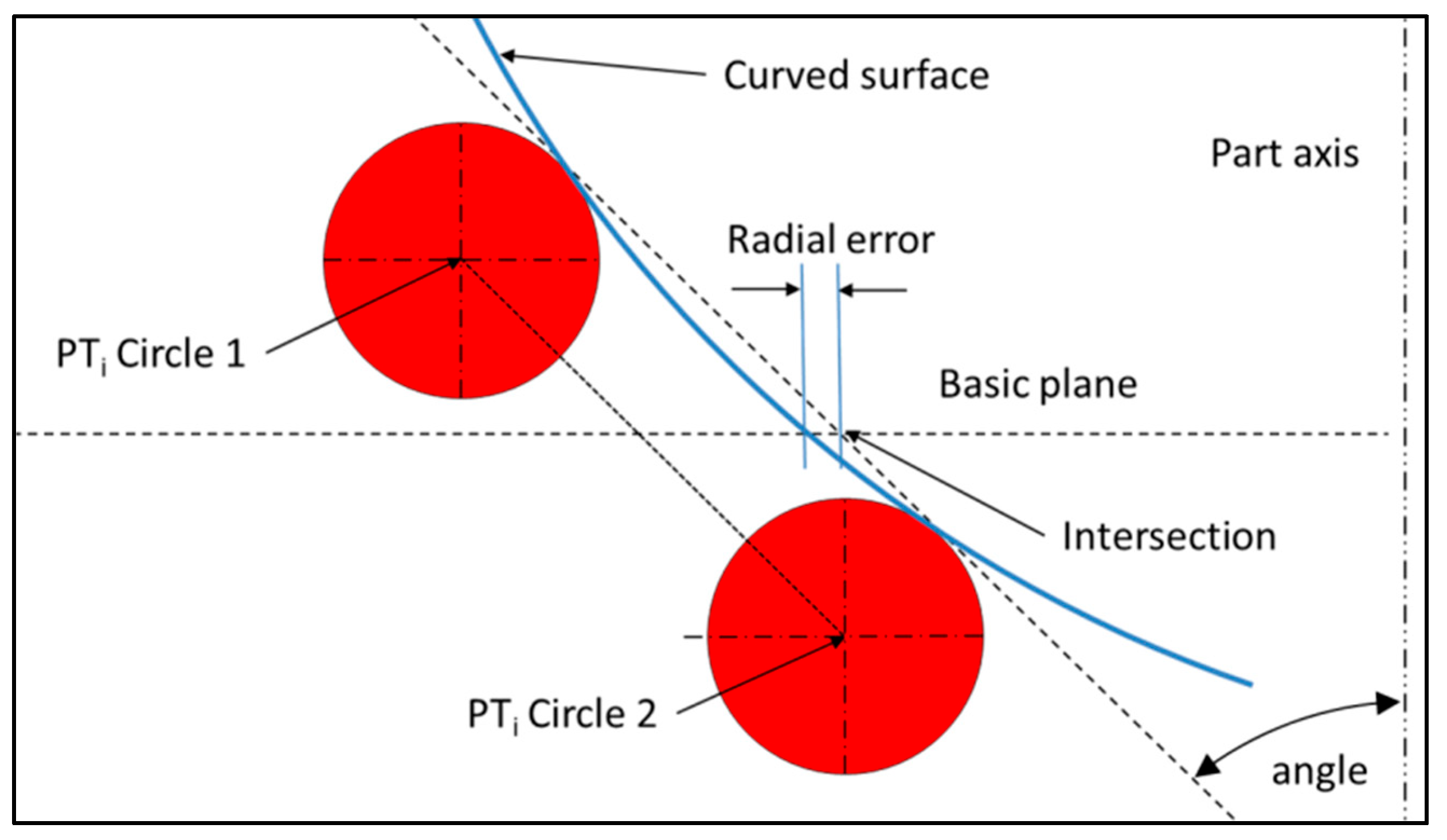
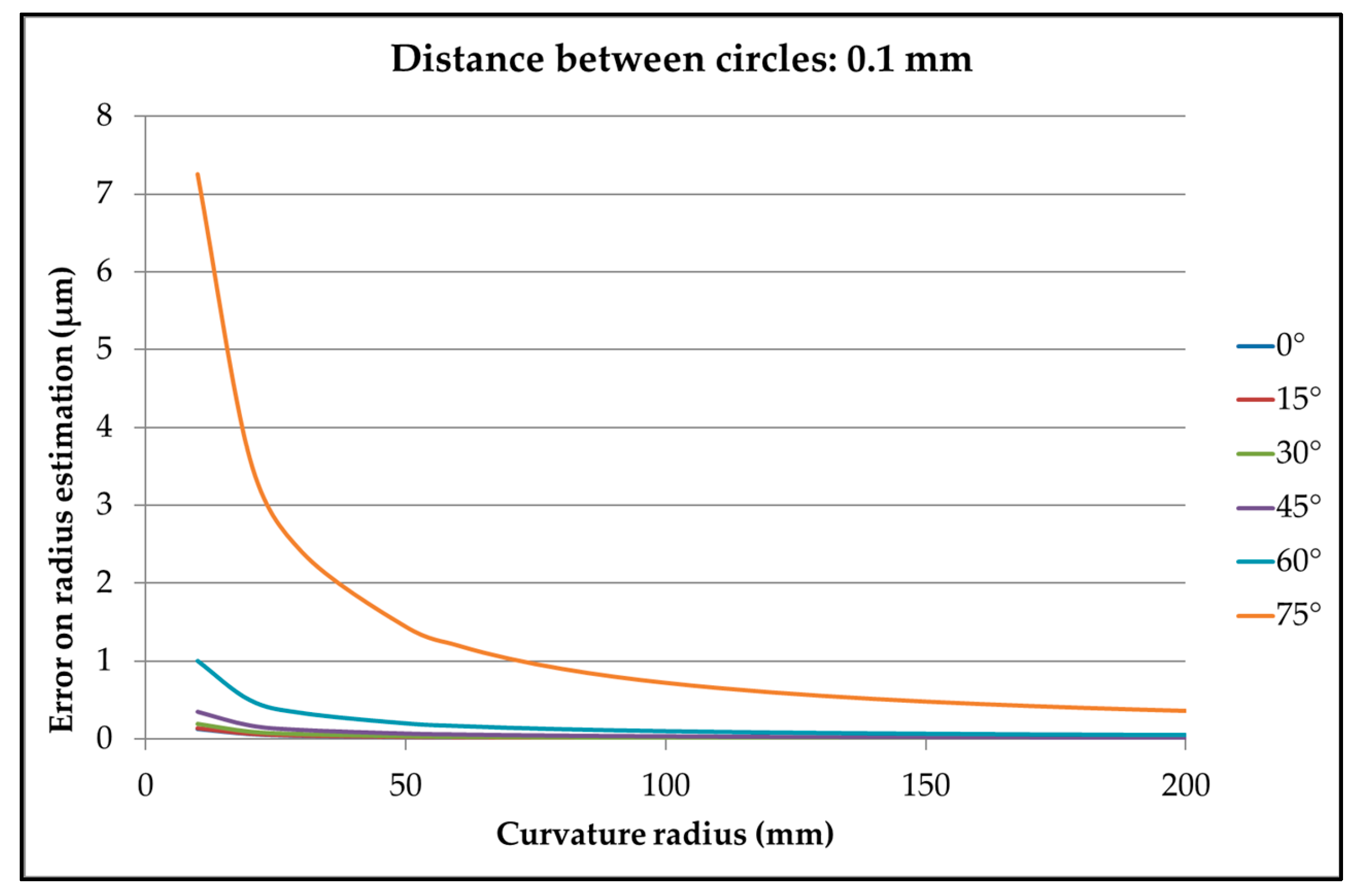
This method generates a defect on the circle diameter, depending on the curvature of the surface, on the angle between the slope and the plane, and on the distance between circles (
Figure 3).
The error on the radius can be limited by reducing the distance between circles. This error should be small in comparison with the error obtained by a direct measurement of the circle.
The calculations below represent a general case for the circularity or for the estimation of a diameter at a given distance from a datum.
The case of the runout is a little different because the part’s defects are measured along a normal vector to the surface (
Figure 4).
Equations (1)–(6) remain unchanged, but the intersection with a plane differs because the tolerance zone is conical. This means that the locally constructed plane must be perpendicular to the tangent plane at the theoretical target point.
In this instance, the line constructed from the contact points must be intersected with a plane containing the theoretical coordinates of a point and the vector normal to the surface at that point. There are as many planes as constructed lines. The direction of the measured deviation must follow the theoretical normal vector [
7], which these constructions allow.
On a cone with a half angle
α, this local plane through a point
Pti (xi,
yi,
zi) belonging to the right cross section can be written thus (
zi is the height of the desired section) (8).
This includes the following conical relations (9).
The vector of the plane comes from the double cross product between the normal vector and the cone axis (here,
z axis—(10)).
So, the plane is defined as follows (11).
Then, Equations (5)–(7) can be used, replacing the vector by the vector .
This method can be used to measure a few circles, for example, to define a circle as a secondary datum. However, should there be many circles, the following method is recommended.
2.3. Second Method
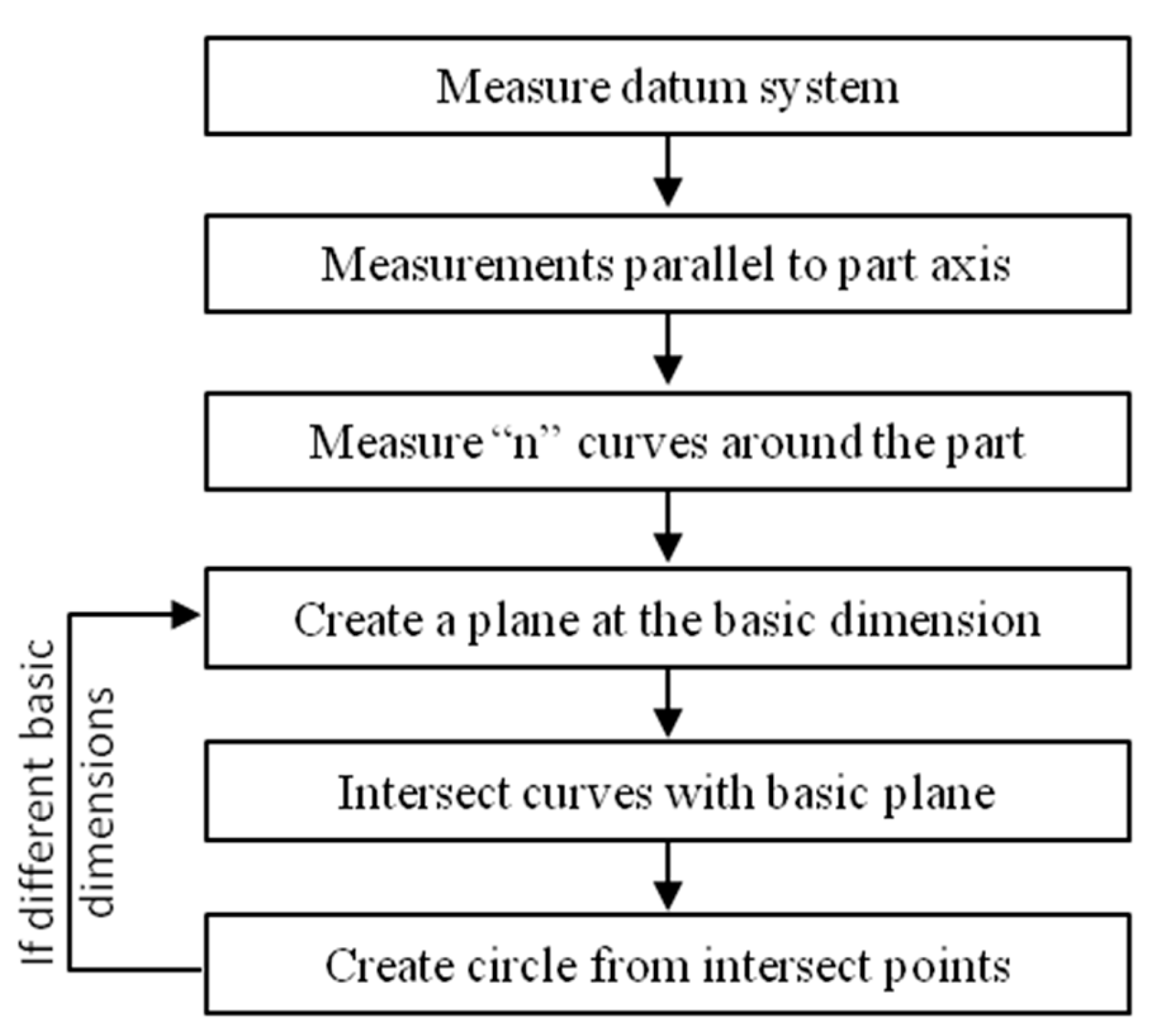
The second solution to avoid the servo-control defect consists of measuring a set of curves around the part, and then intersecting them with a plane to construct a circle (
Figure 5).
The main difference between measuring along the curvature or perpendicularly to it is the distance from the center ball to the contact point along the vector of the plane motion. When the plane motion passes through the part’s axis, this distance is very short. This is also the case while measuring a circle perpendicularly to the curvature.
This second method allows many circles to be constructed by the intersection with different planes, answering the ACS specification [
7], but it needs scanning capabilities to be performed. The point density of the scan should be matched to the curvature in order to maintain sufficient accuracy. On a curved surface, a density from 10 to 20 points per millimeter should suffice, while a density of 4 points per millimeter on a cone may be appropriate.
2.4. Methods Applied to Two Geometrical Configurations
2.4.1. Application to a Calibration Sphere
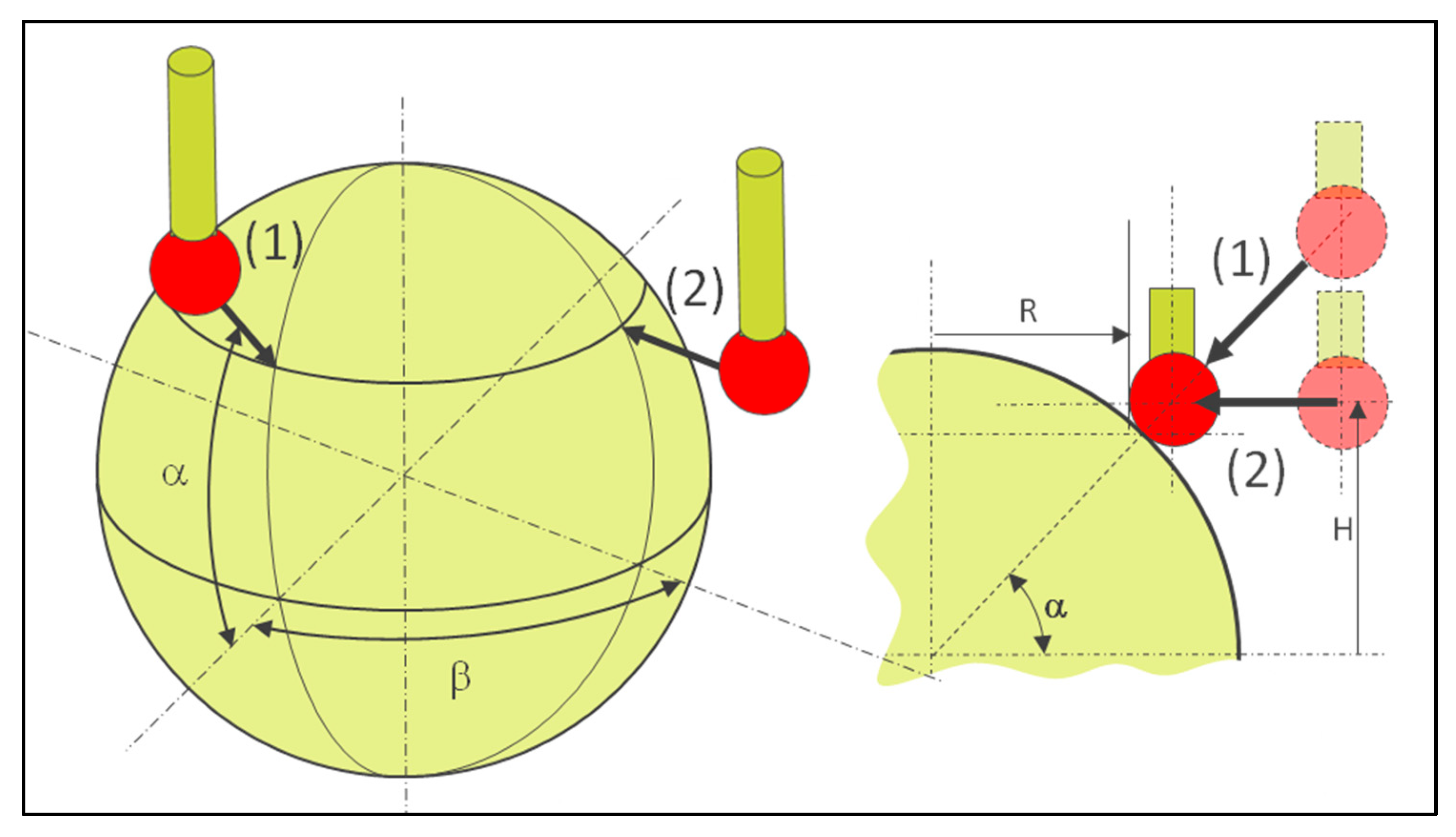
In order for the method to be demonstrated, it needs to be applied to known features, such as standard parts. The method can be used on a calibrated sphere (
Figure 6) at different angles with a gap between circles to minimize the defects. The measured circle is constructed from vector points with a direction perpendicular to the tangent at the target coordinates. In the case of the sphere, the vector is radial.
The coordinates of the target point and the approach vector are calculated as follows (12).
If circle programming is used, the target coordinates have to be calculated considering the theoretical contact point (see
Figure 6).
The coordinates (
H,
R) of the contact point are calculated as follows.
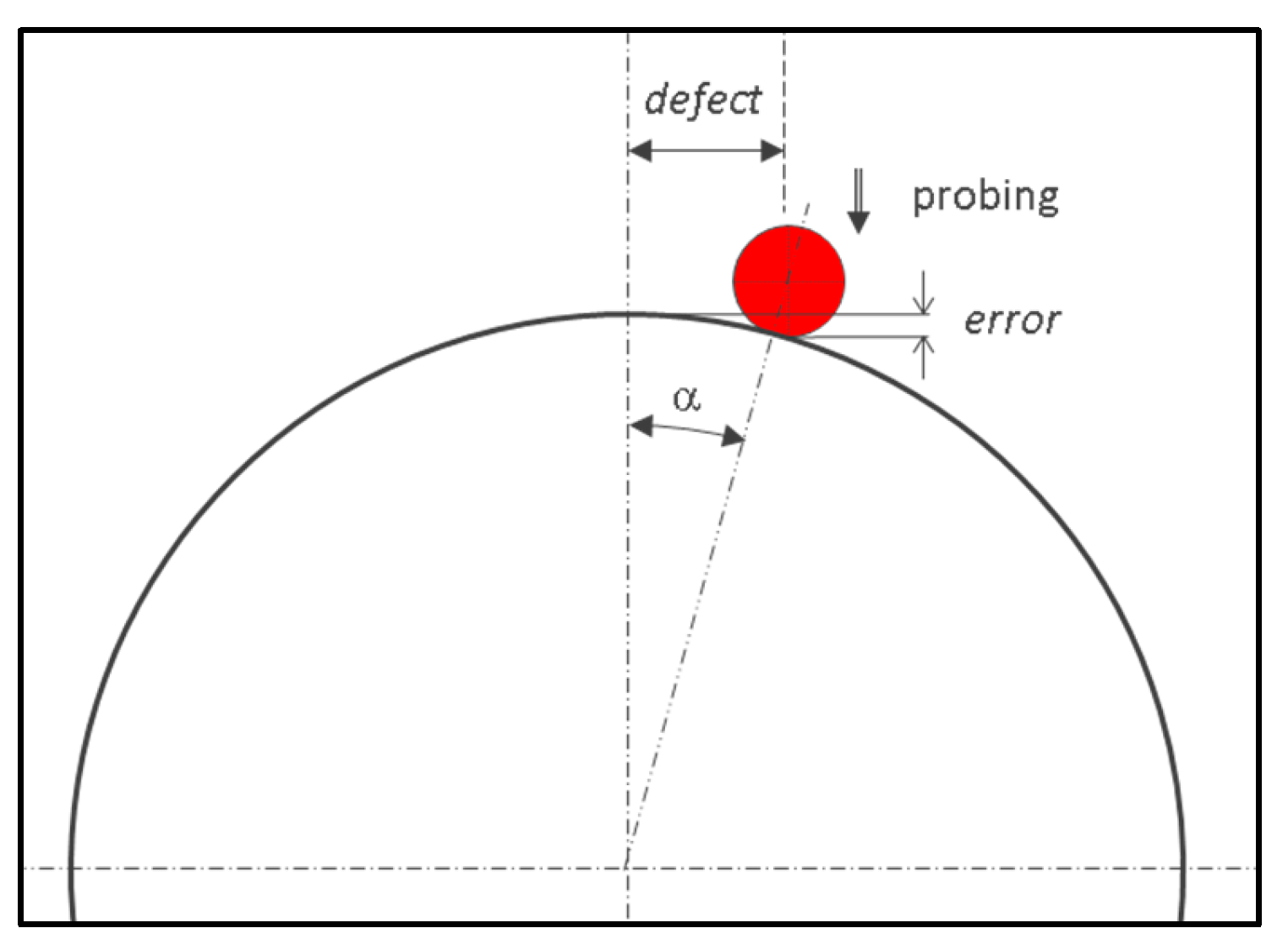
If the measurement is carried out at the equator, the defect is negligible (
Figure 7).
2.4.2. Application to a Torus
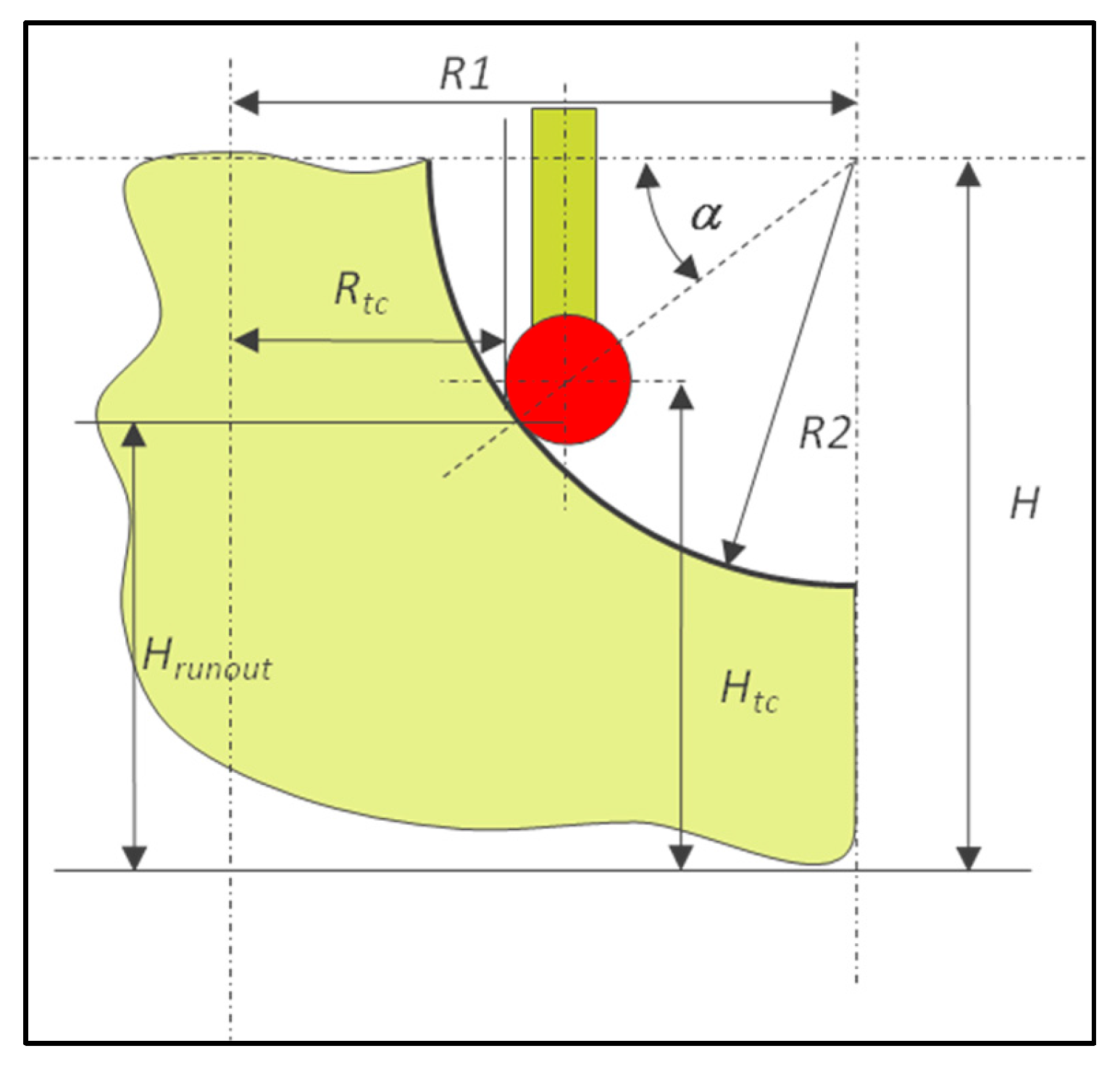
A torus is a warped surface with two owned theoretical dimensions, R1 and R2 (
Figure 8).
The following methods to measure the runout are applied:
Direct measurement with vector points perpendicular to the surface (
Figure 9),
Circle constructed from circle hits (
Figure 9—first method),
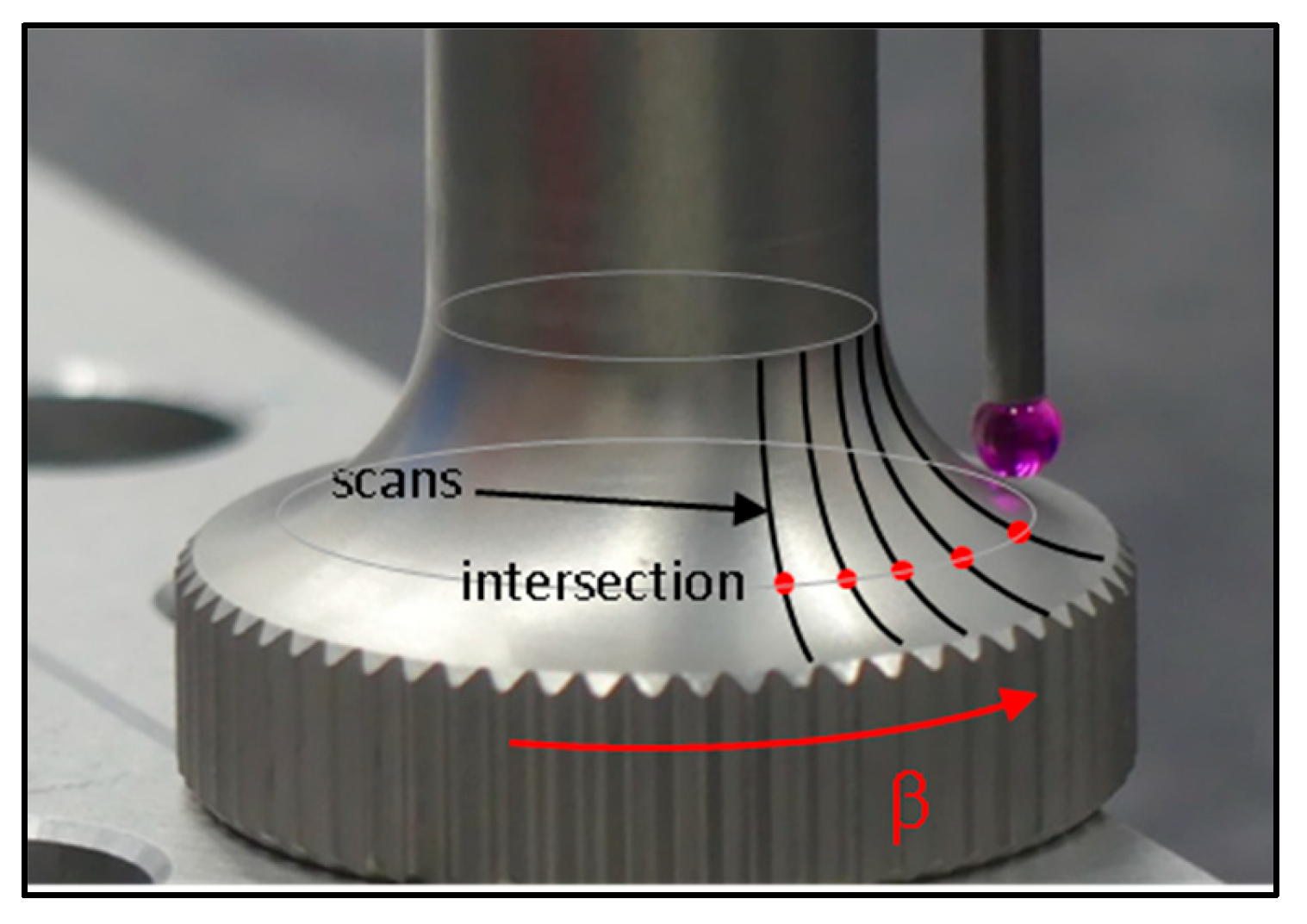
Scanning the radius R2 at different angles around the part and intersecting them with a plane (
Figure 10).
The choice of method depends on various parameters, particularly the size of the part, the number of dimensions to be measured (ACS or not), and the type of probe.
Direct measurement at a given height requires the calculation of the vector direction using (17) and (18).
The target dimensions for the constructed circle method can be calculated using (17) to define α, replacing
Hrunout by
Hrunout ±
d, with
d being the distance around
H (
Figure 9).
Then, the targets for circle hits are determined as follows.
The accuracy for this scanning method depends on the number of hits per millimeter during the scan because the intersection of the scan and the plane to dimension the runout can be a linear interpolation depending on the software.
2.5. Part Defects
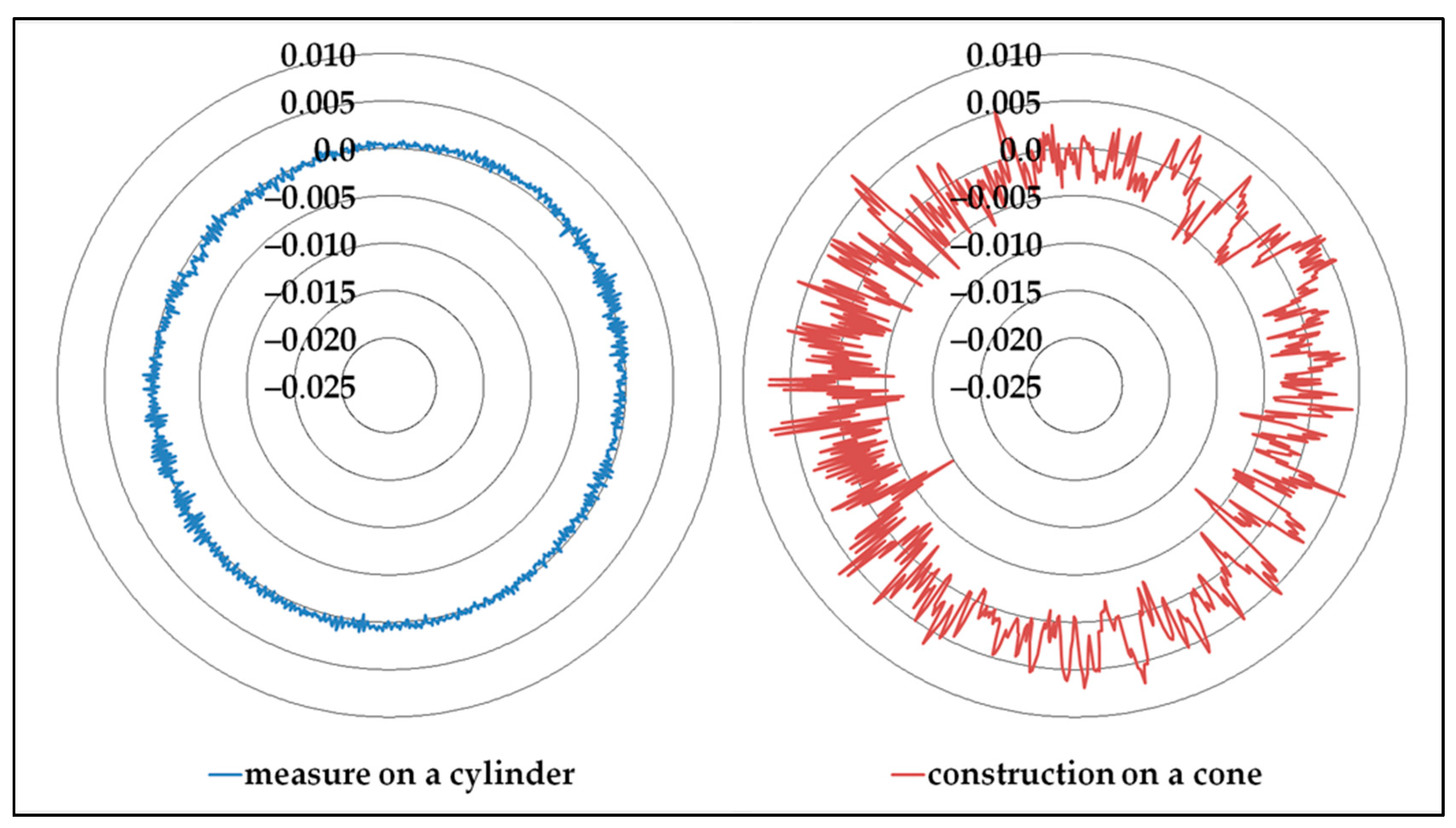
The part itself may present defects equivalent to those created by the servo-control fault, such as roughness or form deviations (
Figure 11). In such cases, the proposed methods can be applied in the same way, thus improving the reliability of measurement results.
4. Conclusions
The use of a CMM facilitates a range of capabilities while simultaneously minimizing the number of expensive machines and the frequency of part displacements between different machines. In this article, we focus on a specific parameter, servo-control, which is not often discussed in the context of CMMs, but rather in that of machine tools. Although this functionality of CMMs rarely leads to significant defects, defects might be introduced to certain dimensions of measured elements. In such cases, it is necessary to construct the elements to be dimensioned, rather than measuring them directly, in order to ensure the highest possible accuracy. The issue arises with roundness and runout, particularly when the latter is dimensioned from a measurement taken on a warped surface. It is important to be aware that direct measurement can lead to the introduction of defects, such as those affecting the diameter, center, and roundness of a circle, which are the only relevant parameters. Furthermore, the results obtained from the direct measurement strategy do not align with the established standard specifications regarding orientation and localization. In sum, the direct measurement method is notable for its simplicity and speed; yet, in some cases, particularly on warped surfaces, the results are not always accurate.
This paper provides an explanation for the causes of these defects and puts forward two different solutions to avoid errors in dimensioning. Both methods are based on the construction of circles from the intersection of segments with a perfect plane. The segment can be constructed in two different ways: from the points of two circles or from linear scans. Whilst both of these methods require a greater investment of time than the direct method, they deliver optimal accuracy and meet the required standard specifications.
By presenting several examples drawn from our CMM or the relevant literature, we illustrate the limitations of servo-control and demonstrate the efficacy of the proposed method. Furthermore, we provide a comprehensive explanation of the role of this hidden parameter in measuring circles on left-handed surfaces as opposed to surfaces that are nominally cylindrical.
In certain instances, the errors caused by servo-control can be of a significantly higher order than the typical uncertainty associated with circle measurements. In such cases, the loss of a small amount of time can result in a significant gain in terms of quality, allowing for a well-informed decision to be made regarding product conformity.
The key benefit of the suggested methodologies lies in their versatility, which allows them to adapt to multiple algorithms, in particular those related to circular datum. It is imperative to apply this method to a specified secondary or tertiary reference when implementing the datum system to ensure its proper construction. Should the software’s options prove inadequate in facilitating the straightforward construction of the intersection points described, a background or post-processing calculation using the equations provided in this paper can ensure a more reliable result.
Our study was conducted using a bridge coordinate measuring machine (CMM), the most common type of CMM. The suggested tests could also be performed on other types, such as gantry CMMs, cantilever CMMs, and horizontal arms, which may exhibit different behaviors. The same holds true for five-axis scanning heads, TTP, or CMMs equipped with a rotary table. High-speed scanning in the shape of a tight sinusoid around the intersection plane would enable the circle to be created with great efficiency. This could be a valuable research area for software publishers.
It would also be beneficial to locate information regarding servo-control within the CMM documentation. In addition, it would be beneficial to incorporate a chapter on this subject into the ISO 10 360 standards, or their equivalent in the American Society of Mechanical Engineers (ASME).
In sum, regardless of the type of CMM or probe, it is essential to perform these tests for two primary reasons. First, they ensure the correction of servo-control defects. Second, they provide a comprehensive understanding of CMM functionality.