Quantification of Lower Limb Kinematics During Swimming in Individuals with Spinal Cord Injury
Abstract
1. Introduction
2. Materials and Methods
2.1. Cohort Definition: Inclusion and Exclusion Criteria
2.2. Study Design and Data Collection
2.3. Sensor-Derived Swimming Parameters
2.4. Statistical Analyses
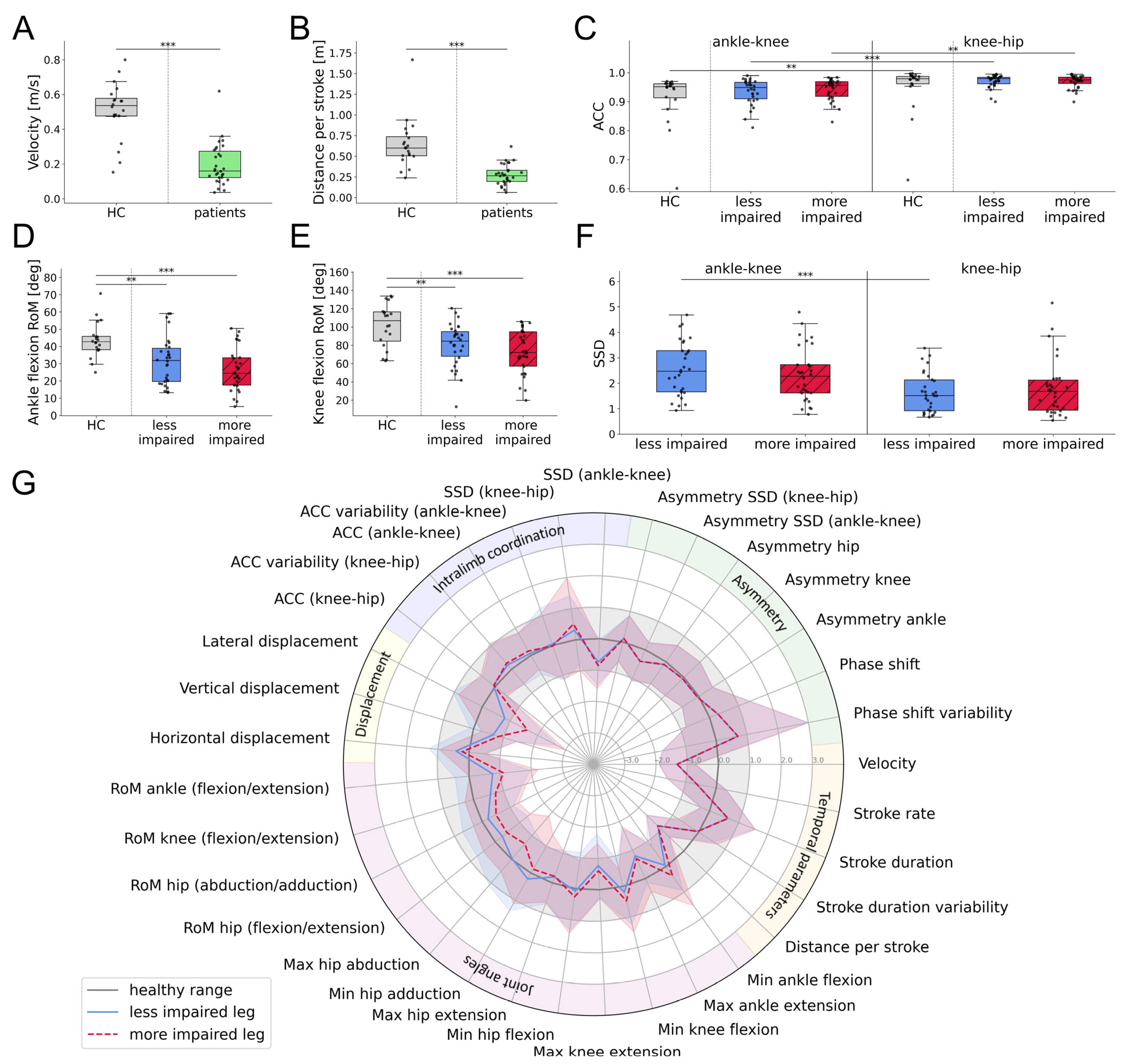
3. Results
3.1. Subjects
3.2. Algorithm
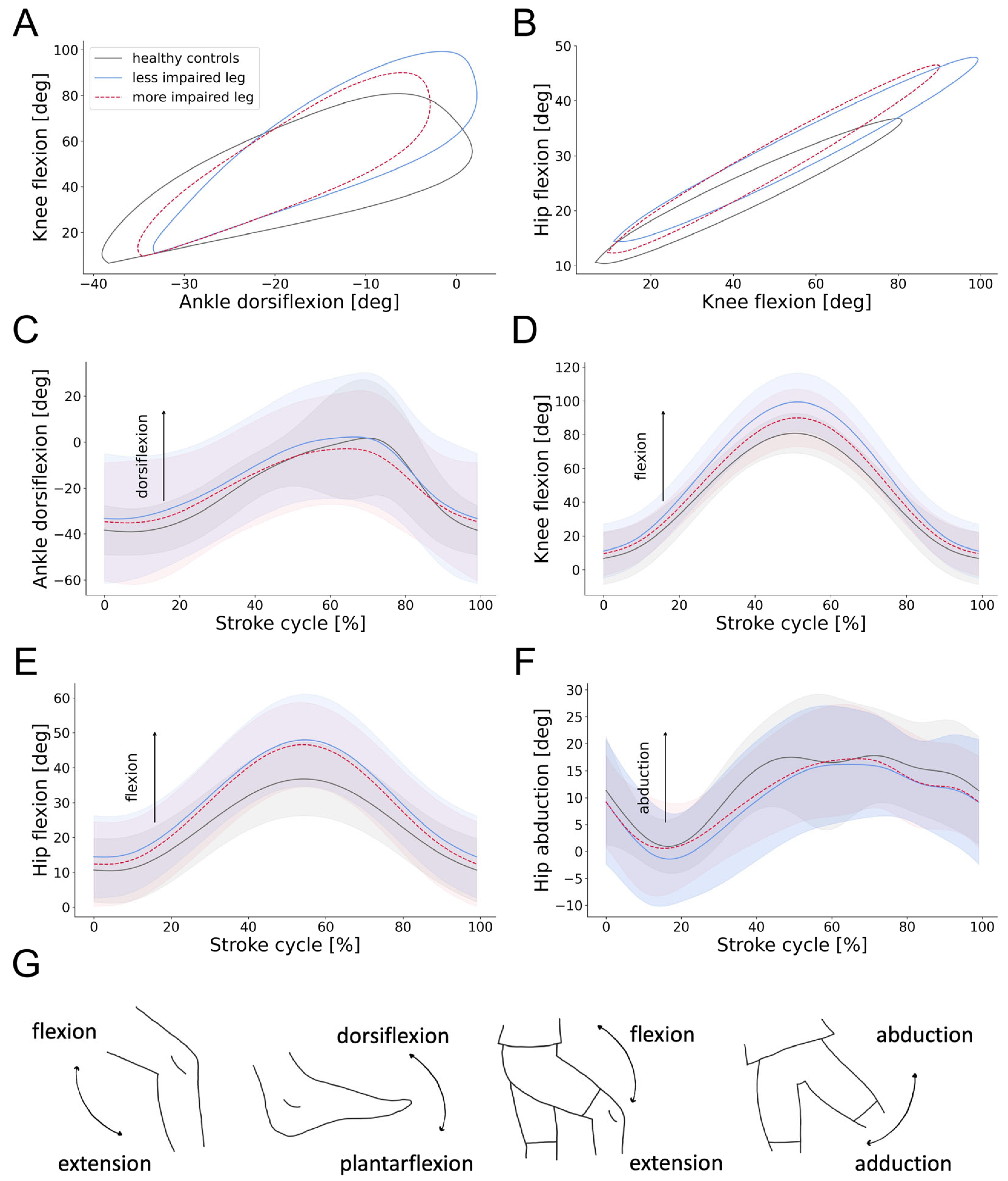
3.3. Swimming Patterns of Healthy Participants
3.4. Swimming Patterns of Individuals with SCI
3.5. Characterization of Swimming Clusters
4. Discussion
4.1. Swimming Patterns of Healthy Controls and Individuals with SCI
4.2. Characterization of Swimming Clusters
4.3. Limitations
4.4. Clinical Applications and Future Work
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ACC | Angular component of coefficient of correspondence |
| AIS | American Spinal Injury Association Impairment Scale |
| BMI | Body mass index |
| IMU | Inertial measurement unit |
| MSD | Mean signed difference |
| NLI | Neurological level of injury |
| RMSE | Root mean squared error |
| SCI | Spinal cord injury |
| SCIM | Spinal Cord Independence Measure |
| SSD | Sum of squared differences |
| 2MWT | 2 min walking test |
| 6MWT | 6 min walking test |
Appendix A

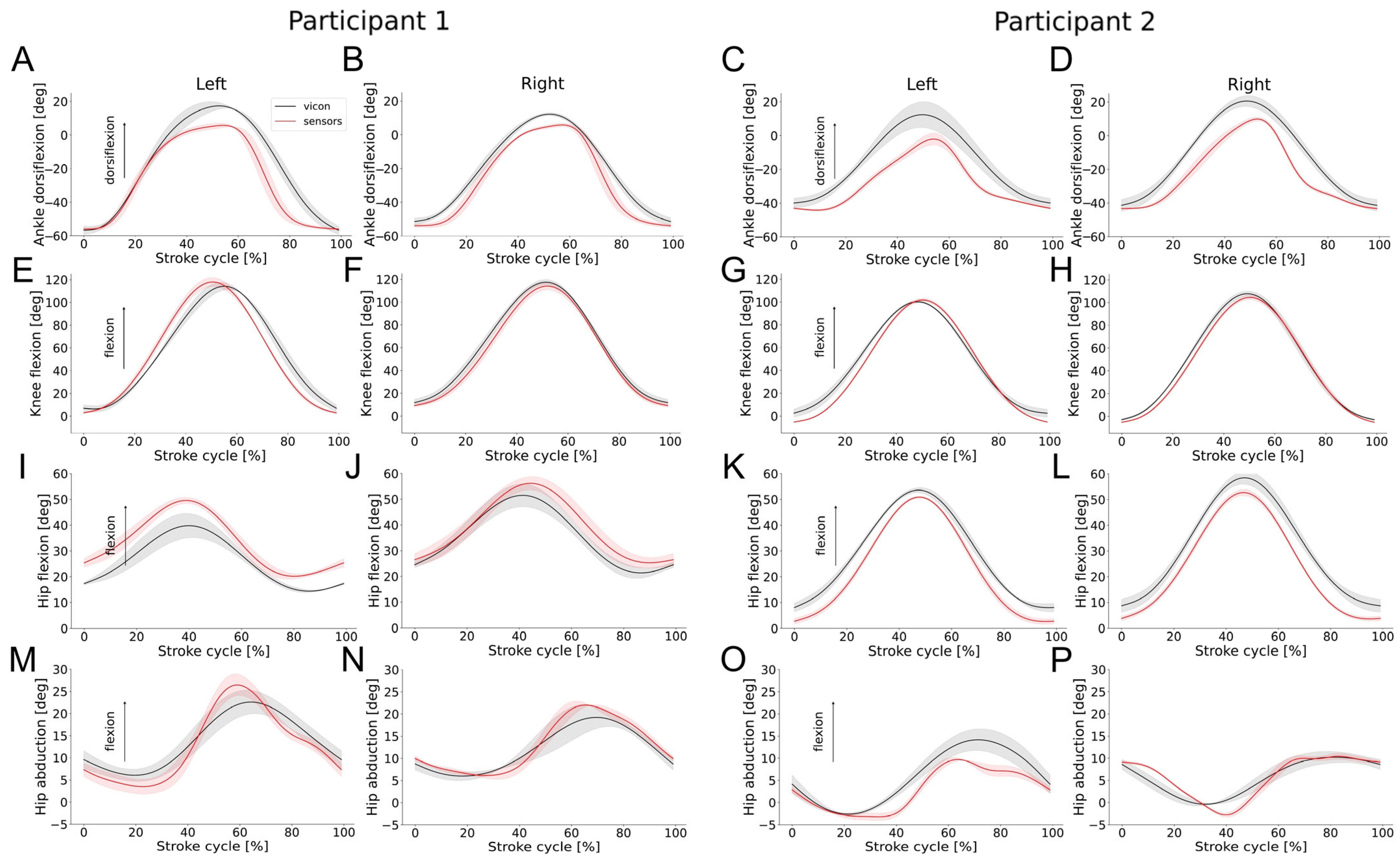
| Joint | RoM IMUs | RoM Vicon | RMSE | MSD | RoM IMUs | RoM Vicon | RMSE | MSD |
|---|---|---|---|---|---|---|---|---|
| Participant 1 | Left | Right | ||||||
| Ankle (plantarflexion/dorsiflexion) | 62.9 (3.5) | 69.5 (7.8) | 7.9 (0.8) | −1.5 (0.1) | 60.6 (0.7) | 64.0 (2.0) | 5.0 (0.4) | −1.7 (0.3) |
| Knee (flexion/extension) | 119.4 (1.0) | 125.0 (22.6) | 7.3 (0.3) | 1.1 (0.9) | 108.7 (2.0) | 105.4 (2.5) | 4.0 (1.7) | −1.2 (0.3) |
| Hip (flexion/extension) | 30.8 (2.4) | 26.2 (3.5) | 2.5 (0.3) | −0.5 (0.3) | 31.2 (3.4) | 30.4 (3.4) | 4.4 (0.3) | −3.4 (0.1) |
| Hip (abduction/adduction) | 18.0 (2.0) | 17.5 (1.7) | 5.9 (0.9) | 4.2 (0.7) | 14.0 (2.8) | 13.5 (3.6) | 2.3 (0.2) | 0.6 (0.5) |
| Participant 2 | Left | Right | ||||||
| Ankle (plantarflexion/dorsiflexion) | 53.2 (7.1) | 52.6 (9.2) | 9.6 (1.1) | −8.6 (1.2) | 57.4 (3.0) | 62.9 (4.9) | 9.4 (0.1) | −7.7 (0.1) |
| Knee (flexion/extension) | 103.7 (3.8) | 96.7 (3.0) | 4.4 (0.4) | −3.3 (0.3) | 111.6 (2.2) | 109.4 (3.0) | 4.3 (0.3) | −2.8 (0.3) |
| Hip (flexion/extension) | 50.1 (1.7) | 46.6 (2.1) | 3.5 (0.3) | −3.1 (0.4) | 51.16 (1.1) | 50.61 (4.6) | 4.1 (0.4) | −3.0 (0.3) |
| Hip (abduction/adduction) | 15.1 (0.2) | 16.9 (2.1) | 2.8 (0.6) | 2.0 (0.7) | 14.1 (1.7) | 11.3 (0.8) | 2.0 (0.1) | 0.1 (0.5) |
| Swimming Parameter | Features | Dominant Leg | Non-Dominant Leg | p-Values |
|---|---|---|---|---|
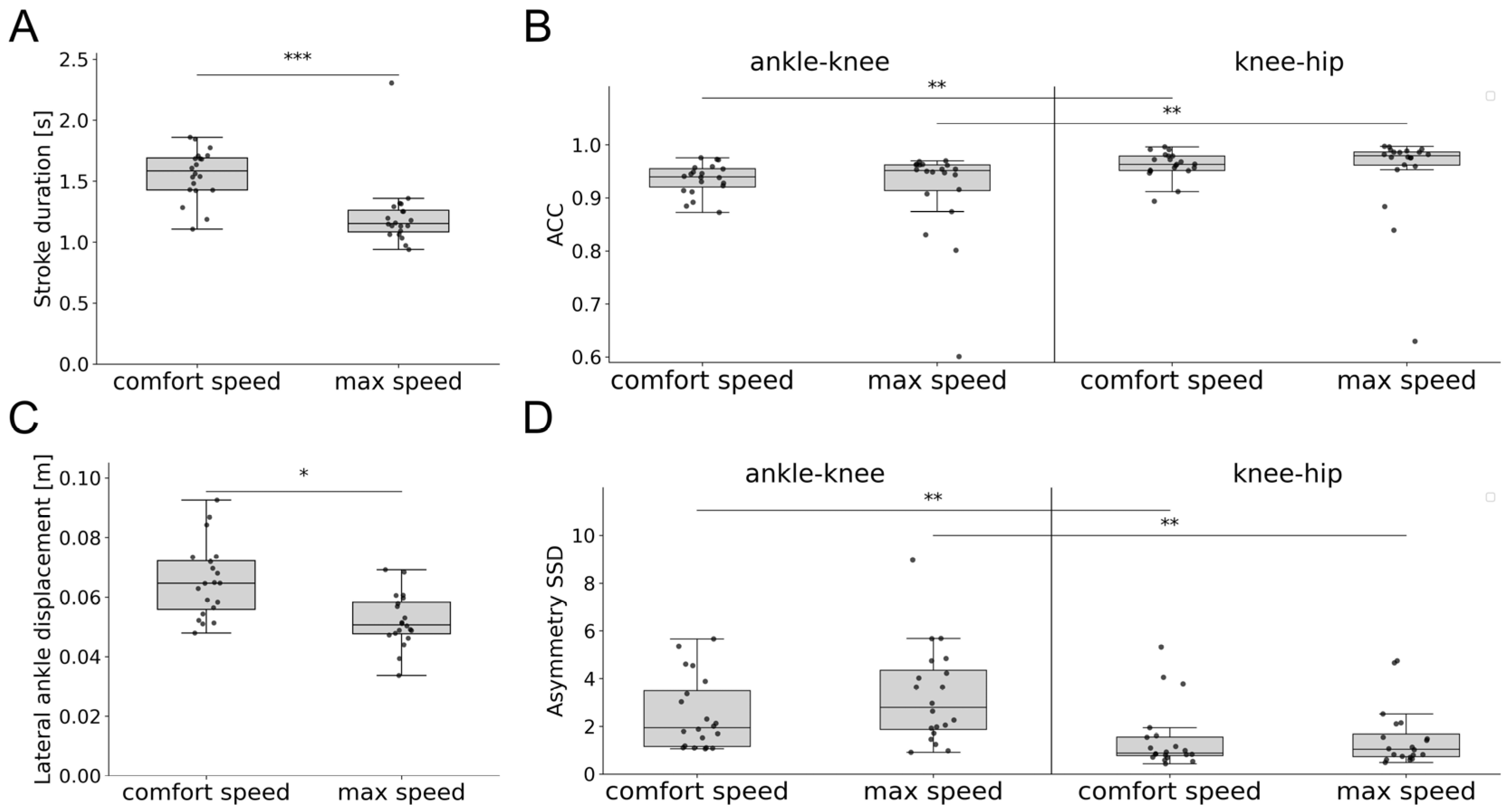
| Stroke duration [s], mean (SD) | 1.22 (0.3) | 1.22 (0.3) | 1.000 | |
| Stroke duration variability [s], mean (SD) | 0.08 (0.07) | 0.1 (0.09) | 1.000 | |
| Joint angles [deg], mean (SD) | Min ankle dorsi-/plantarflexion | −9.5 (14.6) | −7.8 (14.4) | 1.000 |
| Max ankle dorsi-/plantarflexion | 34.5 (13.6) | 35.6 (14.6) | 1.000 | |
| Min knee flexion/extension | −6.0 (13.2) | −2.1 (20.5) | 1.000 | |
| Max knee flexion/extension | 100.6 (20.3) | 94.8 (25.5) | 1.000 | |
| Min hip flexion/extension | 8.0 (12.4) | 8.5 (13.1) | 1.000 | |
| Max hip flexion/extension | 52.7 (12.6) | 53.1 (9.5) | 1.000 | |
| Min hip adduction/abduction | 3.9 (9.5) | 3.2 (9.1) | 1.000 | |
| Max hip adduction/abduction | 20.9 (8.8) | 23.4 (9.0) | 1.000 | |
| Range of motion [deg], mean (SD) | Ankle dorsi-/plantarflexion | 43.4 (12.0) | 44.0 (10.8) | 1.000 |
| Knee flexion/extension | 96.9 (27.1) | 106.6 (22.0) | 0.073 | |
| Hip flexion/extension | 44.5 (14.6) | 44.8 (15.1) | 1.000 | |
| Hip adduction/abduction | 26.5 (6.5) | 24.9 (6.9) | 1.000 | |
| Displacement [m], mean (SD) | Horizontal | 0.07 (0.03) | 0.06 (0.02) | 0.286 |
| Vertical | 0.03 (0.02) | 0.03 (0.02) | 1.000 | |
| Lateral | 0.05 (0.01) | 0.05 (0.01) | 1.000 | |
| ACC, mean (SD) | Ankle/knee | 0.91 (0.09) | 0.92 (0.09) | 1.000 |
| Knee/hip | 0.95 (0.09) | 0.95 (0.08) | 1.000 |
| Cohort | Cluster 1 | Cluster 2 | p-Value |
|---|---|---|---|
| Number, n | 15 | 15 | |
| Age [years], mean (SD) | 59.3 (11.6) | 51.5 (15.1) | 0.164 |
| Sex [female], n (%) | 3 (20.0) | 6 (40.0) | 0.427 |
| BMI [kg/m2] | 25.4 (3.5) | 24.8 (4.4) | 0.534 |
| AIS D, n (%) | 15 (100.0) | 15 (100.0) | <1.000 |
| NLI, n (%) | 5 (33.3) cervical 10 (66.7) thoracic | 7 (46.7) cervical 8 (53.3) thoracic | 0.710 |
| Etiology, n (%) | 5 (33.3) traumatic 10 (66.7) non-traumatic | 6 (40.0) traumatic 9 (60.0) non-traumatic | <1.000 |
| SCIM Mob., mean (SD) | 37.5 (2.5) | 32.9 (6.1) | 0.026 |
References
- Field-Fote, E.C. Spinal Cord Control of Movement: Implications for Locomotor Rehabilitation Following Spinal Cord Injury. Phys. Ther. 2000, 80, 477–484. [Google Scholar] [CrossRef] [PubMed]
- Motiei-Langroudi, R.; Sadeghian, H. Traumatic Spinal Cord Injury: Long-Term Motor, Sensory, and Urinary Outcomes. Asian. Spine J. 2017, 11, 412–418. [Google Scholar] [CrossRef]
- Wyndaele, M.; Wyndaele, J.J. Incidence, Prevalence and Epidemiology of Spinal Cord Injury: What Learns a Worldwide Literature Survey? Spinal Cord 2006, 44, 523–529. [Google Scholar] [CrossRef] [PubMed]
- Werner, C.; Gönel, M.; Lerch, I.; Curt, A.; Demkó, L. Data-Driven Characterization of Walking after a Spinal Cord Injury Using Inertial Sensors. J. Neuroeng. Rehabil. 2023, 20, 55. [Google Scholar] [CrossRef] [PubMed]
- Schroeder, S.; Jaeger, S.; Schwer, J.; Seitz, A.M.; Hamann, I.; Werner, M.; Thorwaechter, C.; Santos, I.; Wendler, T.; Nebel, D.; et al. Accuracy Measurement of Different Marker Based Motion Analysis Systems for Biomechanical Applications: A Round Robin Study. PLoS ONE 2022, 17, e0271349. [Google Scholar] [CrossRef] [PubMed]
- Merriaux, P.; Dupuis, Y.; Boutteau, R.; Vasseur, P.; Savatier, X. A Study of Vicon System Positioning Performance. Sensors 2017, 17, 1591. [Google Scholar] [CrossRef]
- Hamidi Rad, M.; Gremeaux, V.; Dadashi, F.; Aminian, K. A Novel Macro-Micro Approach for Swimming Analysis in Main Swimming Techniques Using IMU Sensors. Front. Bioeng. Biotechnol. 2021, 8, 597738. [Google Scholar] [CrossRef]
- Werner, C.; Easthope, C.A.; Curt, A.; Demkó, L. Towards a Mobile Gait Analysis for Patients with a Spinal Cord Injury: A Robust Algorithm Validated for Slow Walking Speeds. Sensors 2021, 21, 7381. [Google Scholar] [CrossRef]
- Werner, C.; Schneider, S.; Gassert, R.; Curt, A.; Demko, L. Complementing Clinical Gait Assessments of Spinal Cord Injured Individuals Using Wearable Movement Sensors. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 2020, 2020, 3142–3145. [Google Scholar] [CrossRef]
- Camomilla, V.; Bergamini, E.; Fantozzi, S.; Vannozzi, G. Trends Supporting the In-Field Use of Wearable Inertial Sensors for Sport Performance Evaluation: A Systematic Review. Sensors 2018, 18, 873. [Google Scholar] [CrossRef]
- Willi, R.; Werner, C.; Demkó, L.; de Bie, R.; Filli, L.; Zörner, B.; Curt, A.; Bolliger, M. Reliability of Patient-Specific Gait Profiles with Inertial Measurement Units during the 2-Min Walk Test in Incomplete Spinal Cord Injury. Sci. Rep. 2024, 14, 3049. [Google Scholar] [CrossRef] [PubMed]
- Ellapen, T.J.; Hammill, H.V.; Swanepoel, M.; Strydom, G.L. The Benefits of Hydrotherapy to Patients with Spinal Cord Injuries. Afr. J. Disabil. 2018, 7, a450. [Google Scholar] [CrossRef] [PubMed]
- Marinho-Buzelli, A.R.; Gauthier, C.; Chan, K.; Bonnyman, A.M.; Mansfield, A.; Musselman, K.E. The State of Aquatic Therapy Use for Clients with Spinal Cord Injury or Disorder: Knowledge and Current Practice. J. Spinal Cord Med. 2022, 45, 82–90. [Google Scholar] [CrossRef]
- Palladino, L.; Ruotolo, I.; Berardi, A.; Carlizza, A.; Galeoto, G. Efficacy of Aquatic Therapy in People with Spinal Cord Injury: A Systematic Review and Meta-Analysis. Spinal Cord 2023, 61, 317–322. [Google Scholar] [CrossRef]
- Komar, J.; Sanders, R.H.; Chollet, D.; Seifert, L. Do Qualitative Changes in Interlimb Coordination Lead to Effectiveness of Aquatic Locomotion Rather than Efficiency? J. Appl. Biomech. 2014, 30, 189–196. [Google Scholar] [CrossRef]
- Seifert, L.; Didier, C. Inter-Limb Coordination in the Four Competitive Strokes; Nova Science Publishers: Hauppauge, NY, USA, 2011; ISBN 9781616682026. [Google Scholar]
- Seifert, L.; Komar, J.; Barbosa, T.; Toussaint, H.; Millet, G.; Davids, K. Coordination Pattern Variability Provides Functional Adaptations to Constraints in Swimming Performance. Sports Med. 2014, 44, 1333–1345. [Google Scholar] [CrossRef]
- de Magalhaes, F.A.; Vannozzi, G.; Gatta, G.; Fantozzi, S. Wearable Inertial Sensors in Swimming Motion Analysis: A Systematic Review. J. Sports Sci. 2015, 33, 732–745. [Google Scholar] [CrossRef] [PubMed]
- Dadashi, F.; Arami, A.; Crettenand, F.; Millet, G.P.; Komar, J.; Seifert, L.; Aminian, K. A Hidden Markov Model of the Breaststroke Swimming Temporal Phases Using Wearable Inertial Measurement Units. In Proceedings of the 2013 IEEE International Conference on Body Sensor Networks, BSN 2013, Cambridge, MA, USA, 6–9 May 2013. [Google Scholar]
- Rupp, R.; Biering-Sørensen, F.; Burns, S.P.; Graves, D.E.; Guest, J.; Jones, L.; Read, M.S.; Rodriguez, G.M.; Schuld, C.; Tansey, K.E.; et al. International Standards for Neurological Classification of Spinal Cord Injury: Revised 2019. Top. Spinal Cord Inj. Rehabil. 2021, 27, 1–22. [Google Scholar] [CrossRef]
- Khamnon, N.; Amatachaya, S.; Wattanapan, P.; Musika, N.; Jitmongkolsri, P.; Kongngoen, N.; Haisirikul, M.; Jaikarsen, K.; Thaweewannakij, T.; Namwong, W. Reliability and Concurrent Validity of the Spinal Cord Independence Measure III among Rehabilitation Professionals. Spinal Cord 2022, 60, 875–881. [Google Scholar] [CrossRef]
- Filli, L.; Sutter, T.; Easthope, C.S.; Killeen, T.; Meyer, C.; Reuter, K.; Lörincz, L.; Bolliger, M.; Weller, M.; Curt, A.; et al. Profiling Walking Dysfunction in Multiple Sclerosis: Characterisation, Classification and Progression over Time. Sci. Rep. 2018, 8, 4984. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, D.; Zhou, Z.; Mai, J.; He, Z.; Wang, Q. IMU-Based Underwater Sensing System for Swimming Stroke Classification and Motion Analysis. In Proceedings of the 2017 IEEE International Conference on Cyborg and Bionic Systems (CBS), Shenzhen, China, 17–19 October 2017; pp. 268–272. [Google Scholar]
- Madgwick, S.O.H.; Harrison, A.J.L.; Vaidyanathan, R. Estimation of IMU and MARG Orientation Using a Gradient Descent Algorithm. In Proceedings of the IEEE International Conference on Rehabilitation Robotics Rehab Week Zurich, Zurich, Switzerland, 29 June–1 July 2011; pp. 1–7. [Google Scholar]
- Awai, L.; Curt, A. Intralimb Coordination as a Sensitive Indicator of Motor-Control Impairment after Spinal Cord Injury. Front. Hum. Neurosci. 2014, 8, 148. [Google Scholar] [CrossRef] [PubMed]
- Field-Fote, E.C.; Tepavac, D. Improved Intralimb Coordination in People with Incomplete Spinal Cord Injury Following Training with Body Weight Support and Electrical Stimulation. Phys. Ther. 2002, 82, 707–715. [Google Scholar] [CrossRef]
- Frye, S.K.; Geigle, P.R.; York, H.S.; Sweatman, W.M. Functional Passive Range of Motion of Individuals with Chronic Cervical Spinal Cord Injury. J. Spinal Cord Med. 2020, 43, 257–263. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer series in statistics; Springer: Berlin/Heidelberg, Germany, 2009; p. 282. [Google Scholar]
- Lever, J.; Krzywinski, M.; Altman, N. Points of Significance: Principal Component Analysis. Nat. Methods 2017, 14, 641–642. [Google Scholar] [CrossRef]
- Suyal, M.; Sharma, S. A Review on Analysis of K-Means Clustering Machine Learning Algorithm Based on Unsupervised Learning. J. Artif. Intell. Syst. 2024, 6, 85–95. [Google Scholar] [CrossRef]
- Yuan, C.; Yang, H. Research on K-Value Selection Method of K-Means Clustering Algorithm. J 2019, 2, 226–235. [Google Scholar] [CrossRef]
- Silva, M.D.C.; Woodward, A.P.; Fearon, A.M.; Perriman, D.M.; Spencer, T.J.; Couldrick, J.M.; Scarvell, J.M. Minimal Clinically Important Change of Knee Flexion in People with Knee Osteoarthritis after Non-Surgical Interventions Using a Meta-Analytical Approach. Syst. Rev. 2024, 13, 50. [Google Scholar] [CrossRef]
- Ohgi, Y.; Ichikawa, H.; Homma, M.; Miyaji, C. Stroke Phase Discrimination in Breaststroke Swimming Using a Tri-Axial Acceleration Sensor Device. Sports Eng. 2003, 6, 113–123. [Google Scholar] [CrossRef]
- Zemková, E.; Zapletalová, L. The Role of Neuromuscular Control of Postural and Core Stability in Functional Movement and Athlete Performance. Front. Physiol. 2022, 13, 796097. [Google Scholar] [CrossRef]
- Sisto, S.A.; Evans, N. Activity and Fitness in Spinal Cord Injury: Review and Update. Curr. Phys. Med. Rehabil. Rep. 2014, 2, 147–157. [Google Scholar] [CrossRef]
- Carles, L. Neuromuscular Reeducation: Fine-Tuning Movement Patterns for Rehabilitation, Performance Enhancement, and Enhanced Quality of Life Neuromuscular Reeducation: Fine-Tuning Movement Patterns for Rehabilitation, Performance Enhancement, and Enhanced Quality of Life. J. Neurol. Neurorehab. Res. 2023, 8, 164. [Google Scholar] [CrossRef]
- Garrino, L.; Curto, N.; Decorte, R.; Felisi, N.; Matta, E.; Gregorino, S.; Actis, M.V.; Marchisio, C.; Carone, R. Towards Personalized Care for Persons with Spinal Cord Injury: A Study on Patients’ Perceptions. J. Spinal Cord Med. 2011, 34, 67–75. [Google Scholar] [CrossRef] [PubMed]
- Gupta, S.; Jaiswal, A.; Norman, K.; DePaul, V. Heterogeneity and Its Impact on Rehabilitation Outcomes and Interventions for Community Reintegration in People With Spinal Cord Injuries: An Integrative Review. Top. Spinal Cord Inj. Rehabil. 2019, 25, 164–185. [Google Scholar] [CrossRef] [PubMed]
- Faber, J.; Fonseca, L.M. How Sample Size Influences Research Outcomes. Dent. Press J. Orthod. 2014, 19, 27–29. [Google Scholar] [CrossRef]
- Patrick, J.H.; Farmer, S.E.; Bromwich, W. Muscle Stretching for Treatment and Prevention of Contracture in People with Spinal Cord Injury. Spinal Cord 2002, 40, 421–422. [Google Scholar] [CrossRef][Green Version]
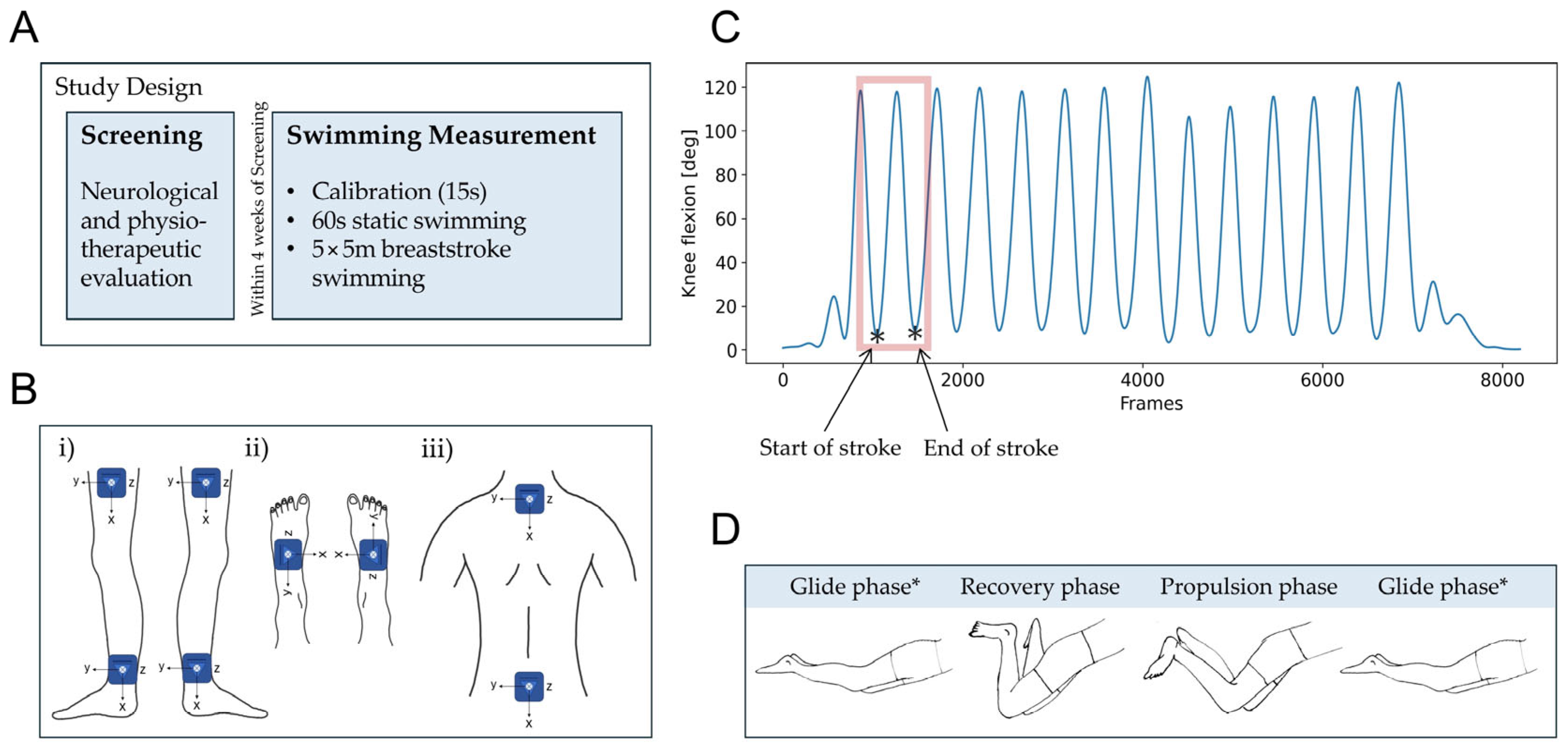

| Swimming Parameter (Features) | Unit | Description |
|---|---|---|
| Velocity (mean) | Meters per second (m/s) | Swimming speed |
| Stroke rate (mean) | Strokes per minute (strokes/min) | Stroke cadence |
| Stroke duration (mean, SD) | Seconds (s) | Time between consecutive glide phases |
| Distance per stroke (mean) | Meters (m) | Distance covered with each stroke |
| Joint angles (min, max) | Degrees (deg) | Angles of the ankle, knee, and hip joints |
| Range of motion (mean) | Degrees (deg) | Range of motion of the ankle, knee, and hip joints |
| Ankle displacement (mean) | Meters (m) | Lateral, horizontal, and vertical displacements of the ankle during the propulsion phase |
| ACC (mean, SD) | Range [0, 1] | Intra-limb coordination |
| SSD (mean) | Degrees squared (deg2) | Deviation from the healthy pattern of intra-limb coordination |
| Asymmetry (mean) | Percentage (%) | Percentage difference in joint angles between left and right legs |
| Asymmetry SSD (mean) | Degrees squared (deg2) | Deviation of intra-limb coordination between left and right legs |
| Phase shift (mean, SD) | Percentage (%) | Inter-limb coordination |
| Cohort | Individuals with SCI | Healthy Controls | p-Values |
|---|---|---|---|
| Number, n | 30 | 20 | |
| Age [years], mean (SD) | 55.4 (14.0) | 37.3 (12.7) | <0.001 |
| Sex [female], n (%) | 9 (30.0) | 10 (50.0) | 0.235 |
| BMI [kg/m2], mean (SD) | 25.1 (4.0) | 22.1 (2.2) | 0.004 |
| AIS D, n (%) | 30 (100.0) | ||
| NLI, n (%) | 12 (40.0) cervical 18 (60.0) thoracic | ||
| Etiology, n (%) | 11 (36.7) traumatic 19 (63.3) non-traumatic | ||
| SCIM Mob., mean (SD) | 35.2 (5.2) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giagiozis, M.; Imhof, S.; Achermann, S.; Jutzeler, C.R.; Demkó, L.; Zörner, B. Quantification of Lower Limb Kinematics During Swimming in Individuals with Spinal Cord Injury. Sensors 2025, 25, 3950. https://doi.org/10.3390/s25133950
Giagiozis M, Imhof S, Achermann S, Jutzeler CR, Demkó L, Zörner B. Quantification of Lower Limb Kinematics During Swimming in Individuals with Spinal Cord Injury. Sensors. 2025; 25(13):3950. https://doi.org/10.3390/s25133950
Chicago/Turabian StyleGiagiozis, Melina, Sabrina Imhof, Sibylle Achermann, Catherine R. Jutzeler, László Demkó, and Björn Zörner. 2025. "Quantification of Lower Limb Kinematics During Swimming in Individuals with Spinal Cord Injury" Sensors 25, no. 13: 3950. https://doi.org/10.3390/s25133950
APA StyleGiagiozis, M., Imhof, S., Achermann, S., Jutzeler, C. R., Demkó, L., & Zörner, B. (2025). Quantification of Lower Limb Kinematics During Swimming in Individuals with Spinal Cord Injury. Sensors, 25(13), 3950. https://doi.org/10.3390/s25133950







