WiPIHT: A WiFi-Based Position-Independent Passive Indoor Human Tracking System
Abstract
1. Introduction
- Propose a method to extract human motion trajectory features using CSI by performing amplitude and phase error correction and denoising on raw CSI data, making the CSI data more representative of human activities.
- Utilize only two non-parallel WiFi device links to ensure real-time reconstruction of motion trajectory shapes, regardless of the position, speed, and direction of human movement, even when the relative positions of the TXs and RXs to the human body are unknown. Calculations of initial position and initial motion angle provide absolute trajectory coordinates.
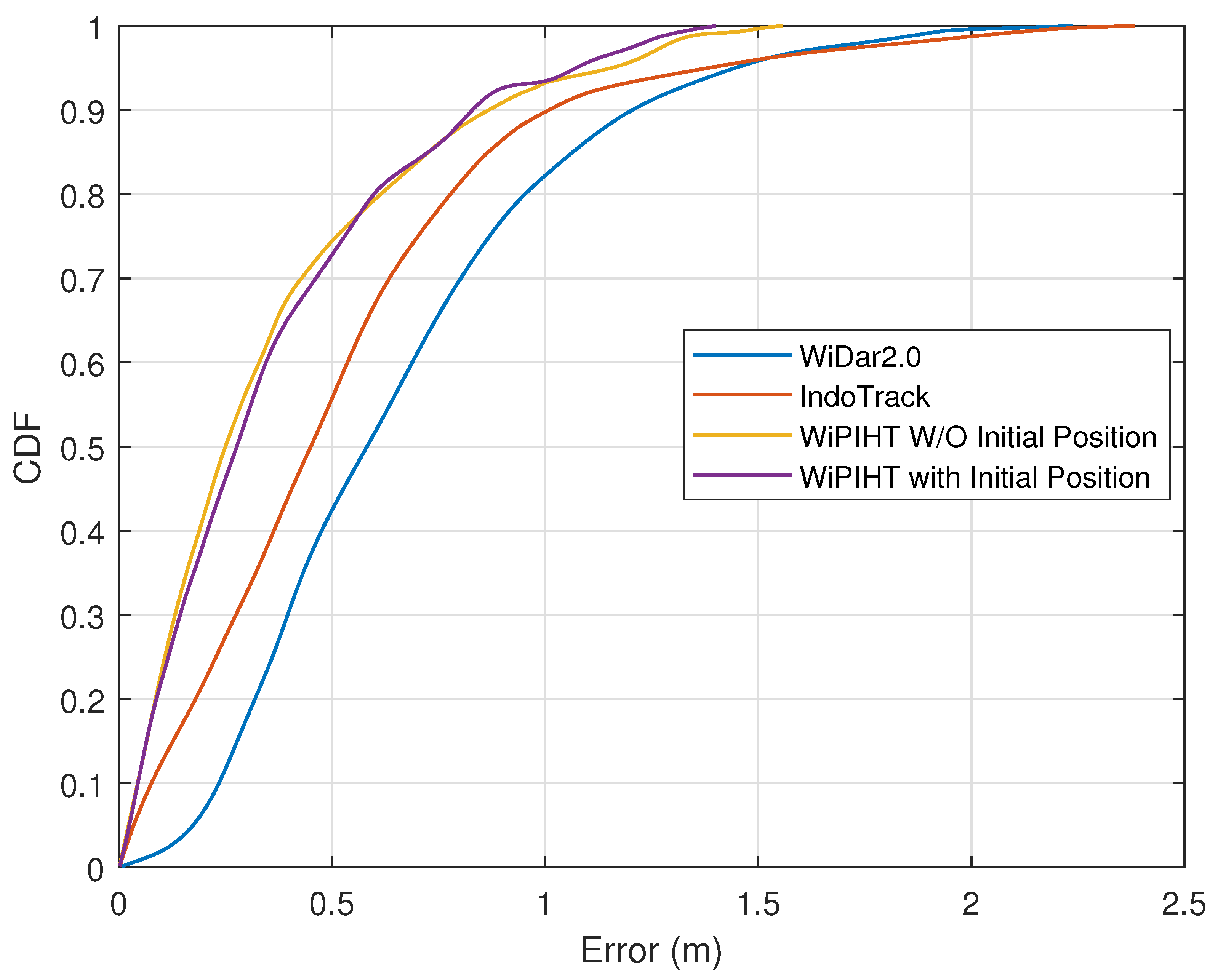
- Implement WiPIHT on regular commercial WiFi devices and conduct extensive experiments and evaluations, validating the efficiency and high precision of the trajectory reconstruction. Evaluation on five test subjects following four different predefined trajectories show that, in a typical indoor environment, WiPIHT achieves a median tracking error of less than 0.3 m in trajectory reconstruction.
2. Related Works
2.1. Non-RF-Based Human Activity Tracking
2.2. RF-Based Human Activity Tracking
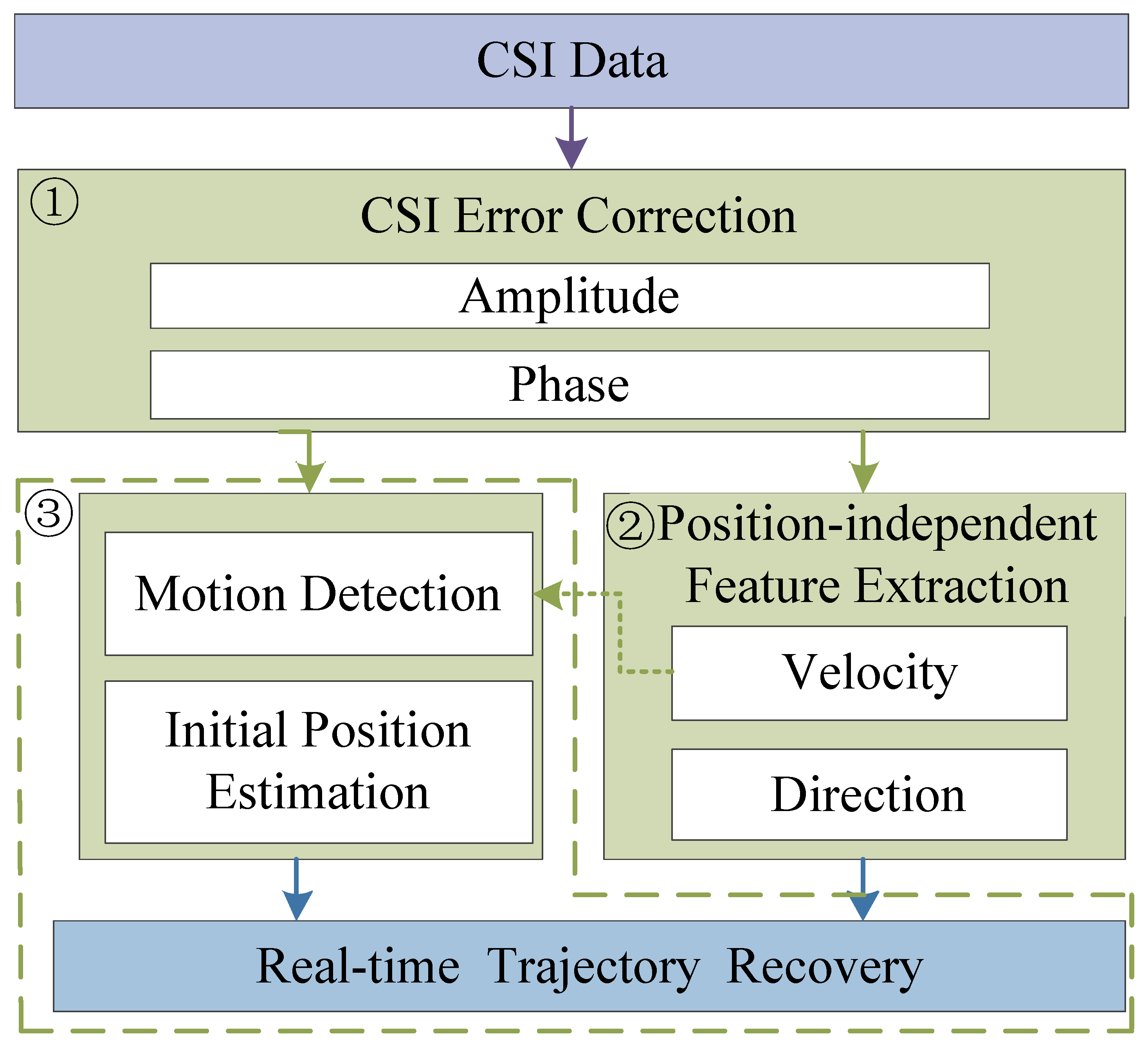
3. System Overview
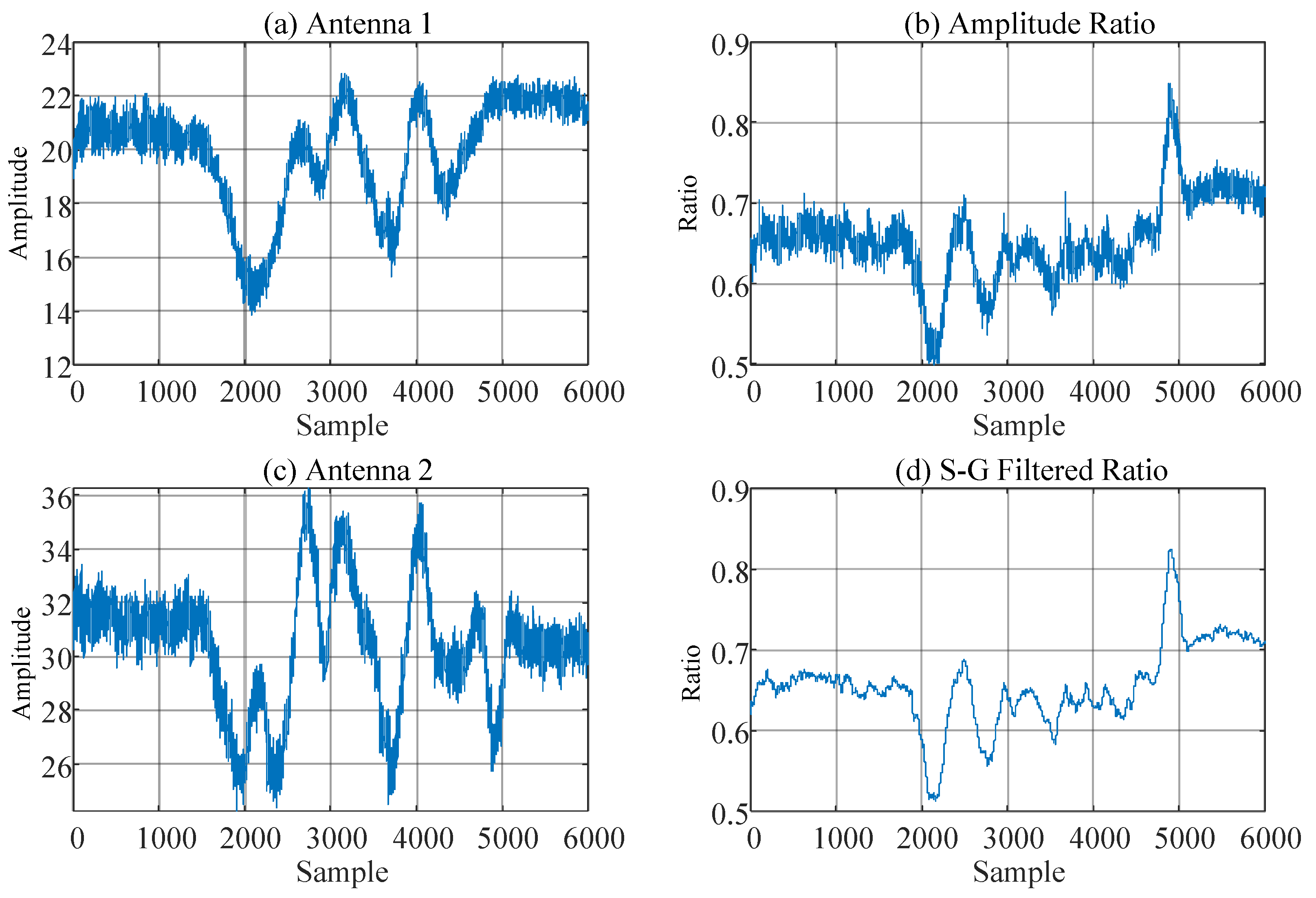
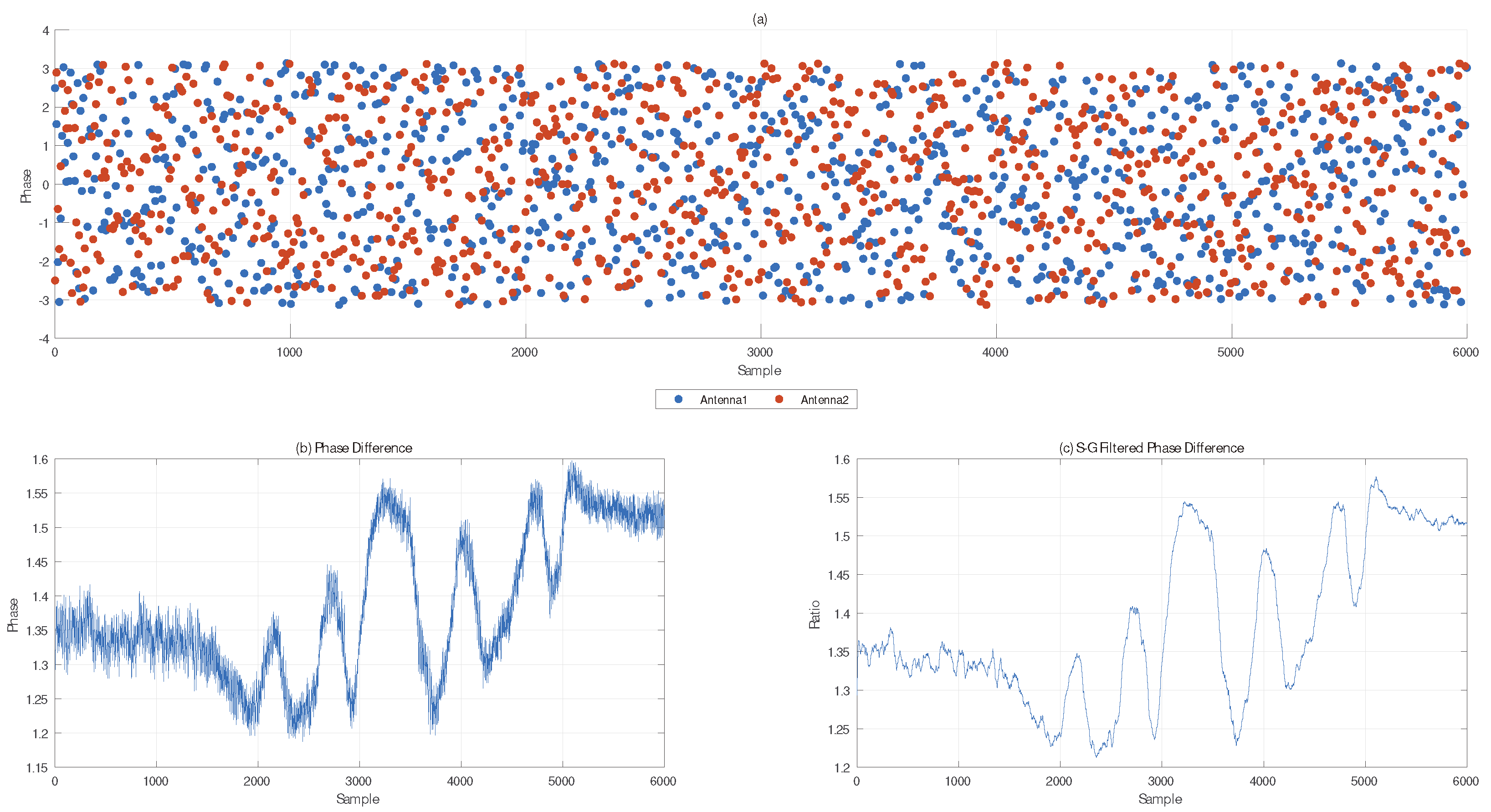
4. CSI Error Correction
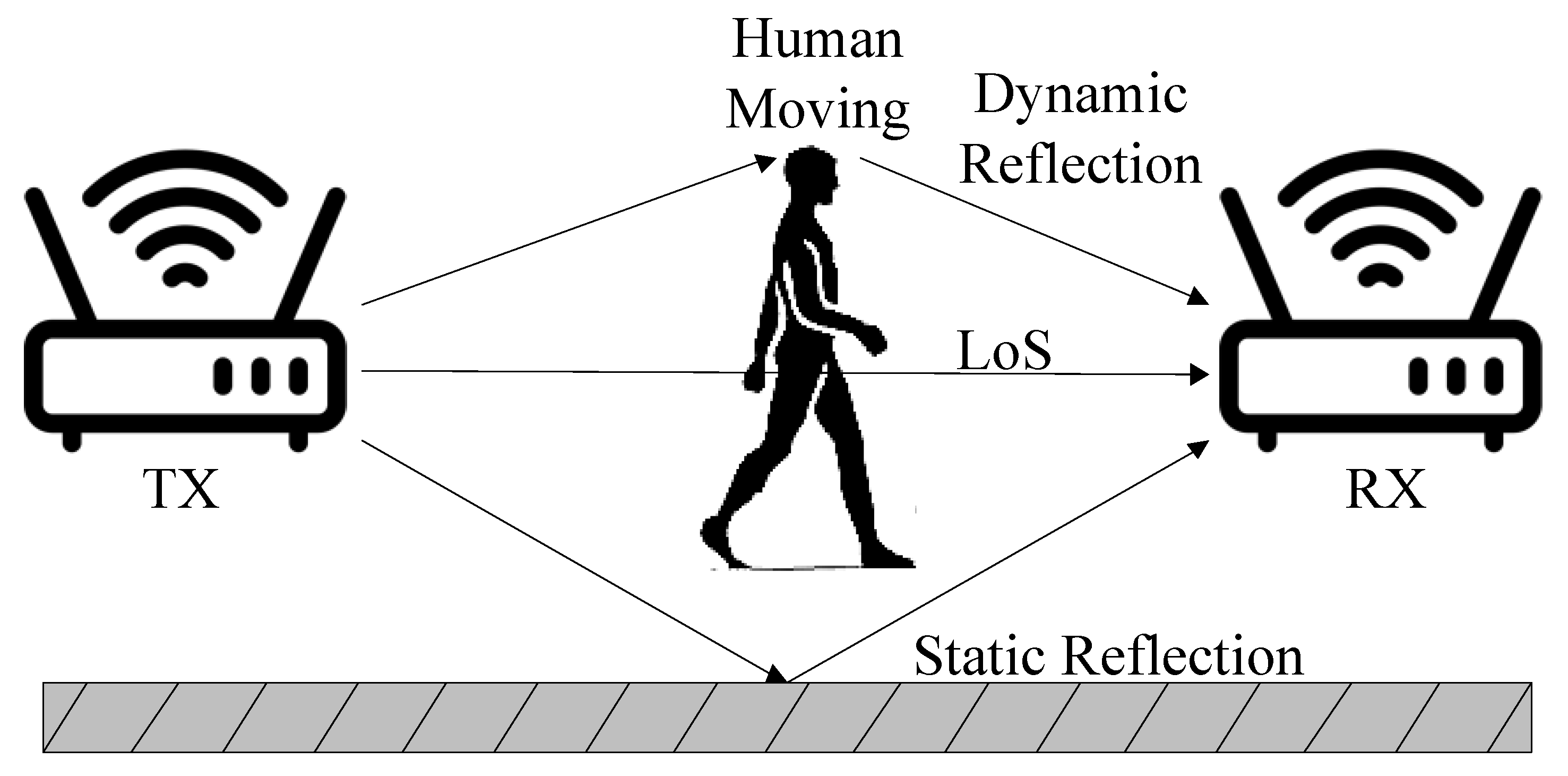
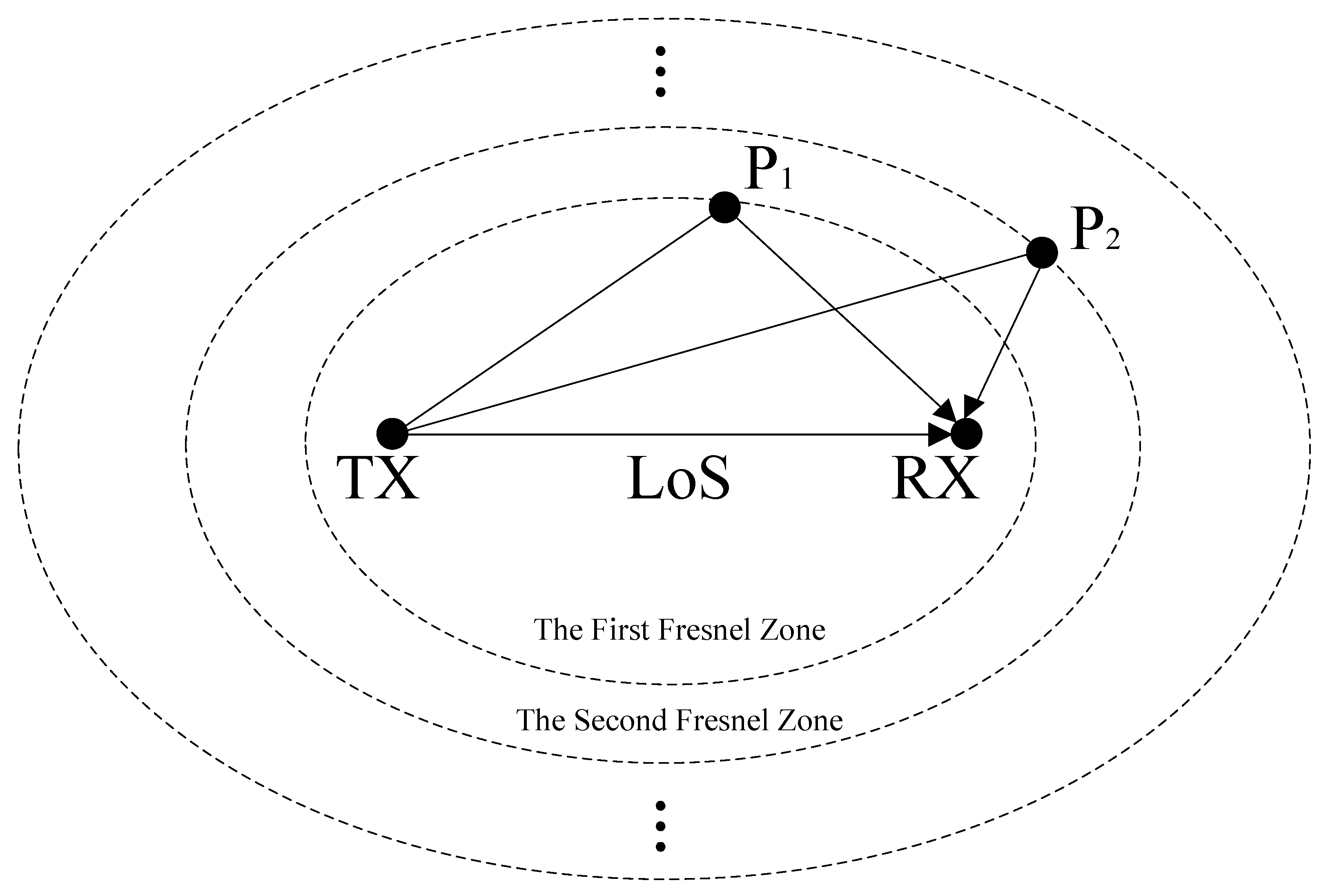
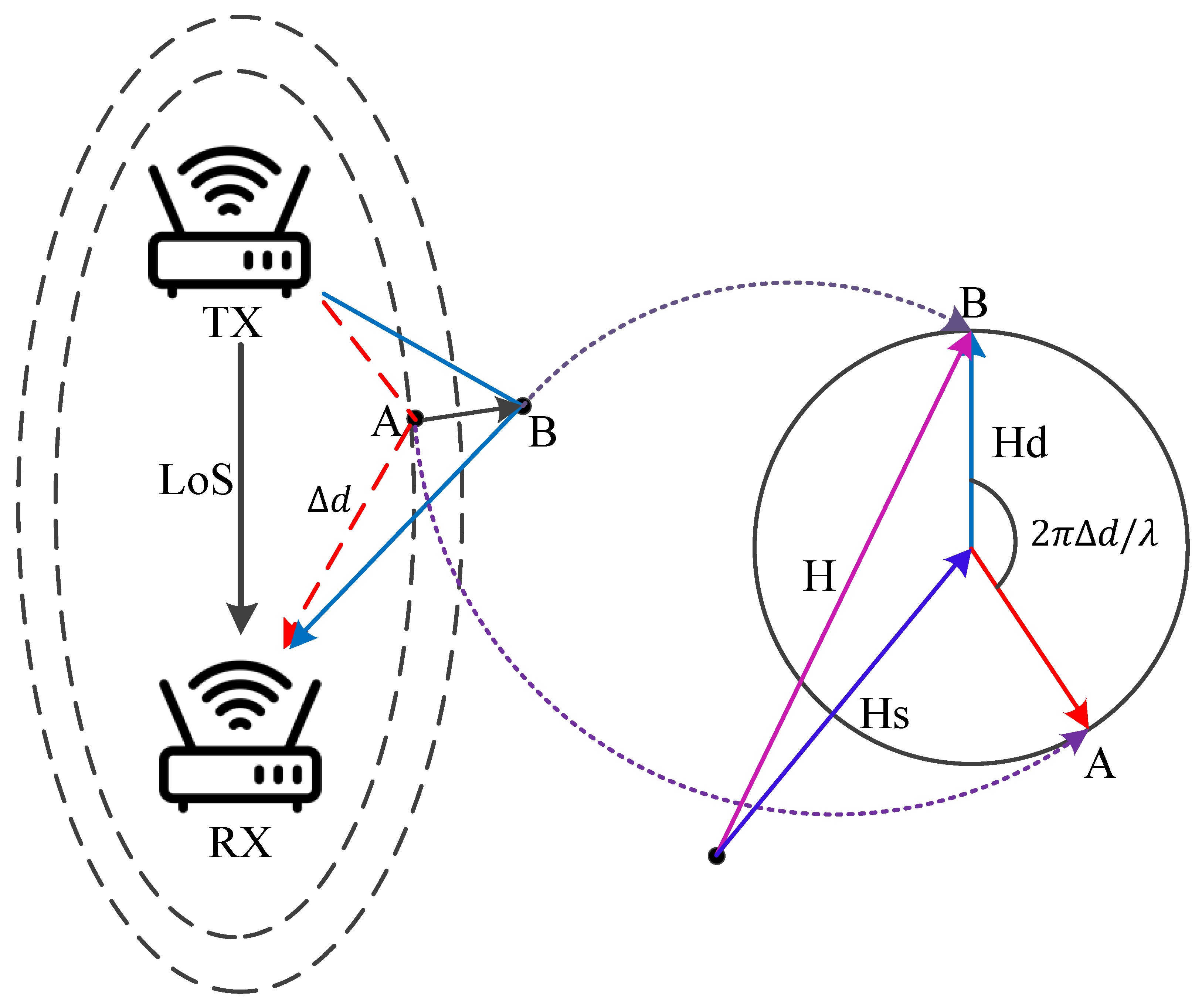
4.1. Fresnel Zone and CSI Phase Rotation
4.2. CSI Error Correction and Denoising Based on Amplitude and Phase
5. Position-Independent Feature Extraction
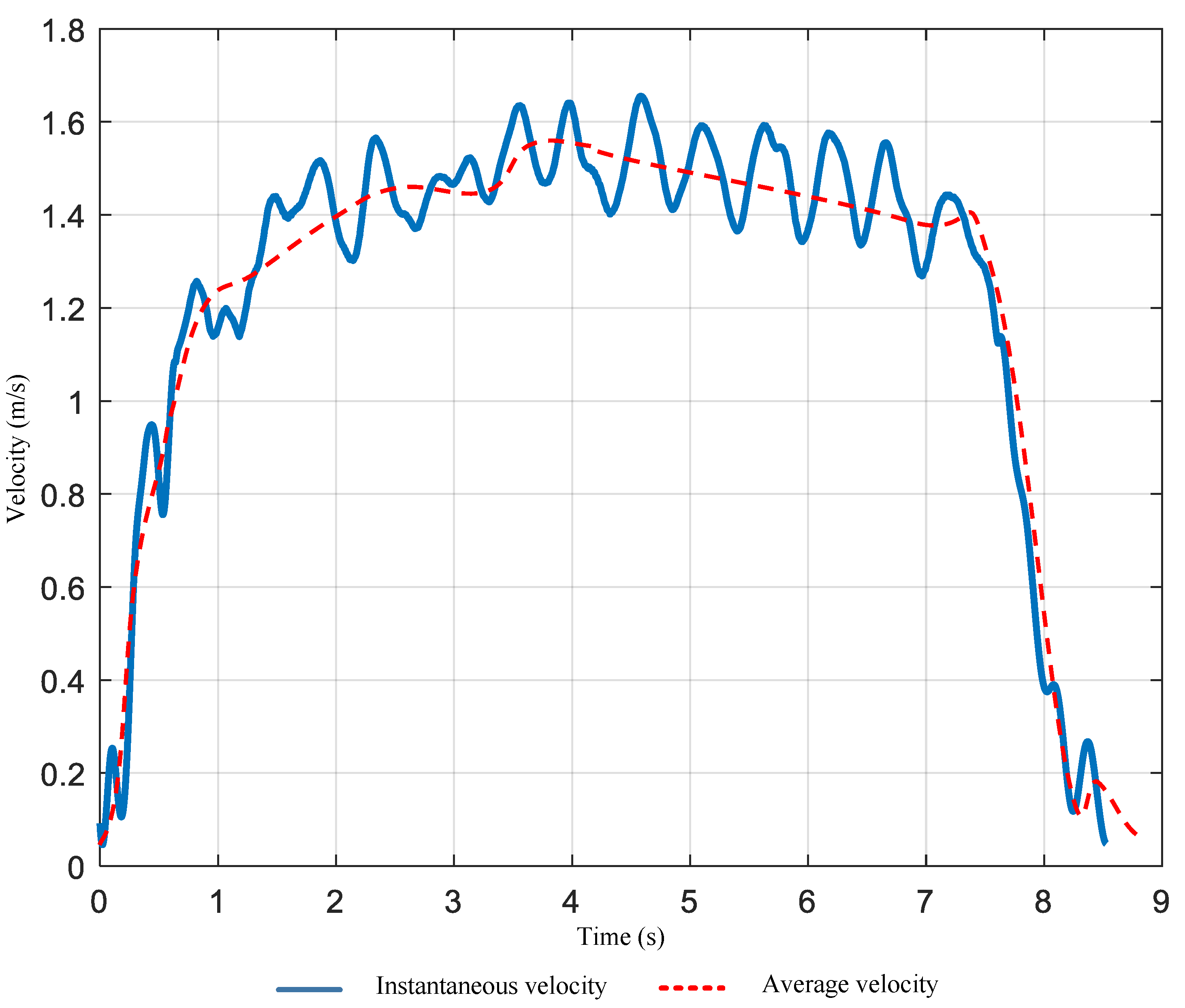
5.1. Position-Independent Real-Time Velocity
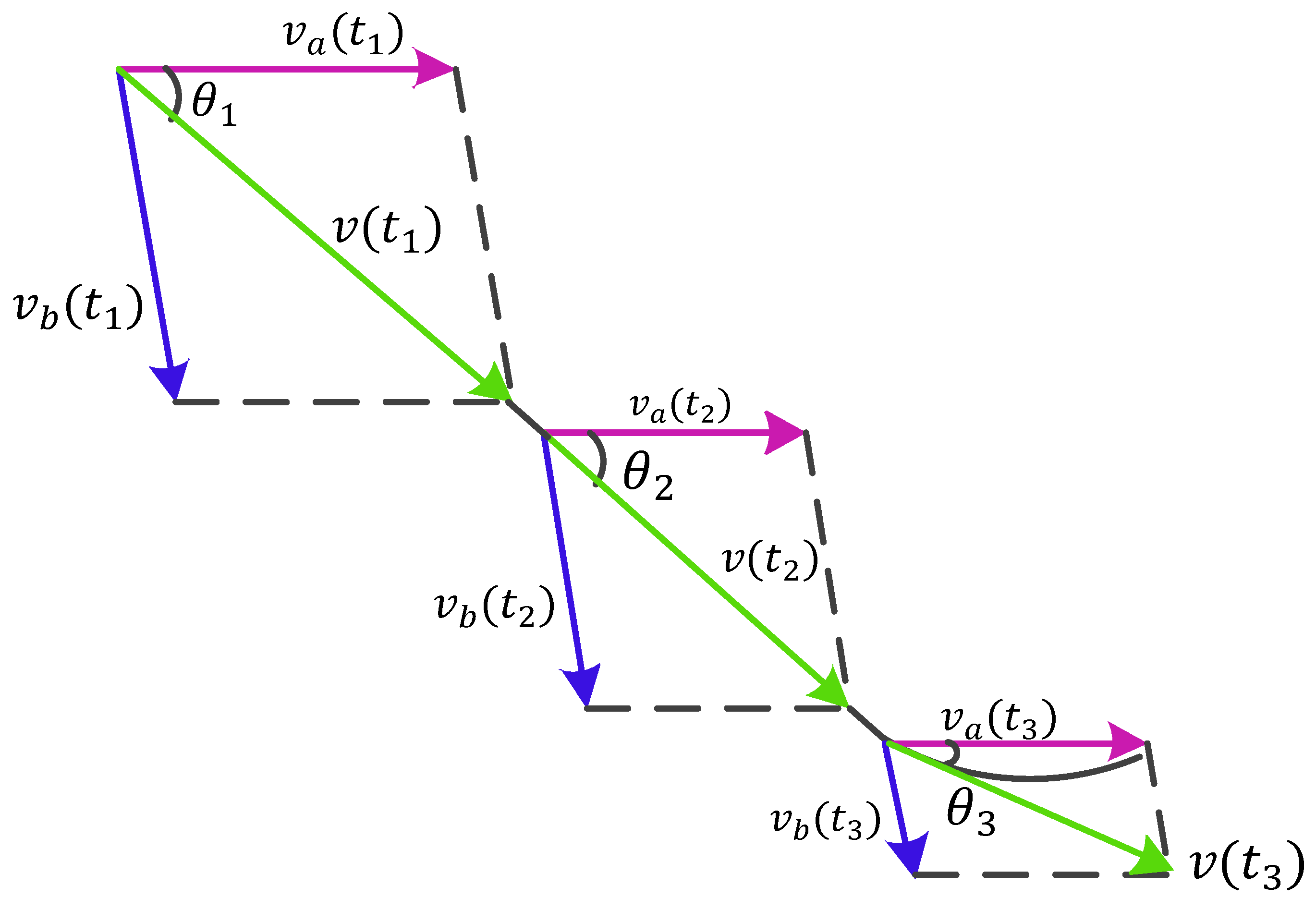
5.2. Position-Independent Real-Time Motion Direction
6. Real-Time Trajectory Recovery
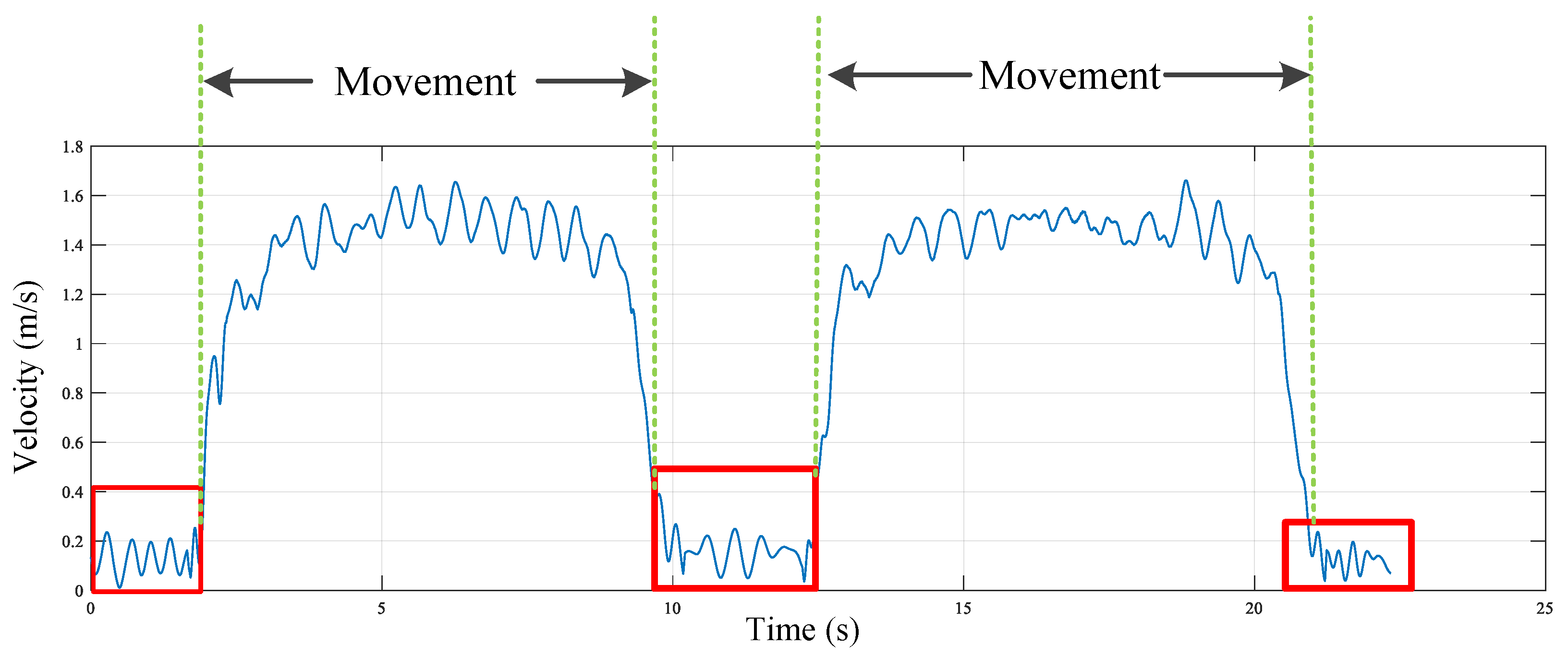
6.1. Motion Detection
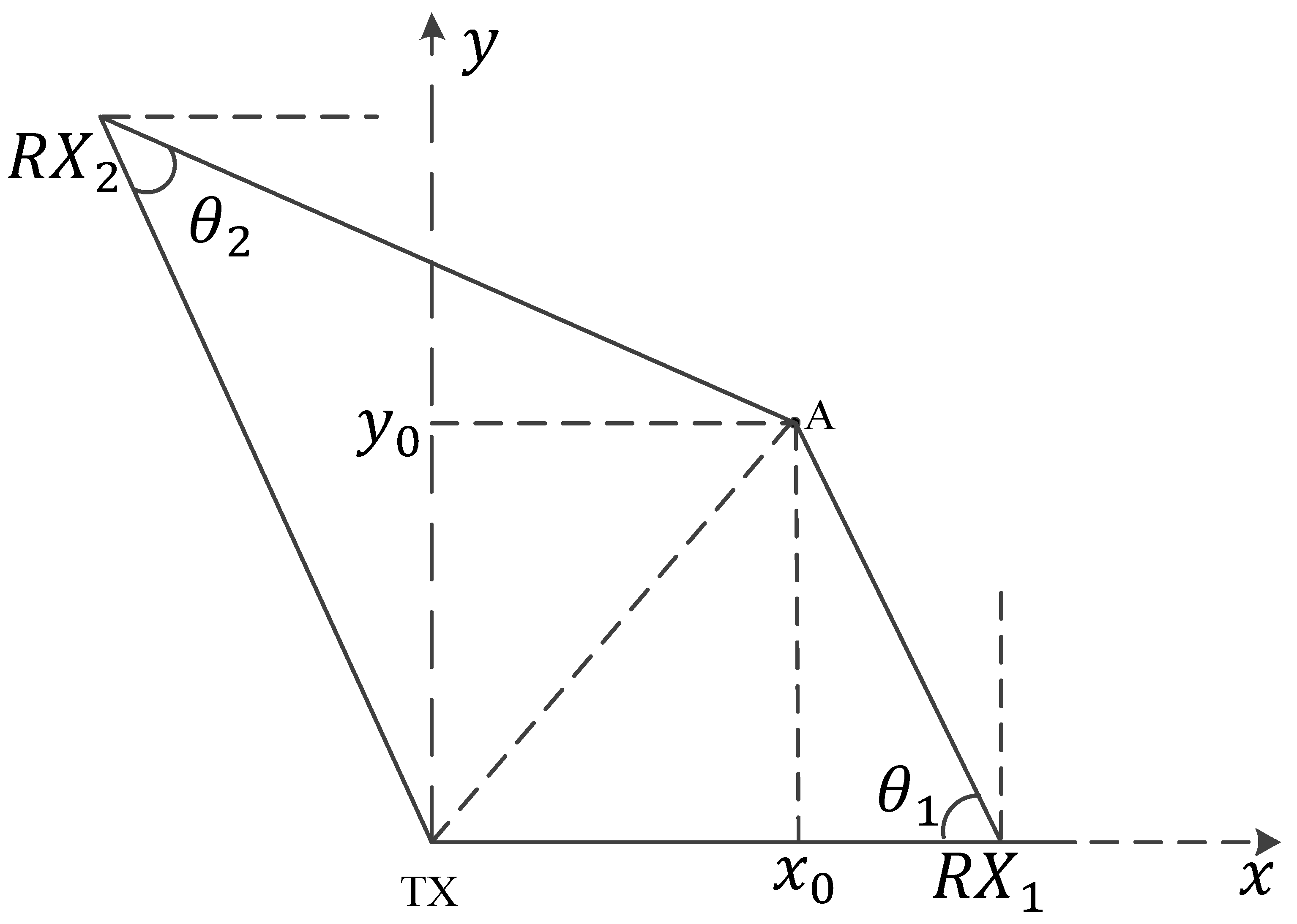
6.2. Initial Position Estimation
6.3. Trajectory Recovery
| Algorithm 1: WiPIHT Trajectory Recovery |
 |
7. Experiment and Evaluation
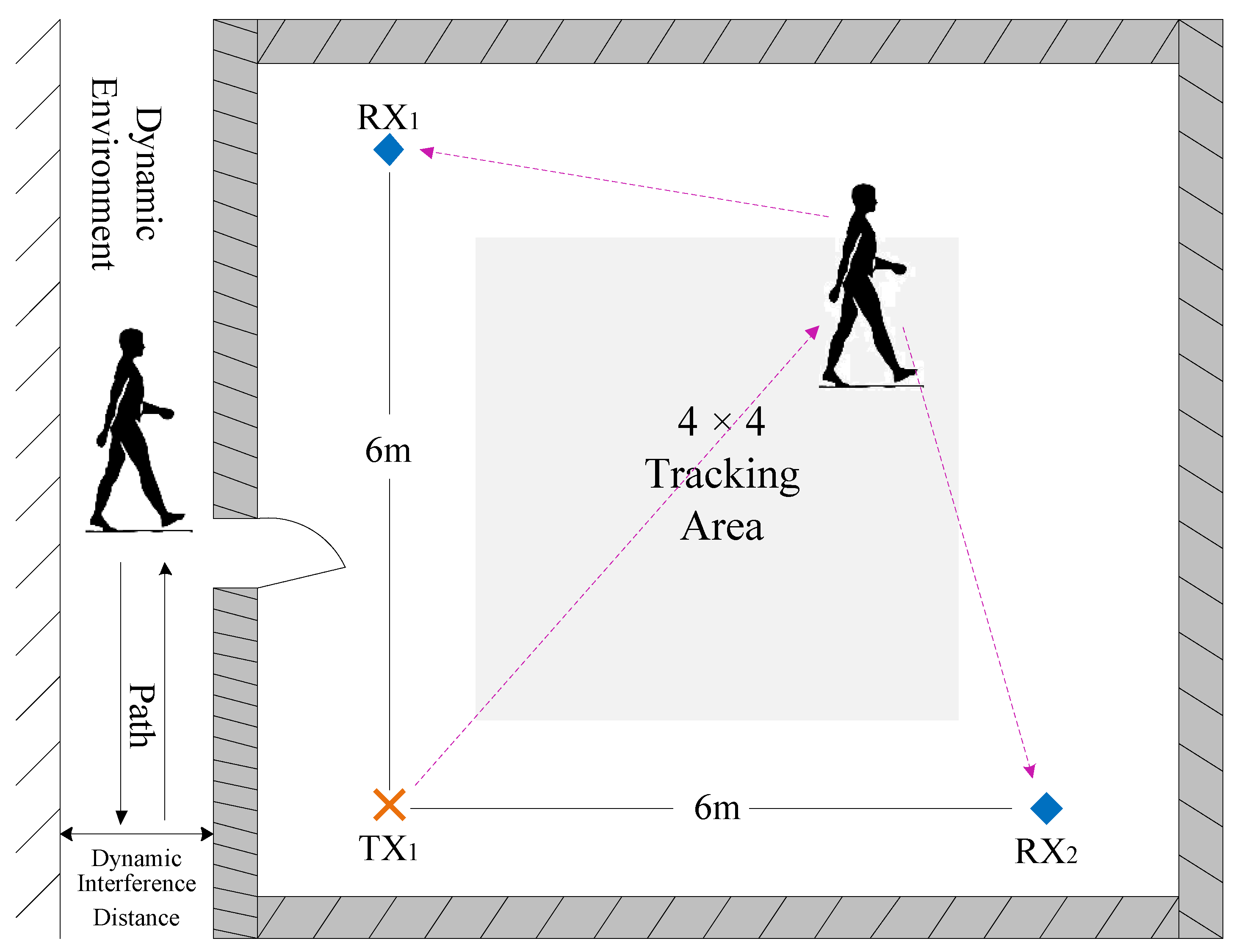
7.1. Experimental Setup
7.2. Experimental Results
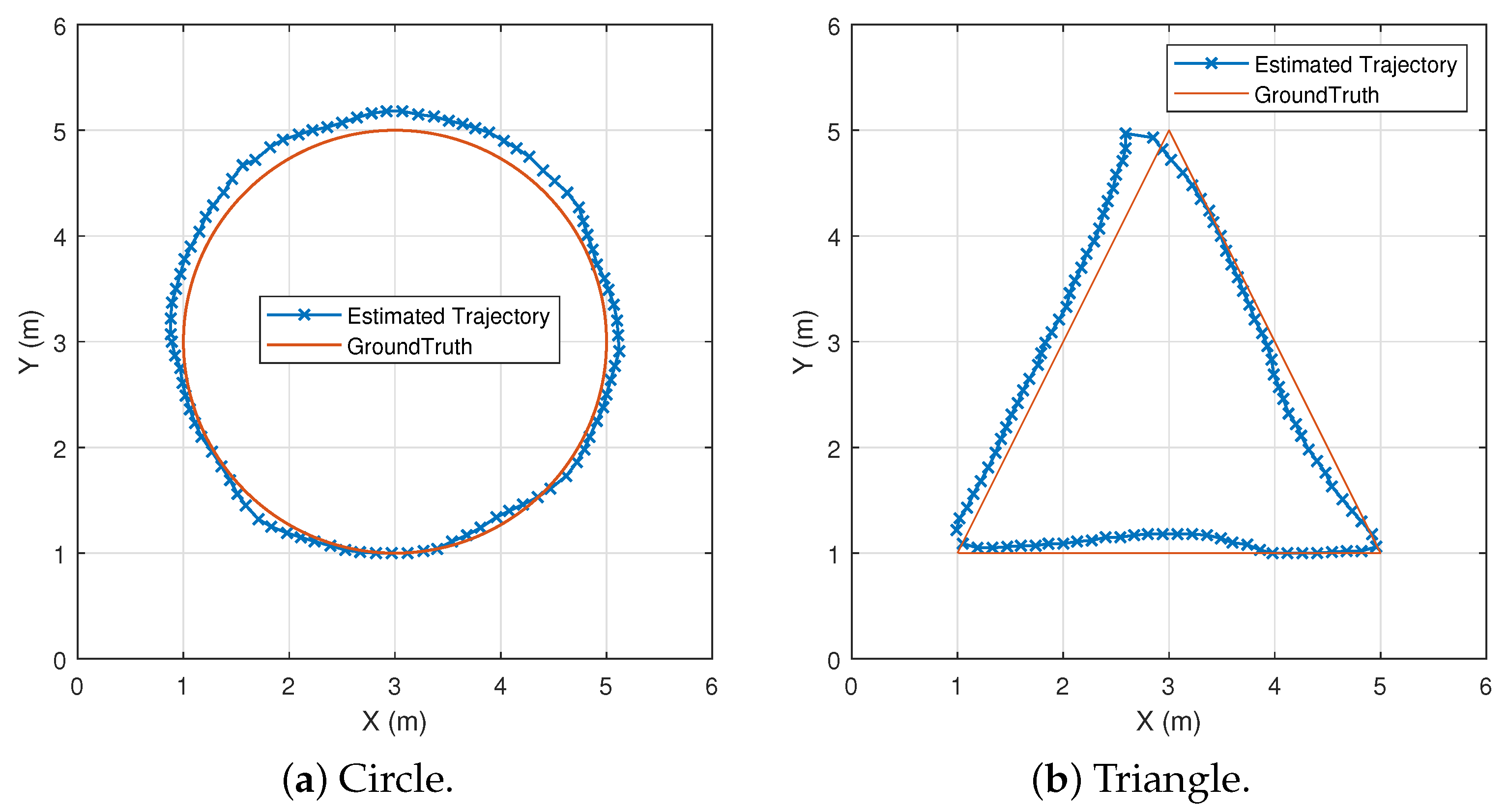
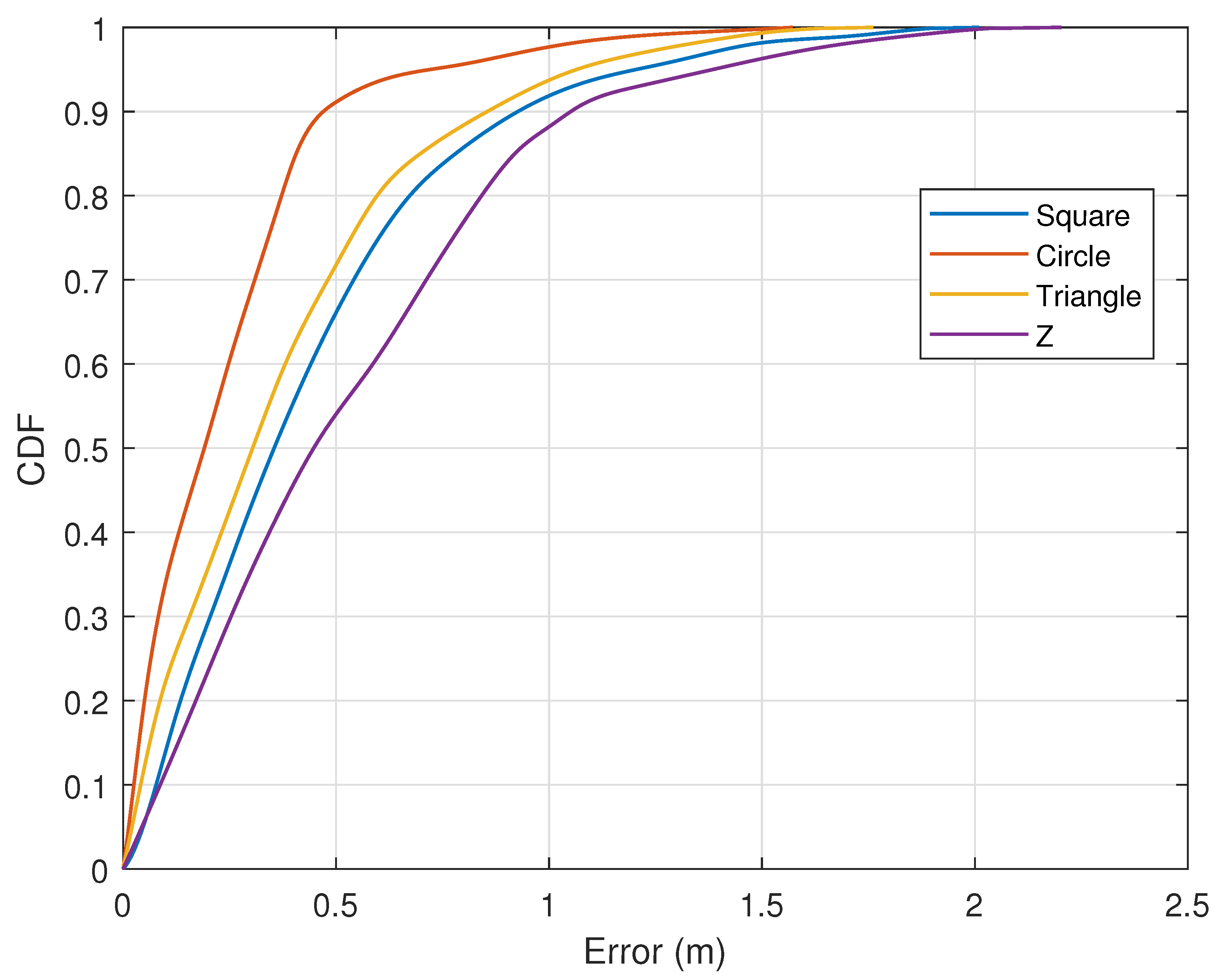
7.2.1. Trajectory Recovery Error
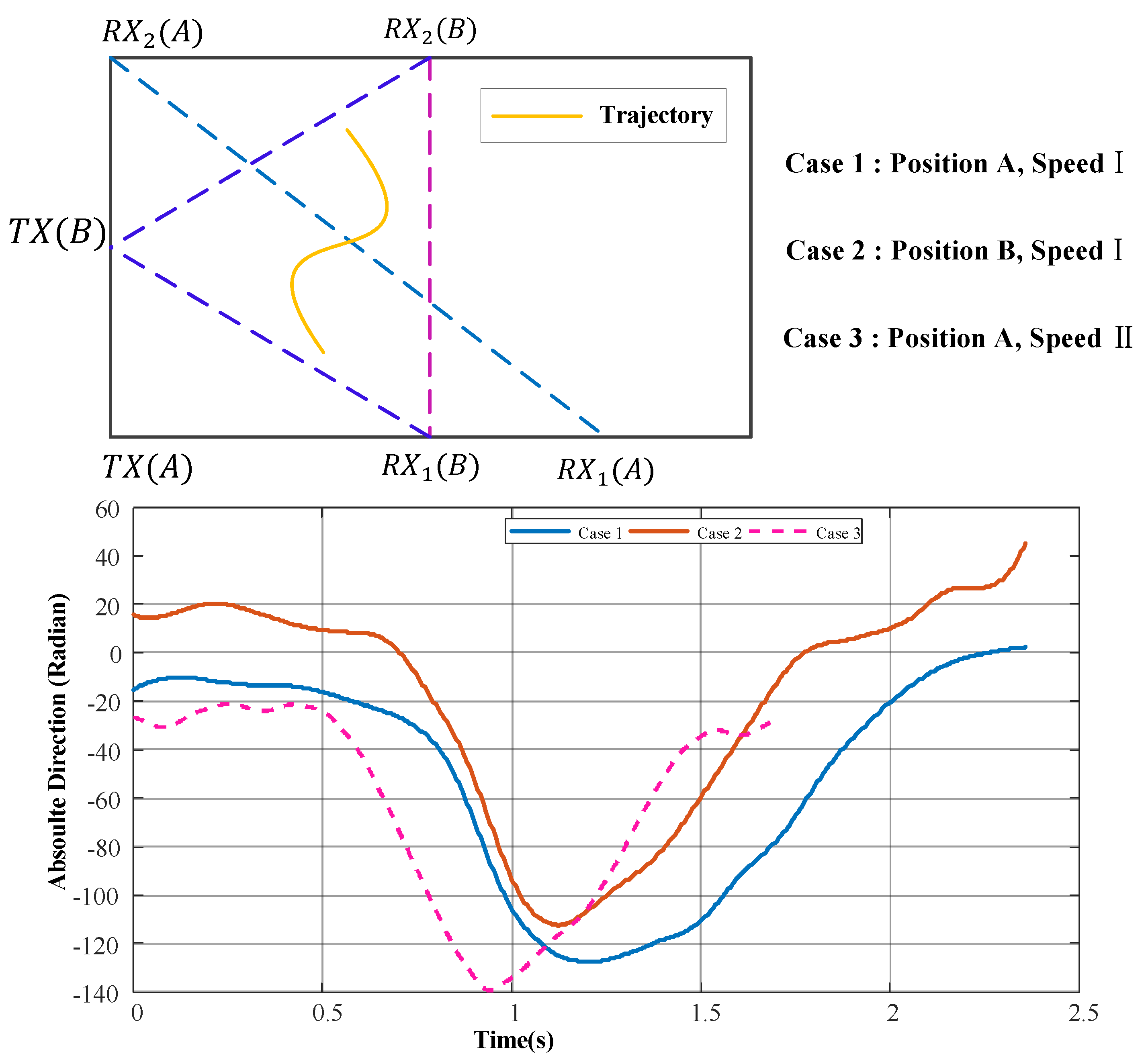
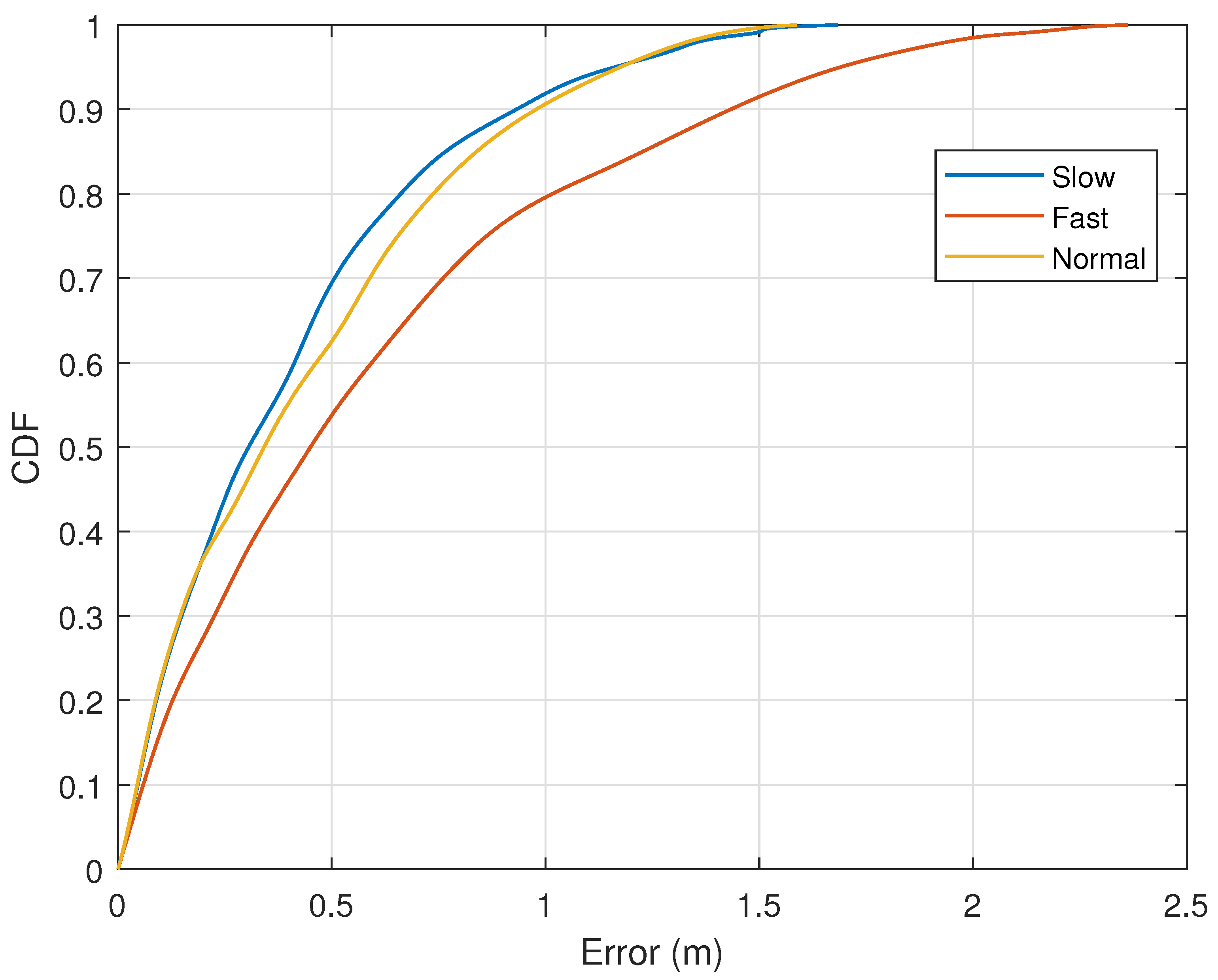
7.2.2. Impact of Movement Speed
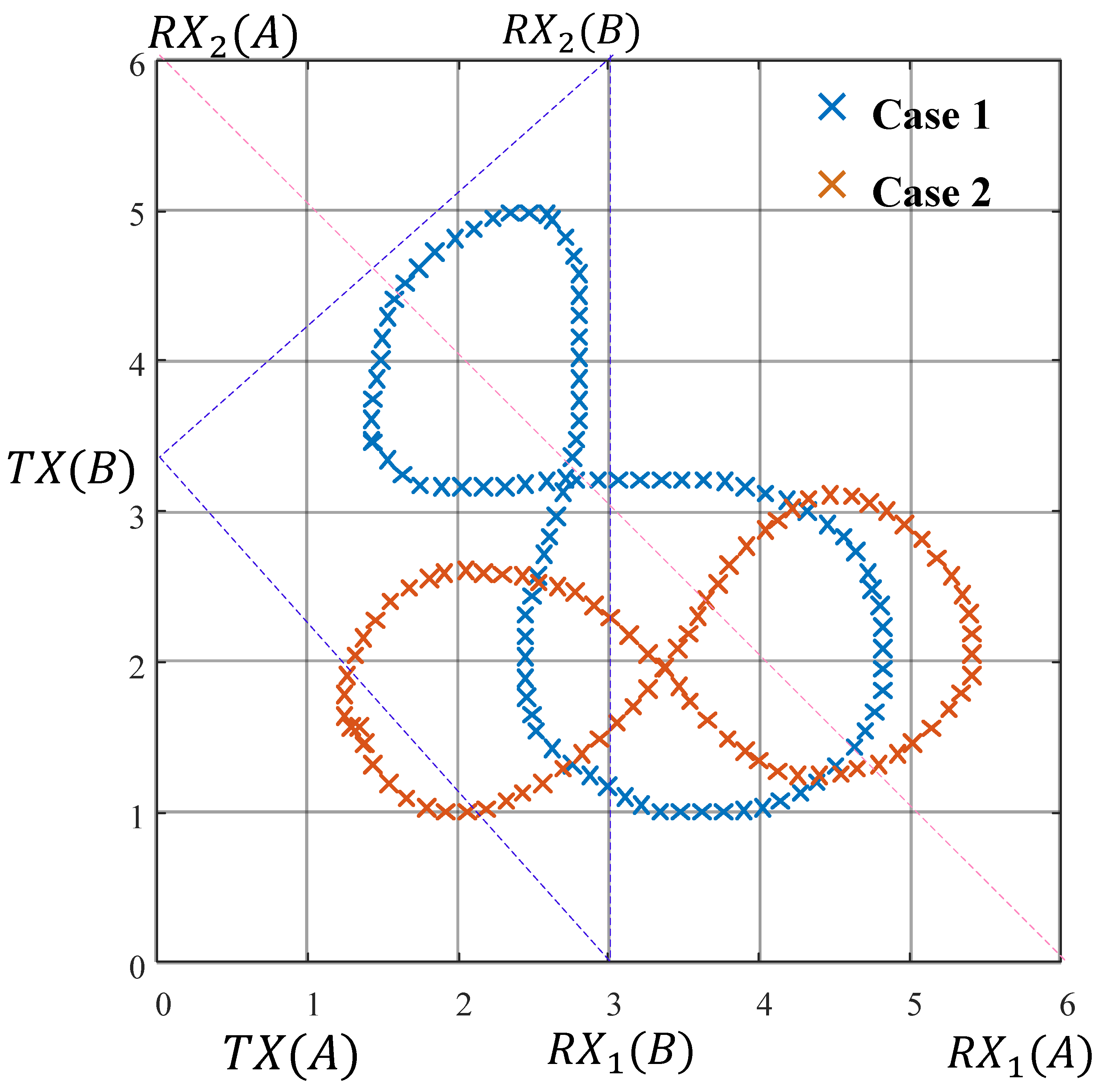
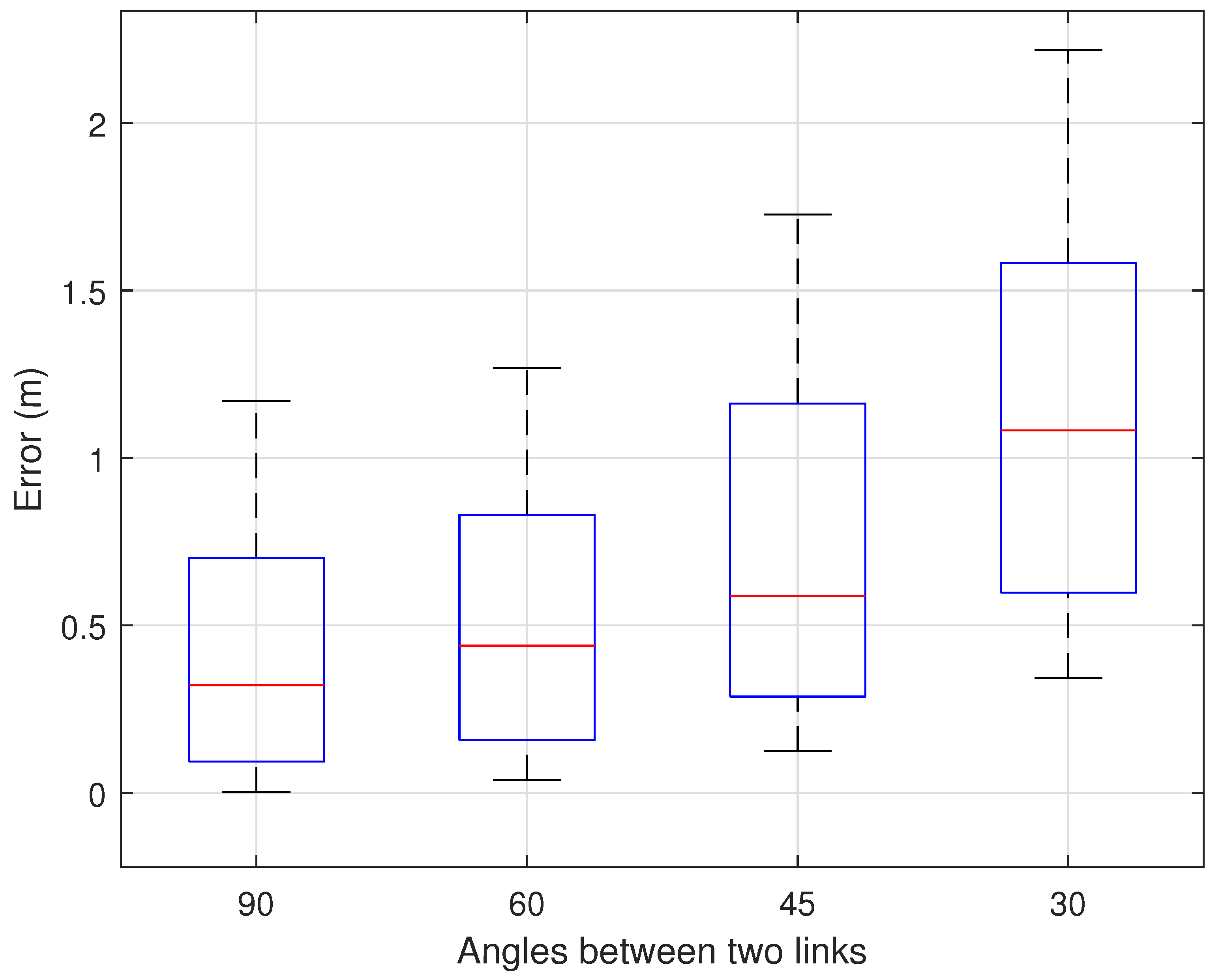
7.2.3. Impact of Static Layout
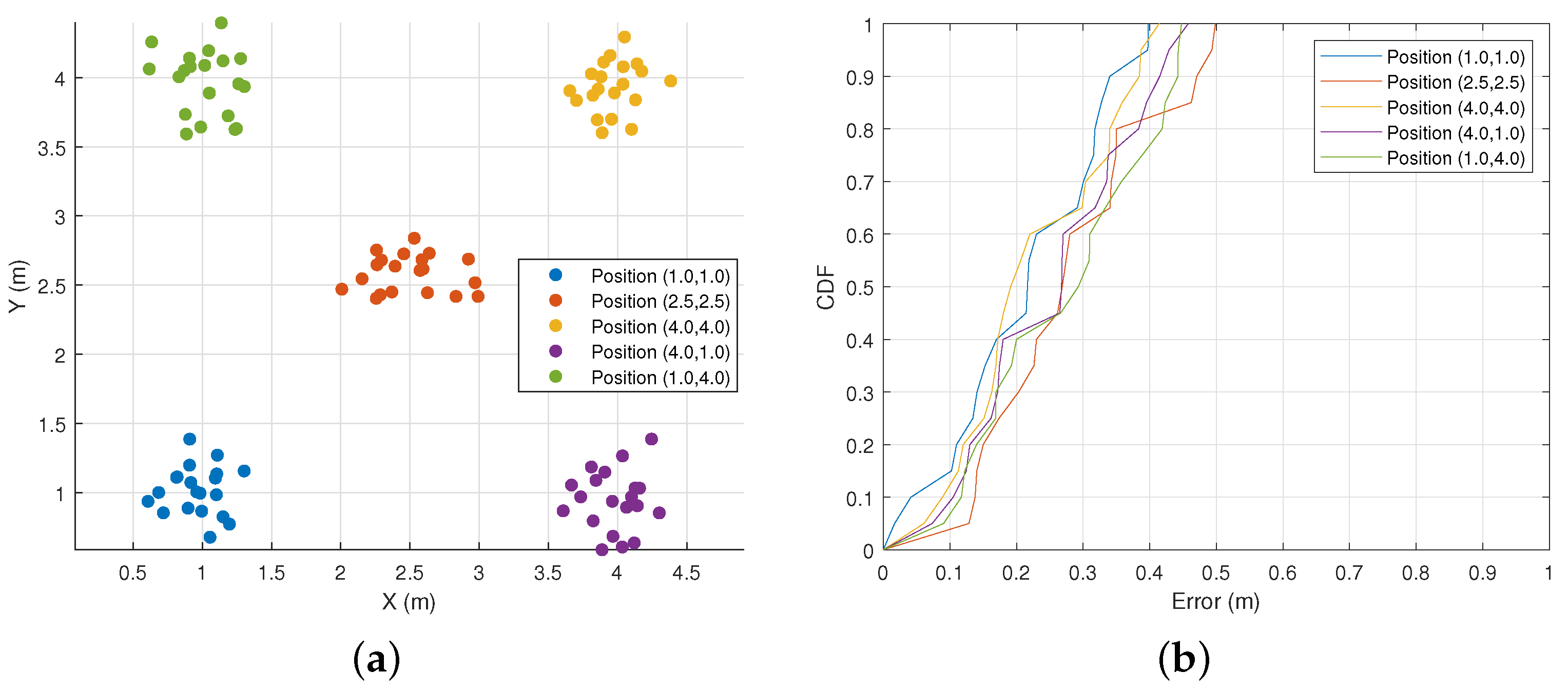
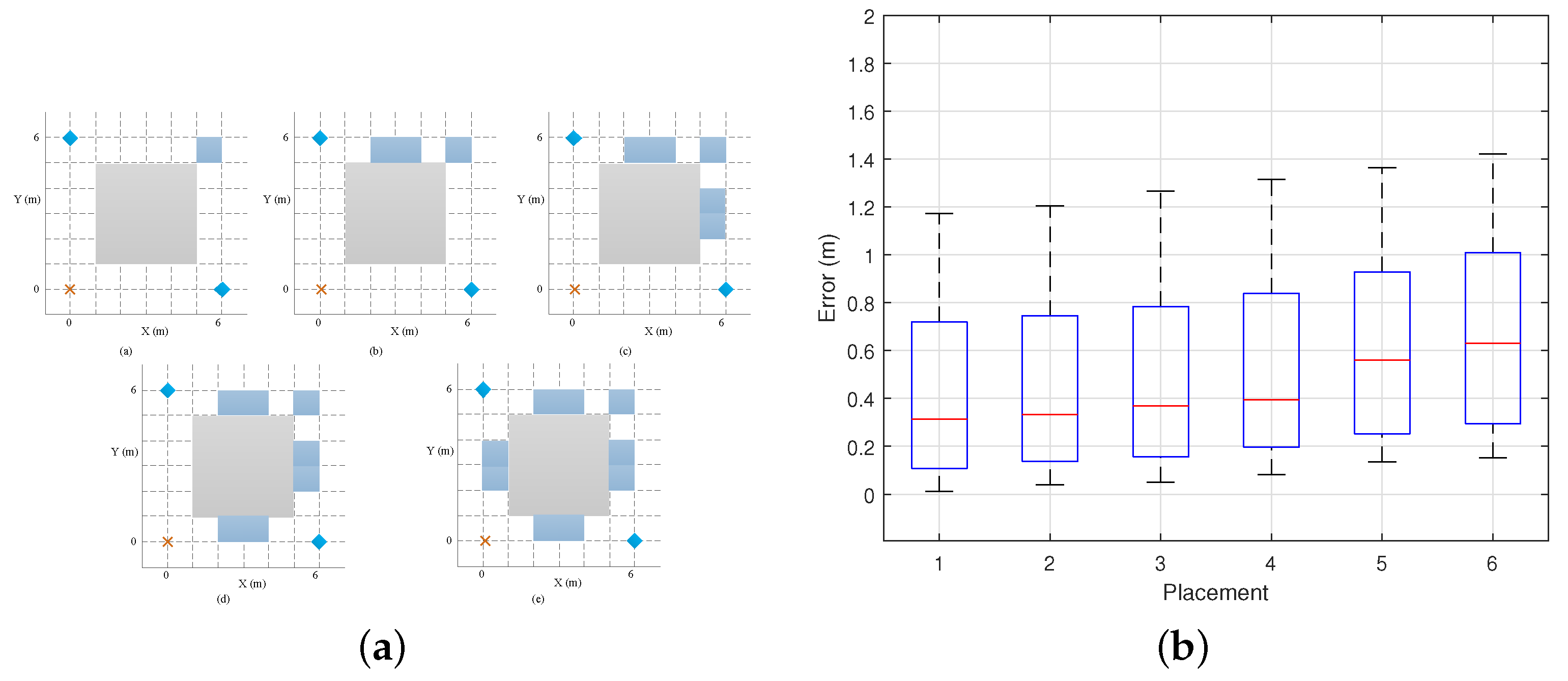
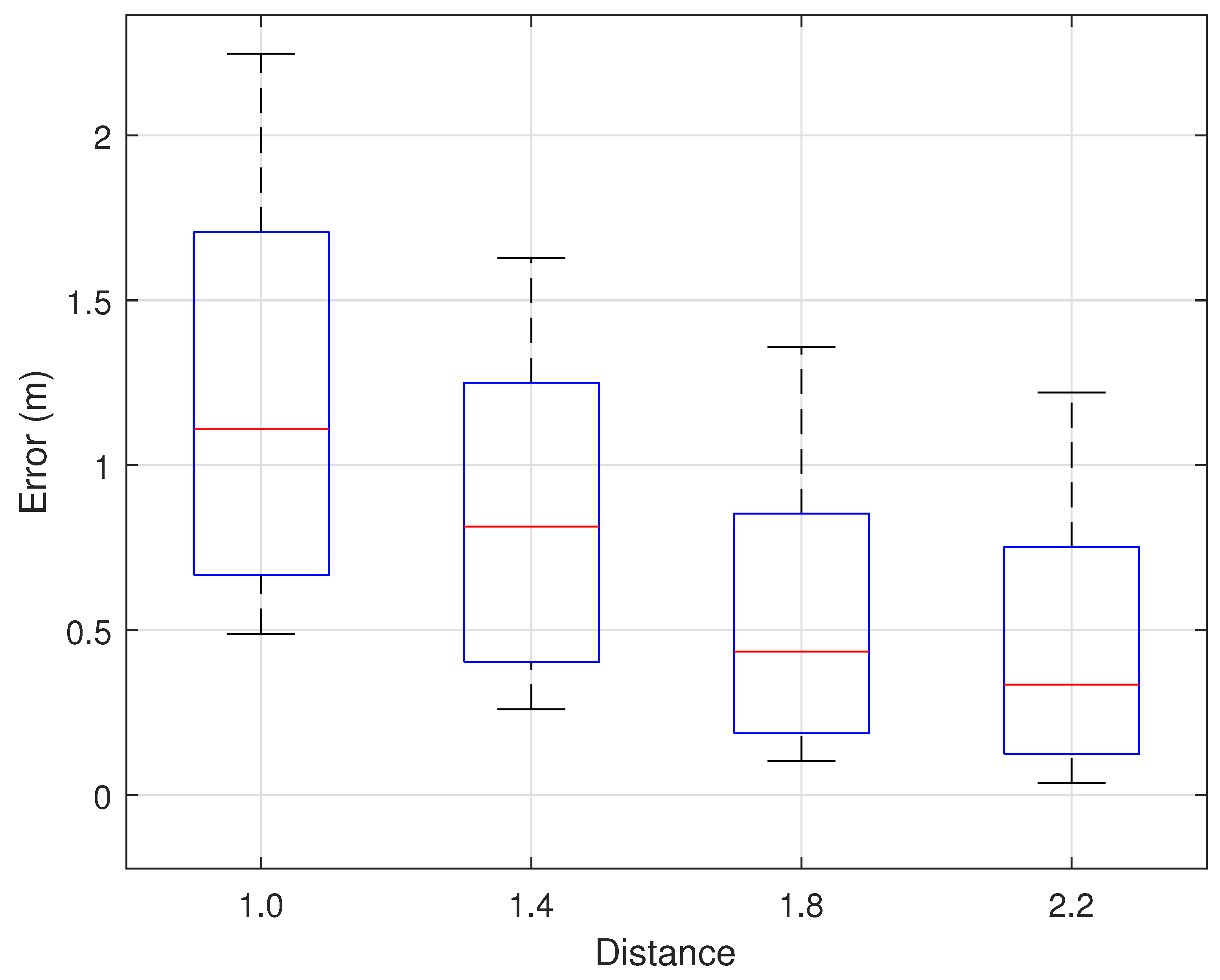
7.2.4. Impact of Transceiver Initial Position
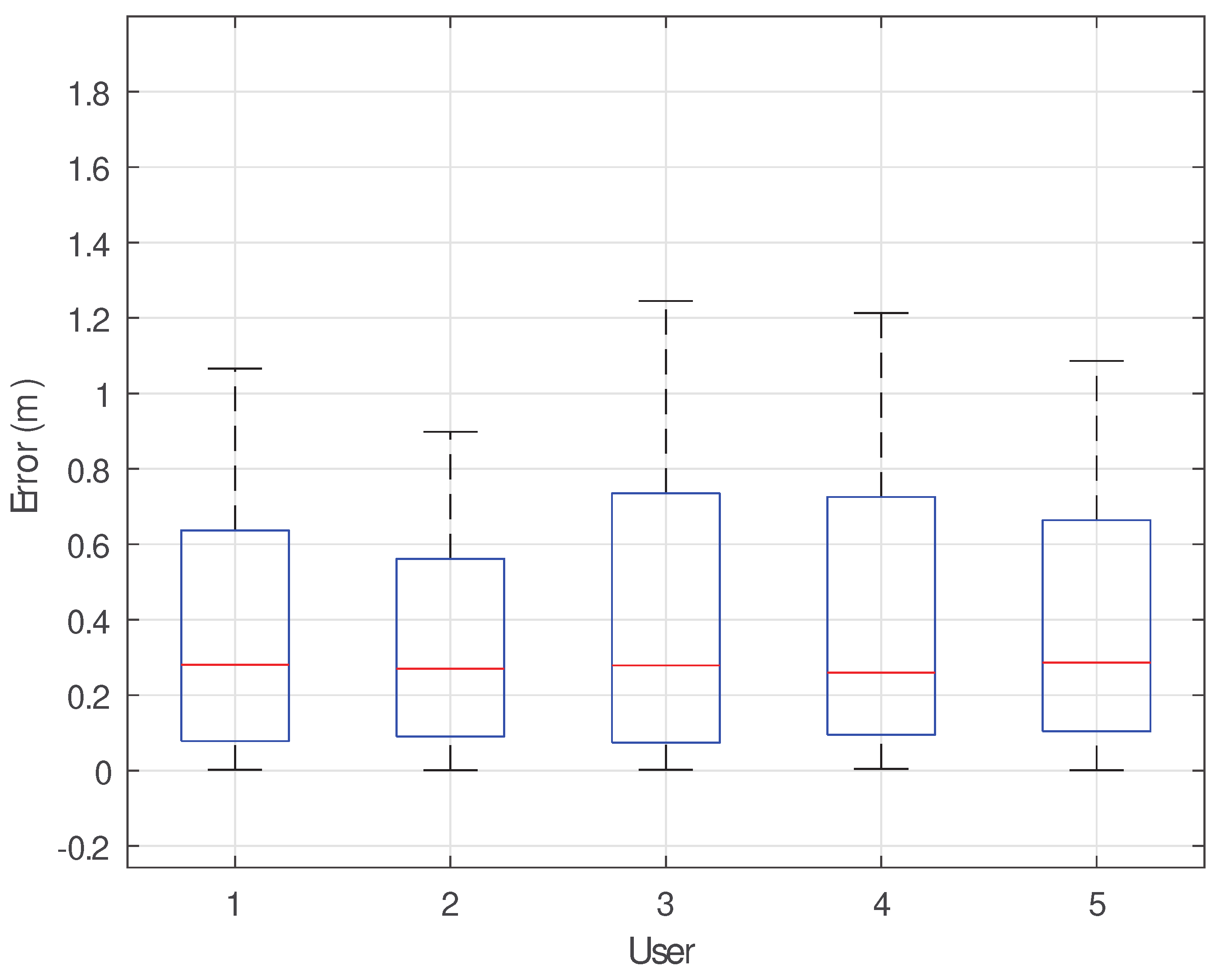
7.2.5. Impact of User Diversity and Preset Trajectory Diversity
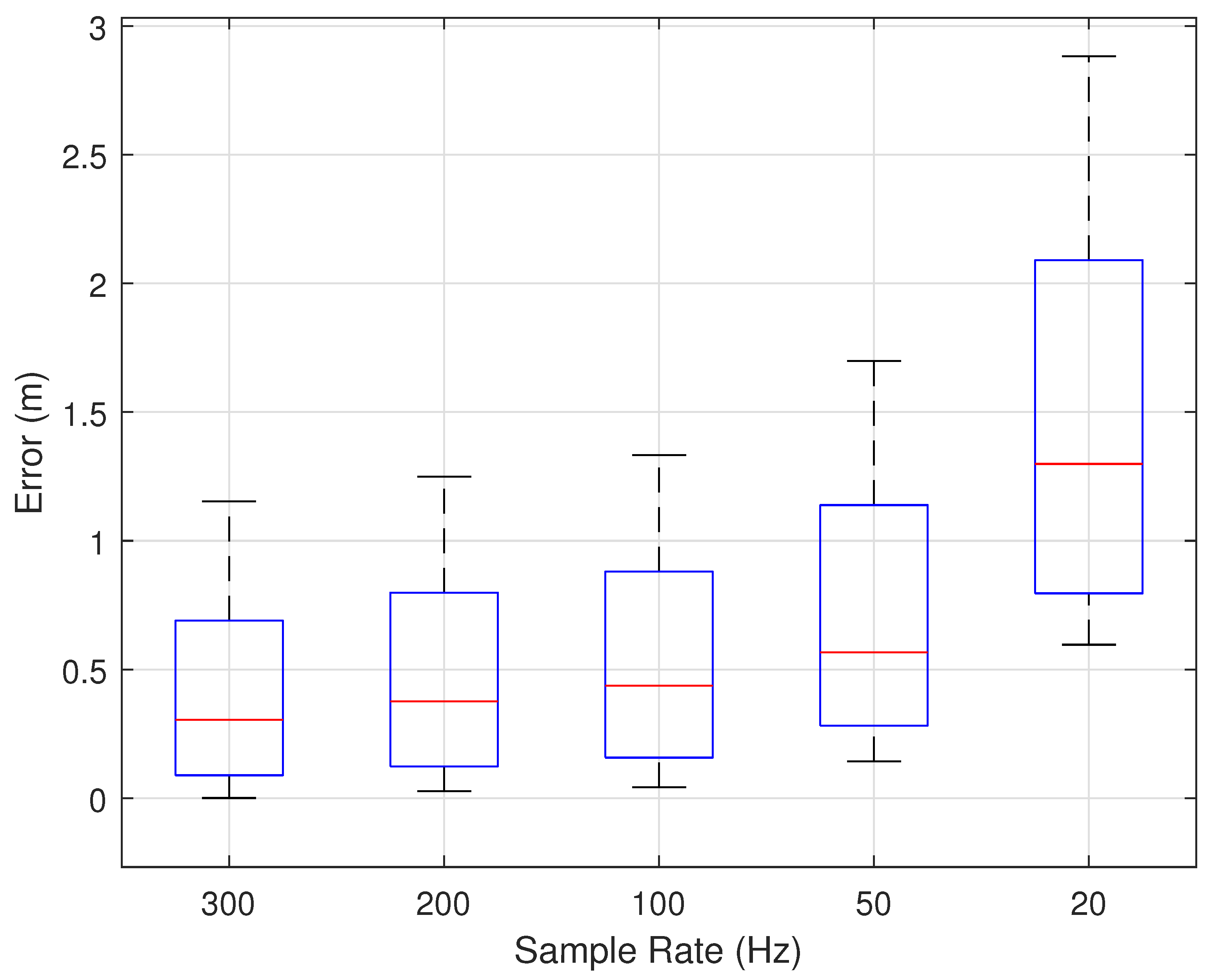
7.2.6. Impact of Sample Rate
7.2.7. Impact of Other Dynamic Objects
8. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sertatıl, C.; Altınkaya, M.A.; Raoof, K. A novel acoustic indoor localization system employing CDMA. Digit. Signal Process. 2012, 22, 506–517. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J.; Wang, W.; Wang, Z.; Liu, Y. Vernier: Accurate and fast acoustic motion tracking using mobile devices. In Proceedings of the IEEE INFOCOM 2018—IEEE Conference on Computer Communications, Honolulu, HI, USA, 15–19 April 2018; pp. 1709–1717. [Google Scholar]
- Mao, W.; He, J.; Qiu, L. Cat: High-precision acoustic motion tracking. In Proceedings of the 22nd Annual International Conference on Mobile Computing and Networking, New York, NY, USA, 3–7 October 2016; pp. 69–81. [Google Scholar]
- Wang, W.; Liu, A.X.; Sun, K. Device-free gesture tracking using acoustic signals. In Proceedings of the 22nd Annual International Conference on Mobile Computing and Networking, New York, NY, USA, 3–7 October 2016; pp. 82–94. [Google Scholar]
- Yun, S.; Chen, Y.C.; Qiu, L. Turning a mobile device into a mouse in the air. In Proceedings of the 13th Annual International Conference on Mobile Systems, Applications, and Services, Florence Italy, 18–22 May 2015; pp. 15–29. [Google Scholar]
- Gorostiza, E.M.; Lázaro Galilea, J.L.; Meca Meca, F.J.; Salido Monzú, D.; Espinosa Zapata, F.; Pallarés Puerto, L. Infrared sensor system for mobile-robot positioning in intelligent spaces. Sensors 2011, 11, 5416–5438. [Google Scholar] [CrossRef] [PubMed]
- Kotaru, M.; Katti, S. Position tracking for virtual reality using commodity WiFi. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 68–78. [Google Scholar]
- Kotaru, M.; Joshi, K.; Bharadia, D.; Katti, S. Spotfi: Decimeter level localization using wifi. In Proceedings of the 2015 ACM Conference on Special Interest Group on Data Communication, London, UK, 17–21 August 2015; pp. 269–282. [Google Scholar]
- Xie, Y.; Xiong, J.; Li, M.; Jamieson, K. mD-Track: Leveraging multi-dimensionality for passive indoor Wi-Fi tracking. In Proceedings of the 25th Annual International Conference on Mobile Computing and Networking, Los Cabos, Mexico, 21–25 October 2019; pp. 1–16. [Google Scholar]
- Xiao, J.; Wu, K.; Yi, Y.; Wang, L.; Ni, L.M. Pilot: Passive device-free indoor localization using channel state information. In Proceedings of the 2013 IEEE 33rd International Conference on Distributed Computing Systems, Philadelphia, PA, USA, 8–11 July 2013; pp. 236–245. [Google Scholar]
- Abdel-Nasser, H.; Samir, R.; Sabek, I.; Youssef, M. MonoPHY: Mono-stream-based device-free WLAN localization via physical layer information. In Proceedings of the 2013 IEEE Wireless Communications and Networking Conference (WCNC), Shanghai, China, 7–10 April 2013; pp. 4546–4551. [Google Scholar]
- Xiao, J.; Wu, K.; Yi, Y.; Wang, L.; Ni, L.M. Fimd: Fine-grained device-free motion detection. In Proceedings of the 2012 IEEE 18th International Conference on Parallel and Distributed Systems, Singapore, 17–19 December 2012; pp. 229–235. [Google Scholar]
- Mallik, M.; Das, S.; Chowdhury, C. Rank based iterative clustering (RBIC) for indoor localization. Eng. Appl. Artif. Intell. 2023, 121, 106061. [Google Scholar] [CrossRef]
- Kakisim, A.G.; Turgut, Z. Multi-channel convolutional neural network with attention mechanism using dual-band WiFi signals for indoor positioning systems in smart buildings. Internet Things 2025, 29, 101435. [Google Scholar] [CrossRef]
- Kerdjidj, O.; Himeur, Y.; Atalla, S.; Copiac, A.; Sohail, S.S.; Fadli, F.; Amira, A.; Mansoor, W.; Gawanmeh, A. Exploring 2D representation and transfer learning techniques for people identification in indoor localization. In Proceedings of the 2023 6th International Conference on Signal Processing and Information Security (ICSPIS), Dubai, United Arab Emirates, 8–9 November 2023; pp. 173–177. [Google Scholar]
- Prasad, G.; Tiwary, P.; Pandey, A.; Kumar, S. A Lightweight α-μ Fading Environment Based Localization Towards Edge Implementation. IEEE Wirel. Commun. Lett. 2024, 13, 3054–3058. [Google Scholar] [CrossRef]
- Abdullah, A.; Aziz, O.A.; Rashid, R.A.; Haris, M.; Sarijari, M.A. Robust and fast algorithm design for efficient Wi-Fi fingerprinting based indoor positioning systems. J. King Saud Univ.-Comput. Inf. Sci. 2023, 35, 101696. [Google Scholar] [CrossRef]
- Abdullah, A.; Haris, M.; Aziz, O.A.; Rashid, R.A.; Abdullah, A.S. UTMInDualSymFi: A dual-band Wi-Fi dataset for fingerprinting positioning in symmetric indoor environments. Data 2023, 8, 14. [Google Scholar] [CrossRef]
- Qian, K.; Wu, C.; Yang, Z.; Liu, Y.; Jamieson, K. Widar: Decimeter-level passive tracking via velocity monitoring with commodity Wi-Fi. In Proceedings of the 18th ACM International Symposium on Mobile Ad Hoc Networking and Computing, Chennai, India, 10–14 July 2017; pp. 1–10. [Google Scholar]
- Li, X.; Zhang, D.; Lv, Q.; Xiong, J.; Li, S.; Zhang, Y.; Mei, H. IndoTrack: Device-free indoor human tracking with commodity Wi-Fi. Proc. ACM Interact. Mob. Wearable Ubiquitous Technol. 2017, 1, 1–22. [Google Scholar] [CrossRef]
- Qian, K.; Wu, C.; Zhang, Y.; Zhang, G.; Yang, Z.; Liu, Y. Widar2. 0: Passive human tracking with a single Wi-Fi link. In Proceedings of the 16th Annual International Conference on Mobile Systems, Applications, and Services, Munich, Germany, 10–15 June 2018; pp. 350–361. [Google Scholar]
- Wang, Z.; Zhang, J.A.; Xu, M.; Guo, Y.J. Single-target real-time passive WiFi tracking. IEEE Trans. Mob. Comput. 2022, 22, 3724–3742. [Google Scholar] [CrossRef]
- Wu, C.; Zhang, F.; Hu, Y.; Liu, K.R. GaitWay: Monitoring and recognizing gait speed through the walls. IEEE Trans. Mob. Comput. 2020, 20, 2186–2199. [Google Scholar] [CrossRef]
- Zhang, F.; Chen, C.; Wang, B.; Liu, K.R. WiSpeed: A statistical electromagnetic approach for device-free indoor speed estimation. IEEE Internet Things J. 2018, 5, 2163–2177. [Google Scholar] [CrossRef]
- Li, X.; Li, S.; Zhang, D.; Xiong, J.; Wang, Y.; Mei, H. Dynamic-MUSIC: Accurate device-free indoor localization. In Proceedings of the 2016 ACM International Joint Conference on Pervasive and Ubiquitous Computing, Heidelberg, Germany, 12–16 September 2016; pp. 196–207. [Google Scholar]
- Han, Z.; Lu, Z.; Wen, X.; Zheng, W.; Zhao, J.; Guo, L. CentiTrack: Towards centimeter-level passive gesture tracking with commodity WiFi. IEEE Internet Things J. 2023, 10, 13012–13027. [Google Scholar] [CrossRef]
- Han, Z.; Lu, Z.; Wen, X.; Guo, L.; Zhao, J. Towards 3D centimeter-level passive gesture tracking with two WiFi links. IEEE Trans. Mob. Comput. 2021, 22, 3031–3045. [Google Scholar] [CrossRef]
- Mautz, R.; Tilch, S. Survey of optical indoor positioning systems. In Proceedings of the 2011 International Conference on Indoor Positioning and Indoor Navigation, Guimarpes, Portugal, 21–23 September 2011; pp. 1–7. [Google Scholar]
- Zhang, C.; Tabor, J.; Zhang, J.; Zhang, X. Extending mobile interaction through near-field visible light sensing. In Proceedings of the 21st Annual International Conference on Mobile Computing and Networking, Paris, France, 7–11 September 2015; pp. 345–357. [Google Scholar]
- Song, J.; Sörös, G.; Pece, F.; Fanello, S.R.; Izadi, S.; Keskin, C.; Hilliges, O. In-air gestures around unmodified mobile devices. In Proceedings of the 27th Annual ACM Symposium on User Interface Software and Technology, Honolulu, HI, USA, 5–8 October 2014; pp. 319–329. [Google Scholar]
- Chen, X.; Schwarz, J.; Harrison, C.; Mankoff, J.; Hudson, S.E. Air+ touch: Interweaving touch & in-air gestures. In Proceedings of the 27th Annual ACM Symposium on User Interface Software and Technology, Honolulu, HI, USA, 5–8 October 2014; pp. 519–525. [Google Scholar]
- Ma, Y.; Selby, N.; Adib, F. Minding the billions: Ultra-wideband localization for deployed RFID tags. In Proceedings of the 23rd Annual International Conference on Mobile Computing and Networking, Snowbird, UT, USA, 16–20 October 2017; pp. 248–260. [Google Scholar]
- Ma, Y.; Selby, N.; Adib, F. Drone relays for battery-free networks. In Proceedings of the Conference of the ACM Special Interest Group on Data Communication, Los Angeles, CA, USA, 21–25 August 2017; pp. 335–347. [Google Scholar]
- Luo, Z.; Zhang, Q.; Ma, Y.; Singh, M.; Adib, F. 3D Backscatter Localization for {Fine-Grained} Robotics. In Proceedings of the 16th USENIX Symposium on Networked Systems Design and Implementation (NSDI 19), Boston, MA, USA, 26–28 February 2019; pp. 765–782. [Google Scholar]
- Xu, H.; Wang, D.; Zhao, R.; Zhang, Q. AdaRF: Adaptive RFID-based indoor localization using deep learning enhanced holography. Proc. ACM Interact. Mob. Wearable Ubiquitous Technol. 2019, 3, 1–22. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, M.; Ye, N.; Xiao, F.; Wang, R.; Huang, H. Computer vision-assisted 3D object localization via COTS RFID devices and a monocular camera. IEEE Trans. Mob. Comput. 2019, 20, 893–908. [Google Scholar] [CrossRef]
- Karanam, C.R.; Korany, B.; Mostofi, Y. Tracking from one side: Multi-person passive tracking with WiFi magnitude measurements. In Proceedings of the 18th International Conference on Information Processing in Sensor Networks, Montreal, QC, Canada, 15–18 April 2019; pp. 181–192. [Google Scholar]
- Tadayon, N.; Rahman, M.T.; Han, S.; Valaee, S.; Yu, W. Decimeter ranging with channel state information. IEEE Trans. Wirel. Commun. 2019, 18, 3453–3468. [Google Scholar] [CrossRef]
- Chen, X.; Li, H.; Zhou, C.; Liu, X.; Wu, D.; Dudek, G. Fido: Ubiquitous fine-grained wifi-based localization for unlabelled users via domain adaptation. In Proceedings of the Web Conference 2020, Taipei, Taiwan, 20–24 April 2020; pp. 23–33. [Google Scholar]
- Venkatnarayan, R.H.; Shahzad, M.; Yun, S.; Vlachou, C.; Kim, K.H. Leveraging polarization of WiFi signals to simultaneously track multiple people. Proc. ACM Interact. Mob. Wearable Ubiquitous Technol. 2020, 4, 1–24. [Google Scholar] [CrossRef]
- Tan, S.; Yang, J. WiFinger: Leveraging commodity WiFi for fine-grained finger gesture recognition. In Proceedings of the 17th ACM International Symposium on Mobile Ad Hoc Networking and Computing, Paderborn, Germany, 5–8 July 2016; pp. 201–210. [Google Scholar]
- Zhang, J.; Wei, B.; Hu, W.; Kanhere, S.S. Wifi-id: Human identification using wifi signal. In Proceedings of the 2016 International Conference on Distributed Computing in Sensor Systems (DCOSS), Washington, DC, USA, 26–28 May 2016; pp. 75–82. [Google Scholar]
- Zhou, R.; Lu, X.; Zhao, P.; Chen, J. Device-free presence detection and localization with SVM and CSI fingerprinting. IEEE Sens. J. 2017, 17, 7990–7999. [Google Scholar] [CrossRef]
- Wang, L.; Sun, K.; Dai, H.; Liu, A.X.; Wang, X. WiTrace: Centimeter-level passive gesture tracking using WiFi signals. In Proceedings of the 2018 15th Annual IEEE International Conference on Sensing, Communication, and Networking (SECON), Hong Kong, China, 11–13 June 2018; pp. 1–9. [Google Scholar]
- Sun, L.; Sen, S.; Koutsonikolas, D.; Kim, K.H. Widraw: Enabling hands-free drawing in the air on commodity wifi devices. In Proceedings of the 21st Annual International Conference on Mobile Computing and Networking, Paris, France, 7–11 September 2015; pp. 77–89. [Google Scholar]
- Xie, Y.; Li, Z.; Li, M. Precise power delay profiling with commodity WiFi. In Proceedings of the 21st Annual international conference on Mobile Computing and Networking, Paris, France, 7–11 September 2015; pp. 53–64. [Google Scholar]
- Wu, D.; Zhang, D.; Xu, C.; Wang, Y.; Wang, H. WiDir: Walking direction estimation using wireless signals. In Proceedings of the 2016 ACM International Joint Conference on Pervasive and Ubiquitous Computing, Heidelberg, Germany, 12–16 September 2016; pp. 351–362. [Google Scholar]
- Zhang, D.; Wang, H.; Wu, D. Toward centimeter-scale human activity sensing with Wi-Fi signals. Computer 2017, 50, 48–57. [Google Scholar] [CrossRef]
- Zhuo, Y.; Zhu, H.; Xue, H.; Chang, S. Perceiving accurate CSI phases with commodity WiFi devices. In Proceedings of the IEEE INFOCOM 2017-IEEE Conference on Computer Communications, Atlanta, GA, USA, 1–4 May 2017; pp. 1–9. [Google Scholar]
- Zhu, J.; Im, Y.; Mishra, S.; Ha, S. Calibrating time-variant, device-specific phase noise for COTS WiFi devices. In Proceedings of the 15th ACM Conference on Embedded Network Sensor Systems, Delft, The Netherlands, 6–8 November 2017; pp. 1–12. [Google Scholar]
- Han, Z.; Guo, L.; Lu, Z.; Wen, X.; Zheng, W. Deep adaptation networks based gesture recognition using commodity WiFi. In Proceedings of the 2020 IEEE Wireless Communications and Networking Conference (WCNC), Seoul, Republic of Korea, 25–28 May 2020; pp. 1–7. [Google Scholar]
- Zhu, H.; Zhuo, Y.; Liu, Q.; Chang, S. π-splicer: Perceiving accurate CSI phases with commodity WiFi devices. IEEE Trans. Mob. Comput. 2018, 17, 2155–2165. [Google Scholar] [CrossRef]
- Wu, D.; Gao, R.; Zeng, Y.; Liu, J.; Wang, L.; Gu, T.; Zhang, D. FingerDraw: Sub-wavelength level finger motion tracking with WiFi signals. Proc. ACM Interact. Mob. Wearable Ubiquitous Technol. 2020, 4, 1–27. [Google Scholar] [CrossRef]
- Zeng, Y.; Wu, D.; Xiong, J.; Yi, E.; Gao, R.; Zhang, D. FarSense: Pushing the range limit of WiFi-based respiration sensing with CSI ratio of two antennas. Proc. ACM Interact. Mob. Wearable Ubiquitous Technol. 2019, 3, 1–26. [Google Scholar] [CrossRef]
- Zeng, Y.; Wu, D.; Xiong, J.; Liu, J.; Liu, Z.; Zhang, D. MultiSense: Enabling multi-person respiration sensing with commodity WiFi. Proc. ACM Interact. Mob. Wearable Ubiquitous Technol. 2020, 4, 1–29. [Google Scholar] [CrossRef]
- Wu, D.; Zeng, Y.; Gao, R.; Li, S.; Li, Y.; Shah, R.C.; Lu, H.; Zhang, D. WiTraj: Robust indoor motion tracking with WiFi signals. IEEE Trans. Mob. Comput. 2021, 22, 3062–3078. [Google Scholar] [CrossRef]
- Ali, K.; Liu, A.X.; Wang, W.; Shahzad, M. Keystroke recognition using wifi signals. In Proceedings of the 21st Annual International Conference on Mobile Computing and Networking, Paris, France, 7–11 September 2015; pp. 90–102. [Google Scholar]
- Gao, R.; Zhang, M.; Zhang, J.; Li, Y.; Yi, E.; Wu, D.; Wang, L.; Zhang, D. Towards position-independent sensing for gesture recognition with Wi-Fi. Proc. ACM Interact. Mob. Wearable Ubiquitous Technol. 2021, 5, 1–28. [Google Scholar] [CrossRef]
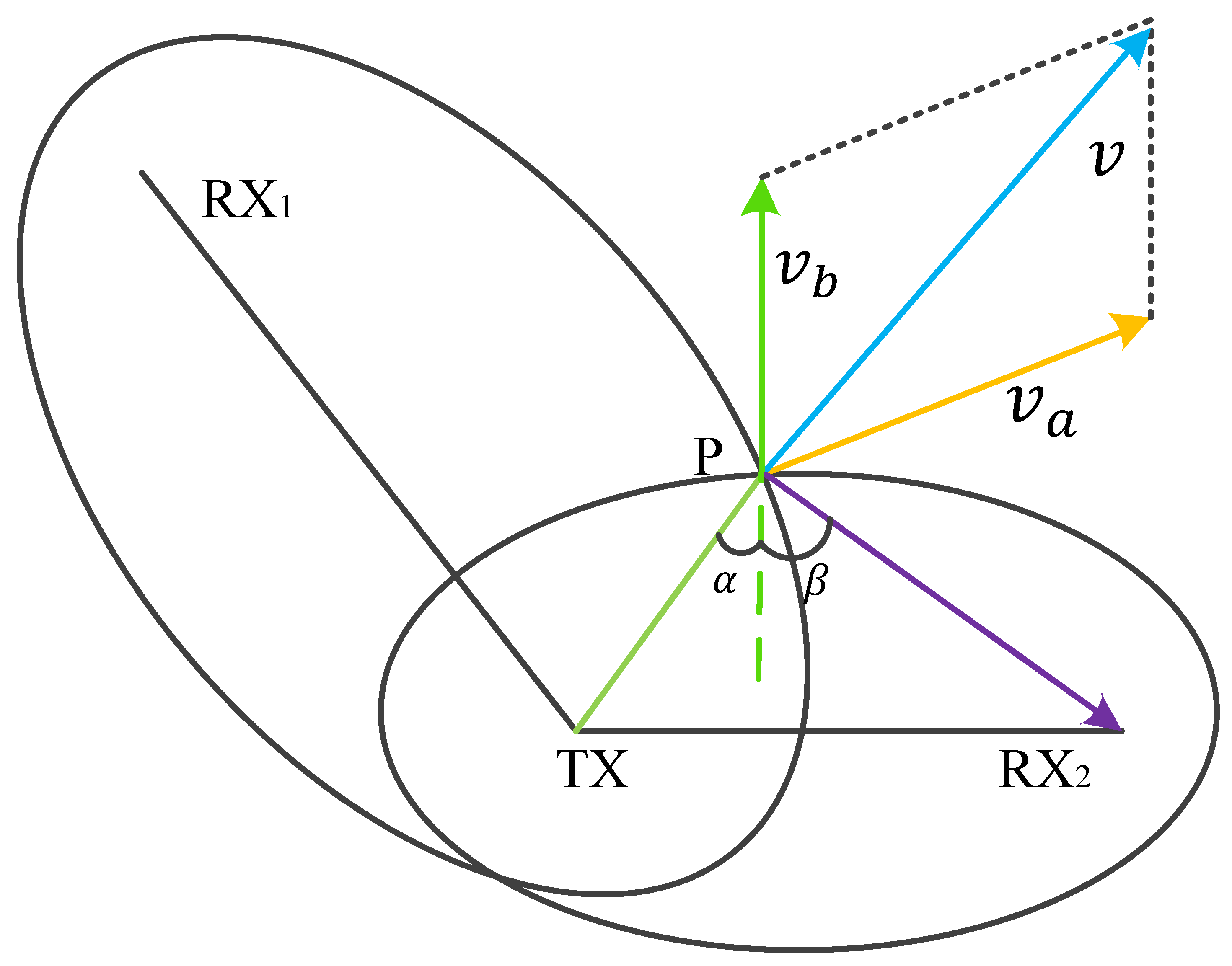
| Method | TX-RX Location | Training | Facility | Real Time | Initial Position |
|---|---|---|---|---|---|
| RSSI | ✓ | high | Commercial WiFi | medium | ✓ |
| WiDAR | ✓ | medium | Commercial WiFi | high | ✓ |
| IndoTrack | ✓ | ✗ | Dedicated device | high | ✓ |
| WiPIHT | ✗ | ✗ | Commercial WiFi | high | ✗ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Che, X.; Meng, X.; Li, L.; Liu, Z.; Shao, S. WiPIHT: A WiFi-Based Position-Independent Passive Indoor Human Tracking System. Sensors 2025, 25, 3936. https://doi.org/10.3390/s25133936
Xu X, Che X, Meng X, Li L, Liu Z, Shao S. WiPIHT: A WiFi-Based Position-Independent Passive Indoor Human Tracking System. Sensors. 2025; 25(13):3936. https://doi.org/10.3390/s25133936
Chicago/Turabian StyleXu, Xu, Xilong Che, Xianqiu Meng, Long Li, Ziqi Liu, and Shuai Shao. 2025. "WiPIHT: A WiFi-Based Position-Independent Passive Indoor Human Tracking System" Sensors 25, no. 13: 3936. https://doi.org/10.3390/s25133936
APA StyleXu, X., Che, X., Meng, X., Li, L., Liu, Z., & Shao, S. (2025). WiPIHT: A WiFi-Based Position-Independent Passive Indoor Human Tracking System. Sensors, 25(13), 3936. https://doi.org/10.3390/s25133936








