SGDO-SLAM: A Semantic RGB-D SLAM System with Coarse-to-Fine Dynamic Rejection and Static Weighted Optimization
Abstract
1. Introduction
- (1)
- We propose a semantic visual SLAM system base, called SGDO-SLAM, based on multi-constraint rejection and static quality-weighted optimization. Compared to existing advanced methods, SGDO-SLAM has higher accuracy in dynamic environments. The system also builds semantic point cloud maps to assist the robot in understanding the environment.
- (2)
- A dynamic feature rejection strategy from coarse to fine is proposed. Coarse culling is first performed by combining priori semantic information with the results of the epipolar geometric constraints. Then, finer rejection is performed by projecting the feature points in the current frames to the key frames according to the depth consistency constraints. Meanwhile, static quality weights are quantified and used to assess the merits of static features.
- (3)
- A static weighting-based optimization method for the SLAM back end is proposed. The method is based on the front-end static quantization weighting drive, which distinguishes the static superior and inferior features after the dynamic features are rejected. High-quality visual features are prioritized for pose estimation and back-end optimization. This approach ensures accurate localization and high-quality mapping.
2. Related Works
2.1. Methods Based on Geometric Information
2.2. Methods Based on Semantic Information
2.3. Fusion Methods
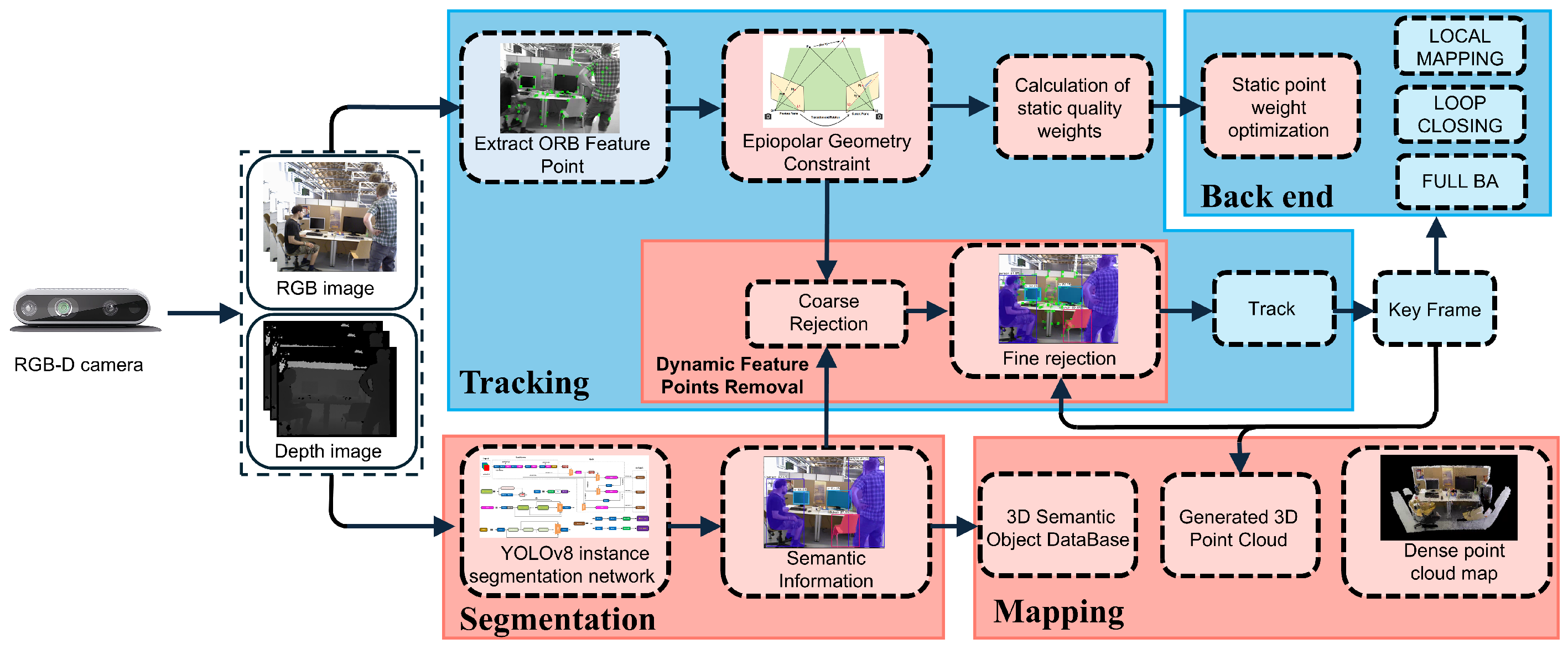
3. System Overview
3.1. System Architecture
3.2. Instance Segmentation
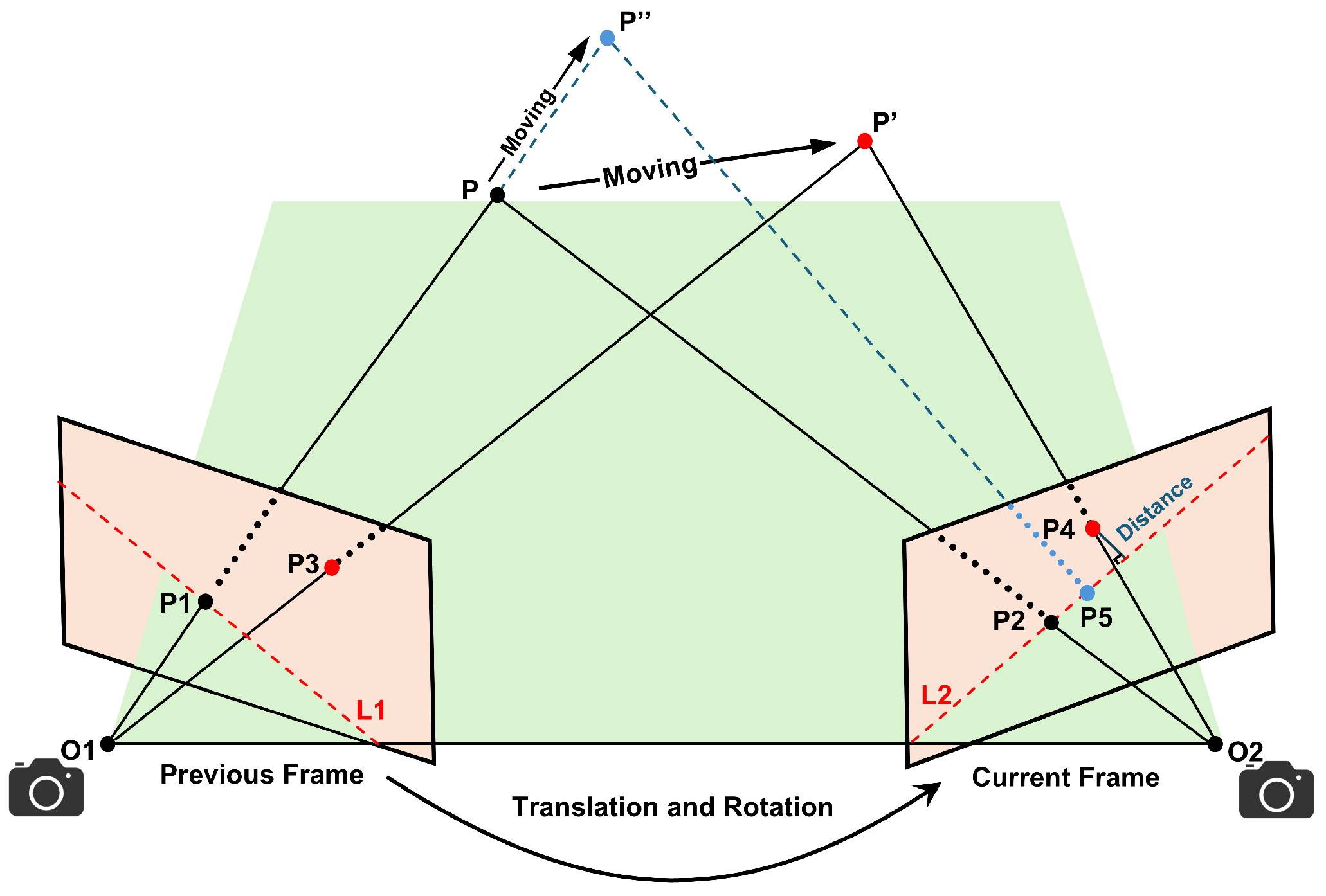
3.3. Epipolar Constraints
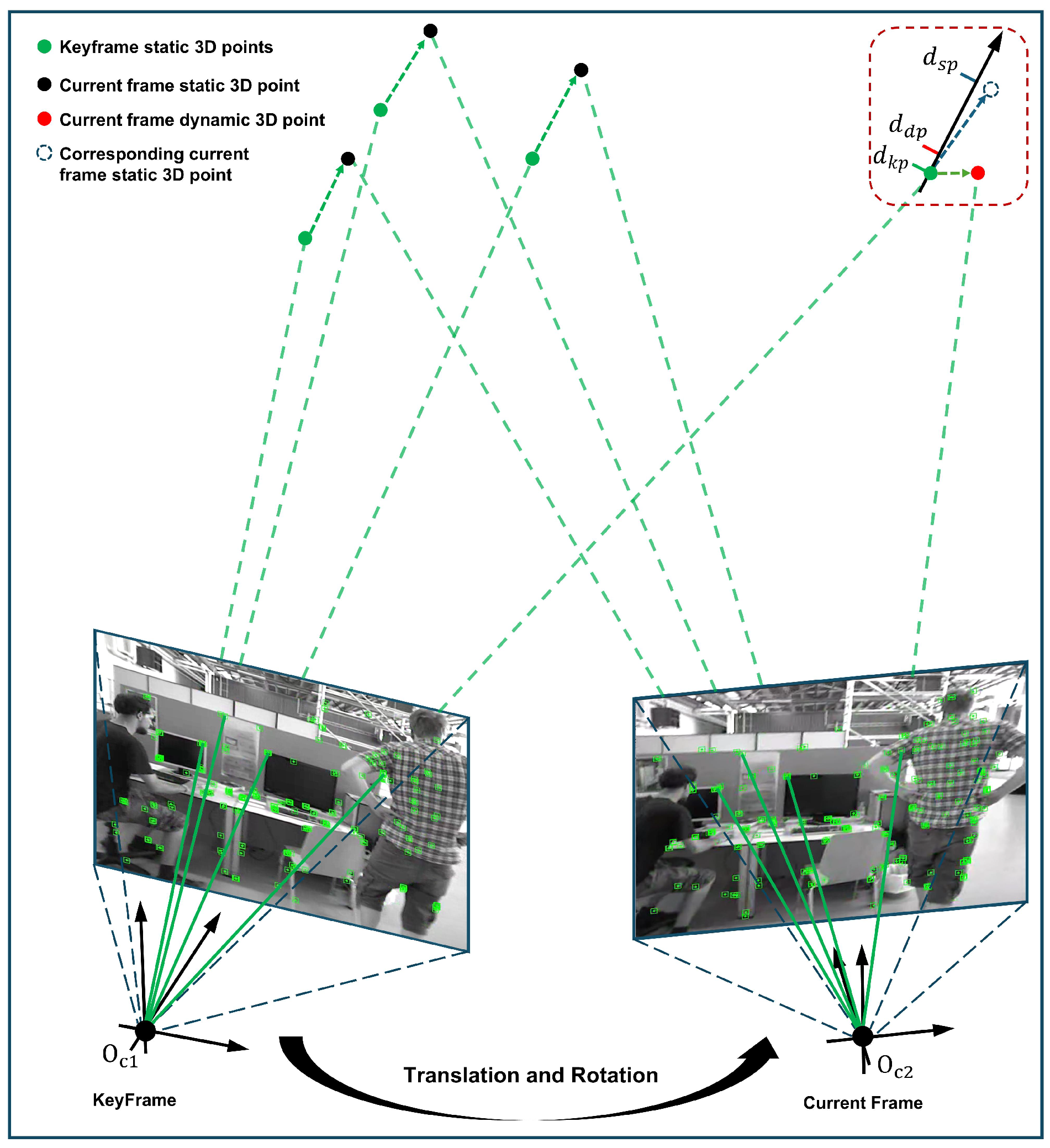
3.4. Depth Consistency Constraint Rejection Strategy
3.5. Static Point Weighted Optimization
3.6. Dense Mapping
4. Experimental Results
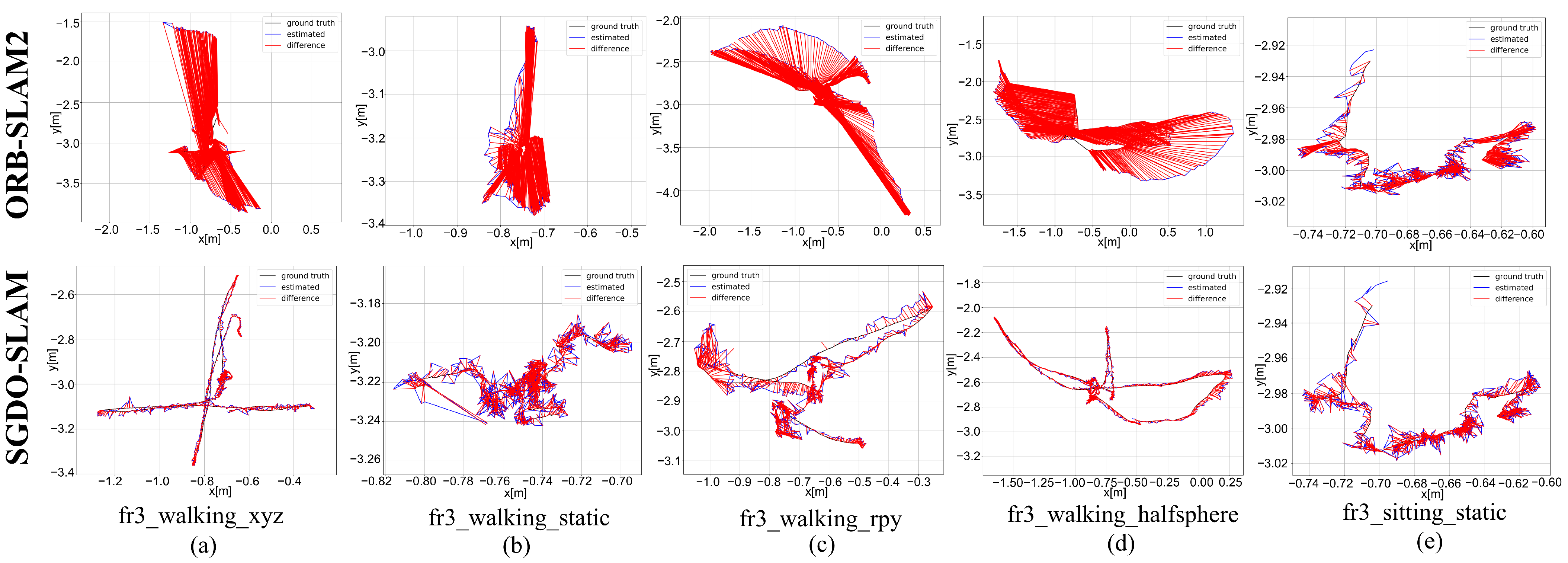
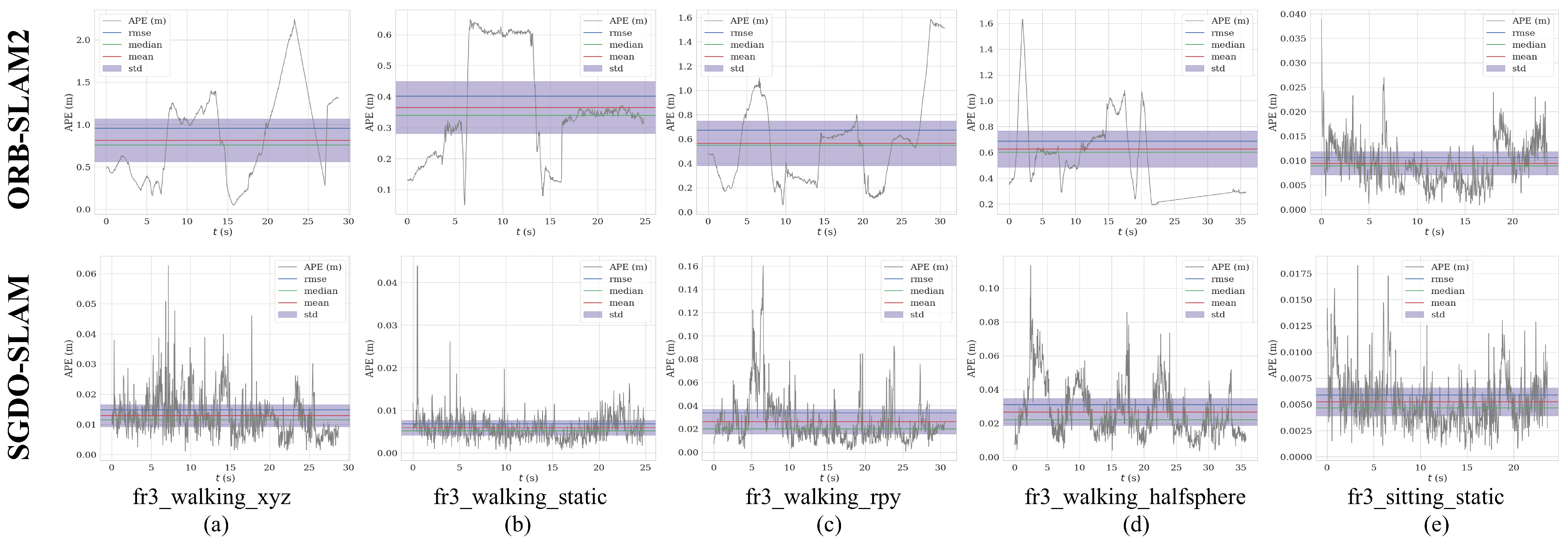
4.1. Performance Evaluation on TUM RGB-D Dataset
4.1.1. Comparison of Baseline Algorithm
4.1.2. Comparison of State-of-the-Art Algorithms
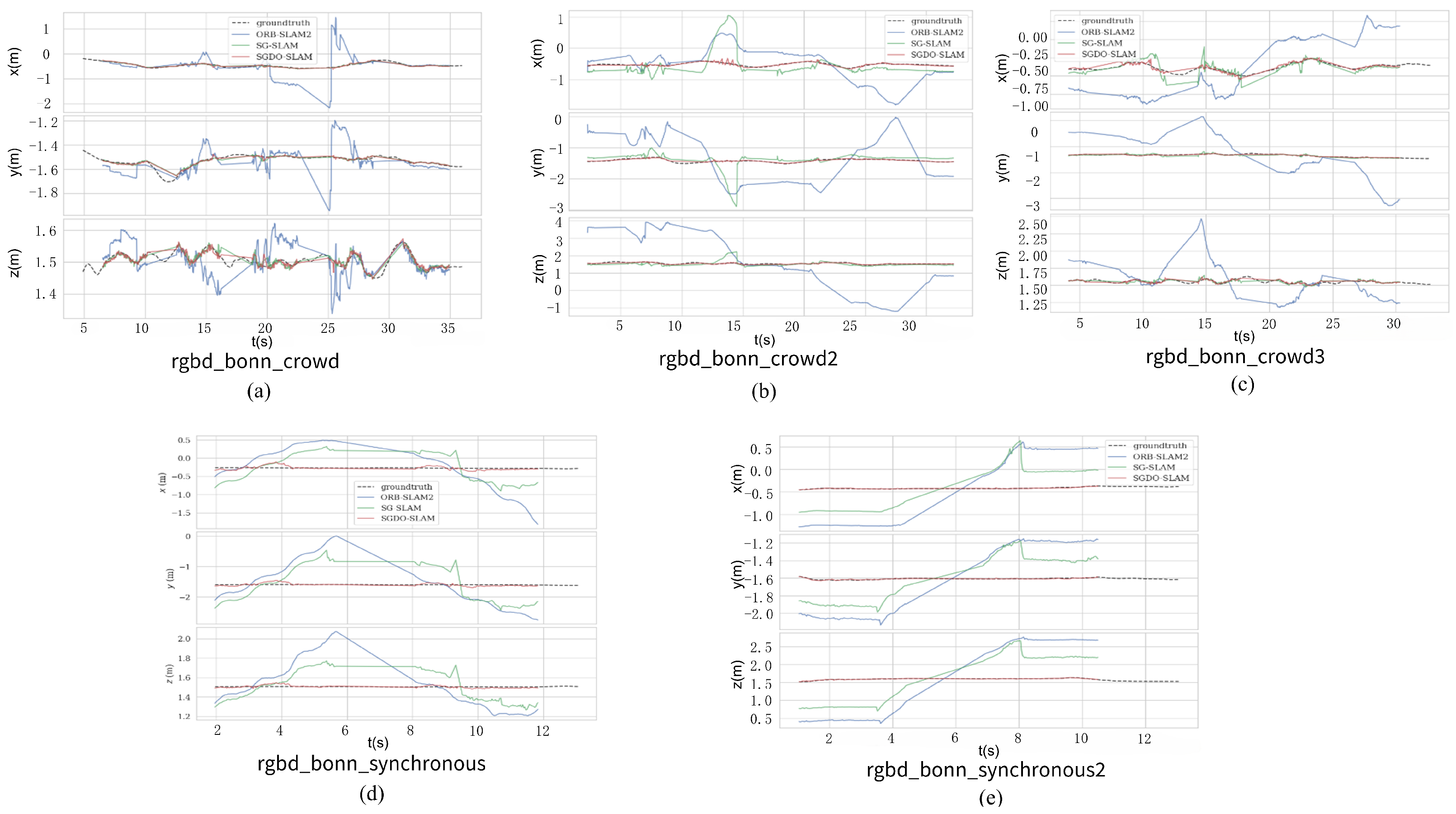
4.2. Performance Evaluation on Bonn RGB-D Dataset
4.3. Ablation Experiment
4.4. Time Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Durrant-Whyte, H.; Bailey, T. Simultaneous localization and mapping: Part I. IEEE Robot. Autom. Mag. 2006, 13, 99–110. [Google Scholar] [CrossRef]
- Wen, S.; Tao, S.; Liu, X.; Babiarz, A.; Yu, F.R. Cd-slam: A real-time stereo visual–inertial slam for complex dynamic environments with semantic and geometric information. IEEE Trans. Instrum. Meas. 2024, 73, 2517808. [Google Scholar] [CrossRef]
- Al-Tawil, B.; Candemir, A.; Jung, M.; Al-Hamadi, A. Mobile Robot Navigation with Enhanced 2D Mapping and Multi-Sensor Fusion. Sensors 2025, 25, 2408. [Google Scholar] [CrossRef]
- Afzal Maken, F.; Muthu, S.; Nguyen, C.; Sun, C.; Tong, J.; Wang, S.; Tsuchida, R.; Howard, D.; Dunstall, S.; Petersson, L. Improving 3D Reconstruction Through RGB-D Sensor Noise Modeling. Sensors 2025, 25, 950. [Google Scholar] [CrossRef] [PubMed]
- Fuentes-Pacheco, J.; Ruiz-Ascencio, J.; Rendón-Mancha, J.M. Visual simultaneous localization and mapping: A survey. Artif. Intell. Rev. 2015, 43, 55–81. [Google Scholar] [CrossRef]
- Bokovoy, A.; Muraviev, K. Assessment of map construction in vSLAM. In Proceedings of the 2021 International Siberian Conference on Control and Communications (SIBCON), Kazan, Russia, 13–15 May 2021; pp. 1–6. [Google Scholar]
- Mur-Artal, R.; Tardós, J.D. Orb-slam2: An open-source slam system for monocular, stereo, and rgb-d cameras. IEEE Trans. Robot. 2017, 33, 1255–1262. [Google Scholar] [CrossRef]
- Qin, T.; Li, P.; Shen, S. Vins-mono: A robust and versatile monocular visual-inertial state estimator. IEEE Trans. Robot. 2018, 34, 1004–1020. [Google Scholar] [CrossRef]
- Campos, C.; Elvira, R.; Rodríguez, J.J.G.; Montiel, J.M.; Tardós, J.D. Orb-slam3: An accurate open-source library for visual, visual–inertial, and multimap slam. IEEE Trans. Robot. 2021, 37, 1874–1890. [Google Scholar] [CrossRef]
- Engel, J.; Schöps, T.; Cremers, D. LSD-SLAM: Large-scale direct monocular SLAM. In Proceedings of the 13th European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; Springer: Cham, Switzerland, 2014; pp. 834–849. [Google Scholar]
- Cheng, S.; Sun, C.; Zhang, S.; Zhang, D. SG-SLAM: A real-time RGB-D visual SLAM toward dynamic scenes with semantic and geometric information. IEEE Trans. Instrum. Meas. 2022, 72, 7501012. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Zhong, M.; Hong, C.; Jia, Z.; Wang, C.; Wang, Z. DynaTM-SLAM: Fast filtering of dynamic feature points and object-based localization in dynamic indoor environments. Robot. Auton. Syst. 2024, 174, 104634. [Google Scholar] [CrossRef]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. Ssd: Single shot multibox detector. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Proceedings, Part I 14. Springer: Cham, Switzerland, 2016; pp. 21–37. [Google Scholar]
- Redmon, J.; Farhadi, A. Yolov3: An incremental improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. Segnet: A deep convolutional encoder-decoder architecture for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef]
- Bescos, B.; Fácil, J.M.; Civera, J.; Neira, J. DynaSLAM: Tracking, mapping, and inpainting in dynamic scenes. IEEE Robot. Autom. Lett. 2018, 3, 4076–4083. [Google Scholar] [CrossRef]
- Yu, C.; Liu, Z.; Liu, X.J.; Xie, F.; Yang, Y.; Wei, Q.; Fei, Q. DS-SLAM: A semantic visual SLAM towards dynamic environments. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 1168–1174. [Google Scholar]
- Wu, W.; Guo, L.; Gao, H.; You, Z.; Liu, Y.; Chen, Z. YOLO-SLAM: A semantic SLAM system towards dynamic environment with geometric constraint. Neural Comput. Appl. 2022, 34, 6011–6026. [Google Scholar] [CrossRef]
- Chang, J.; Dong, N.; Li, D. A real-time dynamic object segmentation framework for SLAM system in dynamic scenes. IEEE Trans. Instrum. Meas. 2021, 70, 2513709. [Google Scholar] [CrossRef]
- Kan, X.; Shi, G.; Yang, X.; Hu, X. YPR-SLAM: A SLAM System Combining Object Detection and Geometric Constraints for Dynamic Scenes. Sensors 2024, 24, 6576. [Google Scholar] [CrossRef]
- Li, S.; Lee, D. RGB-D SLAM in dynamic environments using static point weighting. IEEE Robot. Autom. Lett. 2017, 2, 2263–2270. [Google Scholar] [CrossRef]
- Li, A.; Wang, J.; Xu, M.; Chen, Z. DP-SLAM: A visual SLAM with moving probability towards dynamic environments. Inf. Sci. 2021, 556, 128–142. [Google Scholar] [CrossRef]
- Kundu, A.; Krishna, K.M.; Sivaswamy, J. Moving object detection by multi-view geometric techniques from a single camera mounted robot. In Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2009; pp. 4306–4312. [Google Scholar]
- Yang, S.; Fan, G.; Bai, L.; Zhao, C.; Li, D. Geometric constraint-based visual SLAM under dynamic indoor environment. Comput. Eng. Appl. 2021, 16, 203–212. [Google Scholar]
- Zou, D.; Tan, P. Coslam: Collaborative visual slam in dynamic environments. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 35, 354–366. [Google Scholar] [CrossRef]
- Nguyen, D.; Hughes, C.; Horgan, J. Optical flow-based moving-static separation in driving assistance systems. In Proceedings of the 2015 IEEE 18th International Conference on Intelligent Transportation Systems, Gran Canaria, Spain, 15–18 September 2015; pp. 1644–1651. [Google Scholar]
- Zhang, T.; Zhang, H.; Li, Y.; Nakamura, Y.; Zhang, L. Flowfusion: Dynamic dense rgb-d slam based on optical flow. In Proceedings of the 2020 IEEE international conference on robotics and automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 7322–7328. [Google Scholar]
- Zhang, L.; Wei, L.; Shen, P.; Wei, W.; Zhu, G.; Song, J. Semantic SLAM based on object detection and improved octomap. IEEE Access 2018, 6, 75545–75559. [Google Scholar] [CrossRef]
- Sheng, C.; Pan, S.; Gao, W.; Tan, Y.; Zhao, T. Dynamic-DSO: Direct sparse odometry using objects semantic information for dynamic environments. Appl. Sci. 2020, 10, 1467. [Google Scholar] [CrossRef]
- Xiao, L.; Wang, J.; Qiu, X.; Rong, Z.; Zou, X. Dynamic-SLAM: Semantic monocular visual localization and mapping based on deep learning in dynamic environment. Robot. Auton. Syst. 2019, 117, 1–16. [Google Scholar] [CrossRef]
- Liu, Y.; Miura, J. RDS-SLAM: Real-time dynamic SLAM using semantic segmentation methods. IEEE Access 2021, 9, 23772–23785. [Google Scholar] [CrossRef]
- Lu, Y.; Wang, H.; Sun, J.; Zhang, J.A. Enhanced Simultaneous Localization and Mapping Algorithm Based on Deep Learning for Highly Dynamic Environment. Sensors 2025, 25, 2539. [Google Scholar] [CrossRef] [PubMed]
- Pan, Z.; Hou, J.; Yu, L. Optimization RGB-D 3-D reconstruction algorithm based on dynamic SLAM. IEEE Trans. Instrum. Meas. 2023, 72, 5008413. [Google Scholar] [CrossRef]
- He, L.; Li, S.; Qiu, J.; Zhang, C. DIO-SLAM: A Dynamic RGB-D SLAM Method Combining Instance Segmentation and Optical Flow. Sensors 2024, 24, 5929. [Google Scholar] [CrossRef] [PubMed]
- Jiao, J.; Wang, C.; Li, N.; Deng, Z.; Xu, W. An Adaptive Visual Dynamic-SLAM Method Based on Fusing the Semantic Information. IEEE Sens. J. 2022, 22, 17414–17420. [Google Scholar] [CrossRef]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 580–587. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Spatial pyramid pooling in deep convolutional networks for visual recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1904–1916. [Google Scholar] [CrossRef]
- Girshick, R. Fast r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1440–1448. [Google Scholar]
- Shelhamer, E.; Long, J.; Darrell, T. Fully convolutional networks for semantic segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 640–651. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; Proceedings, Part III 18. Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Lin, T.Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft coco: Common objects in context. In Proceedings of the Computer Vision–ECCV 2014: 13th European Conference, Zurich, Switzerland, 6–12 September 2014; Proceedings, Part V 13. Springer: Cham, Switzerland, 2014; pp. 740–755. [Google Scholar]
- Lucas, B.D.; Kanade, T. An iterative image registration technique with an application to stereo vision. In Proceedings of the IJCAI’81: 7th International Joint Conference on Artificial Intelligence, Vancouver, BC, Canada, 24–28 August 1981; Volume 2, pp. 674–679. [Google Scholar]
- Sturm, J.; Engelhard, N.; Endres, F.; Burgard, W.; Cremers, D. A benchmark for the evaluation of RGB-D SLAM systems. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 573–580. [Google Scholar]
- Palazzolo, E.; Behley, J.; Lottes, P.; Giguere, P.; Stachniss, C. ReFusion: 3D reconstruction in dynamic environments for RGB-D cameras exploiting residuals. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 7855–7862. [Google Scholar]
- Min, F.; Wu, Z.; Li, D.; Wang, G.; Liu, N. Coeb-slam: A robust vslam in dynamic environments combined object detection, epipolar geometry constraint, and blur filtering. IEEE Sens. J. 2023, 23, 26279–26291. [Google Scholar] [CrossRef]
- Huai, S.; Cao, L.; Zhou, Y.; Guo, Z.; Gai, J. A Multi-Strategy Visual SLAM System for Motion Blur Handling in Indoor Dynamic Environments. Sensors 2025, 25, 1696. [Google Scholar] [CrossRef] [PubMed]
- Ruan, C.; Zang, Q.; Zhang, K.; Huang, K. Dn-slam: A visual slam with orb features and nerf mapping in dynamic environments. IEEE Sens. J. 2023, 24, 5279–5287. [Google Scholar] [CrossRef]




| Sequences | ORB-SLAM2 | SGDO-SLAM (Ours) | Improvements | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | Mean | Median | S.D. | RMSE | Mean | Median | S.D. | RMSE (%) | Mean (%) | Median (%) | S.D. (%) | |
| fr3_walking_xyz | 0.9574 | 0.8148 | 0.7589 | 0.5027 | 0.0147 | 0.0127 | 0.0105 | 0.0068 | 98.46 | 98.44 | 98.62 | 98.64 |
| fr3_walking_static | 0.4021 | 0.3648 | 0.3399 | 0.1689 | 0.0068 | 0.0059 | 0.0052 | 0.0034 | 98.31 | 98.38 | 98.47 | 97.99 |
| fr3_walking_rpy | 0.6726 | 0.5642 | 0.5506 | 0.3661 | 0.0339 | 0.0263 | 0.0201 | 0.0213 | 94.96 | 95.34 | 96.35 | 94.18 |
| fr3_walking_half | 0.6871 | 0.6271 | 0.6021 | 0.2807 | 0.0258 | 0.0223 | 0.0182 | 0.0122 | 96.25 | 96.44 | 96.98 | 95.65 |
| fr3_sitting_static | 0.0106 | 0.0093 | 0.0089 | 0.0048 | 0.0059 | 0.0052 | 0.0046 | 0.0026 | 44.34 | 44.08 | 48.31 | 45.83 |
| Sequences | ORB-SLAM2 | SGDO-SLAM (Ours) | Improvements | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | Mean | Median | S.D. | RMSE | Mean | Median | S.D. | RMSE (%) | Mean (%) | Median (%) | S.D. (%) | |
| fr3_walking_xyz | 0.5363 | 0.4245 | 0.5044 | 0.3276 | 0.0175 | 0.0152 | 0.0137 | 0.0085 | 96.73 | 96.41 | 97.28 | 97.40 |
| fr3_walking_static | 0.3063 | 0.1546 | 0.0265 | 0.2643 | 0.0064 | 0.0060 | 0.0062 | 0.0019 | 97.91 | 96.11 | 76.60 | 99.28 |
| fr3_walking_rpy | 0.4902 | 0.3568 | 0.2622 | 0.3361 | 0.0473 | 0.0380 | 0.0297 | 0.0281 | 90.35 | 89.34 | 88.67 | 91.63 |
| fr3_walking_half | 0.6580 | 0.4676 | 0.2569 | 0.4628 | 0.0374 | 0.0328 | 0.0265 | 0.0179 | 94.31 | 92.98 | 89.68 | 96.13 |
| fr3_sitting_static | 0.0148 | 0.0111 | 0.0087 | 0.0098 | 0.0084 | 0.0072 | 0.0066 | 0.0044 | 43.24 | 35.13 | 24.13 | 55.10 |
| Sequences | ORB-SLAM2 | SGDO-SLAM (Ours) | Improvements | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | Mean | Median | S.D. | RMSE | Mean | Median | S.D. | RMSE (%) | Mean (%) | Median (%) | S.D. (%) | |
| fr3_walking_xyz | 10.5042 | 8.2556 | 9.4303 | 6.4947 | 0.4694 | 0.4377 | 0.4221 | 0.1696 | 95.53 | 94.69 | 95.52 | 97.38 |
| fr3_walking_static | 5.5499 | 2.8426 | 0.5174 | 4.7666 | 0.2524 | 0.2324 | 0.2150 | 0.0985 | 95.45 | 91.82 | 58.44 | 97.93 |
| fr3_walking_rpy | 9.2766 | 6.8413 | 4.1514 | 6.2651 | 0.8542 | 0.7117 | 0.5411 | 0.4723 | 90.79 | 89.59 | 86.96 | 92.46 |
| fr3_walking_half | 14.7136 | 10.5943 | 5.5201 | 10.2103 | 0.8603 | 0.7729 | 0.6321 | 0.3777 | 94.15 | 92.70 | 88.54 | 96.30 |
| fr3_sitting_static | 0.3969 | 0.3350 | 0.3343 | 0.2128 | 0.2482 | 0.2649 | 0.2469 | 0.1458 | 27.46 | 25.91 | 20.75 | 31.48 |
| Seq. | YOLO-SLAM | DS-SLAM | SG-SLAM | COEB-SLAM | RDS-SLAM | DynaSLAM | ORB-SLAM3 | SGDO-SLAM (Ours) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | S.D. | RMSE | S.D. | RMSE | S.D. | RMSE | S.D. | RMSE | S.D. | RMSE | S.D. | RMSE | S.D. | RMSE | S.D. | |
| fr3_w_xyz | 0.0146 | 0.0070 | 0.0247 | 0.0161 | 0.0184 | 0.0096 | 0.0188 | 0.0092 | 0.0571 | 0.0229 | 0.0156 | 0.0079 | 0.7012 | 0.3018 | 0.0131 | 0.0068 |
| fr3_w_static | 0.0073 | 0.0035 | 0.0081 | 0.0067 | 0.0076 | 0.0037 | 0.0073 | 0.0034 | 0.0206 | 0.0120 | 0.0079 | 0.0043 | 0.4218 | 0.2246 | 0.0068 | 0.0034 |
| fr3_w_rpy | 0.2164 | 0.1001 | 0.4442 | 0.2350 | 0.0386 | 0.0233 | 0.0364 | 0.0227 | 0.1604 | 0.0874 | 0.0325 | 0.0194 | 0.8656 | 0.4526 | 0.0339 | 0.0213 |
| fr3_w_half | 0.0283 | 0.0138 | 0.0303 | 0.0283 | 0.0300 | 0.0156 | 0.0315 | 0.0148 | 0.0807 | 0.0454 | 0.0261 | 0.0123 | 0.6280 | 0.2926 | 0.0188 | 0.0092 |
| fr3_s_static | 0.0066 | 0.0033 | 0.0065 | 0.0033 | 0.0063 | 0.0030 | 0.0075 | 0.0037 | 0.0084 | 0.0043 | 0.0067 | 0.0028 | 0.0090 | 0.0043 | 0.0059 | 0.0026 |
| Mean | 0.0546 | 0.0255 | 0.1027 | 0.0578 | 0.0201 | 0.0110 | 0.0203 | 0.0107 | 0.0654 | 0.0344 | 0.0177 | 0.0093 | 0.5251 | 0.2551 | 0.0157 | 0.0086 |
| Seq. | ORB-SLAM2 | YOLO-SLAM | SG-SLAM | DN-SLAM | Huai et al. [48] | SGDO-SLAM (Ours) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | S.D. | RMSE | S.D. | RMSE | S.D. | RMSE | S.D. | RMSE | S.D. | RMSE | S.D. | |
| crowd1 | 0.8632 | 0.5918 | 0.033 | - | 0.0234 | 0.0143 | 0.025 | 0.016 | 0.016 | 0.008 | 0.0206 | 0.0126 |
| crowd2 | 1.3573 | 0.6207 | 0.423 | - | 0.0584 | 0.0406 | 0.028 | 0.017 | 0.031 | 0.018 | 0.0278 | 0.0148 |
| crowd3 | 1.0772 | 0.3823 | 0.069 | - | 0.0319 | 0.0219 | 0.026 | 0.014 | 0.026 | 0.017 | 0.0290 | 0.0157 |
| moving_no_box1 | 0.1174 | 0.0710 | 0.027 | - | 0.0192 | 0.0081 | 0.026 | 0.014 | - | - | 0.0014 | 0.0093 |
| moving_no_box2 | 0.1142 | 0.0598 | 0.035 | - | 0.0299 | 0.0030 | 0.120 | 0.061 | - | - | 0.0246 | 0.0095 |
| person_tracking1 | 0.7959 | 0.3617 | 0.157 | - | 0.0400 | 0.0139 | 0.038 | 0.015 | 0.038 | 0.012 | 0.0232 | 0.0101 |
| person_tracking2 | 1.0679 | 0.4699 | 0.037 | - | 0.0376 | 0.0154 | 0.042 | 0.017 | 0.034 | 0.013 | 0.0301 | 0.0140 |
| synchronous1 | 1.1411 | 0.5703 | 0.014 | - | 0.3229 | 0.1824 | - | - | - | - | 0.0093 | 0.0046 |
| synchronous2 | 1.4069 | 1.3201 | 0.007 | - | 0.0164 | 0.0126 | - | - | - | - | 0.0071 | 0.0039 |
| Seq. | SGDO-SLAM (G) | SGDO-SLAM (O) | SGDO-SLAM (S+G) | SGDO-SLAM (S+G+O) | SGDO-SLAM (S+G+D) | SGDO-SLAM (S+G+D+O) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | S.D. | RMSE | S.D. | RMSE | S.D. | RMSE | S.D. | RMSE | S.D. | RMSE | S.D. | |
| fr3_w_xyz | 0.0416 | 0.0130 | 0.0346 | 0.0096 | 0.0157 | 0.0079 | 0.0142 | 0.0076 | 0.0148 | 0.0076 | 0.0131 | 0.0068 |
| fr3_w_static | 0.0226 | 0.0102 | 0.0165 | 0.0088 | 0.0071 | 0.0036 | 0.0080 | 0.0038 | 0.0081 | 0.0040 | 0.0068 | 0.0034 |
| fr3_w_rpy | 0.1333 | 0.0675 | 0.0862 | 0.0468 | 0.0412 | 0.0256 | 0.0393 | 0.0248 | 0.0379 | 0.0238 | 0.0339 | 0.0213 |
| fr3_w_half | 0.0375 | 0.0241 | 0.0246 | 0.0198 | 0.0231 | 0.0113 | 0.0222 | 0.0096 | 0.0204 | 0.0101 | 0.0188 | 0.0092 |
| fr3_s_static | 0.0072 | 0.0036 | 0.0071 | 0.0030 | 0.0062 | 0.0029 | 0.0060 | 0.0027 | 0.0060 | 0.0027 | 0.0059 | 0.0026 |
| Systems | Average Processing Time per Frame (ms) | Hardware Platform |
|---|---|---|
| ORB-SLAM2 | 31.21 | AMD Ryzen 7 4800H CPU, NVIDIA RTX 2060 GPU |
| SG-SLAM | 40.61 | AMD Ryzen 7 4800H CPU, NVIDIA RTX 2060 GPU |
| COEB-SLAM | 50.63 | AMD Ryzen 7 4800H CPU, NVIDIA RTX 2060 GPU |
| YOLO-SLAM | 696.09 | Intel Core i5-4288U CPU |
| DynaSLAM | 195.00 | Intel i7 CPU, P4000 GPU |
| VINS-Fusion | 57.50 | i7-9700K CPU, Nvidia RTX 2080, 48GB RAM |
| SGDO-SLAM(ours) | 38.81 | AMD Ryzen 7 4800H CPU, NVIDIA RTX 2060 GPU |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Q.; Wang, S.; Chen, N.; Li, W.; Yuan, J.; Zheng, E.; Wang, G.; Chen, W. SGDO-SLAM: A Semantic RGB-D SLAM System with Coarse-to-Fine Dynamic Rejection and Static Weighted Optimization. Sensors 2025, 25, 3734. https://doi.org/10.3390/s25123734
Hu Q, Wang S, Chen N, Li W, Yuan J, Zheng E, Wang G, Chen W. SGDO-SLAM: A Semantic RGB-D SLAM System with Coarse-to-Fine Dynamic Rejection and Static Weighted Optimization. Sensors. 2025; 25(12):3734. https://doi.org/10.3390/s25123734
Chicago/Turabian StyleHu, Qiming, Shuwen Wang, Nanxing Chen, Wei Li, Jiayu Yuan, Enhui Zheng, Guirong Wang, and Weimin Chen. 2025. "SGDO-SLAM: A Semantic RGB-D SLAM System with Coarse-to-Fine Dynamic Rejection and Static Weighted Optimization" Sensors 25, no. 12: 3734. https://doi.org/10.3390/s25123734
APA StyleHu, Q., Wang, S., Chen, N., Li, W., Yuan, J., Zheng, E., Wang, G., & Chen, W. (2025). SGDO-SLAM: A Semantic RGB-D SLAM System with Coarse-to-Fine Dynamic Rejection and Static Weighted Optimization. Sensors, 25(12), 3734. https://doi.org/10.3390/s25123734






