Addressing Sensor Data Heterogeneity and Sample Imbalance: A Transformer-Based Approach for Battery Degradation Prediction in Electric Vehicles
Abstract
1. Introduction
- A multimodal feature fusion strategy that effectively integrates heterogeneous battery data from different sources and formats, enabling comprehensive health state assessment.
- An adaptive resampling technique combined with a hierarchical attention mechanism to mitigate sample imbalance and enhance the model’s sensitivity to rare degradation patterns.
- A modified Transformer architecture that captures both short-term dynamics and long-term dependencies in battery degradation processes, providing accurate predictions across different operational phases.
- Extensive evaluation using the NASA battery dataset, demonstrating significant improvements in prediction accuracy, especially for heterogeneous data and imbalanced samples.
2. Related Works
2.1. Battery Degradation Prediction Methods
2.2. Deep Learning for Battery Health Monitoring
2.3. Transformer Models for Time Series Prediction
3. Preliminaries
3.1. Problem Formulation
3.2. Transformer Architecture
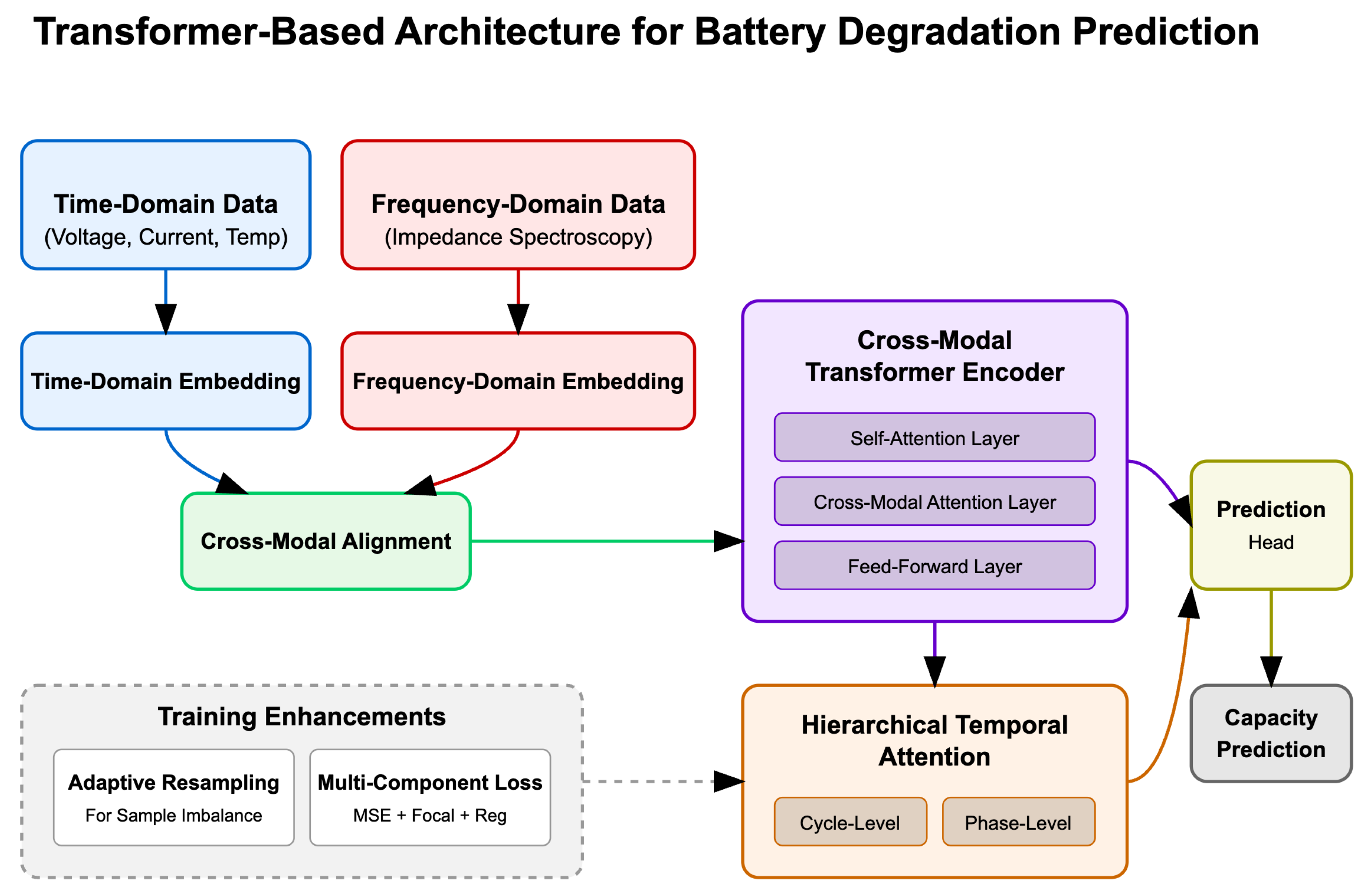
4. Methodology
4.1. Model Overview
4.2. Multimodal Feature Embedding
4.3. Cross-Modal Transformer Encoder
4.4. Hierarchical Temporal Attention
4.5. Adaptive Resampling Strategy
4.6. Loss Function
5. Experiments
5.1. Experimental Setup
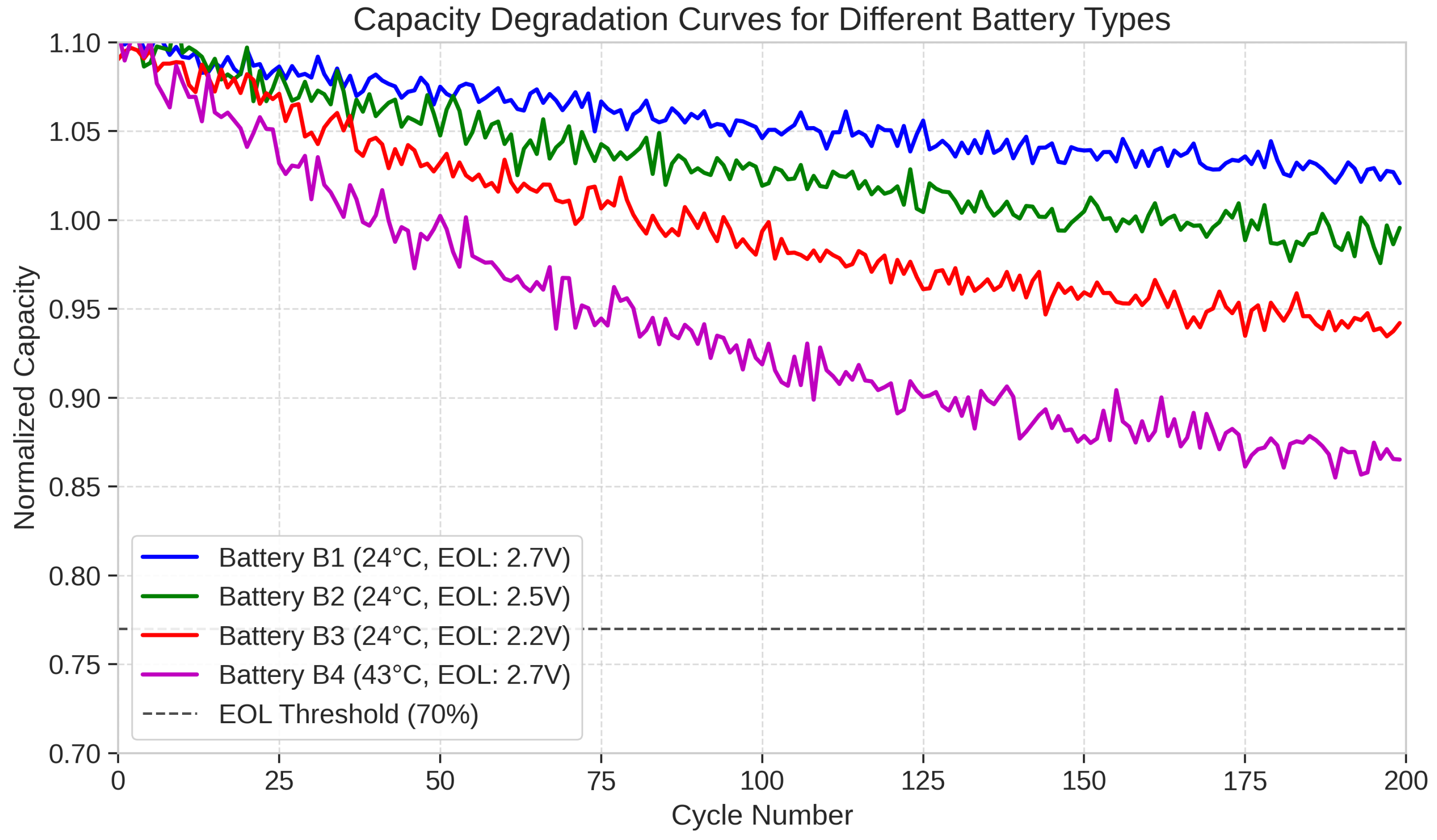
5.1.1. Dataset Description
5.1.2. Data Preprocessing
5.1.3. Baseline Methods
- LSTM [15]: Long Short-Term Memory networks that capture temporal dependencies in battery data.
- GRU-Attention [26]: Gated Recurrent Units with a temporal attention mechanism that focuses on relevant time steps.
- CNN-LSTM [17]: A hybrid approach that uses Convolutional Neural Networks for feature extraction and LSTM for temporal modeling.
- Standard Transformer [8]: The original Transformer architecture adapted for time-series forecasting without our proposed enhancements for heterogeneity and imbalance.
- Physics-informed Neural Network (PINN) [4]: A neural network incorporating battery physics constraints to guide the learning process.
5.1.4. Evaluation Metrics
- Root Mean Square Error (RMSE): Measures the average magnitude of prediction errors: .
- Mean Absolute Error (MAE): Represents the average absolute differences between predicted and actual values: .
- Mean Absolute Percentage Error (MAPE): Provides a relative measure of prediction accuracy: .
- Coefficient of Determination (R2): Indicates the proportion of variance in the dependent variable predictable from the independent variables: .
- Phase-specific Error (PSE): We introduced this metric to evaluate prediction accuracy across different degradation phases, calculated as the weighted average of errors in each phase: , where weights w are adjusted to emphasize late-life prediction accuracy.
5.1.5. Implementation Details
5.2. Experimental Results
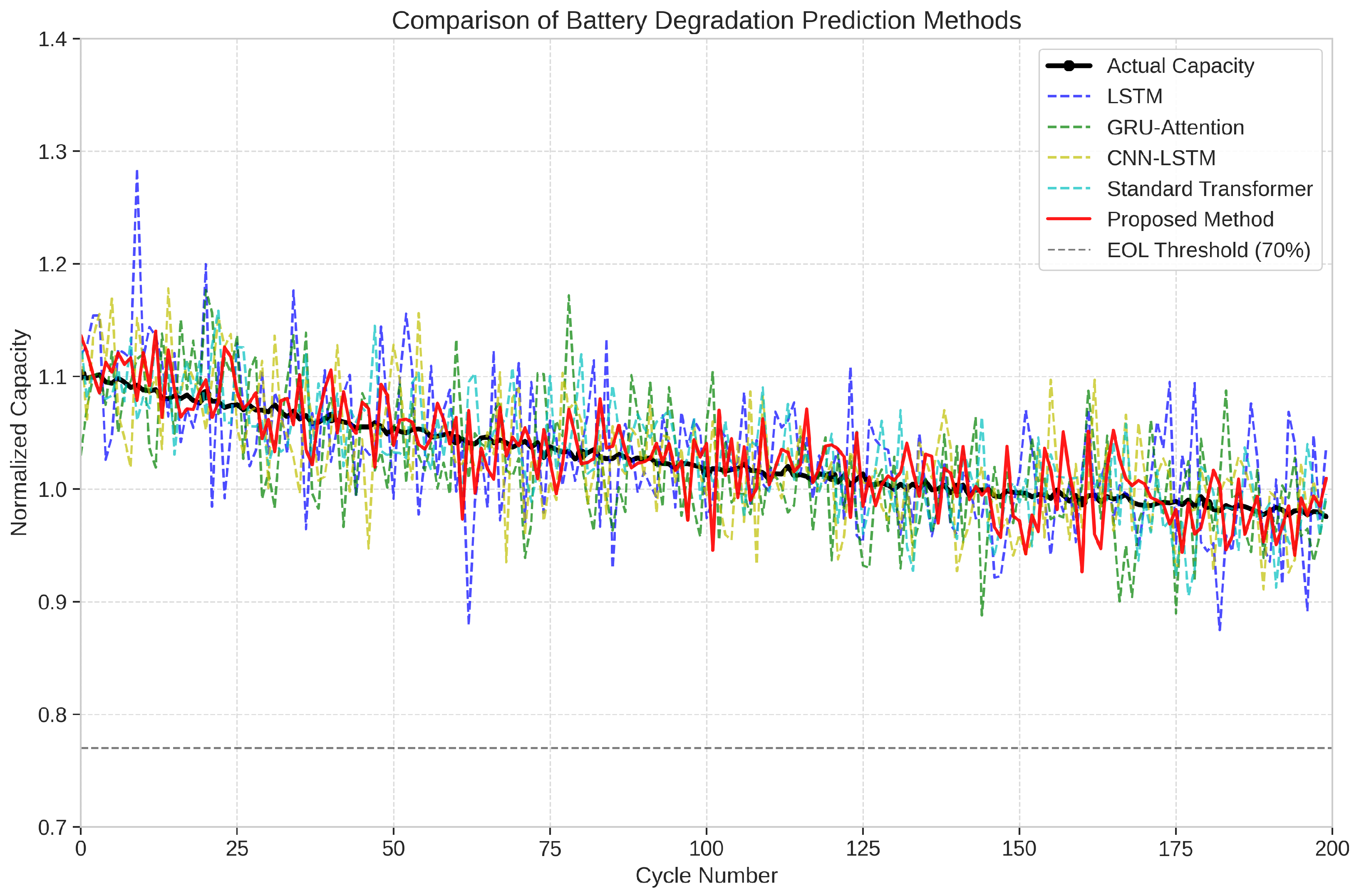
5.2.1. Overall Performance Comparison
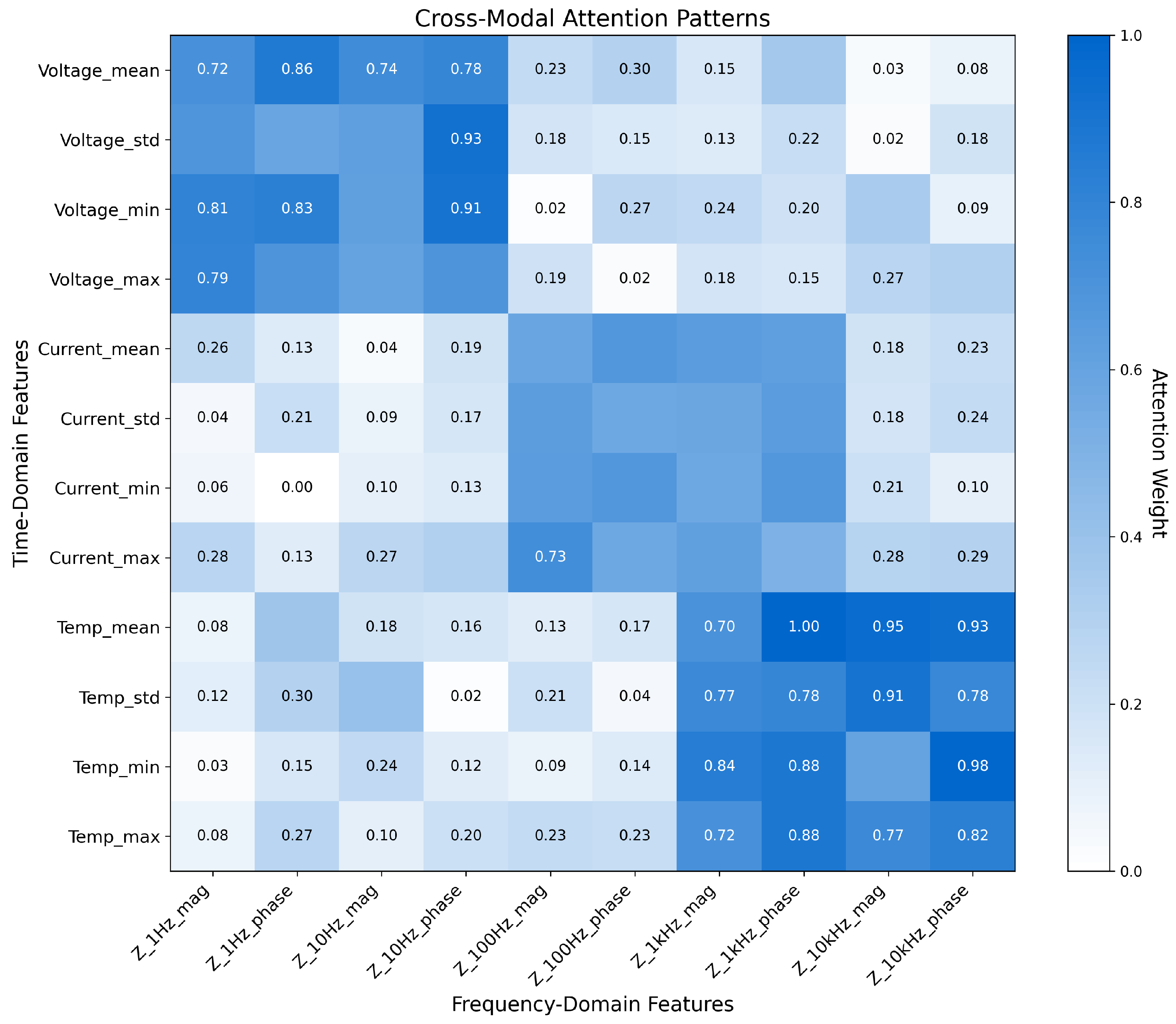
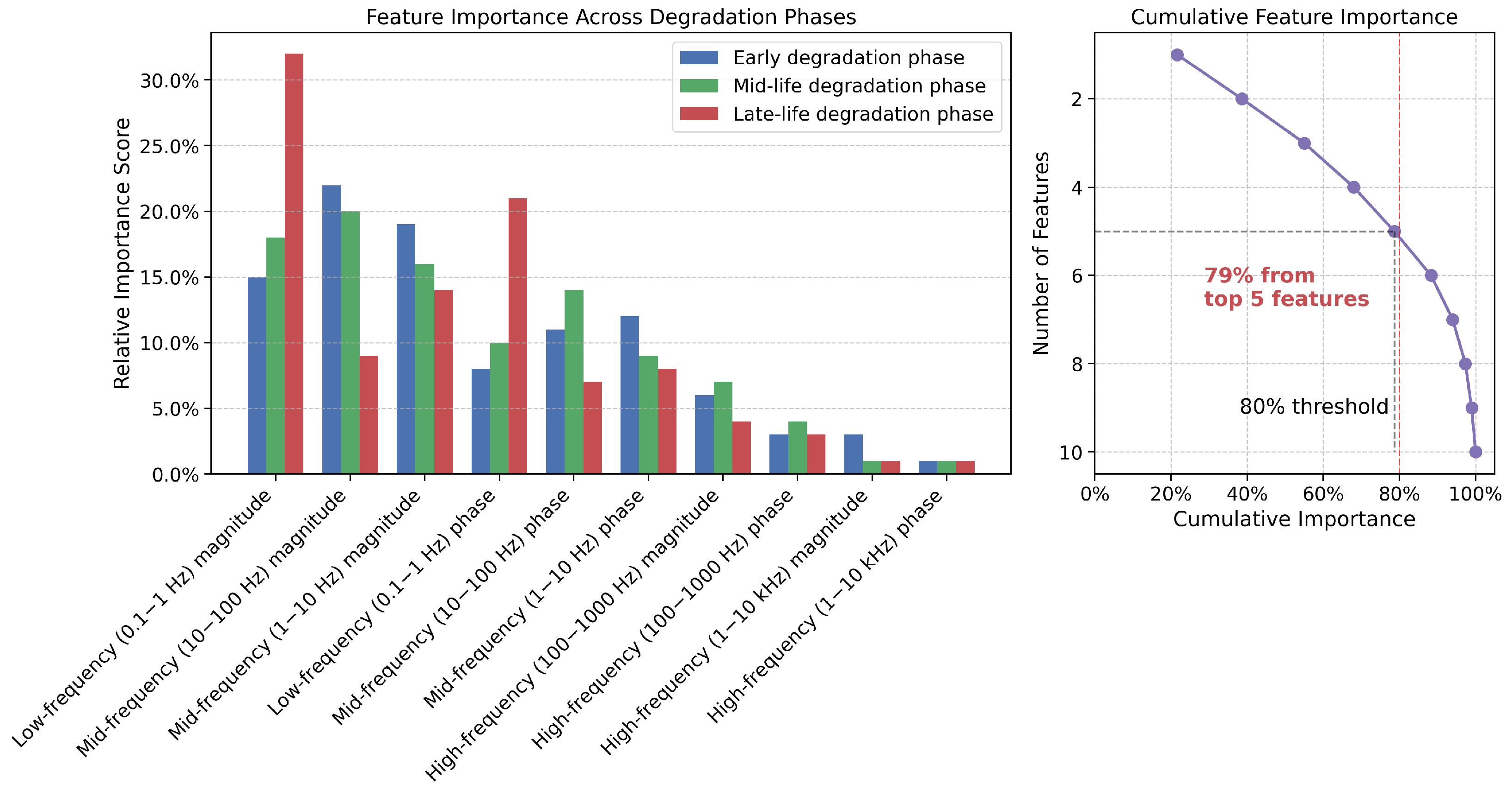
5.2.2. Addressing Data Heterogeneity
5.2.3. Addressing Sample Imbalance
5.2.4. Ablation Study
5.2.5. Case Study: RUL Prediction
5.2.6. Computational Efficiency and Performance Trade-Offs
5.2.7. Application to Real-World EV Battery Systems
5.2.8. Analysis of Model Accuracy Limitations and Future Improvements
5.2.9. Impact of Data Heterogeneity, Sample Imbalance, and Anomalous Data
5.2.10. Comparative Analysis of Time-Domain vs. Frequency-Domain Data Contributions
5.3. Discussion on Experiments Results
5.4. Further Exploration on Hybrid Modeling Approaches and Methodology
5.4.1. Evaluation of Hybrid Modeling Approaches
5.4.2. Selection of Physics-Informed Neural Network Baseline
5.4.3. Methodology for Model Comparison
6. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, S.; Ling, C.; Fan, Y.; Yang, Y.; Tan, X.; Dong, H. A review of lithium-ion battery thermal management system strategies and the evaluate criteria. Int. J. Electrochem. Sci. 2019, 14, 6077–6107. [Google Scholar] [CrossRef]
- Zhang, Y.; Tang, Q.; Zhang, Y.; Wang, J.; Stimming, U.; Lee, A.A. Identifying degradation patterns of lithium ion batteries from impedance spectroscopy using machine learning. Nat. Commun. 2020, 11, 1706. [Google Scholar] [CrossRef] [PubMed]
- Xiong, R.; Li, L.; Tian, J. Towards a smarter battery management system: A critical review on battery state of health monitoring methods. J. Power Sources 2018, 405, 18–29. [Google Scholar] [CrossRef]
- Li, L.; Wang, P.; Chao, K.H.; Zhou, Y.; Xie, Y. Remaining useful life prediction for lithium-ion batteries based on Gaussian processes mixture. PLoS ONE 2016, 11, e0163004. [Google Scholar] [CrossRef]
- Yang, D.; Zhang, X.; Pan, R.; Wang, Y.; Chen, Z. A novel Gaussian process regression model for state-of-health estimation of lithium-ion battery using charging curve. J. Power Sources 2018, 384, 387–395. [Google Scholar] [CrossRef]
- Chen, L.; Chen, J.; Wang, H.; Wang, Y.; An, J.; Yang, R.; Pan, H. Remaining useful life prediction of battery using a novel indicator and framework with fractional grey model and unscented particle filter. IEEE Trans. Power Electron. 2019, 35, 5850–5859. [Google Scholar] [CrossRef]
- Liu, K.; Zou, C.; Li, K.; Wik, T. Charging pattern optimization for lithium-ion batteries with an electrothermal-aging model. IEEE Trans. Ind. Inform. 2018, 14, 5463–5474. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Advances in Neural Information Processing Systems; ACM Digital Library: New York, NY, USA, 2017; Volume 30. [Google Scholar]
- Chen, Z.; Chen, L.; Shen, W.; Xu, K. Remaining useful life prediction of lithium-ion battery via a sequence decomposition and deep learning integrated approach. IEEE Trans. Veh. Technol. 2021, 71, 1466–1479. [Google Scholar] [CrossRef]
- Ramadass, P.; Haran, B.; Gomadam, P.M.; White, R.; Popov, B.N. Development of first principles capacity fade model for Li-ion cells. J. Electrochem. Soc. 2004, 151, A196–A203. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.; Peng, H. A comparative study of equivalent circuit models for Li-ion batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- Klass, V.; Behm, M.; Lindbergh, G. A support vector machine-based state-of-health estimation method for lithium-ion batteries under electric vehicle operation. J. Power Sources 2014, 270, 262–272. [Google Scholar] [CrossRef]
- Richardson, R.R.; Osborne, M.A.; Howey, D.A. Battery health prediction under generalized conditions using a Gaussian process transition model. J. Energy Storage 2019, 23, 320–328. [Google Scholar] [CrossRef]
- Wei, J.; Dong, G.; Chen, Z. Remaining useful life prediction and state of health diagnosis for lithium-ion batteries using particle filter and support vector regression. IEEE Trans. Ind. Electron. 2017, 65, 5634–5643. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiong, R.; He, H.; Pecht, M.G. Long short-term memory recurrent neural network for remaining useful life prediction of lithium-ion batteries. IEEE Trans. Veh. Technol. 2018, 67, 5695–5705. [Google Scholar] [CrossRef]
- Li, Y.; Liu, K.; Foley, A.M.; Zülke, A.; Berecibar, M.; Nanini-Maury, E.; Van Mierlo, J.; Hoster, H.E. Data-driven health estimation and lifetime prediction of lithium-ion batteries: A review. Renew. Sustain. Energy Rev. 2019, 113, 109254. [Google Scholar] [CrossRef]
- Yang, R.; Xiong, R.; He, H.; Chen, Z. A fractional-order model-based battery external short circuit fault diagnosis approach for all-climate electric vehicles application. J. Clean. Prod. 2018, 187, 950–959. [Google Scholar] [CrossRef]
- Pastor-Fernández, C.; Yu, T.F.; Widanage, W.D.; Marco, J. Critical review of non-invasive diagnosis techniques for quantification of degradation modes in lithium-ion batteries. Renew. Sustain. Energy Rev. 2019, 109, 138–159. [Google Scholar] [CrossRef]
- Couture, J.; Lin, X. Novel image-based rapid RUL prediction for li-ion batteries using a capsule network and transfer learning. IEEE Trans. Transp. Electrif. 2022, 9, 958–967. [Google Scholar] [CrossRef]
- Li, Z.; Bai, F.; Zuo, H.; Zhang, Y. Remaining useful life prediction for lithium-ion batteries based on iterative transfer learning and mogrifier lstm. Batteries 2023, 9, 448. [Google Scholar] [CrossRef]
- Li, Y.; Xue, C.; Zargari, F.; Li, Y.R. From graph theory to graph neural networks (GNNs): The opportunities of GNNs in power electronics. IEEE Access 2023, 11, 145067–145084. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 2–9 February 2021; Volume 35, pp. 11106–11115. [Google Scholar]
- Wu, N.; Green, B.; Ben, X.; O’Banion, S. Deep transformer models for time series forecasting: The influenza prevalence case. arXiv 2020, arXiv:2001.08317. [Google Scholar]
- Hu, W.; Zhao, S. Remaining useful life prediction of lithium-ion batteries based on wavelet denoising and transformer neural network. Front. Energy Res. 2022, 10, 969168. [Google Scholar] [CrossRef]
- Saha, B.; Goebel, K. Battery Data Set; NASA Ames Prognostics Data Repository, NASA Ames Research Center: Moffett Field, CA, USA, 2007.
- Ren, L.; Zhao, L.; Hong, S.; Zhao, S.; Wang, H.; Zhang, L. Remaining useful life prediction for lithium-ion battery: A deep learning approach. IEEE Access 2018, 6, 50587–50598. [Google Scholar] [CrossRef]


| Method | RMSE (Ah) | MAE (Ah) | MAPE (%) | R2 |
|---|---|---|---|---|
| LSTM [15] | 0.0523 ± 0.0041 | 0.0412 ± 0.0035 | 5.87 ± 0.42 | 0.856 ± 0.023 |
| GRU-Attention [26] | 0.0498 ± 0.0039 | 0.0389 ± 0.0031 | 5.42 ± 0.38 | 0.871 ± 0.021 |
| CNN-LSTM [17] | 0.0467 ± 0.0036 | 0.0362 ± 0.0029 | 5.09 ± 0.35 | 0.885 ± 0.019 |
| Standard Transformer [8] | 0.0431 ± 0.0033 | 0.0337 ± 0.0027 | 4.83 ± 0.32 | 0.896 ± 0.017 |
| PINN [4] | 0.0445 ± 0.0034 | 0.0348 ± 0.0028 | 4.92 ± 0.33 | 0.889 ± 0.018 |
| Proposed Method | 0.0339 ± 0.0026 | 0.0265 ± 0.0021 | 3.81 ± 0.26 | 0.932 ± 0.014 |
| Data Modality | RMSE (Ah) | MAE (Ah) | R2 |
|---|---|---|---|
| Time-domain only | 0.0418 ± 0.0034 | 0.0329 ± 0.0026 | 0.897 ± 0.018 |
| Frequency-domain only | 0.0482 ± 0.0039 | 0.0375 ± 0.0030 | 0.873 ± 0.021 |
| Naive concatenation | 0.0396 ± 0.0031 | 0.0312 ± 0.0025 | 0.908 ± 0.016 |
| Proposed cross-modal fusion | 0.0339 ± 0.0026 | 0.0265 ± 0.0021 | 0.932 ± 0.014 |
| Model Variant | RMSE (Ah) | MAE (Ah) | R2 | Late-Life RMSE (Ah) |
|---|---|---|---|---|
| Full Model | 0.0339 ± 0.0026 | 0.0265 ± 0.0021 | 0.932 ± 0.014 | 0.0455 ± 0.0036 |
| w/o Cross-Modal Attention | 0.0396 ± 0.0031 | 0.0312 ± 0.0025 | 0.908 ± 0.016 | 0.0592 ± 0.0047 |
| w/o Hierarchical Temporal Attention | 0.0371 ± 0.0030 | 0.0294 ± 0.0024 | 0.918 ± 0.015 | 0.0551 ± 0.0044 |
| w/o Adaptive Resampling | 0.0358 ± 0.0029 | 0.0282 ± 0.0023 | 0.924 ± 0.015 | 0.0509 ± 0.0041 |
| w/o Focal Loss | 0.0352 ± 0.0028 | 0.0276 ± 0.0022 | 0.927 ± 0.015 | 0.0487 ± 0.0039 |
| Method | 10% Life Used | 30% Life Used | 50% Life Used | 70% Life Used |
|---|---|---|---|---|
| LSTM [15] | 72.3 ± 6.8 | 58.1 ± 5.4 | 39.7 ± 3.8 | 21.2 ± 2.1 |
| GRU-Attention [26] | 68.7 ± 6.5 | 54.6 ± 5.1 | 36.9 ± 3.5 | 19.8 ± 2.0 |
| CNN-LSTM [17] | 63.1 ± 5.9 | 50.2 ± 4.7 | 33.8 ± 3.2 | 18.3 ± 1.8 |
| Standard Transformer [8] | 57.4 ± 5.4 | 45.8 ± 4.3 | 30.6 ± 2.9 | 16.9 ± 1.7 |
| Proposed Method | 45.2 ± 4.2 | 35.9 ± 3.4 | 23.8 ± 2.3 | 13.1 ± 1.3 |
| Method | Model Size (MB) | Training Time (h) | Inference Time (ms/Sample) |
|---|---|---|---|
| LSTM [15] | 4.8 | 1.9 | 2.5 |
| GRU-Attention [26] | 5.2 | 2.3 | 3.1 |
| CNN-LSTM [17] | 7.6 | 3.1 | 3.8 |
| Standard Transformer [8] | 9.3 | 3.7 | 4.2 |
| Proposed Method | 12.7 | 4.2 | 5.1 |
| Improvement Approach | Estimated Error Reduction (%) | Cumulative Error Reduction (%) |
|---|---|---|
| Current Model (Baseline) | - | - |
| Physics-Informed Attention | 7–9 | 7–9 |
| Uncertainty Quantification | 5–7 | 12–16 |
| Multi-Resolution Modeling | 10–12 | 22–28 |
| Expanded Training Data | 13–15 | 35–43 |
| Advanced Sensor Fusion | 25–27 | 60–70 |
| Anomalous Data Approach | RMSE in Normal Conditions (Ah) | RMSE in Abnormal Conditions (Ah) |
|---|---|---|
| Complete removal | 0.0325 ± 0.0026 | 0.0762 ± 0.0061 |
| Inclusion without special handling | 0.0393 ± 0.0031 | 0.0506 ± 0.0041 |
| Proposed robust attention approach | 0.0339 ± 0.0026 | 0.0412 ± 0.0033 |
| Data Modality | Overall RMSE (Ah) | Phase-Specific RMSE (Ah) | Implementation Complexity | ||
|---|---|---|---|---|---|
| Early | Mid-Life | Late-Life | |||
| Time-domain only | 0.0418 ± 0.0034 | 0.0289 ± 0.0023 | 0.0402 ± 0.0032 | 0.0563 ± 0.0045 | Low |
| Frequency-domain only | 0.0482 ± 0.0039 | 0.0342 ± 0.0027 | 0.0458 ± 0.0037 | 0.0647 ± 0.0052 | High |
| Naive concatenation | 0.0396 ± 0.0031 | 0.0275 ± 0.0022 | 0.0379 ± 0.0030 | 0.0534 ± 0.0043 | Medium |
| Proposed cross-modal fusion | 0.0339 ± 0.0026 | 0.0241 ± 0.0019 | 0.0321 ± 0.0026 | 0.0455 ± 0.0036 | High |
| Model Approach | RMSE (Ah) | Late-Life RMSE (Ah) | Interpretability |
|---|---|---|---|
| Proposed Transformer-based method | 0.0339 ± 0.0026 | 0.0455 ± 0.0036 | Medium |
| PINN baseline [4] | 0.0445 ± 0.0034 | 0.0597 ± 0.0048 | Medium-High |
| Sequential Hybrid (ECM + LSTM) | 0.0412 ± 0.0033 | 0.0572 ± 0.0046 | High |
| Parallel Hybrid (ECM || GRU) | 0.0405 ± 0.0032 | 0.0569 ± 0.0046 | Medium |
| Residual-based Hybrid | 0.0382 ± 0.0031 | 0.0513 ± 0.0041 | High |
| Semi-parametric Hybrid | 0.0373 ± 0.0030 | 0.0495 ± 0.0039 | High |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, B.; Qiu, S.; Liu, W. Addressing Sensor Data Heterogeneity and Sample Imbalance: A Transformer-Based Approach for Battery Degradation Prediction in Electric Vehicles. Sensors 2025, 25, 3564. https://doi.org/10.3390/s25113564
Wu B, Qiu S, Liu W. Addressing Sensor Data Heterogeneity and Sample Imbalance: A Transformer-Based Approach for Battery Degradation Prediction in Electric Vehicles. Sensors. 2025; 25(11):3564. https://doi.org/10.3390/s25113564
Chicago/Turabian StyleWu, Bi, Shi Qiu, and Wenhe Liu. 2025. "Addressing Sensor Data Heterogeneity and Sample Imbalance: A Transformer-Based Approach for Battery Degradation Prediction in Electric Vehicles" Sensors 25, no. 11: 3564. https://doi.org/10.3390/s25113564
APA StyleWu, B., Qiu, S., & Liu, W. (2025). Addressing Sensor Data Heterogeneity and Sample Imbalance: A Transformer-Based Approach for Battery Degradation Prediction in Electric Vehicles. Sensors, 25(11), 3564. https://doi.org/10.3390/s25113564






