Adaptive Resource Optimization for LoRa-Enabled LEO Satellite IoT System in High-Dynamic Environments
Abstract
1. Introduction
1.1. Background and Contribution
- This study introduces a novel beacon-triggered framework for LoRa-enabled LEO satellite IoT systems, which includes modifications to the calculation formulas for frame duration and skip probability. Unlike conventional solutions, the proposed architecture explicitly addresses the fundamental disparities between semi-static terrestrial networks and highly dynamic LEO scenarios, where orbital motion-induced channel conditions and received signal power variations significantly impact link reliability. This framework serves as the foundation for subsequent resource optimization algorithms, marking a paradigm shift from traditional semi-static approaches to fully adaptive, space-aware IoT resource management.
- Building upon the beacon-triggered framework, this paper explicitly incorporates the characteristics of on-board satellite processing to analyze the conditions for successful data extraction. By accounting for the energy constraints of satellite IoT terminals and their significantly longer transmission distances compared to terrestrial scenarios, the objective function integrating energy efficiency and data extraction rate is formulated.
- To decouple the intertwined objectives of optimizing energy efficiency and maximizing data extraction rates, an adaptive SF allocation algorithm is proposed. This algorithm aims to mitigate collisions and minimize resource waste. Complementing this, a practical dynamic power control mechanism is introduced to optimize power usage of LoRa devices. Together, these strategies enhance overall system performance by effectively balancing energy efficiency with data throughput.
1.2. Related Works
2. System Model
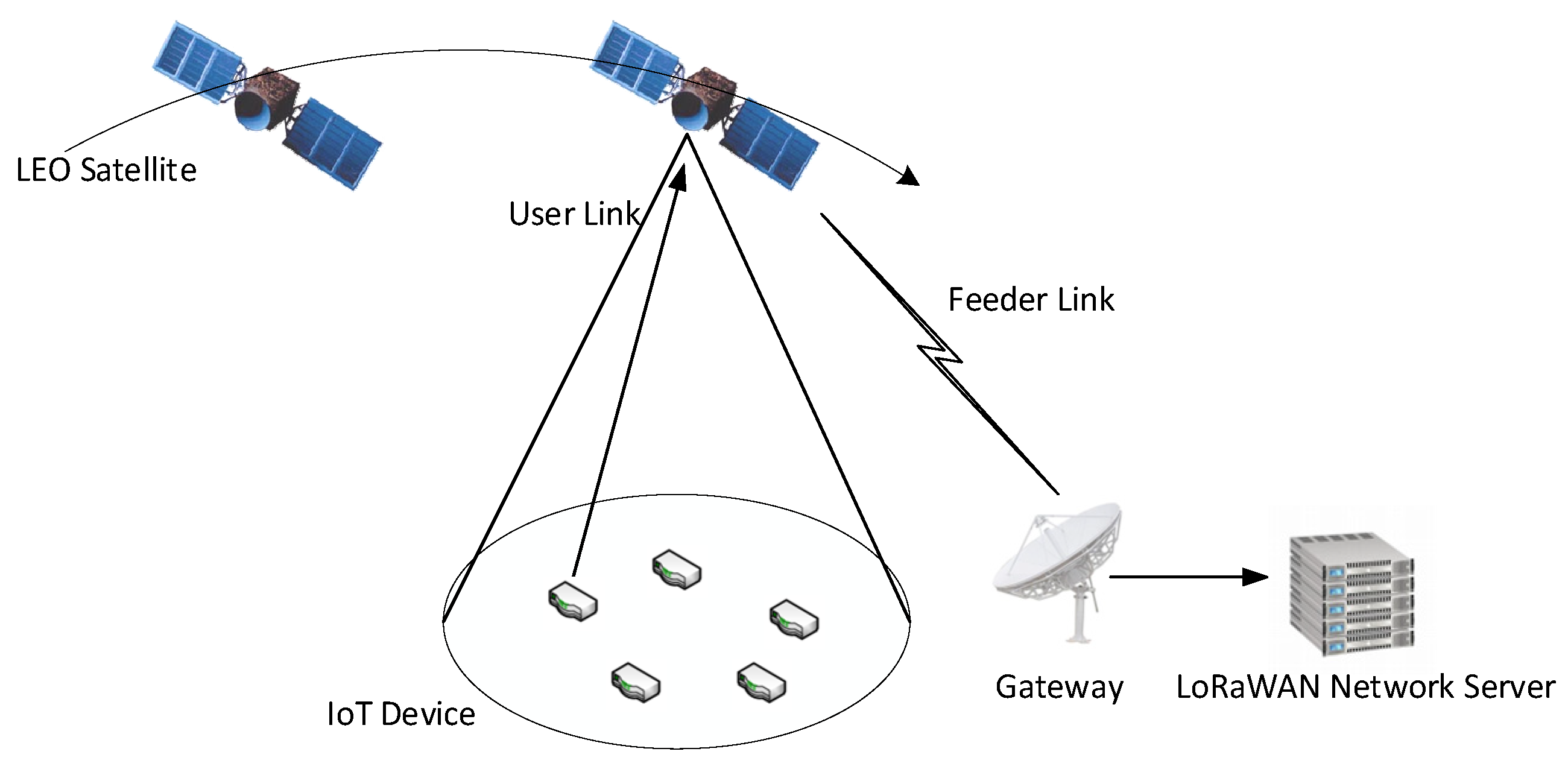
2.1. LEO Satellite IoT Based on LoRa
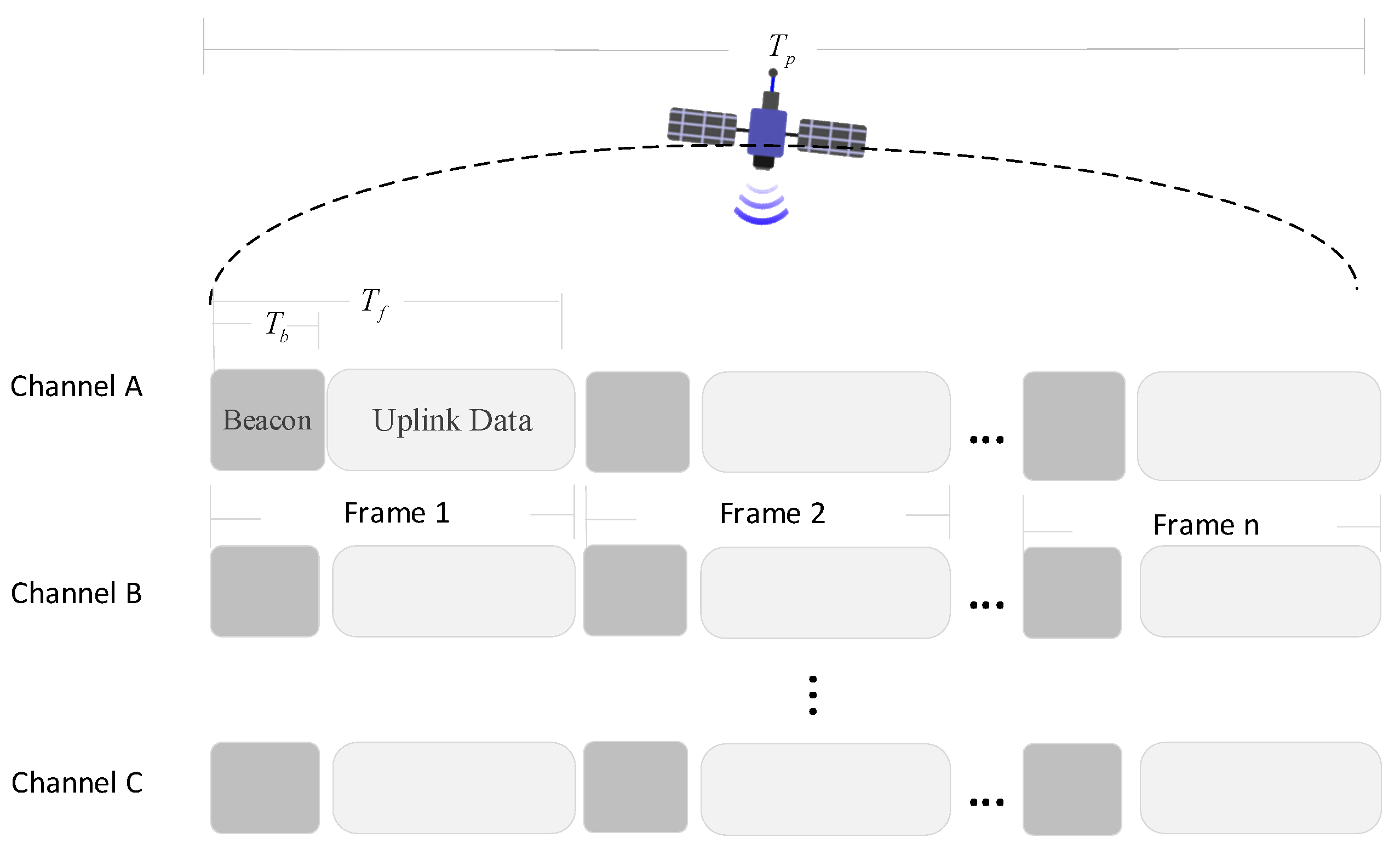
2.2. Beacon Mechanism of LEO Satellite IoT Based on LoRa
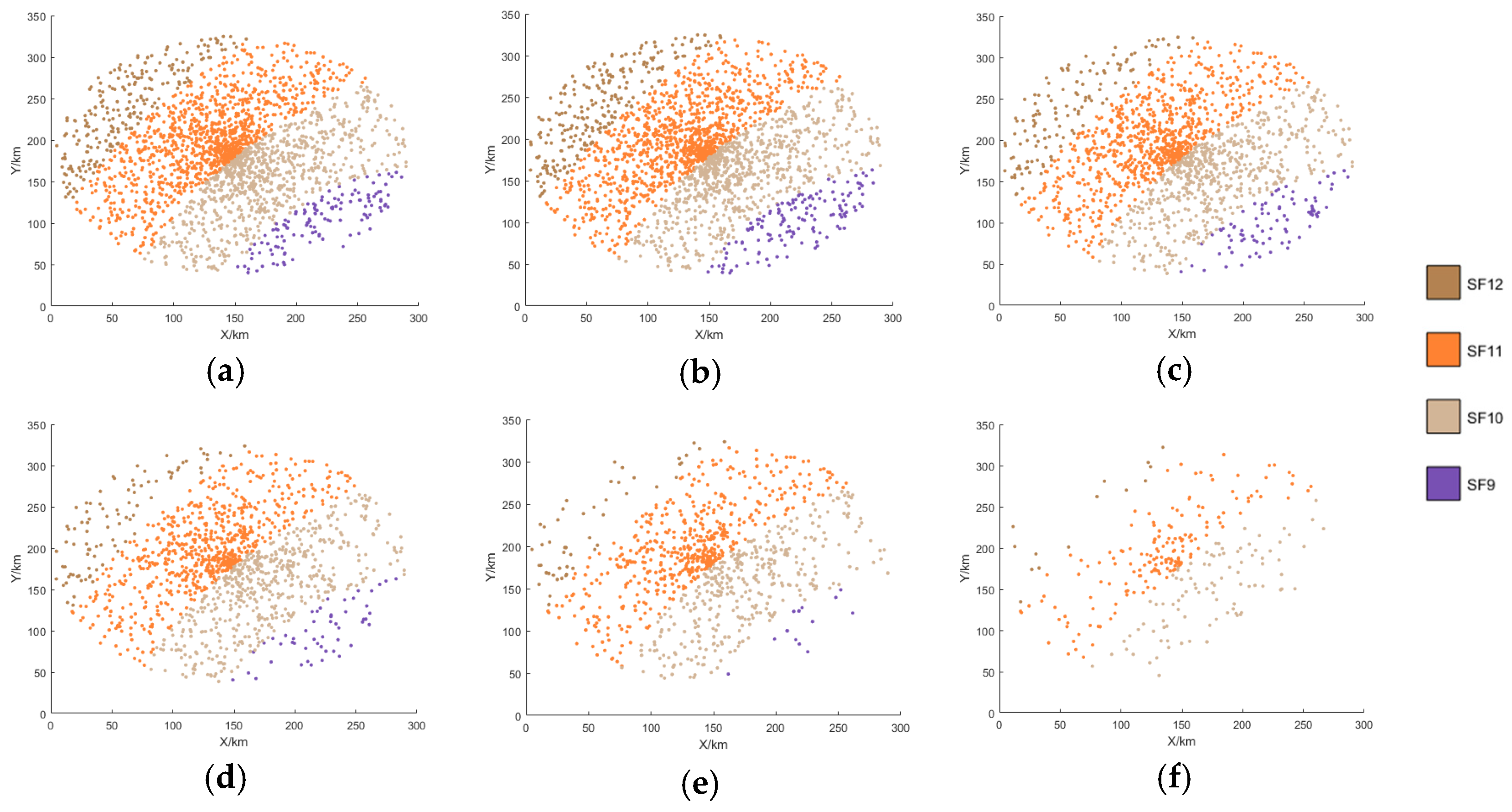
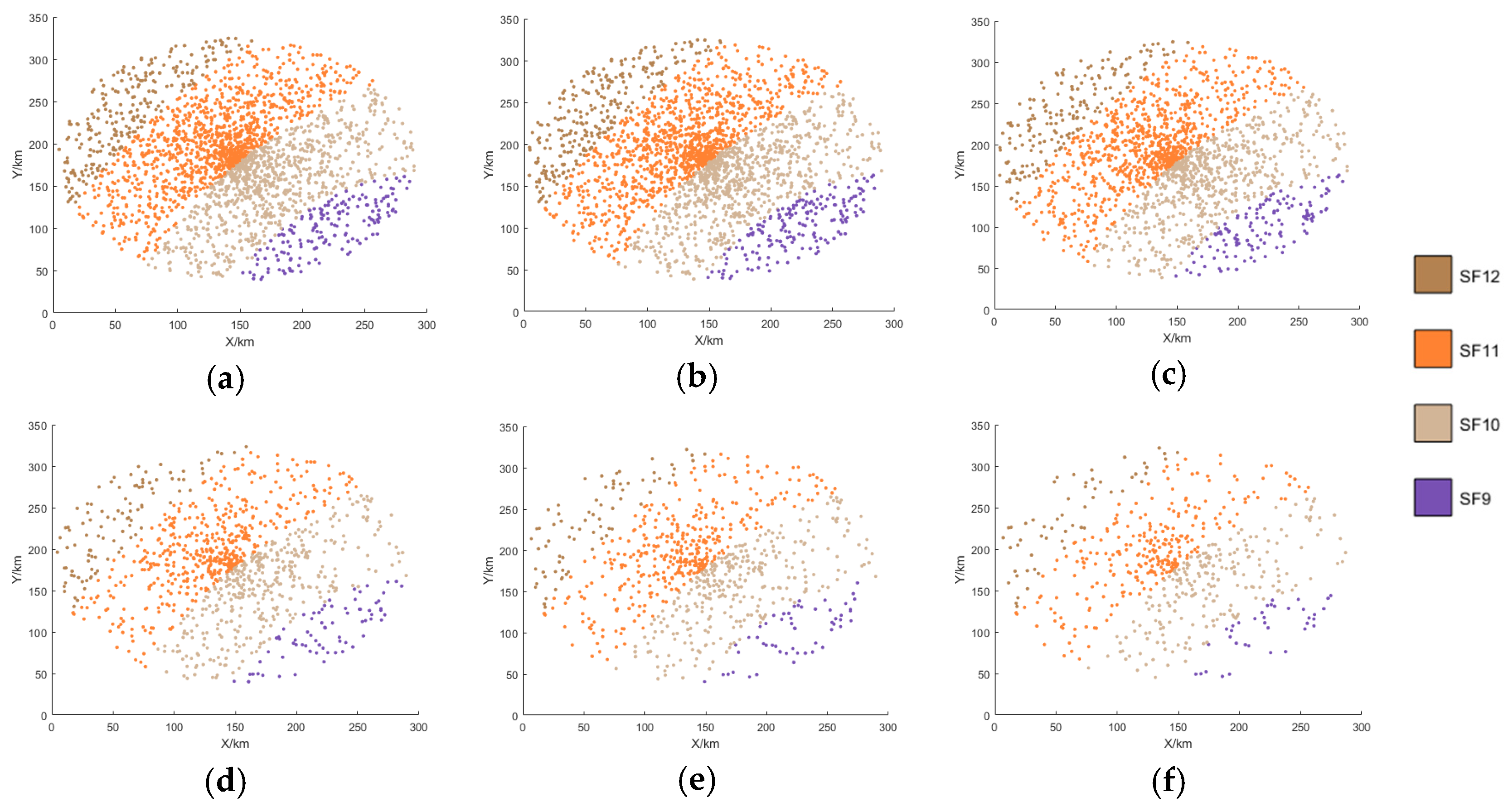
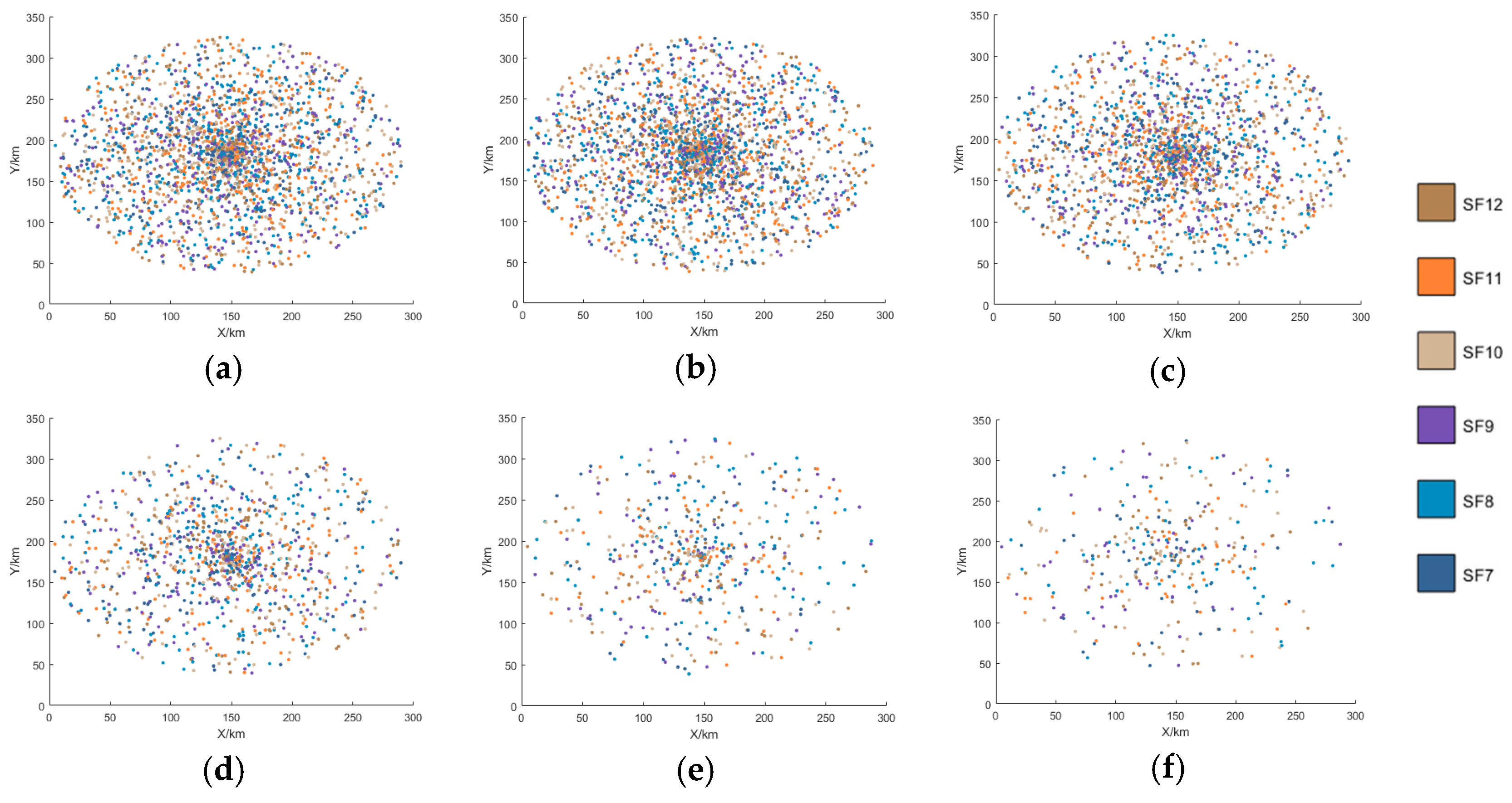
2.3. The Optimal Distribution of SF
3. Adaptive Resource Optimization
3.1. Optimization Problem
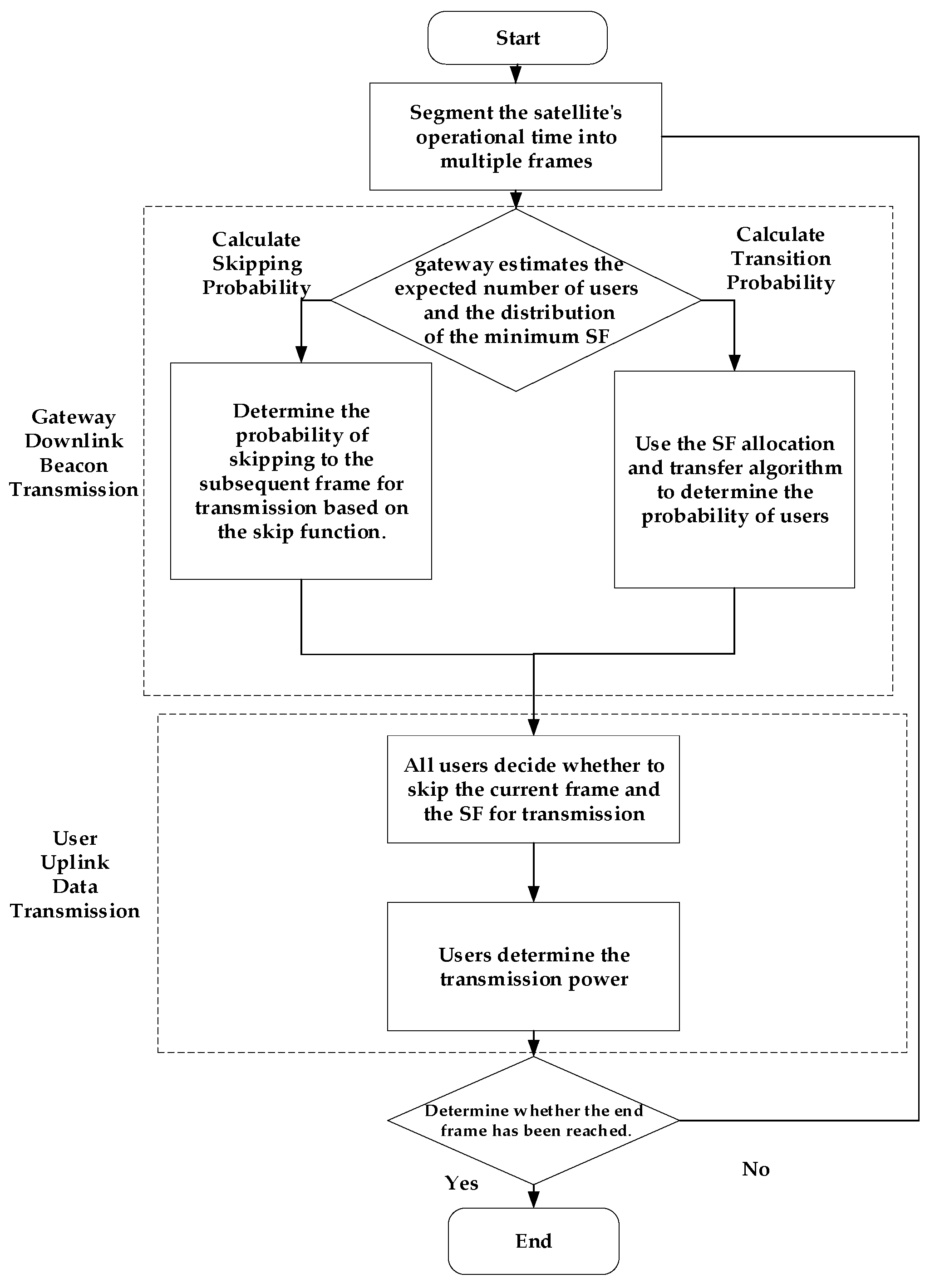
3.2. Resource Optimization Strategy
3.3. Algorithm Design
3.3.1. SF Transfer Algorithm
| Algorithm 1: SF Transfer Algorithm | |
| INPUT | Number of users , Minimum SF distribution , Optimal SF distribution |
| OUTPUT | |
| 1 | Calculate and from and |
| 2 | For k = 7 to 12 |
| 3 | If 0. |
| 4 | point = k, = |
| 6 | = , t = 7 to point − 1 |
| 8 | = , t = point + 1 to 12 |
| 10 | else. |
| 11 | = , t = 7 to 12 |
| 12 | End if |
| 13 | End for |
| 14 | |
| 15 | Initialize and |
| 16 | FOR |
| 17 | |
| 18 | End for |
| 19 | FOR i |
| 20 | FOR j |
| 21 | If |
| 22 | |
| 23 | Else |
| 24 | If i |
| 25 | |
| 26 | else |
| 27 | |
| 28 | End if |
| 29 | End if |
| 30 | End for |
| 31 | End for |
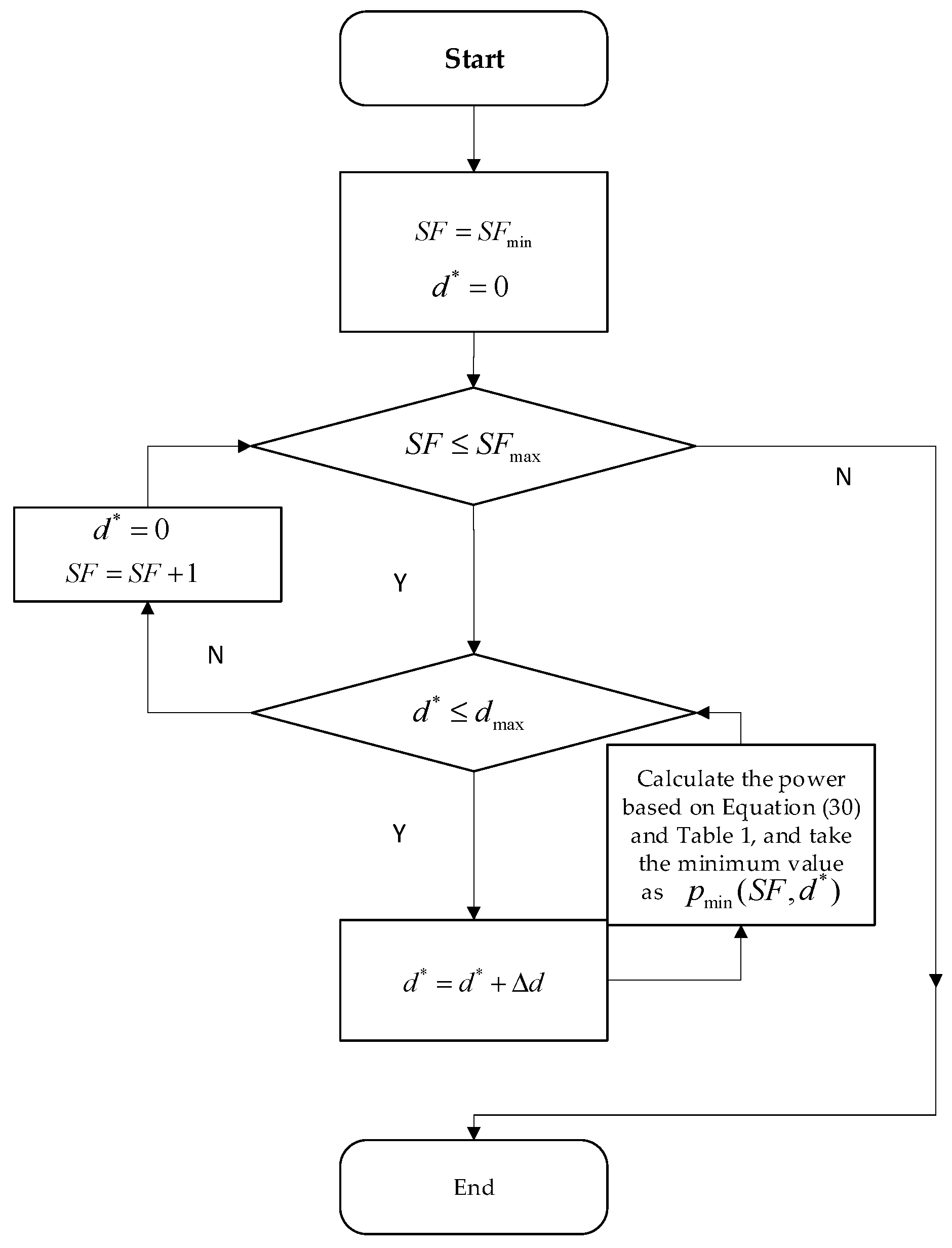
3.3.2. Practical Power Control Mechanism
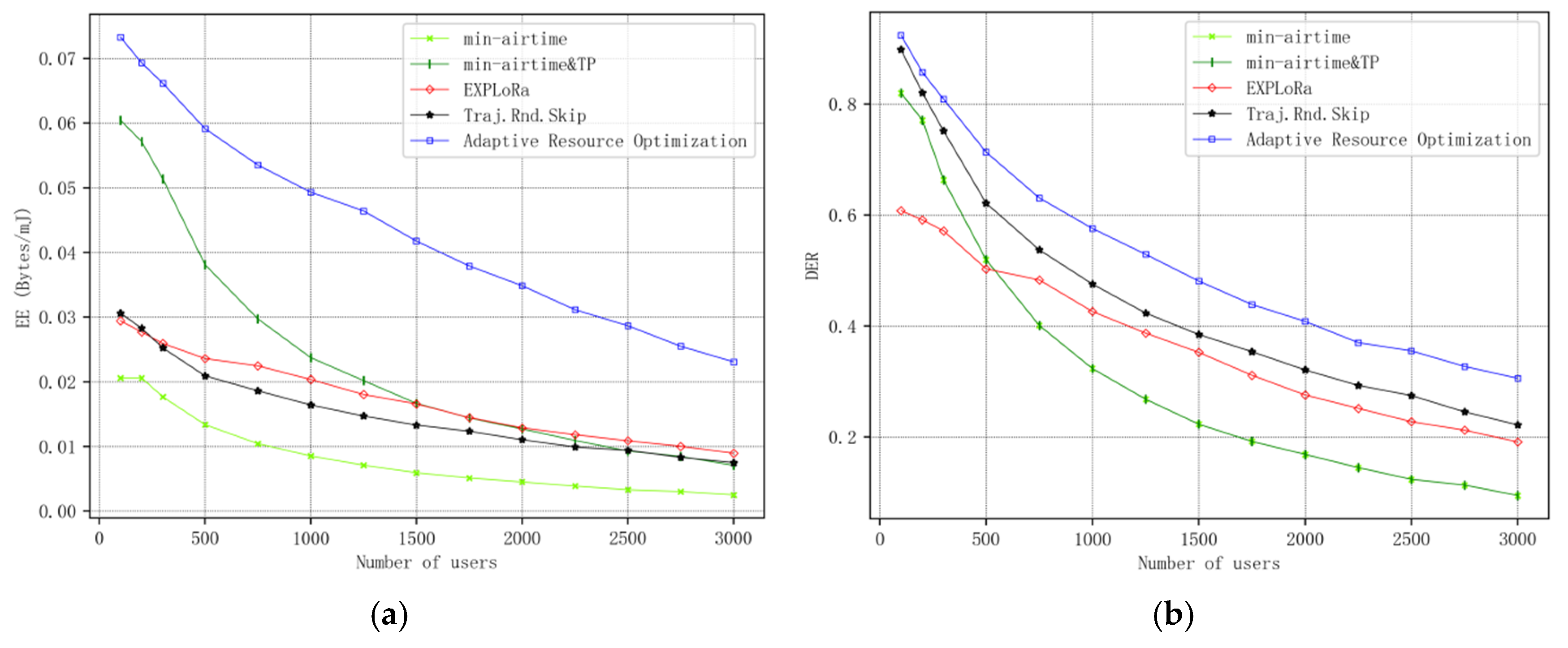
4. Simulation and Analysis
4.1. Simulation
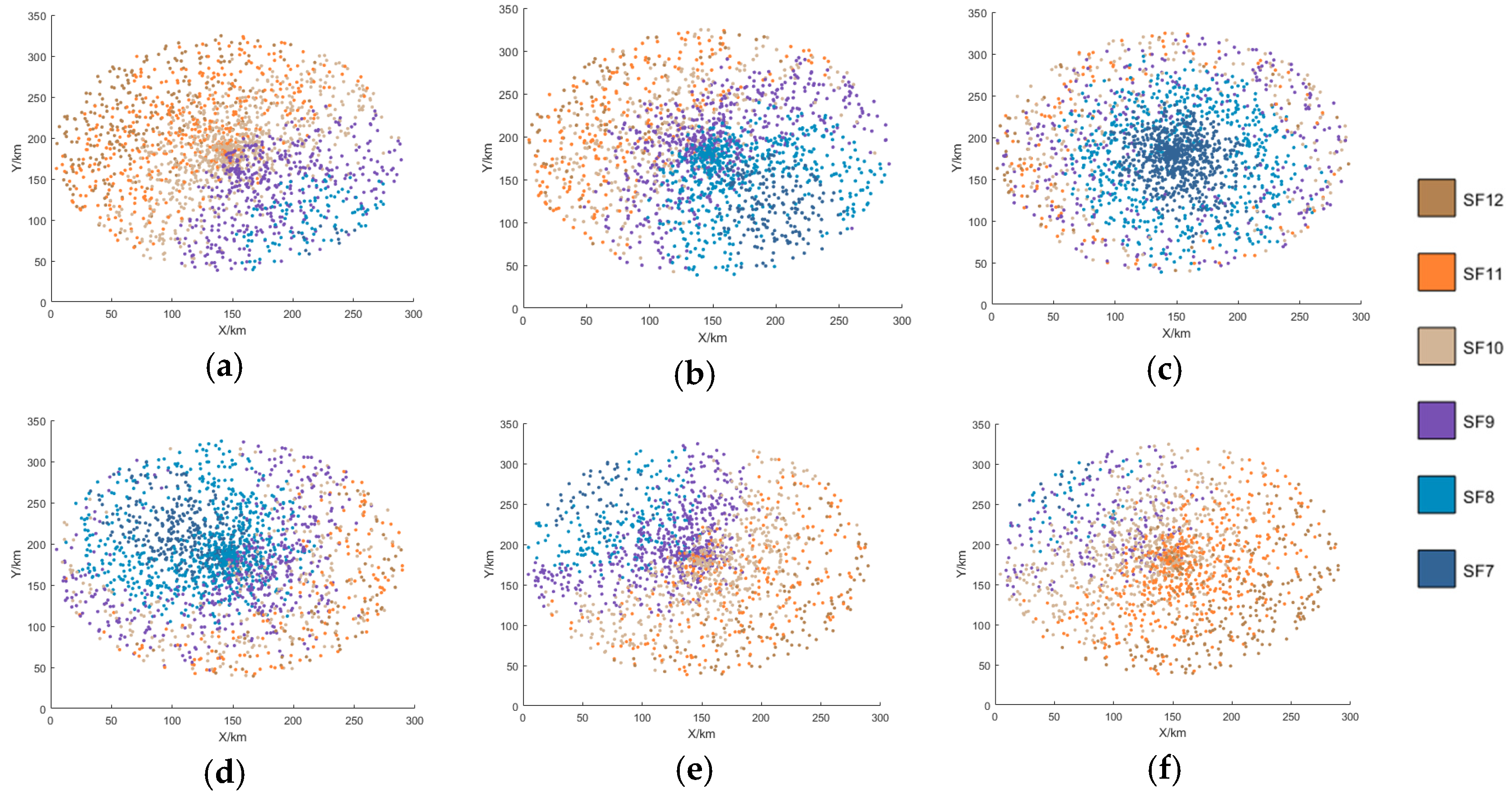
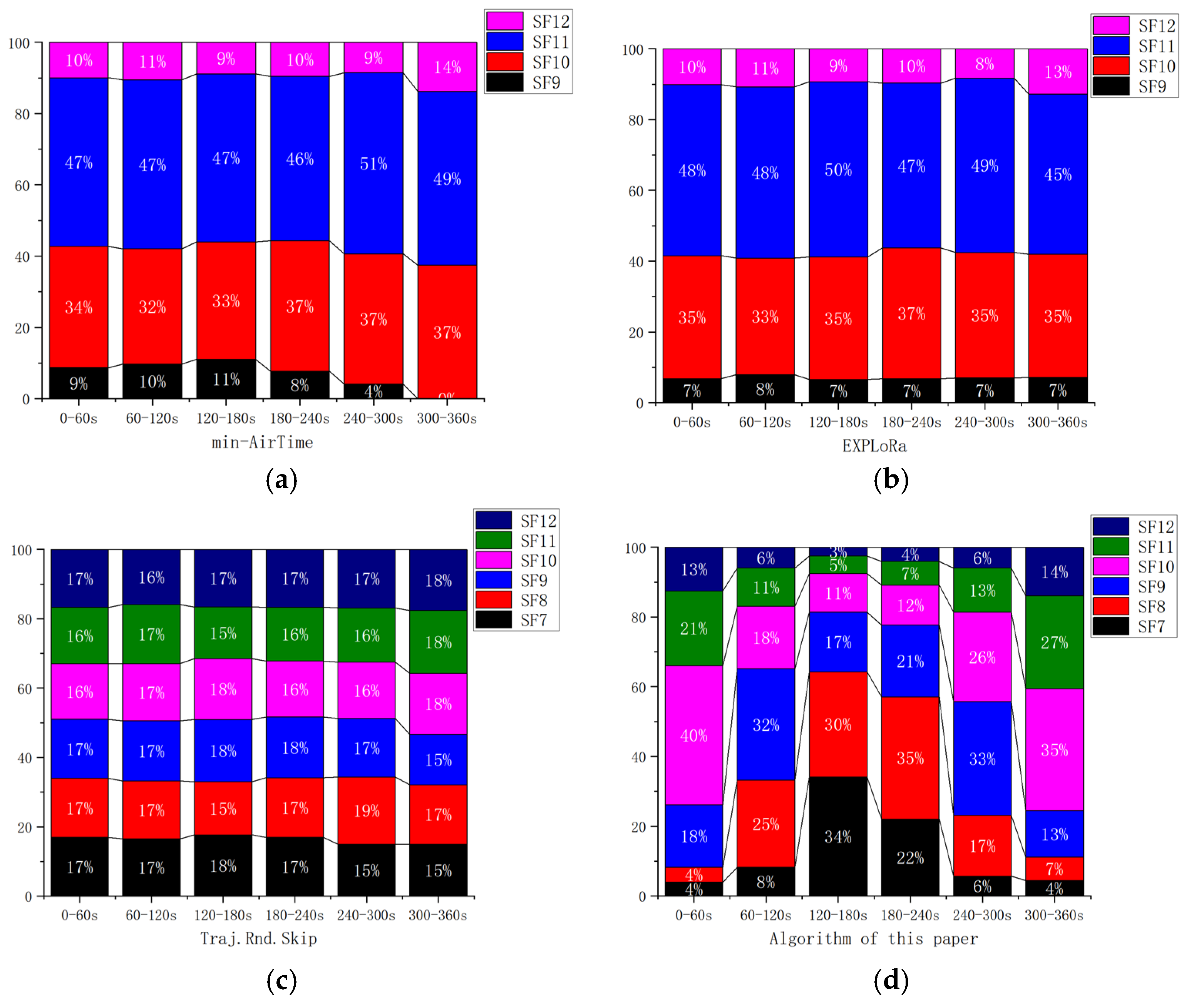
4.2. Performance Analysis and Discussion
5. Future Work
- The proposed dynamic resource optimization algorithm will be extended to multi-satellite constellation scenarios. In these scenarios, inter-satellite handover and coordinated allocation of SFs in overlapping coverage areas will pose new challenges, while also providing opportunities for further optimizing energy efficiency.
- Machine learning techniques, such as deep reinforcement learning, will be integrated to enable the algorithm to adapt to more complex and unpredictable channel conditions.
- To conduct hardware validation tests, a testbed has been set up in the laboratory, including power supplies, signal generators, LEO channel simulators, etc. Opportunities for conducting field tests will be sought in the future.The testbed for hardware validation tests is shown in Figure 13.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Centenaro, M.; Costa, C.E.; Granelli, F.; Sacchi, C.; Vangelista, L. A survey on technologies standards open challenges in satellite IoT. IEEE Commun. Surv. Tutor. 2021, 23, 1693–1720. [Google Scholar] [CrossRef]
- Beshley, M.; Kryvinska, N.; Seliuchenko, M.; Beshley, H.; Shakshuki, E.; Yasar, A. End-to-End QoS “smart queue” management algorithms and traffic prioritization mechanisms for narrow-band internet of things services in 4G/5G networks. Sensors 2020, 20, 2324. [Google Scholar] [CrossRef] [PubMed]
- Bor, M.C.; Roedig, U.; Voigt, T.; Alonso, J. Do LoRa low-power wide-area networks scale? In Proceedings of the 19th ACM International Conference on Modeling, Analysis and Simulation of Wireless and Mobile Systems, Malta, 13–17 November 2016. [Google Scholar]
- Soto-Vergel, A.; Arismendy, L.; Bornacelli-Durán, R.; Cardenas, C.; Montero-Arévalo, B.; Rivera, E.; Candelo-Becerra, J.E. LoRa performance in industrial environments: Analysis of different ADR algorithms. IEEE Trans. Ind. Inform. 2023, 19, 10501–10511. [Google Scholar] [CrossRef]
- Daiwei, H. Research on Cross-layer Resource Allocation Method Based on LoRaWAN Network. Master’s Thesis, Chongqing University of Posts and Telecommunications, Chongqing, China, 24 May 2019. [Google Scholar]
- Cuomo, F.; Campo, M.; Caponi, A.; Bianchi, G.; Rossini, G.; Pisani, P. EXPLoRa: Extending the performance of LoRa by suitable SF allocations. In Proceedings of the 2017 IEEE 13th International Conference on Wireless and Mobile Computing, Rome, Italy, 9–11 October 2017. [Google Scholar]
- Galli, A.; Narduzzi, C.; Peruzzi, G.; Pozzebon, A. Satellite iot for monitoring and tracking of athletes in extreme environments. In Proceedings of the 2022 IEEE International Workshop on Sport, Technology and Research (STAR), Trento-Cavalese, Italy, 6-8 July 2022. [Google Scholar]
- Capez, G.M.; Henn, S.; Fraire, J.A.; Garello, R. Sparse satellite constellation design for global and regional direct-to-satellite IoT services. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 3786–3801. [Google Scholar] [CrossRef]
- Routray, S.K.; Tengshe, R.; Javali, A.; Sarkar, S.; Sharma, L.; Ghosh, A.D. Satellite based IoT for mission critical applications. In Proceedings of the 2019 International Conference on Data Science and Communication (IconDSC), Bangalore, India, 1–2 March 2019. [Google Scholar]
- Afhamisis, M.; Palattella, M. SALSA: A scheduling algorithm for LoRa to LEO satellites. IEEE Access 2022, 10, 11608–11615. [Google Scholar] [CrossRef]
- Álvarez, G.; Fraire, J.; Hassan, K.; Céspedes, S.; Pesch, D. Uplink transmission policies for LoRa-based direct-to-satellite IoT. IEEE Access 2022, 10, 72687–72701. [Google Scholar] [CrossRef]
- Lin, K.; Ullah, M.; Alves, H.; Mikhaylov, K.; Hao, T. Energy Efficiency Optimization for Subterranean LoRaWAN Using A Reinforcement Learning Approach: A Direct-to- Satellite Scenario. IEEE Wirel. Commun. Lett 2023, 13, 308–312. [Google Scholar] [CrossRef]
- Faber, M.J.; van der Zwaag, K.M.; dos Santos, W.G.; Rocha, H.R.; Segatto, M.E.; Silva, J.A. A theoretical and experimental evaluation on the performance of LoRa technology. IEEE Sens. J. 2020, 20, 9480. [Google Scholar] [CrossRef]
- Wu, T.; Qu, D.; Zhang, G. Research on LoRa adaptability in the LEO satellites Internet of Things. In Proceedings of the 2019 15th International Wireless Communications & Mobile Computing Conference, Tangier, Morocco, 24–28 June 2019. [Google Scholar]
- Gkotsiopoulos, P.; Zorbas, D.; Douligeris, C. Performance determinants in LoRa networks: A literature review. IEEE Commun. Surv. Tutor. 2021, 23, 1721. [Google Scholar] [CrossRef]
- Leng, T.; Li, X.; Hu, D.; Cui, G.; Wang, W. Collaborative Computing and Resource Allocation for LEO Satellite-Assisted Internet of Things. Wirel. Commun. Mob. Comput. 2021, 2021, 4212548. [Google Scholar] [CrossRef]
- Kodheli, O.; Maturo, N.; Andrenacci, S.; Chatzinotas, S.; Zimmer, F. Link budget analysis for satellite-based narrowband IoT systems. In Proceedings of the International Conference on Ad-Hoc Networks and Wireless, Luxembourg, 1–3 October 2019. [Google Scholar]
- Ullah, M.A.; Souza, R.D.; Pasolini, G.; de Souza Sant’Ana, J.M.; Höyhtyä, M.; Mikhaylov, K.; Alves, H.; Paolini, E.; Al-Houran, A. Extending the LoRa Direct-to-Satellite Limits: Doppler Shift Pre-Compensation. IEEE Open J. Commun. Soc. 2025, 6, 2256–2273. [Google Scholar] [CrossRef]
- Subramanian, V.; Karunamurthy, J.V.; Ramachandran, B. Hardware doppler shift emulation and compensation for LoRa LEO satellite communication. In Proceedings of the 2023 International Conference on IT Innovation and Knowledge Discovery (ITIKD), Manama, Bahrain, 8–9 March 2025. [Google Scholar]
- Fraire, J.; Henn, S.; Dovis, F.; Garello, R.; Taricco, G. Sparse satellite constellation design for LoRa-based direct-to-satellite Internet of Things. In Proceedings of the GLOBECOM 2020—2020 IEEE Global Communications Conference, Taipei, Taiwan, 7–11 December 2020. [Google Scholar]
- Reynders, B.; Meert, W.; Pollin, S. Power and spreading factor control in low power wide area networks. In Proceedings of the 2017 IEEE International Conference on Communications, Paris, France, 21–25 May 2017. [Google Scholar]
- Ma, Y.; Ma, R.; Lin, Z.; Zhang, R.; Cai, Y.; Wu, W.; Wang, J. Improving age of information for covert communication with time-modulated arrays. IEEE Internet Things J. 2025, 12, 1718–1731. [Google Scholar] [CrossRef]
- Zhang, G.; Wei, X.; Tan, X.; Han, Z.; Zhang, G. AoI Minimization Based on Deep Reinforcement Learning and Matching Game for IoT Information Collection in SAGIN. IEEE Trans. Commun. 2025; early access. [Google Scholar] [CrossRef]
- GitHub Repository for Lora-Space. Available online: https://github.com/alvarezguido/lora-space (accessed on 1 April 2024).



| SF | Sensitivity Threshold/dBm | ||
|---|---|---|---|
| KHz | KHz | KHz | |
| 7 | −123 | −120 | −117 |
| 8 | −126 | −123 | −120 |
| 9 | −129 | −126 | −123 |
| 10 | −132 | −129 | −126 |
| 11 | −134.5 | −131.5 | −128.5 |
| 12 | −137 | −134 | −131 |
| SF | |||||
|---|---|---|---|---|---|
| 7 | 17.71 | 17.84 | 18.04 | 18.31 | 18.64 |
| 8 | 14.71 | 14.84 | 15.04 | 15.31 | 15.64 |
| 9 | 11.71 | 11.84 | 12.04 | 12.31 | 12.64 |
| 10 | 8.71 | 8.84 | 9.04 | 9.31 | 9.64 |
| 11 | 6.21 | 6.34 | 6.54 | 6.81 | 7.14 |
| 12 | 3.71 | 3.84 | 4.04 | 4.31 | 4.64 |
| Parameters | Meaning | Value |
|---|---|---|
| LEO Satellite Altitude | 1000 | |
| Number of users | [100, 3000] | |
| power | [3, 20] | |
| Packet payload length | 20 | |
| Number of cached packets | 5 | |
| channel count | 3 | |
| skip parameter | 4000 | |
| SF | 7–12 | |
| bandwidth | 125 | |
| frame duration | 30 | |
| Satellite transit time | 360 | |
| carrier frequency | 868 | |
| Number of packets processed simultaneously by the satellite | 16 | |
| Antenna Gain | 12 | |
| Atmospheric losses due to gases, rain, etc. | 0.5 | |
| Additional losses due to feedline | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Peng, H.; Ji, Y.; Hong, T.; Zhang, G. Adaptive Resource Optimization for LoRa-Enabled LEO Satellite IoT System in High-Dynamic Environments. Sensors 2025, 25, 3318. https://doi.org/10.3390/s25113318
Zhang C, Peng H, Ji Y, Hong T, Zhang G. Adaptive Resource Optimization for LoRa-Enabled LEO Satellite IoT System in High-Dynamic Environments. Sensors. 2025; 25(11):3318. https://doi.org/10.3390/s25113318
Chicago/Turabian StyleZhang, Chen, Haoyou Peng, Yonghua Ji, Tao Hong, and Gengxin Zhang. 2025. "Adaptive Resource Optimization for LoRa-Enabled LEO Satellite IoT System in High-Dynamic Environments" Sensors 25, no. 11: 3318. https://doi.org/10.3390/s25113318
APA StyleZhang, C., Peng, H., Ji, Y., Hong, T., & Zhang, G. (2025). Adaptive Resource Optimization for LoRa-Enabled LEO Satellite IoT System in High-Dynamic Environments. Sensors, 25(11), 3318. https://doi.org/10.3390/s25113318






