Improving Generalization in Collision Avoidance for Multiple Unmanned Aerial Vehicles via Causal Representation Learning †
Abstract
1. Introduction
2. Related Work
2.1. Drl-Based UAV Collision Avoidance and Navigation
2.2. Causal Representation Learning
3. Approach
3.1. Definitions of Some Key Notations
3.2. Problem Formulation
3.2.1. Survey of Deep Reinforcement Learning in UAV Collision Avoidance
- denotes the state space, representing all possible configurations of the UAV and its environment.
- represents the action space, consisting of all feasible actions that the UAV can execute.
- is the transition probability function, , which specifies the probability of transitioning to state given the current state s and action a.
- is the reward function, , which assigns a scalar reward for taking action a in state s.
- is the observation space, comprising all possible observations that the UAV can make.
- is the observation function, , which provides the probability of observing o given the true state s.
3.2.2. Observation Space
- I represents the accumulation of four consecutive depth images captured by the UAV’s onboard camera. These images provide spatial information about the environment and obstacles.
- V denotes the current velocity of the UAV, which includes its forward, turning, and climbing velocities.
- G represents the Euclidean distance from the UAV’s current position to the target destination. This information helps the UAV navigate towards the goal.
3.2.3. Action Space
3.2.4. Reward Function
3.2.5. Structural Composition of UAV Control in AirSim
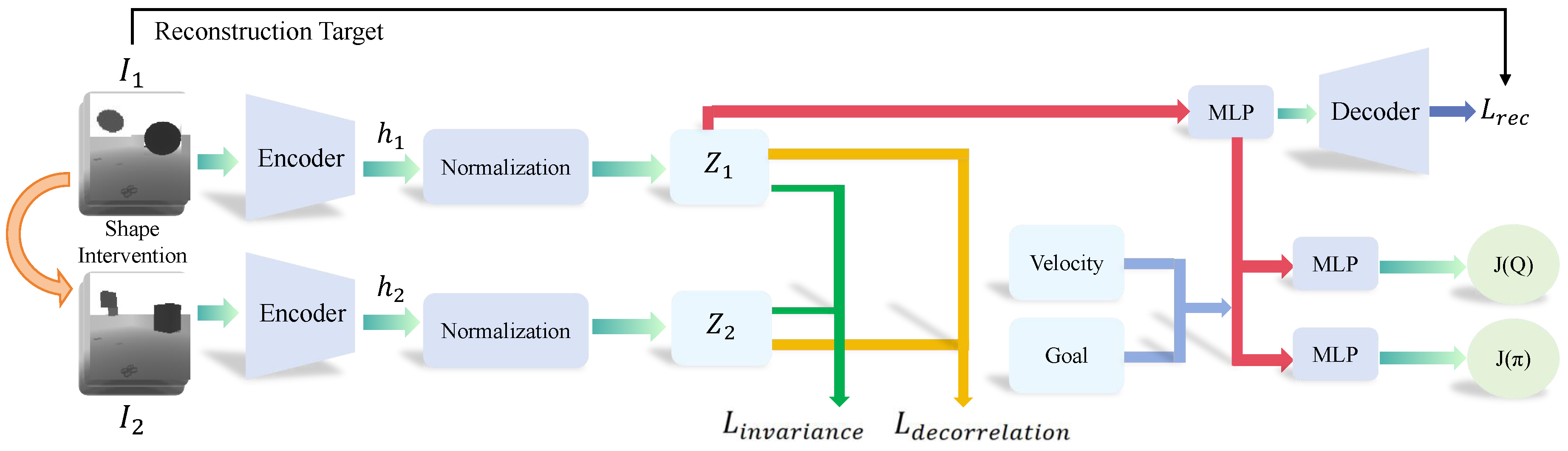
3.3. Architectural Overview
3.4. Extract Invariant Causal Representation
| Algorithm 1 Causal representation learning process. |
| Require: Training environments 1: for each training iteration do 2: Sample batch from training experience // Gather diverse states before intervention 3: Apply shape intervention: // Online causal intervention 4: Encode representations: 5: Compute invariance loss: // Representation invariance enforcement 6: Compute decorrelation loss: // Dimensional decorrelation 7: Compute total representation loss: 8: Update encoder: 9: Train policy network with 10: end for |
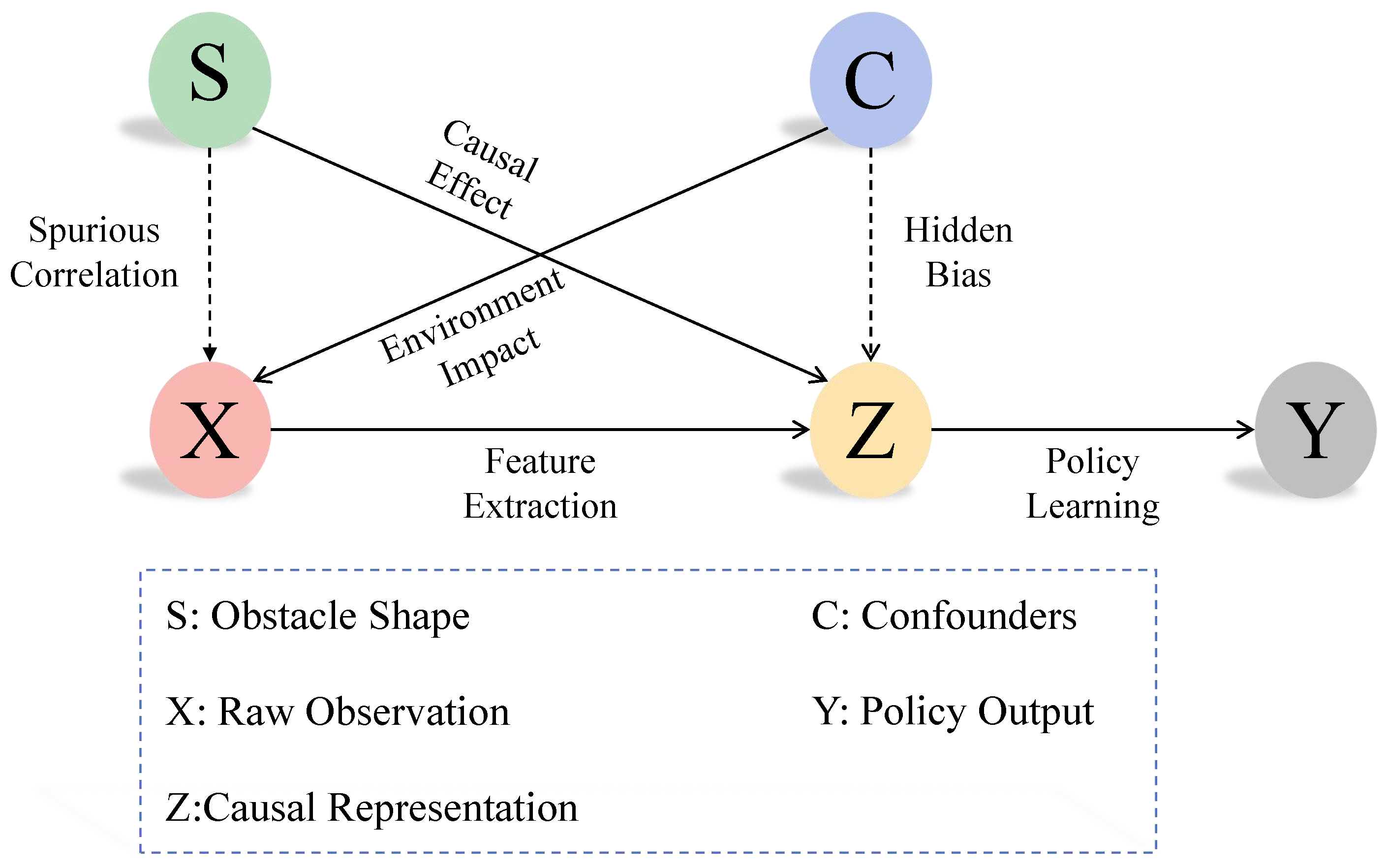
3.5. Causal Identifiability Analysis
- Instance-wise normalization (Equation (9)), removing environment-specific statistics.
- Intervention-invariant representation learning (Equation (10)), enforcing minimization across environments under the same intervention.
4. Results
4.1. Simulation Environment and Experimental Setup
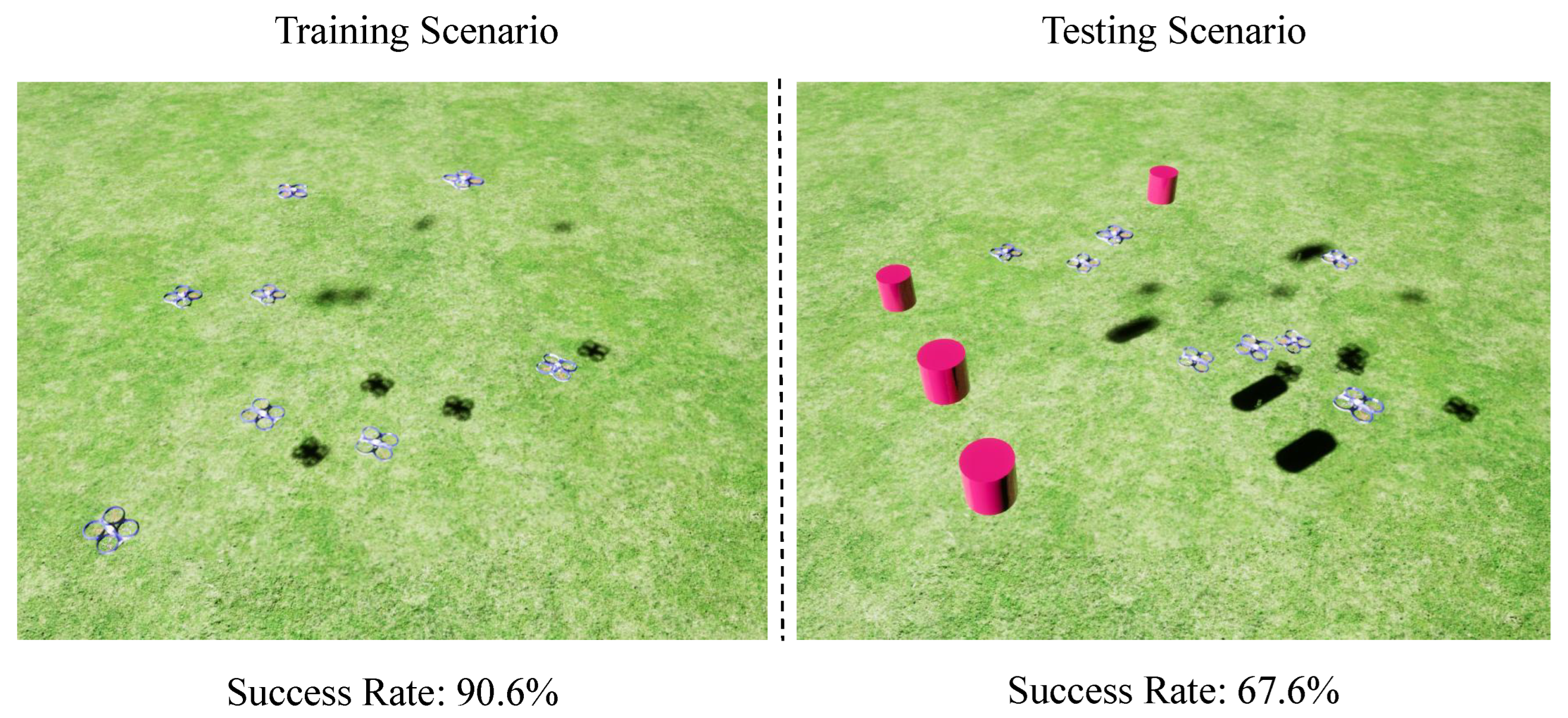
4.2. Evaluation Metrics and Experimental Scenarios
- Success Rate: This metric quantifies the proportion of UAVs that successfully reach their destinations within a predefined time interval, devoid of any collisions.
- Excess Distance: This denotes the supplementary distance traversed by UAVs beyond the direct linear distance between the origin and the target destination.
- Success-weighted Path Length (SPL): This metric amalgamates the success rate with the efficiency of the navigated path, offering a holistic assessment of task accomplishment and path efficacy.
- Average Velocity: This is computed as the quotient of the aggregate flight path length and the time elapsed for the UAV.
4.3. Performance Comparison
4.3.1. Evaluation Obstacle Shapes
4.3.2. Evaluation Under Variable Weather Conditions
4.3.3. More Evaluation Baselines
4.3.4. Ablation Experiment
4.3.5. Scalability Analysis
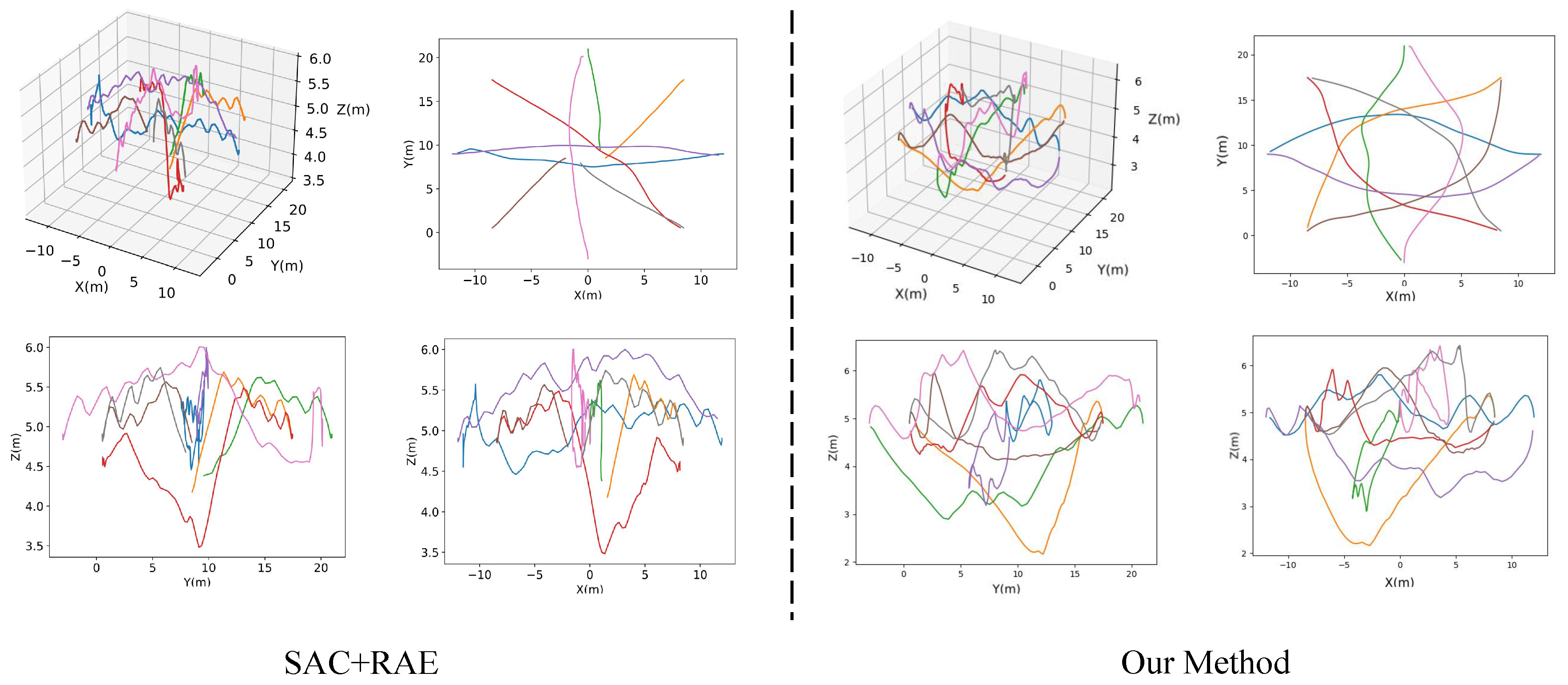
4.4. Visualization of Trajectory
5. Conclusions
6. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| UAV | unmanned aerial vehicle |
| SLAM | simultaneous localization and mapping |
| DRL | deep reinforcement learning |
| RAE | regularized autoencoder |
| CRL | causal representation learning |
References
- Burgués, J.; Marco, S. Environmental chemical sensing using small drones: A review. Sci. Total Environ. 2020, 748, 141172. [Google Scholar] [CrossRef] [PubMed]
- Delmerico, J.; Mintchev, S.; Giusti, A.; Gromov, B.; Melo, K.; Horvat, T.; Cadena, C.; Hutter, M.; Ijspeert, A.; Floreano, D.; et al. The current state and future outlook of rescue robotics. J. Field Robot. 2019, 36, 1171–1191. [Google Scholar] [CrossRef]
- Khan, A.; Gupta, S.; Gupta, S.K. Emerging UAV technology for disaster detection, mitigation, response, and preparedness. J. Field Robot. 2022, 39, 905–955. [Google Scholar] [CrossRef]
- Betti Sorbelli, F. UAV-based delivery systems: A systematic review, current trends, and research challenges. J. Auton. Transp. Syst. 2024, 1, 1–40. [Google Scholar] [CrossRef]
- Tsouros, D.C.; Bibi, S.; Sarigiannidis, P.G. A review on UAV-based applications for precision agriculture. Information 2019, 10, 349. [Google Scholar] [CrossRef]
- Zhuang, L.; Zhong, X.; Xu, L.; Tian, C.; Yu, W. Visual SLAM for unmanned aerial vehicles: Localization and perception. Sensors 2024, 24, 2980. [Google Scholar] [CrossRef] [PubMed]
- Sonugür, G. A Review of quadrotor UAV: Control and SLAM methodologies ranging from conventional to innovative approaches. Robot. Auton. Syst. 2023, 161, 104342. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, H.; Wang, C.; Wang, Y.; Wang, S.; Yang, Z. An improved RANSAC-ICP method for registration of SLAM and UAV-LiDAR point cloud at plot scale. Forests 2024, 15, 893. [Google Scholar] [CrossRef]
- Junior, F.L.; Moreira, L.A.; Moreira, E.M.; Baldivieso, T.J.; Brunaes, M.S.; Rosa, P.F. UAV path automation using visual waypoints acquired from the ground. In Proceedings of the 2020 IEEE 29th International Symposium on Industrial Electronics (ISIE), Delft, The Netherlands, 17–19 June 2020. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Wang, C.; Wang, J.; Shen, Y.; Zhang, X. Autonomous navigation of UAVs in large-scale complex environments: A deep reinforcement learning approach. IEEE Trans. Veh. Technol. 2019, 68, 2124–2136. [Google Scholar] [CrossRef]
- Hu, K.; Li, H.; Zhuang, J.; Hao, Z.; Fan, Z. Efficient focus autoencoders for fast autonomous flight in intricate wild scenarios. Drones 2023, 7, 609. [Google Scholar] [CrossRef]
- Huang, H.; Zhu, G.; Fan, Z.; Zhai, H.; Cai, Y.; Shi, Z.; Dong, Z.; Hao, Z. Vision-based distributed multi-UAV collision avoidance via deep reinforcement learning for navigation. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022. [Google Scholar]
- Fan, Z.; Xia, Z.; Lin, C.; Han, G.; Li, W.; Wang, D.; Chen, Y.; Hao, Z.; Cai, R.; Zhuang, J. UAV Collision Avoidance in Unknown Scenarios with Causal Representation Disentanglement. Drones 2024, 9, 10. [Google Scholar] [CrossRef]
- Zhuang, J.; Han, G.; Xia, Z.; Wang, B.; Li, W.; Wang, D.; Hao, Z.; Cai, R.; Fan, Z. Robust policy learning for multi-uav collision avoidance with causal feature selection. arXiv 2024, arXiv:2407.04056. [Google Scholar]
- Brehmer, J.; De Haan, P.; Lippe, P.; Cohen, T.S. Weakly supervised causal representation learning. Adv. Neural Inf. Process. Syst. 2022, 35, 38319–38331. [Google Scholar]
- Han, G.; Wu, Q.; Wang, B.; Lin, C.; Zhuang, J.; Li, W.; Hao, Z.; Fan, Z. Deep Reinforcement Learning Based Multi-UAV Collision Avoidance with Causal Representation Learning. In Proceedings of the 2024 10th International Conference on Big Data and Information Analytics (BigDIA), Chiang Mai, Thailand, 25–28 October 2024; pp. 833–839. [Google Scholar] [CrossRef]
- Çetin, E.; Barrado, C.; Muñoz, G.; Macias, M.; Pastor, E. Drone Navigation and Avoidance of Obstacles Through Deep Reinforcement Learning. In Proceedings of the 2019 IEEE/AIAA 38th Digital Avionics Systems Conference (DASC), San Diego, CA, USA, 8–12 September 2019; pp. 1–7. [Google Scholar] [CrossRef]
- Ouahouah, S.; Bagaa, M.; Prados-Garzon, J.; Taleb, T. Deep-reinforcement-learning-based collision avoidance in UAV environment. IEEE Internet Things J. 2021, 9, 4015–4030. [Google Scholar] [CrossRef]
- Shin, S.Y.; Kang, Y.W.; Kim, Y.G. Obstacle avoidance drone by deep reinforcement learning and its racing with human pilot. Appl. Sci. 2019, 9, 5571. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, K.; Liu, D.; Song, H. Autonomous UAV Navigation in Dynamic Environments with Double Deep Q-Networks. In Proceedings of the 2020 AIAA/IEEE 39th Digital Avionics Systems Conference (DASC), San Antonio, TX, USA, 11–15 October 2020; pp. 1–7. [Google Scholar] [CrossRef]
- Yu, Y.; Liu, Y.; Wang, J.; Noguchi, N.; He, Y. Obstacle avoidance method based on double DQN for agricultural robots. Comput. Electron. Agric. 2023, 204, 107546. [Google Scholar] [CrossRef]
- Chikhaoui, K.; Ghazzai, H.; Massoud, Y. PPO-based reinforcement learning for UAV navigation in urban environments. In Proceedings of the 2022 IEEE 65th International Midwest Symposium on Circuits and Systems (MWSCAS), Fukuoka, Japan, 7–10 August 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–4. [Google Scholar]
- Liang, C.; Liu, L.; Liu, C. Multi-UAV autonomous collision avoidance based on PPO-GIC algorithm with CNN–LSTM fusion network. Neural Netw. 2023, 162, 21–33. [Google Scholar] [CrossRef] [PubMed]
- Bouhamed, O.; Ghazzai, H.; Besbes, H.; Massoud, Y. Autonomous UAV Navigation: A DDPG-Based Deep Reinforcement Learning Approach. In Proceedings of the 2020 IEEE International Symposium on Circuits and Systems (ISCAS), Sevilla, Spain, 10–12 October 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Yang, M.; Liu, F.; Chen, Z.; Shen, X.; Hao, J.; Wang, J. Causalvae: Disentangled representation learning via neural structural causal models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021. [Google Scholar]
- Zhang, K.; Xie, S.; Ng, I.; Zheng, Y. Causal representation learning from multiple distributions: A general setting. arXiv 2024, arXiv:2402.05052. [Google Scholar]
- Zhao, W.; Tang, D.; Chen, X.; Lv, D.; Ou, D.; Li, B.; Jiang, P.; Gai, K. Disentangled causal embedding with contrastive learning for recommender system. In Proceedings of the Companion Proceedings of the ACM Web Conference 2023, Austin, TX, USA, 30 April–4 May 2023. [Google Scholar]
- Shah, S.; Dey, D.; Lovett, C.; Kapoor, A. Airsim: High-fidelity visual and physical simulation for autonomous vehicles. In Proceedings of the Field and Service Robotics: Results of the 11th International Conference, Zurich, Switzerland, 12–16 June 2017. [Google Scholar]
- Zhang, K.; Gong, M.; Schölkopf, B. Multi-source domain adaptation: A causal view. In Proceedings of the AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015. [Google Scholar]
- Ji, Q.; Li, J.; Hu, J.; Wang, R.; Zheng, C.; Xu, F. Rethinking dimensional rationale in graph contrastive learning from causal perspective. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024. [Google Scholar]
- Hansen, N.; Wang, X. Generalization in reinforcement learning by soft data augmentation. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021. [Google Scholar]
- Raileanu, R.; Goldstein, M.; Yarats, D.; Kostrikov, I.; Fergus, R. Automatic data augmentation for generalization in reinforcement learning. Adv. Neural Inf. Process. Syst. 2021, 34, 5402–5415. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]





| Notations | Definitions |
|---|---|
| S | State space in POMDP |
| A | Action space in POMDP |
| Transition probability function in POMDP | |
| Reward function in POMDP | |
| Observation space in POMDP | |
| Observation function in POMDP | |
| UAV’s observation space, | |
| I | Accumulation of four consecutive depth images (part of ) |
| V | Current velocity of the UAV (part of ) |
| G | Euclidean distance to the target destination (part of ) |
| a | Action vector, |
| Commanded forward velocity | |
| Commanded lateral velocity | |
| Commanded angular velocity | |
| Depth images of UAVs and original obstacles | |
| Depth images of UAVs and obstacles with modified shapes (after intervention) | |
| Normalized latent representations from , respectively, | |
| Invariance loss, | |
| Decorrelation loss to ensure different dimensions capture different information | |
| Reconstruction loss for the autoencoder |
| Controller Type | |||
|---|---|---|---|
| Linear-velocity control | 0.2 | 2.0 | 0.0 |
| Angular-velocity control | 0.25 | 0.0 | 0.0 |
| Item | Parameter |
|---|---|
| Weight | 0.8 kg |
| Number of rotors | 4 |
| Minimum motor thrust | 0 |
| Maximum motor thrust | 1 |
| Minimum tilt throttle | 0.05 |
| Maximum angular velocity | 2.5 rad/s |
| Dimensions (m) | 0.2413 × 0.1143 × 0.0762 |
| Parameter Name | Value |
|---|---|
| Batch size | 128 |
| Max episodes | 150 |
| Update times | 400 |
| Replay buffer capacity | 20,000 |
| Discount | 0.99 |
| Learning Rate | |
| Critic’s target update frequency | 2 |
| Critic’s Q-function soft-update rate | 0.01 |
| Critic’s encoder soft-update rate | 0.05 |
| Actor’s update frequency | 2 |
| Actor’s log stddev bounds | [−10, 2] |
| Optimizer | Adam |
| Obstacle Shape | Unseen/Seen | Method | Success Rate (%) | SPL (%) | Extra Distance (m) | Average Velocity (m/s) |
|---|---|---|---|---|---|---|
| Cube | Seen | SAC + RAE Our method | 67.6 74.4 (↑ 6.8) | 58.3 62.5 (↑ 4.2) | 1.483/1.436 1.542/1.519 | 0.771/0.158 0.806/0.125 |
| Sphere | Seen | SAC + RAE Our method | 68.3 73.4 (↑ 5.1) | 58.4 62.2 (↑ 3.8) | 1.680/1.709 1.735/1.718 | 0.783/0.160 0.814/0.132 |
| Triangle | Unseen | SAC + RAE Our method | 72.5 76.3 (↑ 3.8) | 62.1 64.4 (↑ 2.3) | 1.535/1.622 1.815/1.802 | 0.775/0.164 0.809/0.135 |
| Cylinder | Unseen | SAC + RAE Our method | 67.6 72.1 (↑ 4.5) | 58.6 61.7 (↑ 3.1) | 1.646/1.621 1.853/1.810 | 0.783/0.155 0.810/0.138 |
| Pentahedron | Unseen | SAC + RAE Our method | 67.3 73.8 (↑ 6.5) | 56.7 61.8 (↑ 5.1) | 1.575/1.546 1.651/1.623 | 0.784/0.153 0.813/0.130 |
| Cuboid | Unseen | SAC + RAE Our method | 68.2 74.4 (↑ 6.2) | 59.3 63.0 (↑ 3.7) | 1.635/1.578 1.851/1.820 | 0.799/0.131 0.803/0.136 |
| Mixed | Unseen | SAC + RAE Our method | 67.1 74.2 (↑ 7.1) | 60.4 62.9 (↑ 2.5) | 1.646/1.601 1.858/1.826 | 0.801/0.129 0.805/0.131 |
| Weather Type | Unseen/Seen | Method | Success Rate (%) | SPL (%) | Extra Distance (m) | Average Velocity (m/s) |
|---|---|---|---|---|---|---|
| Rain | Seen | SAC + RAE Our method | 63.6 69.5 (↑ 5.9) | 51.2 54.3 (↑ 3.1) | 2.653/3.143 2.163/3.785 | 0.424/0.137 0.374/0.115 |
| Snow | Unseen | SAC + RAE Our method | 61.8 71.2 (↑ 9.4) | 51.1 56.4 (↑ 5.3) | 2.699/2.685 2.432/3.773 | 0.406/0.131 0.385/0.112 |
| Dust | Unseen | SAC + RAE Our method | 59.8 8.1 (↑ 8.3) | 51.7 58.1 (↑ 6.4) | 3.124/2.620 2.399/4.079 | 0.371/0.131 0.381/0.109 |
| Fog | Unseen | SAC + RAE Our method | 57.9 69.5 (↑ 11.6) | 49.8 59.7 (↑ 9.9) | 2.965/2.545 2.447/4.786 | 0.387/0.134 0.379/0.124 |
| Method | Success Rate (%) | SPL (%) | Extra Distance (m) | Average Velocity (m/s) |
|---|---|---|---|---|
| SAC + RAE | 68.2 | 59.3 | 1.635/1.578 | 0.799/0.131 |
| + AutoAugment [32] | 68.8 | 61.2 | 1.505/2.881 | 0.398/0.131 |
| + DrAC [33] | 69.8 | 61.5 | 1.538/2.693 | 0.379/0.122 |
| + SE [34] | 70.1 | 61.6 | 1.564/2.648 | 0.377/0.122 |
| + Our method | 74.4 | 62.5 | 1.542/1.519 | 0.860/0.125 |
| Success Rate(%) | SPL(%) | Extra Distance (m) | Average Velocity (m/s) | ||
|---|---|---|---|---|---|
| 68.2 | 59.3 | 1.635/1.578 | 0.799/0.131 | ||
| ✓ | 69.6 | 60.1 | 1.584/1.539 | 0.814/0.129 | |
| ✓ | 70.3 | 60.4 | 1.603/1.554 | 0.821/0.122 | |
| ✓ | ✓ | 74.4 | 62.5 | 1.542/1.519 | 0.860/0.125 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, C.; Han, G.; Wu, Q.; Wang, B.; Zhuang, J.; Li, W.; Hao, Z.; Fan, Z. Improving Generalization in Collision Avoidance for Multiple Unmanned Aerial Vehicles via Causal Representation Learning. Sensors 2025, 25, 3303. https://doi.org/10.3390/s25113303
Lin C, Han G, Wu Q, Wang B, Zhuang J, Li W, Hao Z, Fan Z. Improving Generalization in Collision Avoidance for Multiple Unmanned Aerial Vehicles via Causal Representation Learning. Sensors. 2025; 25(11):3303. https://doi.org/10.3390/s25113303
Chicago/Turabian StyleLin, Che, Gaofei Han, Qingling Wu, Boxi Wang, Jiafan Zhuang, Wenji Li, Zhifeng Hao, and Zhun Fan. 2025. "Improving Generalization in Collision Avoidance for Multiple Unmanned Aerial Vehicles via Causal Representation Learning" Sensors 25, no. 11: 3303. https://doi.org/10.3390/s25113303
APA StyleLin, C., Han, G., Wu, Q., Wang, B., Zhuang, J., Li, W., Hao, Z., & Fan, Z. (2025). Improving Generalization in Collision Avoidance for Multiple Unmanned Aerial Vehicles via Causal Representation Learning. Sensors, 25(11), 3303. https://doi.org/10.3390/s25113303






