Efficient Markerless Motion Classification Using Radar
Abstract
Highlights
- A novel markerless motion-classification method that uses radar micro-Doppler features achieves nearly 100% classification accuracy with a compact feature set.
- The method uses cross-correlation between radar signals and basis functions derived from 3D motion-capture data, then applies PCA dimensionality reduction and nearest-neighbor classification.
- The proposed method enables accurate classification of human motion without markers, and thereby ensures privacy and reduces the cost compared to traditional motion-capture systems.
- The approach is accurate across varying SNR conditions, and is therefore suitable for real-world applications such as healthcare monitoring and sports analytics.
Abstract
1. Introduction
2. Signal Modeling and Proposed Method
2.1. Overview
2.2. Signal Modeling and the Proposed Feature
2.3. Limitations in Determining Scatterer Amplitude and the Proposed Method
2.4. Data Compression Using Principal Component Analysis and Classification Using a Simple Classifier
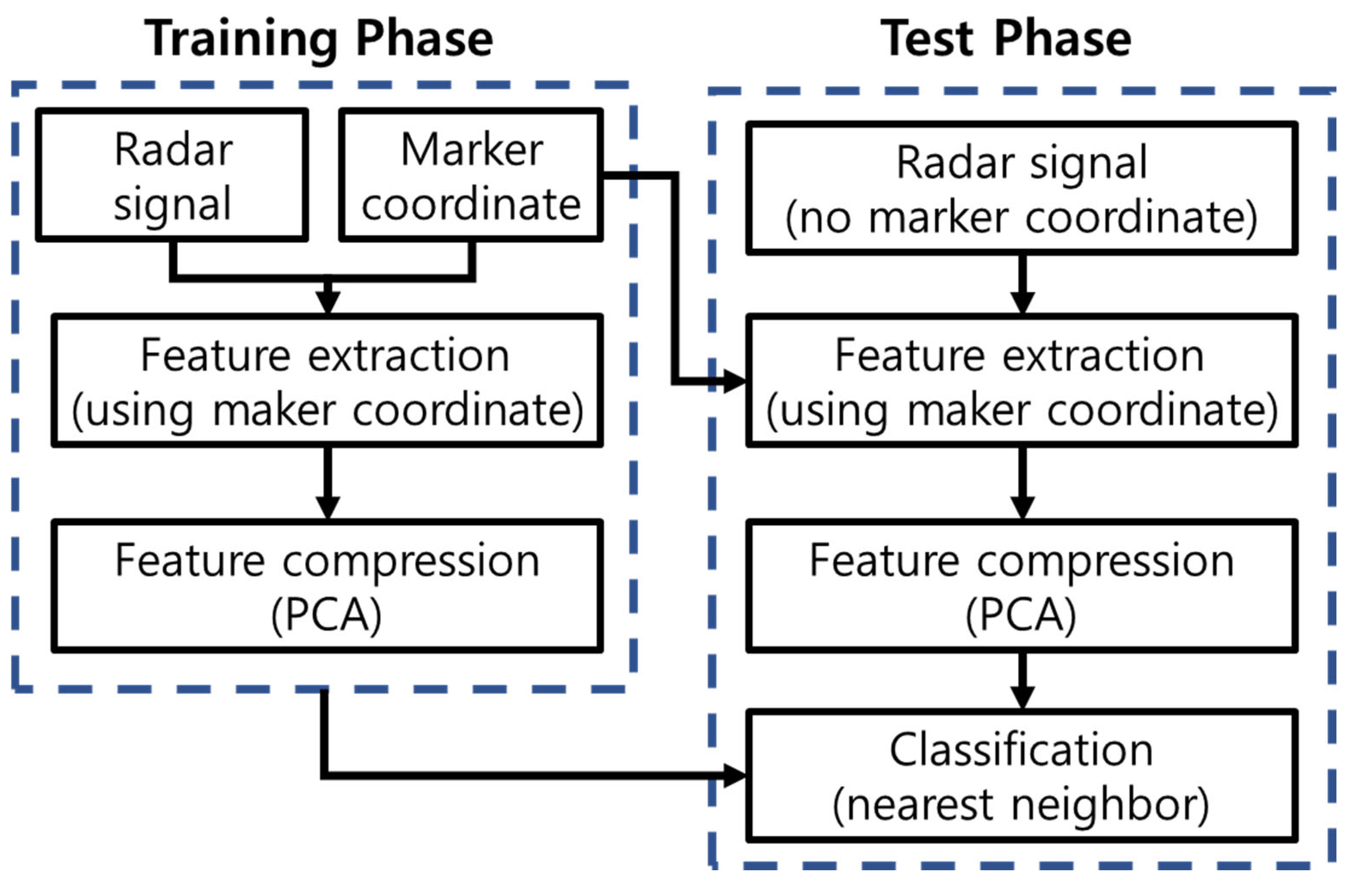
2.5. Overall Procedure
- Data collection: For each of the P MMs, collect Q radar signals and Q × Nc marker coordinates;
- Signal construction: Using the marker coordinates, construct bk(t) as defined in (6);
- Feature vector construction: For each radar signal, construct an Nc × 1 feature vector using the maximum correlation, as described in (11) and formatted in (12);
- Training database construction: Construct the training database F as defined in (13);
- Normalization: Normalize the feature vector in F using the maximum and minimum feature values, as described in (15);
- Compression: Compress the normalized feature vector using PCA;
- Test motion processing: For any randomly selected test motion, repeat steps (1)–(3) and (5)–(6). In this step, the marker coordinates from the training database are used to construct the test feature; (11) is applied to the measured test signal;
- Classification: Classify the motion using a simple nearest neighbor classifier.
3. Experimental Conditions
3.1. Participants
3.2. Motions and Camera System to Extract Marker Information
3.3. Radar and Classification Parameters
4. Classification Results
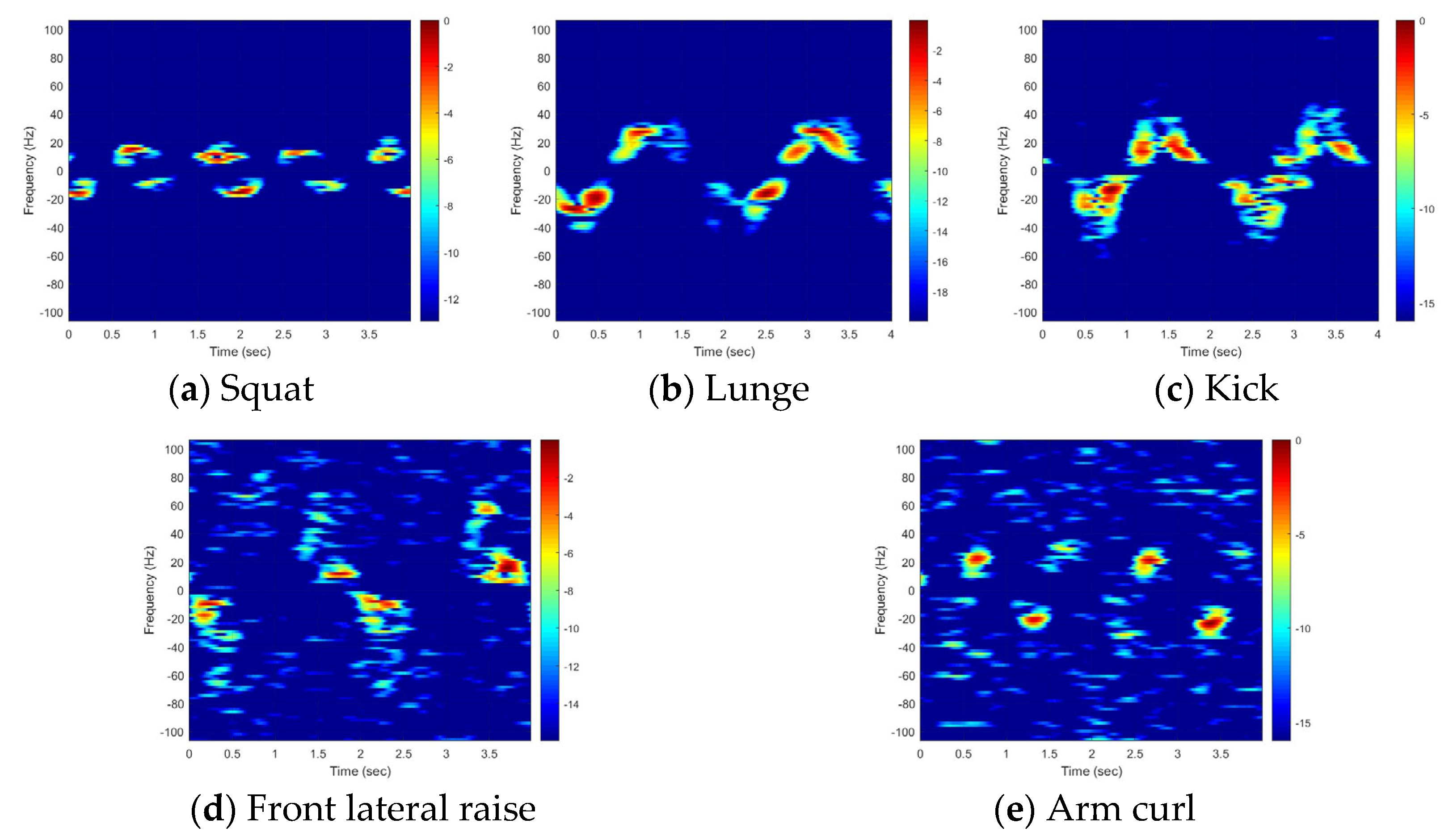
4.1. Analysis of MMs for Each Motion
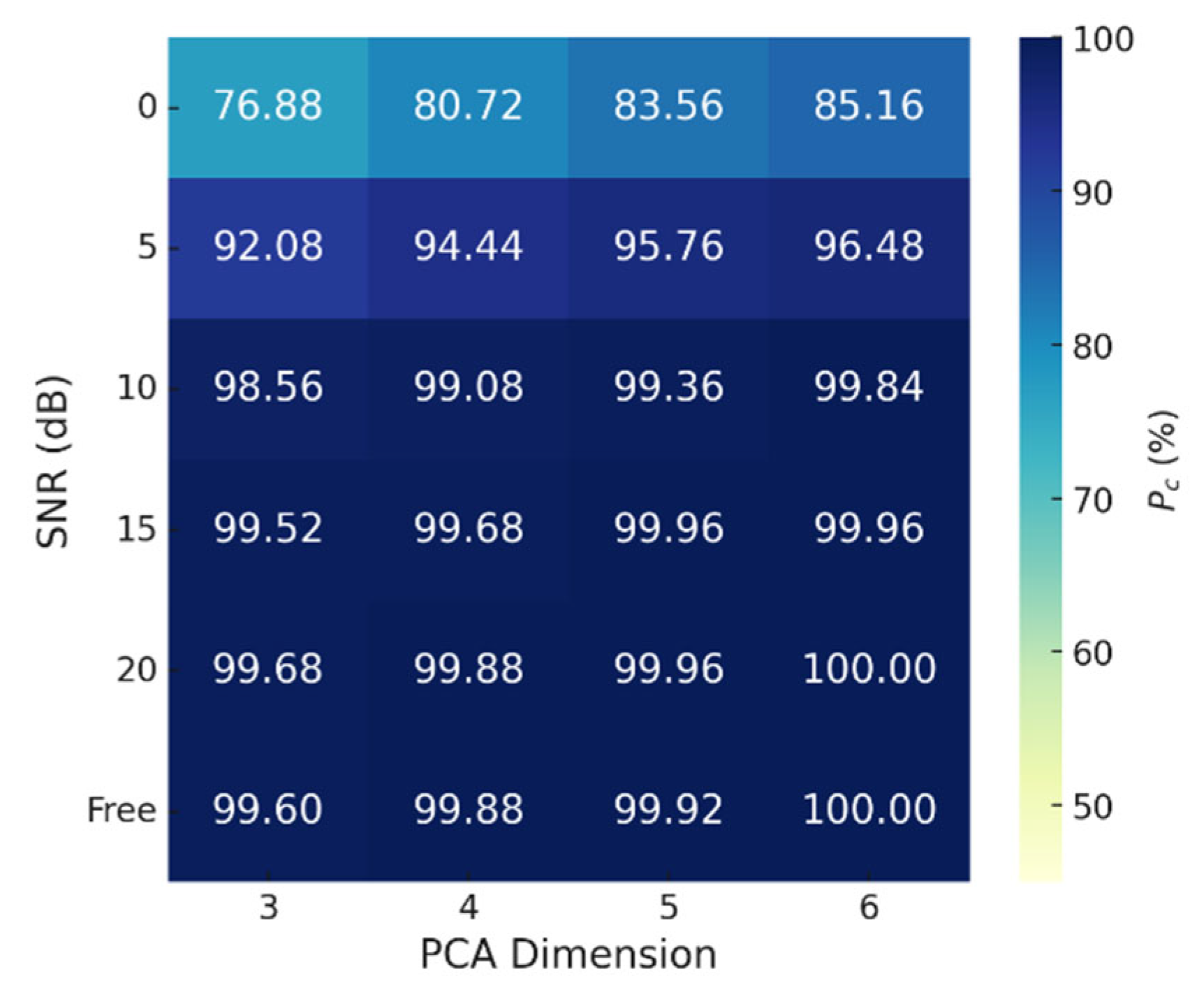
4.2. Classification Result for Various SNRs and Analysis on the Effect of PCA Dimensions
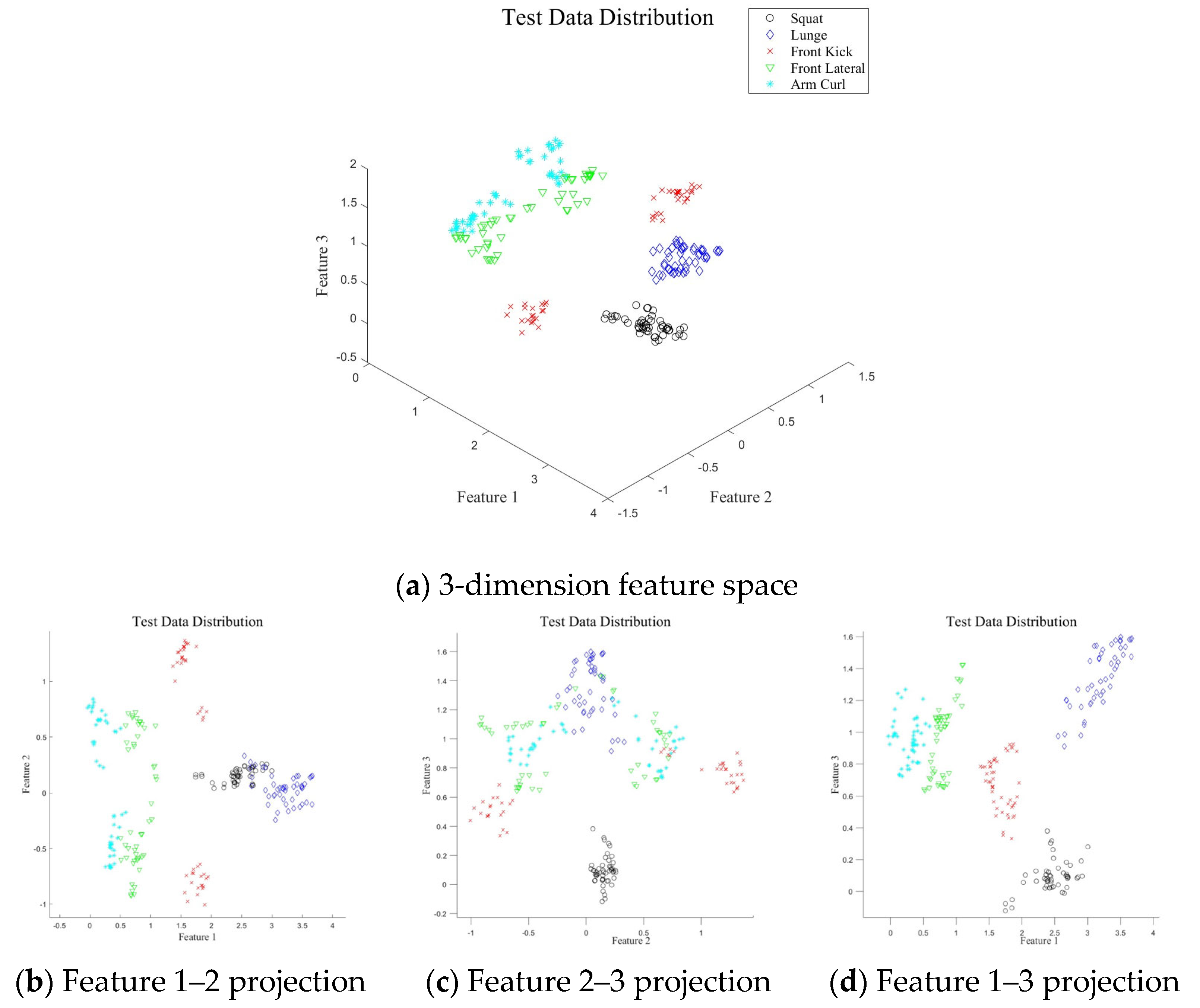
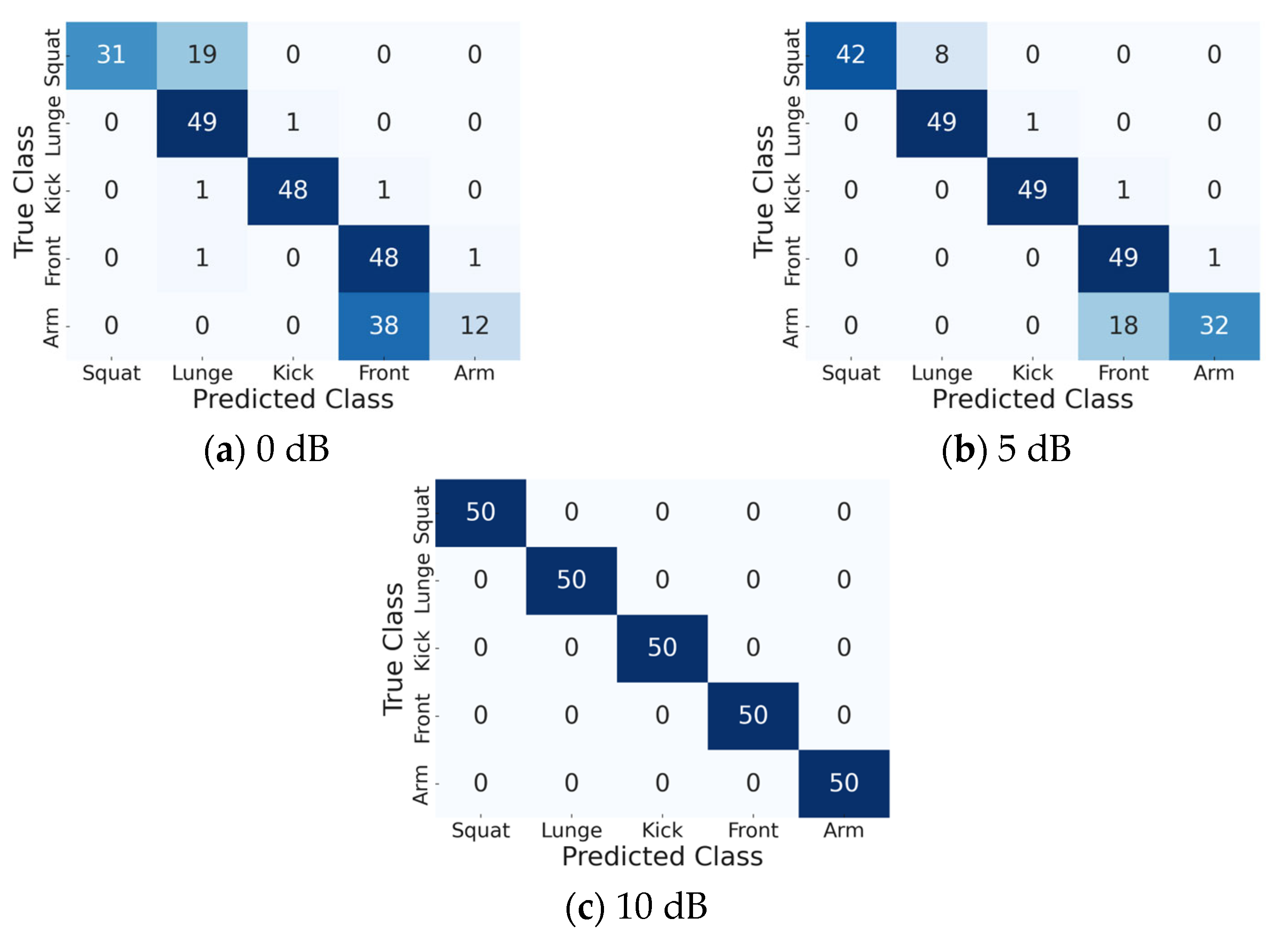
4.3. Analysis of the Classification Accuracy of Each Motion
4.4. Analysis of the Training Database
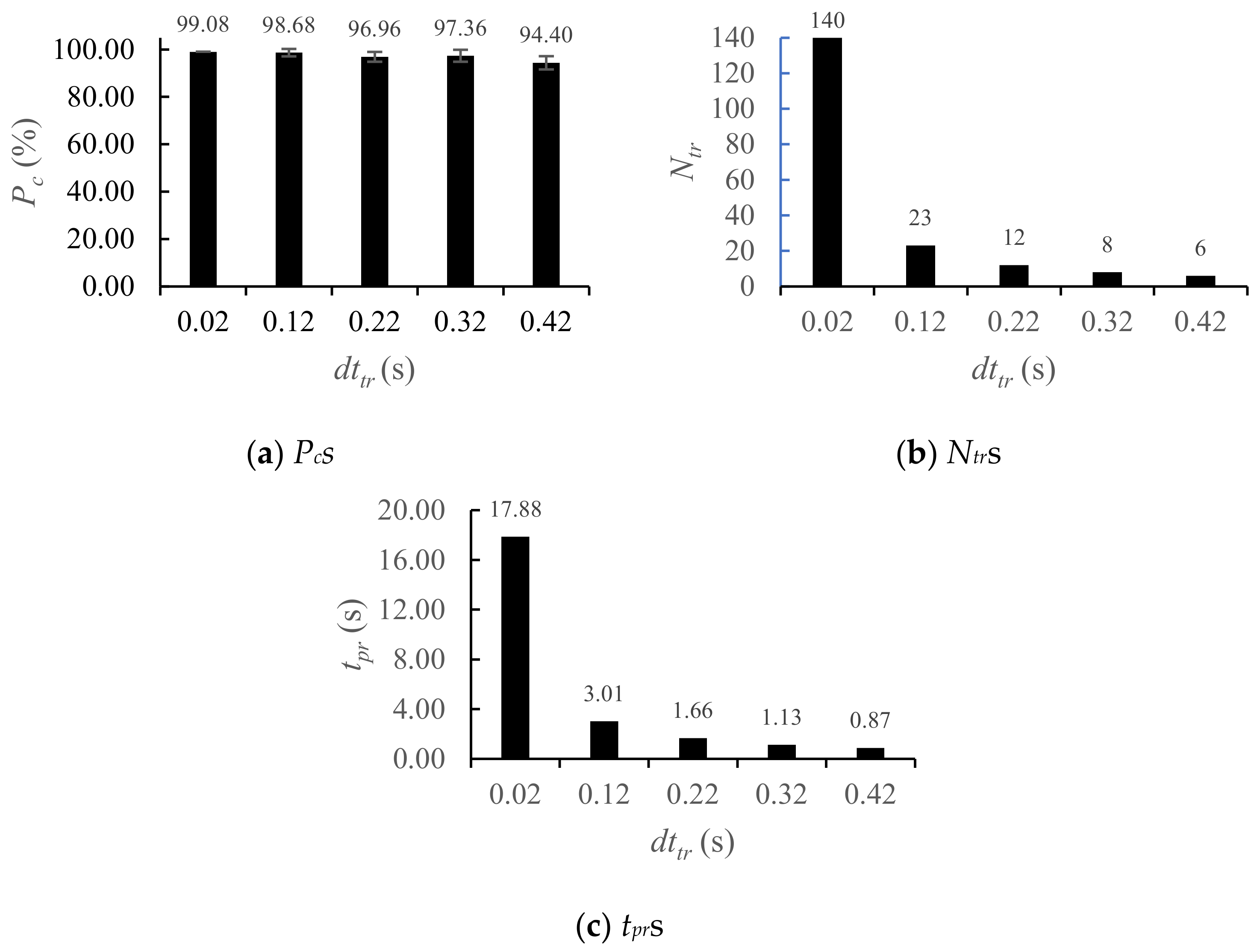
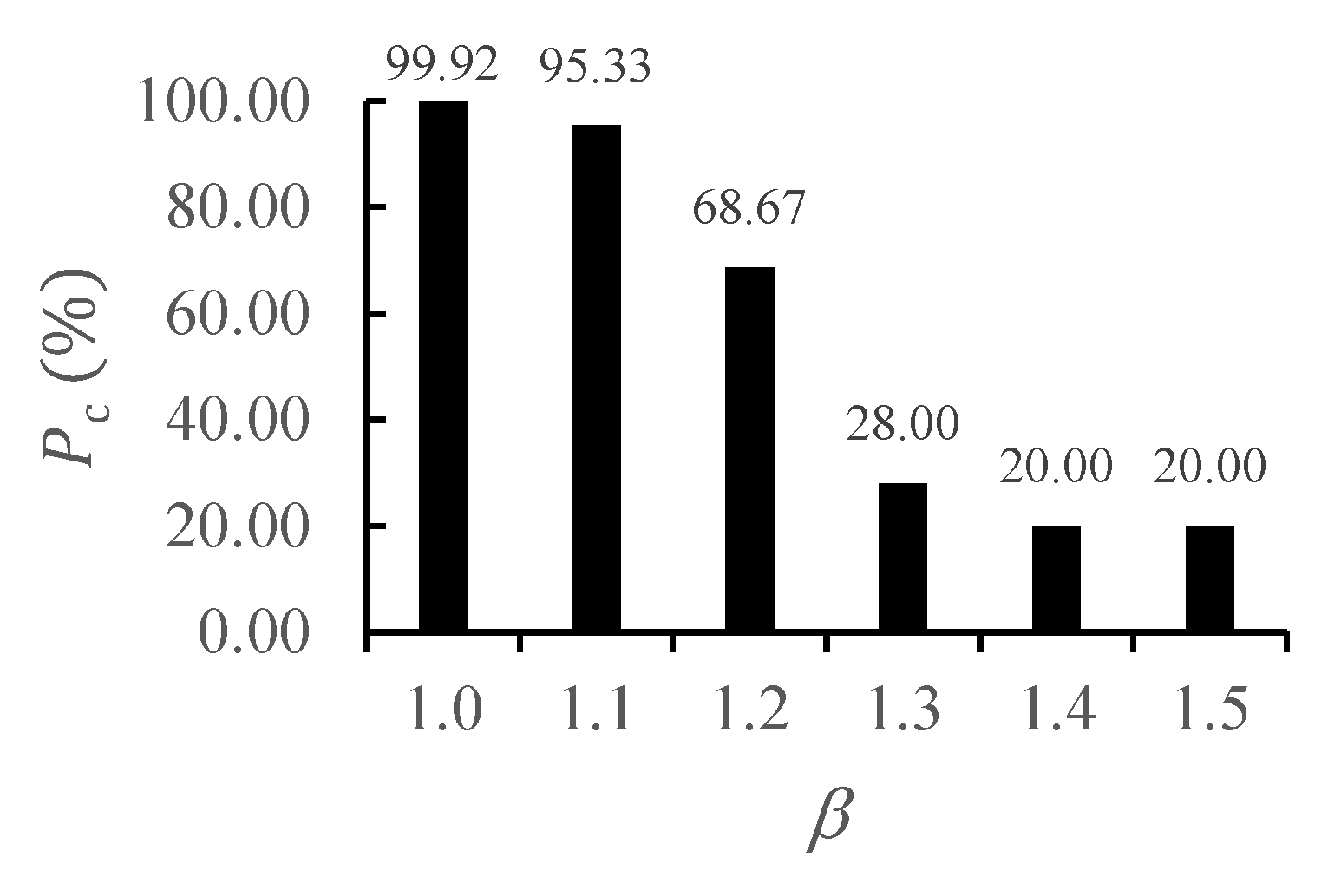
4.4.1. Effect of dttr in the Training Database
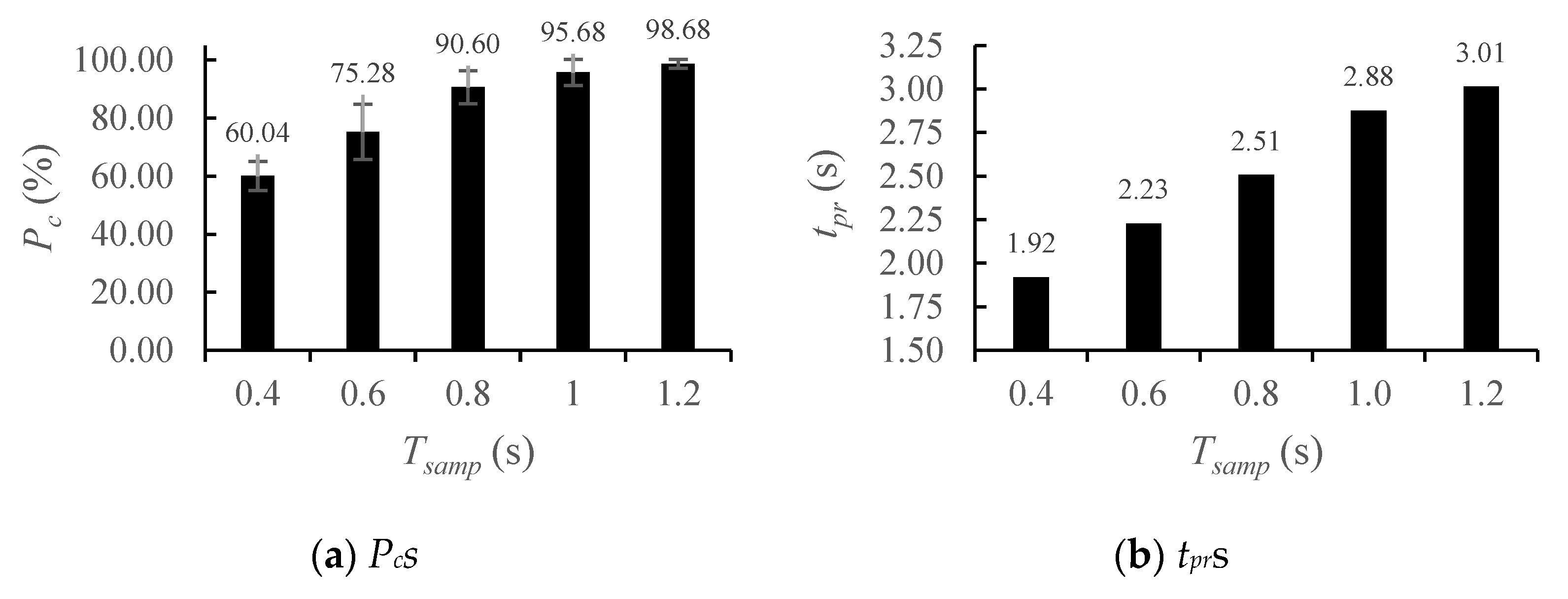
4.4.2. Effect of Tsamp
4.5. Limitations of the Proposed Method and the Solution
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Poppe, R. Vision-Based Human Motion Analysis: An Overview. Comput. Vis. Image Underst. 2007, 108, 4–18. [Google Scholar] [CrossRef]
- Bleser, G.; Taetz, B.; Miezal, M.; Christmann, C.A.; Steffen, D.; Regenspurger, K. Development of an Inertial Motion Capture System for Clinical Application: Potentials and Challenges from the Technology and Application Perspectives. I-Com 2017, 16, 113–129. [Google Scholar] [CrossRef]
- Salim, M.S.; Lim, H.N.; Salim, M.; Baharuddin, M.Y. Motion Analysis of Arm Movement during Badminton Smash. In Proceedings of the IEEE EMBS Conference on Biomedical Engineering and Sciences (IECBES), Kuala Lumpur, Malaysia, 30 November–2 December 2010; pp. 111–114. [Google Scholar]
- Karatzas, N.; Abdelnour, P.; Corban, J.P.A.H.; Zhao, K.Y.; Veilleux, L.; Bergeron, S.G.; Fevens, T.; Rivaz, H.; Babouras, A.; Martineau, P.A. Comparing a Portable Motion Analysis System Against the Gold Standard for Potential Anterior Cruciate Ligament Injury Prevention and Screening. Sensors 2024, 24, 1970. [Google Scholar] [CrossRef] [PubMed]
- Pagnon, D.; Domalain, M.; Reveret, L. Pose2Sim: An End-to-End Workflow for 3D Markerless Sports Kinematics—Part 1: Robustness. Sensors 2021, 21, 6530. [Google Scholar] [CrossRef] [PubMed]
- Seifert, A.; Grimmer, M.; Zoubir, A.M. Doppler Radar for the Extraction of Biomechanical Parameters in Gait Analysis. IEEE J. Biomed. Health Inform. 2020, 25, 547–558. [Google Scholar] [CrossRef] [PubMed]
- Hadjipanayi, C.; Yin, M.; Bannon, A.; Rapeaux, A.; Banger, M.; Haar, S.; Constandinou, T.G. Remote Gait Analysis Using Ultra-Wideband Radar Technology Based on Joint Range-Doppler-Time Representation. IEEE Trans. Biomed. Eng. 2024, 71, 234–245. [Google Scholar] [CrossRef]
- LaHaie, I.J. Overview of an Image-Based Technique for Predicting Far-Field Radar Cross Section from Near-Field Measurements. IEEE Antennas Propag. Mag. 2003, 45, 159–169. [Google Scholar] [CrossRef]
- Sheeny, M.; De Pellegrin, E.; Mukherjee, S.; Ahrabian, A.; Wang, S.; Wallace, A. Radiate: A Radar Dataset for Automotive Perception in Bad Weather. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; IEEE: New York, NY, USA; pp. 1–7. [Google Scholar]
- Chen, V.C.; Li, F.; Ho, S.; Wechsler, H. Micro-Doppler Effect in Radar: Phenomenon, Model, and Simulation Study. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 2–21. [Google Scholar] [CrossRef]
- Kim, Y.; Ling, H. Human Activity Classification Based on Micro-Doppler Signatures Using a Support Vector Machine. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1328–1337. [Google Scholar]
- Jia, Y.; Guo, Y.; Wang, G.; Song, R.; Cui, G.; Zhong, X. Multi-Frequency and Multi-Domain Human Activity Recognition Based on SFCW Radar Using Deep Learning. Neurocomputing 2021, 444, 274–287. [Google Scholar] [CrossRef]
- Deng, F.; Pu, S.; Chen, X.; Shi, Y.; Yuan, T.; Pu, S. Hyperspectral Image Classification with Capsule Network Using Limited Training Samples. Sensors 2018, 18, 3153. [Google Scholar] [CrossRef] [PubMed]
- Lin, Z.; Ji, K.; Kang, M.; Leng, X.; Zou, H. Deep Convolutional Highway Unit Network for SAR Target Classification with Limited Labeled Training Data. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1091–1095. [Google Scholar] [CrossRef]
- Tian, S.; Wang, C.; Zhang, H.; Bhanu, B. SAR Object Classification Using the DAE with a Modified Triplet Restriction. IET Radar Sonar Navig. 2019, 13, 1081–1091. [Google Scholar] [CrossRef]
- Davari, A.; Özkan, H.C.; Maier, A.; Riess, C. Fast and Efficient Limited Data Hyperspectral Remote Sensing Image Classification via GMM-Based Synthetic Samples. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2107–2120. [Google Scholar] [CrossRef]
- Erol, B.; Gurbuz, S.Z.; Amin, M.G. Motion Classification Using Kinematically Sifted Acgan-Synthesized Radar Micro-Doppler Signatures. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 3197–3213. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Z.; Liu, D.; Ling, Q. Dada: Deep Adversarial Data Augmentation for Extremely Low Data Regime Classification. In Proceedings of the ICASSP 2019—2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; IEEE: New York, NY, USA; pp. 2807–2811. [Google Scholar]
- Du, H.; He, Y.; Jin, T. Transfer Learning for Human Activities Classification Using Micro-Doppler Spectrograms. In Proceedings of the IEEE International Conference on Computational Electromagnetics (ICCEM), Chengdu, China, 26–28 March 2018; pp. 1–3. [Google Scholar]
- Du, H.; Jin, T.; Song, Y.; Dai, Y.; Li, M. Efficient Human Activity Classification via Sparsity-Driven Transfer Learning. IET Radar Sonar Navig. 2019, 13, 1741–1746. [Google Scholar] [CrossRef]
- Park, J.; Javier, R.J.; Moon, T.; Kim, Y. Micro-Doppler Based Classification of Human Aquatic Activities via Transfer Learning of Convolutional Neural Networks. Sensors 2016, 16, 1990. [Google Scholar] [CrossRef]
- Seyfioglu, M.S.; Erol, B.; Gurbuz, S.Z.; Amin, M.G. DNN Transfer Learning from Diversified Micro-Doppler for Motion Classification. IEEE Trans. Aerosp. Electron. Syst. 2018, 55, 2164–2180. [Google Scholar] [CrossRef]
- Ricci, R.; Balleri, A. Recognition of Humans Based on Radar Micro-Doppler Shape Spectrum Features. IET Radar Sonar Navig. 2015, 9, 1216–1223. [Google Scholar] [CrossRef]
- van Dorp, P.; Groen, F.C.A. Feature-Based Human Motion Parameter Estimation with Radar. IET Radar Sonar Navig. 2008, 2, 135–145. [Google Scholar] [CrossRef]
- Zeng, Z.; Amin, M.G.; Shan, T. Automatic Arm Motion Recognition Based on Radar Micro-Doppler Signature Envelopes. IEEE Sens. J. 2020, 20, 13523–13532. [Google Scholar] [CrossRef]
- Zhao, R.; Ma, X.; Liu, X.; Li, F. Continuous Human Motion Recognition Using Micro-Doppler Signatures in the Scenario with Micro Motion Interference. IEEE Sens. J. 2020, 21, 5022–5034. [Google Scholar] [CrossRef]
- Ma, D.; Shang, L.; Tang, J.; Bao, Y.; Fu, J.; Yin, J. Classifying Breast Cancer Tissue by Raman Spectroscopy with One-Dimensional Convolutional Neural Network. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2021, 256, 119732. [Google Scholar] [CrossRef]
- Shevgunov, T.; Efimov, E.; Kirdyashkin, V.; Kravchenko, T. The Development of the Algorithm for Estimating the Spectral Correlation Function Based on Two-Dimensional Fast Fourier Transform. In Advances in Signal Processing: Theories, Algorithms, and System Control; Springer: Berlin/Heidelberg, Germany, 2020; pp. 75–86. [Google Scholar]
- Tahmoush, D. Review of Micro-Doppler Signatures. IET Radar Sonar Navig. 2015, 9, 1140–1146. [Google Scholar] [CrossRef]
- Eom, C.; Chun, S.; Kim, B.; Joo, S.; You, J.; Yoon, J.; Han, S.; Park, J.; Park, S. Simulation Study for the Motion Classification Using the Radar and the 3D Motion Analysis System. Korean J. Appl. Biomech. 2024, 34, 240–250. [Google Scholar]
- Kim, K.; Seo, D.; Kim, H. Efficient Radar Target Recognition Using the MUSIC Algorithm and Invariant Features. IEEE Trans. Antennas Propag. 2002, 50, 325–337. [Google Scholar]
- Park, S.; Kim, M.; Jung, J.; Riggs, L.; Kim, K. Automatic Recognition of Range Profiles and ISAR Images of Targets Flying in Formation. IEEE Sens. J. 2019, 19, 515–524. [Google Scholar] [CrossRef]
- Yoon, S.; Kim, S.; Jung, J.; Cha, S.; Baek, Y.; Koo, B.; Choi, I.; Park, S. Efficient Protocol to Use FMCW Radar and CNN to Distinguish Micro-Doppler Signatures of Multiple Drones and Birds. IEEE Access 2022, 10, 26033–26044. [Google Scholar] [CrossRef]

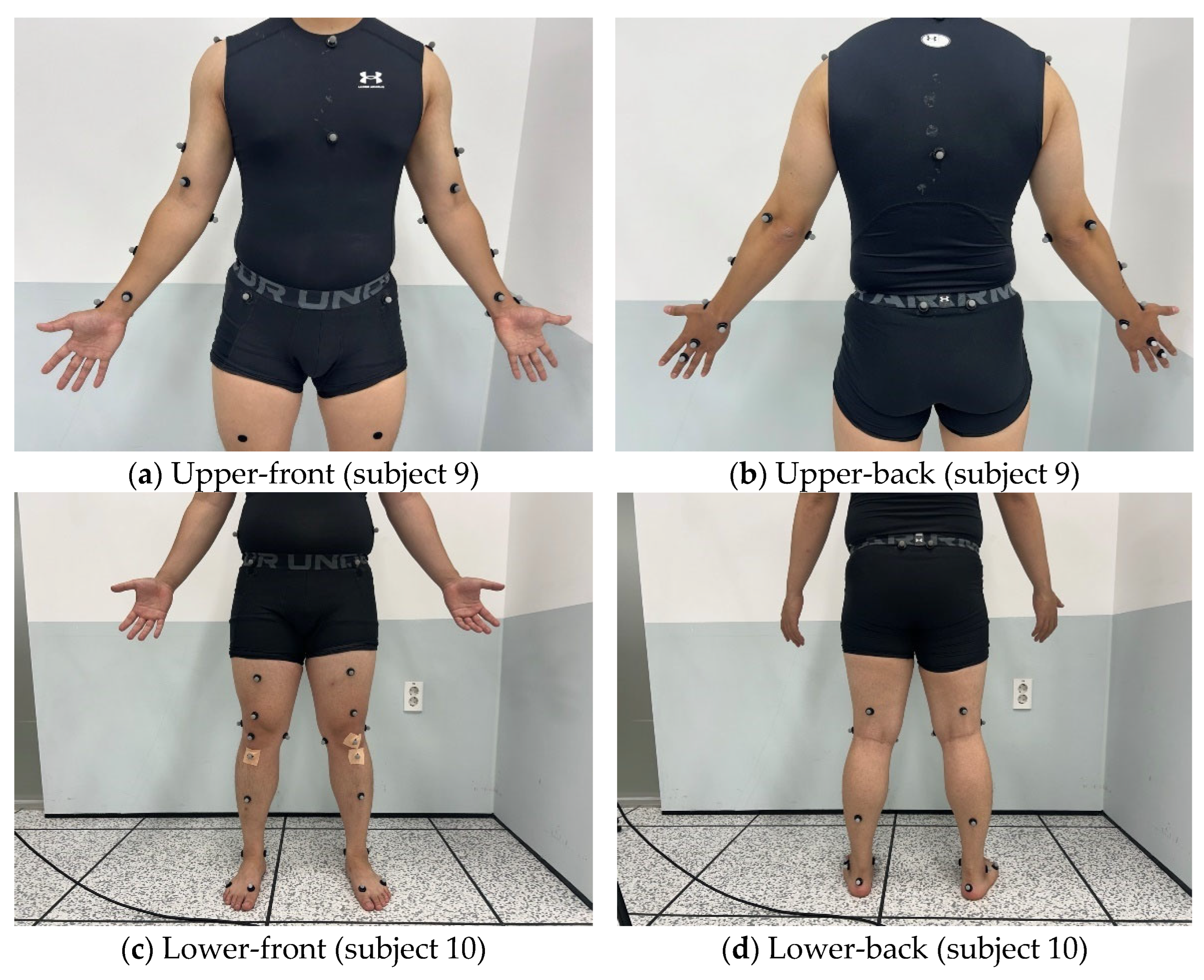



| Variables (Mean ± Std) | 6 Males | 4 Females |
|---|---|---|
| Height (cm) | 174.00 ± 5.33 | 166.38 ± 3.82 |
| Weight (kg) | 82.00 ± 11.03 | 57.50 ± 6.45 |
| Age (y) | 25.67 ± 1.21 | 24.50 ± 2.38 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| fc | 5.80 GHz | λ | 0.05 m |
| Tend | 4.00 s | Tsamp | 1.20 s |
| dttr | 0.02 s | Ntr | 140 |
| d | 4 | SNR | 0–20 dB |
| Single Motion | Two Motions | Body Variation |
|---|---|---|
| 99.12% | 21. 2% | 77.3% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eom, C.; Han, S.; Chun, S.; Joo, S.; Yoon, J.; Kim, M.; Park, J.; Park, S. Efficient Markerless Motion Classification Using Radar. Sensors 2025, 25, 3293. https://doi.org/10.3390/s25113293
Eom C, Han S, Chun S, Joo S, Yoon J, Kim M, Park J, Park S. Efficient Markerless Motion Classification Using Radar. Sensors. 2025; 25(11):3293. https://doi.org/10.3390/s25113293
Chicago/Turabian StyleEom, Changhyeon, Sooji Han, Sabin Chun, Soyoung Joo, Jisu Yoon, Min Kim, Jongchul Park, and Sanghong Park. 2025. "Efficient Markerless Motion Classification Using Radar" Sensors 25, no. 11: 3293. https://doi.org/10.3390/s25113293
APA StyleEom, C., Han, S., Chun, S., Joo, S., Yoon, J., Kim, M., Park, J., & Park, S. (2025). Efficient Markerless Motion Classification Using Radar. Sensors, 25(11), 3293. https://doi.org/10.3390/s25113293








