Handheld Ground-Penetrating Radar Antenna Position Estimation Using Factor Graphs
Abstract
1. Introduction
- A comprehensive development and detailed presentation of a factor-graph-based algorithm for HH-GPR antenna trajectory estimation, including analysis of its computational complexity and memory usage, with a comparison to EKF. The proposed algorithm is used to process distance measurements in a UWB positioning system and uses two variants of motion models and two variants of observation models.
- Presentation of new results of simulative tests for the UWB positioning system with the factor-graph-based algorithm and their comparison with the results obtained with the use of the EKF.
2. Positioning System and Estimation Algorithm
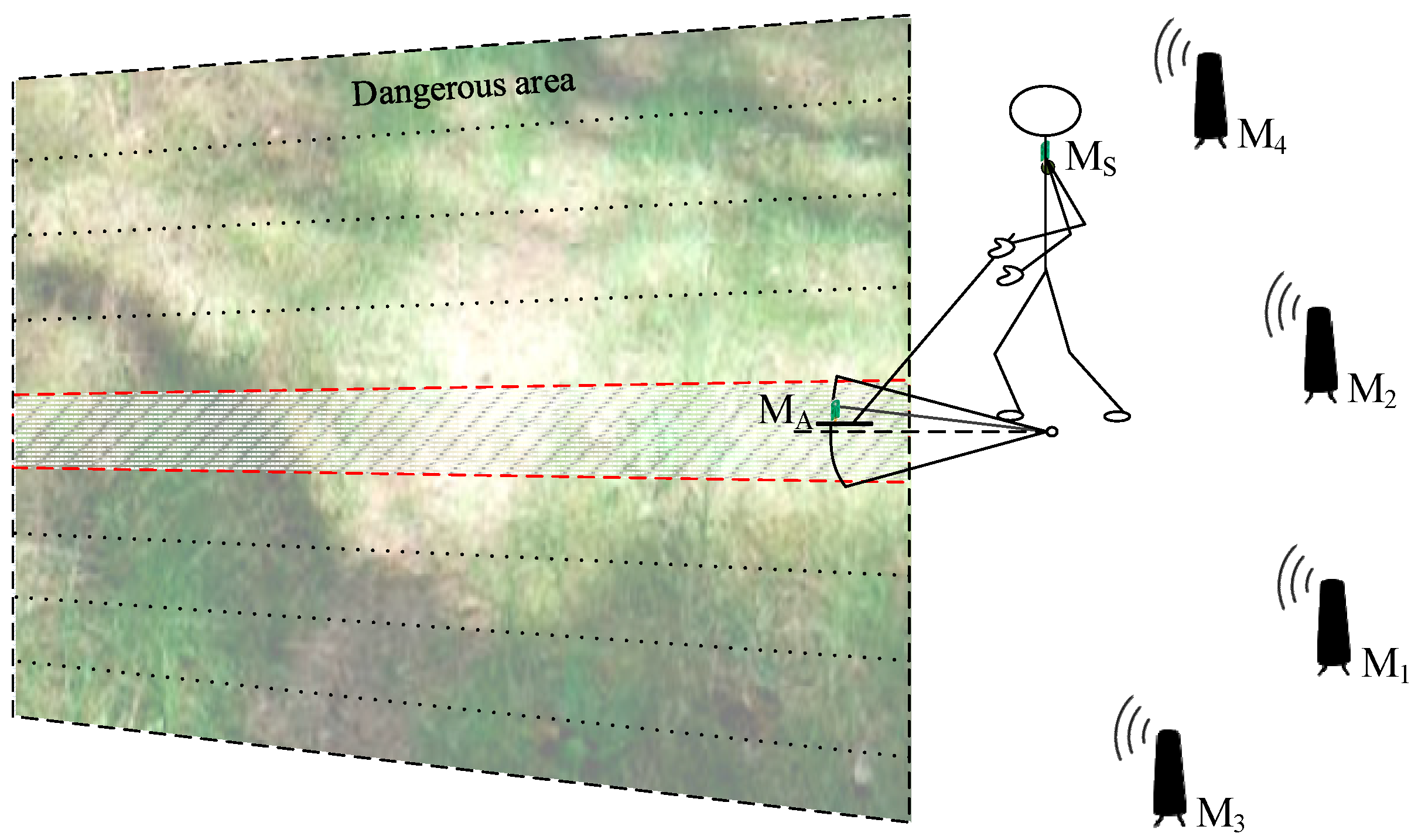
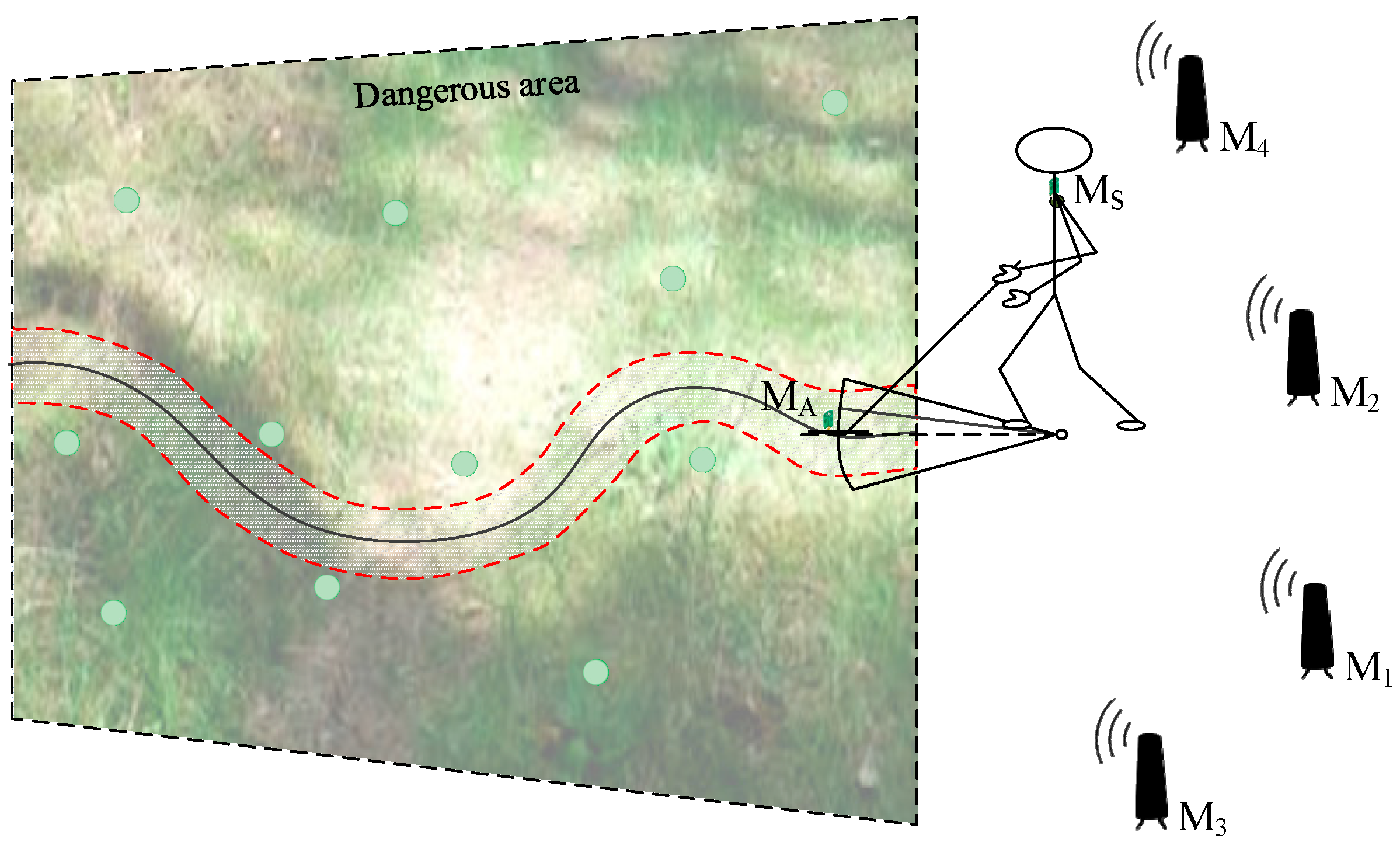
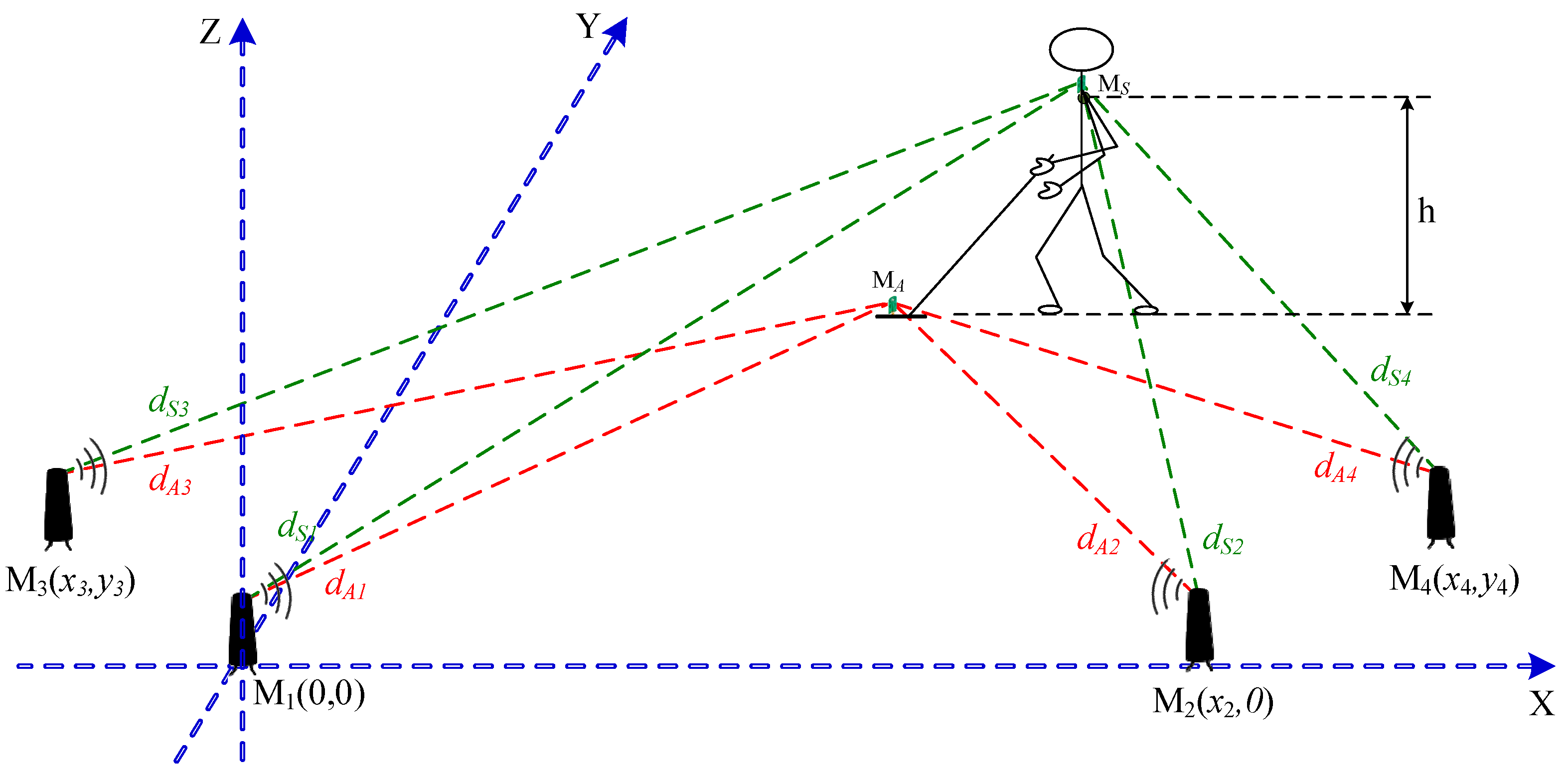
2.1. Positioning System for Handheld Ground-Penetrating Radar
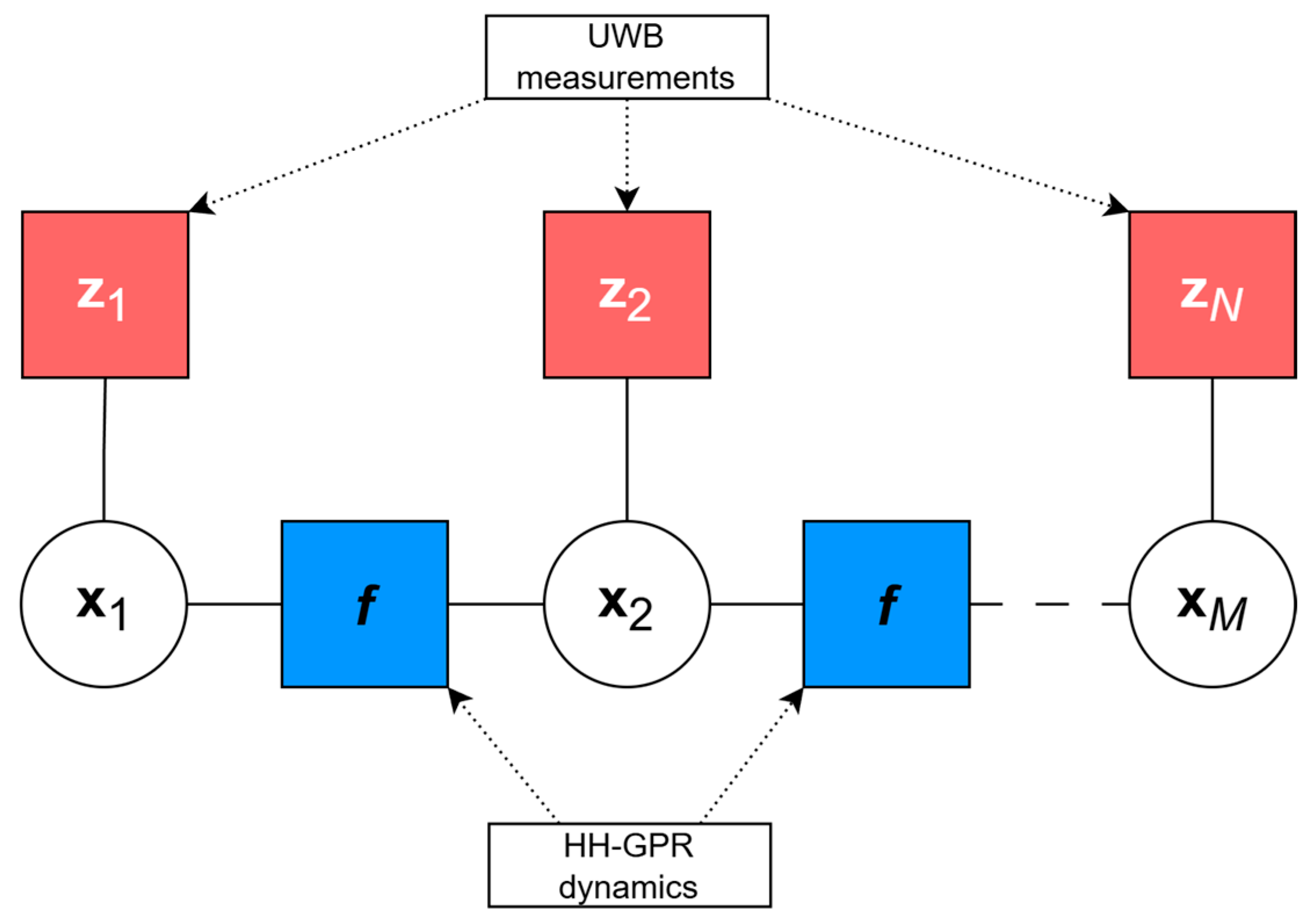
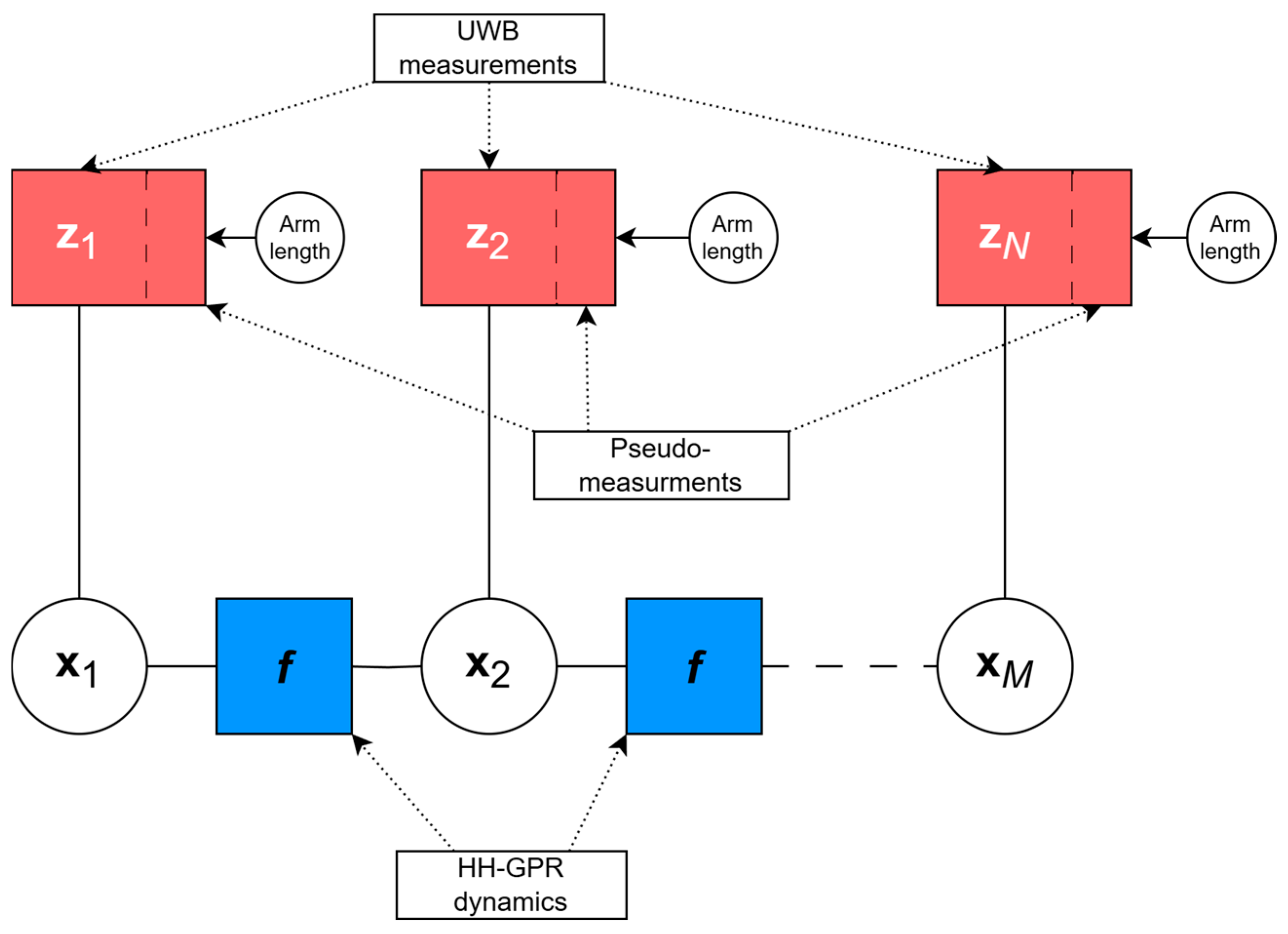
2.2. Application of Factor Graph in Positioning of Handheld Ground-Penetrating Radar
- Variable nodes representing the GPR antenna’s state at different time steps (…), which include its position and velocity with accordance to a given motion model.
2.3. Factor-Graph-Based Estimation Algorithm Details
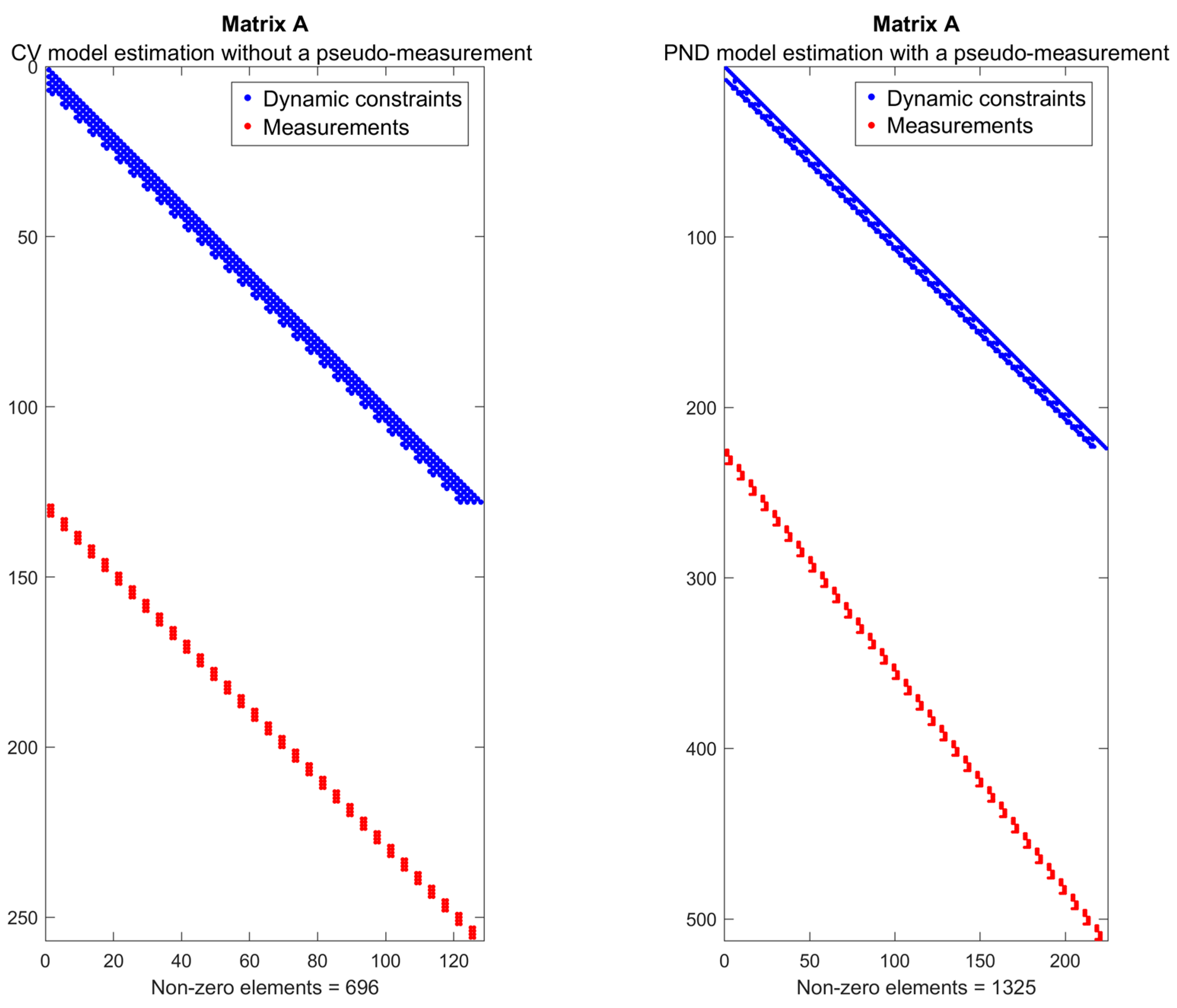
2.4. Computational Complexity and Memory Usage
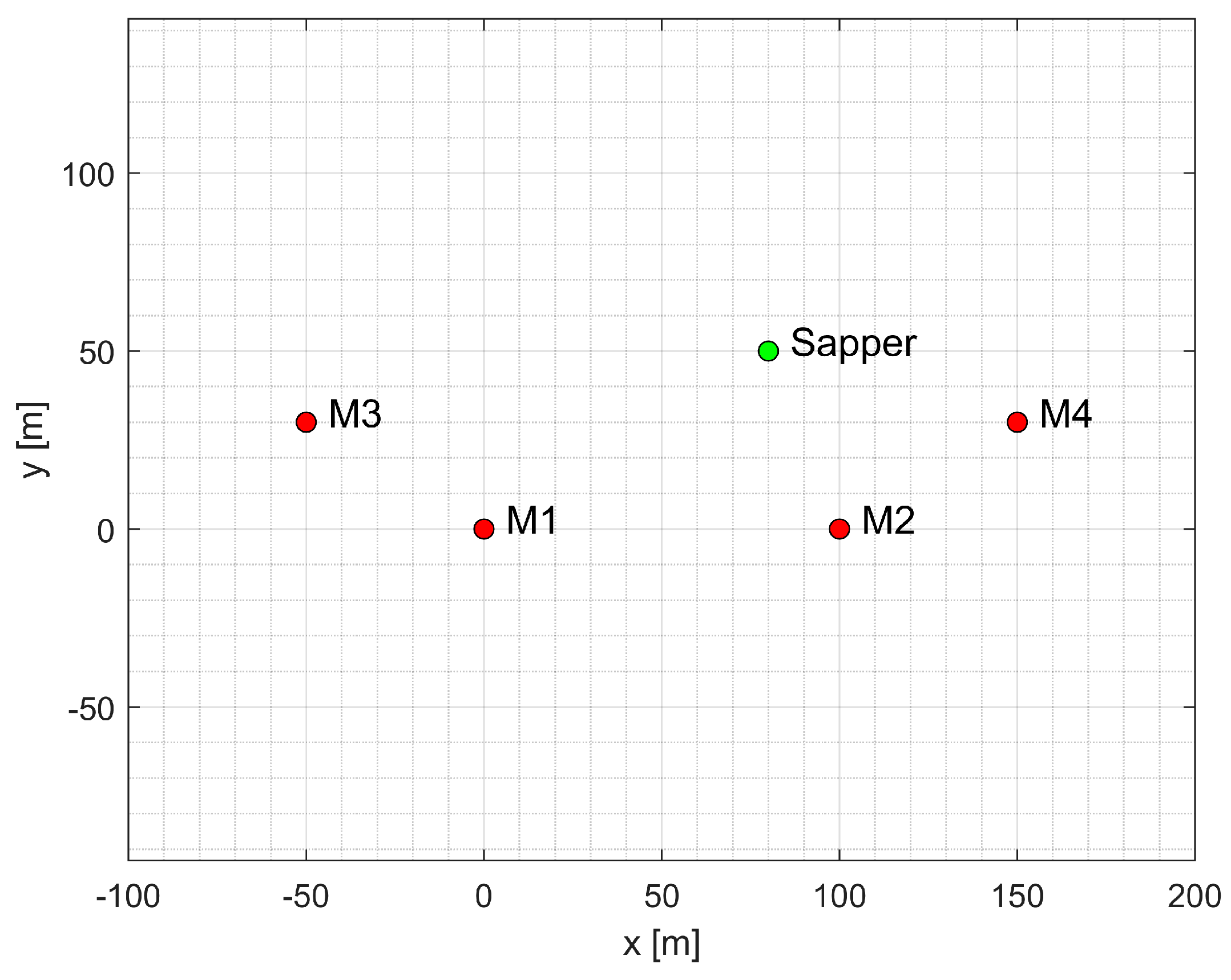
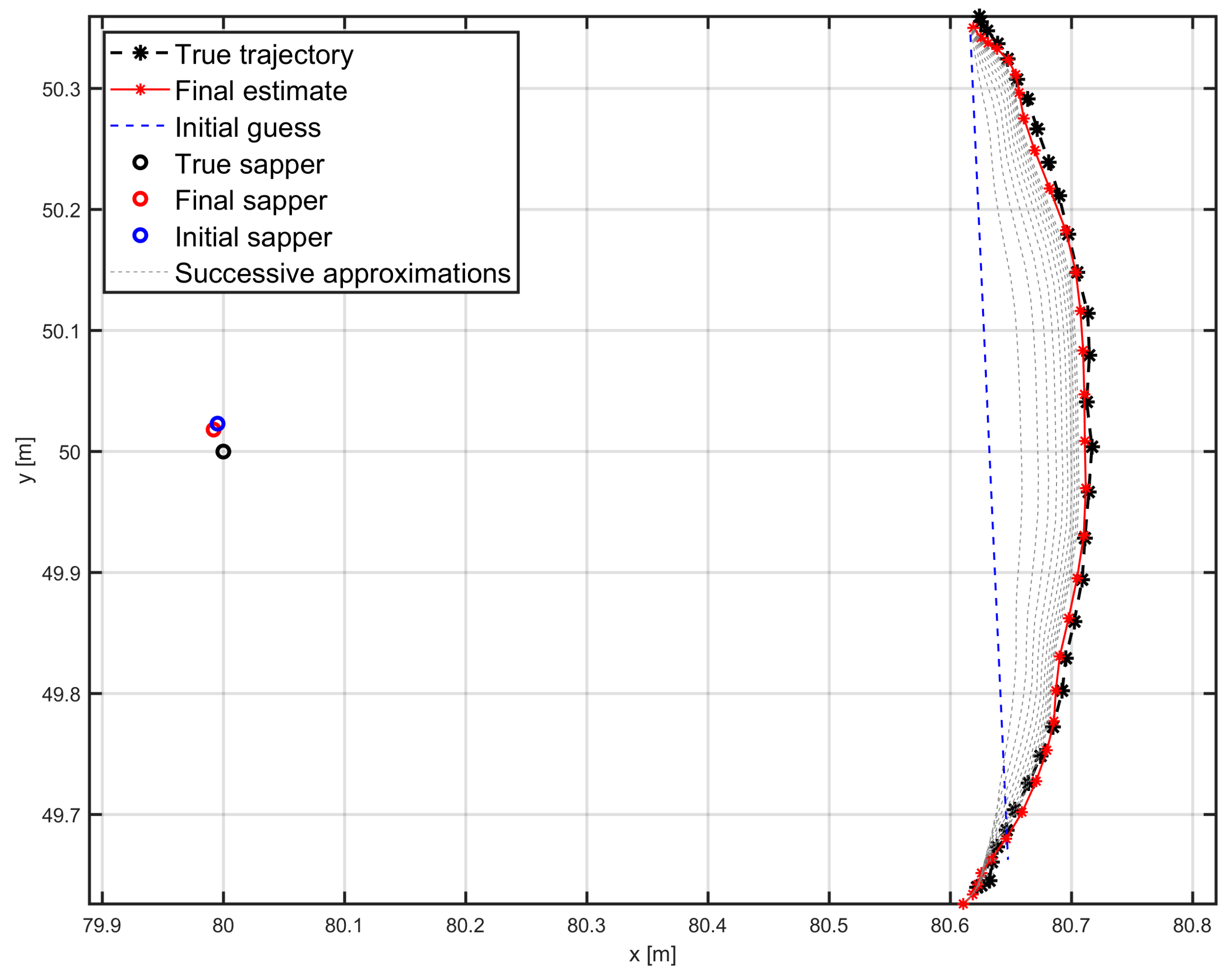
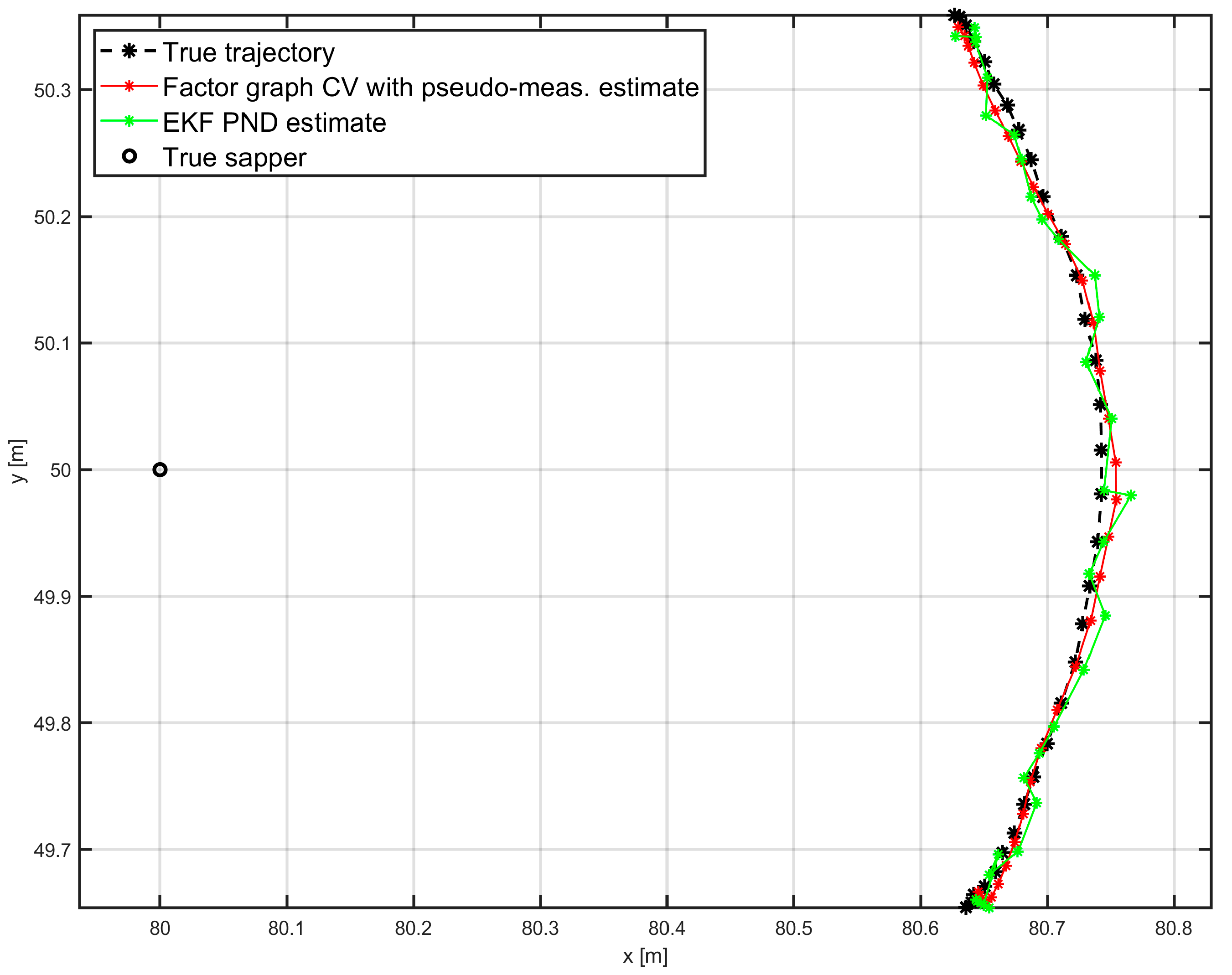
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| HH-GPR | Handheld Ground-Penetrating Radar |
| EKF | Extended Kalman Filter |
| PND | Pendulum |
| KF | Kalman Filter |
| SLAM | Simultaneous Localization and Mapping |
| UWB | Ultrawideband |
| CV | Constant Velocity |
References
- Ahmed, S.A.; El Qassas, R.A.Y.; El Salam, H.F.A. Mapping the possible buried archaeological targets using magnetic and ground penetrating radar data. Egypt. J. Remote Sens. Space Sci. 2020, 23, 321–332. [Google Scholar] [CrossRef]
- Bechtel, T.; Truskavetsky, S.; Capineri, L.; Pochanin, G.; Simic, N.; Viatkin, K.; Sherstyuk, A.; Byndych, T.; Falorni, P.; Bulletti, A.; et al. A survey of electromagnetic characteristics of soils in the Donbass region (Ukraine) for evaluation of the applicability of GPR and MD for landmine detection. In Proceedings of the 16th International Conference on Ground Penetrating Radar (GPR), Hong Kong, China, 13–16 June 2016. [Google Scholar] [CrossRef]
- Iftimi, N.; Savin, A.; Steigmann, R.; Dobrescu, G.S. Underground Pipeline Identification into a Non-Destructive Case Study Based on Ground-Penetrating Radar Imaging. Remote Sens. 2021, 13, 3494. [Google Scholar] [CrossRef]
- Kelly, T.B.; Angel, M.N.; O’Connor, D.E.; Huff, C.C.; Morris, L.E.; Wach, G.D. A novel approach to 3D modelling ground-penetrating radar (GPR) data—A case study of a cemetery and applications for criminal investigation. Forensic Sci. Int. 2021, 325, 110882. [Google Scholar] [CrossRef] [PubMed]
- Urbini, S.; Vittuari, L.; Gandolfi, S. GPR and GPS data integration: Examples of application in Antarctica. Ann. Geophisica 2001, 44, 687–702. [Google Scholar] [CrossRef]
- Wei, S.; Qing, X.; Geng, X.; Xiangyang, S. Application of ground penetrating radar with GPS in underwater topographic survey. In Proceedings of the 2nd International Conference on Artificial Intelligence, Management Science and Electronic Commerce (AIMSEC), Dengfeng, China, 8–10 August 2011. [Google Scholar] [CrossRef]
- Amazeen, C.A.; Locke, M.C. US Army’s new handheld standoff mine detection system (HSTAMIDS). In Proceedings of the EUREL International Conference the Detection of Abandoned Land Mines: A Humanitarian Imperative Seeking a Technical Solution, Edinburgh, UK, 7–9 October 1996. [Google Scholar] [CrossRef]
- Daniels, D.J.; Curtis, P.; Amin, R.; Hunt, N. MINEHOUND production development. In Proceedings of the SPIE 5794, Detection and Remediation Technologies for Mines and Minelike Targets X, Orlando, FL, USA, 10 June 2005. [Google Scholar] [CrossRef]
- Sato, M.; Feng, X.; Fujiwara, J. Handheld GPR and MD sensor for landmine detection. In Proceedings of the IEEE Antennas and Propagation Society International Symposium, Washington, DC, USA, 3–8 July 2005. [Google Scholar] [CrossRef]
- Kraszewski, T. Method for Estimating the Position of the Antenna of a Handheld Ground Penetrating Radar. Ph.D. Thesis, Military University of Technology, Warsaw, Poland, 2023. [Google Scholar]
- Kaniewski, P.; Kraszewski, T. Estimation of Handheld Ground-Penetrating Radar Antenna Position with Pendulum-Model-Based Extended Kalman Filter. Remote Sens. 2023, 15, 741. [Google Scholar] [CrossRef]
- Brown, H.G.; Hwang, P.Y.C. Introduction to Random Signals and Applied Kalman Filtering; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Zarchan, P.; Musoff, H. Fundamentals of Kalman Filtering: A Practical Approach, 3rd ed.; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2009. [Google Scholar]
- Słowak, P.L.; Kaniewski, P. Homography Augmented Particle Filter SLAM. Metrol. Meas. Syst. 2023, 30, 423–439. [Google Scholar] [CrossRef]
- Kschischang, F.R.; Frey, B.J.; Loeliger, H.A. Factor Graphs and the Sum-Product Algorithm. IEEE Trans. Inf. Theory 2001, 47, 498–519. [Google Scholar] [CrossRef]
- Thrun, S.; Burgard, W.; Fox, D. Probabilistic Robotics; MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Mur-Artal, R.; Martinez Montiel, J.M.; Tardos, J.D. ORB-SLAM: A Versatile and Accurate Monocular SLAM System. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar] [CrossRef]
- Taylor, C.; Gross, J. Factor Graphs for Navigation Applications: A Tutorial. NAVIGATION 2024, 71, navi.653. [Google Scholar] [CrossRef]
- Kaess, M.; Dellaert, F. iSAM2: Incremental Smoothing and Mapping Using the Bayes Tree. Int. J. Robot. Res. 2012, 31, 216–235. [Google Scholar] [CrossRef]
- Dong, J.; Boots, B.; Fox, D. Motion Planning as Probabilistic Inference Using Gaussian Processes and Factor Graphs. Robot. Sci. Syst. 2016, 12, 1–9. [Google Scholar] [CrossRef]
- Suzuki, T. First Place Award Winner of the Smartphone Decimeter Challenge: Global Optimization of Position and Velocity by Factor Graph Optimization. In Proceedings of the 34th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2021), St. Louis, MO, USA, 20–24 September 2021. [Google Scholar] [CrossRef]
- Davis, T.A. Algorithm 915, SuiteSparseQR: Multifrontal Multithreaded Rank-Revealing Sparse QR Factorization. ACM Trans. Math. Softw. 2011, 38, 8. [Google Scholar] [CrossRef]
- Gnanasekaran, A.; Darve, E. Hierarchical Orthogonal Factorization: Sparse Least Squares Problems. J. Sci. Comput. 2022, 91, 50. [Google Scholar] [CrossRef]
| Estimation Method | RMSE [m] | Improvement [%] |
|---|---|---|
| EKF PND | 0.0149 | - |
| Factor graph (CV) | 0.0097 | 34.9 |
| Factor graph (CV + pseudo-measurement) | 0.0091 | 39.0 |
| Factor graph (PND) | 0.0080 | 46.3 |
| Factor graph (PND + pseudo-measurement) | 0.0076 | 49.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Słowak, P.; Kraszewski, T.; Kaniewski, P. Handheld Ground-Penetrating Radar Antenna Position Estimation Using Factor Graphs. Sensors 2025, 25, 3275. https://doi.org/10.3390/s25113275
Słowak P, Kraszewski T, Kaniewski P. Handheld Ground-Penetrating Radar Antenna Position Estimation Using Factor Graphs. Sensors. 2025; 25(11):3275. https://doi.org/10.3390/s25113275
Chicago/Turabian StyleSłowak, Paweł, Tomasz Kraszewski, and Piotr Kaniewski. 2025. "Handheld Ground-Penetrating Radar Antenna Position Estimation Using Factor Graphs" Sensors 25, no. 11: 3275. https://doi.org/10.3390/s25113275
APA StyleSłowak, P., Kraszewski, T., & Kaniewski, P. (2025). Handheld Ground-Penetrating Radar Antenna Position Estimation Using Factor Graphs. Sensors, 25(11), 3275. https://doi.org/10.3390/s25113275







