AIMP-Based Power Allocation for Radar Network Tracking Under Countermeasures Environment
Abstract
1. Introduction
1.1. Main Contributions
- (1)
- Build an optimization model of the power allocation for the radar network tracking in a countermeasures environment: On one hand, if a radar is jammed by electronic suppressive jamming, the SINR of the radar will drastically decrease, which negatively affects the tracking accuracy. The target RCS can also affect the SINR, on the other hand. Therefore, the threat of suppressive jamming and the variation in target RCS during the target motion are both considered to build the power allocation optimization model for a radar network in tracking applications. Specifically, at a certain frame, the impact of the jamming on the echo pulses is regarded as the feedback, combined with the target RCS prediction at the next frame; these two factors jointly guide the transmit power adjustment of the radar network at the next frame.
- (2)
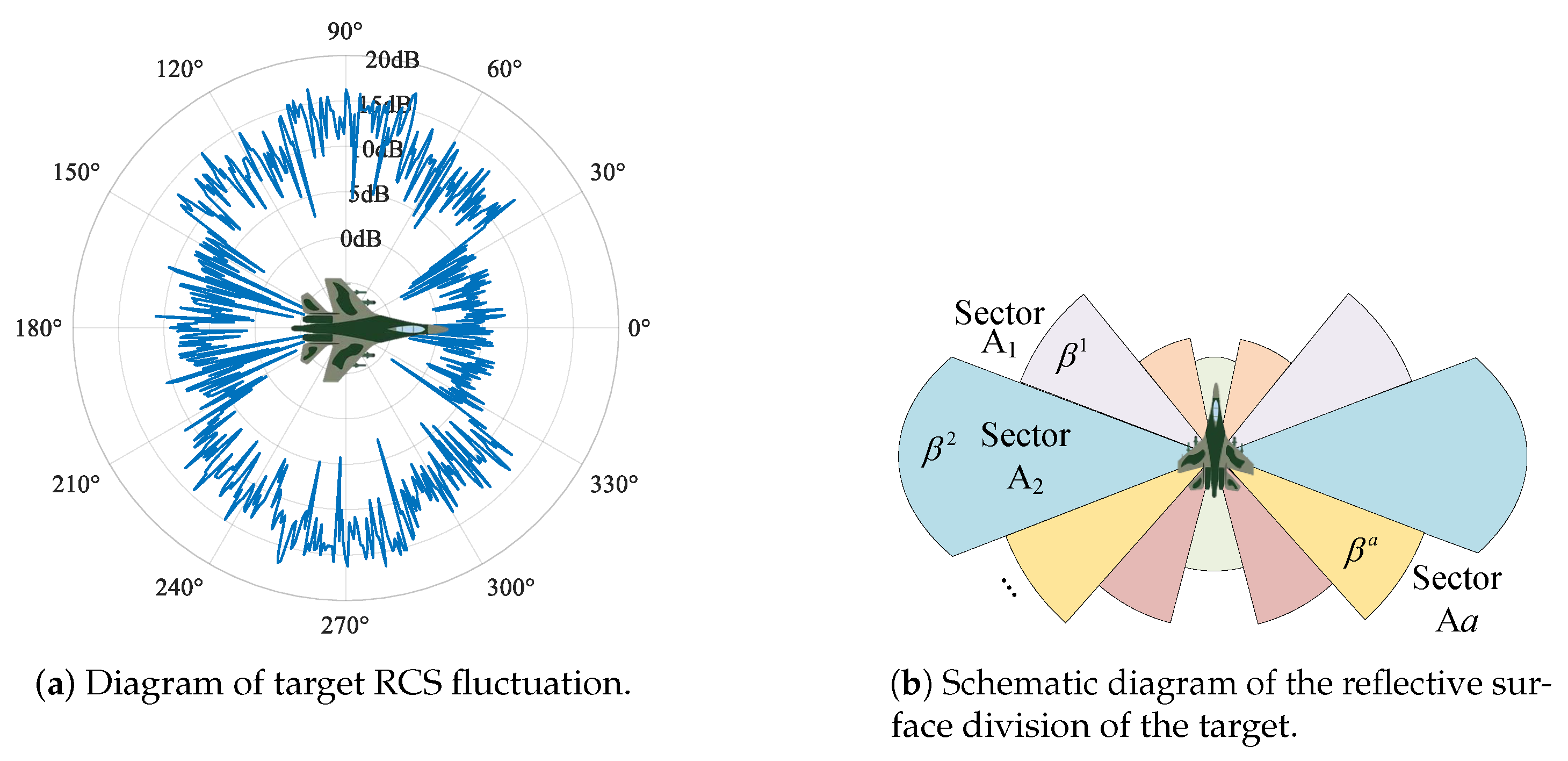
- Develop a target motion trajectory-based RCS prediction method: In general, the target RCS depends on the sector where the radar radiates, and the sector can be described as the incidence angle with which the radar illuminates the target. With the target maneuvering, the incidence angle is decided by the trajectory within two frames of the target. The target state (i.e., the position) at the next frame is first predicted, and in turn, the geometric relationship between the target position within the two successive frames is obtained. The cosine theorem is then utilized to calculate the predicted radar incidence angle, and the target sector radiated by the radar can be determined. Combined with the sector-based RCS value distribution obtained from the prior knowledge, the predicted target RCS at the next frame can finally be obtained.
- (3)
- Propose an adaptive interacting multiple power (AIMP)-based power allocation algorithm for radar network tracking: Predictably, in a countermeasures environment, there exists an optimal transmit power under a given target RCS that the radar network can achieve high SINR while maintaining better LPI performance. To achieve this strategy, based on our previous work, a power allocation strategy based on the IMP algorithm [17], combined with the prediction of target RCS to create an AIMP-based power allocation algorithm for the radar network, is proposed.
1.2. Organization of This Paper
2. System Modeling
2.1. Signal Model and SINR
2.2. Target Motion Model and Radar Measurement Model
2.3. Pulse Interception and Signal Identification
3. Problem Modeling
- (1)
- Obviously, increasing the transmit power is an important way to improve the tracking accuracy. However, the excessive transmit power will also increase the probability in a countermeasures environment, thus raising the risk that the radar will be jammed, negatively affecting the SINR of the radar network and thus decreasing the tracking accuracy;
- (2)
- Reducing the radar transmit power to excessively pursue a lower probability of intercept is also unwise for the radar, which will result in a low SINR, and the strength of the radar will not be fully utilized. For example, the easiest way to achieve the lowest probability of intercept is to radiate no energy into its surveillance area (usually called radio silence), but at the same time, the radar is unable to perform the tracking task (unless it is required to perform a reconnaissance task).
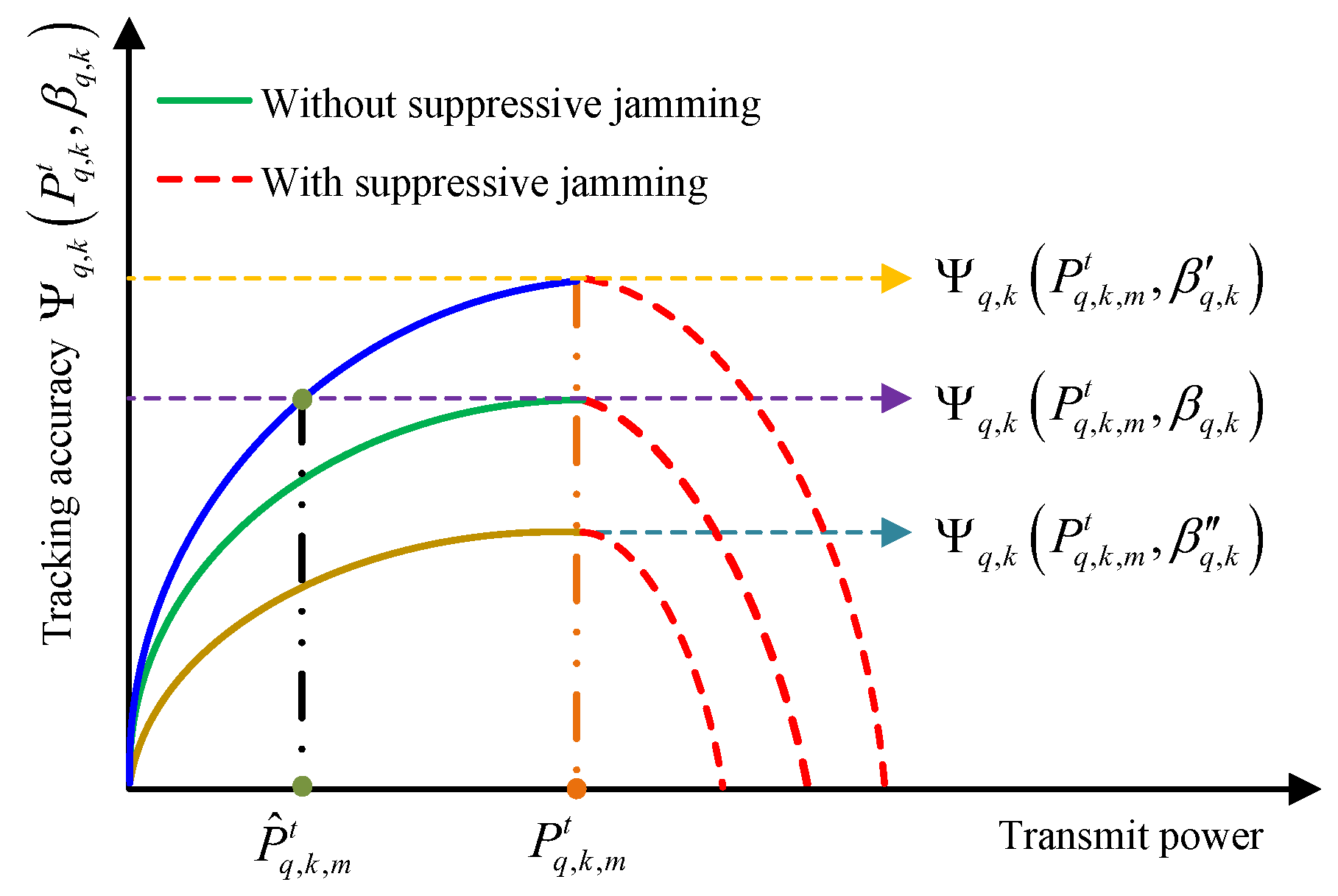
3.1. Relationship Between Tracking Accuracy and SINR
- •
- If the radar is not jammed and , then the increasing transmit power will improve SINR, where the SINR is equal to the SNR;
- •
- As the transmit power of the radar continues to increase, it will suffer from suppressive jamming, resulting in a sharp decrease in SINR.
3.2. Optimization Model
- (1)
- From the perspective of radar transmit power, the SINR will decrease due to the radar being jammed, which in turn leads to a decrease in tracking accuracy. Therein, the intercept probability of the radar pulse is related to the transmit power of the radar and the radar–target range.
- (2)
- In the target RCS perspective, different RCSs will yield different echo power and lead to different SINRs under the same transmit power, which is only related to the target RCS.
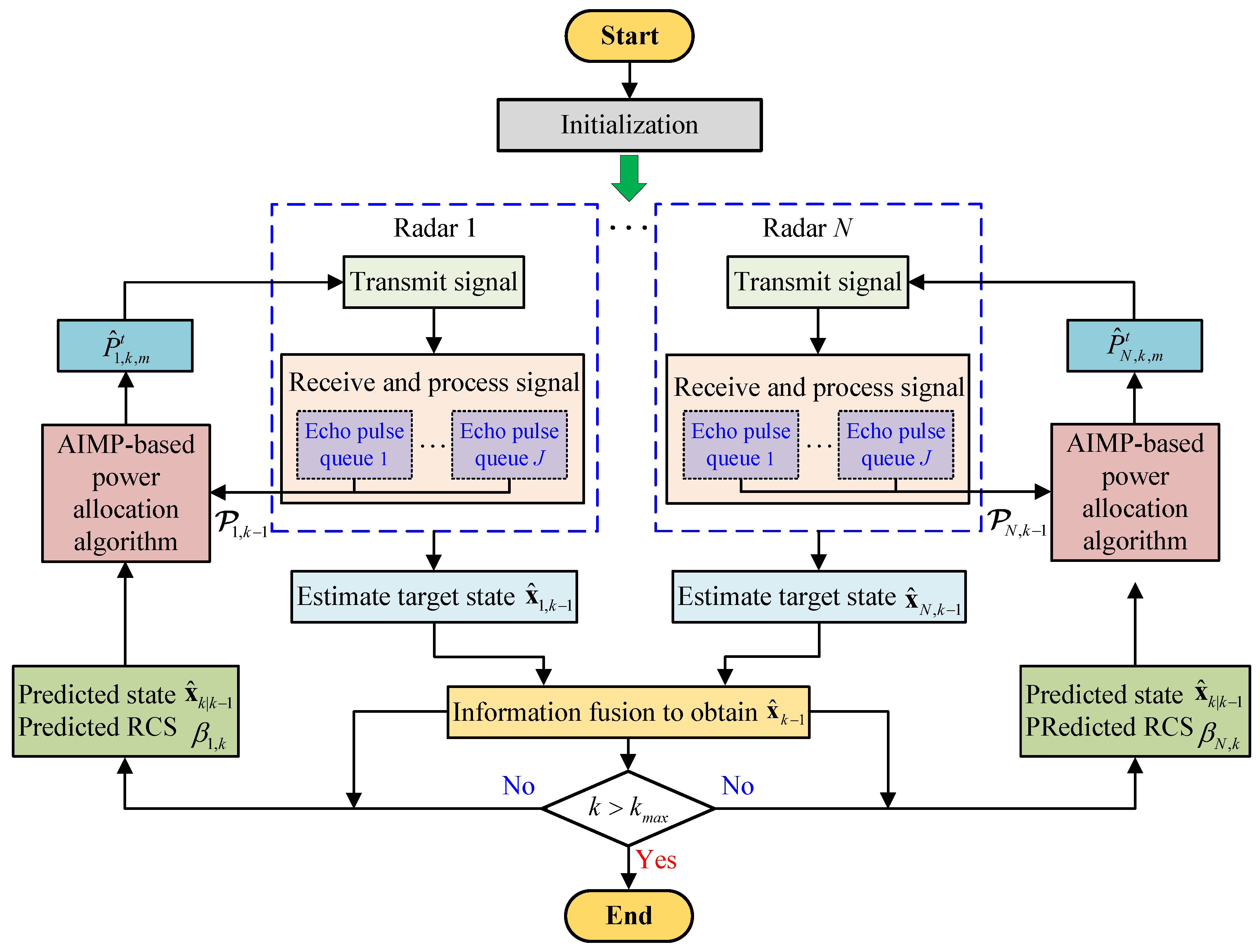
4. AIMP-Based Power Allocation Algorithm
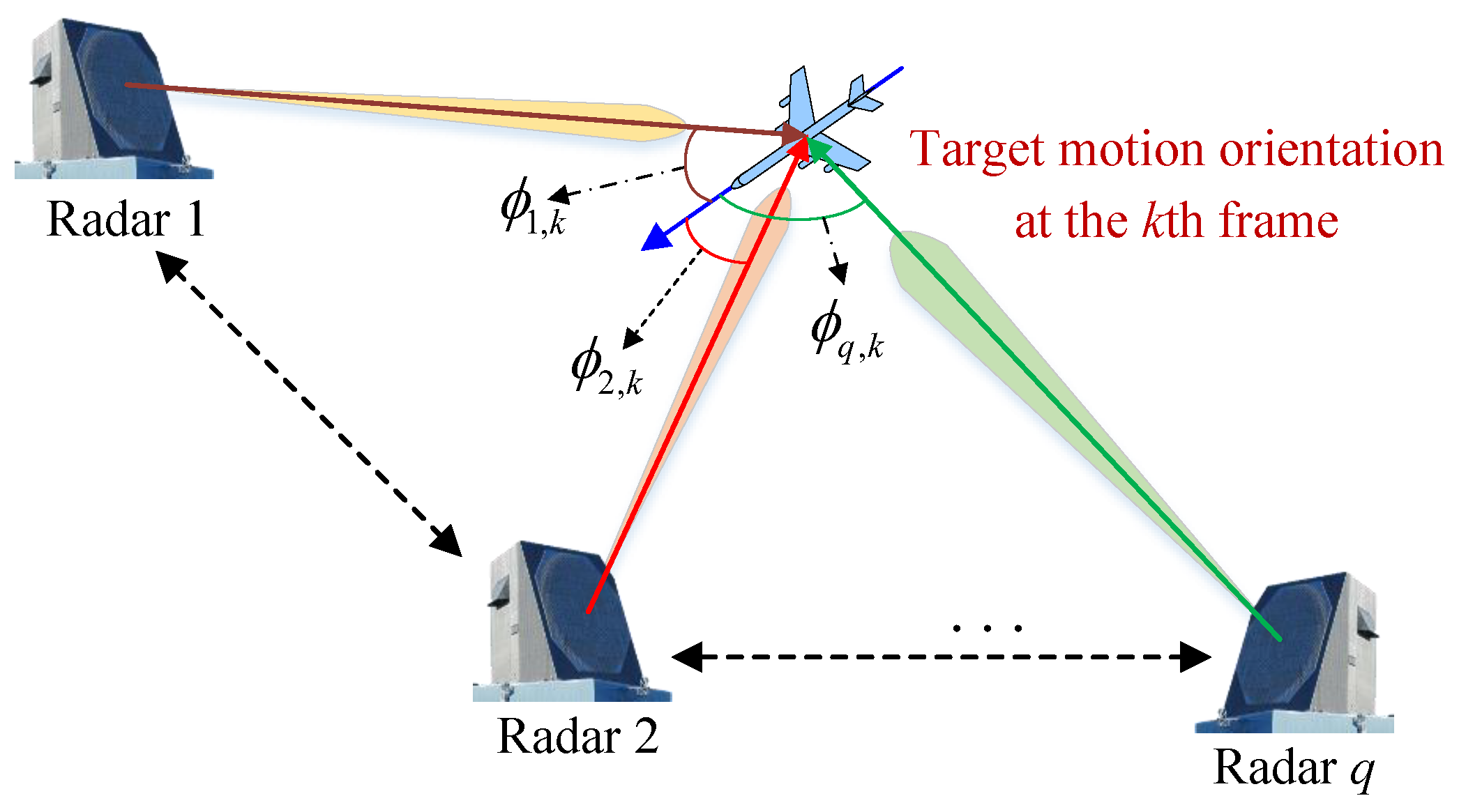
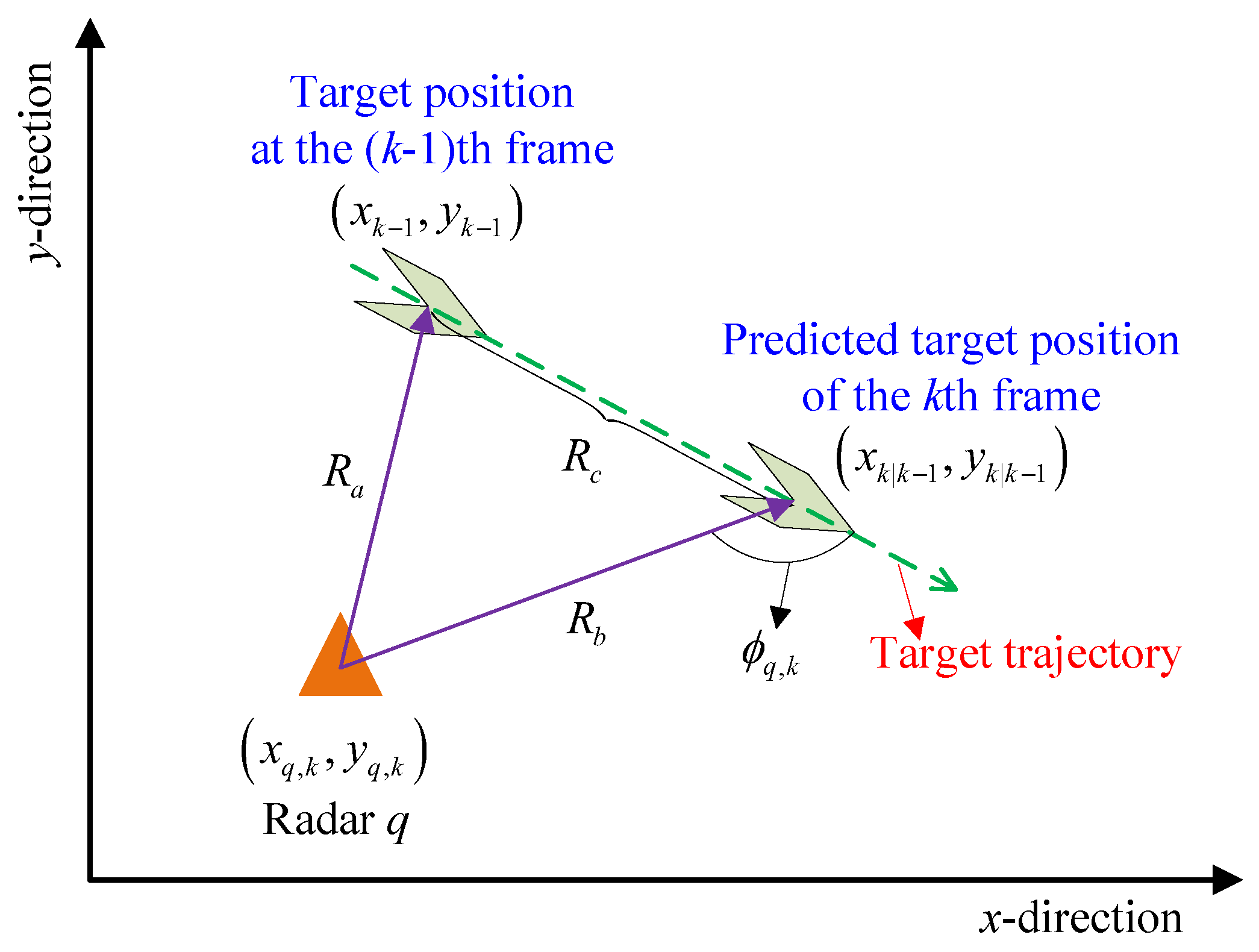
4.1. Radar Incidence Angle
4.2. Target Motion Trajectory-Based RCS Prediction Method
| Algorithm 1: Target motion trajectory-based RCS prediction method. |
Input: The state of the target at the th frame and the RCS value distribution. Output: The target RCS values at the kth frame.
|
4.3. AIMP-Based Power Allocation Algorithm
5. Simulation Results
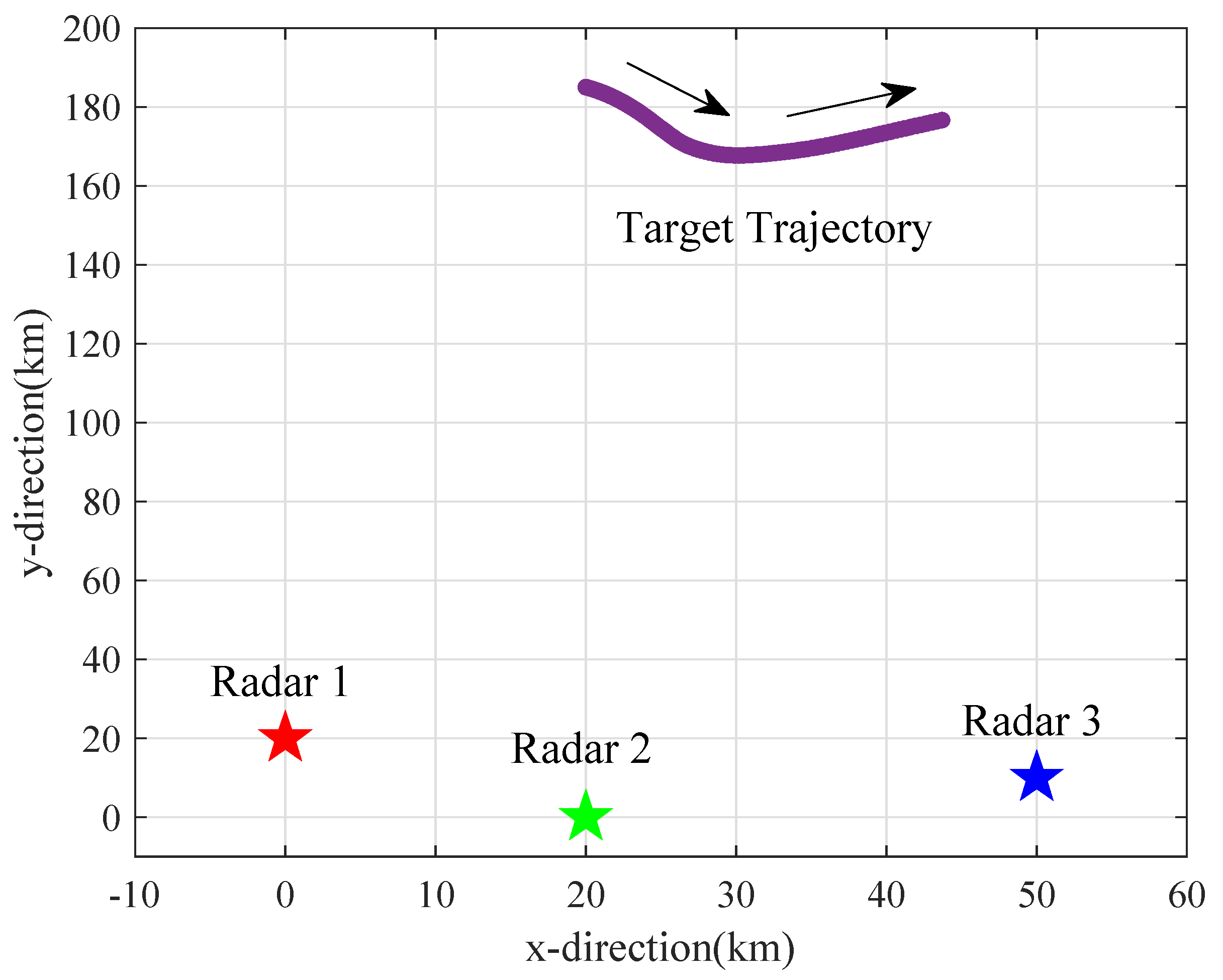
5.1. Simulation Scenario
5.2. Simulation Parameters
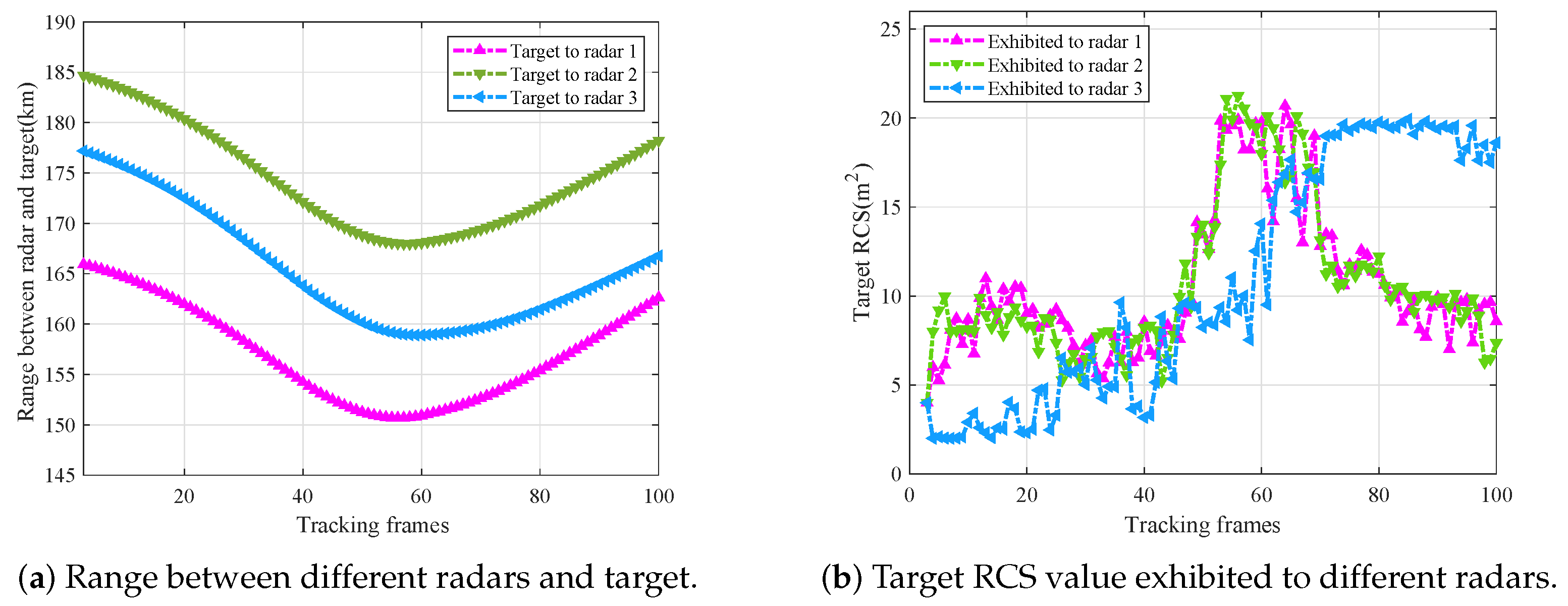
5.3. Target Range and RCS Values Exhibited to Different Radars
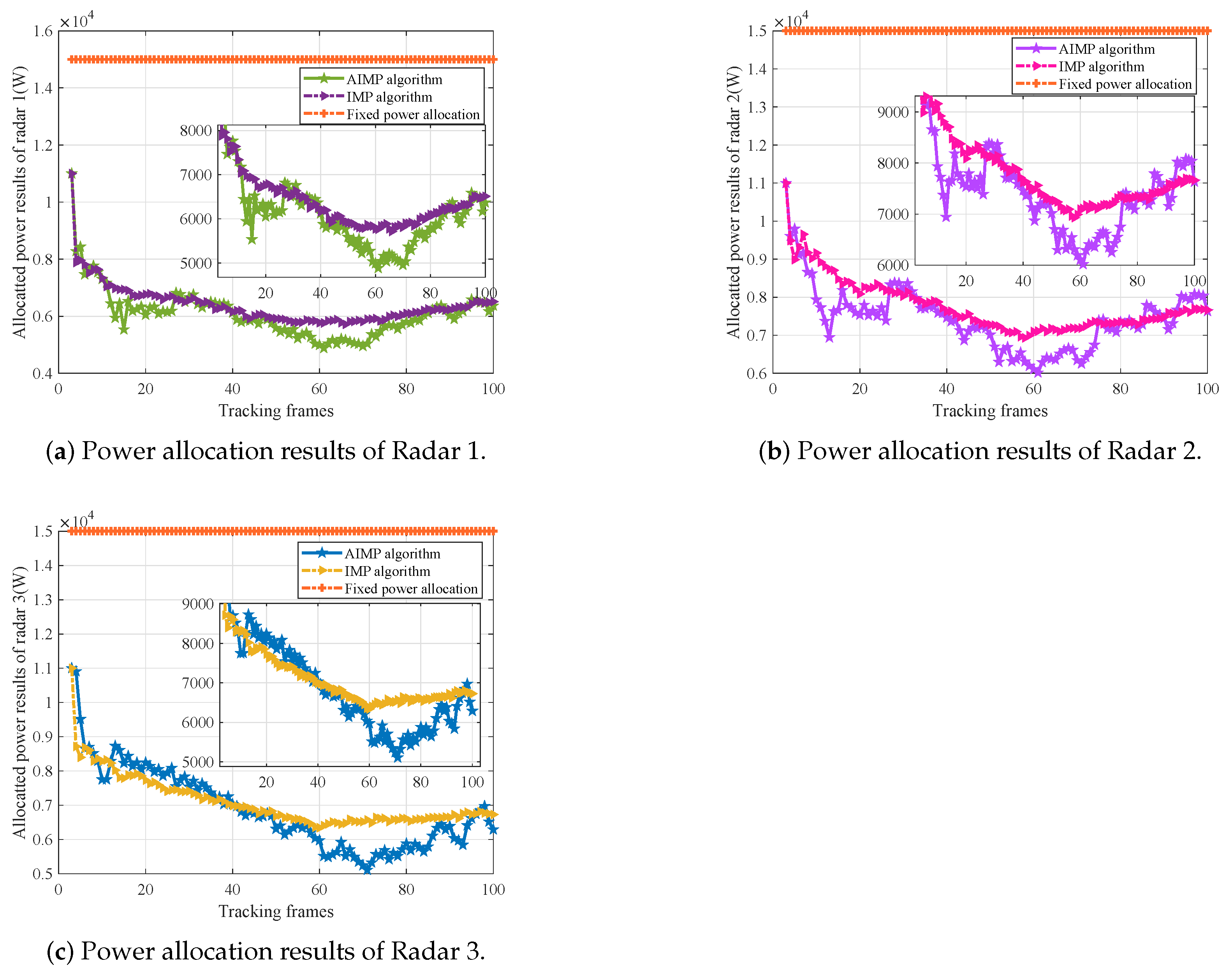
5.4. Power Allocation Results and Tracking Performance Comparison
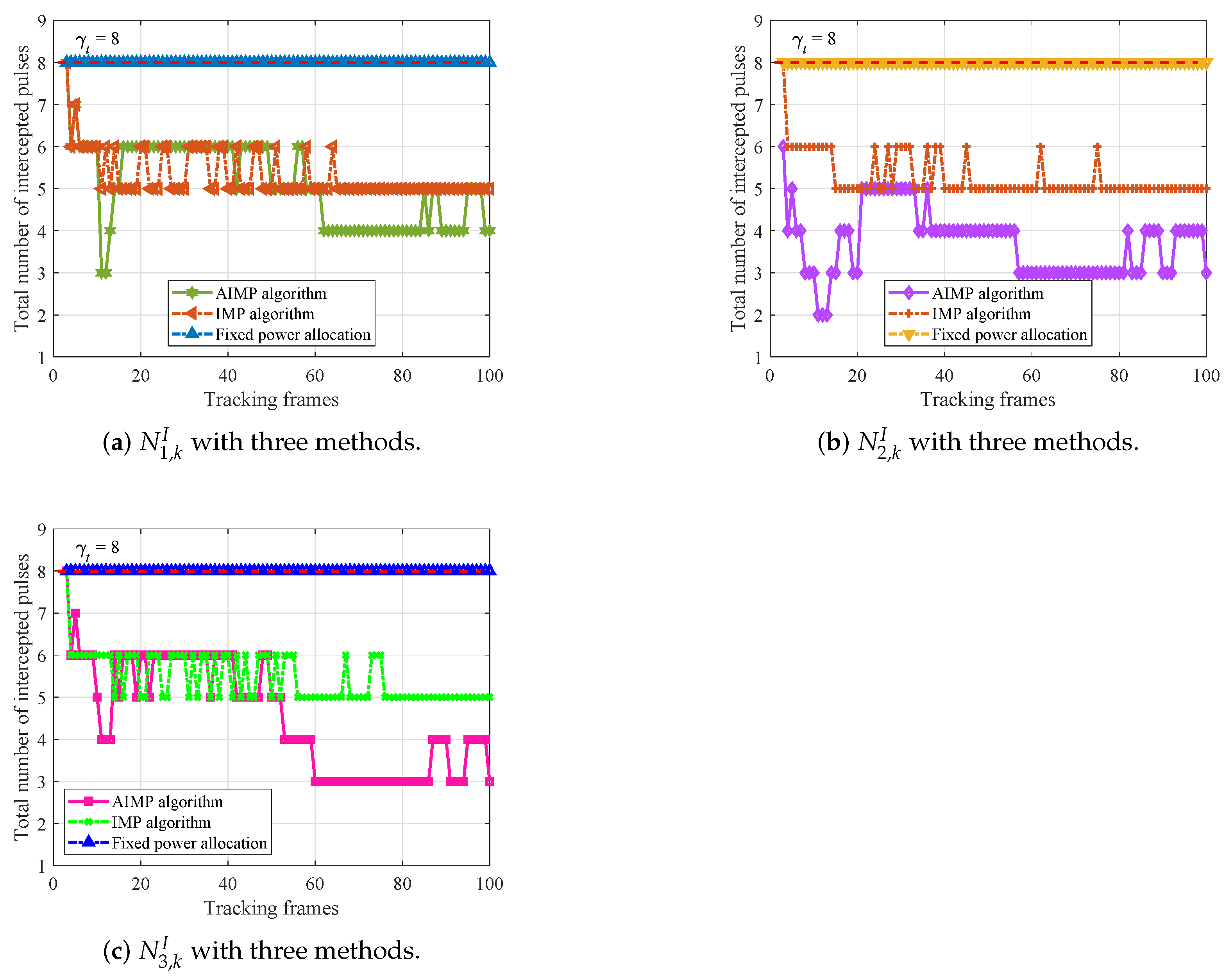
5.5. LPI Performance Comparison
5.6. Limitations of the AIMP-Based Power Allocation Algorithm
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yan, J.; Pu, W.; Zhou, S.; Liu, H.; Greco, M.S. Optimal Resource Allocation for Asynchronous Multiple Targets Tracking in Heterogeneous Radar Networks. IEEE Trans. Signal Process. 2020, 68, 4055–4068. [Google Scholar] [CrossRef]
- Yi, W.; Yuan, Y.; Hoseinnezhad, R.; Kong, L. Resource Scheduling for Distributed Multi-Target Tracking in Netted Colocated MIMO Radar Systems. IEEE Trans. Signal Process. 2020, 68, 1602–1617. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, B.; Zhang, K.; Shi, J.; Li, Z.; Huang, C.; Zhou, Q. Efficient waveform design with jamming characteristics for precision electronic warfare. Signal Process. 2023, 212, 109162. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, T.; Yu, X.; Shi, Q.; Cui, G.; Kong, L. LPI waveform design for radar system against cyclostationary analysis intercept processing. Signal Process. 2022, 201, 108681. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, Y.; Ma, Z.; Kong, L. Task Assignment in UAV-Enabled Front Jammer Swarm: A Coalition Formation Game Approach. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 9562–9575. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, T.; Kong, L.; Ma, Z. Strategy Optimization for Range Gate Pull-Off Track-Deception Jamming Under Black-Box Circumstance. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 4262–4273. [Google Scholar] [CrossRef]
- Lynch, J.D. Introduction to RF Stealth; North California: Sci Tech Publishing Inc.: Irvine, CA, USA, 2024. [Google Scholar]
- Song, J.; Cheng, T.; Wang, Y.; Liu, L.; He, Z. LPI-based Resource Allocation Strategy for Multiple Targets Tracking in CMIMO Radar System with Array Division. Signal Process. 2024, 225, 109625. [Google Scholar] [CrossRef]
- Shi, C.; Ding, L.; Wang, F.; Salous, S.; Zhou, J. Joint Target Assignment and Resource Optimization Framework for Multitarget Tracking in Phased Array Radar Network. IEEE Syst. J. 2021, 15, 4379–4390. [Google Scholar] [CrossRef]
- Meller, M. On Bayesian Tracking and Prediction of Radar Cross Section. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 1756–1768. [Google Scholar] [CrossRef]
- Richards, M.A. Fundamentals of Radar Signal Processing, 2nd ed.; McGraw-Hill Education: New York, NY, USA, 2014. [Google Scholar]
- Yan, J.; Liu, H.; Pu, W.; Zhou, S.; Liu, Z.; Bao, Z. Joint Beam Selection and Power Allocation for Multiple Target Tracking in Netted Colocated MIMO Radar System. IEEE Trans. Signal Process. 2016, 64, 6417–6427. [Google Scholar] [CrossRef]
- Yan, J.; Liu, H.; Pu, W.; Liu, H.; Liu, Z.; Bao, Z. Joint Threshold Adjustment and Power Allocation for Cognitive Target Tracking in Asynchronous Radar Network. IEEE Trans. Signal Process. 2017, 65, 3094–3106. [Google Scholar] [CrossRef]
- Yan, J.; Pu, W.; Liu, H.; Jiu, B.; Bao, Z. Robust Chance Constrained Power Allocation Scheme for Multiple Target Localization in Colocated MIMO Radar System. IEEE Trans. Signal Process. 2018, 66, 3946–3957. [Google Scholar] [CrossRef]
- Haimovich, A.; Blum, R.; Cimini, L. MIMO Radar with Widely Separated Antennas. IEEE Signal Process. Mag. 2008, 25, 116–129. [Google Scholar] [CrossRef]
- Fishler, E.; Haimovich, A.; Blum, R.; Cimini, L.; Chizhik, D.; Valenzuela, R. Spatial Diversity in Radars-Models and Detection Performance. IEEE Trans. Signal Process. 2006, 54, 823–838. [Google Scholar] [CrossRef]
- Xu, L.; Zhang, T.; Ma, Z.; Wang, Y. Power Allocation for Radar Tracking with LPI Constraint and Suppressive Jamming Threat. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 1194–1207. [Google Scholar] [CrossRef]
- Yuan, Y.; Yi, W.; Hoseinnezhad, R.; Varshney, P. Robust Power Allocation for Resource-Aware Multi-Target Tracking with Colocated MIMO Radars. IEEE Trans. Signal Process. 2021, 69, 443–458. [Google Scholar] [CrossRef]
- Shi, C.; Ding, L.; Wang, F.; Salous, S.; Zhou, J. Low Probability of Intercept-Based Collaborative Power and Bandwidth Allocation Strategy for Multi-Target Tracking in Distributed Radar Network System. IEEE Sens. J. 2020, 20, 6367–6377. [Google Scholar] [CrossRef]
- Yan, J.; Jiu, B.; Liu, H.; Chen, B.; Bao, Z. Prior Knowledge-Based Simultaneous Multibeam Power Allocation Algorithm for Cognitive Multiple Targets Tracking in Clutter. IEEE Trans. Signal Process. 2015, 63, 512–527. [Google Scholar] [CrossRef]
- Shalom, Y.; Li, X. Estimation and Tracking-Principles, Techniques, and Software; Artech House Inc.: Norwood, MA, USA, 2023. [Google Scholar]
- Wang, Y.; Zhang, T.; Kong, L.; Ma, Z. A Stochastic Simulation Optimization based Range Gate Pull-off Jamming Method. IEEE Trans. Evol. Comput. 2023, 27, 580–594. [Google Scholar] [CrossRef]
- Schleher, D. LPI radar: Fact or fiction. IEEE Aerosp. Electron. Syst. Mag. 2009, 21, 3–6. [Google Scholar] [CrossRef]
- Shi, C.; Dai, X.; Wang, Y.; Zhou, J.; Salous, S. Joint Route Optimization and Multidimensional Resource Management Scheme for Airborne Radar Network in Target Tracking Application. IEEE Syst. J. 2022, 16, 6669–6680. [Google Scholar] [CrossRef]
- Shi, C.; Zhou, J.; Wang, F. LPI based resource management for target tracking in distributed radar network. In Proceedings of the 2016 IEEE Radar Conference (RadarConf), Philadelphia, PA, USA, 2–6 May 2016. [Google Scholar]
- Martino, A. Introduction to Modern EW Systems, Second Edition; Artech House Inc.: Norwood, MA, USA, 2018. [Google Scholar]
- Costley, A.; Christensen, R.; Leishman, R.; Droge, G. Sensitivity of Single-Pulse Radar Detection to Aircraft Pose Uncertainties. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 2286–2295. [Google Scholar] [CrossRef]
- Shalom, Y.; Chang, K.; Blom, H. Tracking a maneuvering target using input estimation versus the interacting multiple model algorithm. IEEE Trans. Aerosp. Electron. Syst. 1989, 25, 296–300. [Google Scholar] [CrossRef]
- Svensson, D.; Svensson, L. A New Multiple Model Filter with Switch Time Conditions. IEEE Trans. Signal Process. 2010, 58, 11–25. [Google Scholar] [CrossRef]





| Extent of (in Degrees) | Average RCS Value |
|---|---|
| m2 | |
| m2 | |
| m2 | |
| m2 | |
| other | m2 |
| Average Transmit Power | ||||
|---|---|---|---|---|
| Radar | Radar 1 | Radar 2 | Radar 3 | |
| Algorithm | ||||
| AIMP-based algorithm | 6100.2 W | 7438.9 W | 6869.7 W | |
| IMP-based algorithm | 6391.0 W | 7772.3 W | 7087.5 W | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, X.; Xu, L.; Nie, L.; Li, X. AIMP-Based Power Allocation for Radar Network Tracking Under Countermeasures Environment. Sensors 2025, 25, 3163. https://doi.org/10.3390/s25103163
Xing X, Xu L, Nie L, Li X. AIMP-Based Power Allocation for Radar Network Tracking Under Countermeasures Environment. Sensors. 2025; 25(10):3163. https://doi.org/10.3390/s25103163
Chicago/Turabian StyleXing, Xiaoyou, Longxiao Xu, Lvwan Nie, and Xueting Li. 2025. "AIMP-Based Power Allocation for Radar Network Tracking Under Countermeasures Environment" Sensors 25, no. 10: 3163. https://doi.org/10.3390/s25103163
APA StyleXing, X., Xu, L., Nie, L., & Li, X. (2025). AIMP-Based Power Allocation for Radar Network Tracking Under Countermeasures Environment. Sensors, 25(10), 3163. https://doi.org/10.3390/s25103163






