A Semi-Supervised Attention-Temporal Ensembling Method for Ground Penetrating Radar Target Recognition
Abstract
1. Introduction
2. Underground Target Recognition Based on Semi-Supervised Attention-TE
2.1. Temporal Ensembling
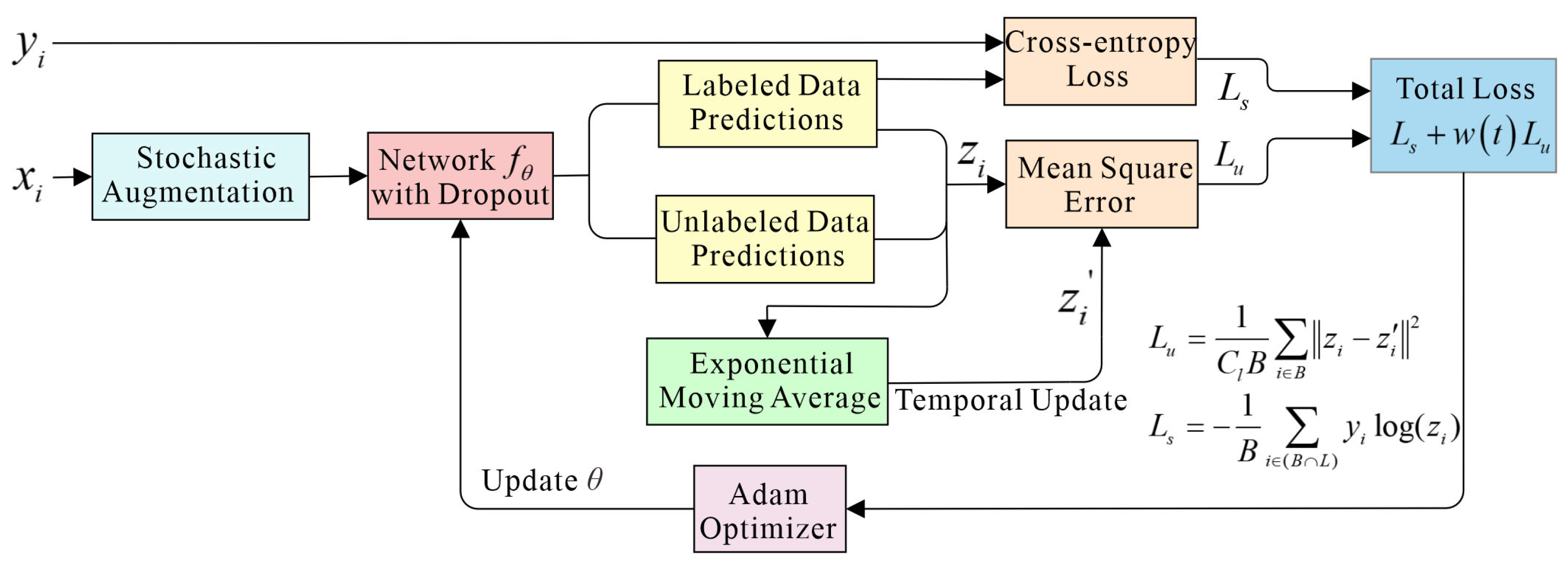
| Algorithm 1: Temporal ensembling pseudocode |
| Input: xi: Training sample, i∈N yi: Labels for labeled samples, i∈L L: Set of training sample indices with known labels |
| fθ(·): Neural network with trainable parameters θ g(·): Stochastic augmentation function w(t): Weighting function α: Momentum factor, 0 < α < 1 Initialization: ▷Initialize ensemble predictions ▷Initialize target vectors 1. For t in [1, epochs] do 2. For each minibatch B do 3. zi fθ (g(xi)) ▷Evaluate network outputs 4. ▷Supervised loss component ▷Unsupervised loss component 5. update θ via Adam optimizer ▷Update network parameters 6. end for 7. ▷Accumulate ensemble predictions 8. ▷Construct target vectors by bias correction 9. end for 10. return θ |
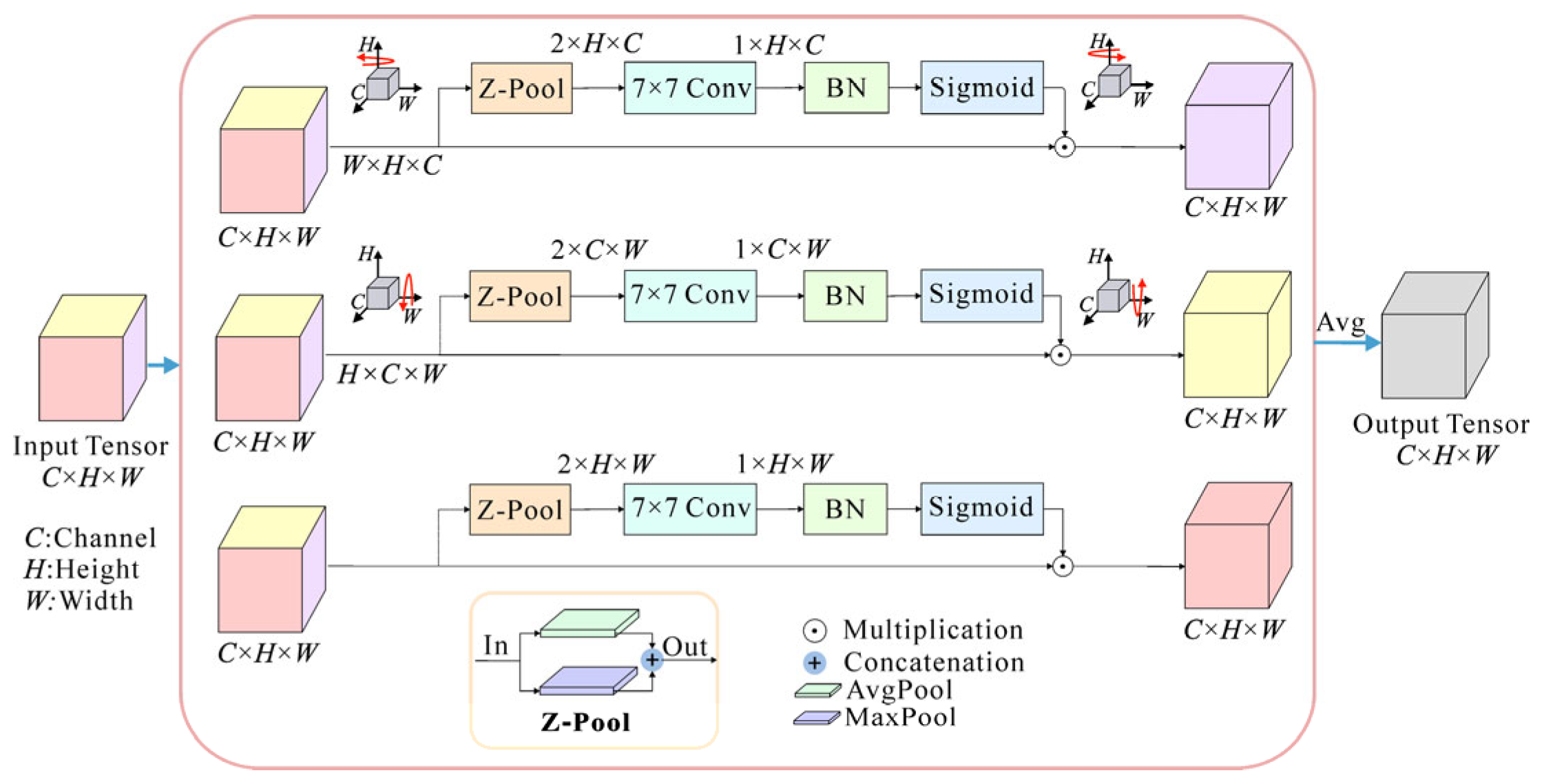
2.2. Triplet Attention
2.3. Attention-TE Method
3. Laboratory Experiments
3.1. Laboratory Data Acquisition
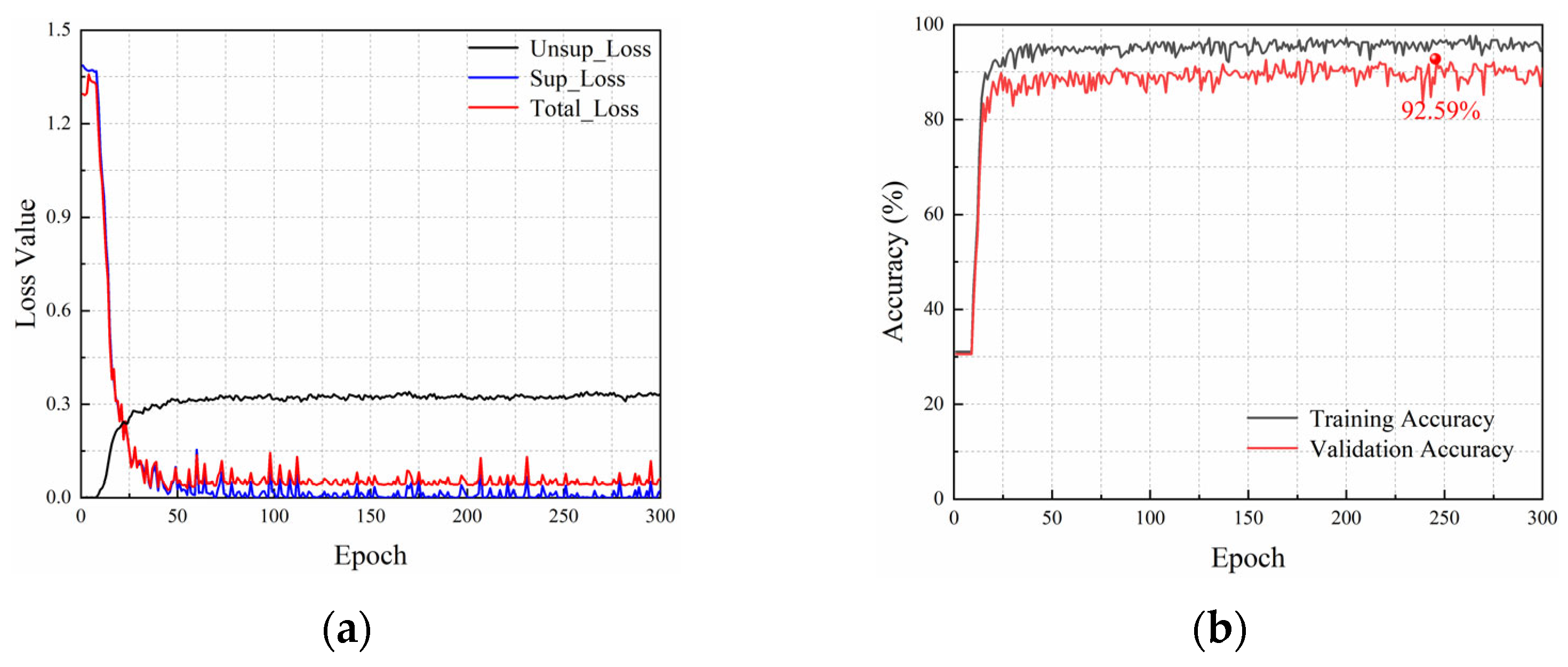
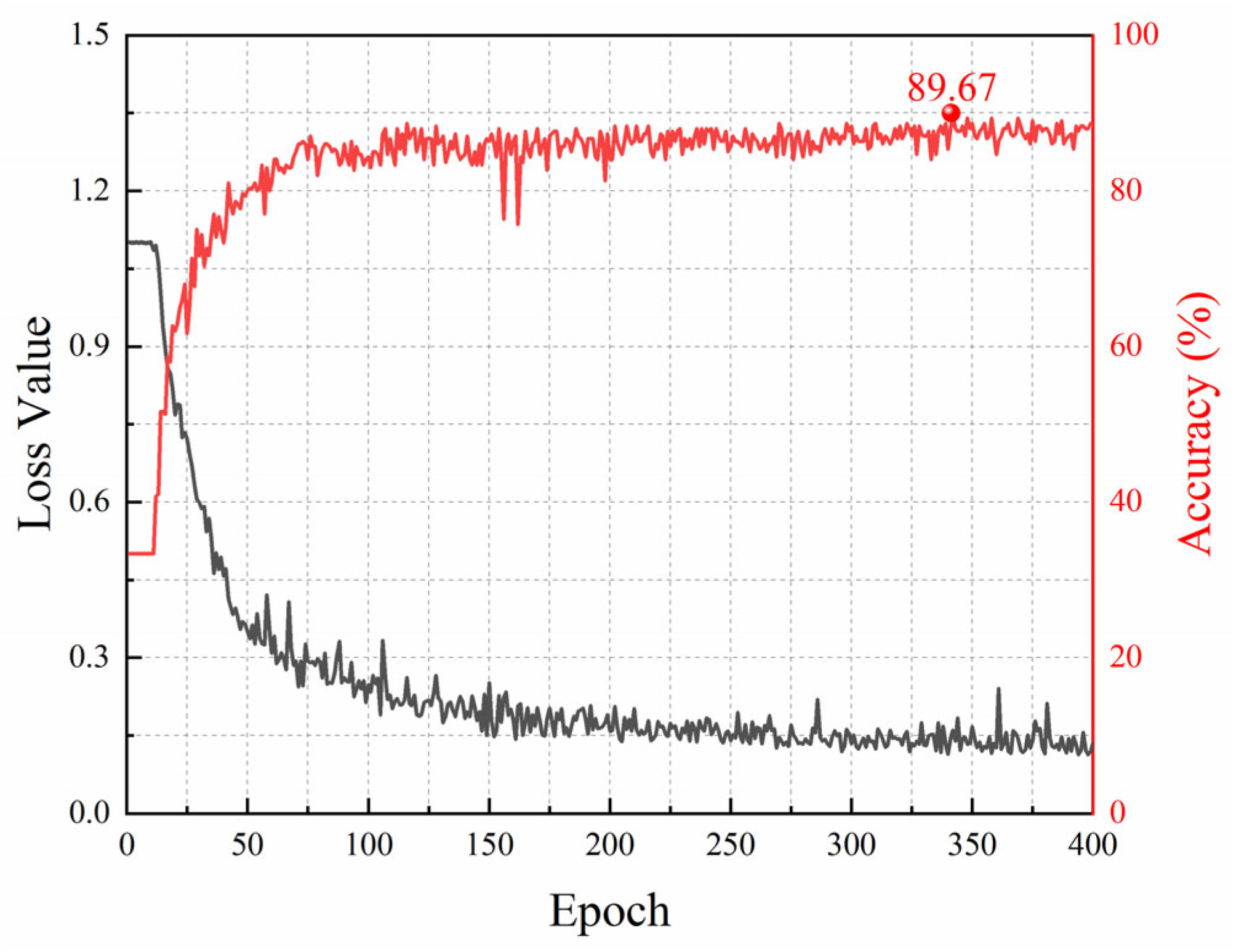
3.2. Network Training for Laboratory Data
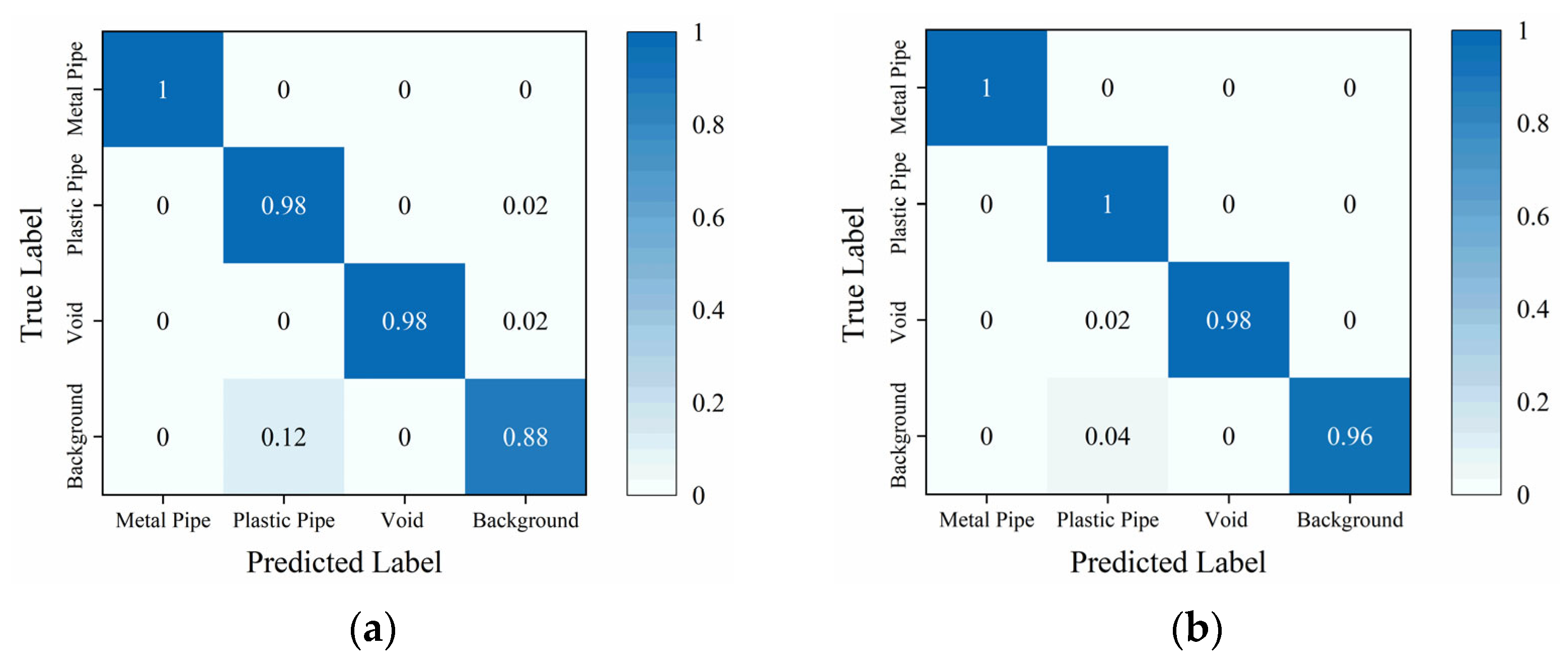
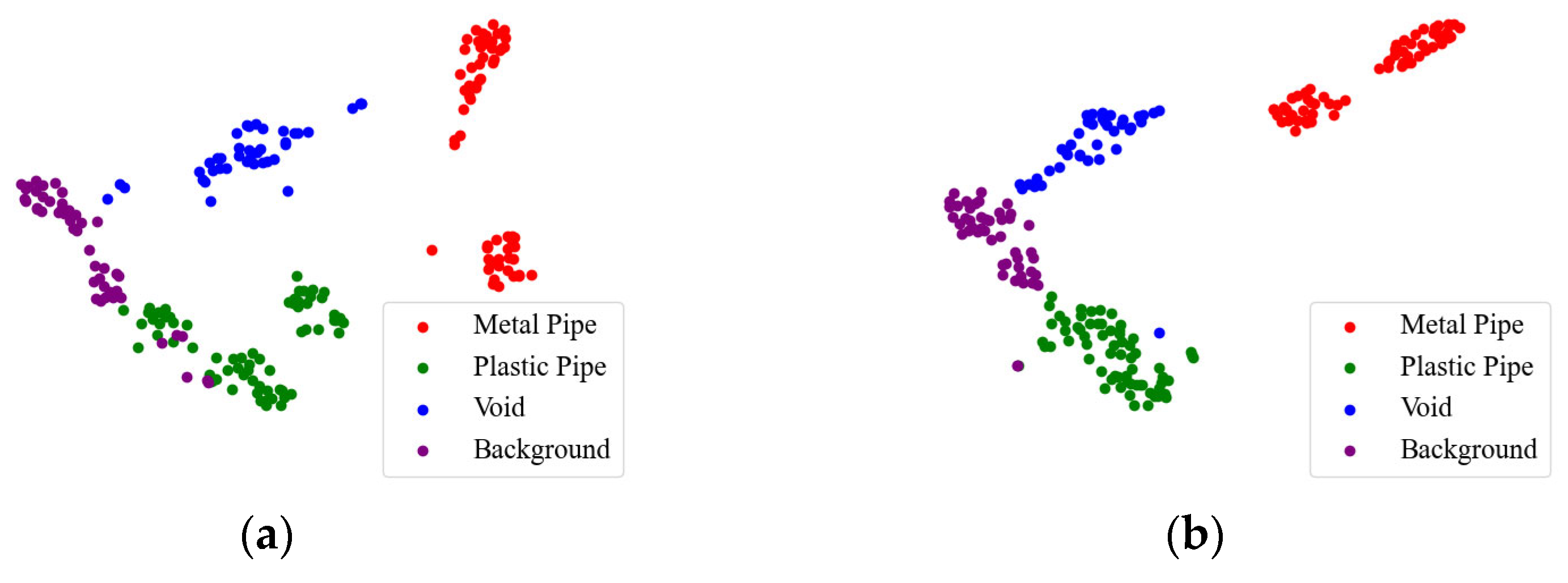
3.3. Classification Results of Laboratory Data
3.4. Ablation Experiments for Laboratory Data
3.5. Comparison with State-of-the-Art Methods for Laboratory Data
4. Field Experiment
4.1. Field Data Acquisition
4.2. Network Training for Field Data
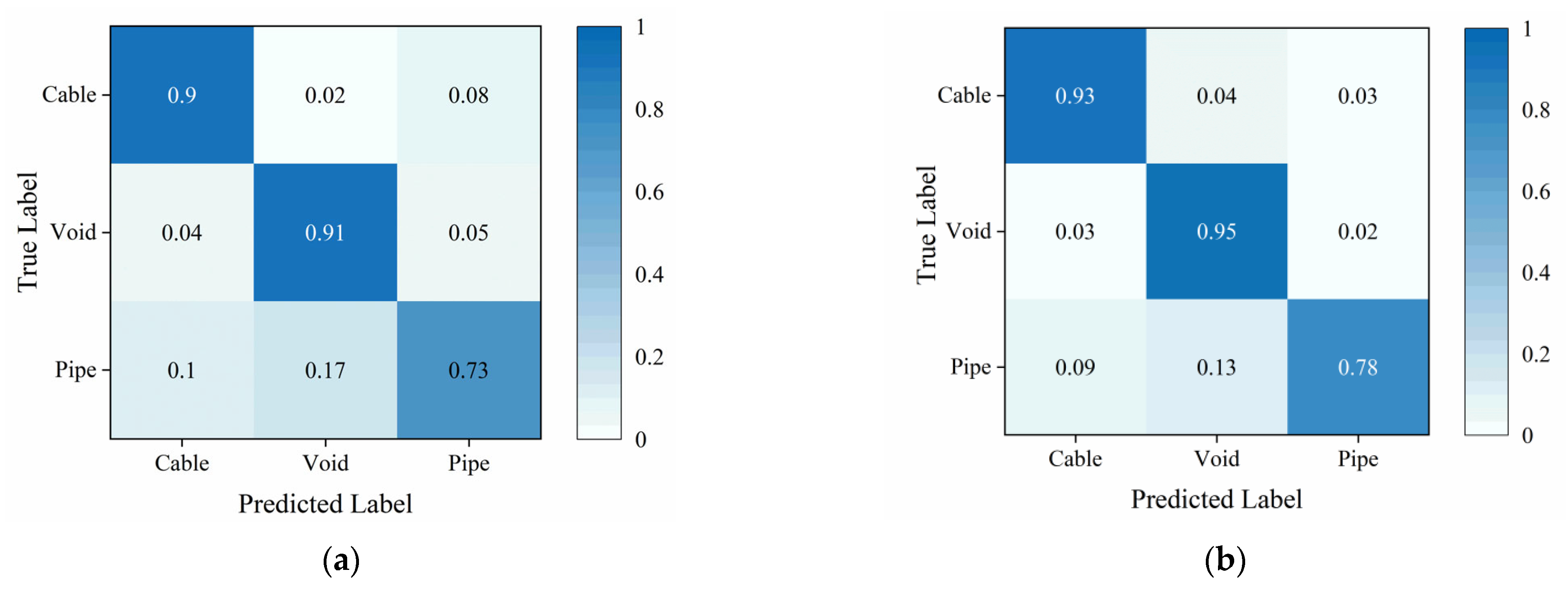
4.3. Classification Results of Field Data
4.4. Ablation Experiments for Field Data
4.5. Comparison with State-of-the-Art Methods for Field Data
5. Conclusions and Discussions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lai, W.W.-L.; Dérobert, X.; Annan, P. A review of Ground Penetrating Radar application in civil engineering: A 30-year journey from Locating and Testing to Imaging and Diagnosis. NDT E Int. 2018, 96, 58–78. [Google Scholar]
- Qin, H.; Zhang, D.; Tang, Y.; Wang, Y. Automatic recognition of tunnel lining elements from GPR images using deep convolutional networks with data augmentation. Autom. Constr. 2021, 130, 103830. [Google Scholar] [CrossRef]
- Li, Y.; Liu, C.; Yue, G.; Gao, Q.; Du, Y. Deep learning-based pavement subsurface distress detection via ground penetrating radar data. Autom. Constr. 2022, 142, 104516. [Google Scholar] [CrossRef]
- Xie, X.; Qin, H.; Yu, C.; Liu, L. An automatic recognition algorithm for GPR images of RC structure voids. J. Appl. Geophys. 2013, 99, 125–134. [Google Scholar] [CrossRef]
- El-Mahallawy, M.S.; Hashim, M. Material classification of underground utilities from GPR images using DCT-based SVM approach. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1542–1546. [Google Scholar] [CrossRef]
- Shao, W.; Bouzerdoum, A.; Phung, S.L.; Su, L.; Indraratna, B.; Rujikiatkamjorn, C. Automatic classification of ground-penetrating-radar signals for railway-ballast assessment. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3961–3972. [Google Scholar] [CrossRef]
- Meşecan, İ.; Çiço, B.; Bucak, I.Ö. Feature vector for underground object detection using B-scan images from GprMax. Microprocess. Microsyst. 2020, 76, 103116. [Google Scholar] [CrossRef]
- Tong, Z.; Gao, J.; Yuan, D. Advances of deep learning applications in ground-penetrating radar: A survey. Constr. Build. Mater. 2020, 258, 120371. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, J.; Sun, W. Recognition of the typical distress in concrete pavement based on GPR and 1D-CNN. Remote Sens. 2021, 13, 2375. [Google Scholar] [CrossRef]
- Besaw, L.E.; Stimac, P.J. Deep convolutional neural networks for classifying GPR B-scans. In Detection and Sensing of Mines, Explosive Objects, and Obscured Targets XX; International Society for Optics and Photonics: Washington, DC, USA, 2015; Volume 9454, pp. 385–394. [Google Scholar]
- Tong, Z.; Gao, J.; Zhang, H. Innovative method for recognizing subgrade defects based on a convolutional neural network. Constr. Build. Mater. 2018, 169, 69–82. [Google Scholar] [CrossRef]
- Ahmed, H.; La, H.M.; Tran, K. Rebar detection and localization for bridge deck inspection and evaluation using deep residual networks. Autom. Constr. 2020, 120, 103393. [Google Scholar] [CrossRef]
- Rosso, M.M.; Marasco, G.; Aiello, S.; Aloisio, A.; Chiaia, B.; Marano, G.C. Convolutional networks and transformers for intelligent road tunnel investigations. Comput. Struct. 2023, 275, 106918. [Google Scholar] [CrossRef]
- Khudoyarov, S.; Kim, N.; Lee, J.-J. Three-dimensional convolutional neural network–based underground object classification using three-dimensional ground penetrating radar data. Struct. Health Monit. 2020, 19, 1884–1893. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Mizutani, T.; Meguro, K.; Hirano, T. Detecting subsurface voids from GPR images by 3-D convolutional neural network using 2-D finite difference time domain method. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 3061–3073. [Google Scholar] [CrossRef]
- Bralich, J.; Reichman, D.; Collins, L.M.; Malof, J.M. Improving convolutional neural networks for buried target detection in ground penetrating radar using transfer learning via pretraining. In Detection and Sensing of Mines, Explosive Objects, and Obscured Targets XXII; SPIE: Bellingham, WA, USA, 2017; Volume 10182, pp. 198–208. [Google Scholar]
- Veal, C.; Dowdy, J.; Brockner, B.; Anderson, D.T.; Ball, J.E.; Scott, G. Generative adversarial networks for ground penetrating radar in hand held explosive hazard detection. In Detection and Sensing of Mines, Explosive Objects, and Obscured Targets XXIII; International Society for Optics and Photonics: Washington, DC, USA, 2015; Volume 10628, pp. 306–323. [Google Scholar]
- Gao, F.; Yang, Y.; Wang, J.; Sun, J.; Yang, E.; Zhou, H. A deep convolutional generative adversarial networks (DCGANs)-based semi-supervised method for object recognition in synthetic aperture radar (SAR) images. Remote Sens. 2018, 10, 846. [Google Scholar] [CrossRef]
- Yan, S.; Zhang, Y.; Gao, F.; Sun, J.; Hussain, A.; Zhou, H. A Trimodel SAR Semisupervised Recognition Method Based on Attention-Augmented Convolutional Networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 9566–9583. [Google Scholar] [CrossRef]
- Seyfioglu, M.S.; Ozbayoglu, A.M.; Gurbuz, S.Z. Deep convolutional autoencoder for radar-based classification of similar aided and unaided human activities. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 1709–1723. [Google Scholar] [CrossRef]
- Ding, Y.; Jin, B.; Zhang, J.; Liu, R.; Zhang, Y. Human motion recognition using doppler radar based on semi-supervised learning. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Wu, D.; Shi, J.; Li, Z.; Du, M.; Liu, F.; Zeng, F. Contrastive Semi-supervised Learning with Pseudo-label for Radar Signal Automatic Modulation Recognition. IEEE Sens. J. 2024, 24, 30399–30411. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, S.; Li, X.; Zhao, H.; Zhu, L.; Chen, S. Ground target recognition using carrier-free UWB radar sensor with a semi-supervised stacked convolutional denoising autoencoder. IEEE Sens. J. 2021, 21, 20685–20693. [Google Scholar] [CrossRef]
- Reid, G. Landmine detection using semi-supervised learning. Electron. Theses Diss. 2018, 3132, 1–19. [Google Scholar]
- Todkar, S.S.; Le Bastard, C.; Baltazart, V.; Ihamouten, A.; Derobort, X. Comparative study of classification algorithms to detect interlayer debondings within pavement structures from Step-frequency radar data. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Valencia, Spain, 22–27 July 2018; pp. 6820–6823. [Google Scholar]
- Liu, H.; Wang, J.; Zhang, J.; Jiang, H.; Xu, J.; Jiang, P.; Zhang, F.; Sui, Q.; Wang, Z. Semi-supervised deep neural network-based cross-frequency ground-penetrating radar data inversion. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–19. [Google Scholar]
- Ma, Y.; Song, X.; Li, Z.; Li, H.; Qu, Z. A Prior Knowledge Guided Semi-Supervised Deep Learning Method for Improving Buried Pipe Detection on GPR Data. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–15. [Google Scholar] [CrossRef]
- Teng, J.; Long, X.; Yang, Q.; Jing, G.; Liu, H. Semi-Conv-DETR: A railway ballast bed defect detection model integrating convolutional augmentation and semi-supervised DETR. Transp. Geotech. 2024, 48, 101334. [Google Scholar] [CrossRef]
- Laine, S.; Aila, T. Temporal ensembling for semi-supervised learning. arXiv 2016, arXiv:1610.02242. [Google Scholar]
- Meel, P.; Vishwakarma, D.K. A temporal ensembling based semi-supervised ConvNet for the detection of fake news articles. Expert Syst. Appl. 2021, 177, 115002. [Google Scholar] [CrossRef]
- Zhu, Q.; Chen, Z.; Soh, Y.C. A novel semisupervised deep learning method for human activity recognition. IEEE Trans. Ind. Inform. 2018, 15, 3821–3830. [Google Scholar] [CrossRef]
- Shi, H.; He, Z.; Hwang, K.S. Domain adaptation with temporal ensembling to local attention region search for object detection. Knowl.-Based Syst. 2025, 309, 112846. [Google Scholar] [CrossRef]
- Misra, D.; Nalamada, T.; Arasanipalai, A.U.; Hou, Q. Rotate to attend: Convolutional triplet attention module. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2021; pp. 3139–3148. [Google Scholar]
- Maaten, L.V.D.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Lee, D. Others Pseudo-label: The simple and efficient semi-supervised learning method for deep neural networks. Workshop Chall. Represent. Learn. ICML 2013, 3, 896. [Google Scholar]
- Odena, A. Semi-Supervised Learning with Generative Adversarial Networks. arXiv 2016, arXiv:1606.01583. [Google Scholar]
- Rasmus, A.; Berglund, M.; Honkala, M.; Valpola, H.; Raiko, T. Semi-supervised learning with ladder networks. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2015; pp. 3546–3554. [Google Scholar]







| Block1 | Block2 | Block3 | FC |
|---|---|---|---|
| Conv 3 × 3, F = 32, S = 1 Conv 3 × 3, F = 32, S = 1 Conv 3 × 3, F = 32, S = 1 Triplet Attention MaxPool 3 × 3, F = 32, S = 2, D = 0.5 | Conv 3 × 3, F = 64, S = 1 Conv 3 × 3, F = 64, S = 1 Conv 3 × 3, F = 64, S = 1 Triplet Attention MaxPool 3 × 3, F = 64, S = 2, D = 0.5 | Conv 3 × 3, F = 32, S = 1 Conv 3 × 3, F = 16, S = 1 Conv 3 × 3, F = 16, S = 1 Triplet Attention MaxPool 3 × 3, F = 16, S = 2, D = 0.5 | FC1 128 FC2 Cl |
| Target | Total | Training | Validation | Testing |
|---|---|---|---|---|
| Metal pipe | 868 | 744 | 62 | 62 |
| Plastic pipe | 924 | 792 | 66 | 66 |
| Void | 560 | 480 | 40 | 40 |
| Background | 672 | 576 | 48 | 48 |
| Total | 3024 | 2592 | 216 | 216 |
| Labeling Rate | Metal Pipe | Plastic Pipe | Void | Background | Average Accuracy |
|---|---|---|---|---|---|
| 5% | 94.35 ± 4.04 | 89.09 ± 3.56 | 74.25 ± 5.28 | 79.17 ± 10.1 | 84.21 ± 2.91 |
| 10% | 99.52 ± 0.78 | 97.27 ± 1.72 | 88.50 ± 4.89 | 79.38 ± 3.47 | 91.17 ± 0.92 |
| 15% | 100.0 ± 0.00 | 98.03 ± 1.76 | 99.00 ± 1.75 | 84.79 ± 2.95 | 95.46 ± 0.72 |
| 20% | 99.36 ± 0.83 | 99.24 ± 1.07 | 98.00 ± 1.58 | 96.87 ± 2.03 | 98.37 ± 0.70 |
| 25% | 99.68 ± 0.68 | 99.24 ± 1.64 | 99.00 ± 2.42 | 96.67 ± 1.76 | 98.65 ± 0.62 |
| Labeling Rate | TE | TE + SE | Ours |
|---|---|---|---|
| 5% | 81.75 ± 3.20 | 82.62 ± 2.66↑0.87 | 84.21 ± 2.91↑2.46 |
| 10% | 90.53 ± 0.55 | 91.05 ± 1.21↑0.52 | 91.17 ± 0.92↑0.64 |
| 15% | 94.35 ± 0.46 | 94.55 ± 0.70↑0.20 | 95.46 ± 0.72↑1.11 |
| 20% | 96.28 ± 0.56 | 96.51 ± 0.33↑0.23 | 98.37 ± 0.70↑2.09 |
| 25% | 97.10 ± 0.69 | 97.54 ± 0.29↑0.44 | 98.65 ± 0.62↑1.55 |
| Methods | Pseudo-Label [35] | SCAE [20] | SGAN [36] | Ladder Network [37] | VGG16 | Ours |
|---|---|---|---|---|---|---|
| Accuracy (%) | 88.11 ± 2.30 | 82.78 ± 3.11 | 78.47 ± 3.54 | 76.63 ± 2.01 | 89.45 ± 0.29 | 91.17 ± 0.92 |
| Precision (%) | 90.28 ± 3.06 | 83.95 ± 3.75 | 80.47 ± 3.24 | 77.79 ± 2.22 | 89.82 ± 0.36 | 93.27 ± 0.72 |
| Recall (%) | 88.11 ± 2.30 | 82.78 ± 3.11 | 78.47 ± 3.54 | 76.63 ± 2.01 | 89.45 ± 0.29 | 91.17 ± 0.92 |
| F1-score (%) | 89.18 ± 2.59 | 83.36 ± 3.42 | 79.45 ± 3.33 | 77.21 ± 2.11 | 89.63 ± 0.32 | 92.20 ± 0.76 |
| Target | Total | Training | Validation | Testing |
|---|---|---|---|---|
| Pipe | 1000 | 800 | 100 | 100 |
| Void | 940 | 740 | 100 | 100 |
| Cable | 1000 | 800 | 100 | 100 |
| Total | 2940 | 2340 | 300 | 300 |
| Methods | Pseudo-Label | SCAE | SGAN | Ladder Network | VGG16 | Ours |
|---|---|---|---|---|---|---|
| Accuracy (%) | 83.60 ± 3.77 | 77.30 ± 1.85 | 63.70 ± 3.96 | 65.63 ± 1.67 | 85.93 ± 0.83 | 88.57 ± 1.75 |
| Precision (%) | 84.06 ± 3.55 | 78.60 ± 1.53 | 64.08 ± 3.89 | 66.45 ± 1.63 | 86.12 ± 0.94 | 89.06 ± 1.41 |
| Recall (%) | 83.60 ± 3.77 | 77.30 ± 1.85 | 63.70 ± 3.96 | 65.63 ± 1.67 | 85.93 ± 0.83 | 88.57 ± 1.75 |
| F1-score (%) | 83.83 ± 3.65 | 77.94 ± 1.58 | 63.89 ± 3.92 | 66.04 ± 1.64 | 86.03 ± 0.88 | 88.81 ± 1.57 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Yu, D.; Zhang, X.; Xu, H.; Li, J.; Zhou, L.; Wang, B. A Semi-Supervised Attention-Temporal Ensembling Method for Ground Penetrating Radar Target Recognition. Sensors 2025, 25, 3138. https://doi.org/10.3390/s25103138
Liu L, Yu D, Zhang X, Xu H, Li J, Zhou L, Wang B. A Semi-Supervised Attention-Temporal Ensembling Method for Ground Penetrating Radar Target Recognition. Sensors. 2025; 25(10):3138. https://doi.org/10.3390/s25103138
Chicago/Turabian StyleLiu, Li, Dajiang Yu, Xiping Zhang, Hang Xu, Jingxia Li, Lijun Zhou, and Bingjie Wang. 2025. "A Semi-Supervised Attention-Temporal Ensembling Method for Ground Penetrating Radar Target Recognition" Sensors 25, no. 10: 3138. https://doi.org/10.3390/s25103138
APA StyleLiu, L., Yu, D., Zhang, X., Xu, H., Li, J., Zhou, L., & Wang, B. (2025). A Semi-Supervised Attention-Temporal Ensembling Method for Ground Penetrating Radar Target Recognition. Sensors, 25(10), 3138. https://doi.org/10.3390/s25103138







