1. Introduction
Land cover mapping serves as a fundamental tool for analyzing and monitoring human activities and natural environmental processes [
1]. Advanced remote sensing image processing techniques enable precise land cover identification and robust classification frameworks [
2,
3,
4]. The rapid evolution of remote sensing and Earth observation technologies has revolutionized the way we collect and interpret data, enabling the acquisition of diverse and high-quality information from a multitude of sensors for practical applications [
5,
6,
7]. Among these, hyperspectral imaging (HSI) has emerged as an indispensable tool for land classification due to its unparalleled ability to capture rich spectral information, which allows for the discrimination of subtle differences in land cover characteristics [
8,
9,
10]. Despite its advantages, HSI-based classification is often constrained by limitations in spatial resolution and susceptibility to atmospheric interference and has difficulties in distinguishing different ground objects that produce similar spectral responses. All these factors may reduce the accuracy of the classification results [
11,
12]. On the other hand, Light Detection and Ranging (LiDAR) technology affords a complementary vista by supplying highly precise elevation data, which exhibit a relatively lower susceptibility to weather conditions and atmospheric perturbations [
6,
13,
14]. This inherent flexibility and robustness make LiDAR indispensable in scenarios where spectral data alone prove insufficient. The complementary integration of HSI and LiDAR data thus offers a powerful approach to leverage their combined strengths. By merging the rich spectral signatures from HSI with LiDAR’s precise 3D structural information, this multimodal approach effectively mitigates the individual limitations of each technique, substantially improving land classification accuracy [
15,
16].
In recent years, deep learning-based fusion methods combining HSI and LiDAR data have demonstrated impressive performance due to their robust feature extraction capabilities. Among these approaches, convolutional neural networks (CNNs) and transformer-based methods are the most commonly employed. For instance, Xu et al. [
17] developed a dual-tunnel CNN framework to extract spectral–spatial features from both HSI and LiDAR data. Additionally, Wang et al. [
18] introduced a multi-scale pyramid fusion framework that leverages spatial–spectral cross-modal attention, enhancing classification through effective multi-scale information learning. Wu et al. [
19] proposed a new deep learning framework for multimodal remote sensing data classification, utilizing CNNs as the backbone and incorporating an advanced cross-channel reconstruction module. Traditional CNN-based multimodal fusion classification methods suffer from insufficient contextual awareness. Their limited receptive field design can only extract local features and struggles to model long-range dependencies, resulting in weak global information integration capabilities [
20,
21]. Recently, transformer networks have been introduced to the multimodal remote sensing domain due to their distinctive and powerful global modeling capabilities, demonstrating remarkable performance. The GLT-Net framework utilizes convolutional operators for local spatial feature extraction while employing transformer architecture to model long-range dependencies. Additionally, it incorporates a hybrid strategy combining multi-scale feature fusion with probabilistic decision fusion to enhance performance [
22]. Roy et al. [
23] presented a multimodal fusion transformer (MFT) network that features multi-head cross-patch attention and uses LiDAR to initialize the classification token. Yao et al. [
24] proposed an innovative multimodal deep learning framework designed for processing remote sensing image patches, which utilizes parallel branches of position-sharing vision transformers (ViTs) enhanced with separable convolutional modules. Despite their successes, these methods often face limitations in the number of parameters, necessitating a large number of labeled samples for optimal training and performance.
Graph-based semi-supervised methods enhance classification accuracy by effectively utilizing information from unlabeled samples [
25,
26]. For example, Xia et al. [
27] applied morphological filters to both LiDAR and hyperspectral data to extract features, which were then fused for classification using semi-supervised graph fusion. Du et al. [
28] proposed constructing multimodal graphs for feature fusion, employing graph-based loss functions to guide the feature extraction network. Additionally, Wang et al. [
29] introduced a classification method for HSI and LiDAR data based on a dual-coupled CNN-GCN structure. While these graph-based methods have made notable strides in improving classification accuracy by fusing complementary information from two modalities, many existing approaches overlook the complex higher-order inter-modal and intra-modal correlations prevalent in real-world multimodal data. In traditional graph convolutional neural network methods, pairwise connections among data are employed. However, there are limitations in expressing the correlations of multimodal data. The structure of multimodal data extends beyond pairwise connections, and a hypergraph structure can be used for multimodal data modeling. Hypergraphs are capable of encoding high-order data correlations by using their hyperedges without degree constraints [
30]. Ma et al. proposed a feature fusion hypergraph neural network for HSI classification. It extracts spatial and spectral features to generate hyperedges for constructing a hypergraph representing HSI features [
31]. However, this pixel-wise graph construction method (where each pixel serves as a node and the hyperedge quantity is a multiple of the node count) generates significant computational overhead. EHGNN takes superpixels as the nodes of the hypergraph and uses the KNN algorithm to construct hyperedges for hypergraph feature learning [
32]. Xu et al. established a hypergraph model at the superpixel level. This model not only fuses the local homogeneity and complex correlations of HSI but also consumes very little computational resources [
33]. Although using superpixels as graph nodes reduces the computational load, it leads to the loss of pixel-level features and easily causes over-smoothing. In this paper, we propose to use pixels as the nodes of the hypergraph, extract superpixels from HSI and LiDAR, respectively, and use the superpixels as hyperedges to construct an adjacency matrix for feature learning. This way, not only can the computational load be greatly reduced but also pixel-level features can be effectively retained without over-smoothing. More importantly, it can naturally depict the homogeneous structures of the two modalities. The main contributions can be summarized as follows:
In this study, we pioneer the application of HGCNs to the classification tasks of HSI and LiDAR data, enabling the capture of long-range dependencies while simultaneously characterizing the spatial structural properties of both HSI and LiDAR. By integrating HGCNs with a lightweight CNN, our approach effectively extracts local features while fully leveraging the synergistic advantages of both architectures.
For HSI and LiDAR data, we employ SLIC [
34] and Felzenszwalb [
35] segmentation methods, respectively. Our innovative strategy of constructing hyperedges using superpixels maximizes the utilization of homogeneous information during feature extraction. This design not only preserves pixel-level discriminative features but also significantly reduces computational overhead.
Extensive experimental results demonstrate that the proposed HGCN-HL model achieves remarkable performance in HSI and LiDAR classification tasks, outperforming state-of-the-art methods. Benefiting from the inherent advantages of its lightweight architecture, HGCN-HL achieves substantial speed improvements in both the training and testing phases, exhibiting superior computational efficiency compared to other leading networks.
The remainder of this paper is structured as follows.
Section 2 introduces the proposed methodology, detailing the framework and key innovations.
Section 3 presents the experimental setup, including datasets, implementation details, and comparative results.
Section 4 provides an in-depth analysis and discussion of the method’s performance and limitations. Finally,
Section 5 concludes this paper with key findings and potential future research directions.
2. Method
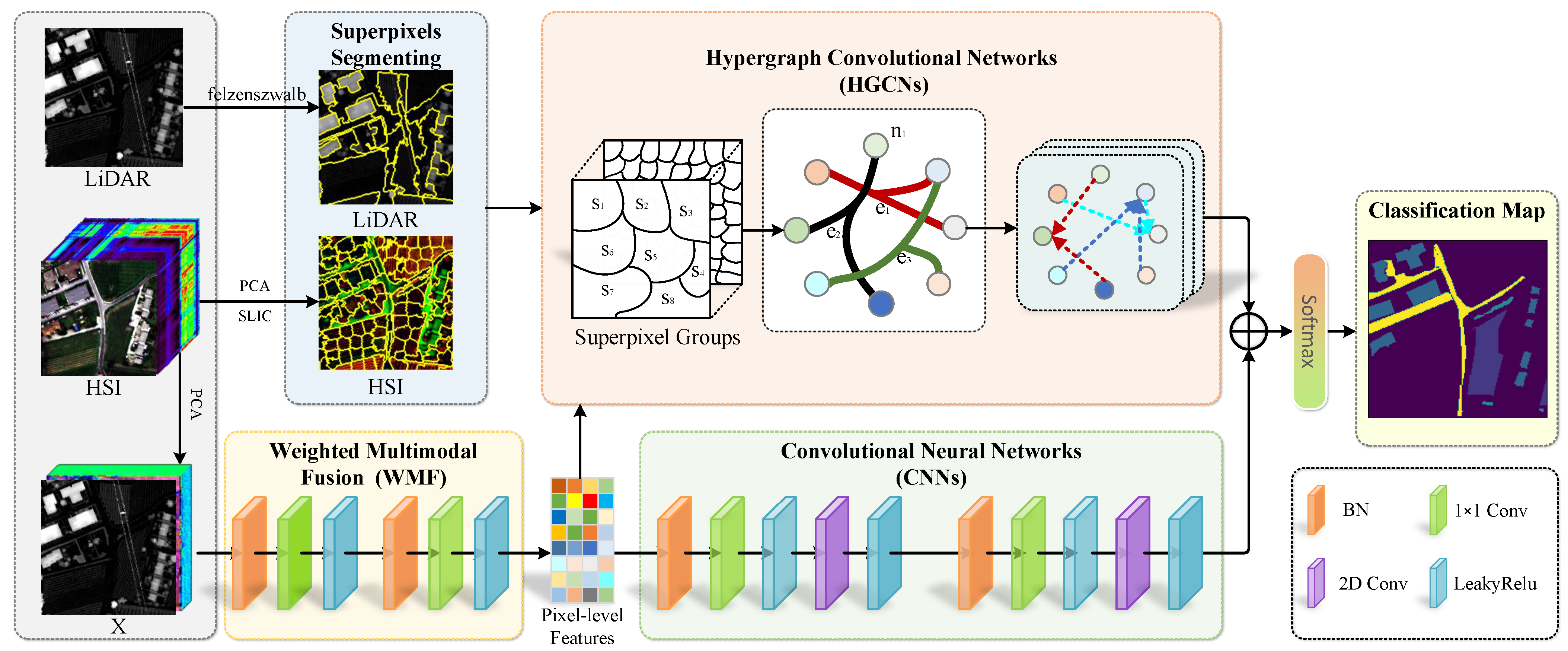
Figure 1 illustrates the framework of the proposed method. We represent the hyperspectral image as
and the corresponding LiDAR image as
, where
H and
W are the spatial dimensions and
B is the number of spectral bands in the hyperspectral image. All pixels are classified into
C categories, denoted as
. First, we normalize
and
on a channel-wise basis to obtain
and
. Next, we perform principal component analysis (PCA) on the normalized hyperspectral image
, reducing it to
spectral bands, represented as
. We then conduct a preliminary fusion of the two modalities along the spectral bands, creating a multimodal dataset defined as
, where
indicates the concatenation operation along the spectral dimension. We provide our source code at
https://github.com/giswl/HGCN-HL (accessed on 9 April 2025) to support the remote sensing research community.
2.1. Weighted Multimodal Fusion (WMF)
The Weighted Multimodal Fusion (WMF) mechanism is proposed to effectively integrate HSI and LiDAR data through adaptive feature weighting. This approach dynamically assigns importance weights to different modalities based on their discriminative contributions to the classification task. The HSI and LiDAR data are processed using a
convolution, where
denotes the
jth output feature in the
lth layer.
where
is the weight parameter of the
lth layer corresponding to the
jth output feature. The notation
indicates that the output
from the
th layer undergoes a batch normalization operation. Additionally,
represents the bias parameter of the
lth layer corresponding to the
jth output feature.
is an activation function, such as LeakyReLU(·).
2.2. Feature Extraction via CNNs
Convolutional neural networks (CNNs) inherently model inter-feature contextual relationships, enabling robust inference and state-of-the-art performance in HSI and LiDAR classification. Their hierarchical architecture extracts high-level abstract features through localized receptive fields, yielding semantically discriminative representations from complex multimodal data. To extract spatial–spectral features from multimodal data and reduce the model parameters, we employ the spatial–spectral convolution proposed by Liu et al. [
36]. The 3D convolution kernel can be decomposed into two simpler convolution kernels: a
convolution kernel and a 2D convolution kernel. Thus, the spatial–spectral convolution layer can be modeled as
where
and
are the
and 2D convolutional filters with multiple kernels, BN(·) represents the batch normalization operation, and ‘*’ denotes the convolution operator.
In a conventional standard convolution, a single kernel processes all the channels of the input feature map simultaneously. This implies that the number of parameters per kernel grows proportionally with the input channels, leading to a rapid escalation in both computational cost and parameter count. In this work, the 2D convolutional layer employs depthwise convolution, where each channel of the input feature map is processed by an independent convolutional kernel. Specifically, for an input feature map with channels, the depthwise convolution utilizes separate kernels, each with a depth of 1. Consequently, each kernel only performs a convolution on a single corresponding input channel, significantly reducing both computational complexity and parameter count.
2.3. Multiple Hyperedge Fusion
In conventional GCN-based approaches, graphs are typically constructed and learned using unimodal features. This limitation stems from their reliance on adjacency matrix A as the input, which inherently constrains the number of edges. By contrast, our method employs incidence matrix
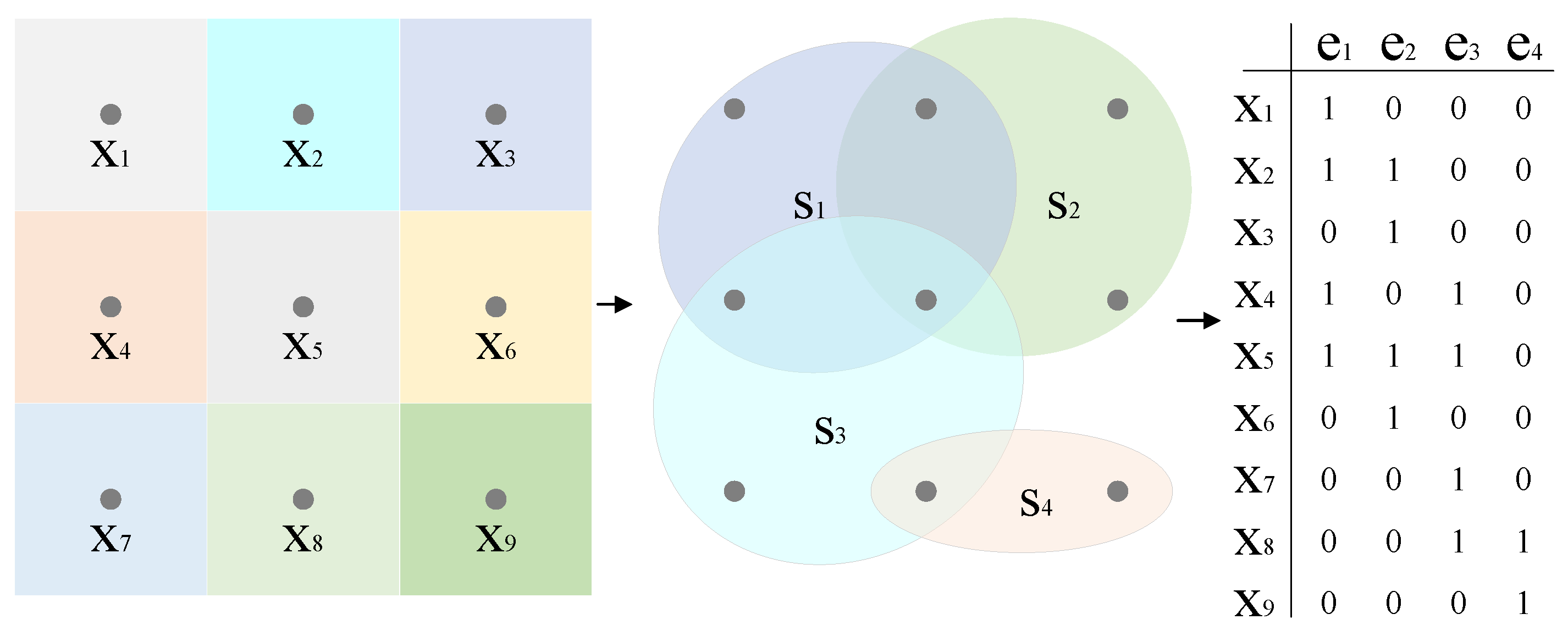
to represent hypergraph topology, enabling the simultaneous modeling of both hyperspectral and LiDAR data modalities. This framework requires joint feature generation from the two distinct data sources. As illustrated in
Figure 2, we developed a multimodal hypergraph to effectively capture the intrinsic relationships within multimodal data by utilizing superpixels. The Simple Linear Iterative Clustering (SLIC) algorithm, an adaptation of k-means clustering, effectively partitions HSI into homogeneous superpixel regions while preserving local spectral–spatial consistency. After applying SLIC, the HSI is divided into
N superpixels, represented as
. Each superpixel serves as a hyperedge, which is then flattened with the dataset
, resulting in
. The relationship between the pixels and superpixels is defined as follows:
where
) indicates whether pixel
) belongs to superpixel
. This binary mapping enables the construction of the incidence matrix.
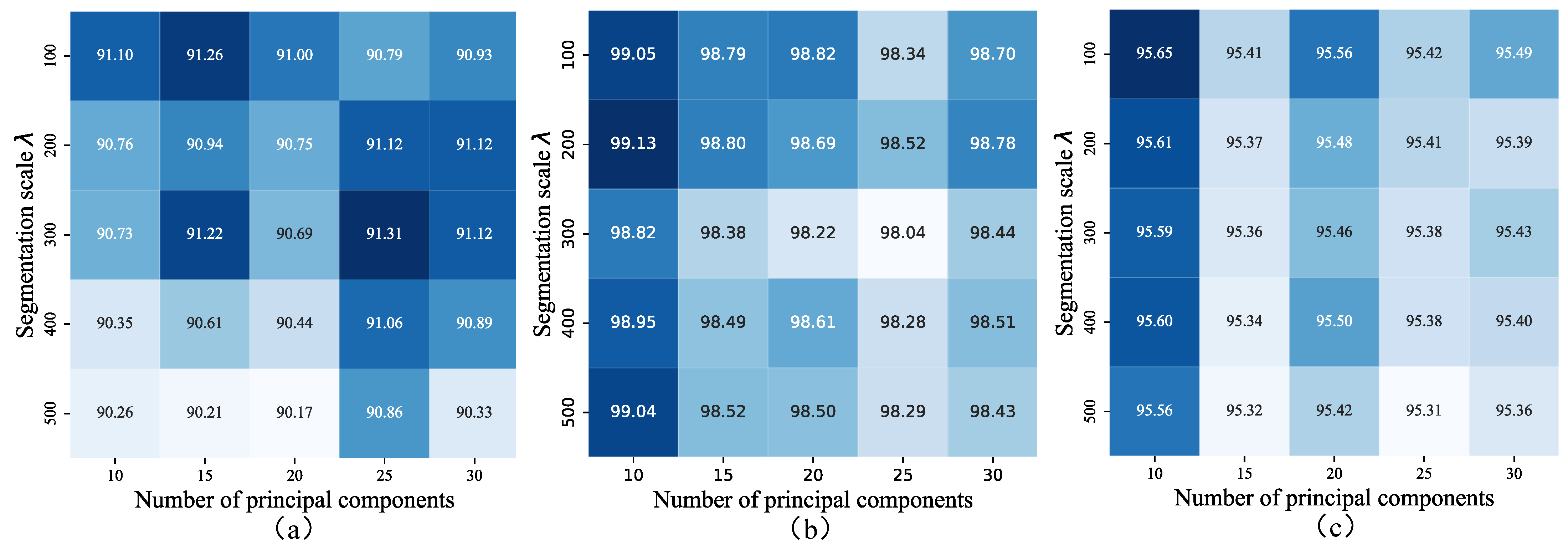
Based on this relationship, an incidence matrix can be constructed. Selecting an appropriate number of superpixels is crucial. An insufficient number of superpixels may cause heterogeneity among the pixels within each superpixel, while an excessive number can elevate computational complexity. For HSI, to appropriately scale for ground objects, we introduce , the number of pixels per superpixel. This leads to the formula , which helps streamline the hyperparameter selection process.
This relationship enables the construction of an incidence matrix
. Selecting the appropriate number of superpixels (
N) is essential; too few superpixels can result in heterogeneous pixels within each superpixel, while too many can lead to increased computational complexity. To properly scale for ground objects in HSI, we introduce
, the number of pixels per superpixel, resulting in the expression
. This method simplifies the hyperparameter selection process in practice. By applying a specific value of
, we generate hyperpixels
and their corresponding incidence matrices
. For LiDAR data, we leverage the Felzenszwalb algorithm, a well-known and effective segmentation method, to create superpixels
along with their associated incidence matrices
. The Felzenszwalb algorithm is adept at exploiting the geometric and intensity information in LiDAR data to produce meaningful superpixel segments. The fusion of hyperedges derived from these multimodal features is accomplished by concatenating the respective incidence matrices, as described by the following equation:
where [·,·] represents the concatenation operation. This concatenation operation effectively combines the complementary information from HSI and LiDAR data. By integrating the incidence matrices, we can take advantage of the rich spectral details from HSI and the accurate geometric information from LiDAR, enabling a more comprehensive and robust representation of the scene.
2.4. Hypergraph Convolution Neural Network
A hypergraph generalizes traditional graphs by allowing hyperedges to connect arbitrary subsets of vertices. Formally defined as
, it consists of vertex set
and hyperedge set
. Unlike graph convolutional networks (GCNs) using adjacency matrices
to model pairwise connections, hypergraphs employ incidence matrices
to capture higher-order relationships. The incidence matrix entries are defined as follows:
The hypergraph Laplacian matrix
is constructed as follows:
where
is the hyperedge weight matrix, and
,
are the diagonal matrices encoding the vertex and hyperedge degrees, respectively. Given a vertex
, its degree
is defined as
. For an edge
, its degree
is given by
. These degree matrices serve to normalize the incidence matrix
, a critical operation for hypergraph analysis.
In the context of HSI and LiDAR fusion, the hypergraph convolution process extends graph convolution principles. For pixel-level feature representation
and hypergraph association matrix
, the
th layer output is computed as follows:
Here, is a diagonal weight matrix with trainable parameters representing hyperedge weights. The vertex and hyperedge degree matrices , ensure proper normalization. The learnable parameters transform input features to output features using the ReLU activation function .
2.5. Feature Fusion and Classification
Due to the distinct nature of HGCNs and CNNs, the feature distributions from these two branches differ. To effectively integrate these features, this study employs additive fusion, multiplicative fusion, concatenation-based fusion, and attention-based fusion strategies [
37], as detailed below:
where
,
, and
represent the outputs of the HGCNs, the CNNs, and the final fused feature map, respectively. [·,·] represents the concatenation operation. The symbol ⊙ denotes the Hadamard product. We use the attention mechanism
(
,
) to learn their corresponding importance (
,
) as follows:
Then, we combine these two embeddings to obtain the final embedding
expressed as follows:
To train the network, we employ a cross-entropy loss function expressed as follows:
Here, N denotes the number of samples, c represents the number of classes, and is the feature representation of the ith sample (where d is 128 in this paper), belonging to class . is the jth column of the weight matrix , and is the bias term.