Introducing a Quality-Driven Approach for Federated Learning
Abstract
1. Introduction
- RQ1. To what extent is DQFed robust in handling class imbalance?
- RQ2. To what extent is DQFed robust in addressing mislabeled data?
- RQ3. How does the robustness of DQFed change with an increasing number of clients?
- RQ4. To what extent is DQFed more effective compared to state-of-the-art (SOA) approaches?
2. Related Work
2.1. Unbalancing in Federated Learning
2.2. Mislabeling in Federated Learning
3. Background
3.1. Federated Learning
- The central server initializes and distributes the global model to participating clients.
- Each client trains the model locally using its private dataset and computes an updated version of the model.
- The server aggregates the clients’ updates to refine the global model.
- x is the data feature;
- y is the data label;
- is the local data size;
- n is the total number of sample pairs;
- C is the client participation ratio;
- l is the loss function;
- k is the client index.
- Horizontal Federated Learning (HFL): This paradigm applies when the datasets across different clients share the same set of features but consist of different samples. In other words, the data of each client correspond to a subset of the population, with identical feature spaces. For example, consider multiple hospitals collaborating to build a machine learning model for predicting disease risks. Each hospital collects data about patients using the same attributes, such as age, medical history, and lab results, but the patient populations do not overlap [40]. HFL is particularly effective in domains where institutions operate in similar contexts but are restricted from sharing sensitive data directly due to privacy concerns or regulations like GDPR.
- Vertical Federated Learning (VFL): This paradigm applies when the datasets across different clients contain the same set of samples but differ in their features. VFL arises in situations where organizations possess complementary information about the same individuals or entities. For instance, a bank may hold transactional and financial data about its customers, while an e-commerce platform has data about their purchasing behavior. By collaboratively training a model without sharing raw data, these organizations can leverage their combined feature spaces to improve model performance [41]. VFL is especially valuable in cross-industry collaborations where the datasets are fragmented but can provide mutual benefits if integrated securely.
- Federated Transfer Learning (FTL): In scenarios where datasets across clients differ in both features and samples, Federated Transfer Learning bridges the gap by leveraging transfer learning techniques. FTL enables knowledge sharing between domains with little or no overlap in data but with related tasks. For example, a healthcare provider in one region may have patient data with a rich set of features, while another region may have fewer features but a larger sample size. By transferring learned representations or knowledge, FTL allows both entities to enhance their models despite the dissimilarity in data distributions.
3.2. The FedAvg Algorithm
| Algorithm 1 Federated averaging (FedAvg) algorithm. |
| Require: K: Total number of clients. F: Fraction of clients selected in each round. E: Number of local training epochs. B: Local batch size. : Initial global model parameters. Ensure: Updated global model parameters after T rounds.
|
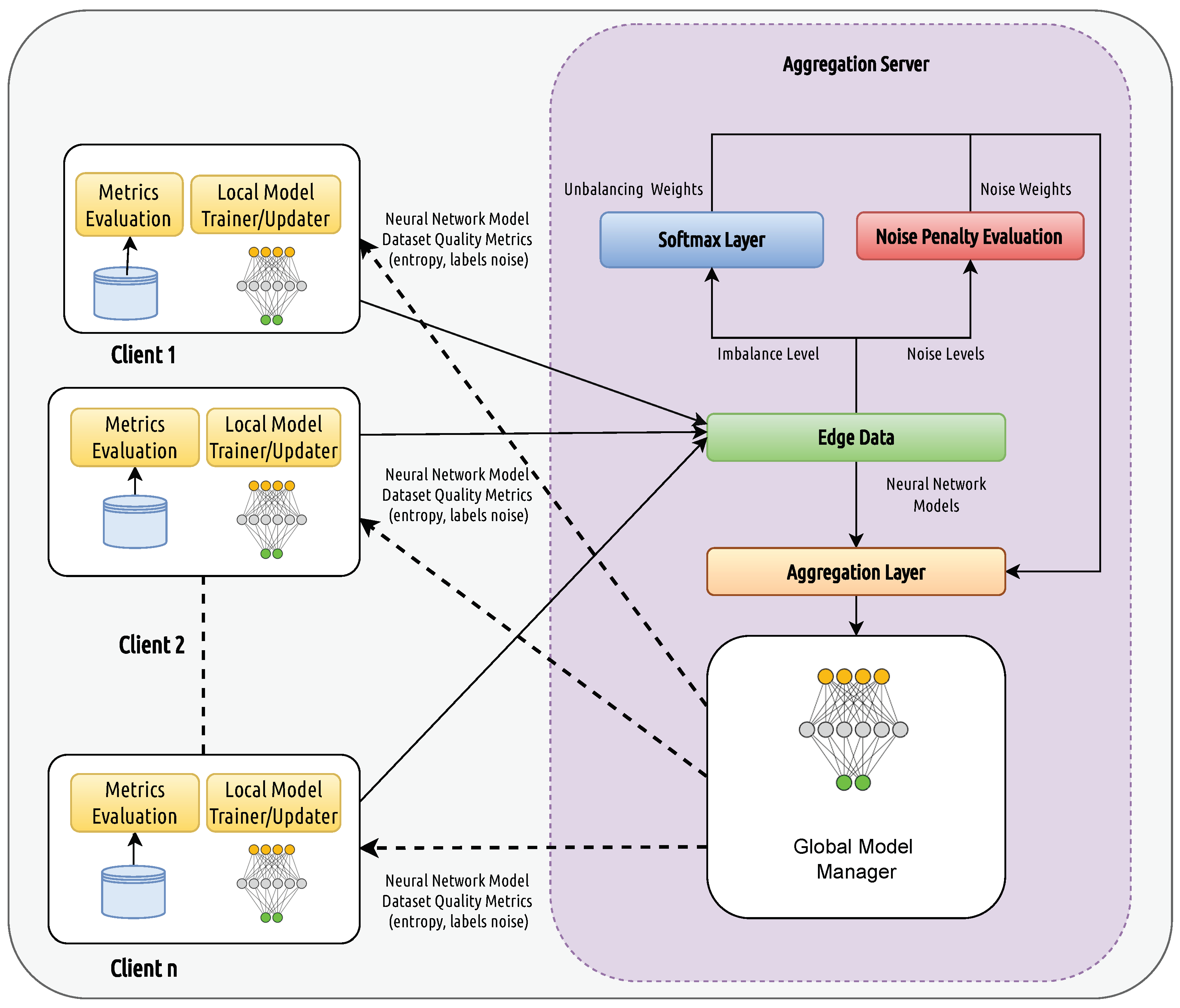
4. The DQFed Approach
- e is the base of the natural logarithm;
- N represents the number of classes;
- is the sum of the exponentials of all elements in z
4.1. The Quality Model
4.1.1. The Shannon Entropy
- V is the number of values in a dataset;
- N represents classes;
- represents the size of class i.
4.1.2. Noise Detection and Penalization Score
| Algorithm 2 VAE training for noise detection. |
| Require: Training dataset D, number of epochs E, batch size B, learning rate , noise rate Ensure: Trained VAE model M
|
4.1.3. Penalization Strategies for Noise and Imbalance
| Algorithm 3 NRP score calculation and DQFed Aggregation. |
Require:
|
5. Empirical Validation
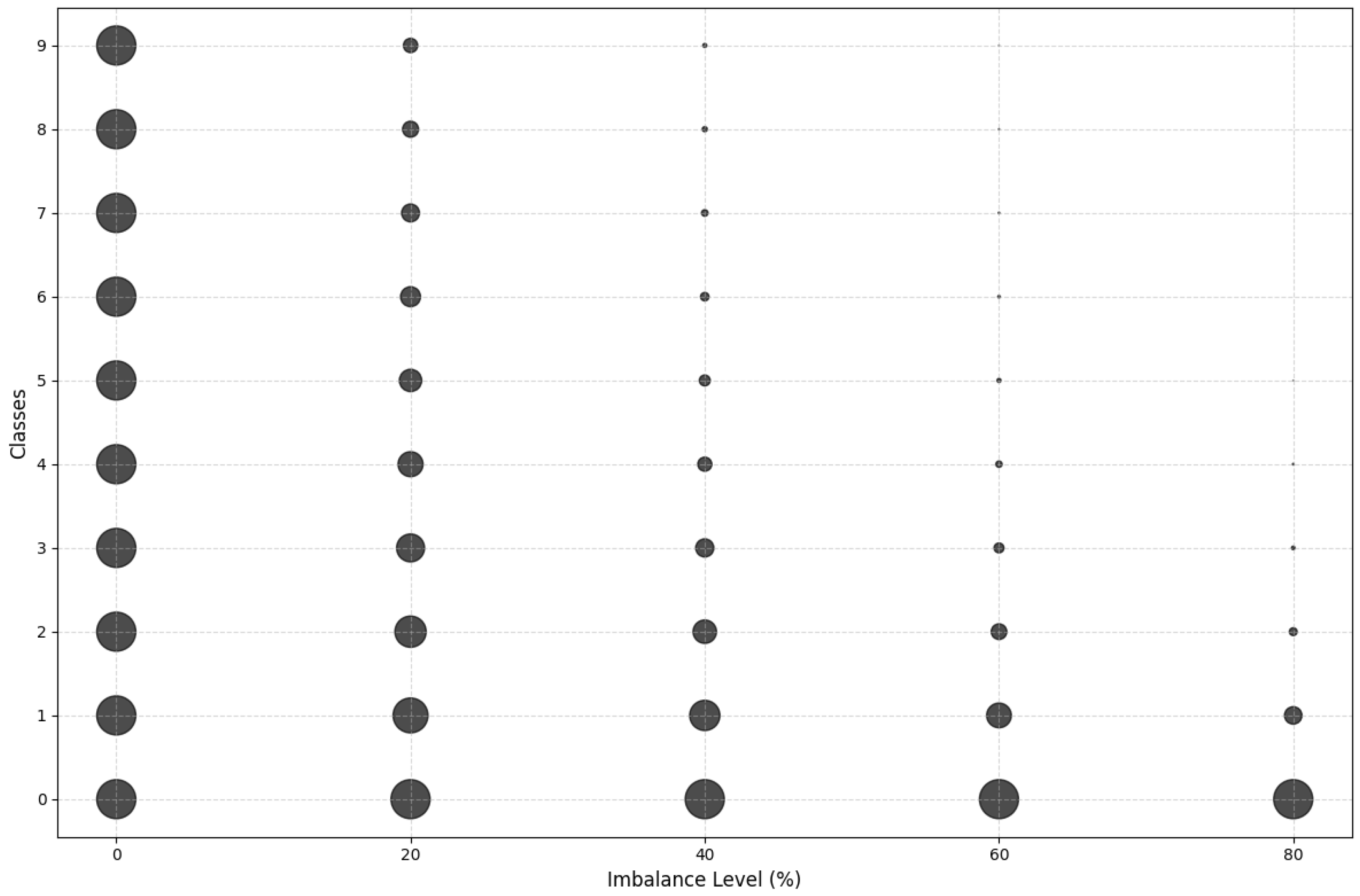
5.1. Datasets and Imbalance Injection
5.2. Datasets and Noise Injection
5.3. The Experiment Setting
6. Results and Discussion
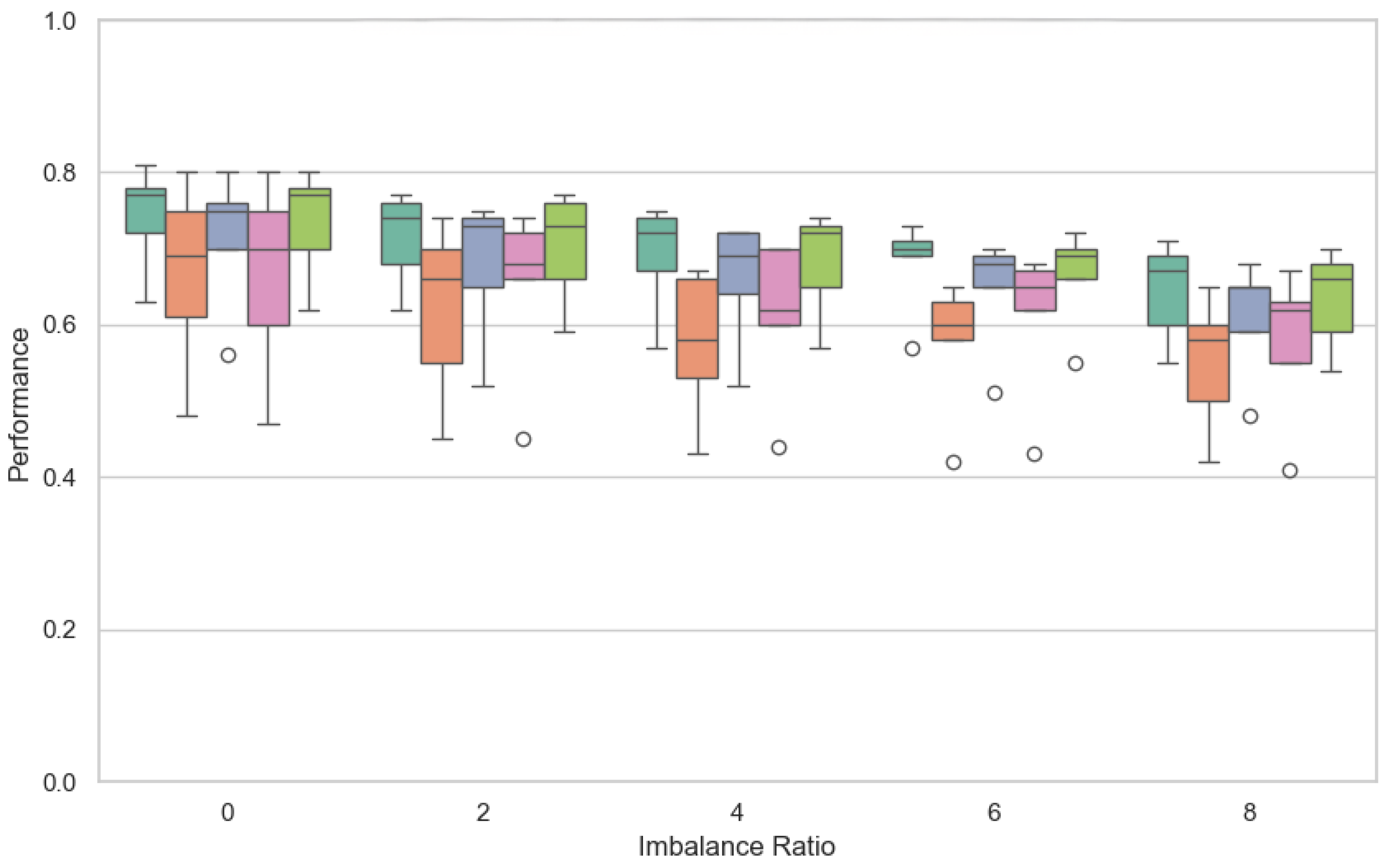
6.1. Results and Discussion for RQ1
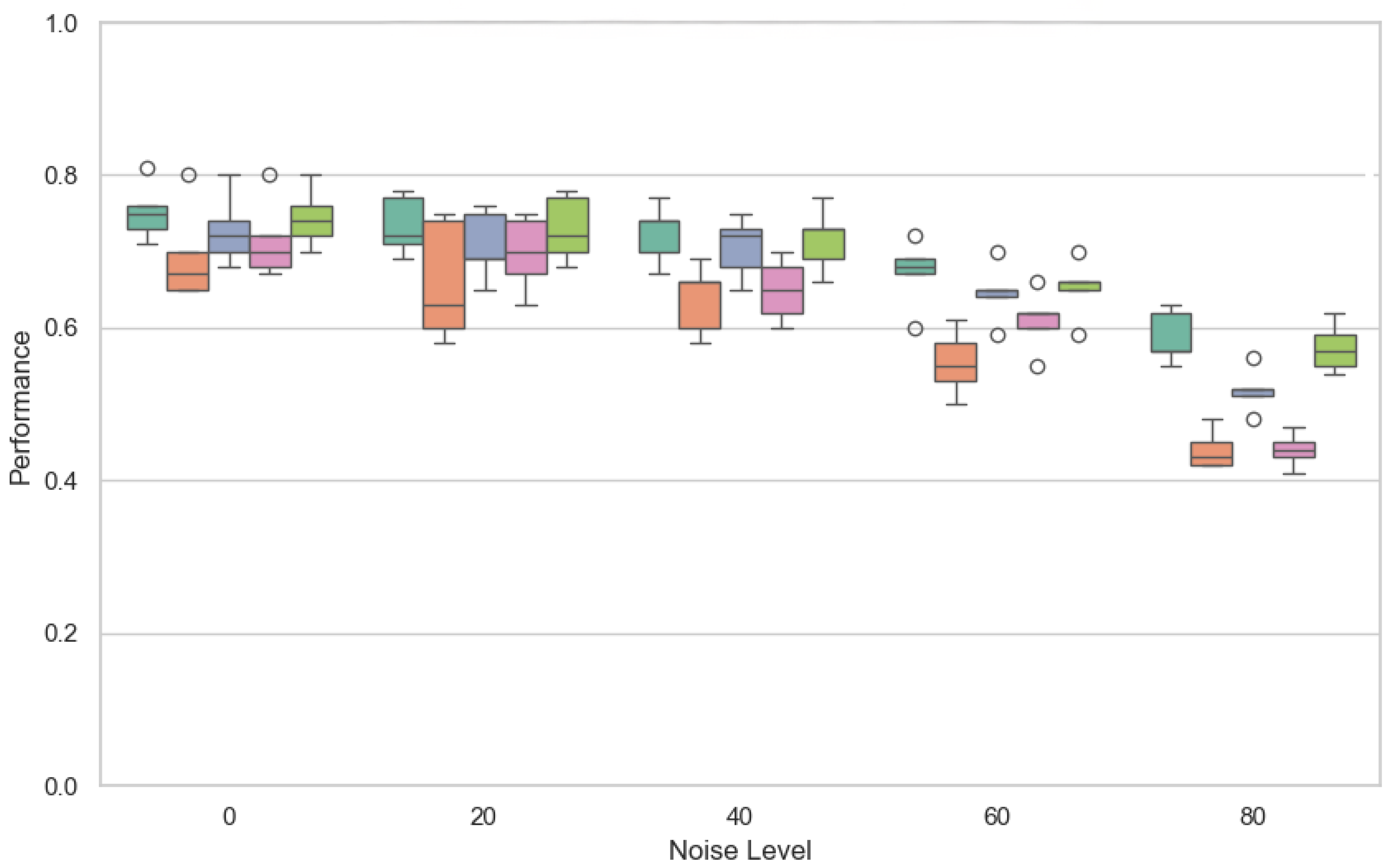
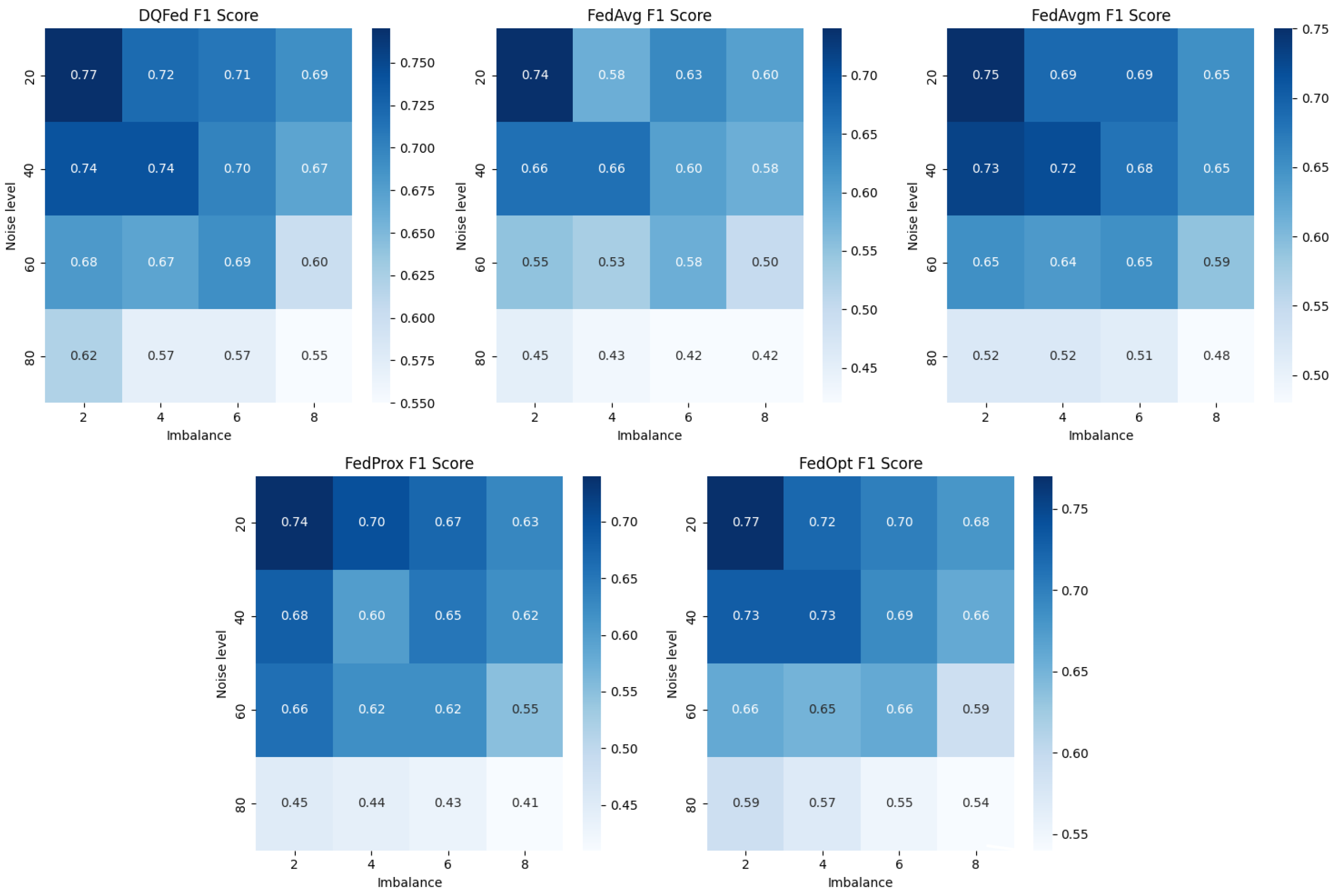
6.2. Results and Discussion for RQ2
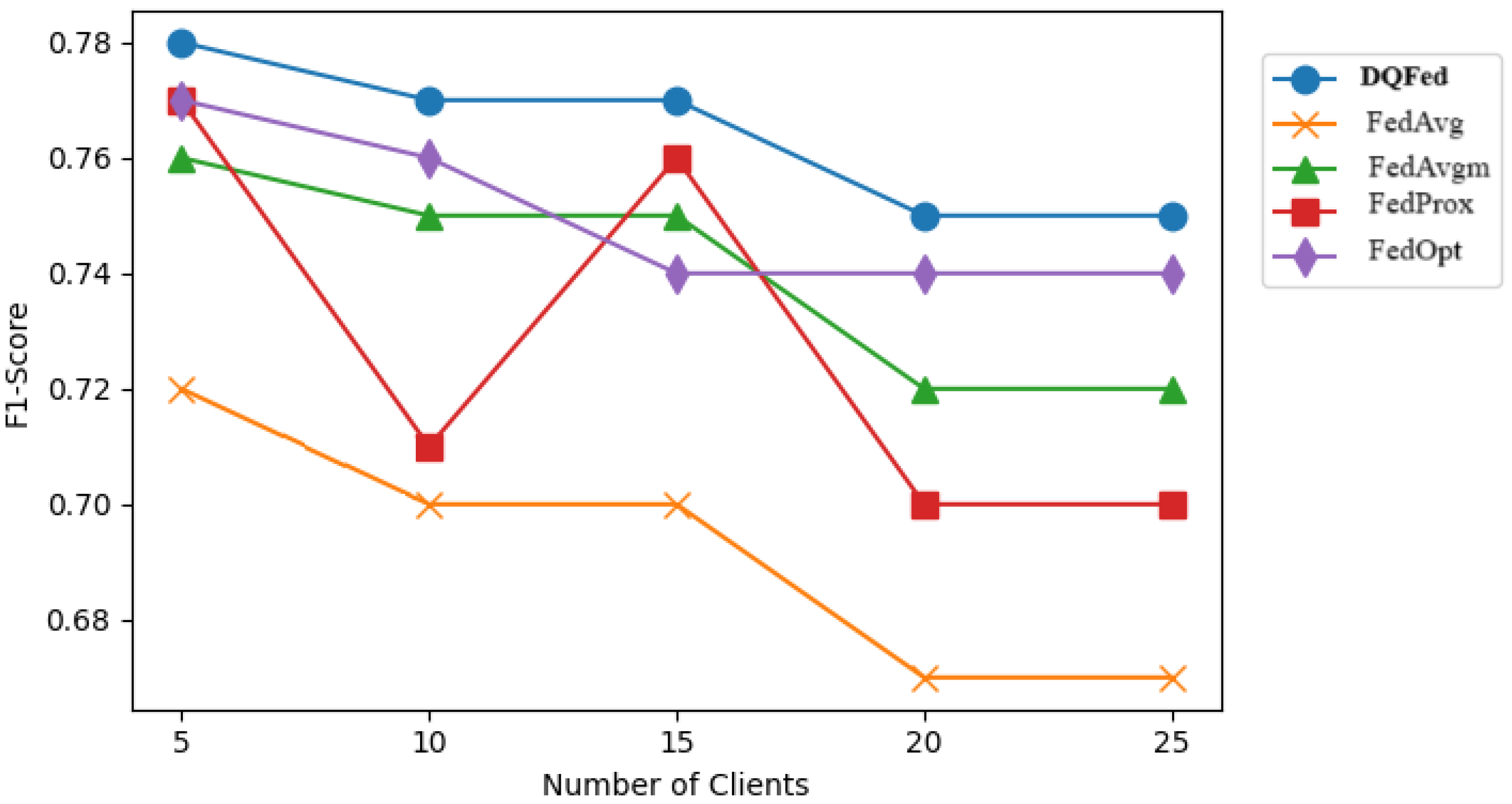
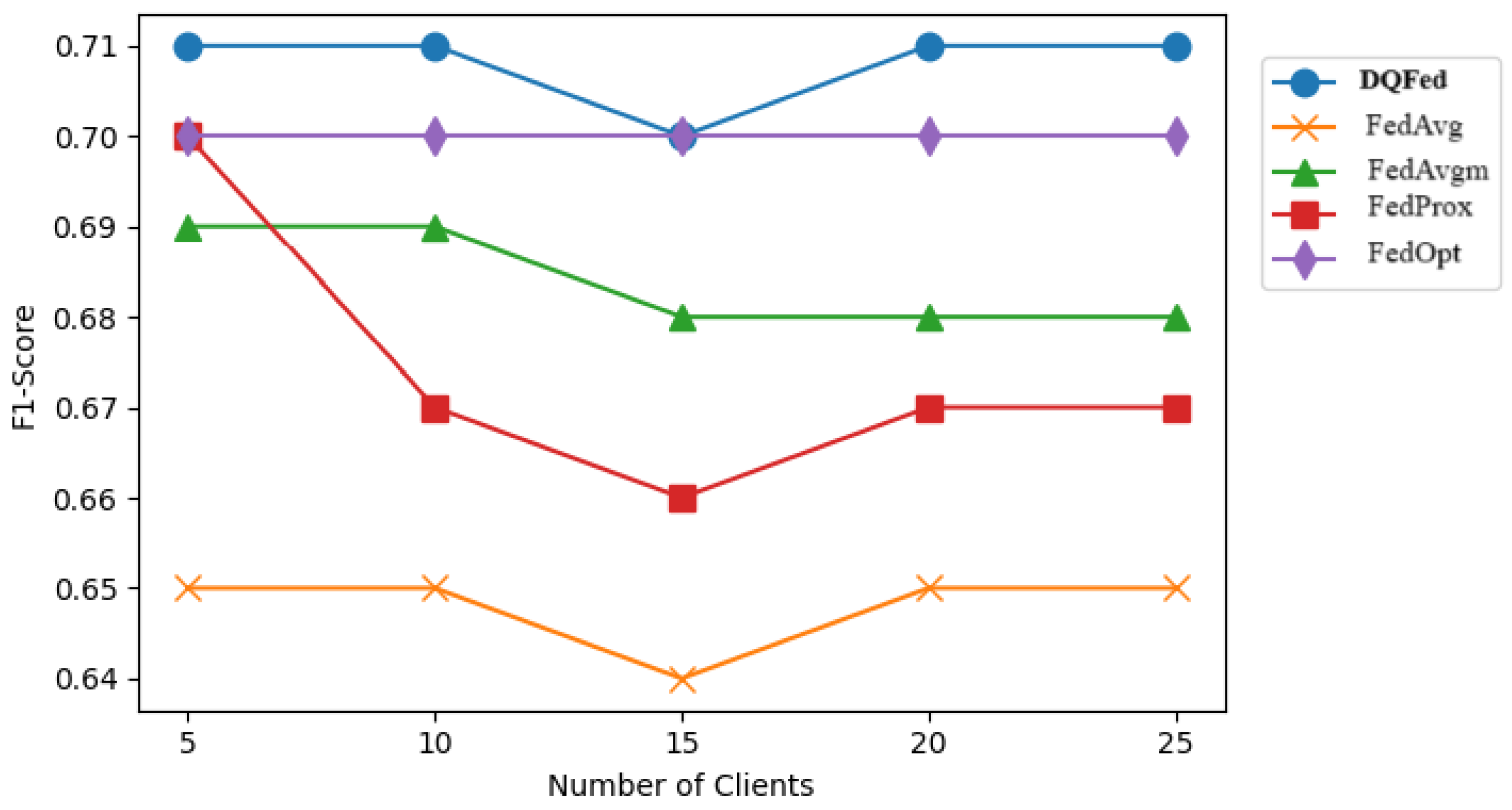
- Entropy-based weighting, as shown in Table 2, provides a relative improvement in F1-score over FedAvg under high imbalance conditions, achieving notably higher performance (0.71 compared to 0.65 at the highest imbalance level).
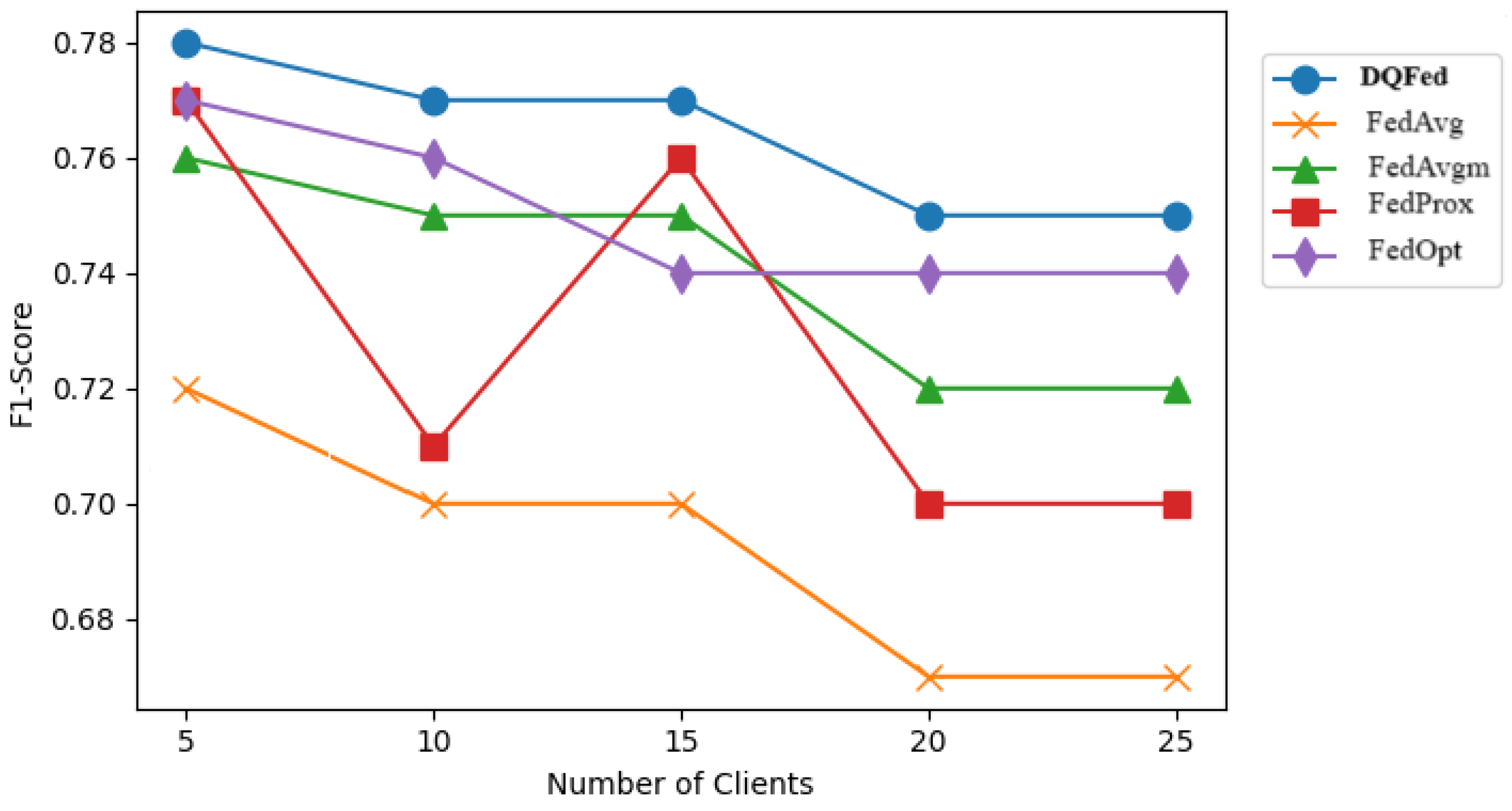
- Noise-based weighting, as demonstrated in Table 3, results in a substantial relative improvement in F1-score over FedAvg under high noise conditions, with performance increasing significantly (0.63 compared to 0.48 at 80% noise).
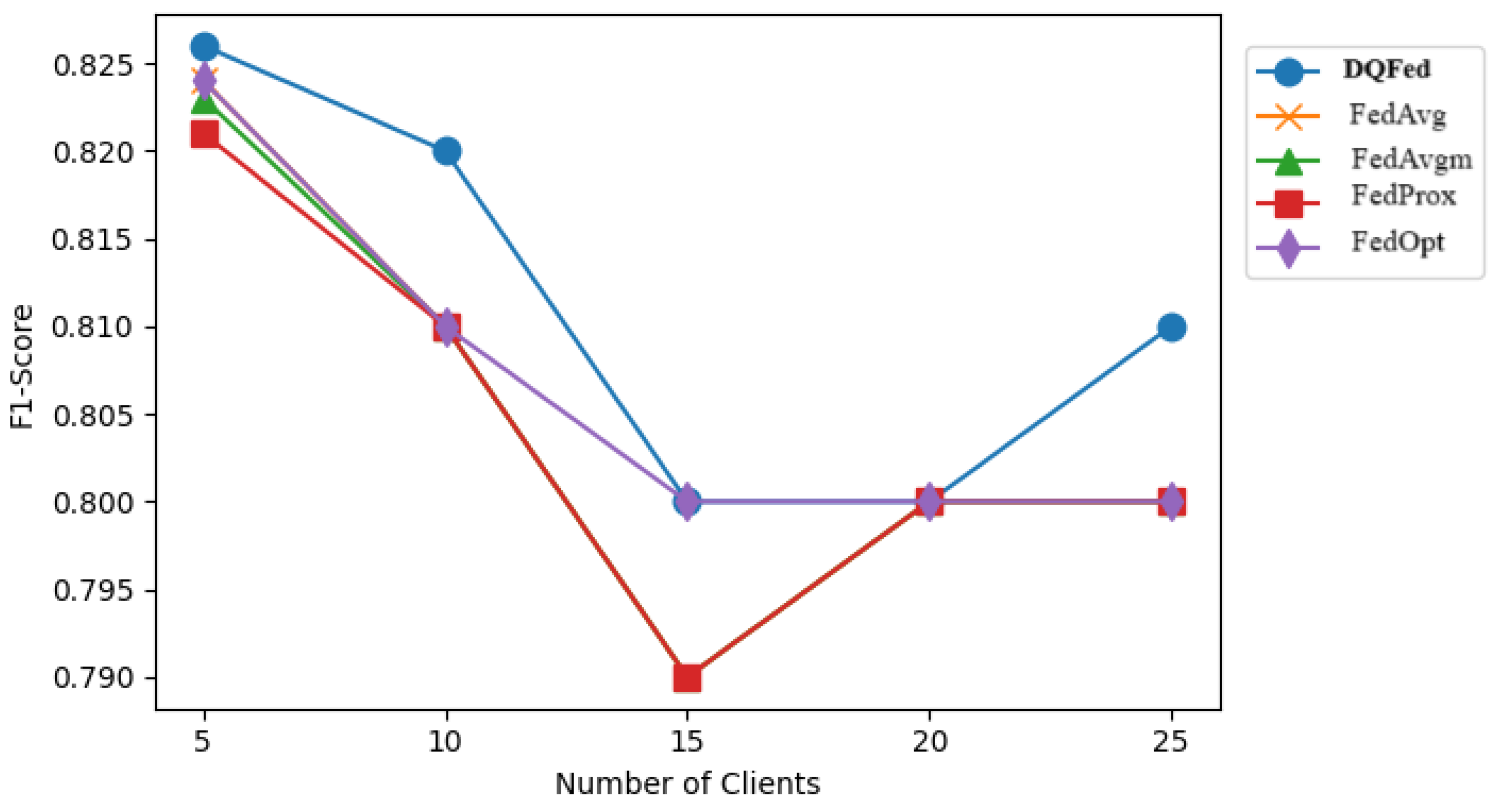
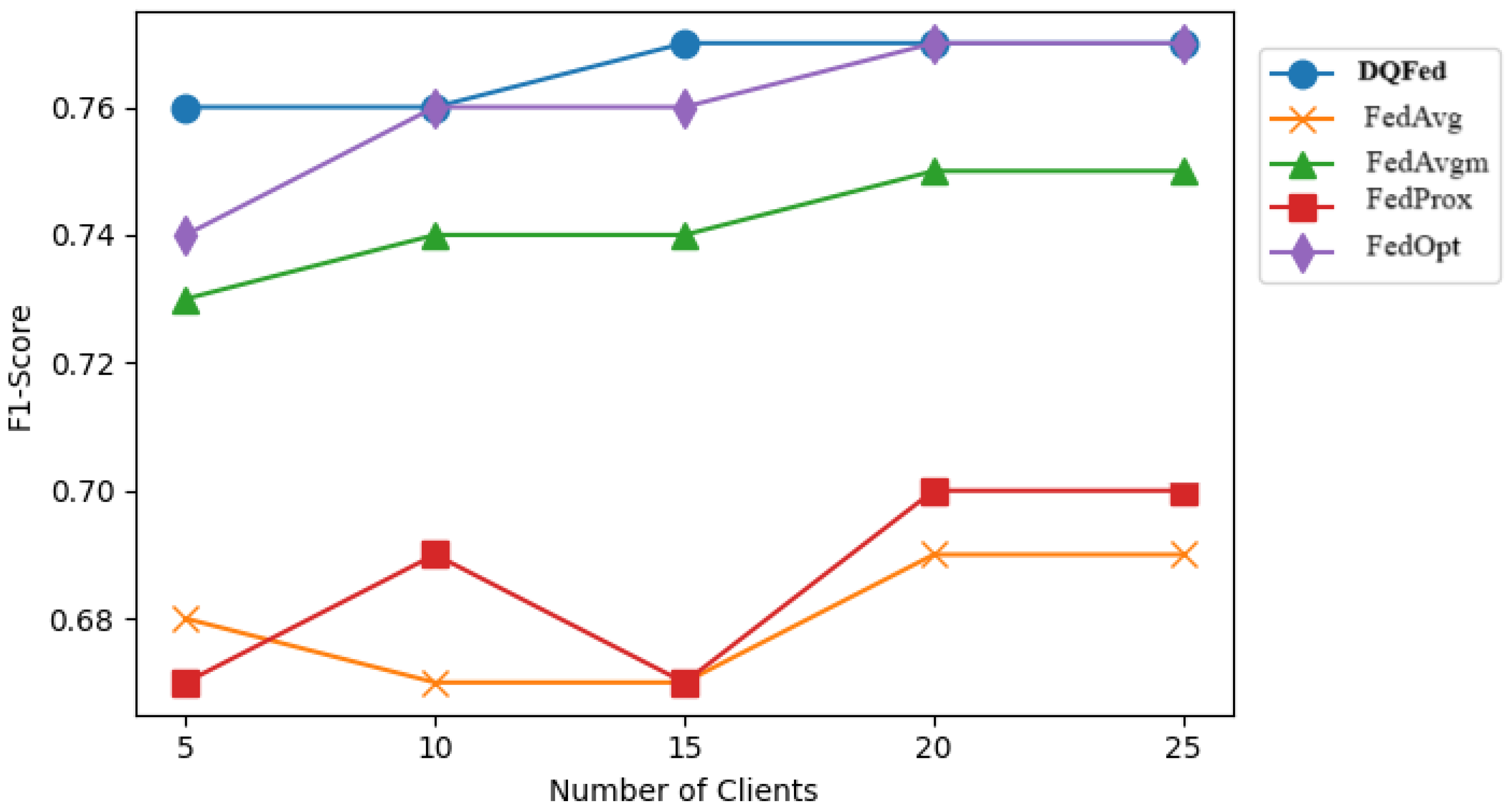
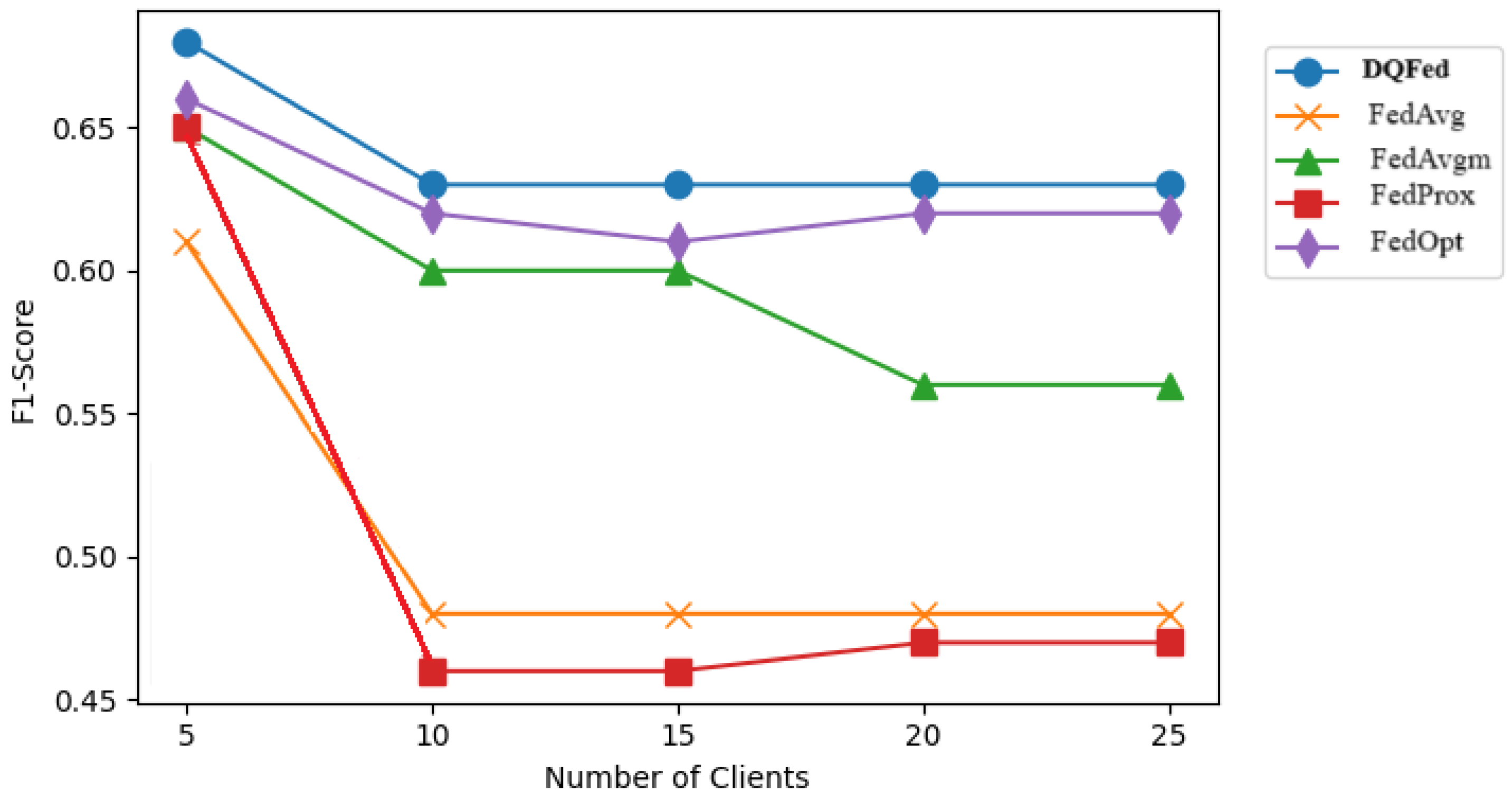
6.3. Results and Discussion for RQ3
6.4. Results and Discussion for RQ4
6.5. Wilcoxon Signed-Rank Test
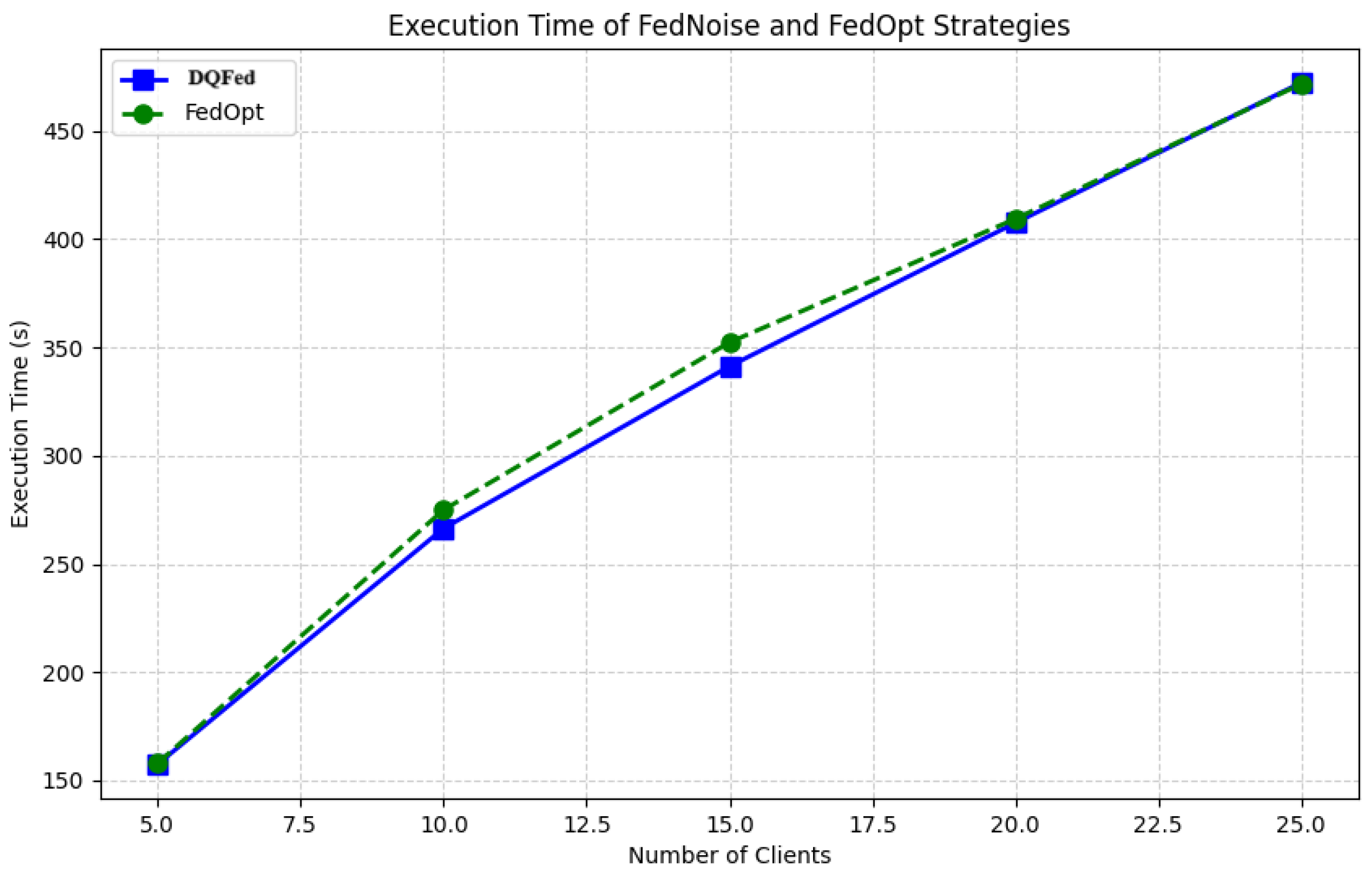
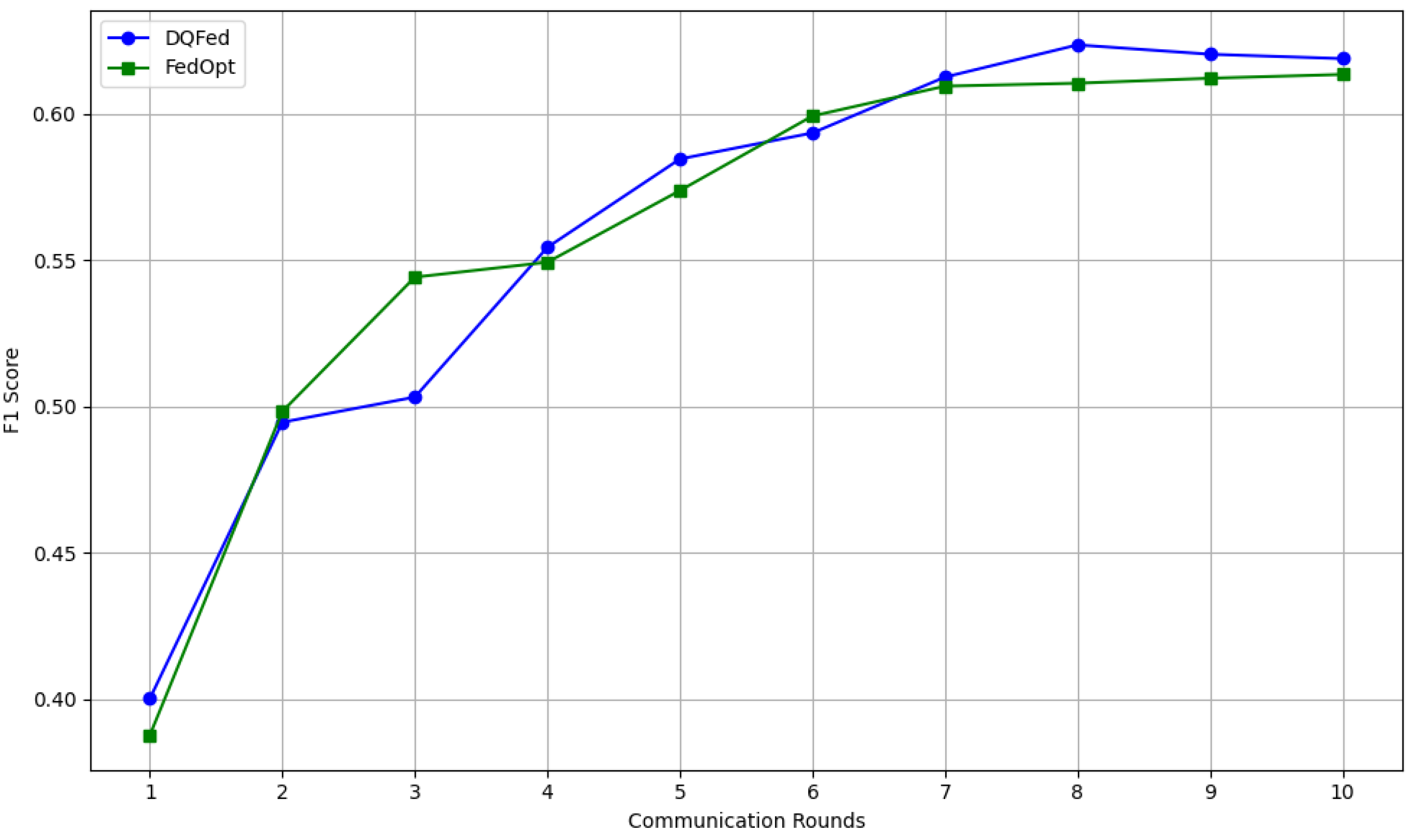
6.6. Convergence Rate over Rounds
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Smith, V.; Chiang, C.K.; Sanjabi, M.; Talwalkar, A. Federated Multi-Task Learning. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS’17), Red Hook, NY, USA, 4–9 December 2017; pp. 4427–4437. [Google Scholar]
- GabAllah, N.; Farrag, I.; Khalil, R.; Sharara, H.; ElBatt, T. IoT systems with multi-tier, distributed intelligence: From architecture to prototype. Pervasive Mob. Comput. 2023, 93, 101818. [Google Scholar] [CrossRef]
- Bimpas, A.; Violos, J.; Leivadeas, A.; Varlamis, I. Leveraging pervasive computing for ambient intelligence: A survey on recent advancements, applications and open challenges. Comput. Netw. 2024, 239, 110156. [Google Scholar] [CrossRef]
- Wang, G.; Ma, J.; Yang, L.T. Guest Editorial: Special Issue on Safety and Security for Ubiquitous Computing and Communications. Inf. Sci. 2020, 522, 317–318. [Google Scholar] [CrossRef]
- Konečný, J.; McMahan, H.B.; Yu, F.X.; Richtárik, P.; Suresh, A.T.; Bacon, D. Federated Learning: Strategies for Improving Communication Efficiency. arXiv 2017, arXiv:1610.05492. [Google Scholar]
- Tan, H. An efficient IoT group association and data sharing mechanism in edge computing paradigm. Cyber Secur. Appl. 2023, 1, 100003. [Google Scholar] [CrossRef]
- Dean, J.; Corrado, G.; Monga, R.; Chen, K.; Devin, M.; Mao, M.; Ranzato, M.a.; Senior, A.; Tucker, P.; Yang, K.; et al. Large Scale Distributed Deep Networks. In Advances in Neural Information Processing Systems; Pereira, F., Burges, C., Bottou, L., Weinberger, K., Eds.; Curran Associates, Inc.: Lake Tahoe, NA, USA, 2012; Volume 25. [Google Scholar]
- Blanco-Justicia, A.; Domingo-Ferrer, J.; Martínez, S.; Sánchez, D.; Flanagan, A.; Tan, K.E. Achieving security and privacy in federated learning systems: Survey, research challenges and future directions. Eng. Appl. Artif. Intell. 2021, 106, 104468. [Google Scholar] [CrossRef]
- Li, Q.; Wen, Z.; Wu, Z.; Hu, S.; Wang, N.; Li, Y.; Liu, X.; He, B. A Survey on Federated Learning Systems: Vision, Hype and Reality for Data Privacy and Protection. IEEE Trans. Knowl. Data Eng. 2023, 35, 3347–3366. [Google Scholar] [CrossRef]
- Voigt, P.; Bussche, A.v.d. The EU General Data Protection Regulation (GDPR): A Practical Guide, 1st ed.; Springer Publishing Company, Incorporated: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Zhao, J.C.; Bagchi, S.; Avestimehr, S.; Chan, K.S.; Chaterji, S.; Dimitriadis, D.; Li, J.; Li, N.; Nourian, A.; Roth, H.R. Federated Learning Privacy: Attacks, Defenses, Applications, and Policy Landscape—A Survey. arXiv 2024, arXiv:2405.03636. [Google Scholar]
- Zheng, W.; Yan, L.; Gou, C.; Wang, F.Y. Federated Meta-Learning for Fraudulent Credit Card Detection. In Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence (IJCAI’20), Virtual, 7–15 January 2021. [Google Scholar]
- Wang, X.; Han, Y.; Wang, C.; Zhao, Q.; Chen, X.; Chen, M. In-Edge AI: Intelligentizing Mobile Edge Computing, Caching and Communication by Federated Learning. IEEE Netw. 2019, 33, 156–165. [Google Scholar] [CrossRef]
- Li, J.; Li, G.; Cheng, H.; Liao, Z.; Yu, Y. FedDiv: Collaborative Noise Filtering for Federated Learning with Noisy Labels. arXiv 2024, arXiv:2312.12263. [Google Scholar] [CrossRef]
- Bernardi, M.L.; Cimitile, M.; Usman, M. DQFed: A Federated Learning Strategy for Non-IID Data based on a Quality-Driven Perspective. In Proceedings of the IEEE International Conference on Fuzzy Systems, Yokohama, Japan, 30 June–5 July 2024. [Google Scholar] [CrossRef]
- Lu, Z.; Pan, H.; Dai, Y.; Si, X.; Zhang, Y. Federated Learning With Non-IID Data: A Survey. IEEE Internet Things J. 2024, 11, 19188–19209. [Google Scholar] [CrossRef]
- Zhu, H.; Xu, J.; Liu, S.; Jin, Y. Federated learning on non-IID data: A survey. Neurocomputing 2021, 465, 371–390. [Google Scholar] [CrossRef]
- Wu, N.; Yu, L.; Jiang, X.; Cheng, K.T.; Yan, Z. FedNoRo: Towards Noise-Robust Federated Learning by Addressing Class Imbalance and Label Noise Heterogeneity. In Proceedings of the Proceedings of the Thirty-Second International Joint Conference on Artificial Intelligence, Macao, 19–25 August 2023; pp. 4424–4432. [Google Scholar]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; Arcas, B.A.y. Communication-Efficient Learning of Deep Networks from Decentralized Data. In Proceedings of the 20th International Conference on Artificial Intelligence and Statistics, PMLR, Fort Lauderdale, FL, USA, 20–22 April 2017; Singh, A., Zhu, J., Eds.; Proceedings of Machine Learning Research. Volume 54, pp. 1273–1282. [Google Scholar]
- Li, T.; Sahu, A.K.; Zaheer, M.; Sanjabi, M.; Talwalkar, A.; Smith, V. Federated Optimization in Heterogeneous Networks. In Proceedings of the Third Conference on Machine Learning and Systems, MLSys 2020, Austin, TX, USA, 2–4 March 2020. [Google Scholar]
- Hsieh, K.; Phanishayee, A.; Mutlu, O.; Gibbons, P. The Non-IID Data Quagmire of Decentralized Machine Learning. In Proceedings of the 37th International Conference on Machine Learning, Virtual, 13–18 July 2020; Singh, A.H.D., III, Ed.; PMLR; Proceedings of Machine Learning Research. Volume 119, pp. 4387–4398. [Google Scholar]
- Zhao, Y.; Li, M.; Lai, L.; Suda, N.; Civin, D.; Chandra, V. Federated Learning with Non-IID Data. arXiv 2018, arXiv:1806.00582. [Google Scholar] [CrossRef]
- Zhang, J.; Li, C.; Qi, J.; He, J. A Survey on Class Imbalance in Federated Learning. arXiv 2023, arXiv:2303.11673. [Google Scholar]
- He, H.; Bai, Y.; Garcia, E.A.; Li, S. ADASYN: Adaptive synthetic sampling approach for imbalanced learning. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–8 June 2008; pp. 1322–1328. [Google Scholar] [CrossRef]
- Wang, L.; Xu, S.; Wang, X.; Zhu, Q. Addressing Class Imbalance in Federated Learning. arXiv 2020, arXiv:2008.06217. [Google Scholar] [CrossRef]
- Sarkar, D.; Narang, A.; Rai, S. Fed-Focal Loss for imbalanced data classification in Federated Learning. arXiv 2020, arXiv:2011.06283. [Google Scholar]
- Chou, Y.H.; Hong, S.; Sun, C.; Cai, D.; Song, M.; Li, H. GRP-FED: Addressing Client Imbalance in Federated Learning via Global-Regularized Personalization. In Proceedings of the 2022 SIAM International Conference on Data Mining (SDM) Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA, USA, 28–30 April 2022; pp. 451–458. [Google Scholar] [CrossRef]
- Cheng, X.; Tian, W.; Shi, F.; Zhao, M.; Chen, S.; Wang, H. A Blockchain-Empowered Cluster-Based Federated Learning Model for Blade Icing Estimation on IoT-Enabled Wind Turbine. IEEE Trans. Ind. Inform. 2022, 18, 9184–9195. [Google Scholar] [CrossRef]
- Duan, S.; Liu, C.; Cao, Z.; Jin, X.; Han, P. Fed-DR-Filter: Using global data representation to reduce the impact of noisy labels on the performance of federated learning. Future Gener. Comput. Syst. 2022, 137, 336–348. [Google Scholar] [CrossRef]
- Yang, S.; Park, H.; Byun, J.; Kim, C. Robust Federated Learning With Noisy Labels. IEEE Intell. Syst. 2022, 37, 35–43. [Google Scholar] [CrossRef]
- Xu, J.; Chen, Z.; Quek, T.S.; Chong, K.E. FedCorr: Multi-Stage Federated Learning for Label Noise Correction. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Los Alamitos, CA, USA, 18–24 June 2022; pp. 10174–10183. [Google Scholar] [CrossRef]
- Zeng, B.; Yang, X.; Chen, Y.; Yu, H.; Zhang, Y. CLC: A Consensus-based Label Correction Approach in Federated Learning. ACM Trans. Intell. Syst. Technol. 2022, 13, 75. [Google Scholar] [CrossRef]
- Zhang, J.; Lv, D.; Dai, Q.; Xin, F.; Dong, F. Noise-aware Local Model Training Mechanism for Federated Learning. ACM Trans. Intell. Syst. Technol. 2023, 14, 65. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, X.; Qin, X.; Yu, H.; Chan, P.; Shen, Z. Dealing with Label Quality Disparity in Federated Learning. In Federated Learning: Privacy and Incentive; Yang, Q., Fan, L., Yu, H., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 108–121. [Google Scholar]
- Zheng, H.; Liu, H.; Liu, Z.; Tan, J. Federated temporal-context contrastive learning for fault diagnosis using multiple datasets with insufficient labels. Adv. Eng. Inform. 2024, 60, 102432. [Google Scholar] [CrossRef]
- Kim, S.; Park, H.; Kang, M.; Jin, K.H.; Adeli, E.; Pohl, K.M.; Park, S. Federated learning with knowledge distillation for multi-organ segmentation with partially labeled datasets. Med. Image Anal. 2024, 95, 103156. [Google Scholar] [CrossRef] [PubMed]
- shahraki, M.; Bidgoly, A.J. Edge model: An efficient method to identify and reduce the effectiveness of malicious clients in federated learning. Future Gener. Comput. Syst. 2024, 157, 459–468. [Google Scholar] [CrossRef]
- Xu, Y.; Liao, Y.; Wang, L.; Xu, H.; Jiang, Z.; Zhang, W. Overcoming Noisy Labels and Non-IID Data in Edge Federated Learning. IEEE Trans. Mob. Comput. 2024, 23, 11406–11421. [Google Scholar] [CrossRef]
- Sergeev, A.; Balso, M.D. Horovod: Fast and easy distributed deep learning in TensorFlow. arXiv 2018, arXiv:1802.05799. [Google Scholar]
- Yang, Q.; Liu, Y.; Chen, T.; Tong, Y. Federated Machine Learning: Concept and Applications. ACM Trans. Intell. Syst. Technol. 2019, 10, 12. [Google Scholar] [CrossRef]
- Liu, Y.; Kang, Y.; Xing, C.; Chen, T.; Yang, Q. A Secure Federated Transfer Learning Framework. IEEE Intell. Syst. 2020, 35, 70–82. [Google Scholar] [CrossRef]
- Casella, B.; Fonio, S. Architecture-Based FedAvg for Vertical Federated Learning. In Proceedings of the IEEE/ACM 16th International Conference on Utility and Cloud Computing (UCC’23), New York, NY, USA, 4–7 December 2024. [Google Scholar] [CrossRef]
- Addabbo, P.; Bernardi, M.L.; Biondi, F.; Cimitile, M.; Clemente, C.; Orlando, D. Temporal Convolutional Neural Networks for Radar Micro-Doppler Based Gait Recognition. Sensors 2021, 21, 381. [Google Scholar] [CrossRef]
- Ardimento, P.; Aversano, L.; Bernardi, M.L.; Cimitile, M.; Iammarino, M. Transfer Learning for Just-in-Time Design Smells Prediction using Temporal Convolutional Networks. In Proceedings of the 16th International Conference on Software Technologies, ICSOFT, Online, 6–8 July 2021; Fill, H., van Sinderen, M., Maciaszek, L.A., Eds.; SCITEPRESS: Setúbal, Portugal, 2021; pp. 310–317. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. SIGMOBILE Mob. Comput. Commun. Rev. 2001, 5, 3–55. [Google Scholar] [CrossRef]

| Hyperparameter | Description |
|---|---|
| Optimization Algorithm | Adam optimizer |
| Learning Rate | 0.001 |
| Batch Size | 128 |
| Training Epochs | 16 |
| Loss Function | Binary Cross-Entropy + KL-Divergence |
| Device | CUDA (if available), otherwise CPU |
| Clients | Imbalance | Dqfed | FedAvg | FedAvgm | FedProx | FedOpt |
|---|---|---|---|---|---|---|
| 25 | 0 | 0.81 | 0.8 | 0.8 | 0.8 | 0.8 |
| 25 | 2 | 0.76 | 0.7 | 0.74 | 0.72 | 0.76 |
| 25 | 4 | 0.75 | 0.67 | 0.72 | 0.7 | 0.74 |
| 25 | 6 | 0.73 | 0.65 | 0.7 | 0.68 | 0.72 |
| 25 | 8 | 0.71 | 0.65 | 0.68 | 0.67 | 0.7 |
| Clients | Noise % | DQFed | FedAvg | FedAvgm | FedProx | FedOpt |
|---|---|---|---|---|---|---|
| 25 | 0 | 0.81 | 0.8 | 0.8 | 0.8 | 0.8 |
| 25 | 20 | 0.78 | 0.75 | 0.76 | 0.75 | 0.78 |
| 25 | 40 | 0.77 | 0.69 | 0.75 | 0.7 | 0.77 |
| 25 | 60 | 0.72 | 0.61 | 0.7 | 0.6 | 0.7 |
| 25 | 80 | 0.63 | 0.48 | 0.56 | 0.47 | 0.62 |
| Comparison | p-Value | Significant ()? |
|---|---|---|
| DQFed vs. FedAvg | 0.0025 | Yes |
| DQFed vs. FedAvgm | 0.041 | Yes |
| DQFed vs. FedProx | 0.034 | Yes |
| DQFed vs. FedOpt | 0.046 | Yes |
| Comparison | p-Value | Significant ()? |
|---|---|---|
| DQFed vs. FedAvg | 0.034 | Yes |
| DQFed vs. FedAvgm | 0.038 | Yes |
| DQFed vs. FedProx | 0.041 | Yes |
| DQFed vs. FedOpt | 0.038 | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Usman, M.; Bernardi, M.L.; Cimitile, M. Introducing a Quality-Driven Approach for Federated Learning. Sensors 2025, 25, 3083. https://doi.org/10.3390/s25103083
Usman M, Bernardi ML, Cimitile M. Introducing a Quality-Driven Approach for Federated Learning. Sensors. 2025; 25(10):3083. https://doi.org/10.3390/s25103083
Chicago/Turabian StyleUsman, Muhammad, Mario Luca Bernardi, and Marta Cimitile. 2025. "Introducing a Quality-Driven Approach for Federated Learning" Sensors 25, no. 10: 3083. https://doi.org/10.3390/s25103083
APA StyleUsman, M., Bernardi, M. L., & Cimitile, M. (2025). Introducing a Quality-Driven Approach for Federated Learning. Sensors, 25(10), 3083. https://doi.org/10.3390/s25103083








