Gearbox Fault Diagnosis Under Noise and Variable Operating Conditions Using Multiscale Depthwise Separable Convolution and Bidirectional Gated Recurrent Unit with a Squeeze-and-Excitation Attention Mechanism
Abstract
1. Introduction
- (1)
- Multiscale feature extraction: The introduction of multiscale depthwise separable convolution enables the efficient extraction of multiscale spatial features from vibration signals through multiscale convolutional kernels, significantly enhancing feature extraction capabilities.
- (2)
- Adaptive feature recalibration: The incorporation of the squeeze-and-excitation attention mechanism dynamically adjusts channel weights, enhancing the model’s focus on critical fault features, and thus promoting the ability of multiscale convolution to capture key information.
- (3)
- Bidirectional temporal modeling: The bidirectional gated recurrent unit is employed to capture temporal dependencies in both directions, allowing the model to simultaneously consider past and future contextual information, thereby improving its sequential modeling ability.
- (4)
- Efficient computation and high diagnostic accuracy: By introducing depthwise separable convolutions, computational complexity is effectively reduced, significantly improving efficiency while maintaining high performance. Moreover, the integration of multiscale feature extraction and time-dependent modeling has significantly improved diagnostic accuracy without compromising efficiency.
2. Related Theoretical Background
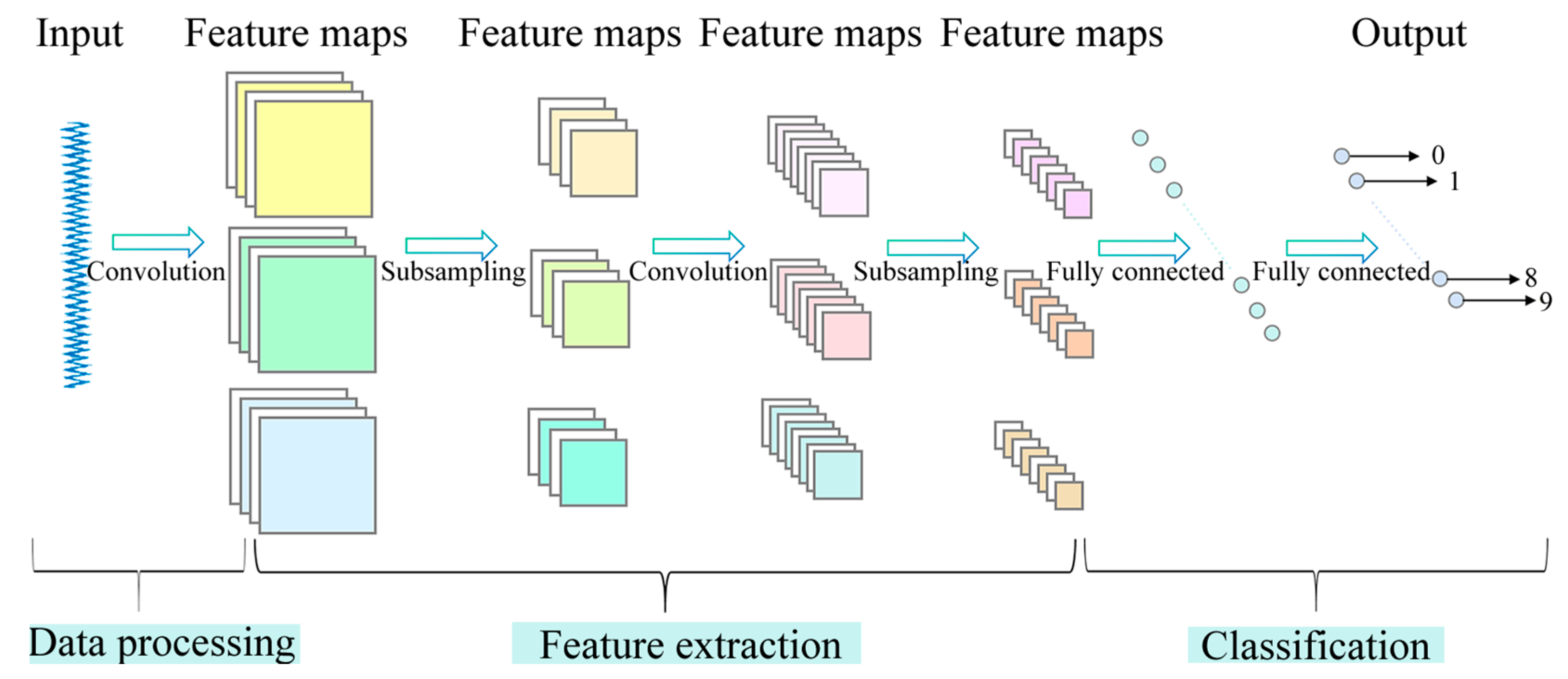
2.1. Multiscale Convolutional Neural Network (MSCNN)
- (a)
- Convolutional Layer: Suppose the input signal is , and the convolution kernel is . The convolution operation is defined as follows:where is the activation function, is the bias term, and ∗ represents the convolution operation. The resulting output feature map is denoted as .
- (b)
- Pooling Layer: Pooling operations are used to reduce dimensionality and extract essential features. Common pooling methods include Max Pooling and average pooling. The output of the pooling layer can be expressed as follows:where represents the elements within the pooling window, and represents the maximum pooling operation.
- (c)
- Multiscale Convolution: A key innovation of MSCNN is its use of multiscale convolutional operations. Suppose there are multiple convolution kernels , each with a different size. These kernels extract features at various scales from the input signal. The final output feature is the fusion of convolution feature maps at multiple scales:where represents the final multiscale feature maps extracted by the MSCNN model.
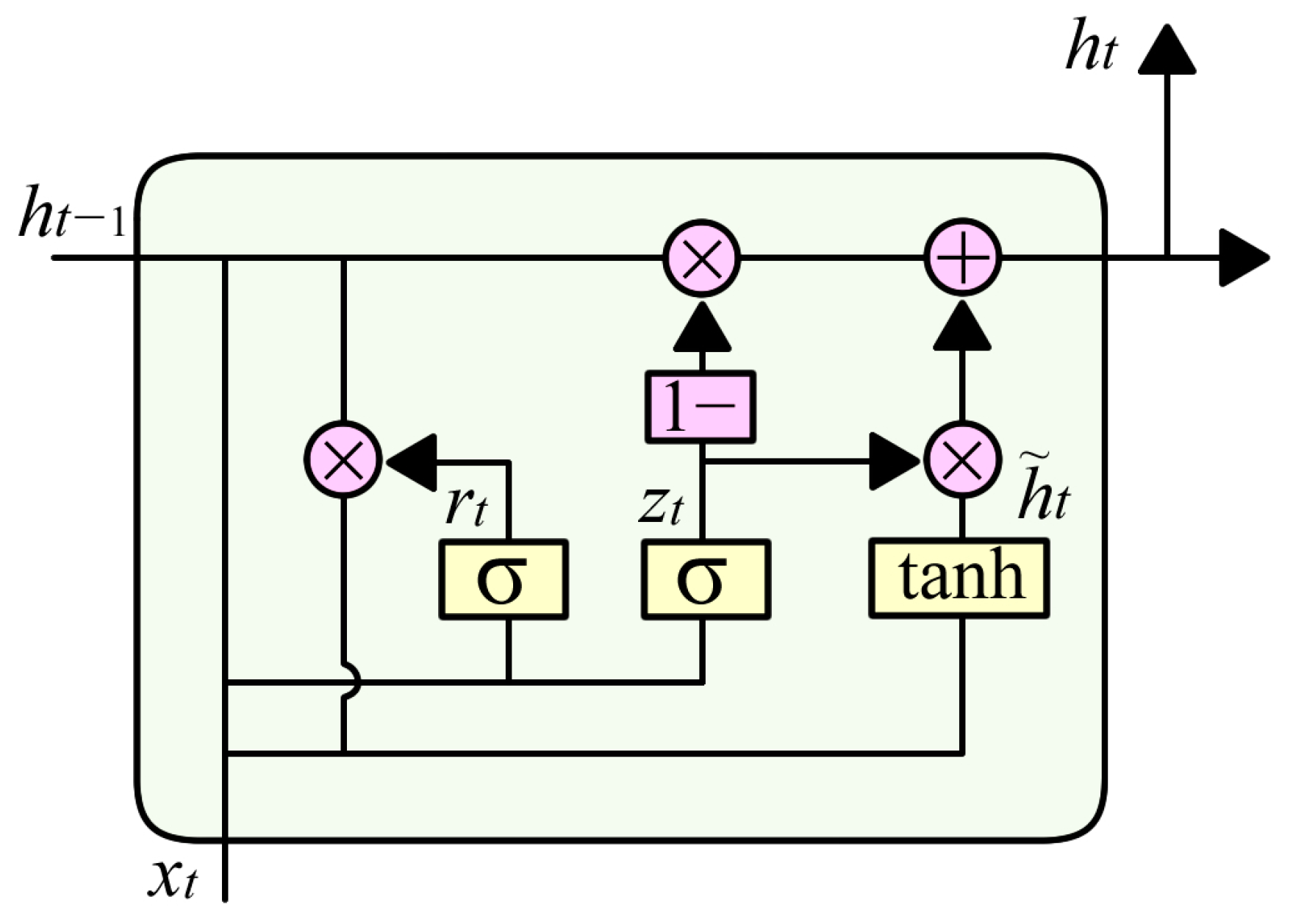
2.2. Gated Recurrent Unit (GRU)
- (a)
- Update Gate: The update gate controls the degree to which the current state is updated. It is computed as follows:where represents the input at time step t, is the previous hidden state, is the Sigmoid activation function, and and are learnable parameters.
- (b)
- Reset Gate: The reset gate determines how much of the past hidden state contributes to the current state. It is defined as follows:where and are the parameter matrices and bias vectors for the reset gate, represents the sigmoid activation function, which bounds the gate values between 0 and 1, is the input vector at time step , is the hidden state from the previous time step;
- (c)
- Candidate Hidden State: The candidate hidden state is computed using the reset gate to determine the current state information:where indicates that the hidden state from the previous time step, is combined with the reset gate to control its influence, are the corresponding weight matrices and biases, and is the hyperbolic tangent activation function.
- (d)
- Final Hidden State: The final hidden state is obtained as a weighted combination of the previous hidden state and the candidate hidden state:where is the update gate, is the previous hidden state, is the candidate hidden state, represents retained historical information, and represents newly acquired information.
- (1)
- Input-to-hidden matrices, which transform the input vector into the respective internal gate and candidate state spaces:
- (a)
- connects to the update gate and maps the input vector to the update gate .
- (b)
- connects to the reset gate and maps the input vector to the reset gate .
- (c)
- connects to the candidate hidden state and maps the input vector to the candidate hidden state .
- (2)
- Hidden-to-hidden (recurrent) matrices, which transform the previous hidden state to each corresponding gate:
- (a)
- recurrent weights for the update gate; maps the hidden state to the update gate .
- (b)
- recurrent weights for the reset gate; maps to the reset gate .
- (c)
- recurrent weights for the candidate hidden state; maps to the candidate hidden state .
2.3. Squeeze-and-Excitation Attention Mechanism (SE)
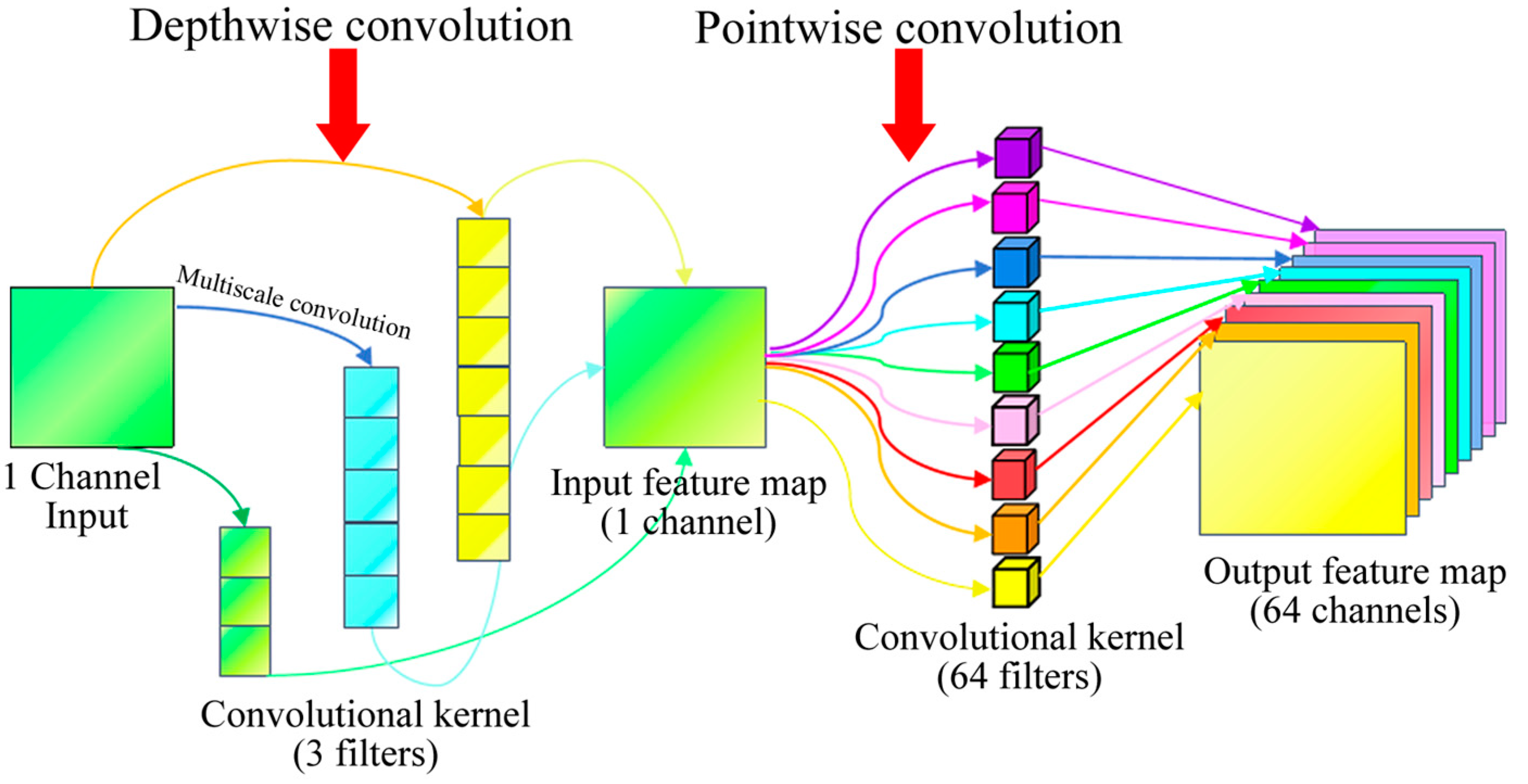
2.4. Multiscale Depthwise Separable Convolution (MDSC)
- (a)
- The 3 × 1 convolution captures fine-grained local structures:
- (b)
- The 5 × 1 convolution extracts mid-range contextual dependencies:
- (c)
- The 7 × 1 convolution focuses on broader global trends:
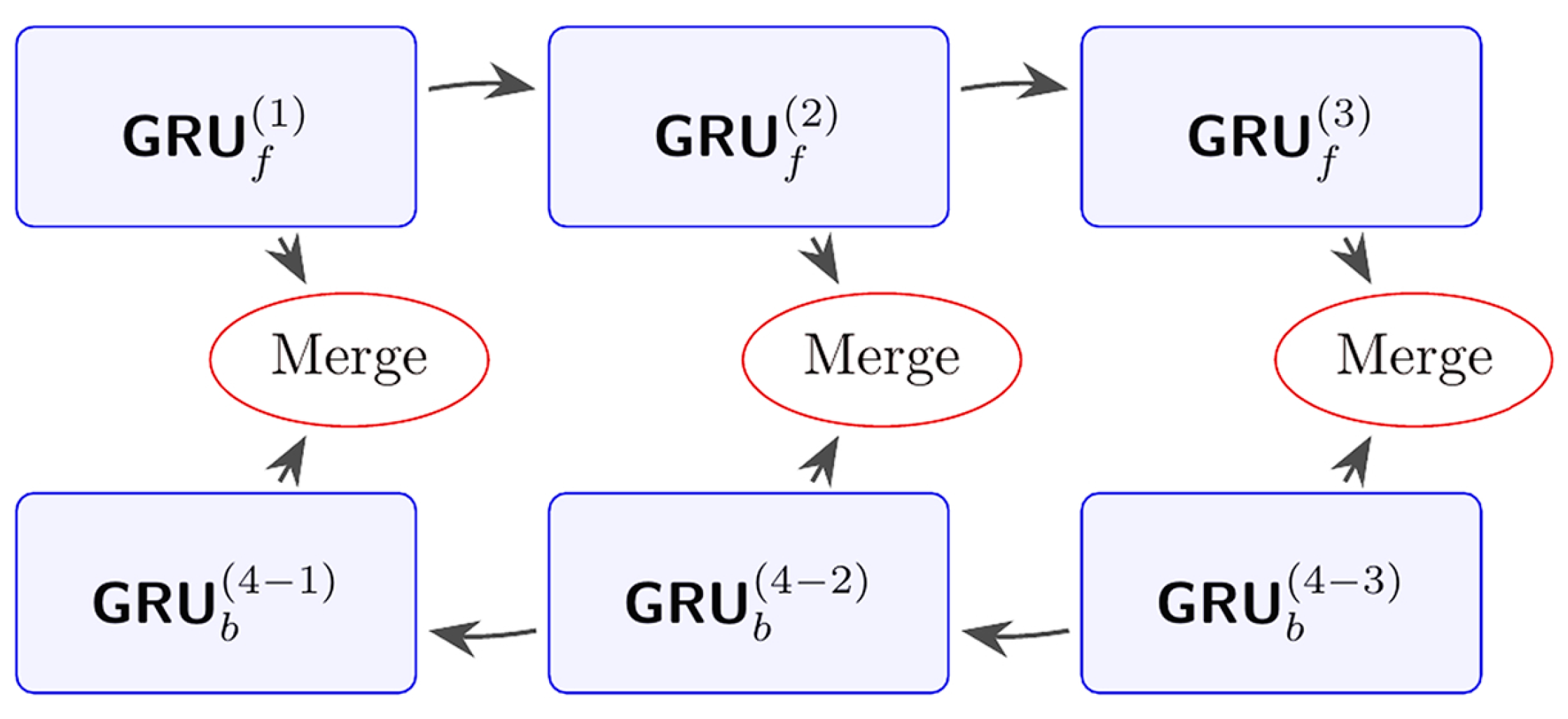
2.5. Bidirectional Gated Recurrent Unit (BiGRU)
- (a)
- Forward GRU
- (b)
- Backward GRU
- (c)
- Output Fusion
3. MDSC-SE-BiGRU Model
4. Results and Discussion
4.1. Case 1: Fault Diagnosis of Planetary Gearbox
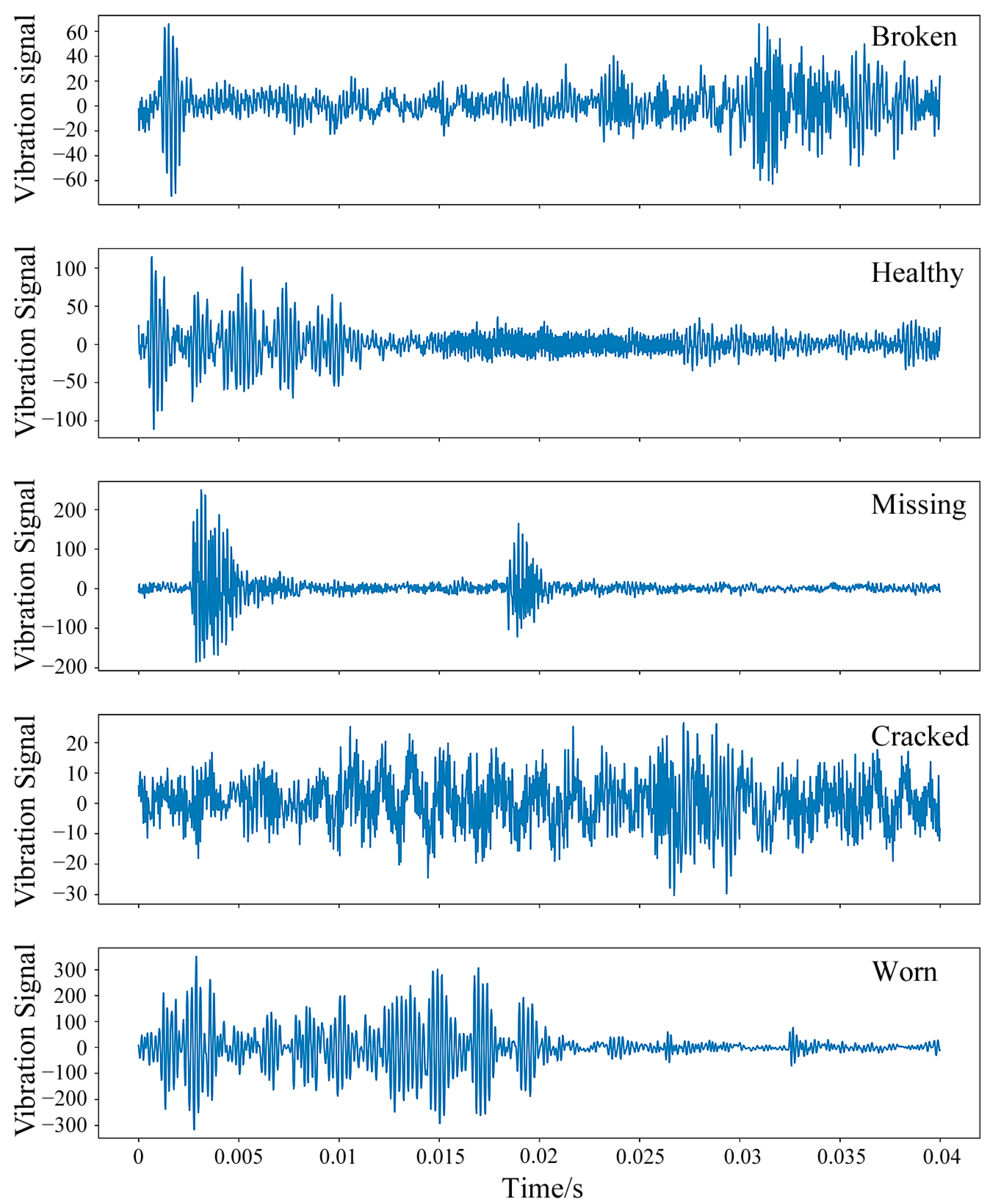
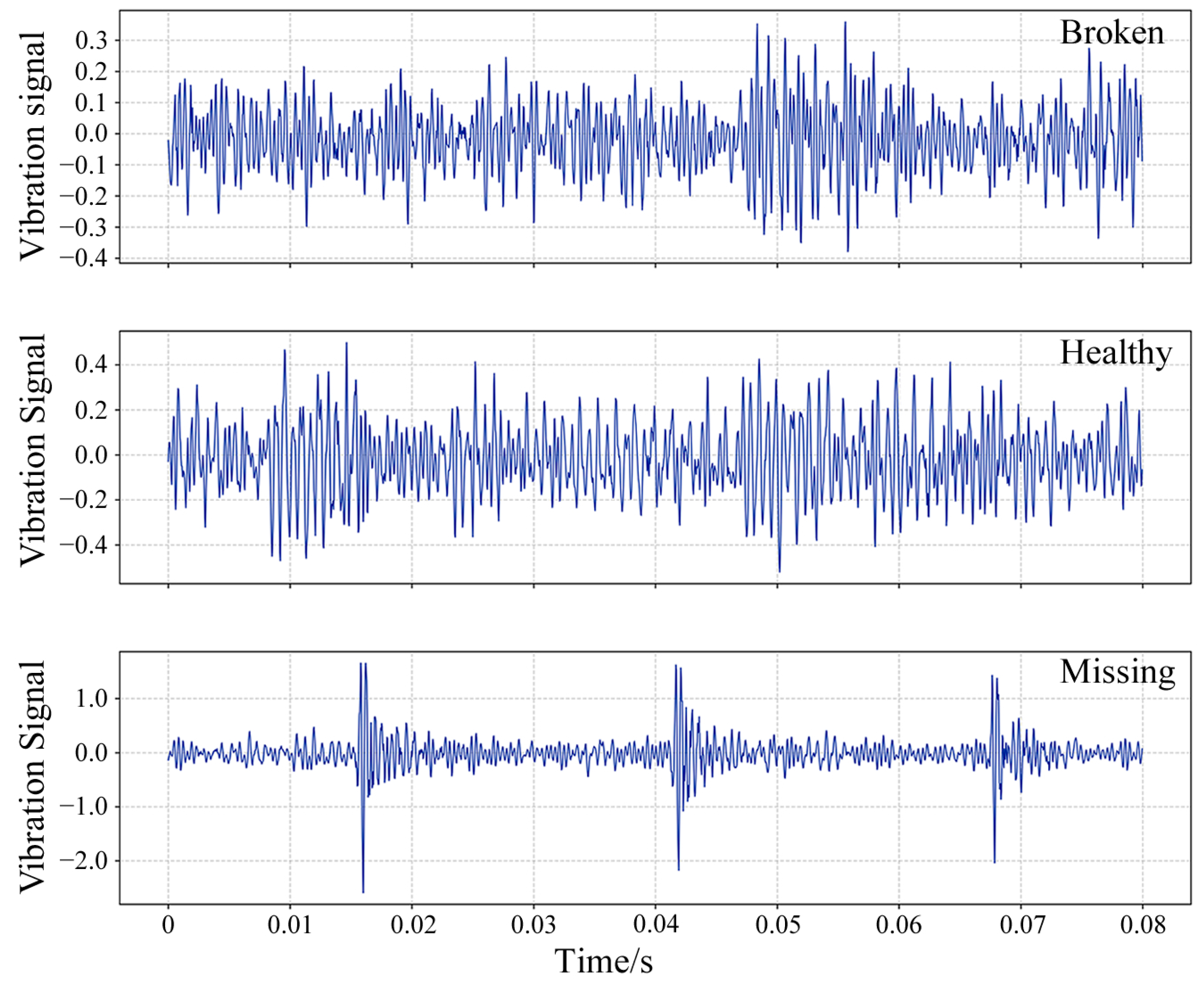
4.1.1. Data Description
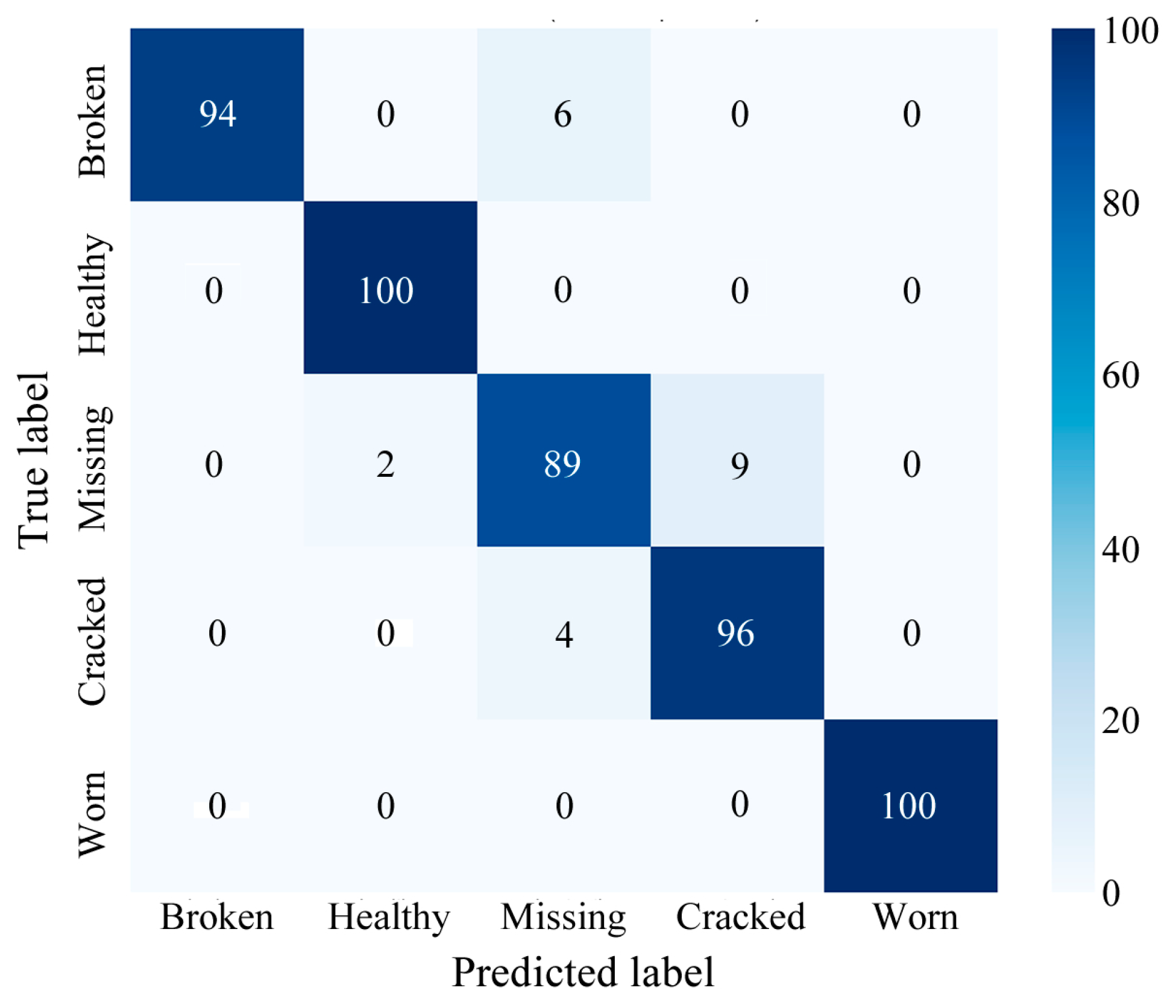
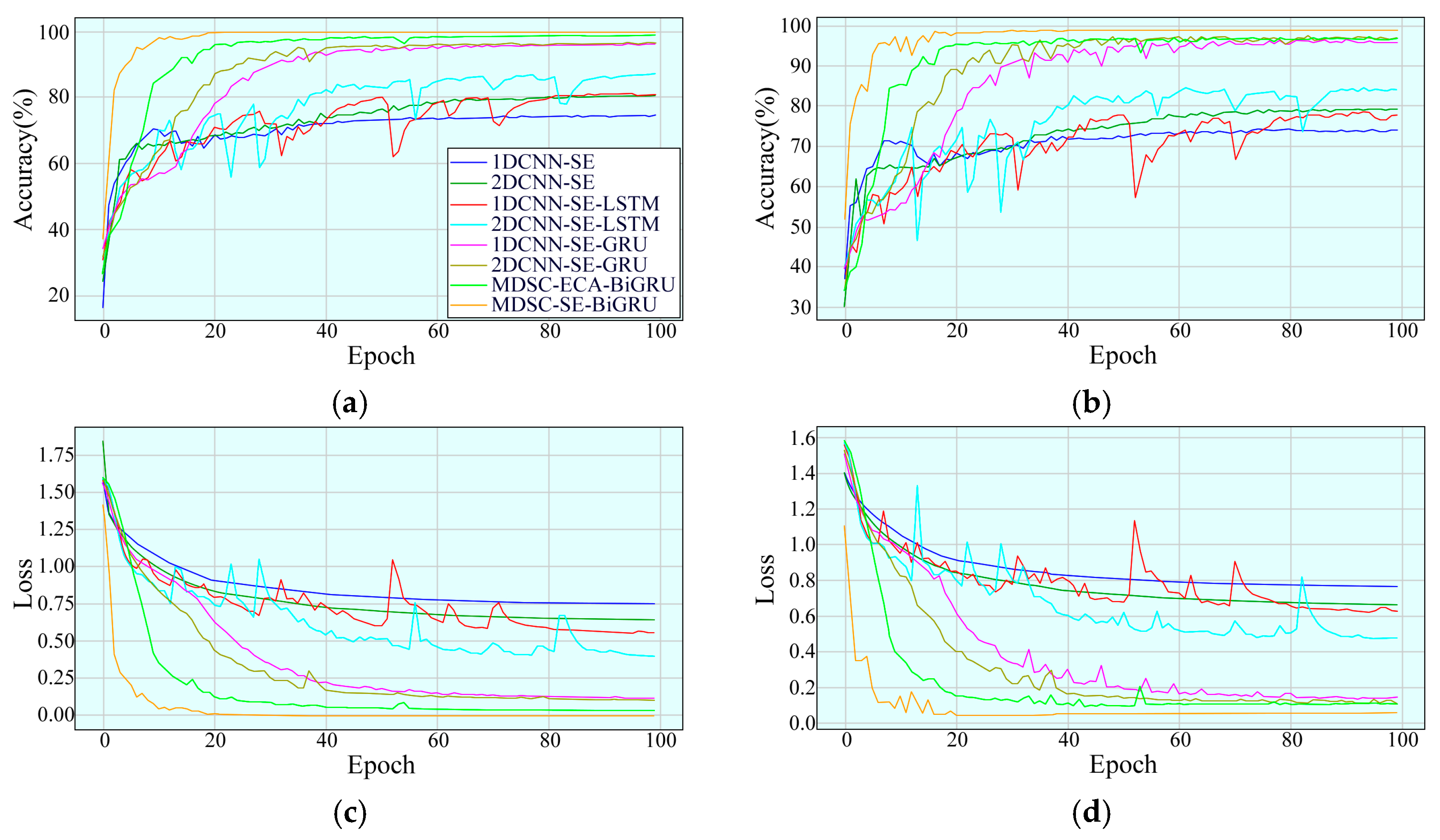
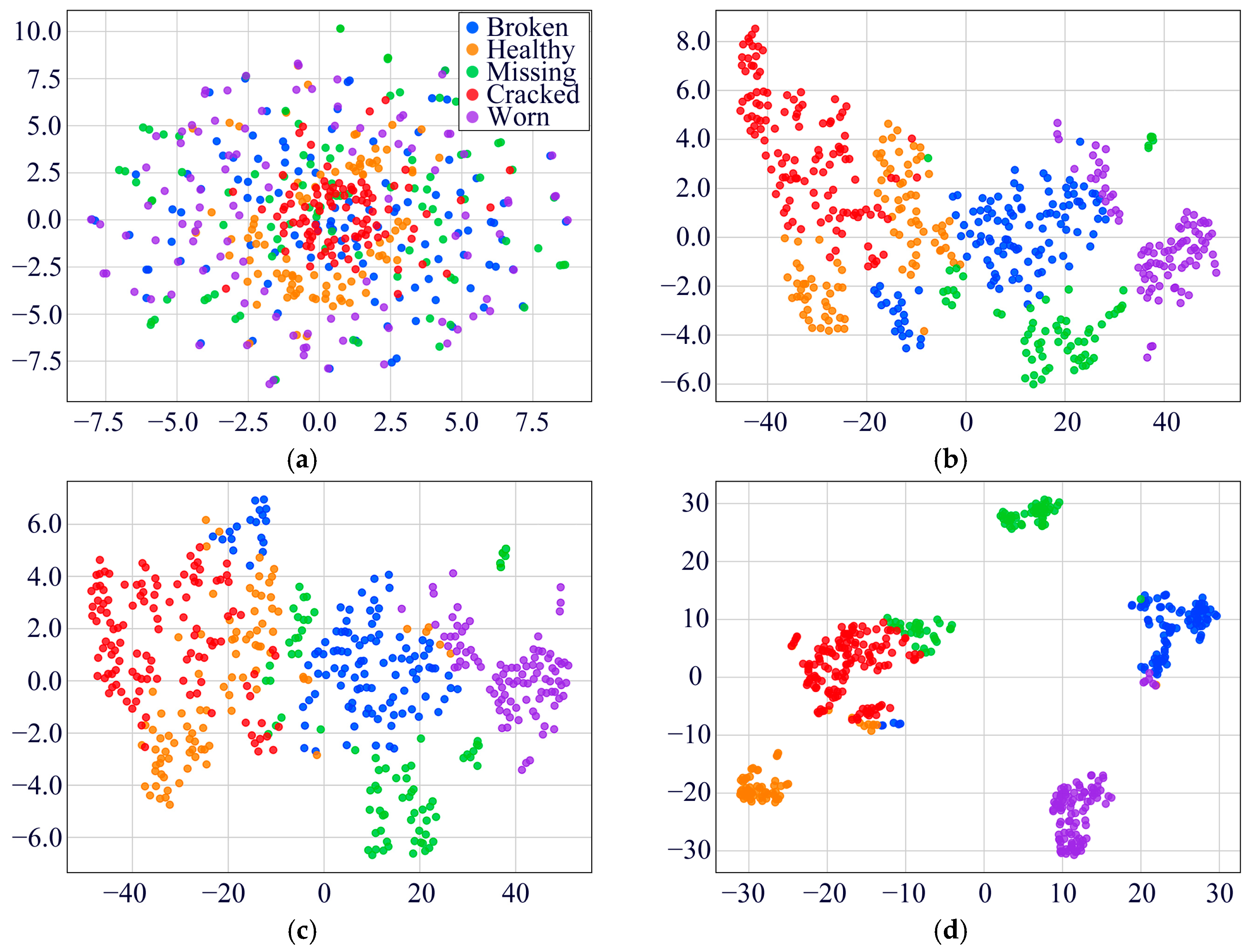
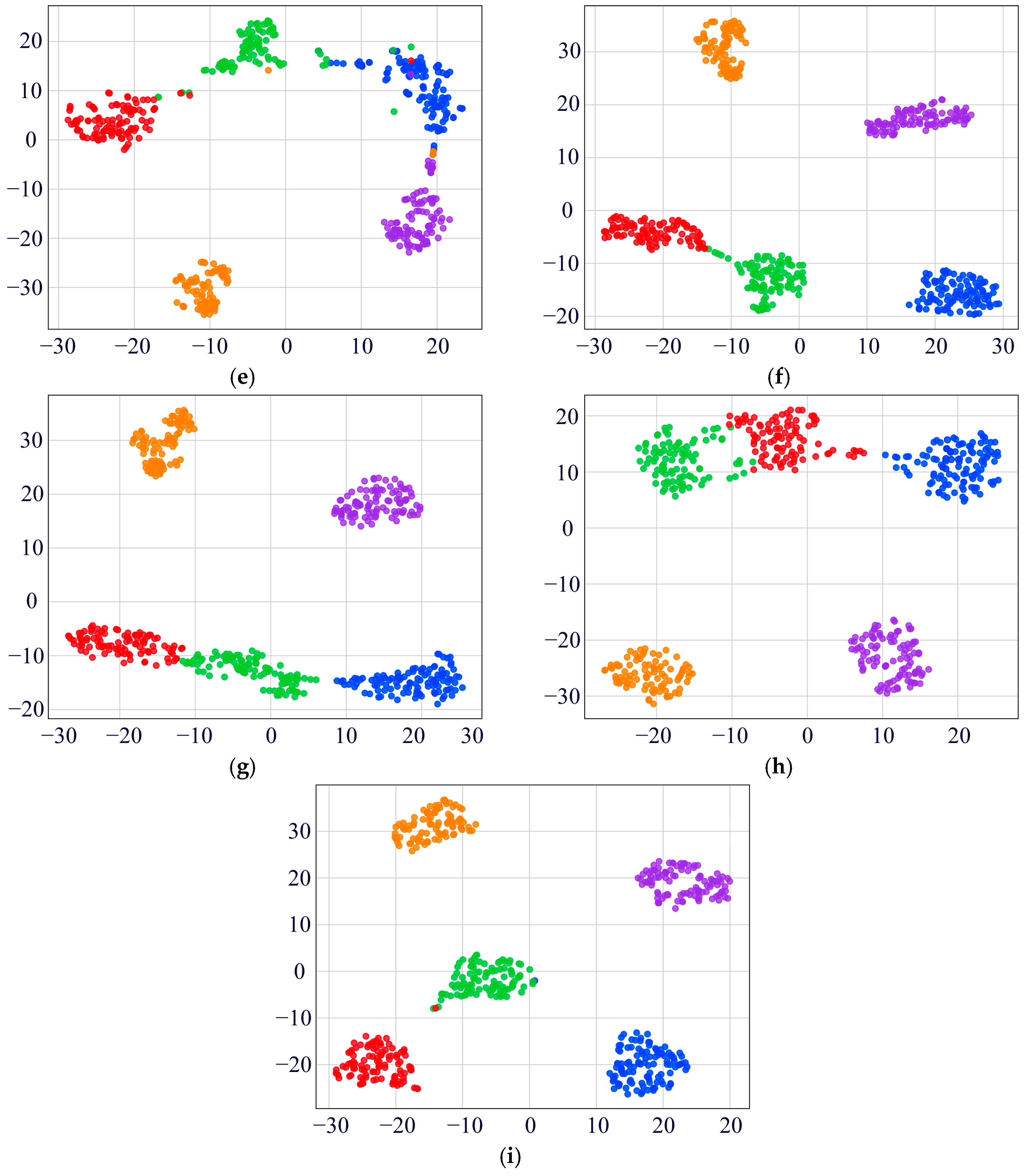
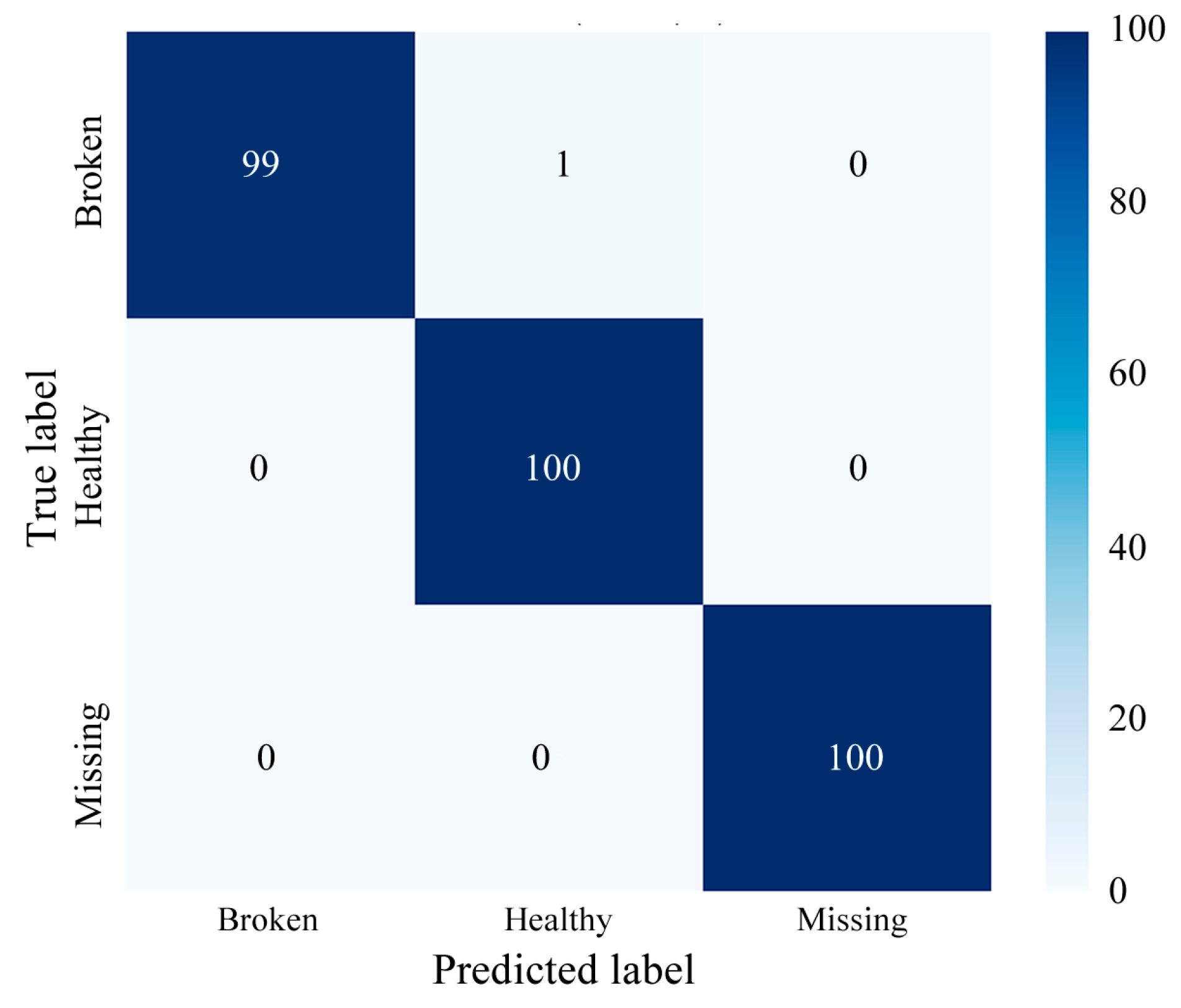
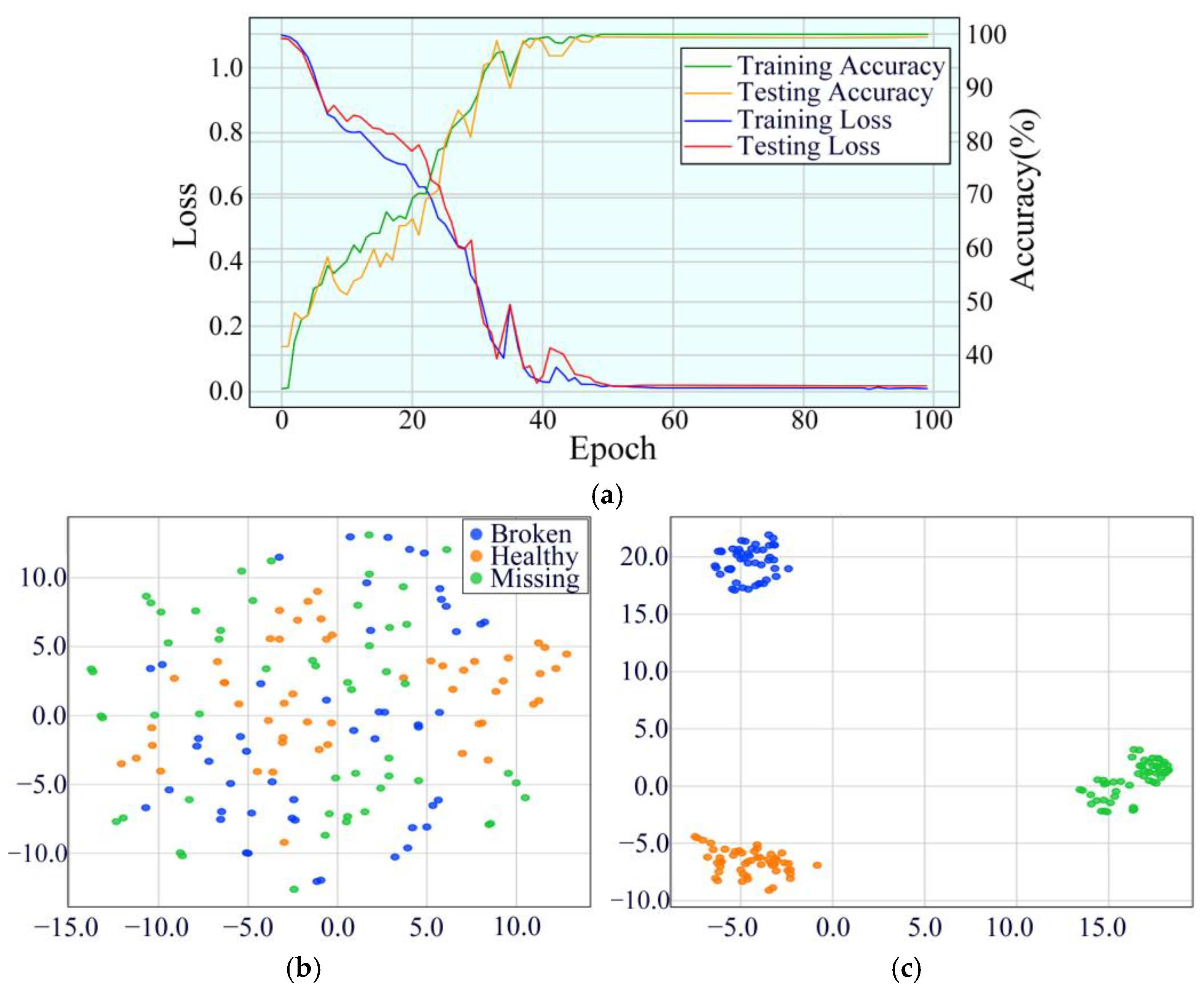
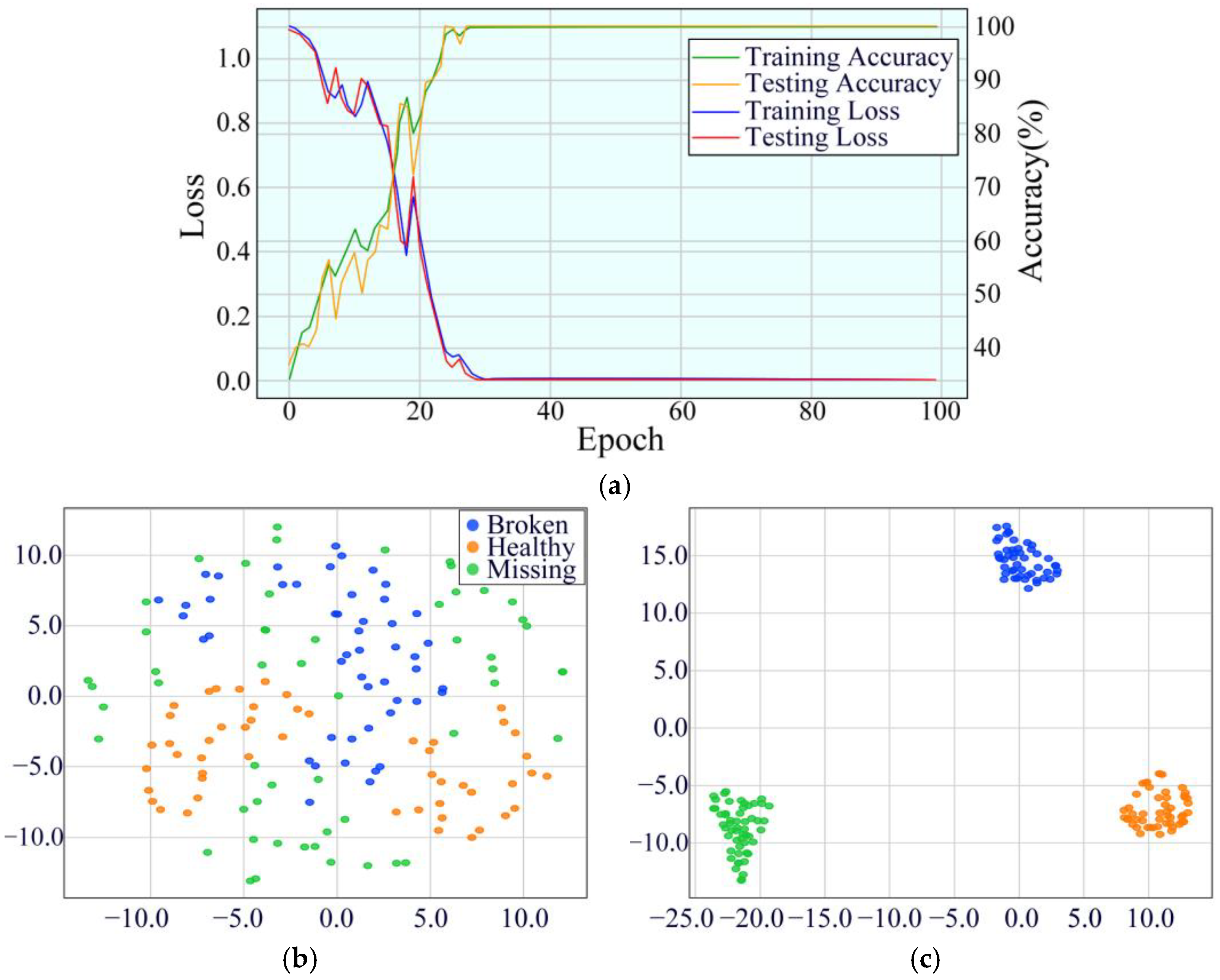
4.1.2. Experimental Results and Analysis
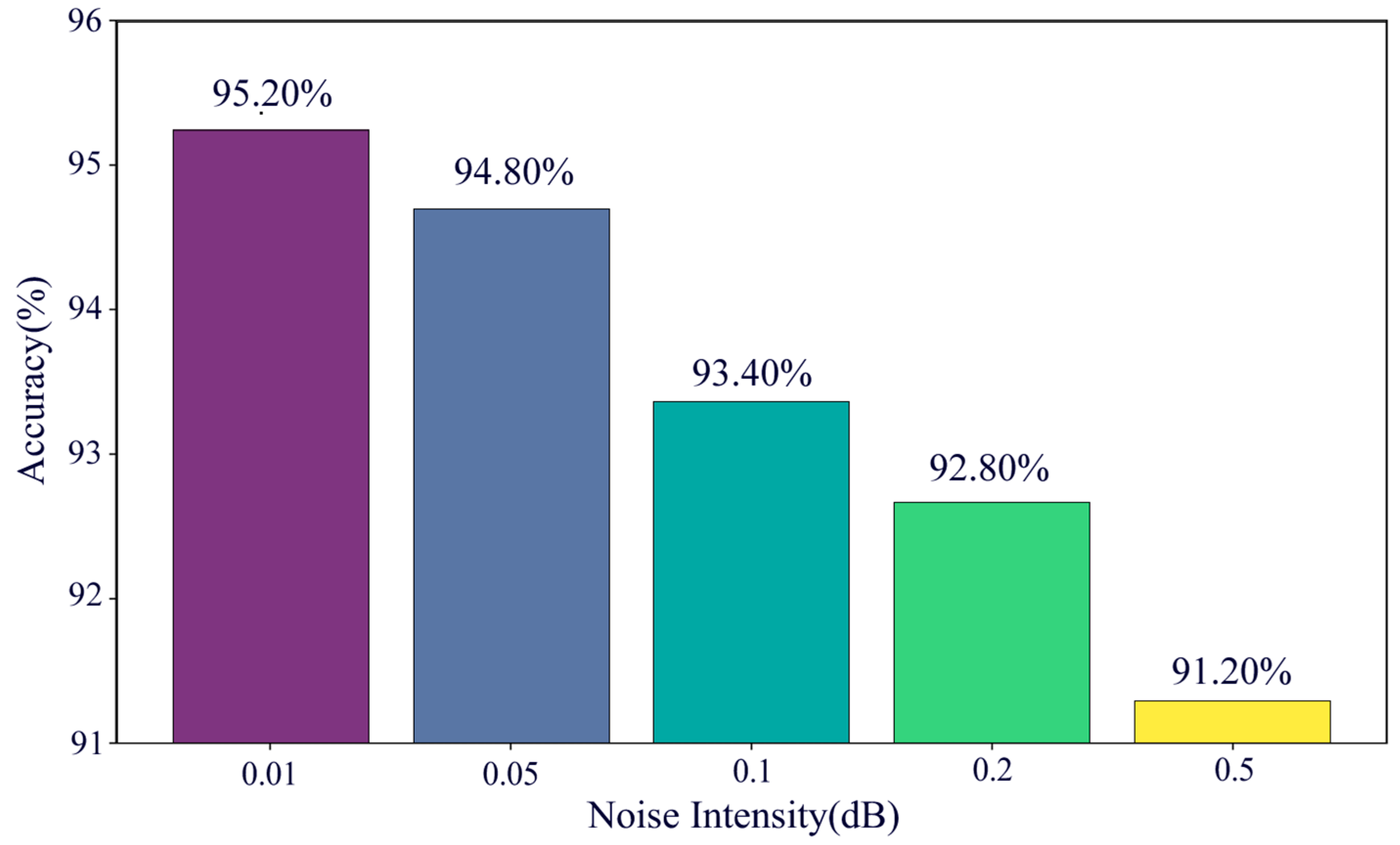
4.1.3. Testing Performance Under Different Noise Intensities
4.2. Case 2: Fault Diagnosis of Standard Gearbox
4.2.1. Data Description
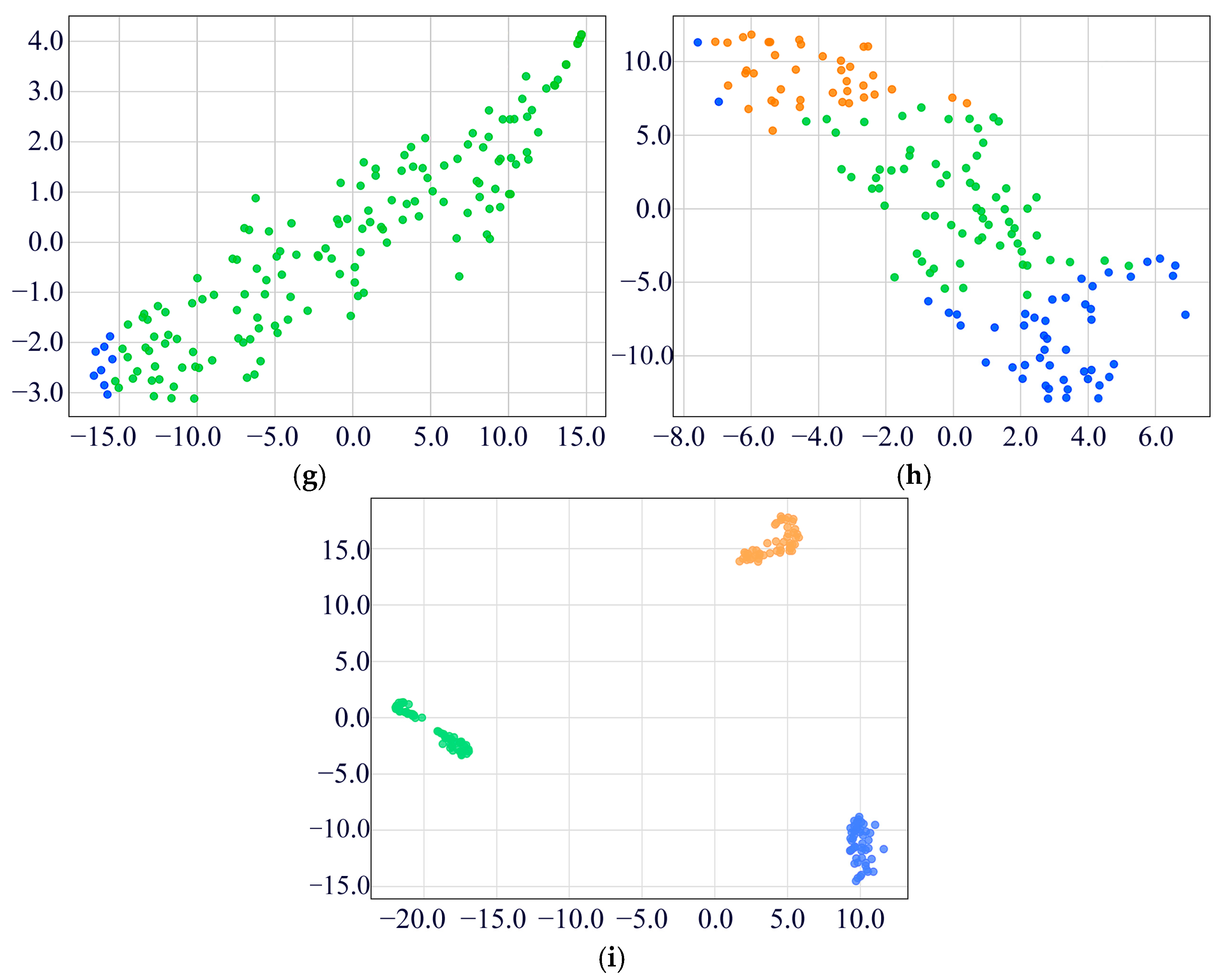
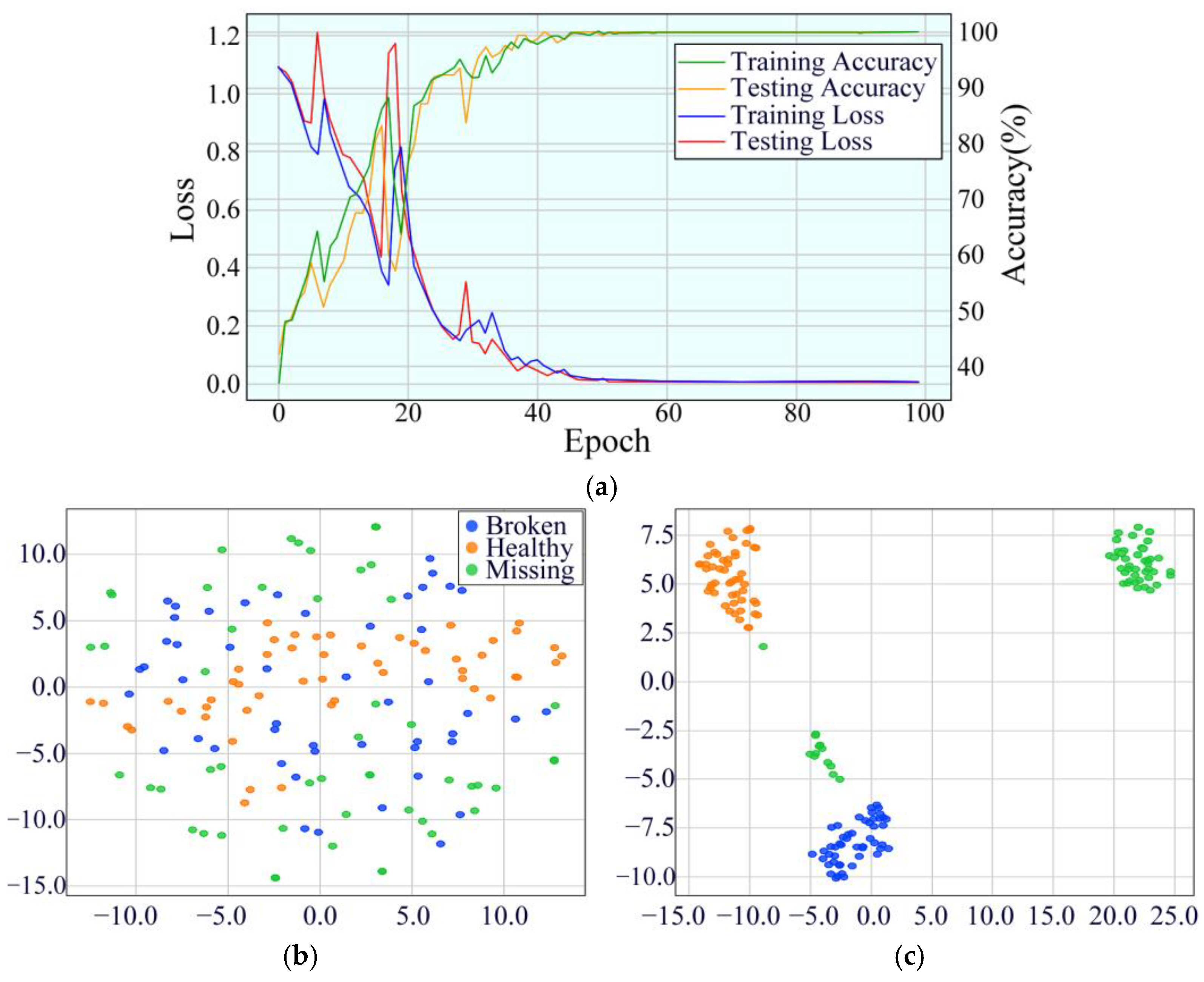
4.2.2. Experimental Results and Analysis
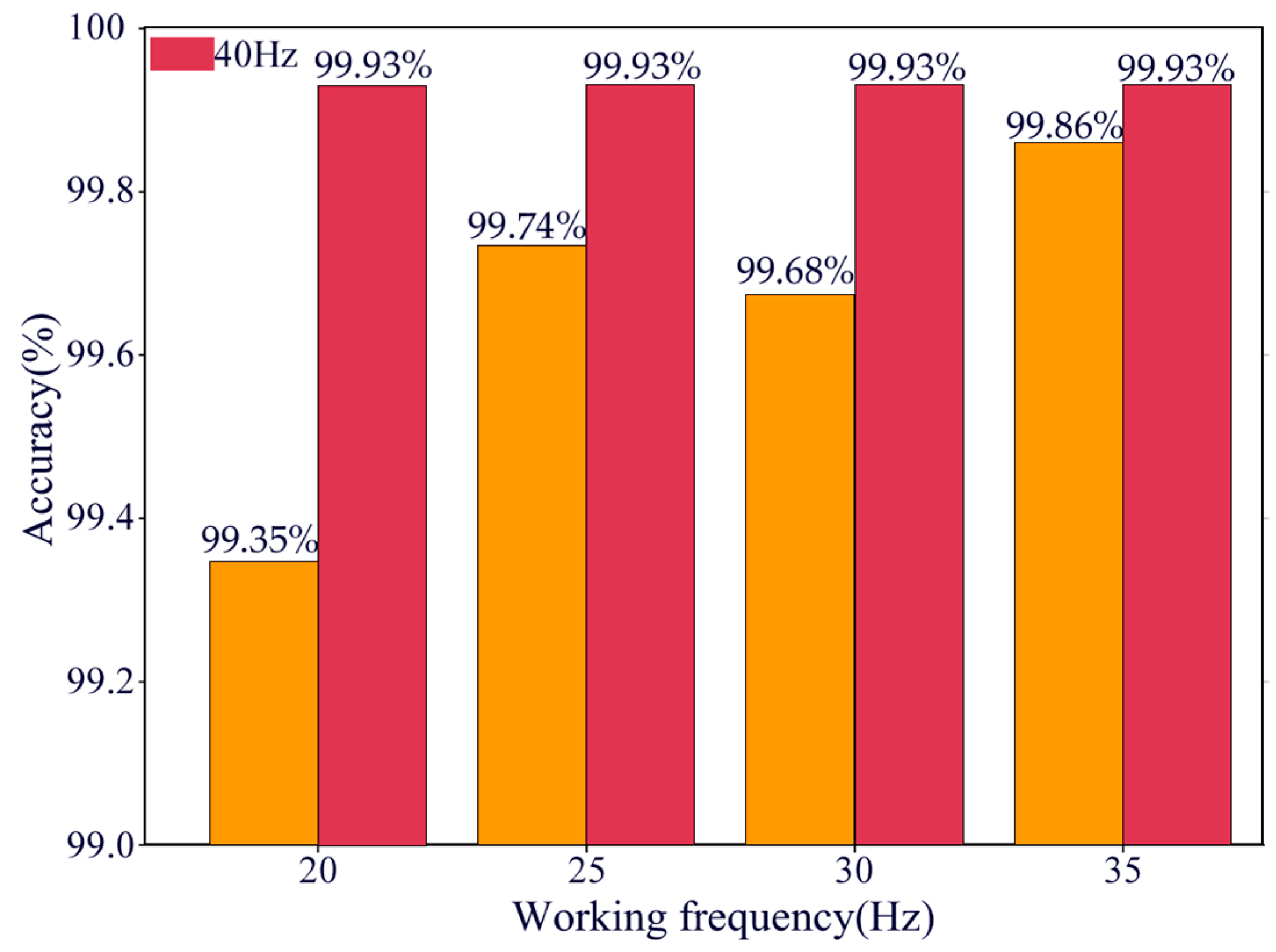
4.2.3. Testing Performance Under Different Operating Conditions
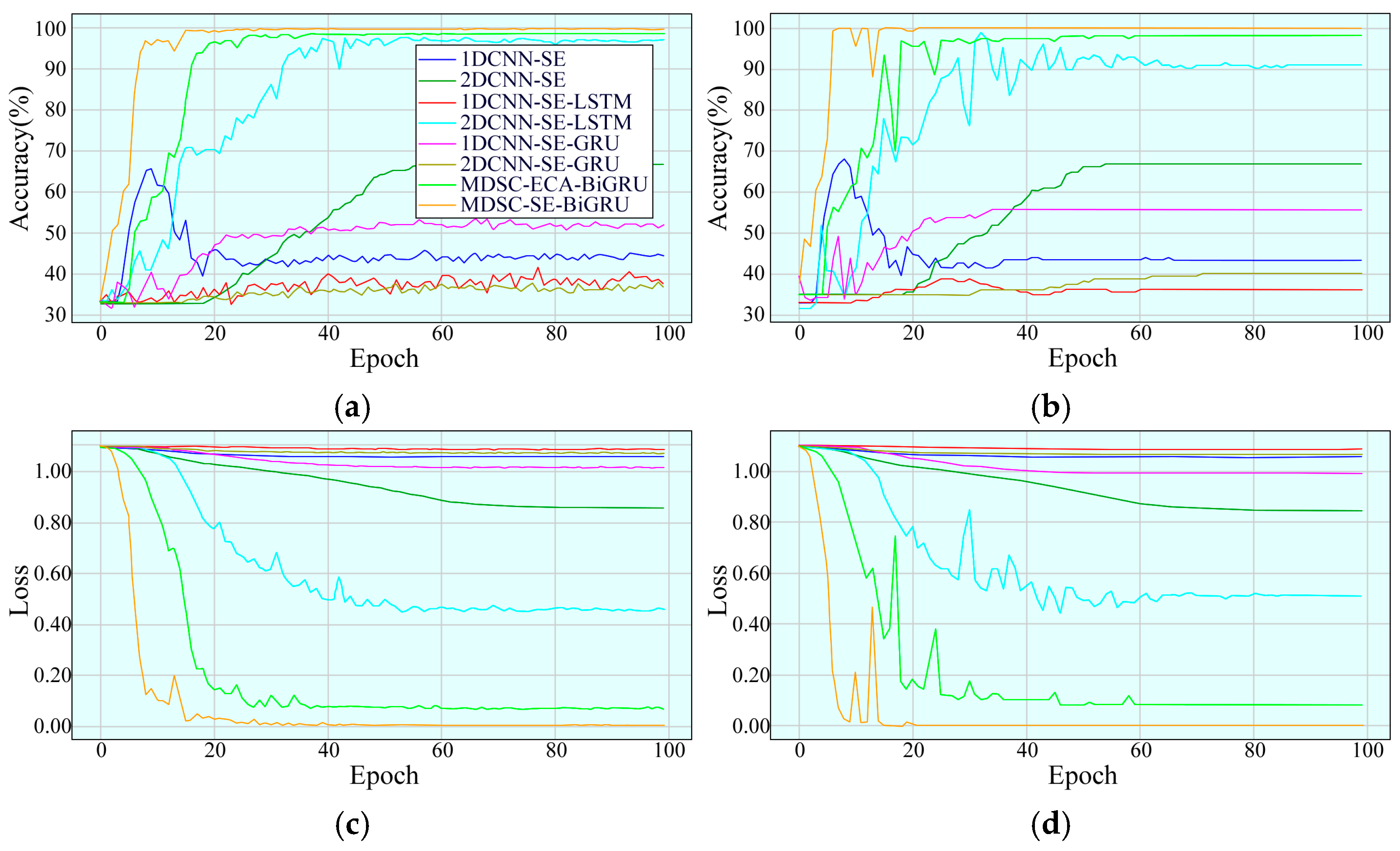
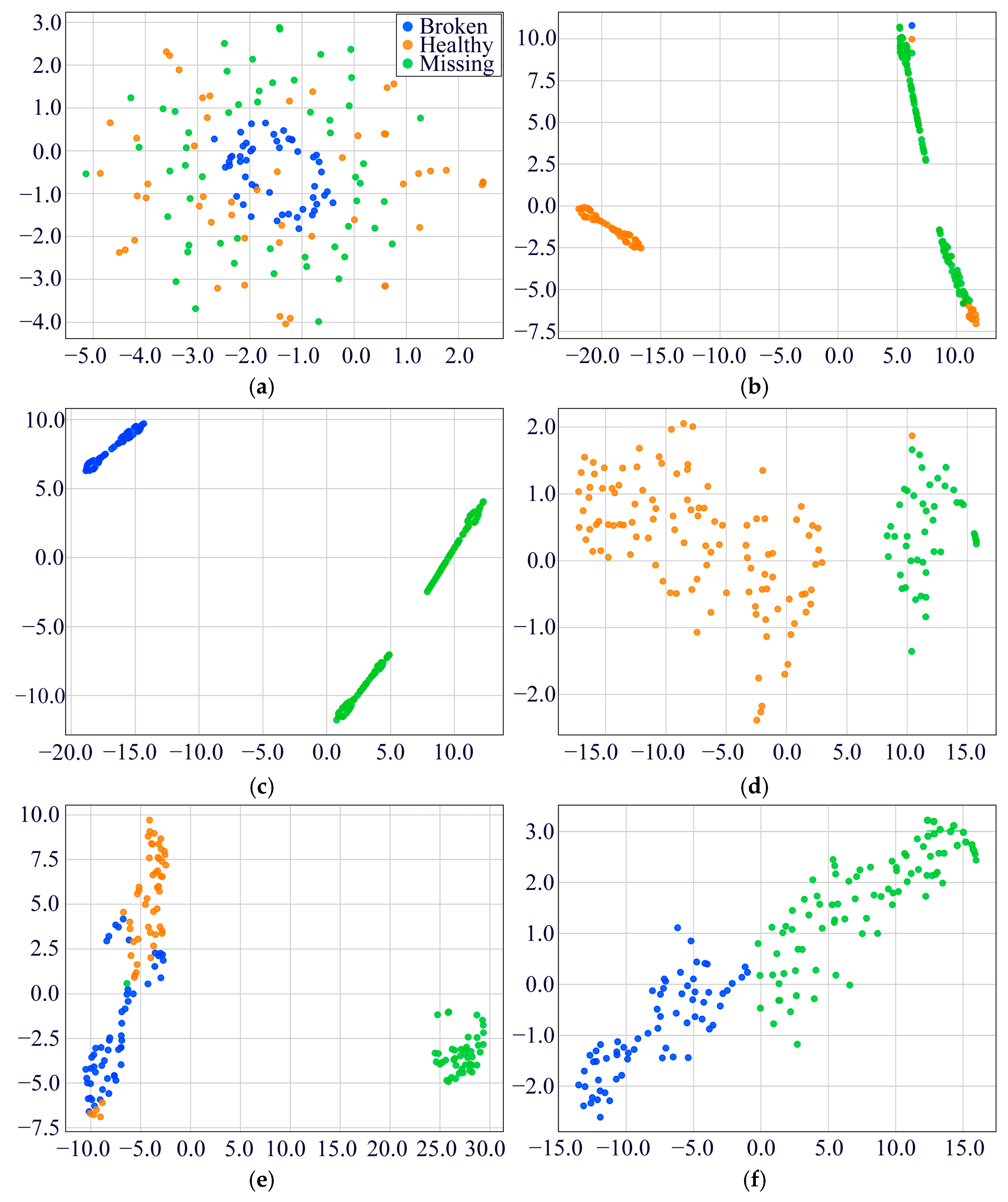
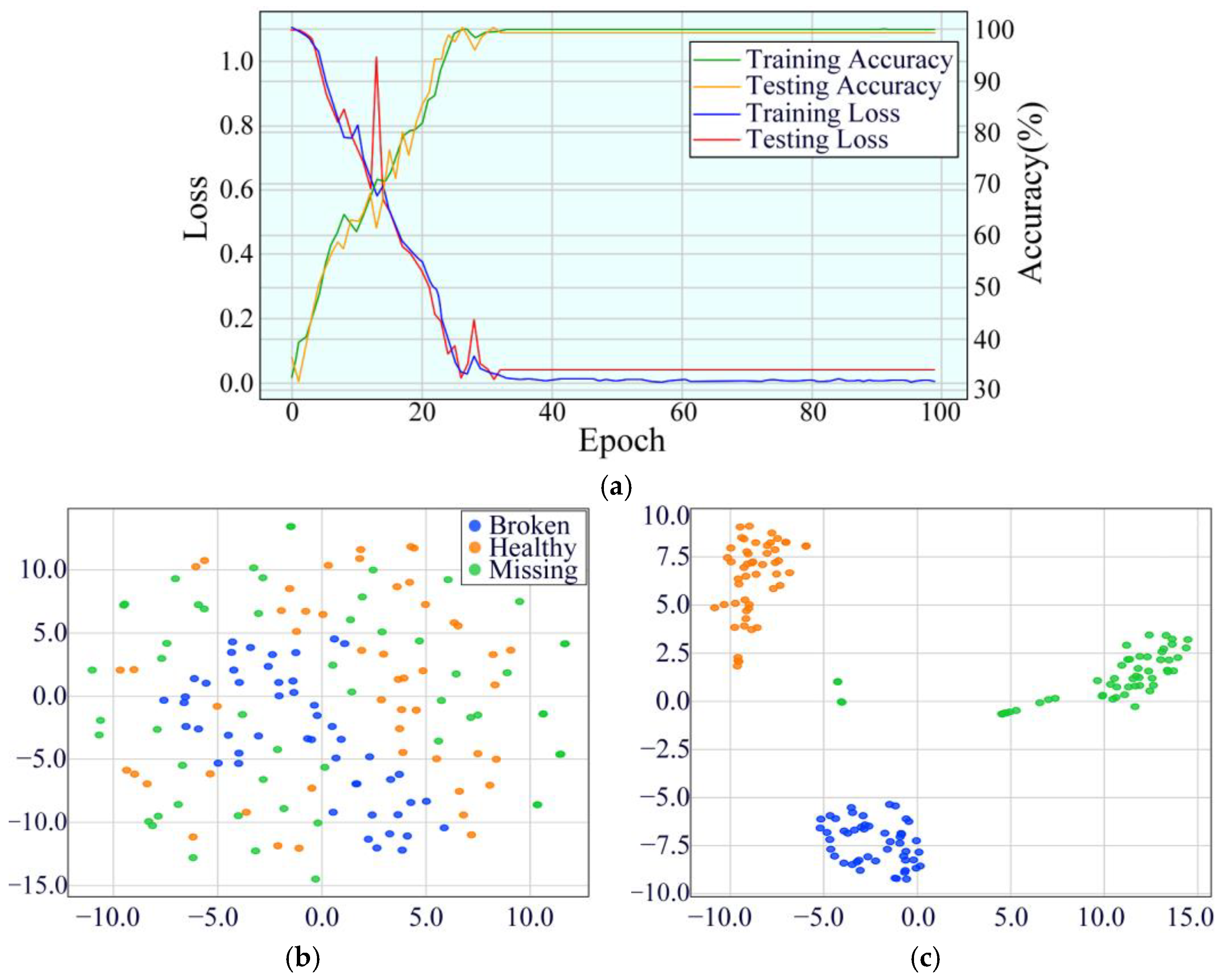
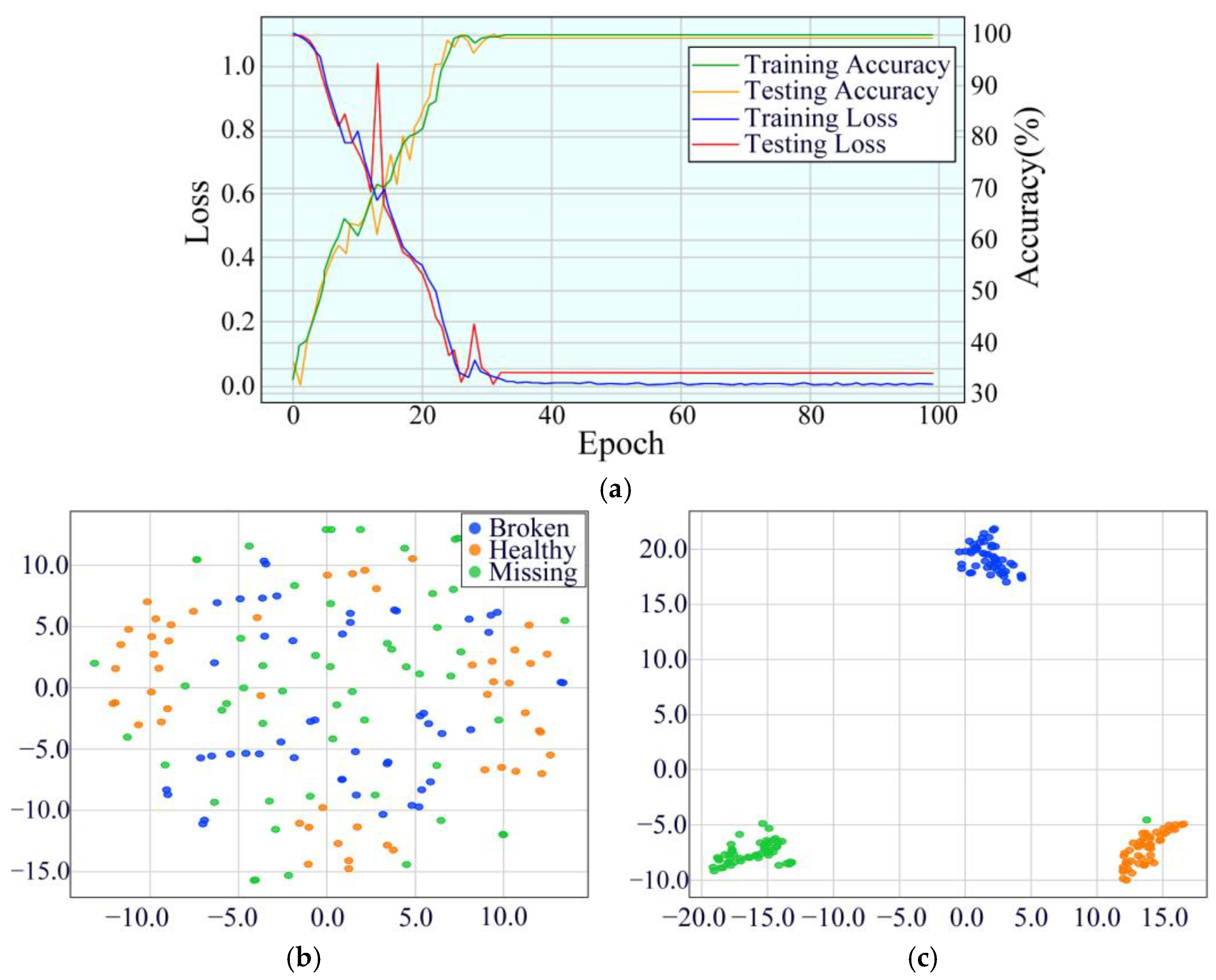
4.3. Ablation Experiments for the Proposed MDSC-SE-BiGRU Model
5. Conclusions
- (1)
- Acquiring real-world industrial fault data to further validate the performance of the MDSC-SE-BiGRU model in practical applications.
- (2)
- Optimizing the computational efficiency of the MDSC-SE-BiGRU model to meet the real-time diagnostic requirements of industrial applications, enabling lightweight deployment on embedded systems and edge computing platforms.
- (3)
- Integrating vibration, temperature, acoustic, and other multi-modal signals to further improve the accuracy and reliability of fault diagnosis.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, T.; Zhu, C.; Chen, J.; Liu, H. A review on gear scuffing studies: Theories, experiments and design. Tribol. Int. 2024, 196, 109741. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, J.; Dong, C.; Guo, J. An analytical calculation of time-varying mesh stiffness of non-circular planetary gear system with crack. Iran. J. Sci. Technol. Trans. Mech. Eng. 2025; in press. [Google Scholar] [CrossRef]
- Gong, Q.; Shi, J.; Nan, W.; Zhao, G.; Qi, P. Multi-state meshing characteristics and global nonlinear dynamics of a spur gear system considering local tooth breakage. Meccanica 2025, 60, 119–140. [Google Scholar] [CrossRef]
- Fan, L.; Zhao, X.; Hao, W.; Miao, C.; Hu, X.; Fang, C. Tribo-dynamic behavior of double-row cylindrical roller bearings under raceway defects and cage fracture. Lubricants 2025, 13, 80. [Google Scholar] [CrossRef]
- Morales-Espejel, G.-E. Thermal damage on rolling/sliding contact surfaces as produced by embedded particles. Tribol. Int. 2024, 199, 109968. [Google Scholar] [CrossRef]
- Ninawe, S.; Deshmukh, R. Efficient vibration analysis system using empirical mode decomposition residual signal and multi-axis data. J. Vib. Control, 2024; in press. [Google Scholar] [CrossRef]
- Nguyen, T.-D.; Nguyen, P.-D. Improvements in the wavelet transform and its variations: Concepts and applications in diagnosing gearbox in non-stationary conditions. Appl. Sci. 2024, 14, 4642. [Google Scholar] [CrossRef]
- Lee, S.; Jeong, H.; Kwon, J. Transformer-based GAN with Multi-STFT for rotating machinery vibration data analysis. Electronics 2024, 13, 4253. [Google Scholar] [CrossRef]
- Luo, X.; Wang, H.; Han, T.; Zhang, Y. FFT-Trans: Enhancing Robustness in Mechanical Fault Diagnosis With Fourier Transform-Based Transformer Under Noisy Conditions. IEEE Trans. Instrum. Meas. 2024, 73, 2515112. [Google Scholar] [CrossRef]
- Wang, J.; Li, J.; Wang, H.; Guo, L. Composite fault diagnosis of gearbox based on empirical mode decomposition and improved variational mode decomposition. J. Low Freq. Noise Vib. Act. Control 2021, 40, 332–346. [Google Scholar] [CrossRef]
- Huang, T.; Yi, C.; Hao, Z.; Tan, X.; Deng, D. Adaptive window rotated second-order synchroextracting transform and its application in fault diagnosis of wind turbine gearbox. Meas. Sci. Technol. 2023, 34, 024005. [Google Scholar] [CrossRef]
- Strömbergsson, D.; Marklund, P.; Berglund, K.; Larsson, P.-E. Bearing monitoring in the wind turbine drivetrain: A comparative study of the FFT and wavelet transforms. Wind. Energy 2020, 23, 1381–1393. [Google Scholar] [CrossRef]
- Hou, S.; Zheng, J.; Pan, H.; Feng, K.; Liu, Q.; Ni, Q. Multivariate multi-scale cross-fuzzy entropy and SSA-SVM-based fault diagnosis method of gearbox. Meas. Sci. Technol. 2024, 35, 056102. [Google Scholar] [CrossRef]
- Felix, L.O.; de Sá Só Martins, D.H.C.; Monteiro, U.A.B.V.; Pinto, L.A.V.; Tarrataca, L.; Martins, C.A.O. Multiple fault diagnosis in a wind turbine gearbox with autoencoder data augmentation and kpca dimension reduction. J. Nondestruct. Eval. 2024, 43, 114. [Google Scholar] [CrossRef]
- Bao, C.; Zhang, T.; Hu, Z.; Feng, W.; Liu, R. Wind turbine condition monitoring based on improved active learning strategy and KNN algorithm. IEEE Access 2023, 11, 13545–13553. [Google Scholar] [CrossRef]
- Hou, Y.; Wang, J.; Chen, Z.; Ma, J.; Li, T. Diagnosisformer: An efficient rolling bearing fault diagnosis method based on improved Transformer. Eng. Appl. Artif. Intell. 2023, 124, 106507. [Google Scholar] [CrossRef]
- Yu, S.; Pang, S.; Ning, J.; Wang, M.; Song, L. ANC-Net: A novel multiscale active noise cancellation network for rotating machinery fault diagnosis based on discrete wavelet transform. Expert Syst. Appl. 2025, 265, 125937. [Google Scholar] [CrossRef]
- Ding, J.; Xiao, D.; Li, X. Gear Fault Diagnosis Based on Genetic Mutation Particle Swarm Optimization VMD and Probabilistic Neural Network Algorithm. IEEE Access 2020, 8, 18456–18474. [Google Scholar] [CrossRef]
- Huang, D.; Zhang, W.-A.; Guo, F.; Liu, W.; Shi, X. Wavelet packet decomposition-based multiscale CNN for fault diagnosis of wind turbine gearbox. IEEE Trans. Cybern. 2023, 53, 443–453. [Google Scholar] [CrossRef]
- Wang, M.-H.; Chen, F.-H.; Lu, S.-D. Research on fault diagnosis of wind turbine gearbox with snowflake graph and deep learning algorithm. Appl. Sci. 2023, 13, 1416. [Google Scholar] [CrossRef]
- Pang, X.; Xue, X.; Jiang, W.; Lu, K. An investigation into fault diagnosis of planetary gearboxes using a bispectrum convolutional neural network. IEEE/ASME Trans. Mechatron. 2021, 26, 2027–2037. [Google Scholar] [CrossRef]
- Mao, G.; Zhang, Z.; Qiao, B.; Li, Y. Fusion domain-adaptation CNN driven by images and vibration signals for fault diagnosis of gearbox cross-working conditions. Entropy 2022, 24, 119. [Google Scholar] [CrossRef] [PubMed]
- Andhale, Y.; Parey, A. Gearbox fault detection using entropy-based feature extraction and hybrid classifier. Proc. Inst. Mech. Eng. Part D—J. Automob. Eng. 2024; in press. [Google Scholar]
- Chen, Y.; Liu, X.; Rao, M.; Qin, Y.; Wang, Z.; Ji, Y. Explicit speed-integrated LSTM network for non-stationary gearbox vibration representation and fault detection under varying speed conditions. Reliab. Eng. Syst. Saf. 2025, 254, 110596. [Google Scholar] [CrossRef]
- Su, X.; Shan, Y.; Li, C.; Mi, Y.; Fu, Y.; Dong, Z. Spatial-temporal attention and GRU based interpretable condition monitoring of offshore wind turbine gearboxes. IET Renew. Power Gener. 2022, 16, 402–415. [Google Scholar] [CrossRef]
- Chen, Y.; Zheng, X. Fault diagnosis of wind turbine based on multi-signal CNN-GRU model. Proc. Inst. Mech. Eng. Part A—J. Power Energy 2023, 237, 1113–1124. [Google Scholar] [CrossRef]
- Li, Z.; Feng, X.; Wang, L.; Xie, Y. DC–DC circuit fault diagnosis based on GWO optimization of 1DCNN-GRU network hyperparameters. Energy Rep. 2023, 9, 536–548. [Google Scholar] [CrossRef]
- Yin, S.; Chen, Z. Research on compound fault diagnosis of bearings using an improved DRSN-GRU dual-channel model. IEEE Sens. J. 2024, 24, 35304–35311. [Google Scholar] [CrossRef]
- Han, S.; Zhong, X.; Shao, H.; Xu, T.; Zhao, R.; Cheng, J. Novel multiscale dilated CNN-LSTM for fault diagnosis of planetary gearbox with unbalanced samples under noisy environment. Meas. Sci. Technol. 2021, 32, 124002. [Google Scholar] [CrossRef]
- Wang, T.; Tang, Y.; Wang, T.; Lei, N. An improved MSCNN and GRU model for rolling bearing fault diagnosis. Strojniski Vestn.-J. Mech. Eng. 2023, 69, 261–274. [Google Scholar] [CrossRef]
- Liu, Y.; Gao, T.; Wu, W.; Sun, Y. Planetary gearboxes fault diagnosis based on markov transition fields and SE-ResNet. Sensors 2024, 24, 7540. [Google Scholar] [CrossRef] [PubMed]
- Shao, Z.; Jiang, H.; Zhang, X.; Zhou, J.; Huang, W. PLL-WCAN: Pseudo-label progressive learning guided wavelet class-aware adaptive network for gearbox cross-domain fault diagnosis. Mech. Syst. Signal Proc. 2025, 230, 112624. [Google Scholar] [CrossRef]
- He, C.; Yasenjiang, J.; Lv, L.; Xu, L.; Lan, Z. Gearbox fault diagnosis based on MSCNN-LSTM-CBAM-SE. Sensors 2024, 24, 4682. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Mao, J.; Zhao, M. Rolling bearing fault diagnosis method based on attention CNN and BiLSTM network. Neural Process. Lett. 2023, 55, 3377–3410. [Google Scholar] [CrossRef]
- Yang, J.; Gao, T.; Jiang, S. A dual-input fault diagnosis model based on SE-MSCNN for analog circuits. Appl. Intell. 2023, 53, 7154–7168. [Google Scholar] [CrossRef]
- Wang, Z.; Xuan, J.; Shi, T.; Li, Y. Multi-label domain adversarial reinforcement learning for unsupervised compound fault recognition. Reliab. Eng. Syst. Saf. 2025, 254, 110638. [Google Scholar] [CrossRef]
- Wang, Z.; Xuan, J.; Shi, T. Domain reinforcement feature adaptation methodology with correlation alignment for compound fault diagnosis of rolling bearing. Expert Syst. Appl. 2025, 262, 125594. [Google Scholar] [CrossRef]
- Wang, Z.; Xuan, J.; Shi, T. An autonomous recognition framework based on reinforced adversarial open set algorithm for compound fault of mechanical equipment. Mech. Syst. Signal Proc. 2024, 219, 111596. [Google Scholar] [CrossRef]
- Wang, Z.; Li, S.; Xuan, J.; Shi, T. Biologically inspired compound defect detection using a spiking neural network with continuous time–frequency gradients. Adv. Eng. Inform. 2025, 65, 103132. [Google Scholar] [CrossRef]
- Liu, D.; Cui, L.; Cheng, W. A review on deep learning in planetary gearbox health state recognition: Methods, applications, and dataset publication. Meas. Sci. Technol. 2024, 35, 012002. [Google Scholar] [CrossRef]
- Zhao, C.; Zio, E.; Shen, W. Domain generalization for cross-domain fault diagnosis: An application-oriented perspective and a benchmark study. Reliab. Eng. Syst. Saf. 2024, 245, 109964. [Google Scholar] [CrossRef]



| Layer Structure | Input Size | Convolutional Kernel Size (Number) | Output Size | Stride |
|---|---|---|---|---|
| Conv_1-BN-ReLU | [1, 1024] | 3 × 1 (64) | [64, 1024] | 1 |
| Conv_2-BN-ReLU | [1, 1024] | 5 × 1 (64) | [64, 1024] | 1 |
| Conv_3-BN-ReLU | [1, 1024] | 7 × 1 (64) | [64, 1024] | 1 |
| Feature Fusion | [64, 1024] × 3 | - | [192, 1024] | - |
| SEBlock | [192, 1024] | - | [192, 1024] | - |
| BiGRU | [192, 1024] | - | [256, 1024] | - |
| Fc_1 | [256] | - | [128] | - |
| Fc_2 | [128] | - | [64] | - |
| Fc_3 | [64] | - | [5] | - |
| Model Name | Kernel Size | Input Size | Output Size | Parameter Number | FC Layers |
|---|---|---|---|---|---|
| 1DCNN-SE | 3 | (1, 1024) | (Batch, 5) | 23,429 | 2 |
| 2DCNN-SE | 5 | (1, 1024) | (Batch, 5) | 23,429 | 2 |
| 1DCNN-SE-LSTM | 3 | (1, 1024) | (Batch, 5) | 173,445 | 2 |
| 2DCNN-SE-LSTM | 5 | (1, 1024) | (Batch, 5) | 173,445 | 2 |
| 1DCNN-SE-GRU | 3 | (1, 1024) | (Batch, 5) | 139,397 | 2 |
| 2DCNN-SE-GRU | 5 | (1, 1024) | (Batch, 5) | 139,397 | 2 |
| MDSC-ECA-BiGRU | 3, 5, 7 | (1, 1024) | (Batch, 5) | 564,933 | 3 |
| MDSC-SE-BiGRU | 3, 5, 7 | (1, 1024) | (Batch, 5) | 564,421 | 3 |
| Model Name | Accuracy | Precision | Recall | F1 Score |
|---|---|---|---|---|
| 1DCNN-SE | 0.7400 | 0.7574 | 0.7400 | 0.7423 |
| 2DCNN-SE | 0.7920 | 0.7962 | 0.7920 | 0.7912 |
| 1DCNN-SE-LSTM | 0.7780 | 0.7987 | 0.7780 | 0.7796 |
| 2DCNN-SE-LSTM | 0.8400 | 0.8406 | 0.8400 | 0.8395 |
| 1DCNN-SE-GRU | 0.9580 | 0.9587 | 0.9580 | 0.9582 |
| 2DCNN-SE-GRU | 0.9700 | 0.9700 | 0.9700 | 0.9700 |
| MDSC-ECA-BiGRU | 0.9680 | 0.9682 | 0.9680 | 0.9680 |
| MDSC-SE-BiGRU | 0.9880 | 0.9880 | 0.9880 | 0.9880 |
| Model Name | Accuracy | Precision | Recall | F1 Score |
|---|---|---|---|---|
| 1DCNN-SE | 0.4351 | 0.2753 | 0.4351 | 0.4351 |
| 2DCNN-SE | 0.6688 | 0.4985 | 0.6688 | 0.5564 |
| 1DCNN-SE-LSTM | 0.3636 | 0.2876 | 0.3636 | 0.3034 |
| 2DCNN-SE-LSTM | 0.9091 | 0.9142 | 0.9091 | 0.9087 |
| 1DCNN-SE-GRU | 0.5584 | 0.5584 | 0.5584 | 0.4493 |
| 2DCNN-SE-GRU | 0.4026 | 0.4479 | 0.4026 | 0.2787 |
| MDSC-ECA-BiGRU | 0.9805 | 0.9682 | 0.9805 | 0.9805 |
| MDSC-SE-BiGRU | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
| Number | MDSC | SE | BiGRU | Accuracy | Precision | Recall | F1 Score |
|---|---|---|---|---|---|---|---|
| 1 | × | × | × | 0.4720 | 0.5408 | 0.4720 | 0.4741 |
| 2 | √ | × | × | 0.6040 | 0.6233 | 0.6040 | 0.6108 |
| 3 | × | √ | × | 0.5660 | 0.5916 | 0.5660 | 0.5627 |
| 4 | × | × | √ | 0.7340 | 0.7345 | 0.7340 | 0.7331 |
| 5 | × | √ | √ | 0.8940 | 0.8952 | 0.8940 | 0.8916 |
| 6 | √ | × | √ | 0.9100 | 0.9102 | 0.9100 | 0.9098 |
| 7 | √ | √ | × | 0.8200 | 0.8219 | 0.8200 | 0.8193 |
| 8 | √ | √ | √ | 0.9940 | 0.9940 | 0.9940 | 0.9940 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, X.; Zhai, K.; Luo, N.; Zhao, Y.; Wang, G. Gearbox Fault Diagnosis Under Noise and Variable Operating Conditions Using Multiscale Depthwise Separable Convolution and Bidirectional Gated Recurrent Unit with a Squeeze-and-Excitation Attention Mechanism. Sensors 2025, 25, 2978. https://doi.org/10.3390/s25102978
Ma X, Zhai K, Luo N, Zhao Y, Wang G. Gearbox Fault Diagnosis Under Noise and Variable Operating Conditions Using Multiscale Depthwise Separable Convolution and Bidirectional Gated Recurrent Unit with a Squeeze-and-Excitation Attention Mechanism. Sensors. 2025; 25(10):2978. https://doi.org/10.3390/s25102978
Chicago/Turabian StyleMa, Xiaoteng, Kejia Zhai, Nana Luo, Yehui Zhao, and Guangming Wang. 2025. "Gearbox Fault Diagnosis Under Noise and Variable Operating Conditions Using Multiscale Depthwise Separable Convolution and Bidirectional Gated Recurrent Unit with a Squeeze-and-Excitation Attention Mechanism" Sensors 25, no. 10: 2978. https://doi.org/10.3390/s25102978
APA StyleMa, X., Zhai, K., Luo, N., Zhao, Y., & Wang, G. (2025). Gearbox Fault Diagnosis Under Noise and Variable Operating Conditions Using Multiscale Depthwise Separable Convolution and Bidirectional Gated Recurrent Unit with a Squeeze-and-Excitation Attention Mechanism. Sensors, 25(10), 2978. https://doi.org/10.3390/s25102978










