Guided Lamb Wave Array Time-Delay-Based MUSIC Algorithm for Impact Imaging †
Abstract
1. Introduction
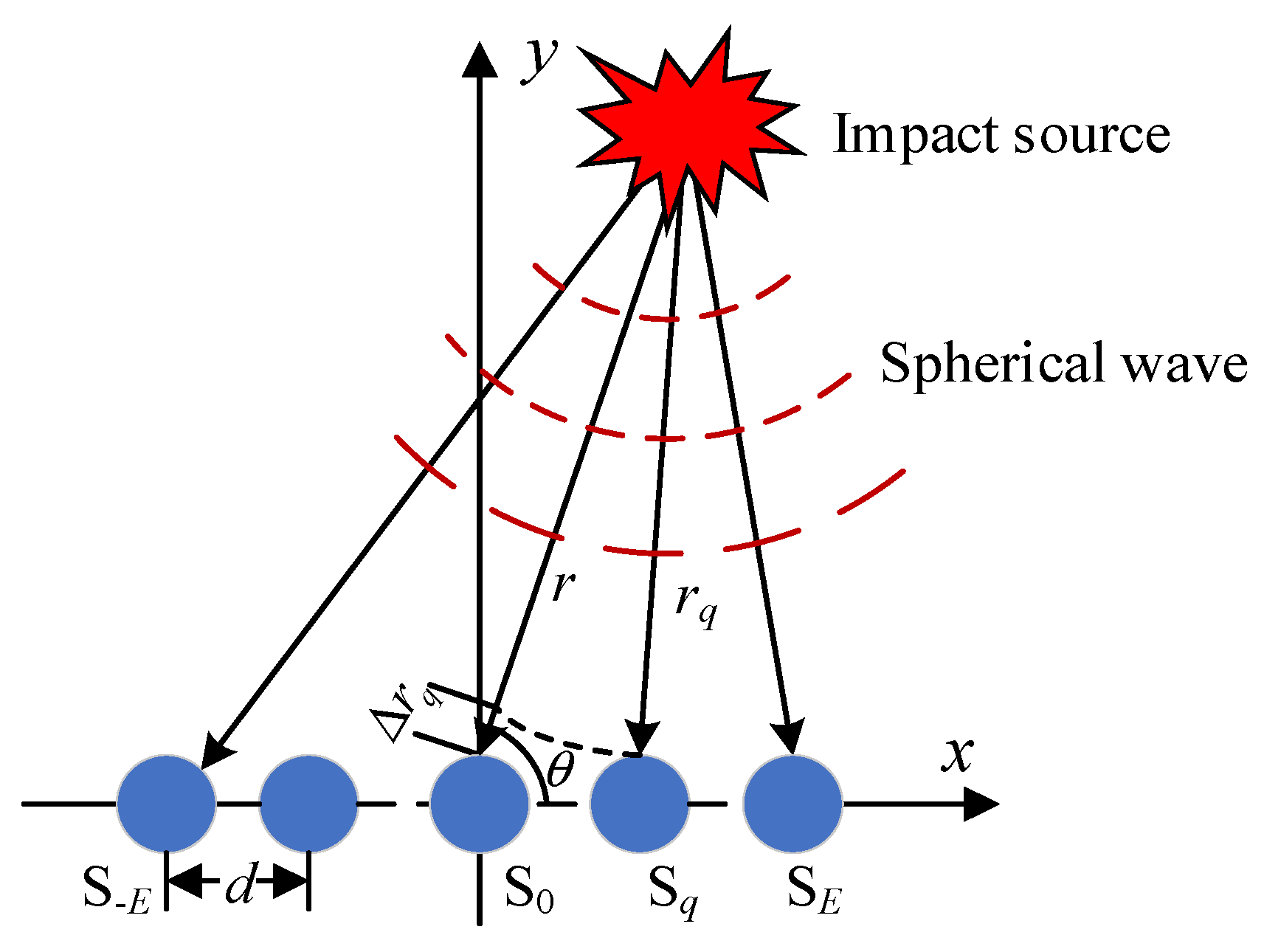
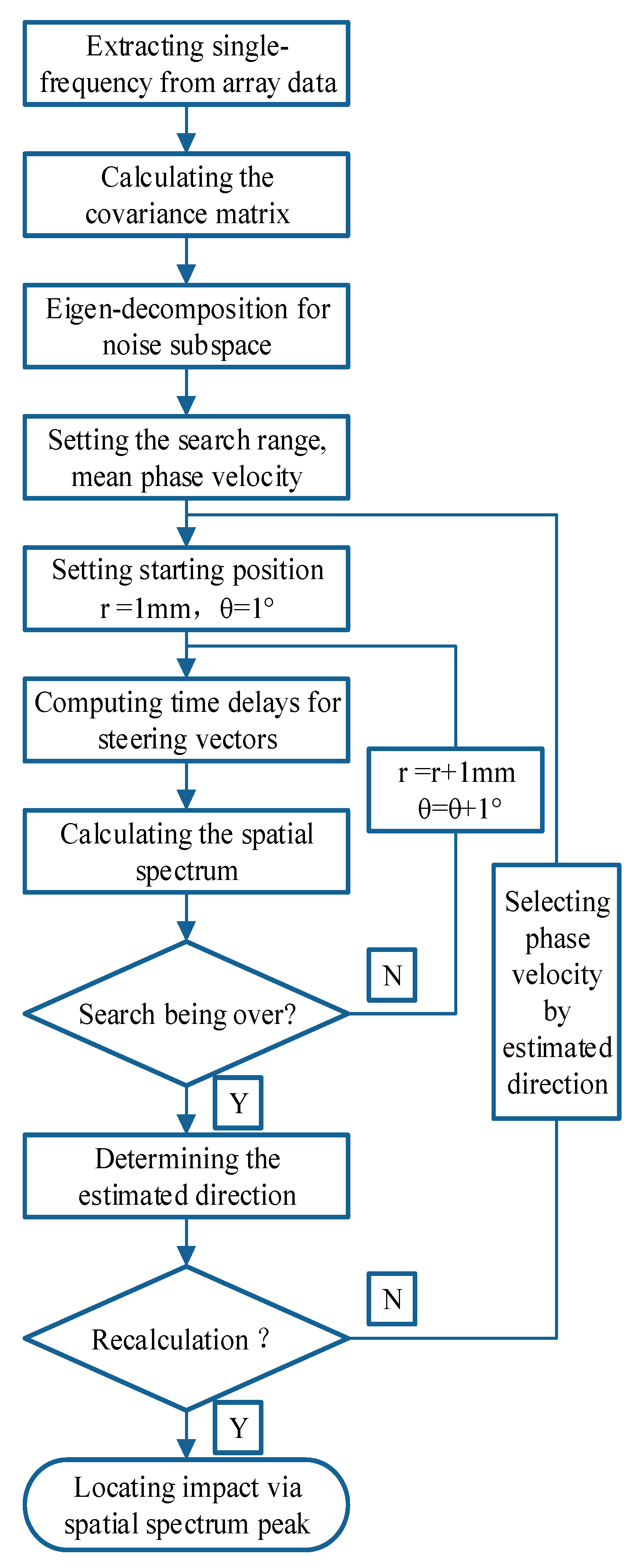
2. Array Time-Delay-Based MUSIC Algorithm
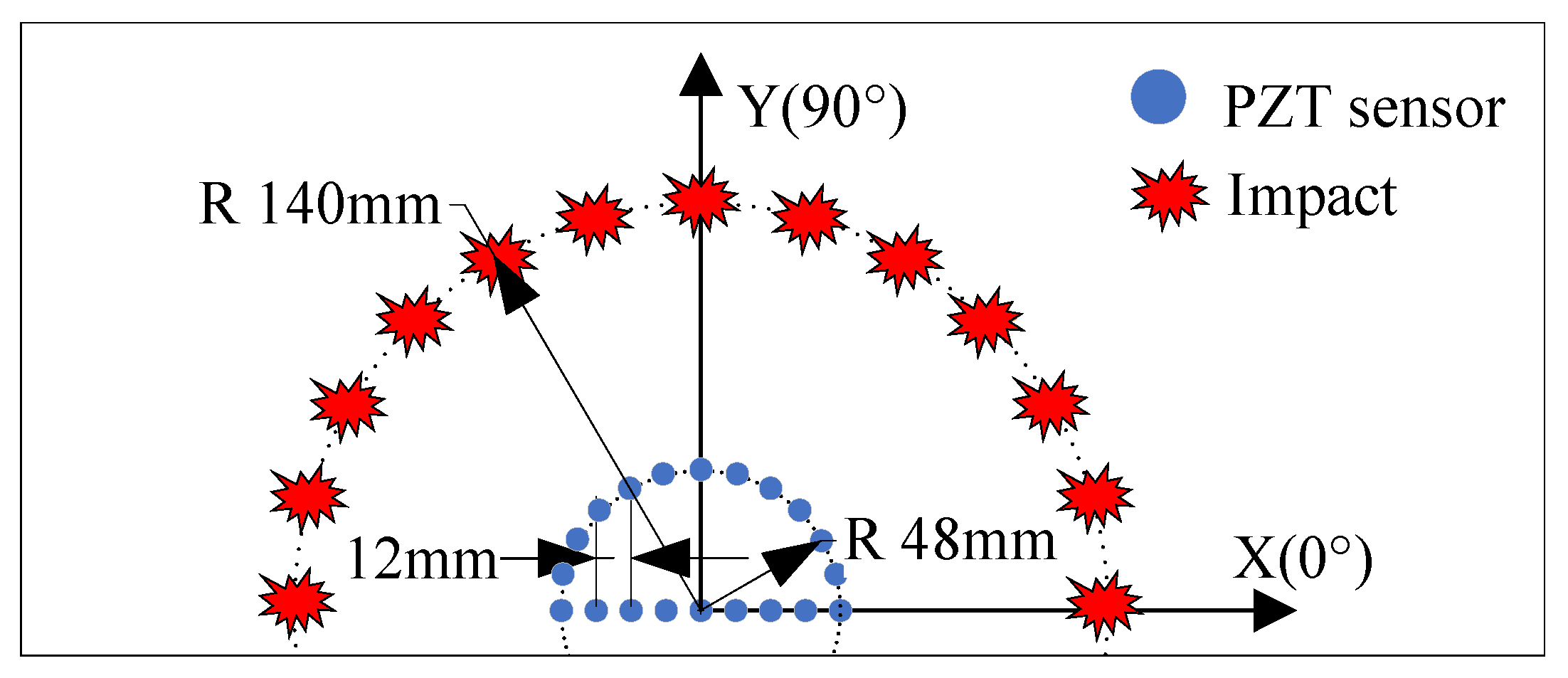
3. Validation of Precise Acquisition of Array Time Delays
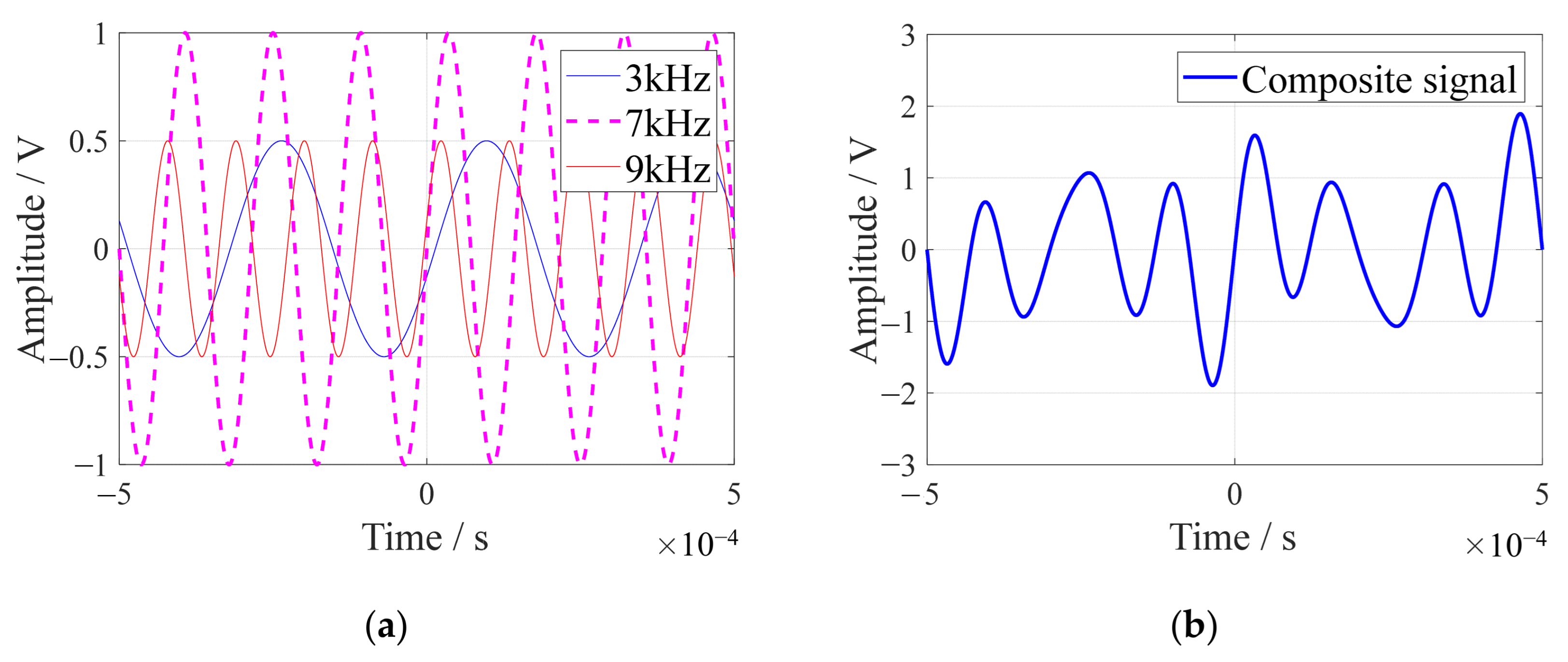
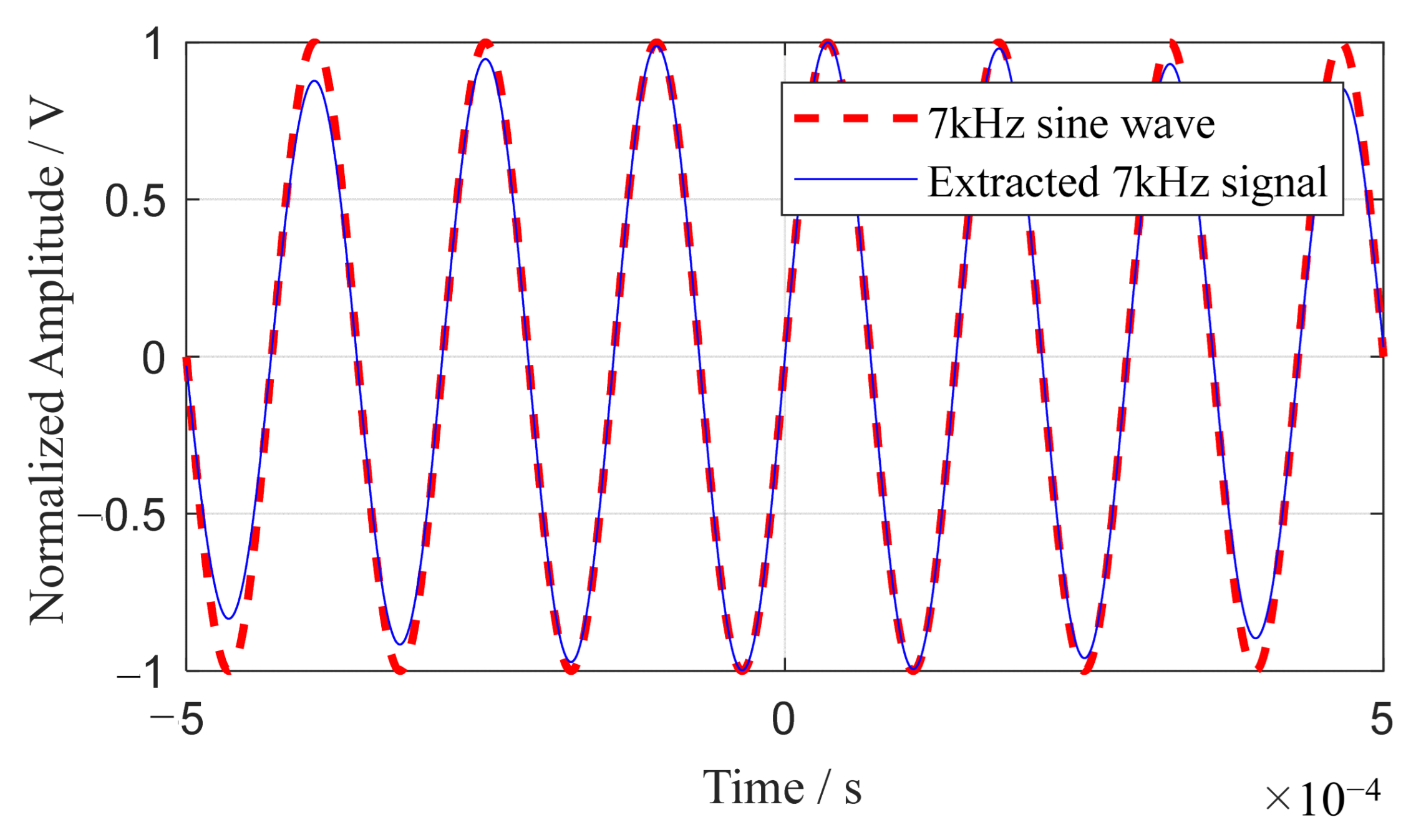
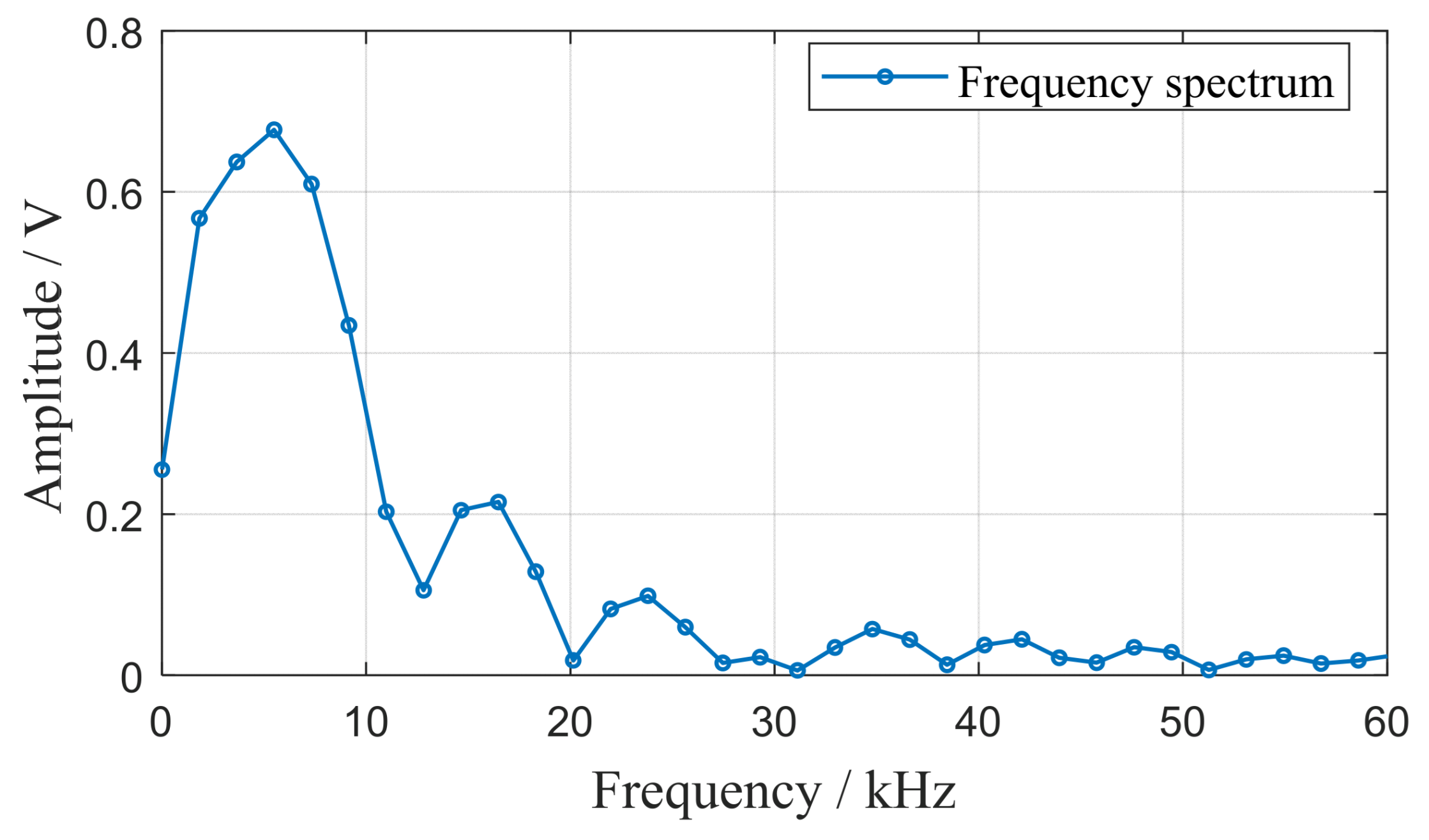
3.1. Verification of Single-Frequency Signal Extraction
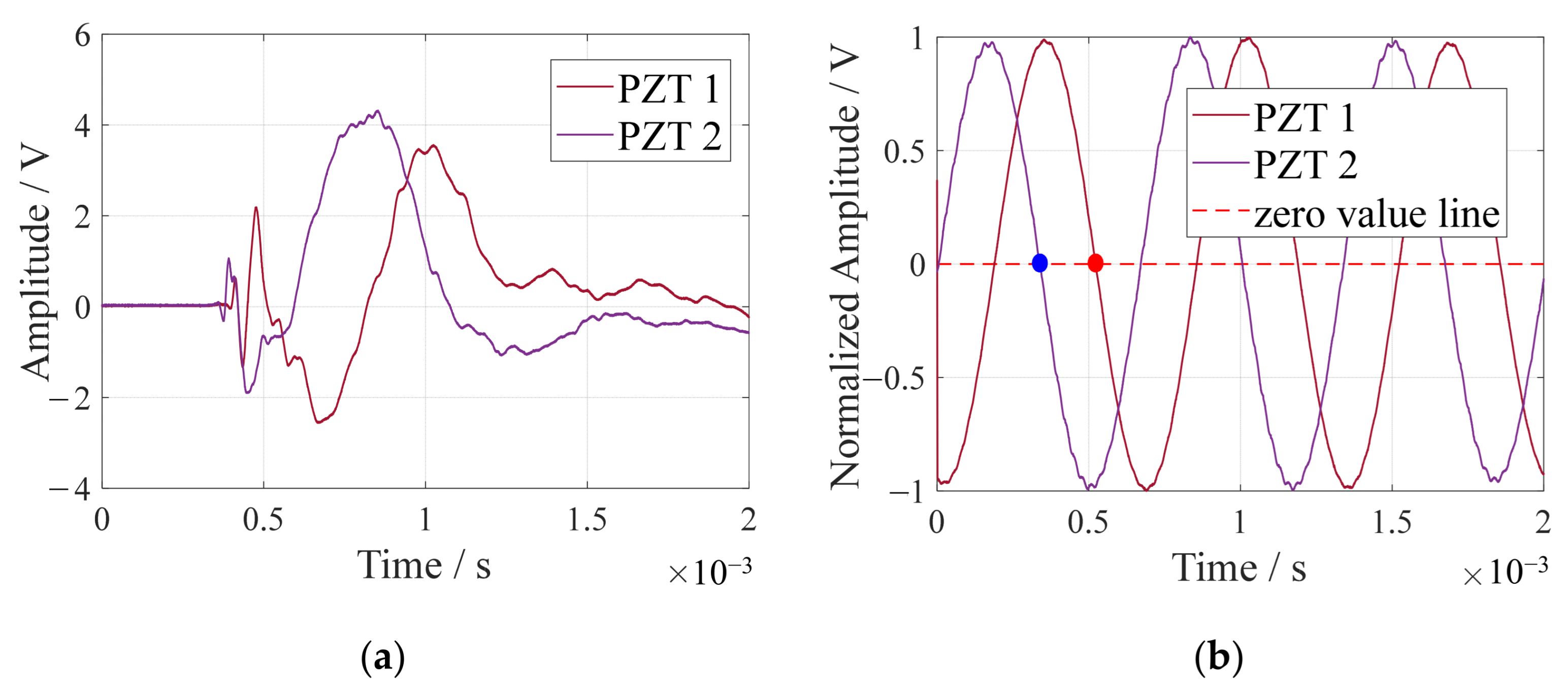
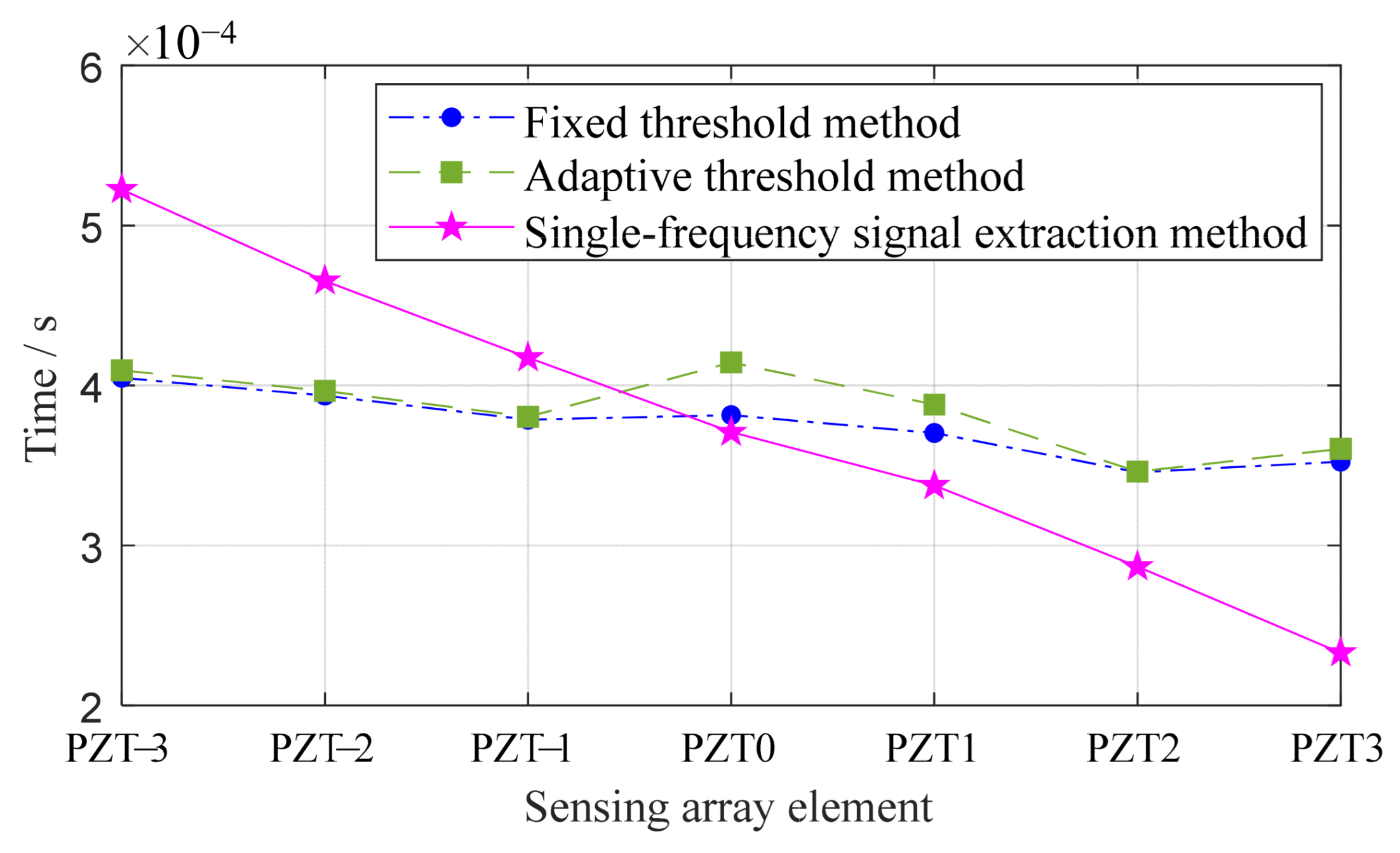
3.2. Comparison of Time Delay Acquisition Accuracy
- (1)
- Fixed threshold method
- (2)
- Adaptive threshold method
- (3)
- Single-frequency signal extraction method
- (4)
- Evaluation of different time delay acquisition methods
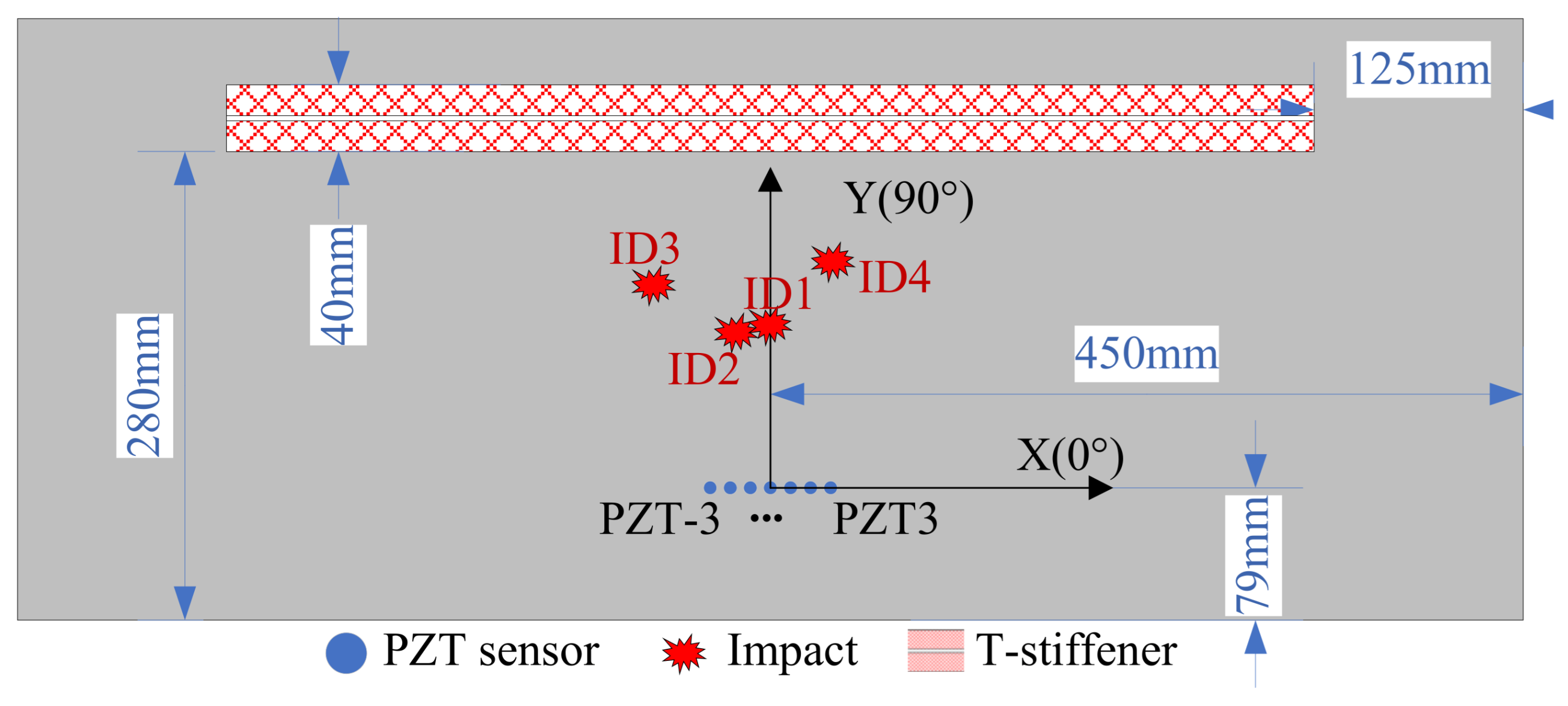
4. Impact Localization on a Composite Structure
4.1. Single-Frequency Signal Velocity Measurement
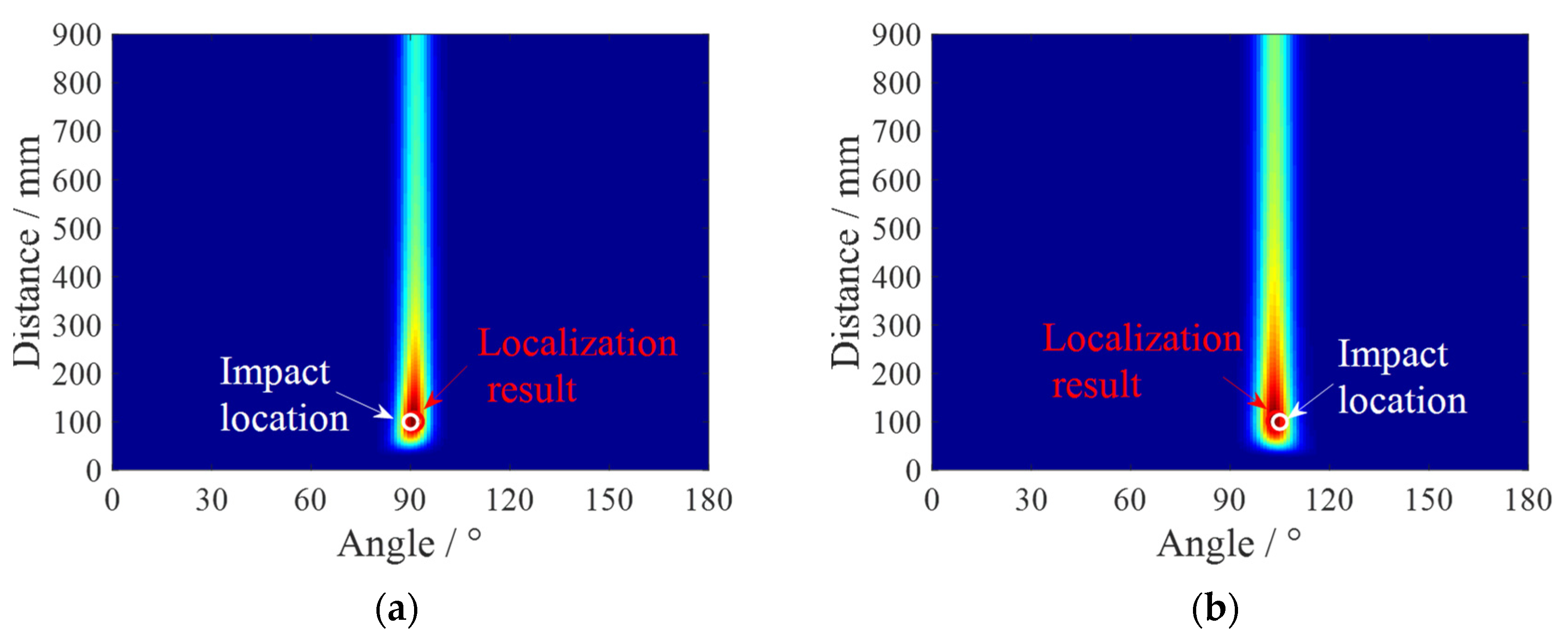
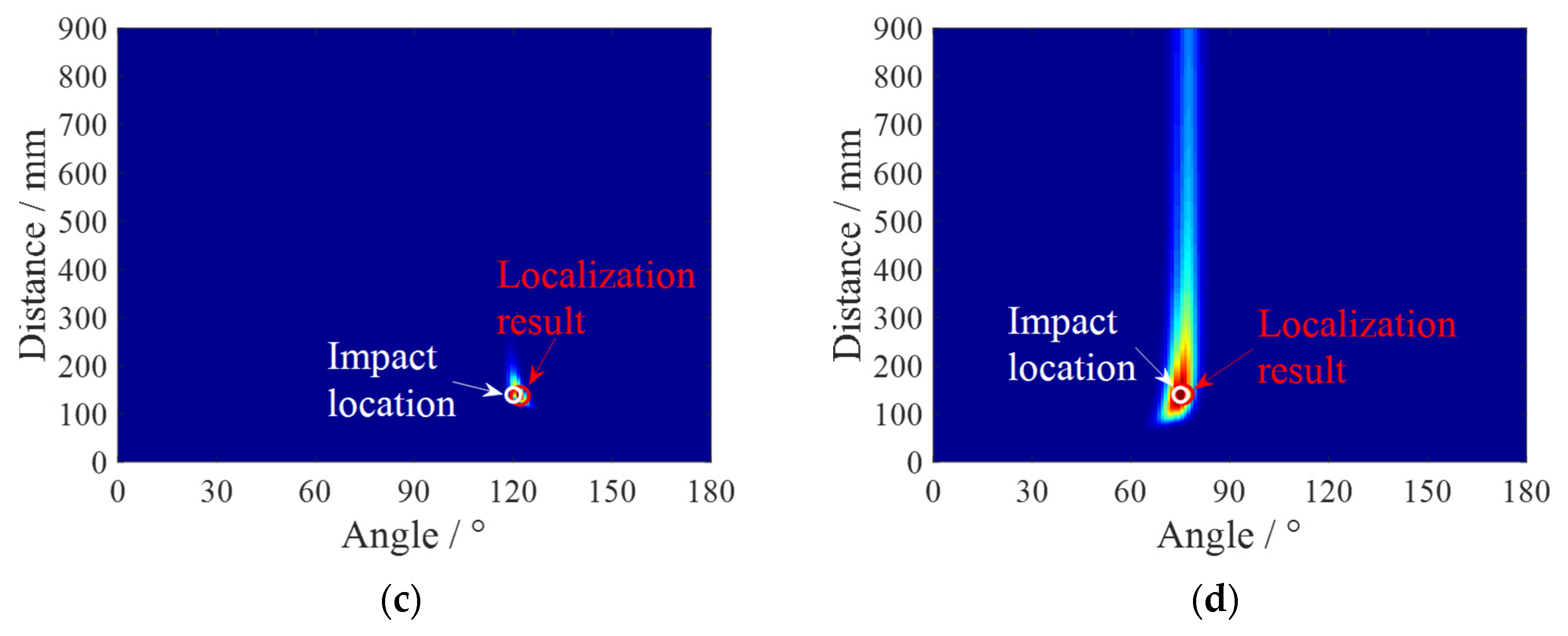
4.2. Impact Localization Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tang, L.; Zhang, J.L.; Tang, Y.S.; Kong, J.; Liu, T.X.; Gu, J.W. Polymer matrix wave-transparent composites: A review. J. Mater. Sci. Technol. 2021, 75, 225–251. [Google Scholar] [CrossRef]
- Islam, M.H.; Afroj, S.; Uddin, M.A.; Andreeva, D.V.; Novoselov, K.S.; Karim, N. Graphene and CNT-Based Smart Fiber-Reinforced Composites: A Review. Adv. Funct. Mater. 2022, 32, 2205723. [Google Scholar] [CrossRef]
- Li, L.; Ortiz, C. A Natural 3D Interconnected Laminated Composite with Enhanced Damage Resistance. Adv. Funct. Mater. 2015, 25, 3463–3471. [Google Scholar] [CrossRef]
- Yang, H.J.; Yang, L.; Yang, Z.Y.; Shan, Y.N.; Gu, H.S.; Ma, J.T.; Zeng, X.; Tian, T.; Ma, S.Y.; Wu, Z.J. Ultrasonic detection methods for mechanical characterization and damage diagnosis of advanced composite materials: A review. Compos. Struct. 2023, 324, 117554. [Google Scholar] [CrossRef]
- Singh, T.; Sehgal, S. Structural Health Monitoring of Composite Materials. Arch. Comput. Method Eng. 2022, 29, 1997–2017. [Google Scholar] [CrossRef]
- Lv, H.; Shi, S.; Chen, B.; Ma, J.; Sun, Z. Low-velocity impact response of composite sandwich structure with grid-honeycomb hybrid core. Int. J. Mech. Sci. 2023, 246, 108149. [Google Scholar] [CrossRef]
- Lemartinel, A.; Castro, M.; Fouche, O.; De Luca, J.C.; Feller, J.F. Impact and strain monitoring in glass fiber reinforced epoxy laminates with embedded quantum resistive sensors (QRSs). Compos. Sci. Technol. 2022, 221, 109352. [Google Scholar] [CrossRef]
- Abdulkarem, M.; Samsudin, K.; Rokhani, F.Z.; Rasid, M.F.A. Wireless sensor network for structural health monitoring: A contemporary review of technologies, challenges, and future direction. Struct. Health Monit. 2020, 19, 693–735. [Google Scholar] [CrossRef]
- Kralovec, C.; Schagerl, M. Review of Structural Health Monitoring Methods Regarding a Multi-Sensor Approach for Damage Assessment of Metal and Composite Structures. Sensors 2020, 20, 826. [Google Scholar] [CrossRef]
- Wang, Q.; Xu, Y.F.; Su, Z.Q.; Cao, M.S.; Yue, D. An Enhanced Time-Reversal Imaging Algorithm-Driven Sparse Linear Array for Progressive and Quantitative Monitoring of Cracks. IEEE Trans. Instrum. Meas. 2019, 68, 3433–3445. [Google Scholar] [CrossRef]
- Qing, X.L.; Li, W.Z.; Wang, Y.S.; Sun, H. Piezoelectric Transducer-Based Structural Health Monitoring for Aircraft Applications. Sensors 2019, 19, 545. [Google Scholar] [CrossRef]
- Ricci, F.; Monaco, E.; Boffa, N.D.; Maio, L.; Memmolo, V. Guided waves for structural health monitoring in composites: A review and implementation strategies. Prog. Aeosp. Sci. 2022, 129, 100790. [Google Scholar] [CrossRef]
- Capineri, L.; Bulletti, A. Ultrasonic Guided-Waves Sensors and Integrated Structural Health Monitoring Systems for Impact Detection and Localization: A Review. Sensors 2021, 21, 2929. [Google Scholar] [CrossRef] [PubMed]
- Summerscales, J. Acoustic Emission Source Location in Fibre-Reinforced Composite Materials; Advanced Composites Manufacturing Centre: Plymouth, England, 2013. [Google Scholar]
- Na, W.S.; Baek, J. A review of the piezoelectric electromechanical impedance based structural health monitoring technique for engineering structures. Sensors 2018, 18, 1307. [Google Scholar] [CrossRef] [PubMed]
- Fan, X.H.; Chen, T.; Du, J.Q.; He, Y.T.; Cui, R.H.; Ma, B.L.; Song, Y.J. Methods for improving sensitivity of crack quantitative monitoring of flexible eddy current array sensor. Smart Mater. Struct. 2020, 29, 085033. [Google Scholar] [CrossRef]
- Roach, D. Real time crack detection using mountable comparative vacuum monitoring sensors. Smart. Struct. Syst. 2009, 5, 317–328. [Google Scholar] [CrossRef]
- Liu, M.B.; Li, B.B.; Li, J.T.; Lian, Y.Y. Smart coating sensor applied in crack detection for aircraft. Appl. Mech. Mater. 2013, 330, 383–388. [Google Scholar] [CrossRef]
- Xu, Z.D.; Zhu, C.; Shao, L.W. Damage identification of pipeline based on ultrasonic guided wave and wavelet denoising. J. Pipel. Syst. Eng. Pract. 2021, 12, 04021051. [Google Scholar] [CrossRef]
- Wang, Z.K.; Yang, Z.B.; Wu, S.M.; Li, H.Q.; Tian, S.H.; Chen, X.F. An Improved Multiple Signal Classification for Nonuniform Sampling in Blade Tip Timing. IEEE Trans. Instrum. Meas. 2020, 69, 7941–7952. [Google Scholar] [CrossRef]
- Montaruli, M.F.; Facchini, L.; Di Lizia, P.; Massari, M.; Pupillo, G.; Bianchi, G.; Naldi, G. Adaptive track estimation on a radar array system for space surveillance. Acta Astronaut. 2022, 198, 111–123. [Google Scholar] [CrossRef]
- Huan, Q.; Chen, M.T.; Su, Z.Q.; Li, F.X. A high-resolution structural health monitoring system based on SH wave piezoelectric transducers phased array. Ultrasonics 2019, 97, 29–37. [Google Scholar] [CrossRef]
- Abedi, M.; Shayanfar, J.; Al-Jabri, K. Damage assessment via machine learning approaches: A systematic review. Asian J. Civ. Eng. 2023, 24, 3823–3852. [Google Scholar] [CrossRef]
- Desai, D.; Mehendale, N. A Review on Sound Source Localization Systems. Arch. Comput. Method Eng. 2022, 29, 4631–4642. [Google Scholar] [CrossRef]
- Park, W.K. Application of MUSIC algorithm in real-world microwave imaging of unknown anomalies from scattering matrix. Mech. Syst. Signal Proc. 2021, 153, 107501. [Google Scholar] [CrossRef]
- Zheng, Q.F.; Luo, L.G.; Song, H.; Sheng, G.H.; Jiang, X.C. A RSSI-AOA-Based UHF Partial Discharge Localization Method Using MUSIC Algorithm. IEEE Trans. Instrum. Meas. 2021, 70, 1–9. [Google Scholar] [CrossRef]
- Cicchetti, R.; Pisa, S.; Piuzzi, E.; Pittella, E.; D’Atanasio, P.; Testa, O. Numerical and Experimental Comparison Among a New Hybrid FT-Music Technique and Existing Algorithms for Through-the-Wall Radar Imaging. IEEE Trans. Microw. Theory Tech. 2021, 69, 3372–3387. [Google Scholar] [CrossRef]
- Liu, Y.J.; Chen, H.X.; Wang, B. DOA estimation based on CNN for underwater acoustic array. Appl. Acoust. 2021, 172, 107594. [Google Scholar] [CrossRef]
- Zhang, R.; Xu, K.J.; Quan, Y.H.; Zhu, S.Q.; Xing, M.D. Signal Subspace Reconstruction for DOA Detection Using Quantum-Behaved Particle Swarm Optimization. Remote Sens. 2021, 13, 2560. [Google Scholar] [CrossRef]
- Su, Y.; Yuan, S.; Wang, Y. Impact localization in composite using multiple signal classification method. Acta Mater. Compos. Sin. 2010, 27, 105–110. [Google Scholar]
- Engholm, M.; Stepinski, T. Direction of arrival estimation of Lamb waves using circular arrays. Struct. Health Monit. 2011, 10, 467–480. [Google Scholar] [CrossRef]
- Yang, H.; Lee, Y.J.; Lee, S.K. Impact source localization in plate utilizing multiple signal classification. Proc. Inst. Mech. Eng. Part C J. Eng. Mech. Eng. Sci. 2013, 227, 703–713. [Google Scholar] [CrossRef]
- Yuan, S.; Zhong, Y.; Qiu, L.; Wang, Z. Two-dimensional near-field multiple signal classification algorithm-based impact localization. J. Intell. Mater. Syst. Struct. 2015, 26, 400–413. [Google Scholar] [CrossRef]
- Zhang, Z.H.; Zhong, Y.T.; Xiang, J.W.; Jiang, Y.Y.; Wang, Z.L. Research on the Performance and Improvement of Uniform Linear Sensors Array-Based Impact Localization Method Under Vibration Conditions. IEEE Sens. J. 2020, 20, 14932–14939. [Google Scholar] [CrossRef]
- Zhu, C.; Xu, Z.Y.; Hou, C.; Lv, X.D.; Jiang, S.; Ye, D.; Huang, Y.A. Flexible, monolithic piezoelectric sensors for large-area structural impact monitoring via MUSIC-assisted machine learning. Struct. Health Monit. 2023, 23, 121–136. [Google Scholar] [CrossRef]
- Chen, H.L.; Xu, K.L.; Liu, Z.H.; Ta, D. Sign coherence factor-based search algorithm for defect localization with laser generated Lamb waves. Mech. Syst. Signal Proc. 2022, 173, 109010. [Google Scholar] [CrossRef]
- Qiu, L.; Yuan, S.; Zhang, X.; Wang, Y. A time reversal focusing based impact imaging method and its evaluation on complex composite structures. Smart Mater. Struct. 2011, 20, 105014. [Google Scholar] [CrossRef]
- Wei, H.; Zhang, Q.H.; Shang, M.H.; Gu, Y. Extreme learning Machine-based classifier for fault diagnosis of rotating Machinery using a residual network and continuous wavelet transform. Measurement 2021, 183, 109864. [Google Scholar] [CrossRef]
- Zheng, F.; Yuan, S.F. Research on composite impact localization by MUSIC based guided wave monitoring. In Proceedings of the 2022 IEEE International Conference on Prognostics and Health Management (ICPHM), Detroit, MI, USA, 6–8 June 2022; pp. 154–160. [Google Scholar]
- Ohtsu, M.; Enoki, M.; Mizutani, Y.; Shigeishi, M. Principles of the acoustic emission (AE) method and signal processing. In Practical Acoustic Emission Testing; Springer: Tokyo, Japan, 2016. [Google Scholar]
- Liu, Y.; Liu, C.; Van Pamel, A.; Cawley, P. Feasibility and Reliability of Grain Noise Suppression in Monitoring of Highly Scattering Materials. J. Nondestruct. Eval. 2017, 36, 1–13. [Google Scholar] [CrossRef]
- Yang, Y.; Peng, Z.K.; Zhang, W.M.; Meng, G. Frequency-varying group delay estimation using frequency domain polynomial chirplet transform. Mech. Syst. Signal Proc. 2014, 46, 146–162. [Google Scholar] [CrossRef]







| Impact | Locations | Array Time-Delay-Based MUSIC Algorithm | |||
|---|---|---|---|---|---|
| Localization Results | Error | ||||
| Angle | Distance | Angle | Distance | ||
| ID1 | (90°, 100 mm) | 91° | 101 mm | 1° | 1 mm |
| ID2 | (105°, 100 mm) | 104° | 102 mm | 1° | 2 mm |
| ID3 | (120°, 140 mm) | 122° | 138 mm | 2° | 2 mm |
| ID4 | (75°, 140 mm) | 76° | 141 mm | 1° | 1 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, F.; Yuan, S. Guided Lamb Wave Array Time-Delay-Based MUSIC Algorithm for Impact Imaging. Sensors 2024, 24, 1882. https://doi.org/10.3390/s24061882
Zheng F, Yuan S. Guided Lamb Wave Array Time-Delay-Based MUSIC Algorithm for Impact Imaging. Sensors. 2024; 24(6):1882. https://doi.org/10.3390/s24061882
Chicago/Turabian StyleZheng, Fei, and Shenfang Yuan. 2024. "Guided Lamb Wave Array Time-Delay-Based MUSIC Algorithm for Impact Imaging" Sensors 24, no. 6: 1882. https://doi.org/10.3390/s24061882
APA StyleZheng, F., & Yuan, S. (2024). Guided Lamb Wave Array Time-Delay-Based MUSIC Algorithm for Impact Imaging. Sensors, 24(6), 1882. https://doi.org/10.3390/s24061882







