Crack Detection and Analysis of Concrete Structures Based on Neural Network and Clustering
Abstract
1. Introduction
2. Related Work
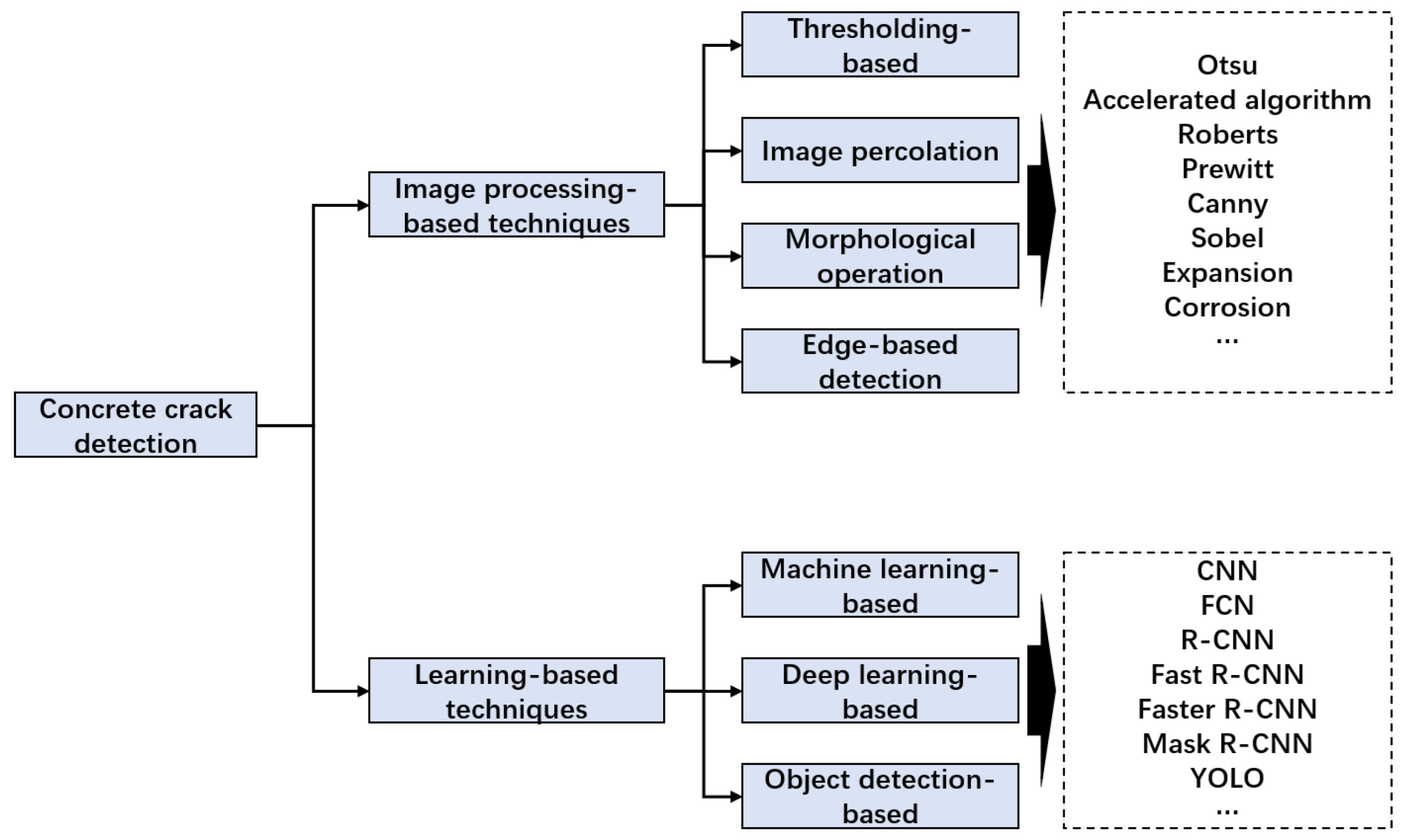
2.1. Concrete Crack Detection
2.2. Crack Clustering
3. Materials and Methods
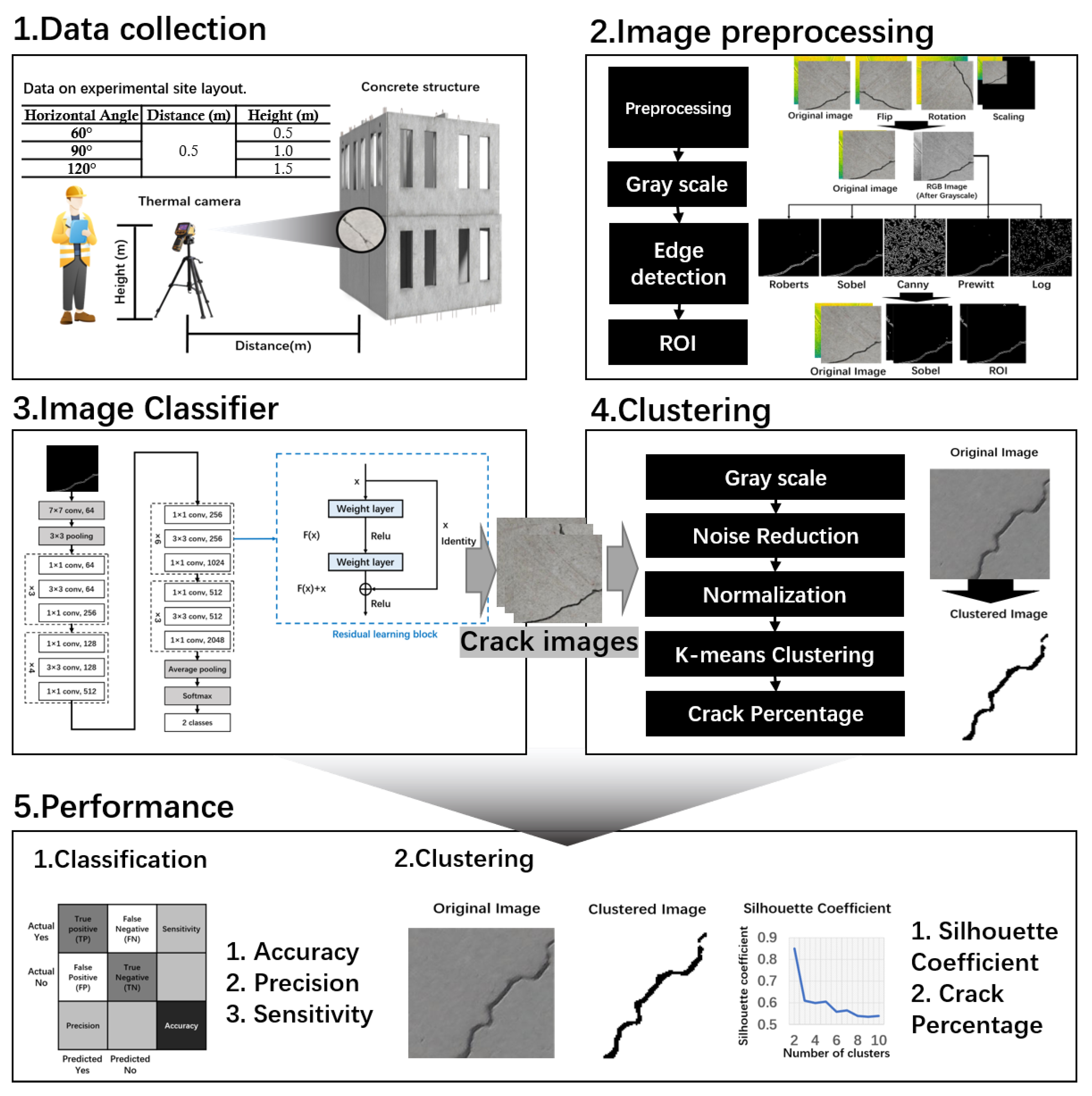
3.1. Data Collection
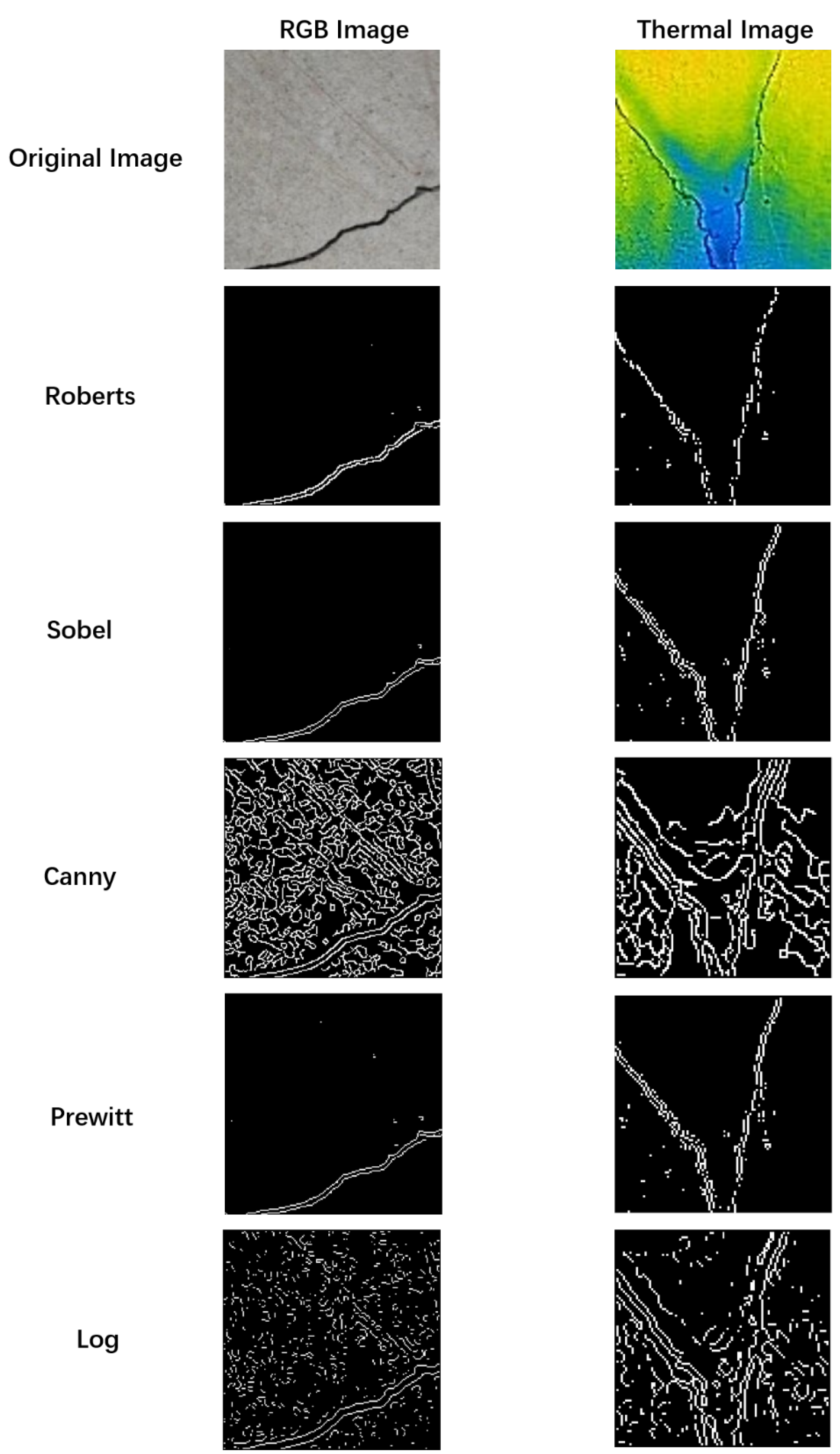
3.2. Algorithm
3.3. Image Classifier
| Architectural Structure 1 | |
| layers = | |
| Image put | [100 100 3] |
| 2-D Convolution | (5, 20) |
| ReLU | |
| 2-D Max Pooling | (2, ‘Stride’, 2) |
| Fully connected | 2 |
| Softmax | |
| Classification output | crossentripyex |
| Options = trainingOptions | |
| sgdm | |
| Execution environment | CPU |
| Max epochs | 100 |
| Validation data | {trainingSet, testingSet} |
| Validation frequency | 5 |
| Initial learn rate | 1 × 10−4 |
| Gradient threshold | 1 |
| Verbose | false |
| Plots | training-progress |
3.4. Crack Clustering
- Number of Clusters: Define the desired number of clusters, denoted as k, into which the dataset will be partitioned.
- Initialize Cluster Centers: Select k data points at random from the dataset to serve as the initial cluster centers, represented by .
- Iterative Process: The iterative process unfolds as follows:
- (a)
- Allocate data points to the closest cluster center: Determine the distance between each cluster center for each data point , and then allocate the data point to the cluster with the closest center. The assignment is determined by the formula , where is the index of the assigned cluster, is the i-th data point, and is the center of the j-th cluster.
- (b)
- Update Cluster Centers: Update the cluster centers in accordance with the mean of each cluster’s data points. The update is performed using the formula , where is the new center of the j-th cluster, is the number of data points in the j-th cluster, and is the j-th data point in the i-th cluster.
- Compute Objective Function (Sum of Squares Within Clusters): Evaluate the objective function , where represents the number of data points in the i-th cluster, and denotes the center of the i-th cluster.
- Output Results: If the objective function converges, output the final cluster centers as the result. Otherwise, return to step 2 and iterate until convergence is achieved.
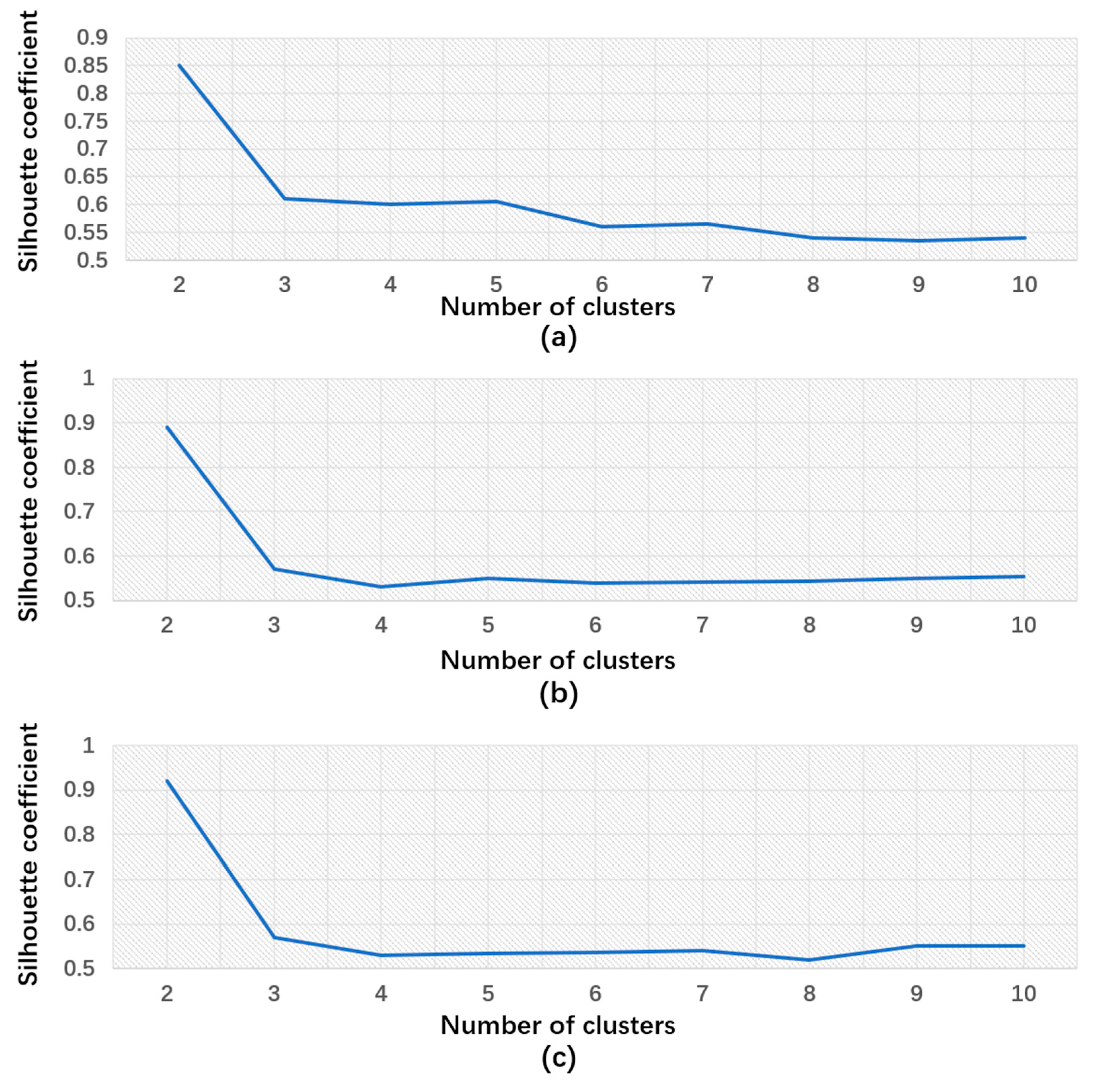
- Number of Clusters: Determining the optimal number of clusters is pivotal to the efficacy of the k-means clustering algorithm. The silhouette coefficient approach is employed to achieve this. The algorithm iterates through various values of k (number of clusters), computing the silhouette coefficient for each. This coefficient gauges an object’s degree of similarity to its cluster compared to others. Plotting these coefficients yields a curve graph. The k value corresponding to the highest silhouette coefficient represents the optimal number of clusters. This approach circumvents the need to manually specify the number of clusters, thereby enhancing the robustness and accuracy of the clustering results.
- Initialize Cluster Centers: The Otsu algorithm is used to determine the initial cluster centers in the clustering algorithm. In addition, it is employed to determine the threshold used as the filtering criterion for initializing the cluster centers. Given that concrete cracks typically involve grayscale level transitions between two adjacent regions with different grayscale levels, an appropriate threshold is derived from the average values of these two regions. Leveraging the Otsu algorithm, an efficient image segmentation method, expedites the convergence of the algorithm by selecting the threshold determined by Otsu as the initial cluster center. This strategy not only improves the quality of the initial cluster centers by achieving rapid initialization, reducing iteration times, and preventing convergence to local optima, but also leverages the advantages of the Otsu algorithm in image data processing, thereby enhancing the efficiency and accuracy of the initialization process.
4. Results and Discussion
4.1. Classifier Model Performance Analysis
4.2. Crack Clustering Model Performance Analysis
4.2.1. The Selection of Cluster Number
4.2.2. Selection of the Initial Cluster Center
4.2.3. Silhouette Coefficient
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Deng, Z.; Huang, M.; Wan, N.; Zhang, J. The Current Development of Structural Health Monitoring for Bridges: A Review. Buildings 2023, 13, 1360. [Google Scholar] [CrossRef]
- Golding, V.P.; Gharineiat, Z.; Munawar, H.S.; Ullah, F. Crack detection in concrete structures using Deep Learning. Sustainability 2022, 14, 8117. [Google Scholar] [CrossRef]
- Broberg, P. Surface crack detection in welds using thermography. NDT E Int. 2013, 57, 69–73. [Google Scholar] [CrossRef]
- Fang, F.; Li, L.; Gu, Y.; Zhu, H.; Lim, J.H. A novel hybrid approach for crack detection. Pattern Recognit. 2020, 107, 107474. [Google Scholar] [CrossRef]
- Hsieh, Y.A.; Tsai, Y.J. Machine learning for crack detection: Review and model performance comparison. J. Comput. Civ. Eng. 2020, 34, 04020038. [Google Scholar] [CrossRef]
- Gupta, P.; Dixit, M. Image-based crack detection approaches: A comprehensive survey. Multimed. Tools Appl. 2022, 81, 40181–40229. [Google Scholar] [CrossRef]
- Talab AM, A.; Huang, Z.; Xi, F.; HaiMing, L. Detection crack in image using Otsu method and multiple filtering in image processing techniques. Optik 2016, 127, 1030–1033. [Google Scholar] [CrossRef]
- Qu, Z.; Lin, L.D.; Guo, Y.; Wang, N. An improved algorithm for image crack detection based on percolation model. IEEJ Trans. Electr. Electron. Eng. 2015, 10, 214–221. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, Z.; Qi, D.; Liu, Y. Automatic crack detection and classification method for subway tunnel safety monitoring. Sensors 2014, 14, 19307–19328. [Google Scholar] [CrossRef]
- Hoang, N.D.; Nguyen, Q.L. Metaheuristic optimized edge detection for recognition of concrete wall cracks: A comparative study on the performances of roberts, prewitt, canny, and sobel algorithms. Adv. Civ. Eng. 2018, 2018, 7163580. [Google Scholar] [CrossRef]
- Rodríguez-Martín, M.; Lagüela, S.; González-Aguilera, D.; Martínez, J. Thermographic test for the geometric characterization of cracks in welding using IR image rectification. Autom. Constr. 2016, 61, 58–65. [Google Scholar] [CrossRef]
- Ai, D.; Jiang, G.; Kei, L.S.; Li, C. Automatic pixel-level pavement crack detection using information of multi-scale neighborhoods. IEEE Access 2018, 6, 24452–24463. [Google Scholar] [CrossRef]
- Luo, Q.; Ge, B.; Tian, Q. A fast adaptive crack detection algorithm based on a double-edge extraction operator of FSM. Constr. Build. Mater. 2019, 204, 244–254. [Google Scholar] [CrossRef]
- Kim, J.J.; Kim, A.R.; Lee, S.W. Artificial neural network-based automated crack detection and analysis for the inspection of concrete structures. Appl. Sci. 2020, 10, 8105. [Google Scholar] [CrossRef]
- Yokoyama, S.; Matsumoto, T. Development of an automatic detector of cracks in concrete using machine learning. Procedia Eng. 2017, 171, 1250–1255. [Google Scholar] [CrossRef]
- Gopalakrishnan, K.; Khaitan, S.K.; Choudhary, A.; Agrawal, A. Deep convolutional neural networks with transfer learning for computer vision-based data-driven pavement distress detection. Constr. Build. Mater. 2017, 157, 322–330. [Google Scholar] [CrossRef]
- Li, B.; Wang, K.C.; Zhang, A.; Yang, E.; Wang, G. Automatic classification of pavement crack using deep convolutional neural network. Int. J. Pavement Eng. 2020, 21, 457–463. [Google Scholar] [CrossRef]
- Patra, S.; Middya, A.I.; Roy, S. PotSpot: Participatory sensing based monitoring system for pothole detection using deep learning. Multimed. Tools Appl. 2021, 80, 25171–25195. [Google Scholar] [CrossRef]
- Dung, C.V. Autonomous concrete crack detection using deep fully convolutional neural network. Autom. Constr. 2019, 99, 52–58. [Google Scholar] [CrossRef]
- Xu, X.; Zhao, M.; Shi, P.; Ren, R.; He, X.; Wei, X.; Yang, H. Crack detection and comparison study based on faster R-CNN and mask R-CNN. Sensors 2022, 22, 1215. [Google Scholar] [CrossRef]
- Li, R.; Yu, J.; Li, F.; Yang, R.; Wang, Y.; Peng, Z. Automatic bridge crack detection using Unmanned aerial vehicle and Faster R-CNN. Constr. Build. Mater. 2023, 362, 129659. [Google Scholar] [CrossRef]
- Qiu, Q.; Lau, D. Real-time detection of cracks in tiled sidewalks using YOLO-based method applied to unmanned aerial vehicle (UAV) images. Autom. Constr. 2023, 147, 104745. [Google Scholar] [CrossRef]
- Yang, C.; Chen, J.; Li, Z.; Huang, Y. Structural crack detection and recognition based on deep learning. Appl. Sci. 2021, 11, 2868. [Google Scholar] [CrossRef]
- Fan, X.; Wu, J.; Shi, P.; Zhang, X.; Xie, Y. A novel automatic dam crack detection algorithm based on local-global clustering. Multimed. Tools Appl. 2018, 77, 26581–26599. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, K.; Wang, Y.; Shen, Y.; Hu, H. Rail crack detection using acoustic emission technique by joint optimization noise clustering and time window feature detection. Appl. Acoust. 2020, 160, 107141. [Google Scholar] [CrossRef]
- Doulamis, A.; Doulamis, N.; Protopapadakis, E.; Voulodimos, A. Combined convolutional neural networks and fuzzy spectral clustering for real time crack detection in tunnels. In Proceedings of the 2018 25th IEEE International Conference on Image Processing (ICIP), Athens, Greece, 7–10 October 2018; pp. 4153–4157. [Google Scholar]
- Li, W.; Huyan, J.; Gao, R.; Hao, X.; Hu, Y.; Zhang, Y. Unsupervised deep learning for road crack classification by fusing convolutional neural network and k_means clustering. J. Transp. Eng. Part B Pavements 2021, 147, 04021066. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, Z.; Zheng, B.; Qin, R.; Wen, G.; Cheng, W.; Chen, X. Acoustic emission technology-based multifractal and unsupervised clustering on crack damage monitoring for low-carbon steel. Measurement 2023, 217, 113042. [Google Scholar] [CrossRef]
- Kamranfar, P.; Lattanzi, D.; Shehu, A.; Stoffels, S. Pavement Distress Recognition via Wavelet-Based Clustering of Smartphone Accelerometer Data. J. Comput. Civ. Eng. 2022, 36, 04022007. [Google Scholar] [CrossRef]
- Liu, Z.; Gu, X.; Chen, J.; Wang, D.; Chen, Y.; Wang, L. Automatic recognition of pavement cracks from combined GPR B-scan and C-scan images using multiscale feature fusion deep neural networks. Autom. Constr. 2023, 146, 104698. [Google Scholar] [CrossRef]
- Tran, Q.H.; Han, D.; Kang, C.; Haldar, A.; Huh, J. Effects of ambient temperature and relative humidity on subsurface defect detection in concrete structures by active thermal imaging. Sensors 2017, 17, 1718. [Google Scholar] [CrossRef]
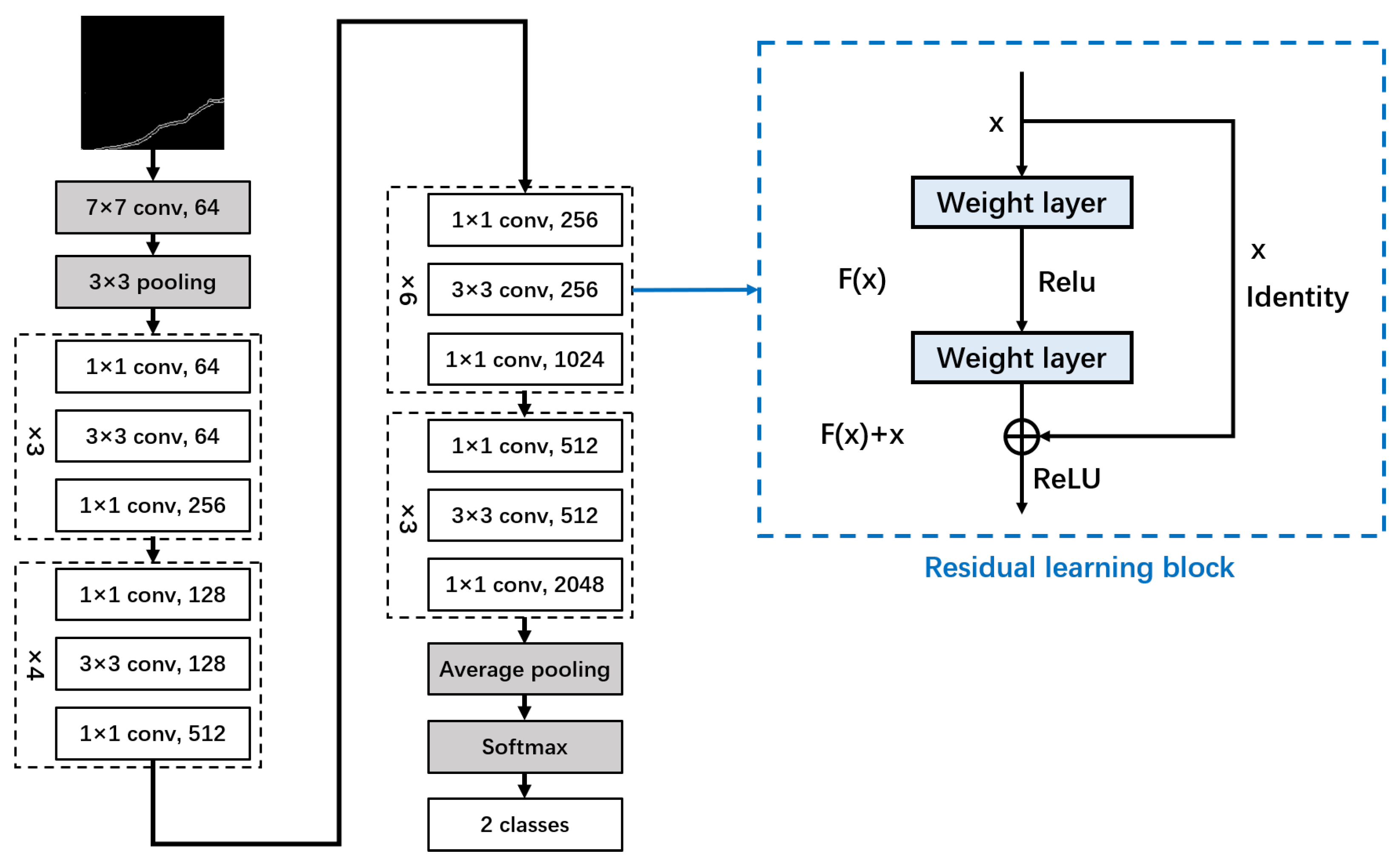
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- MacQueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 21 June–18 July 1967; Volume 1, pp. 281–297. [Google Scholar]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
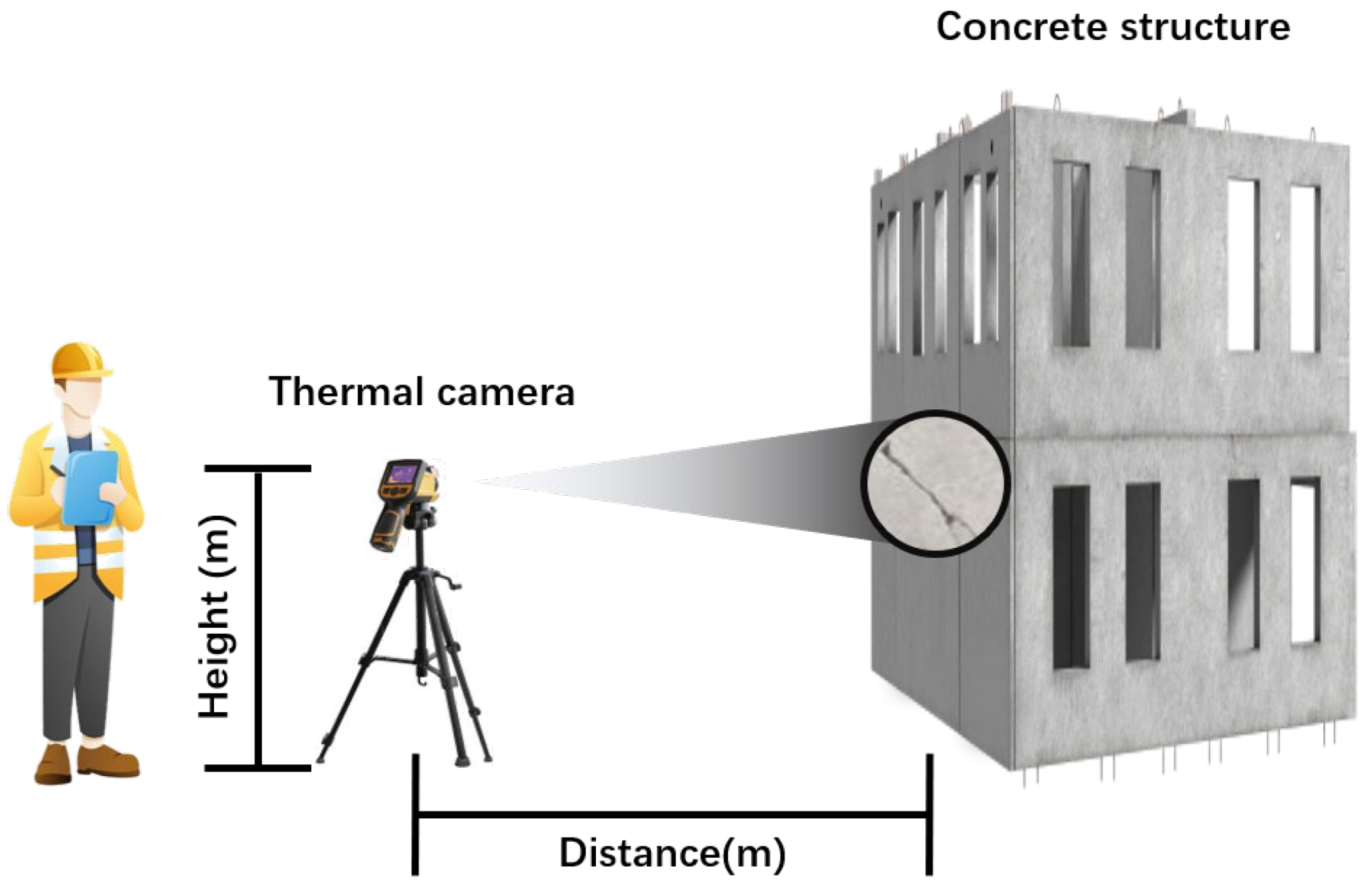







| Brand | FLIR E8 |
| View Field | 45° × 34° |
| Range of Temperatures | −20 °C~250 °C |
| Frequency Images | 9 Hz |
| Temperature Sensitivity | <0.06 °C |
| Accuracy | ±2 °C |
| Onboard Camera | 640 × 480 |
| Horizontal Angle | Distance (m) | Height (m) |
|---|---|---|
| 60° | 0.5 | 0.5 |
| 90° | 1.0 | |
| 120° | 1.5 |
| Total Images | Thermal Images | RGB Images | |
|---|---|---|---|
| Non-Crack | 1500 | 750 | 750 |
| Crack | 3000 | 1500 | 1500 |
| Total | 4500 | 2250 | 2250 |
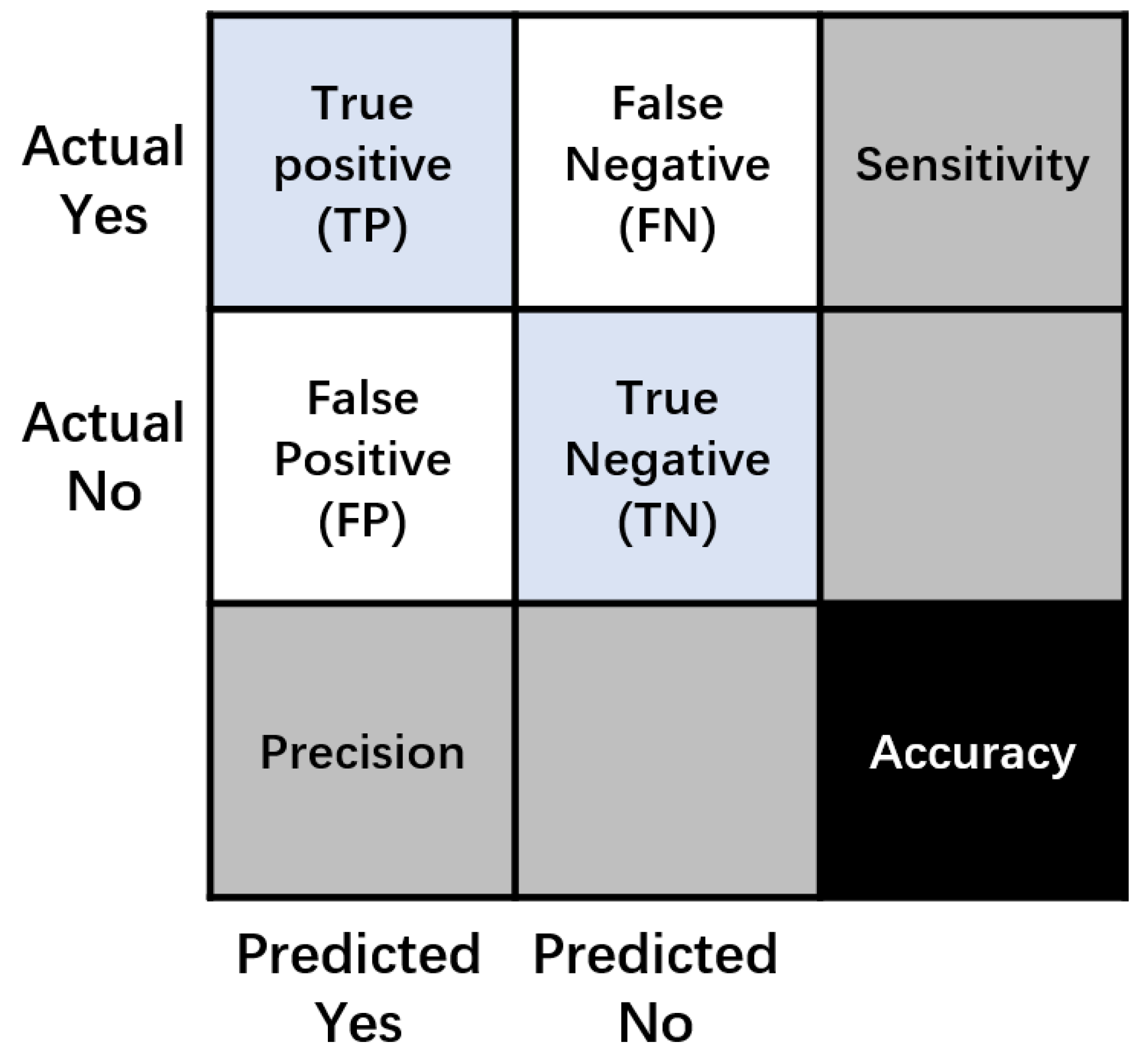
| Total | Predicted Crack (PP) | Predicted Non-Crack (PN) |
|---|---|---|
| Actual crack (P) | TP | FN |
| Actual non-crack (N) | FP | TN |
| Metric | Formula |
|---|---|
| Accuracy (Acc) | |
| Precision (Pr) | |
| Recall (Re) | |
| F1-Score (F1) |
| Concrete Crack and Non-Crack | ||||||
|---|---|---|---|---|---|---|
| Neural Networks | Training | Testing | ||||
| Precision | Recall | F1-Score | Precision | Recall | F1-Score | |
| Sobel | 99.4% | 91.8% | 95.4% | 98.4% | 88.7% | 93.2% |
| Sobel + ROI | 99.9% | 100% | 99.9% | 99.8% | 100% | 99.8% |
| Image 1 | Image 2 | Image 3 |
|---|---|---|
 |  |  |
| Crack Image | Optimal Number of Clusters | Otsu Threshold |
|---|---|---|
| Image 1 | 2 | 120 |
| Image 2 | 2 | 116 |
| Image 3 | 2 | 106 |
| Crack Image | Silhouette Coefficient | Crack Percentage |
|---|---|---|
| Image 1 | 0.8783 | 6.13% |
| Image 2 | 0.8862 | 2.22% |
| Image 3 | 0.9157 | 7.32% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, Y.; Park, H.W.; Mi, Y.; Song, S. Crack Detection and Analysis of Concrete Structures Based on Neural Network and Clustering. Sensors 2024, 24, 1725. https://doi.org/10.3390/s24061725
Choi Y, Park HW, Mi Y, Song S. Crack Detection and Analysis of Concrete Structures Based on Neural Network and Clustering. Sensors. 2024; 24(6):1725. https://doi.org/10.3390/s24061725
Chicago/Turabian StyleChoi, Young, Hee Won Park, Yirong Mi, and Sujeen Song. 2024. "Crack Detection and Analysis of Concrete Structures Based on Neural Network and Clustering" Sensors 24, no. 6: 1725. https://doi.org/10.3390/s24061725
APA StyleChoi, Y., Park, H. W., Mi, Y., & Song, S. (2024). Crack Detection and Analysis of Concrete Structures Based on Neural Network and Clustering. Sensors, 24(6), 1725. https://doi.org/10.3390/s24061725






