Applications of Isosceles Triangular Coupling Structure in Optical Switching and Sensing
Abstract
1. Introduction
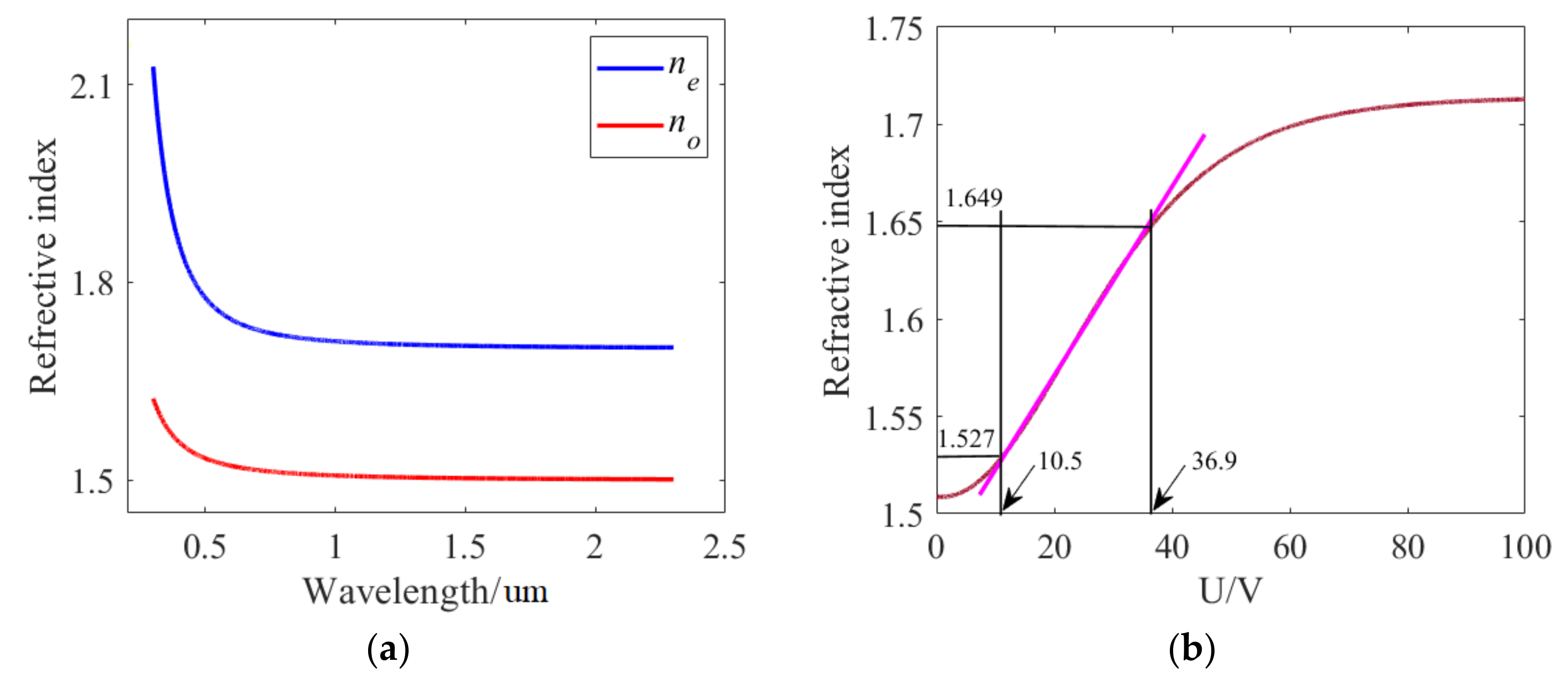
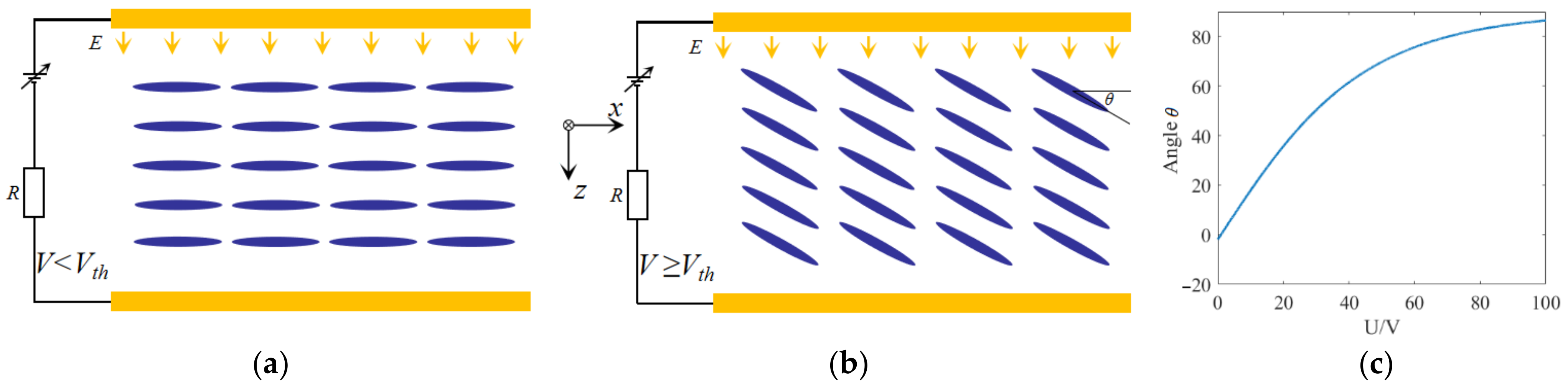
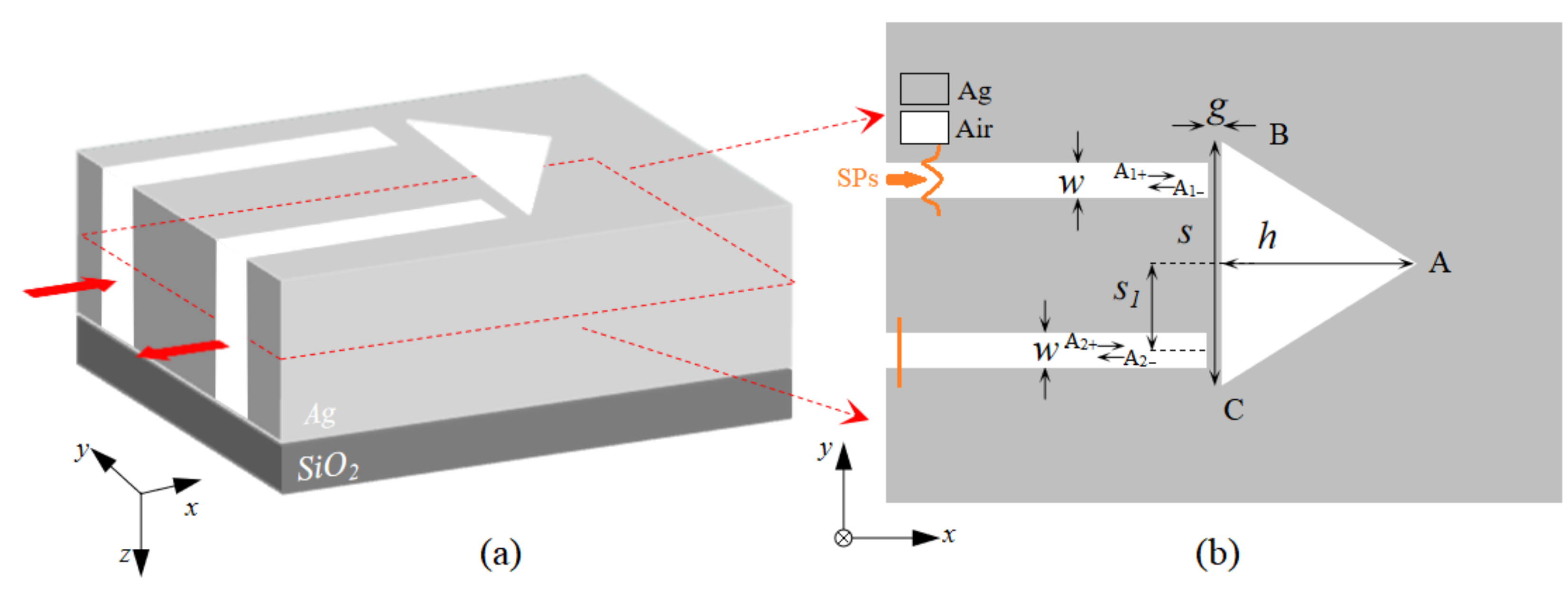
2. Structural Model and Analytical Method
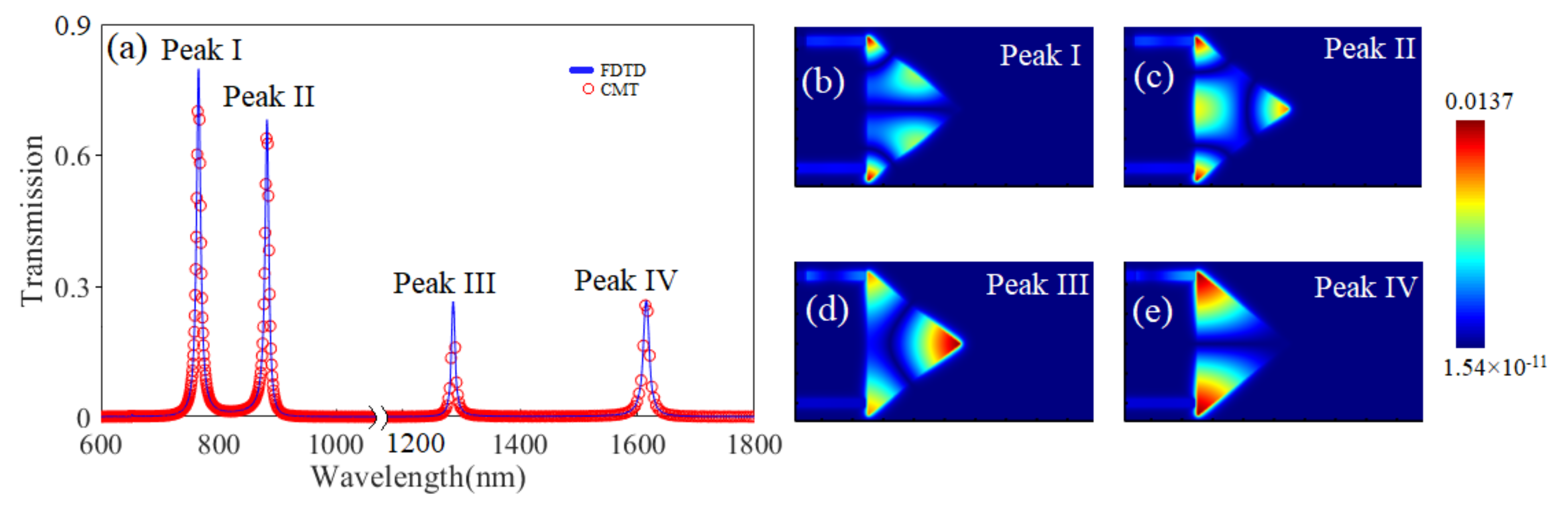
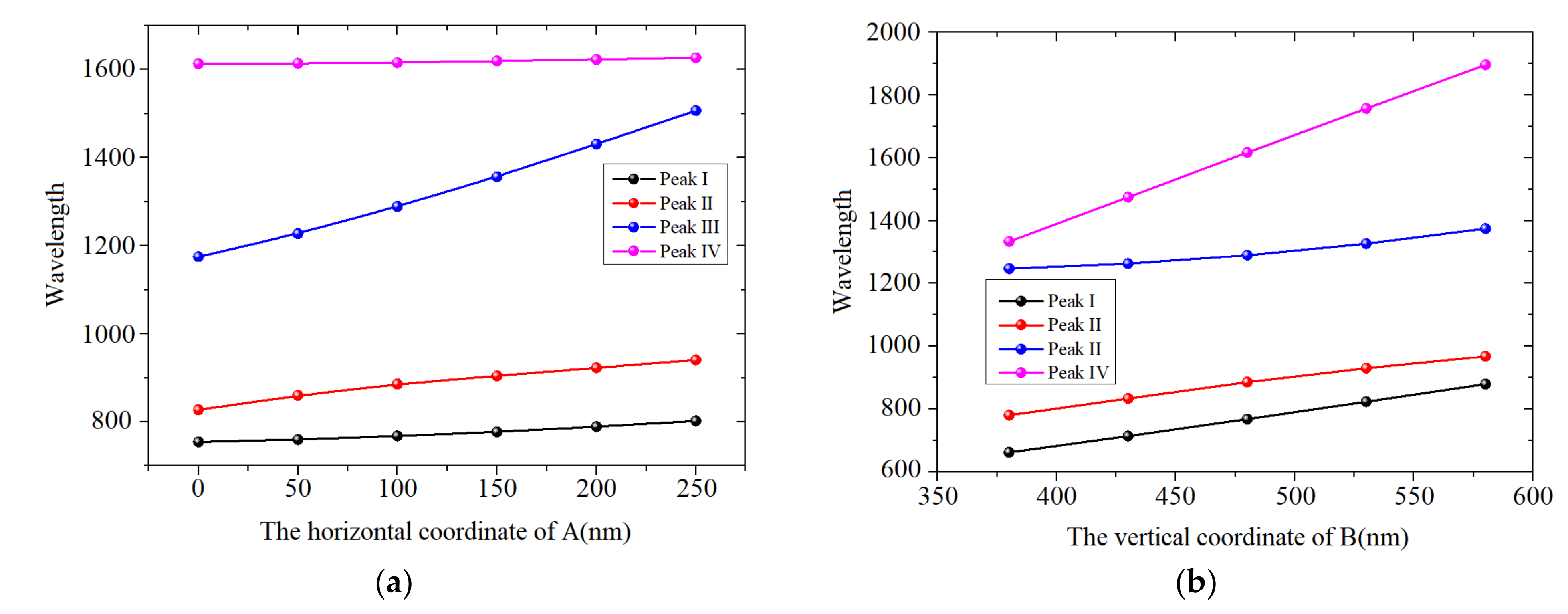
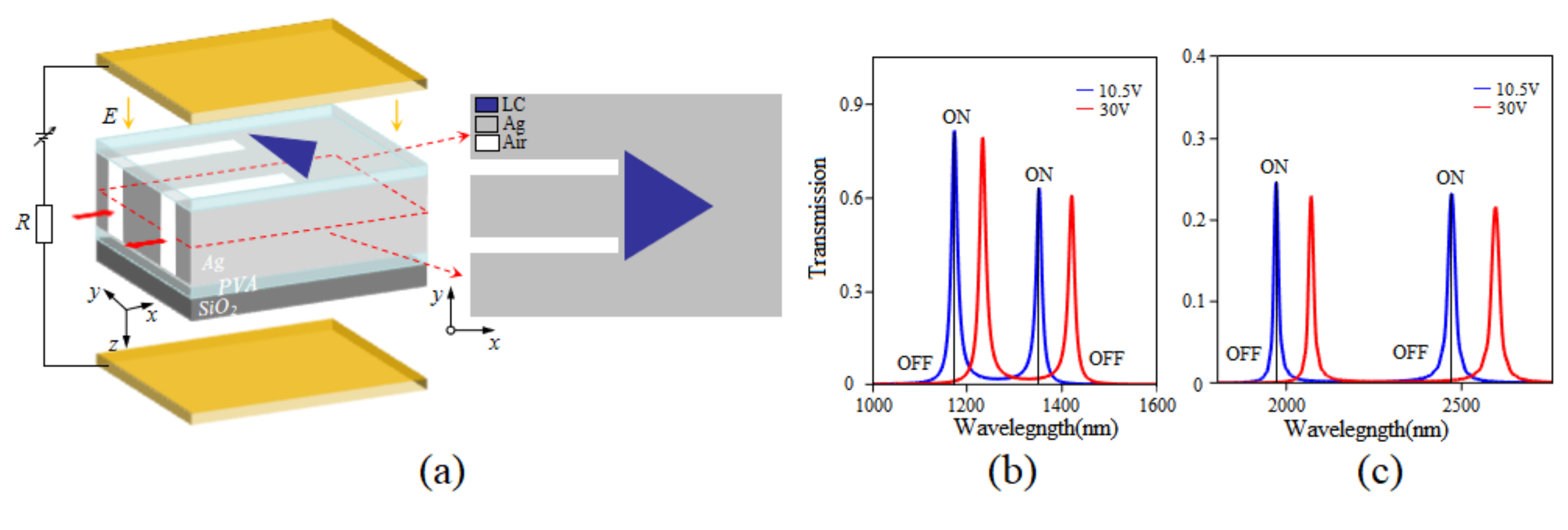
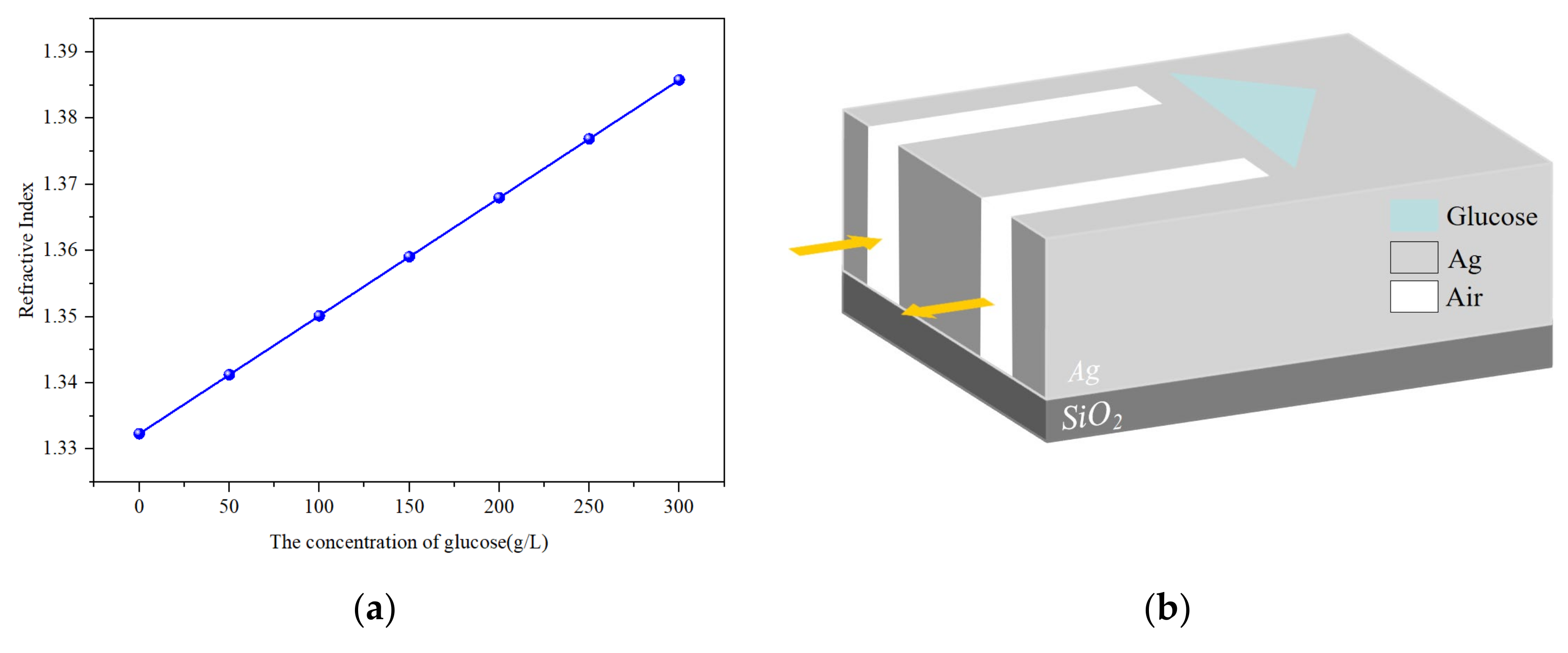
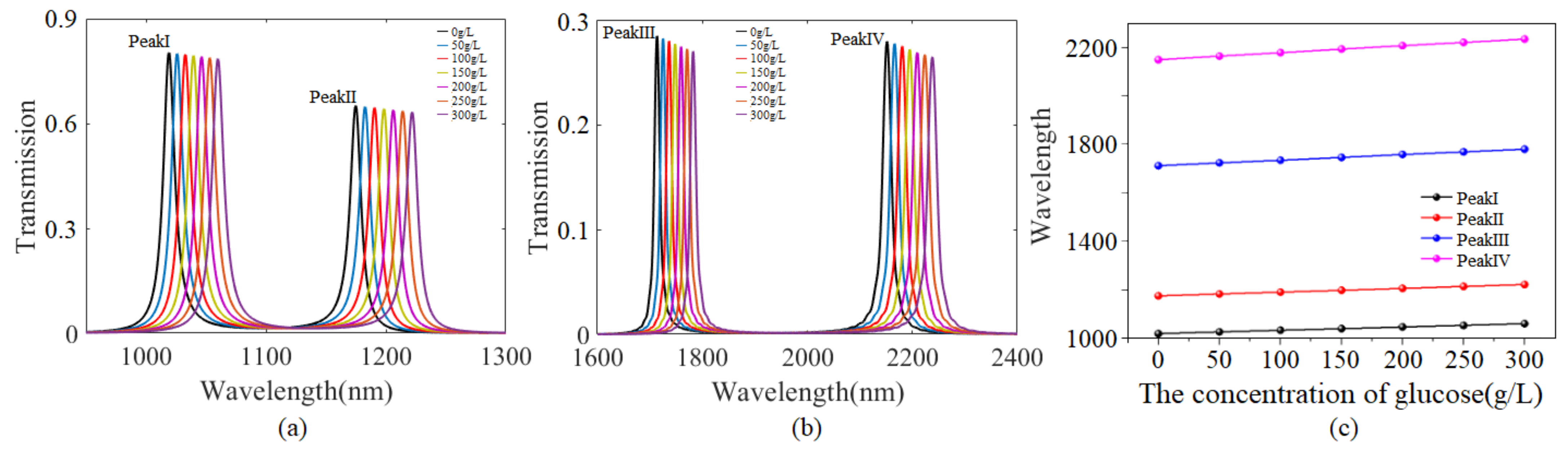
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sun, X.; Lei, Z.; Zhong, H.; He, C.; Liu, S.; Meng, Q.; Liu, Q.; Chen, S.; Kong, X.; Tian, Y. A quasi-3D Fano resonance cavity on optical fiber end-facet for high signal-to-noise ratio dip-and-read surface plasmon sensing. Light Adv. Manuf. 2022, 3, 665–675. [Google Scholar] [CrossRef]
- Wang, M.; Wang, T.; Ojambati, O.S.; Duffin, T.J.; Kang, K.; Lee, T.; Scheer, E.; Xiang, D.; Nijhuis, C.A. Plasmonic phenomena in molecular junctions: Principles and applications. Nat. Rev. Chem. 2022, 6, 681–704. [Google Scholar] [CrossRef] [PubMed]
- Butt, M.A.; Khonina, S.N.; Kazanskiy, N.L. Plasmonics: A necessity in the field of sensing—A review. Fiber Integr. Opt. 2021, 40, 14–47. [Google Scholar] [CrossRef]
- Martínez, J.; Ródenas, A.; Aguiló, M.; Fernandez, T.; Solis, J.; Díaz, F. Mid-infrared surface plasmon polariton chemical sensing on fiber-coupled ITO coated glass. Opt. Lett. 2016, 41, 2493–2496. [Google Scholar] [CrossRef]
- Zhu, P.; Shi, H.; Guo, L.J. SPPs coupling induced interference in metal/dielectric multilayer waveguides and its application for plasmonic lithography. Opt. Express 2012, 20, 12521–12529. [Google Scholar] [CrossRef]
- Gramotnev, D.K.; Bozhevolnyi, S.I. Plasmonics beyond the diffraction limit. Nat. Photonics 2010, 4, 83–91. [Google Scholar] [CrossRef]
- Nishijima, Y.; Rosa, L.; Juodkazis, S. Surface plasmon resonances in periodic and random patterns of gold nano-disks for broadband light harvesting. Opt. Express 2012, 20, 11466–11477. [Google Scholar] [CrossRef]
- Zayats, A.V.; Smolyaninov, I.I.; Maradudin, A.A. Nano-optics of surface plasmon polaritons. Phys. Rep. 2005, 408, 131–134. [Google Scholar] [CrossRef]
- Neutens, P.; Lagae, L.; Borghs, G.; Dorpe, P.V. Plasmon filters and resonators in metal-insulator-metal waveguides. Opt. Express 2012, 20, 3408–3423. [Google Scholar] [CrossRef]
- Tao, J.; Huang, X.; Lin, X.; Zhang, Q.; Jin, X. A narrow-band subwavelength plasmonic waveguide filter with asymmetrical multiple-teethshaped structure. Opt. Express 2009, 17, 13989–13994. [Google Scholar] [CrossRef]
- Ma, F.; Lee, C. Optical nanofilters based on meta-atom side-coupled plasmonics metal-insulator-metal waveguides. J. Light. Technol. 2013, 31, 2876–2880. [Google Scholar] [CrossRef]
- Tao, J.; Wang, Q.; Huang, X. All-optical plasmonic switches based on coupled nano-disk cavity structures containing nonlinear material. Plasmonics 2011, 6, 753–759. [Google Scholar] [CrossRef]
- Min, C.; Veronis, G. Absorption switches in metal-dielectric-metal plasmonic waveguides. Opt. Express 2009, 17, 10757–10766. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Lu, H.; Liu, X.; Gong, Y. Numerical investigation of an alloptical switch in a graded nonlinear plasmonic grating. Nanotechnology 2012, 23, 444009. [Google Scholar] [CrossRef]
- Xu, L.; Wang, S.; Wu, L. Refractive index sensing based on plasmonic waveguide side coupled with bilaterally located double cavities. IEEE Trans. Nanotechnol. 2014, 13, 875–880. [Google Scholar] [CrossRef]
- Zou, S.; Wang, F.; Liang, R.; Xiao, L.; Hu, M. A Nanoscale refractive index sensor based on asymmetric plasmonic waveguide with a ring resonator: A review. IEEE Sens. J. 2015, 15, 646–650. [Google Scholar] [CrossRef]
- Tang, Y.; Zhang, Z.; Wang, R.; Hai, Z.; Xue, C.; Zhang, W.; Yan, S. Refractive index sensor based on fano resonances in metalinsulator-metal waveguides coupled with resonators. Sensors 2017, 17, 784. [Google Scholar] [CrossRef]
- Zhang, B.; Wang, L.; Li, H.; Zhai, X.; Xia, S. Two kinds of double Fano resonances induced by an asymmetric MIM waveguide structure. J. Opt. 2016, 18, 065001. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, H.; Zhang, Z. Fano resonance in a gearshaped nanocavity of the metal-insulator-metal waveguide. Plasmonics 2013, 8, 797801. [Google Scholar] [CrossRef]
- Shi, H.; Yan, S.; Yang, X.; Wu, X.; Wu, W.; Hua, E. A nanosensor based on a metal-insulator-metal bus waveguide with a stub coupled with a racetrack ring resonator. Micromachines 2021, 12, 495. [Google Scholar] [CrossRef]
- Grineviciute, L.; Nikitina, J.; Babayigit, C.; Staliunas, K. Fano-like resonances in nanostructured thin films for spatial filtering. Appl. Phys. Lett. 2021, 118, 131114. [Google Scholar] [CrossRef]
- Chou Chao, C.; Chou Chau, Y.; Chiang, H. Breaking the symmetry of a metal–insulator–metal-based resonator for sensing applications. Nanoscale Res. Lett. 2022, 17, 48. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Jin, G. Detecting the temperature of ethanol based on Fano resonance spectra obtained using a metal-insulator-metal waveguide with SiO2 branches. Opt. Mater. Express 2021, 11, 2787–2799. [Google Scholar] [CrossRef]
- Liu, X.; Li, J.; Chen, J.; Rohimah, S.; Tian, H.; Wang, J. Fano resonance based on D-shaped waveguide structure and its application for human hemoglobin detection. Appl. Opt. 2020, 59, 6424–6430. [Google Scholar] [CrossRef] [PubMed]
- Tathfif, I.; Farhad Hassan, M.; Rashid, K.S.; Yaseer, A.A.; Sagor, R.H. A highly sensitive plasmonic refractive index sensor based on concentric triple ring resonator for cancer biomarker and chemical concentration detection. Opt. Commun. 2022, 519, 128429. [Google Scholar] [CrossRef]
- Li, B.; Zeng, L.; He, B.; Zhang, X.; Liao, K.; Liu, K.; Wang, B.; Ma, W. The sensing applications in U-shape structure based on dual transparency windows. IEEE Photonics J. 2018, 10, 5700808. [Google Scholar] [CrossRef]
- Palik, E.D. Handbook of Optical Constants in Solids; Academic Press: New York, NY, USA, 1998. [Google Scholar]
- Wang, S.; Yu, S.; Zhao, T.; Wang, Y.; Shi, X. A nanosensor with ultra-high FOM based on tunable malleable multiple Fano resonances in a waveguide coupled isosceles triangular resonator. Opt. Commun. 2020, 465, 125614. [Google Scholar] [CrossRef]
- Li, J.; Wu, S. Extended Cauchy equations for the refractive indices of liquidcrystals. J. Appl. Phys. 2004, 95, 896–901. [Google Scholar] [CrossRef]
- Li, J.; Wu, S.; Brugioni, S.; Meucci, R.; Faetti, S. Infrared refractive indices of liquid crystals. J. Appl. Phys. 2005, 97, 073501. [Google Scholar] [CrossRef]
- Li, X.; Feng, N.; Xu, Y.; Huang, Z.; Wen, K.; Xiong, X. Theoretical and simulation study of dynamically tunable sensor based on liquid crystal-modulated Fano resonator in terahertz band. Opt. Laser Technol. 2022, 155, 108350. [Google Scholar] [CrossRef]
- Wang, Z.; Cheng, L.; Wu, Y.; Li, C.; Gong, M.; Cao, P.; He, X.; Niu, T. Plasmonic demultiplexer with tunable output power ratio based on metal-dielectric-metal structure and E7 liquid crystal arrays. IEEE Photonics J. 2020, 12, 4800410. [Google Scholar] [CrossRef]
- Humbatov, S.; Ramazanov, M.; İmamaliyev, A. The study of BaTiO3 nanoparticles effect on threshold properties of Liquid Crystal 5CB. Mol. Cryst. Liq. Cryst. 2017, 646, 263–267. [Google Scholar] [CrossRef]
- Raynes, E.P.; Tough, R.J.A.; Davies, K.A. Voltage dependence of the capacitance of a twisted nematic liquid crystal layer. Mol. Cryst. Liq. Cryst. 1979, 56, 63–68. [Google Scholar] [CrossRef]
- Stoltzfus, C.; Barbour, R.; Atherton, D.; Barber, Z. Micro-sized tunable liquid crystal optical filters. Opt. Lett. 2017, 42, 2090–2093. [Google Scholar] [CrossRef]
- Guo, S.; Liang, X.; Zhang, H.; Shen, W.; Li, C.; Wang, X. An electrically light-transmittance-controllable film with a low-driving voltage from a coexistent system of polymer-dispersed and polymer-stabilised cholesteric liquid crystals. Liq. Cryst. 2018, 45, 1854–1860. [Google Scholar] [CrossRef]
- He, Q.; Huo, Y.; Guo, Y.; Niu, Q.; Hao, X.; Cui, P.; Wang, Y.; Song, M. Multiple adjustable Fano resonance based on double half ring resonator and its application. Phys. Scripta 2021, 96, 065504. [Google Scholar] [CrossRef]
- Chou Chau, Y.; Ming, T.; Chou Chao, C.; Thotagamuge, R.; Kooh, M.R.R.; Huang, H.; Lim, C.; Chiang, H. Significantly enhanced coupling effect and gap plasmon resonance in a MIM-cavity based sensing structure. Sci. Rep. 2021, 11, 18515. [Google Scholar] [CrossRef]
- Rohimah, S.; Tian, H.; Wang, J.; Chen, J.; Li, J.; Liu, X.; Cui, J.; Xu, Q.; Hao, Y. Fano resonance in the plasmonic structure of MIM waveguide with r-shaped resonator for refractive index sensor. Plasmonics 2022, 17, 1681–1689. [Google Scholar] [CrossRef]
- Kumari, S.; Verma, Y.K.; Tripathi, S.M. Plasmonic Ring Resonator Sensor with High Figure of Merit and Sensitivity Using Degenerate N-Doped Silicon for SPP Excitation. Plasmonics 2024, 19, 2743–2751. [Google Scholar] [CrossRef]
| Structure | Materials | Year | S | Reference |
|---|---|---|---|---|
| Double half-ring resonator | Ag | 2021 | 0.145 nm·L/g | [37] |
| MIM cavity | Ag | 2021 | 0.19 nm·L/g | [38] |
| MIM waveguide with r-shaped resonator | Ag | 2022 | 0.16 nm·L/g | [39] |
| Nano-ring resonator | N-doped Si | 2024 | 0.21 nm·L/g | [40] |
| Isosceles triangular coupling structure | Ag | 2024 | 0.283 nm·L/g | This work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, L.; Zhang, X.; Guo, Q.; Fan, Y.; Deng, Y.; Ma, Z.; Li, B. Applications of Isosceles Triangular Coupling Structure in Optical Switching and Sensing. Sensors 2024, 24, 8221. https://doi.org/10.3390/s24248221
Zeng L, Zhang X, Guo Q, Fan Y, Deng Y, Ma Z, Li B. Applications of Isosceles Triangular Coupling Structure in Optical Switching and Sensing. Sensors. 2024; 24(24):8221. https://doi.org/10.3390/s24248221
Chicago/Turabian StyleZeng, Lili, Xingjiao Zhang, Qinghua Guo, Yang Fan, Yuanwen Deng, Zhengchao Ma, and Boxun Li. 2024. "Applications of Isosceles Triangular Coupling Structure in Optical Switching and Sensing" Sensors 24, no. 24: 8221. https://doi.org/10.3390/s24248221
APA StyleZeng, L., Zhang, X., Guo, Q., Fan, Y., Deng, Y., Ma, Z., & Li, B. (2024). Applications of Isosceles Triangular Coupling Structure in Optical Switching and Sensing. Sensors, 24(24), 8221. https://doi.org/10.3390/s24248221






