Accurate Arrhythmia Classification with Multi-Branch, Multi-Head Attention Temporal Convolutional Networks
Abstract
:1. Introduction
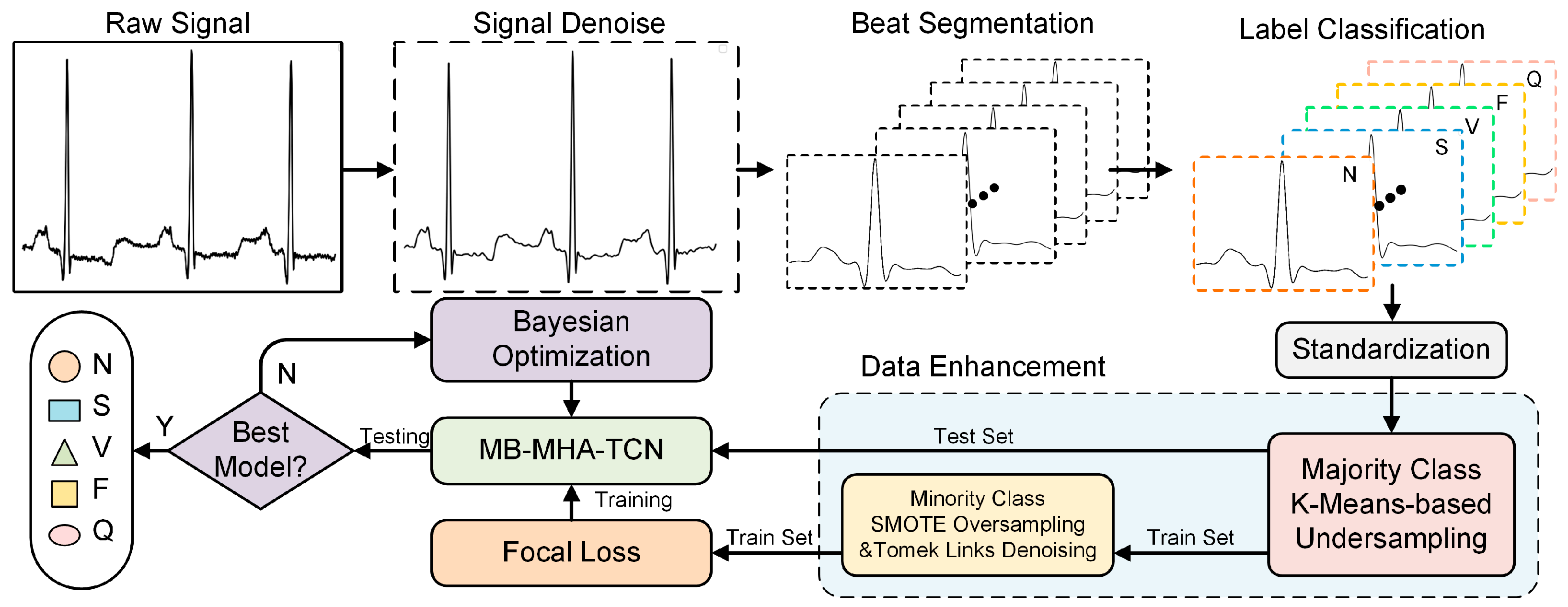
2. Materials and Methods
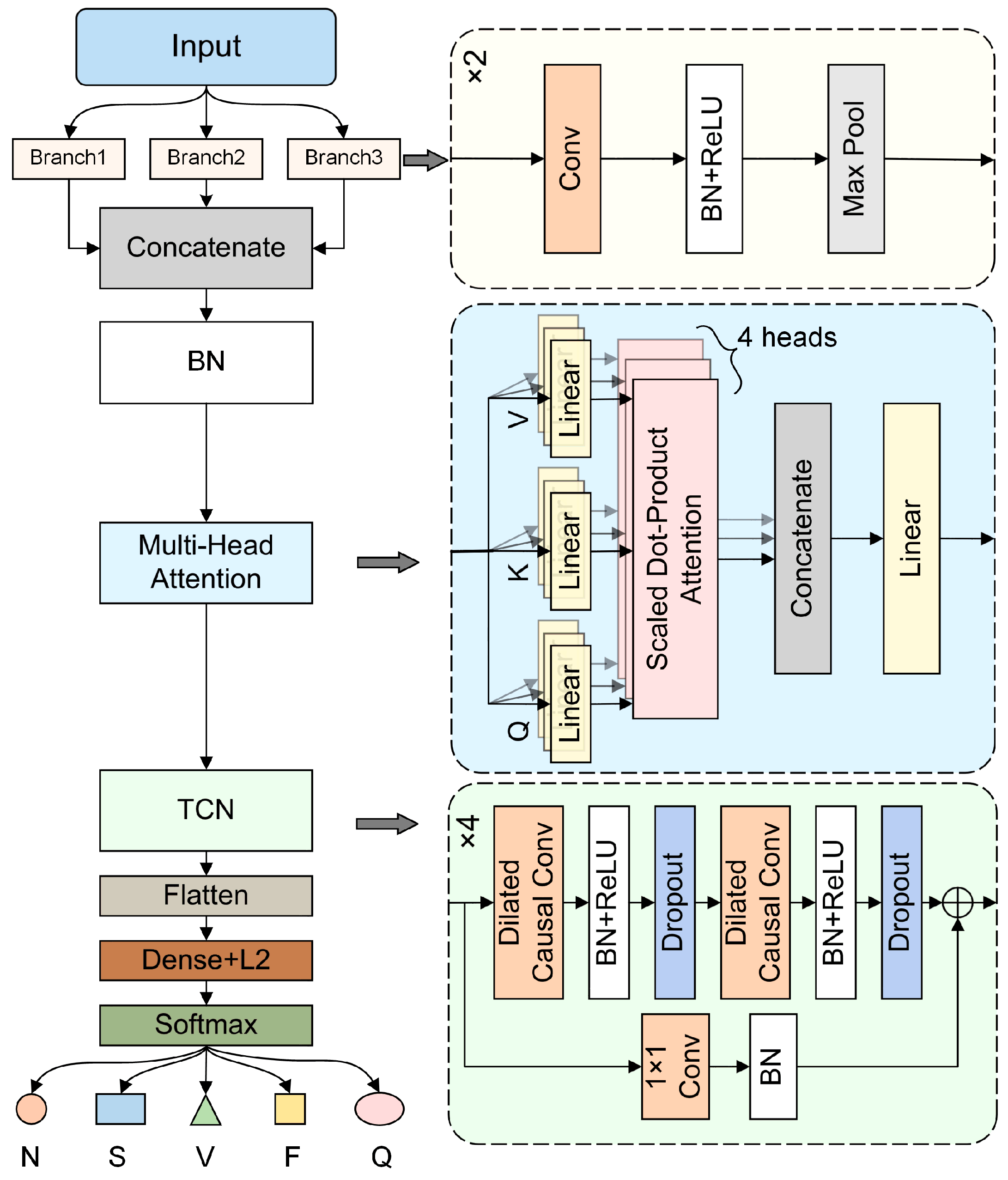
2.1. MB-MHA-TCN Model
2.1.1. Multi-Branch Dilation Convolution
2.1.2. Multi-Head Self-Attention Mechanism
2.1.3. Temporal Convolutional Network
2.2. Dataset and Preprocessing
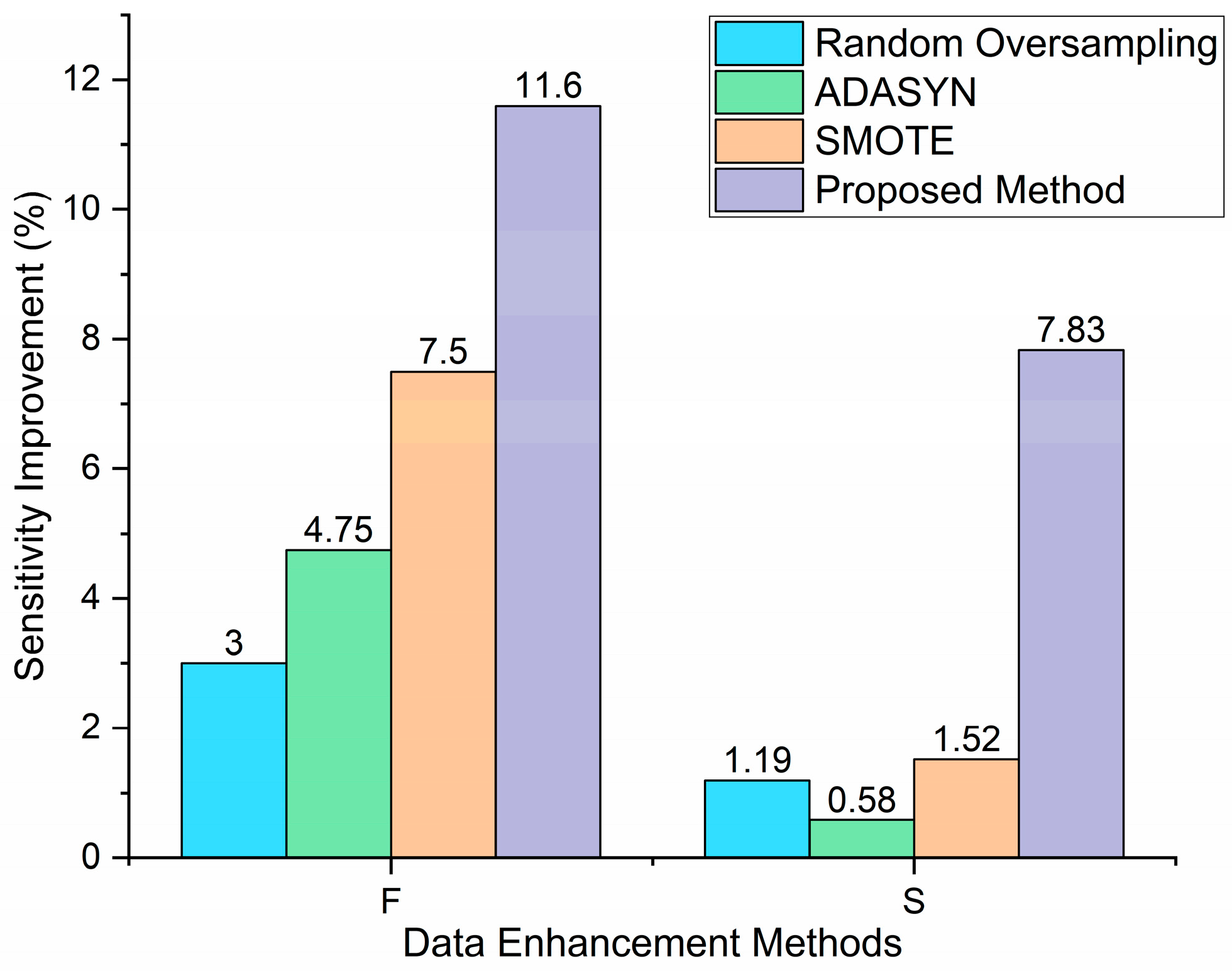
2.3. Data Augmentation
3. Results and Discussion
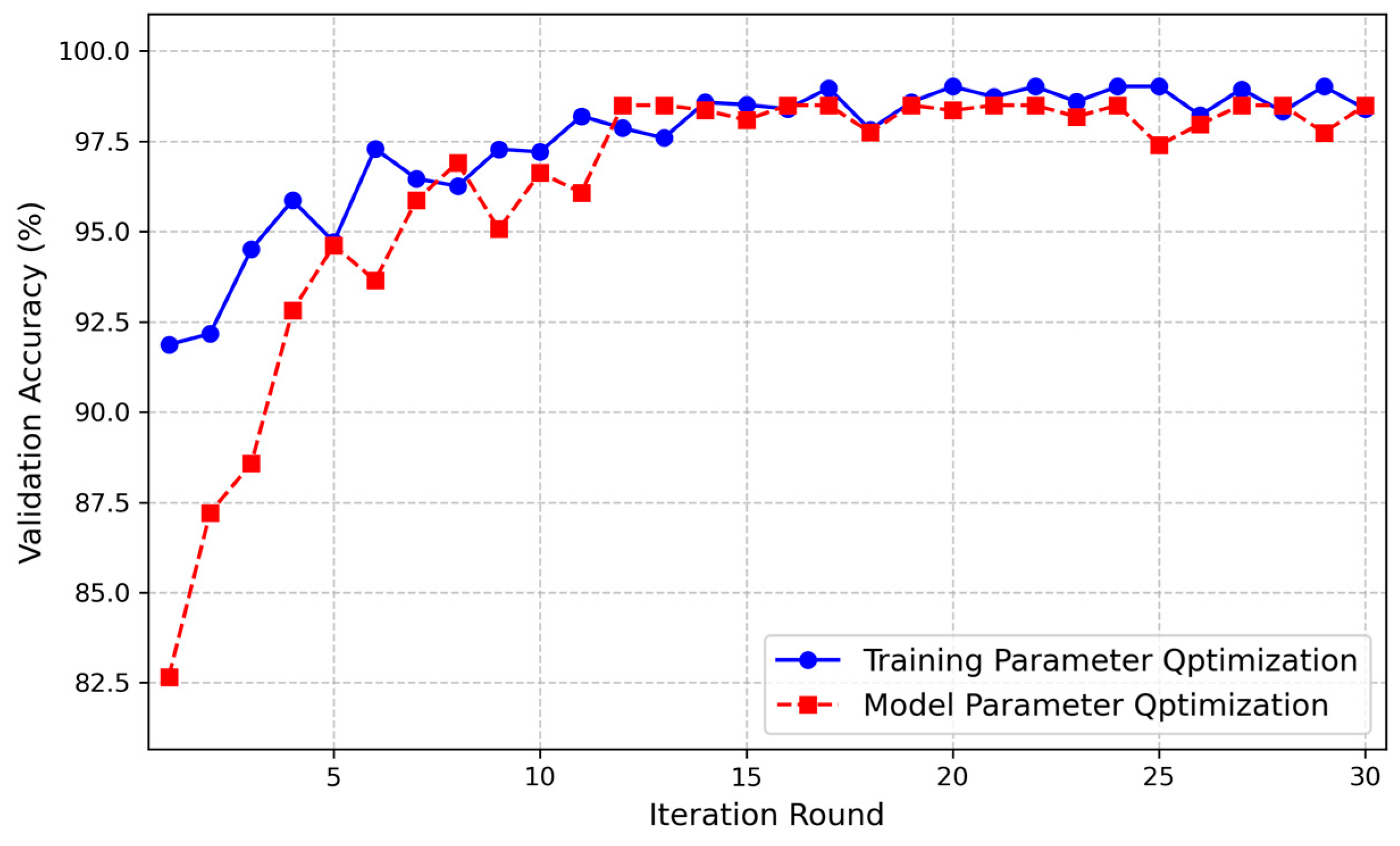
3.1. Experimental Setup
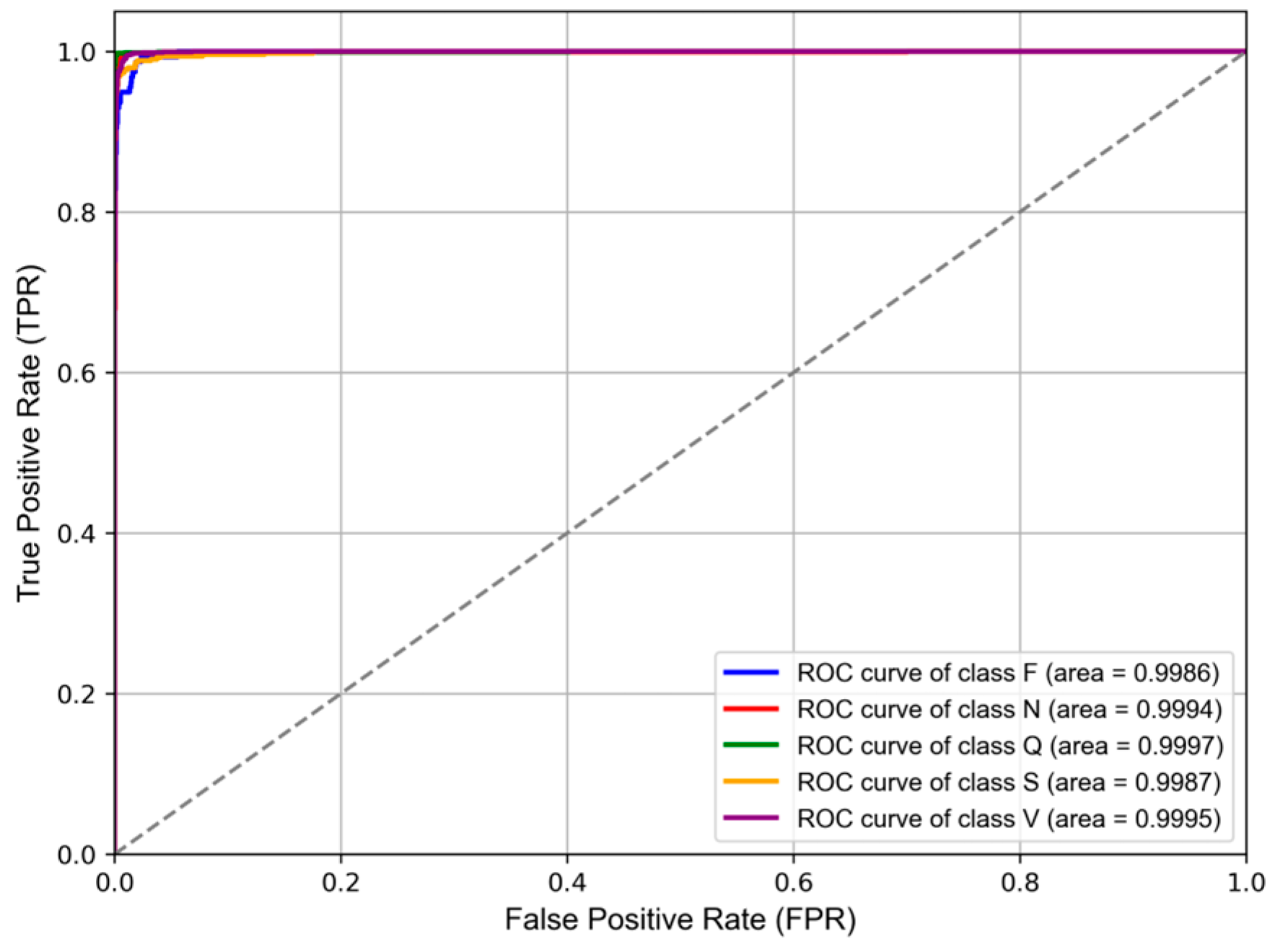
3.2. Performance Matrices
3.3. Performance of the Proposed Method
3.4. Ablation Experiment
3.5. Comparison of the Proposed Method to Other Previous Works
4. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gopinathannair, R.; Etheridge, S.P.; Marchlinski, F.E.; Spinale, F.G.; Lakkireddy, D.; Olshansky, B. Arrhythmia-induced cardiomyopathies: Mechanisms, recognition, and management. J. Am. Coll. Cardiol. 2015, 66, 1714–1728. [Google Scholar] [CrossRef] [PubMed]
- Lippi, G.; Sanchis-Gomar, F.; Cervellin, G. Global epidemiology of atrial fibrillation: An increasing epidemic and public health challenge. Int. J. Stroke 2021, 16, 217–221. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. Cardiovascular Diseases (CVDs) Fact Sheet. 2021. Available online: https://www.who.int/news-room/fact-sheets/detail/cardiovascular-diseases-(cvds) (accessed on 22 October 2024).
- Goldberger, A.L.; Amaral, L.A.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.-K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a new research resource for complex physiologic signals. Circulation 2000, 101, e215–e220. [Google Scholar] [CrossRef] [PubMed]
- Martínez, J.P.; Almeida, R.; Olmos, S.; Rocha, A.P.; Laguna, P. A wavelet-based ECG delineator: Evaluation on standard databases. IEEE Trans. Biomed. Eng. 2004, 51, 570–581. [Google Scholar] [CrossRef]
- Gañán-Calvo, A.M.; Fajardo-López, J. Universal structures of normal and pathological heart rate variability. Sci. Rep. 2016, 6, 21749. [Google Scholar] [CrossRef]
- Gañán-Calvo, A.M.; Hnatkova, K.; Romero-Calvo, Á.; Fajardo-López, J.; Malik, M. Risk stratifiers for arrhythmic and non-arrhythmic mortality after acute myocardial infarction. Sci. Rep. 2018, 8, 9897. [Google Scholar] [CrossRef]
- Yang, W.; Si, Y.; Wang, D.; Guo, B. Automatic recognition of arrhythmia based on principal component analysis network and linear support vector machine. Comput. Biol. Med. 2018, 101, 22–32. [Google Scholar] [CrossRef]
- Theerthagiri, P.; Vidya, J. Cardiovascular disease prediction using recursive feature elimination and gradient boosting classification techniques. Expert Syst. 2022, 39, e13064. [Google Scholar] [CrossRef]
- Sahoo, S.; Dash, P.; Mishra, B.; Sabut, S.K. Deep learning-based system to predict cardiac arrhythmia using hybrid features of transform techniques. Intell. Syst. Appl. 2022, 16, 200127. [Google Scholar] [CrossRef]
- Pandey, S.K.; Janghel, R.R. ECG arrhythmia classification using artificial neural networks. In Proceedings of the 2nd International Conference on Communication, Computing and Networking: ICCCN 2018, NITTTR, Chandigarh, India, 29–30 March 2018; pp. 645–652. [Google Scholar]
- Asl, B.M.; Setarehdan, S.K.; Mohebbi, M. Support vector machine-based arrhythmia classification using reduced features of heart rate variability signal. Artif. Intell. Med. 2008, 44, 51–64. [Google Scholar] [CrossRef]
- Alickovic, E.; Subasi, A. Medical decision support system for diagnosis of heart arrhythmia using DWT and random forests classifier. J. Med. Syst. 2016, 40, 108. [Google Scholar] [CrossRef] [PubMed]
- Castillo, O.; Melin, P.; Ramírez, E.; Soria, J. Hybrid intelligent system for cardiac arrhythmia classification with Fuzzy K-Nearest Neighbors and neural networks combined with a fuzzy system. Expert Syst. Appl. 2012, 39, 2947–2955. [Google Scholar] [CrossRef]
- Sahoo, S.; Subudhi, A.; Dash, M.; Sabut, S. Automatic classification of cardiac arrhythmias based on hybrid features and decision tree algorithm. Int. J. Autom. Comput. 2020, 17, 551–561. [Google Scholar] [CrossRef]
- Padmavathi, S.; Ramanujam, E. Naïve Bayes classifier for ECG abnormalities using multivariate maximal time series motif. Procedia Comput. Sci. 2015, 47, 222–228. [Google Scholar] [CrossRef]
- Hanbay, K. Deep neural network based approach for ECG classification using hybrid differential features and active learning. IET Signal Process. 2019, 13, 165–175. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Ince, T.; Gabbouj, M. Real-time patient-specific ECG classification by 1-D convolutional neural networks. IEEE Trans. Biomed. Eng. 2015, 63, 664–675. [Google Scholar] [CrossRef]
- Hannun, A.Y.; Rajpurkar, P.; Haghpanahi, M.; Tison, G.H.; Bourn, C.; Turakhia, M.P.; Ng, A.Y. Cardiologist-level arrhythmia detection and classification in ambulatory electrocardiograms using a deep neural network. Nat. Med. 2019, 25, 65–69. [Google Scholar] [CrossRef]
- Ahmed, A.A.; Ali, W.; Abdullah, T.A.; Malebary, S.J. Classifying cardiac arrhythmia from ECG signal using 1D CNN deep learning model. Mathematics 2023, 11, 562. [Google Scholar] [CrossRef]
- Acharya, U.R.; Oh, S.L.; Hagiwara, Y.; Tan, J.H.; Adam, M.; Gertych, A.; San Tan, R. A deep convolutional neural network model to classify heartbeats. Comput. Biol. Med. 2017, 89, 389–396. [Google Scholar] [CrossRef]
- Kachuee, M.; Fazeli, S.; Sarrafzadeh, M. Ecg heartbeat classification: A deep transferable representation. In Proceedings of the 2018 IEEE International Conference on Healthcare Informatics (ICHI), New York, NY, USA, 4–7 June 2018; pp. 443–444. [Google Scholar]
- Jeong, D.U.; Lim, K.M. Convolutional neural network for classification of eight types of arrhythmia using 2D time–frequency feature map from standard 12-lead electrocardiogram. Sci. Rep. 2021, 11, 20396. [Google Scholar] [CrossRef]
- Degirmenci, M.; Ozdemir, M.A.; Izci, E.; Akan, A. Arrhythmic heartbeat classification using 2d convolutional neural networks. IRBM 2022, 43, 422–433. [Google Scholar] [CrossRef]
- Katrompas, A.; Ntakouris, T.; Metsis, V. Recurrence and self-attention vs the transformer for time-series classification: A comparative study. In Proceedings of the International Conference on Artificial Intelligence in Medicine, Halifax, NS, Canada, 14–17 June 2022; pp. 99–109. [Google Scholar]
- Park, J.; Lee, K.; Park, N.; You, S.C.; Ko, J. Self-Attention LSTM-FCN model for arrhythmia classification and uncertainty assessment. Artif. Intell. Med. 2023, 142, 102570. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Yang, G.; Li, S.; Li, Y.; He, L.; Liu, D. Arrhythmia classification algorithm based on multi-head self-attention mechanism. Biomed. Signal Process. Control. 2023, 79, 104206. [Google Scholar] [CrossRef]
- Xu, Z.; Zang, M.; Liu, T.; Zhou, S.; Liu, C.; Wang, Q. Multi-modality Multi-attention Network for Ventricular Arrhythmia Classification. In Proceedings of the 2023 3rd International Conference on Bioinformatics and Intelligent Computing, Sanya, China, 10–12 February 2023; pp. 331–336. [Google Scholar]
- Chen, A.; Wang, F.; Liu, W.; Chang, S.; Wang, H.; He, J.; Huang, Q. Multi-information fusion neural networks for arrhythmia automatic detection. Comput. Methods Progr. Biomed. 2020, 193, 105479. [Google Scholar] [CrossRef]
- Wang, M.; Rahardja, S.; Fränti, P.; Rahardja, S. Single-lead ECG recordings modeling for end-to-end recognition of atrial fibrillation with dual-path RNN. Biomed. Signal Process. Control. 2023, 79, 104067. [Google Scholar] [CrossRef]
- Mousavi, S.; Afghah, F. Inter-and intra-patient ecg heartbeat classification for arrhythmia detection: A sequence to sequence deep learning approach. In Proceedings of the ICASSP 2019—2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 1308–1312. [Google Scholar]
- Xu, X.; Jeong, S.; Li, J. Interpretation of electrocardiogram (ECG) rhythm by combined CNN and BiLSTM. IEEE Access 2020, 8, 125380–125388. [Google Scholar] [CrossRef]
- Essa, E.; Xie, X. An ensemble of deep learning-based multi-model for ECG heartbeats arrhythmia classification. IEEE Access 2021, 9, 103452–103464. [Google Scholar] [CrossRef]
- Bai, S.; Kolter, J.Z.; Koltun, V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar]
- Ingolfsson, T.M.; Wang, X.; Hersche, M.; Burrello, A.; Cavigelli, L.; Benini, L. ECG-TCN: Wearable cardiac arrhythmia detection with a temporal convolutional network. In Proceedings of the 2021 IEEE 3rd International Conference on Artificial Intelligence Circuits and Systems (AICAS), Washington, DC, USA, 6–9 June 2021; pp. 1–4. [Google Scholar]
- Zhao, X.; Zhou, R.; Ning, L.; Guo, Q.; Liang, Y.; Yang, J. Atrial Fibrillation Detection with Single-Lead Electrocardiogram Based on Temporal Convolutional Network—ResNet. Sensors 2024, 24, 398. [Google Scholar] [CrossRef]
- Vaswani, A. Attention is all you need. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 6000–6010. [Google Scholar]
- Moody, G.B.; Mark, R.G. The impact of the MIT-BIH arrhythmia database. IEEE Eng. Med. Biol. Mag. 2001, 20, 45–50. [Google Scholar] [CrossRef]
- De Chazal, P.; O’Dwyer, M.; Reilly, R.B. Automatic classification of heartbeats using ECG morphology and heartbeat interval features. IEEE Trans. Biomed. Eng. 2004, 51, 1196–1206. [Google Scholar] [CrossRef]
- Wu, W.; Huang, Y.; Wu, X. SRT: Improved transformer-based model for classification of 2D heartbeat images. Biomed. Signal Process. Control. 2024, 88, 105017. [Google Scholar] [CrossRef]


| Layer Type | Branch | Filter | Kernel/Pool Size | Dilation Rate | Stride | Activation Function | Batch Normalization | Other |
|---|---|---|---|---|---|---|---|---|
| Input Layer | - | - | - | - | - | - | - | 250 × 1 |
| Conv Layer 1 | 1 | 48 | 12 | 1 | 1 | ReLU | Yes | - |
| Max Pooling 1 | 1 | - | 2 | - | 2 | - | - | - |
| Conv Layer 2 | 1 | 64 | 6 | 1 | 1 | ReLU | Yes | - |
| Max Pooling 2 | 1 | - | 2 | - | 2 | - | - | - |
| Conv Layer 1 | 2 | 48 | 22 | 1 | 1 | ReLU | Yes | - |
| Max Pooling 1 | 2 | - | 2 | - | 2 | - | - | - |
| Conv Layer 2 | 2 | 64 | 11 | 2 | 1 | ReLU | Yes | - |
| Max Pooling 2 | 2 | - | 2 | - | 2 | - | - | - |
| Conv Layer 1 | 3 | 48 | 48 | 1 | 1 | ReLU | Yes | - |
| Max Pooling 1 | 3 | - | 2 | - | 2 | - | - | - |
| Conv Layer 2 | 3 | 64 | 24 | 4 | 1 | ReLU | Yes | - |
| Max Pooling 2 | 3 | - | 2 | - | 2 | - | - | - |
| Concatenate | - | - | - | - | - | - | Yes | - |
| MHA | - | - | - | - | - | - | - | 4 heads |
| TCN Layer | - | 6 | 8 | - | - | ReLU | Yes | Dropout |
| Flatten Layer | - | - | - | - | - | - | - | - |
| Dense Layer | - | 5 | - | - | - | - | - | L2 |
| Output Layer | - | - | - | - | - | Softmax | - |
| Category | Class | Number/% of Total 1 |
|---|---|---|
| N | Normal beat (N) | 73,520/68.5 |
| Left bundle branch block beat (L) | 8030/7.5 | |
| Right bundle branch block beat (R) | 7187/6.7 | |
| Atrial escape beat (e) | 15/0.0 | |
| Nodal (Junctional) beat (j) | 216/0.2 | |
| SVEB | Atrial premature beat (A) | 2454/2.3 |
| Aberrated atrial premature beat (a) | 138/0.1 | |
| Nodal (Junctional) premature beat (J) | 69/0.1 | |
| Supraventricular premature beat (S) | 2/0.0 | |
| VEB | Premature ventricular contraction (V) | 6854/6.4 |
| Ventricular escape beat (E) | 106/0.1 | |
| F | Fusion of ventricular and normal beat (F) | 785/0.7 |
| Q | Paced beat (/) | 6969/6.5 |
| Fusion of paced and normal beat (f) | 977/0.9 | |
| Unclassified beat (Q) | 32/0.0 | |
| Total | - | 107,354/100.0 |
| Datasets | N | S | V | F | Q | Total |
|---|---|---|---|---|---|---|
| Training set | 12,746 | 5561 | 4455 | 4817 | 5135 | 32,714 |
| Test set | 3074 | 532 | 1391 | 157 | 1572 | 6726 |
| Validation set | 2492 | 433 | 1108 | 128 | 1244 | 5405 |
| Total/% of total | 18,312/40.8 | 6526/14.6 | 6954/15.5 | 5102/11.4 | 7951/17.7 | 44,845/100.0 |
| Strategy | Parameters | Value |
|---|---|---|
| Warmup | initial_lr | 0.0001 |
| target_lr | 0.0007 | |
| Exponential Decay | decay_steps | 1500 |
| decay_rate | 0.97 | |
| min_lr | 0.00001 |
| Optimization Strategy | Hyperparameters | Search Space | Value | |
|---|---|---|---|---|
| Optimum Model | CNN | kernel_size_branch1 | [2, 16] | 4 |
| kernel_size_branch2 | [8, 32] | 14 | ||
| kernel_size_branch3 | [16, 128] | 62 | ||
| filt_ | [16, 64] | 16 | ||
| MHA | num_heads | [4, 16] | 4 | |
| TCN | kernel_size_tcn | [4, 16] | 8 | |
| layers | [2, 5] | 4 | ||
| filt_tcn | [6, 20] | 10 | ||
| Optimum Training Effect | Training parameter | epochs | [40, 200] | 80 |
| batch_size | [32, 128] | 64 | ||
| drop_rate1 | [0.1, 0.5] | 0.4 | ||
| Focal Loss | α | [0.1, 2.0] | 0.76943 | |
| γ | [1, 5] | 2 | ||
| Folds | OA * | Pre * | Sen * | F1 * | AUC * |
|---|---|---|---|---|---|
| Fold 0 | 98.68% | 95.93% | 97.21% | 96.54% | 99.68% |
| Fold 1 | 99.02% | 97.58% | 97.94% | 97.76% | 99.92% |
| Fold 2 | 98.59% | 95.99% | 97.06% | 96.51% | 99.83% |
| Fold 3 | 98.72% | 96.56% | 96.99% | 96.77% | 99.77% |
| Fold 4 | 98.75% | 96.93% | 96.86% | 96.89% | 99.80% |
| Average | 98.75% | 96.60% | 97.21% | 96.89% | 99.80% |
| Predicted Label | Performance (%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| N | S | V | F | Q | Pre | Sen | F1 | OA | ||
| True label | N | 3052 | 11 | 8 | 1 | 2 | 99.71% | 99.28% | 99.49% | 99.02% |
| S | 4 | 520 | 5 | 1 | 2 | 96.47% | 97.74% | 97.11% | ||
| V | 4 | 6 | 1373 | 5 | 3 | 98.49% | 98.71% | 98.60% | ||
| F | 0 | 2 | 7 | 148 | 0 | 93.67% | 94.27% | 93.97% | ||
| Q | 1 | 0 | 1 | 3 | 1567 | 99.56% | 99.68% | 99.62% | ||
| Classes | Metrics 1 | TCN | MB-TCN | MHA-TCN | Proposed Method 2 |
|---|---|---|---|---|---|
| N | Pre | 98.19% | 99.26% | 98.99% | 99.34% |
| Sen | 98.31% | 98.94% | 99.12% | 99.40% | |
| F1 | 98.25% | 99.10% | 99.05% | 99.37% | |
| S | Pre | 89.75% | 92.29% | 93.93% | 96.71% |
| Sen | 94.18% | 96.96% | 95.57% | 97.07% | |
| F1 | 91.90% | 94.55% | 94.73% | 96.89% | |
| V | Pre | 98.01% | 98.37% | 98.18% | 98.34% |
| Sen | 94.36% | 96.13% | 96.42% | 97.96% | |
| F1 | 96.15% | 97.24% | 97.29% | 98.15% | |
| F | Pre | 76.97% | 82.04% | 84.01% | 88.92% |
| Sen | 92.10% | 92.74% | 90.32% | 92.23% | |
| F1 | 83.83% | 87.03% | 87.05% | 90.52% | |
| Q | Pre | 99.02% | 99.60% | 99.39% | 99.68% |
| Sen | 98.41% | 99.20% | 99.36% | 99.40% | |
| F1 | 98.71% | 99.40% | 99.38% | 99.54% | |
| Average | Pre | 92.39% | 94.31% | 94.90% | 96.60% |
| Sen | 95.47% | 96.79% | 96.16% | 97.21% | |
| F1 | 93.77% | 95.46% | 95.50% | 96.89% | |
| OA | 97.04% | 98.12% | 98.13% | 98.75% |
| Loss Function | Classes | Pre | Sen | F1 | OA |
|---|---|---|---|---|---|
| Categorical Crossentropy Loss | N | 99.22% | 99.43% | 99.32% | 98.61% |
| S | 96.28% | 95.98% | 96.13% | ||
| V | 98.56% | 97.43% | 97.99% | ||
| F | 87.18% | 91.46% | 89.25% | ||
| Q | 99.48% | 99.68% | 99.58% | ||
| Focal Loss | N | 99.34% | 99.40% | 99.37% | 98.75% |
| S | 96.71% | 97.07% | 96.89% | ||
| V | 98.34% | 97.96% | 98.15% | ||
| F | 88.92% | 92.23% | 90.52% | ||
| Q | 99.68% | 99.40% | 99.54% |
| Author | Preprocessing | Approach * | Pre/% | Sen/% | Spe/% | F1/% | OA/% |
|---|---|---|---|---|---|---|---|
| Proposed method | Butterworth Bandpass Filter, K-Means, SMOTE, Tomek Links | MB-MHA-TCN | 97.58 | 97.94 | 99.75 | 97.76 | 99.02 |
| Wu et al., 2024 [40] | DPI, SMOTE | CNN + Transformer | - | 88.1 | - | 82.6 | 95.7 |
| Xu et al., 2023 [28] | Modal Conversion, Sample Enrichment | Multi-Head Attention | 90.36 | 91.01 | 91.01 | 90.68 | 97.72 |
| Essa et al., 2021 [33] | Baseline Correction, Low-Pass Filter | CNN + LSTM | 74.97 | 69.20 | 94.56 | 71.06 | 95.81 |
| Xu et al., 2020 [32] | Downsampling (125 Hz), Zero Padding | CNN + BiLSTM | 96.34 | 95.9 | - | 95.92 | 95.9 |
| Mousavi et al., 2019 [31] | SMOTE | CNN + BiLSTM | 97.21 | 96.19 | 98.58 | - | 99.53 |
| Hanbay et al., 2019 [17] | Median Filter, Low-Pass Filter | DNN | - | 86.41 | 96.41 | - | 96.4 |
| Kachuee et al., 2018 [22] | Zero Padding | 1D-CNN | 95.2 | 95.1 | - | - | 95.9 |
| Acharya et al., 2017 [21] | Wavelet Filter (db6), Data Augmentation (Z-Score) | 9-layer CNN model | - | 96.71 | 91.54 | - | 94.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bi, S.; Lu, R.; Xu, Q.; Zhang, P. Accurate Arrhythmia Classification with Multi-Branch, Multi-Head Attention Temporal Convolutional Networks. Sensors 2024, 24, 8124. https://doi.org/10.3390/s24248124
Bi S, Lu R, Xu Q, Zhang P. Accurate Arrhythmia Classification with Multi-Branch, Multi-Head Attention Temporal Convolutional Networks. Sensors. 2024; 24(24):8124. https://doi.org/10.3390/s24248124
Chicago/Turabian StyleBi, Suzhao, Rongjian Lu, Qiang Xu, and Peiwen Zhang. 2024. "Accurate Arrhythmia Classification with Multi-Branch, Multi-Head Attention Temporal Convolutional Networks" Sensors 24, no. 24: 8124. https://doi.org/10.3390/s24248124
APA StyleBi, S., Lu, R., Xu, Q., & Zhang, P. (2024). Accurate Arrhythmia Classification with Multi-Branch, Multi-Head Attention Temporal Convolutional Networks. Sensors, 24(24), 8124. https://doi.org/10.3390/s24248124







