Design and Monitoring Application of an Adjustable Intelligent Bearing Based on Pressure Sensing
Abstract
1. Introduction
2. Bridge Overturning Risk Analysis
2.1. Current Situation Analysis
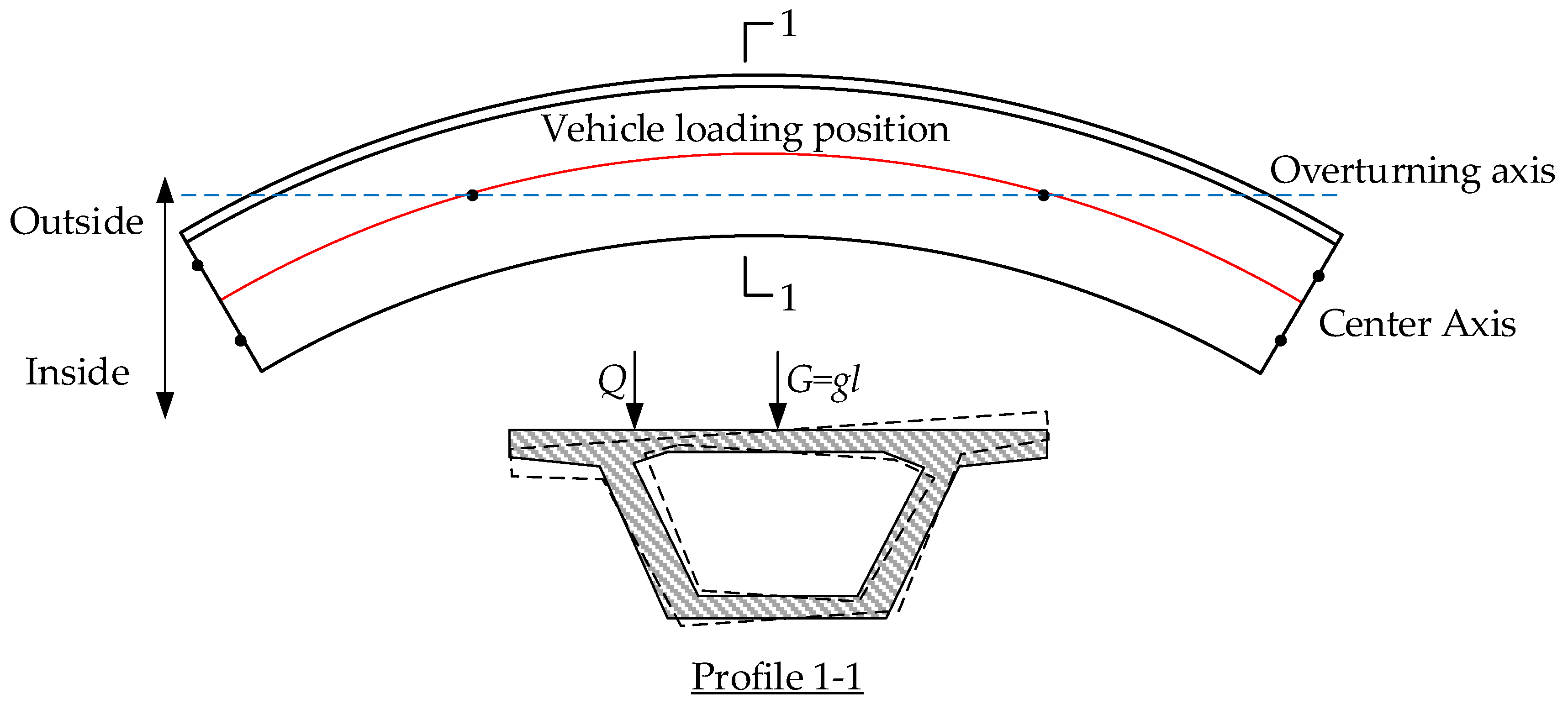
2.2. Overturning Mechanism Analysis
3. Adjustable Intelligent Force Measurement Bearing Design
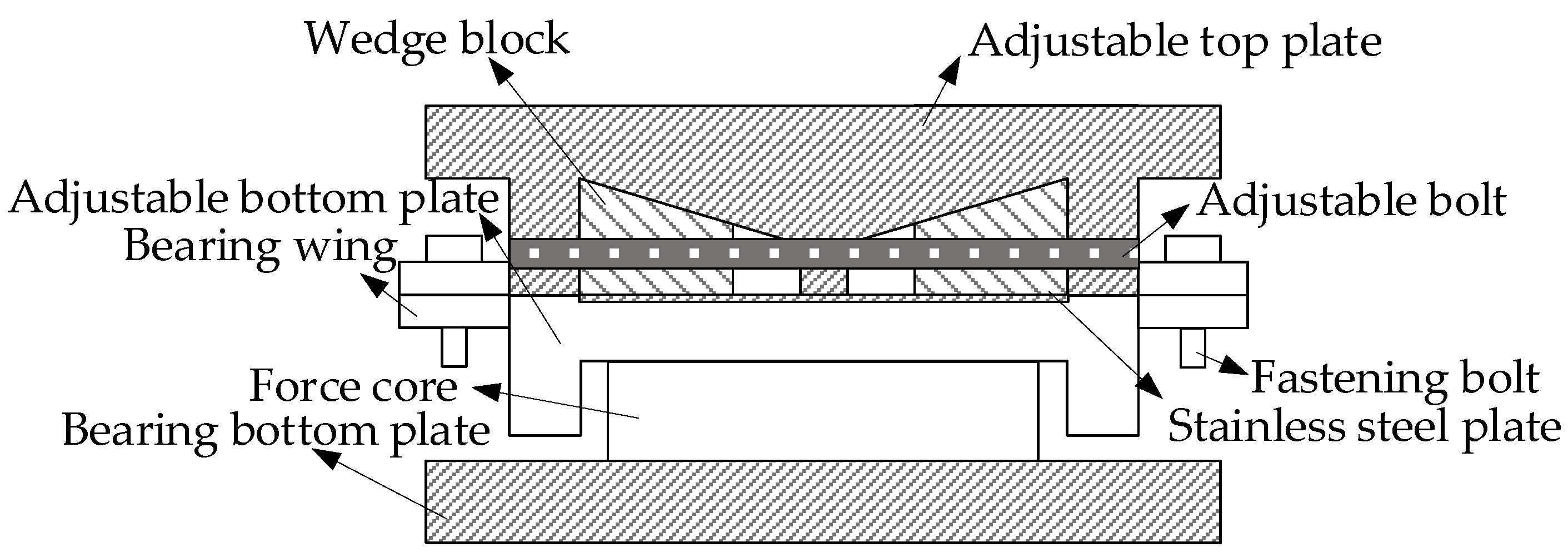
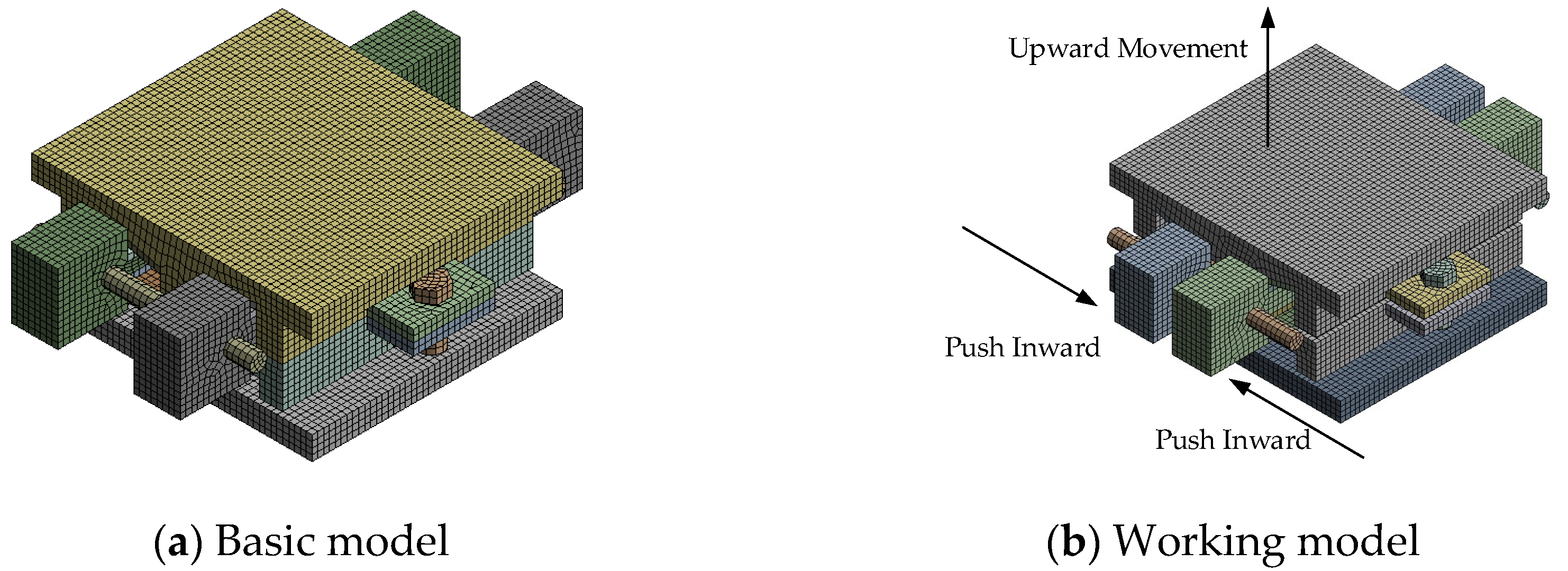
3.1. Structural Design
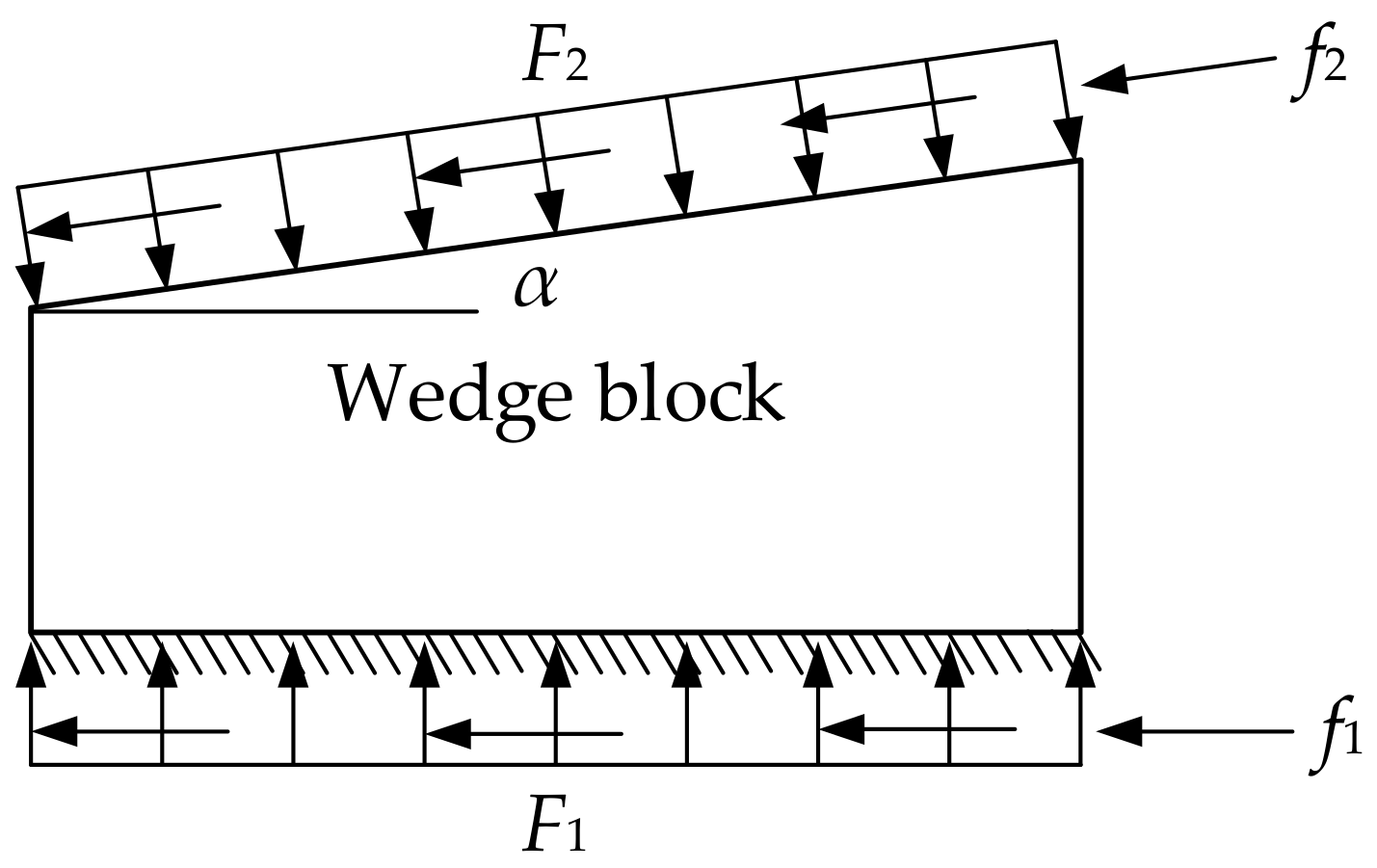
3.2. Theoretical Formula Derivation
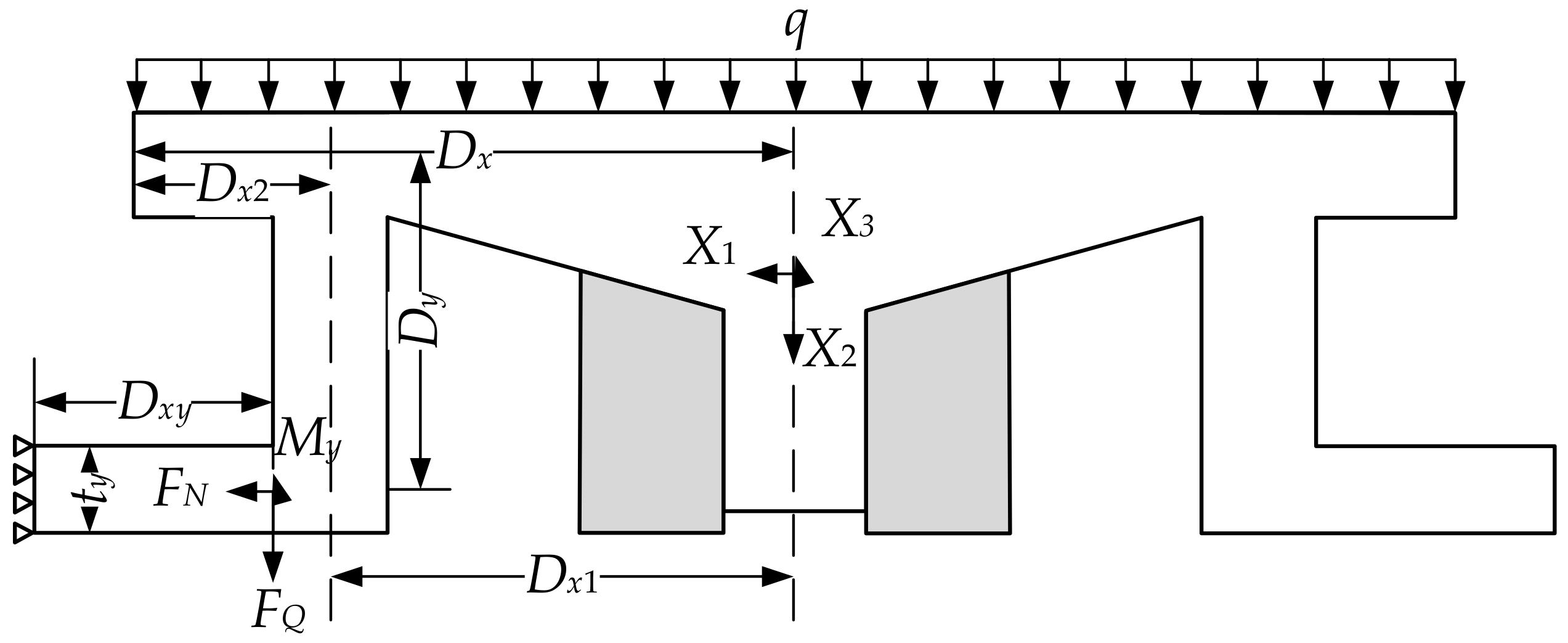
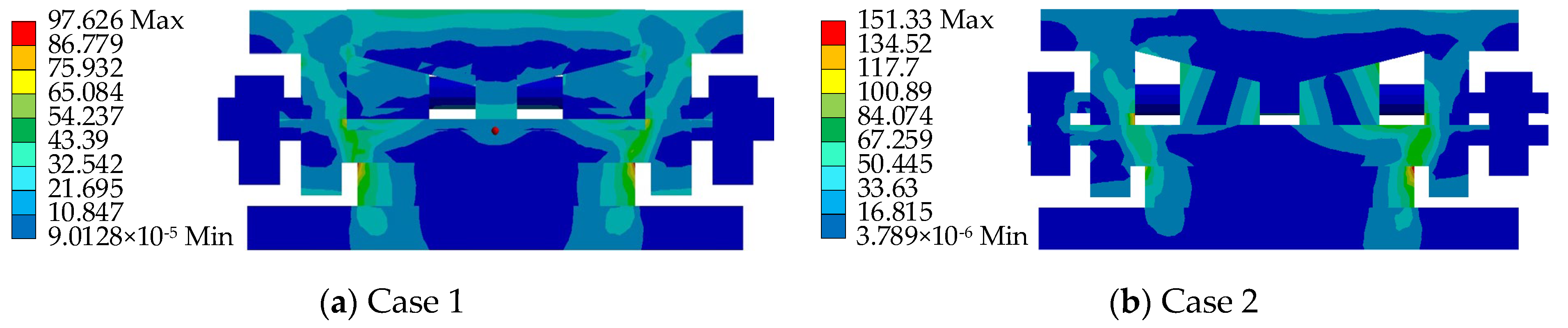
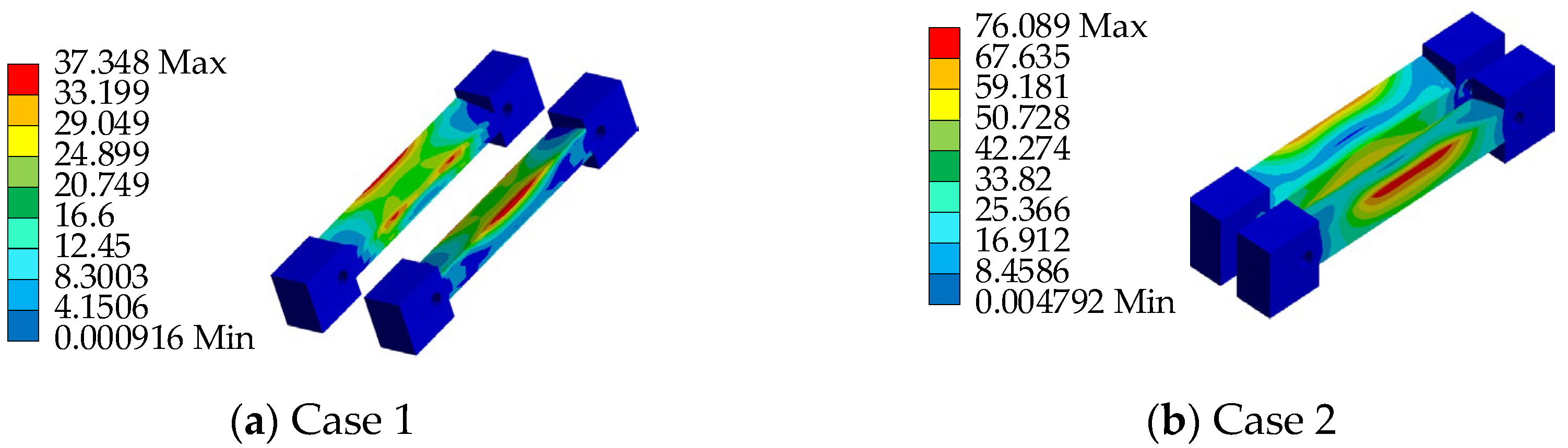
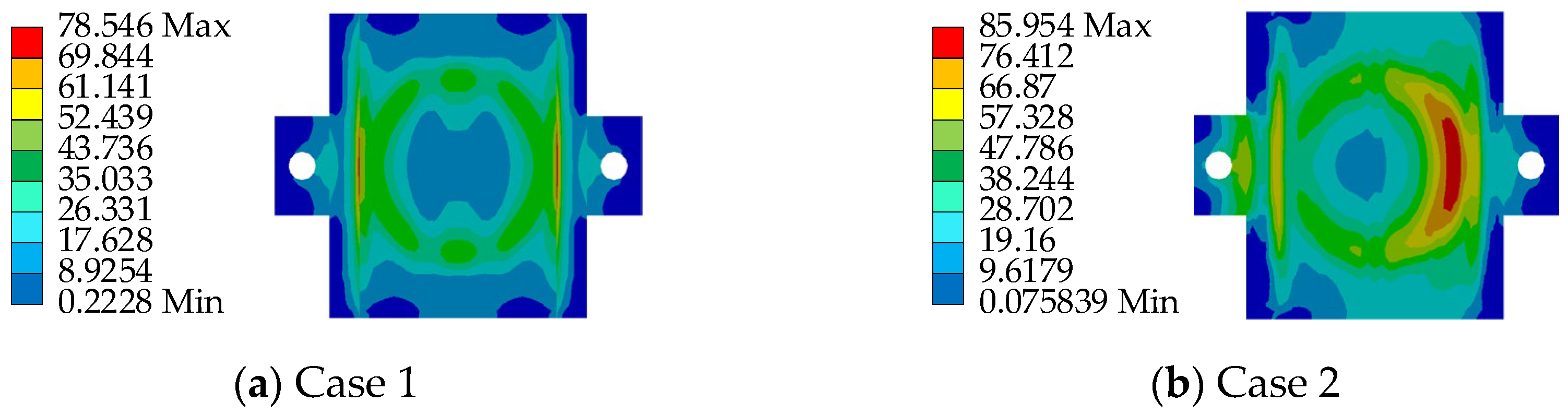
3.3. Ultimate Strength Analysis
4. Field Application of AIFMB in Bridge Monitoring
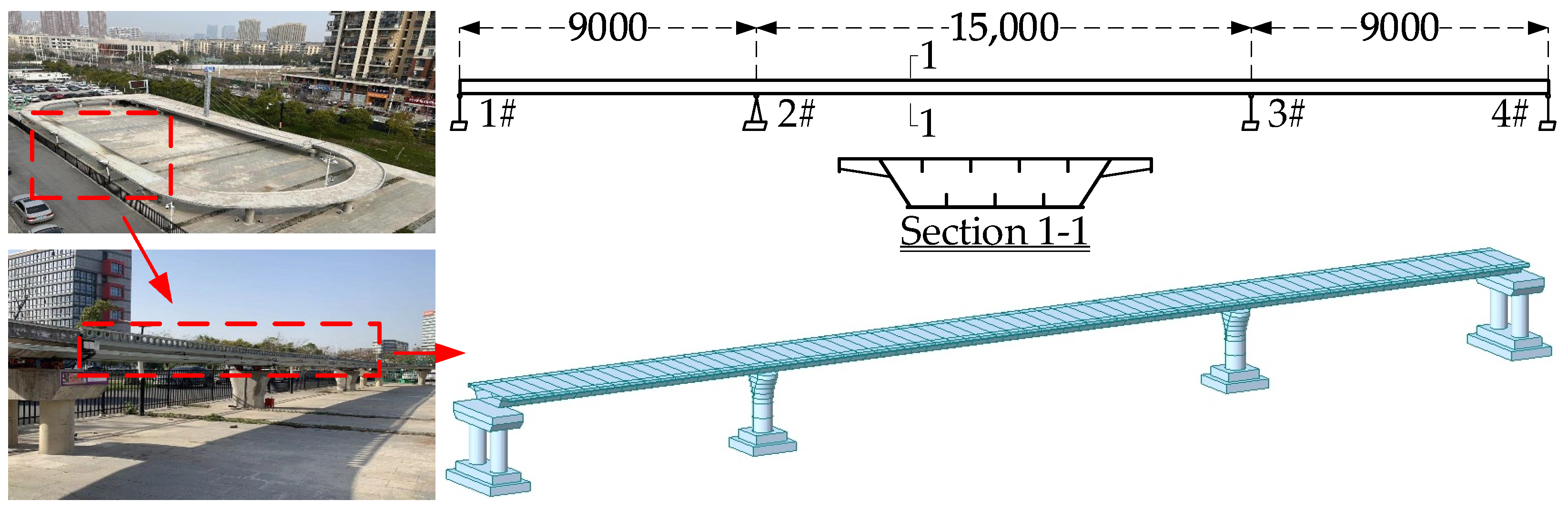
4.1. Bridge Profile
4.2. Experimental Condition
4.3. Application Result Analysis
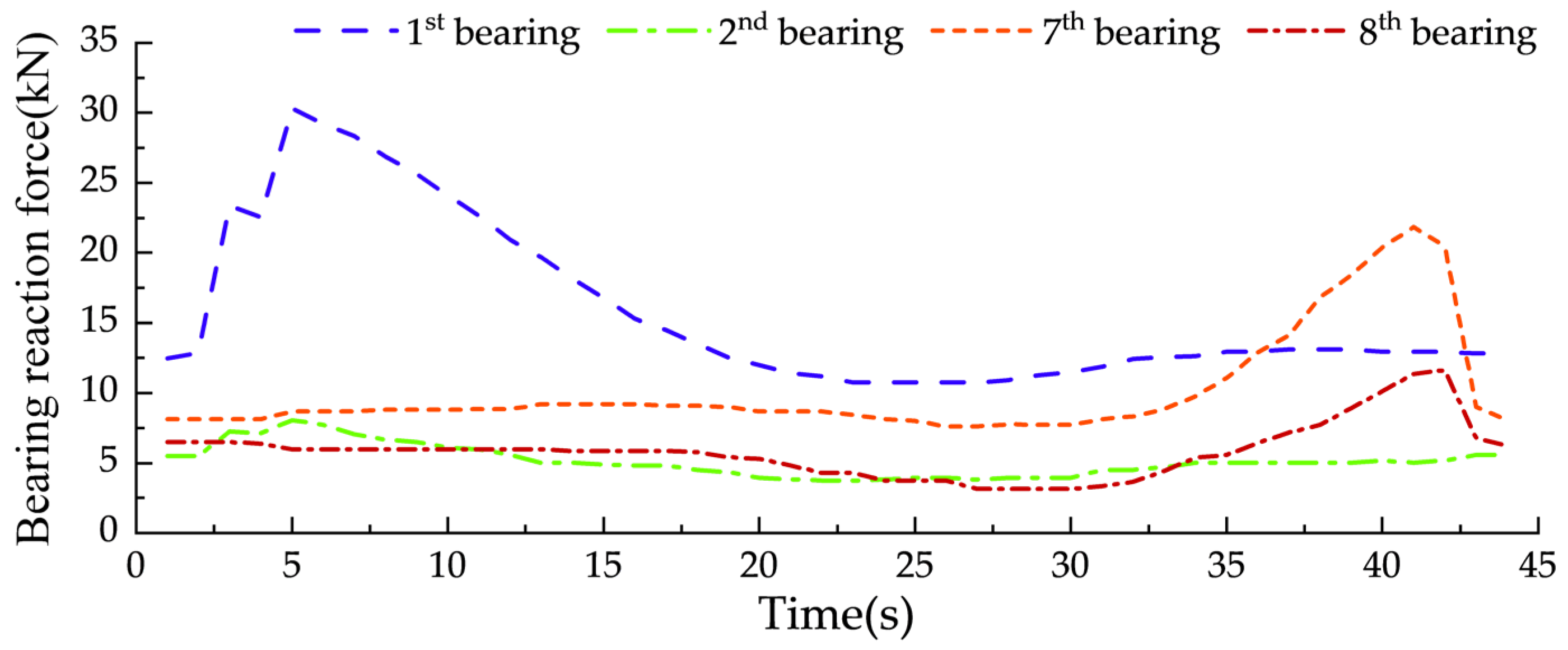
4.3.1. Force Measurement Result
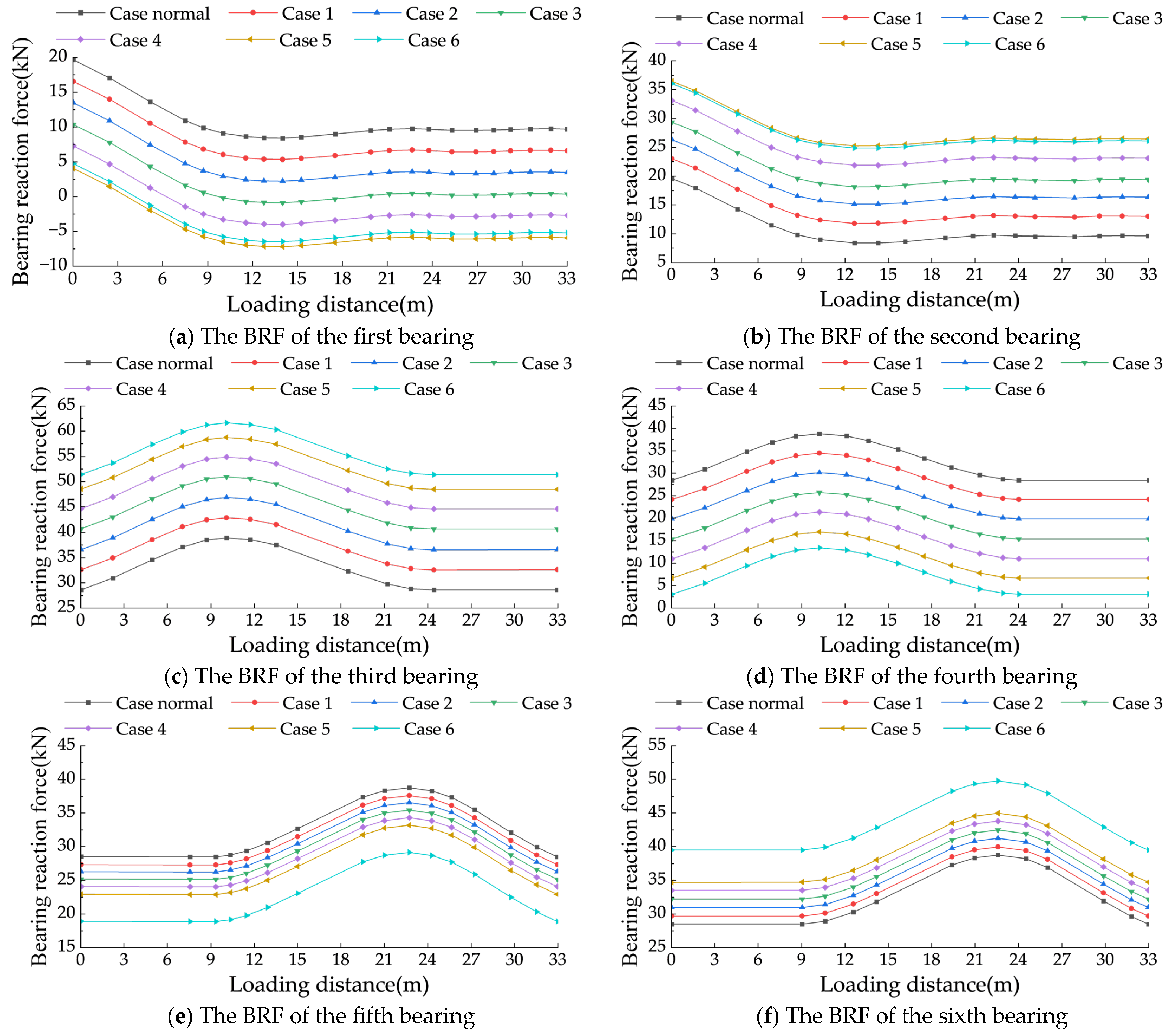
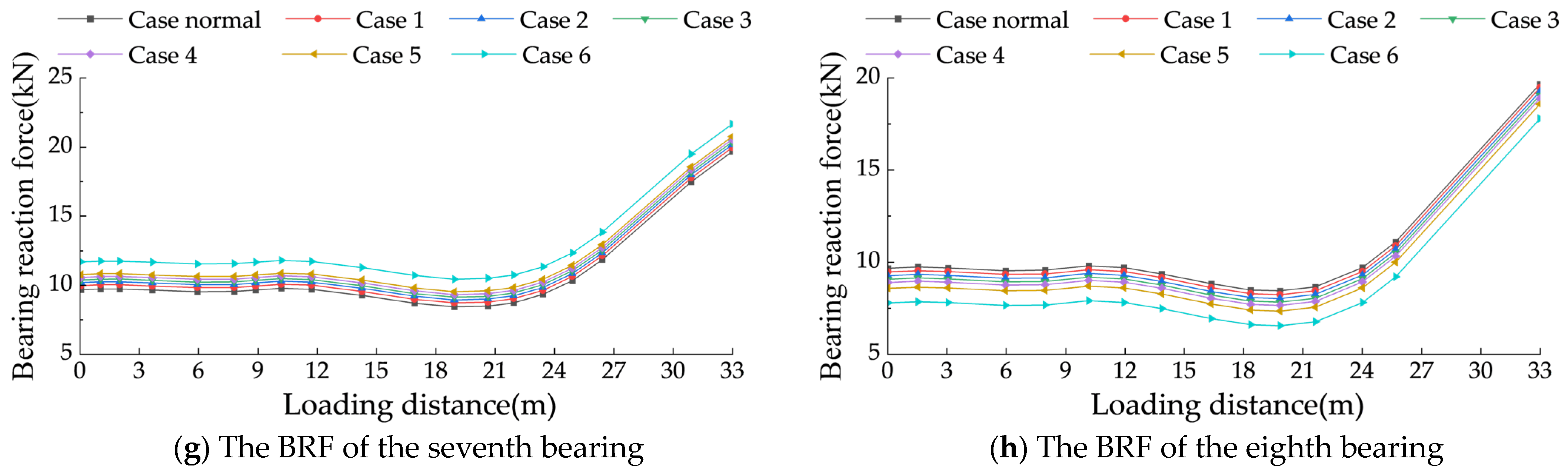
4.3.2. Height Adjustment Results
5. Discussion
- Future research could combine real-time eigen perturbation techniques by introducing vibration modal parameter analysis. This method would improve the ability of the device to detect changes in bridge stiffness. Adding modal parameter changes to bearing reaction force data would enable the monitoring of both global and local risks. This approach can help address the current lack of an overall health assessment.
- The AIFMB now uses bearing reaction forces as the only monitoring parameter. This approach makes it hard to identify multiple risk sources under complex conditions. Future work could include multi-modal data, such as vibration, temperature, and displacement. This combination of data will improve adaptability and accuracy when analyzing risks in complex scenarios.
- To improve early warnings for instability and potential risks, new prediction modules based on historical reaction forces and modal data should be developed. Computer vision and deep learning can be used to analyze historical data and predict long-term changes in bridge performance. This method would improve the overall monitoring and prediction abilities of the device.
6. Conclusions
- The derived relationships between lifting force-vertical force and horizontal displacement-vertical displacement validate the feasibility of the AIFMB structure. Under the design load, the stresses of each component remain within reasonable strength design limits under adverse conditions. This indicates that the new bearing design has an effective structure and accurate parameter selection.
- The AIFMB accurately measures the changes in bearing reaction force caused by the test vehicle and sensitively detects the instantaneous impacts. This verifies that its sensitivity in force measurement meets the requirements for vehicle speed and axle spacing identification. This new bearing can monitor abnormal bearing reactions in real time, ensuring the safe operation of the bridge.
- The moving load is sensitive to the settlement of the bridge piers, and the reaction force at the mid-span bearing is significantly affected by the settlement. After the AIFMB is raised, the reaction force of the bridge bearings approaches normal values, leading to safer and more reasonable stress distribution in the bridge. The AIFMB effectively addresses the issue of bridge pier settlement.
- Future work could enhance the device by integrating real-time eigen perturbation techniques to improve its sensitivity to bridge stiffness changes. Combining modal parameter analysis with bearing reaction force data could improve the monitoring of both global and local risks. This approach would help address current limitations in comprehensive health assessments.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rizzo, P.; Enshaeian, A. Challenges in Bridge Health Monitoring: A Review. Sensors 2021, 21, 4336. [Google Scholar] [CrossRef] [PubMed]
- Vijayan, D.S.; Sivasuriyan, A.; Devarajan, P.; Krejsa, M.; Chalecki, M.; Zóltowski, M.; Kozarzewska, A.; Koda, E. Development of Intelligent Technologies in SHM on the Innovative Diagnosis in Civil Engineering-A Comprehensive Review. Buildings 2023, 13, 1903. [Google Scholar] [CrossRef]
- Bhowmik, B. Advancements in online modal identification: A recursive simultaneous diagonalization comprehensive framework for real-time applications. Eng. Struct. 2024, 305, 117770. [Google Scholar] [CrossRef]
- Tripura, T.; Panda, S.; Hazra, B.; Chakraborty, S. Data-driven discovery of interpretable Lagrangian of stochastically excited dynamical systems. Comput. Method Appl. M. 2024, 427, 117032. [Google Scholar] [CrossRef]
- Zhou, J.T.; Li, X.G.; Xia, R.C.; Yang, J.; Zhang, H. Health Monitoring and Evaluation of Long-Span Bridges Based on Sensing and Data Analysis: A Survey. Sensors 2017, 17, 603. [Google Scholar] [CrossRef]
- Vafaei, M.; Alih, S.C. An Ideal strain gage placement plan for structural health monitoring under seismic loadings. Earthq. Struct. 2015, 8, 541–553. [Google Scholar] [CrossRef]
- Capova, K.; Velebil, L.; Vcelak, J. Laboratory and In-Situ Testing of Integrated FBG Sensors for SHM for Concrete and Timber Structures. Sensors 2020, 20, 1661. [Google Scholar] [CrossRef]
- Helmi, K.; Taylor, T.; Zarafshan, A.; Ansari, F. Reference free method for real time monitoring of bridge deflections. Eng. Struct. 2015, 103, 116–124. [Google Scholar] [CrossRef]
- Bing, X.; Yang, W.N.; Yang, X. Research on Bridge Deflection Linear Data Monitoring Based on Tilt Sensor. J. Nanoelectron. Optoelectron. 2017, 12, 1406–1411. [Google Scholar] [CrossRef]
- Peng, W.B.; Zhu, Z.X.; Li, C.H.; Shen, Z.N.; Taciroglu, E. Modified Method for Accurate Evaluation of Overturning Limit on Restrainer-Reinforced Single-Column Pier Bridges. J. Bridge Eng. 2024, 29, 04024067. [Google Scholar] [CrossRef]
- Chang, S.P.; Yee, J.; Lee, J. Necessity of the bridge health monitoring system to mitigate natural and man-made disasters. Struct. Infrastruct. Eng. 2009, 5, 173–197. [Google Scholar] [CrossRef]
- Feng, K.; Casero, M.; Gonzalez, A. Characterization of the road profile and the rotational stiffness of supports in a bridge based on axle accelerations of a crossing vehicle. Comput.-Aided. Civ. Inf. 2023, 38, 1935–1954. [Google Scholar] [CrossRef]
- Gonzalez, A.; Feng, K.; Casero, M. The Use of the Forced Frequency of a Bridge Due to a Truck Fleet for Estimating Stiffness Losses at Low Speed. Appl. Sci. 2022, 12, 11380. [Google Scholar] [CrossRef]
- Almutairi, M.; Nikitas, N.; Abdeljaber, O.; Avci, O.; Bocian, M. A methodological approach towards evaluating structural damage severity using 1D CNNs. Structures 2021, 34, 4435–4446. [Google Scholar] [CrossRef]
- Gong, X.Y.; Song, X.D.; Cai, C.S.; Li, G.Q.; Xiong, W. Early warning for abnormal strains of continuous bridges using a proposed temperature-strain mapping model. Smart Mater. Struct. 2011, 7, 597–611. [Google Scholar] [CrossRef]
- Deng, N.C.; Yu, M.S.; Yao, X.Y. Intelligent Active Correction Technology and Application of Tower Displacement in Arch Bridge Cable Lifting Construction. Appl. Sci. 2021, 11, 9808. [Google Scholar] [CrossRef]
- Han, W.; Wu, J.; Cai, C.S.; Chen, S. Characteristics and dynamic impact of overloaded extra heavy trucks on typical highway bridges. J. Bridge Eng. 2015, 20, 05014011. [Google Scholar] [CrossRef]
- Dan, D.H.; Yu, X.W.; Yan, X.F.; Zhang, K.L. Monitoring and Evaluation of Overturning Resistance of Box Girder Bridges Based on Time-Varying Reliability Analysis. J. Perform. Constr. Facil. 2020, 34, 04019101. [Google Scholar] [CrossRef]
- Ghahremani, B.; Enshaeian, A.; Rizzo, P. Bridge Health Monitoring Using Strain Data and High-Fidelity Finite Element Analysis. Sensors 2022, 22, 5172. [Google Scholar] [CrossRef]
- Martinez, D.; Malekjafarian, A.; OBrien, E. Bridge health monitoring using deflection measurements under random traffic. Struct. Control. Health 2020, 27, e2593. [Google Scholar] [CrossRef]
- Tang, D.N.; Huang, M.S. The Sustainable Development of Bridges in China: Collapse Cause Analysis, Existing Management Dilemmas and Potential Solutions. Buildings 2024, 14, 419. [Google Scholar] [CrossRef]
- Xiong, W.; Cai, C.S.; Kong, B.; Ye, J.S. Overturning-Collapse Modeling and Safety Assessment for Bridges Supported by Single-Column Piers. J. Bridge Eng. 2017, 22, 04017084. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Y.D. Study on the Safety of Bridge Structure. Appl. Mech. Mater. 2013, 340, 59–63. [Google Scholar] [CrossRef]
- Luo, X. Research on anti-overturning performance of multi-span curved girder bridge with small radius. Acta Mech. Malays. 2018, 2, 4–7. [Google Scholar]
- Shi, X.F.; Cao, Z.; Ma, H.Y.; Ruan, X. Failure Analysis on a Curved Girder Bridge Collapse under Eccentric Heavy Vehicles Using Explicit Finite Element Method: Case Study. J. Bridge Eng. 2018, 23, 05018001. [Google Scholar] [CrossRef]
- Hirt, M.; Lebet, J.P. Steel Bridges: Conceptual and Structural Design of Steel and Steelconcrete Composite Bridges; EPFL Press: Lausanne, Switzerland, 2013. [Google Scholar]
- Shi, X.; Zhou, Z.; Ruan, X. Failure analysis of a girder bridge collapse under eccentric heavy vehicles. J. Bridge Eng. 2016, 21, 05016009. [Google Scholar] [CrossRef]
- Peng, W.; Zhao, H.; Dai, F.; Taciroglu, E. Analytical method for overturning limit analysis of single-column pier bridges. J. Perform. Constr. Facil. 2017, 31, 04017007. [Google Scholar] [CrossRef]
- Li, S.; Gan, L.Y.; Zhao, R.A.; Wang, S.A.; Zhou, Y. Research on Bridge Integrity Assessment and Early Warning Monitoring Methods Based on Bearing Reaction Force. Buildings 2024, 14, 763. [Google Scholar] [CrossRef]
- Sengsri, P.; Kaewunruen, S. Influences of Flood Conditions on Dynamic Characteristics of Novel 3D-Printed Porous Bridge Bearings. Materials 2023, 16, 2288. [Google Scholar] [CrossRef]
- Ma, F.B.; Wang, H.C.; Cheng, X.X.; Feng, D.M.; Wu, G.; Hou, S.T. Experimental investigation and application evaluation case of an adjustable height temporary support for bearing replacement in large-tonnage HSR Bridges. J. Bridge Eng. 2022, 27, 05022003. [Google Scholar] [CrossRef]
- Jing, D.H.; Cao, S.Y.; Krevaikas, T.; Bian, J. A self-locking steel bearing connection for circular reinforced concrete columns. Adv. Struct. Eng. 2019, 22, 2605–2619. [Google Scholar] [CrossRef]
- Huang, P.; Yang, Q.Q. Theory and contents of frictional mechanics. Friction 2014, 2, 27–39. [Google Scholar] [CrossRef]






| Date | Location | Accident | Consequence |
|---|---|---|---|
| 23 October 2007 | Minzu East Road Viaduct, Baotou City, Nei Mongol, China | Main girder of the viaduct suddenly overturned [21] | Many people were injured |
| 15 July 2009 | Shanxi-Tianjin Expressway, Tianjin City, China | Ramp bridge A overturned [21] | 6 dead and 4 injured |
| 26 November 2010 | Rapid Inner Ring West Line, Nanjing City, Jiangsu, China | Side tumbling of steel box beam [18] | 7 dead and 3 injured |
| 21 February 2011 | Chunhui Interchange, Shangyu City, Zhejiang, China | On-ramp collapsed [22] | 3 injured |
| 24 August 2012 | Qunli Viaduct, Harbin City, Heilongjiang, China | Overall overturning of approach bridge box girder [23] | 3 dead and 5 injured |
| 19 June 2015 | Guangdong-Jiangxi Expressway, Heyuan City, Guangdong, China | Ramp bridge collapsed [24] | 1 dead and 4 injured |
| 23 May 2016 | Center Line Viaduct, Shanghai City, China | Damage on bridge surface [25] | No casualties |
| Category | Elasticity Modulus | Poisson Ratio | Size (mm) | Thickness (mm) |
|---|---|---|---|---|
| Adjustable top plate | 2.1 × 105 MPa | 0.3 | 240 × 215 | 20 |
| Adjustable bottom plate | 190 × 215 | 20 | ||
| Wedge block | 40 × 215 | 10–20 | ||
| Adjustable bolt | R20 | \ |
| Loading Conditions | Detail | Vertical Load (kN) | Horizontal Load (kN) |
|---|---|---|---|
| Case 1 | Basic model | 300 | 30 |
| Case 2 | Working model | 300 | 30 |
| Conditions | Detail | Height Adjustment Position | Height Adjustment Degree |
|---|---|---|---|
| Case normal | Force measurement | / | / |
| Case 1 | Height adjustment | Fourth bearing | 0.2 mm |
| Case 2 | 0.4 mm | ||
| Case 3 | 0.6 mm | ||
| Case 4 | 0.8 mm | ||
| Case 5 | 1.0 mm | ||
| Case 6 | 1.2 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Zhang, Z.; Gan, L.; Yin, J.; Fu, M. Design and Monitoring Application of an Adjustable Intelligent Bearing Based on Pressure Sensing. Sensors 2024, 24, 7820. https://doi.org/10.3390/s24237820
Li S, Zhang Z, Gan L, Yin J, Fu M. Design and Monitoring Application of an Adjustable Intelligent Bearing Based on Pressure Sensing. Sensors. 2024; 24(23):7820. https://doi.org/10.3390/s24237820
Chicago/Turabian StyleLi, Shu, Zaiyu Zhang, Luyi Gan, Jiheng Yin, and Ming Fu. 2024. "Design and Monitoring Application of an Adjustable Intelligent Bearing Based on Pressure Sensing" Sensors 24, no. 23: 7820. https://doi.org/10.3390/s24237820
APA StyleLi, S., Zhang, Z., Gan, L., Yin, J., & Fu, M. (2024). Design and Monitoring Application of an Adjustable Intelligent Bearing Based on Pressure Sensing. Sensors, 24(23), 7820. https://doi.org/10.3390/s24237820







