A High-Precision Real-Time Temperature Acquisition Method Based on Magnetic Nanoparticles
Abstract
1. Introduction
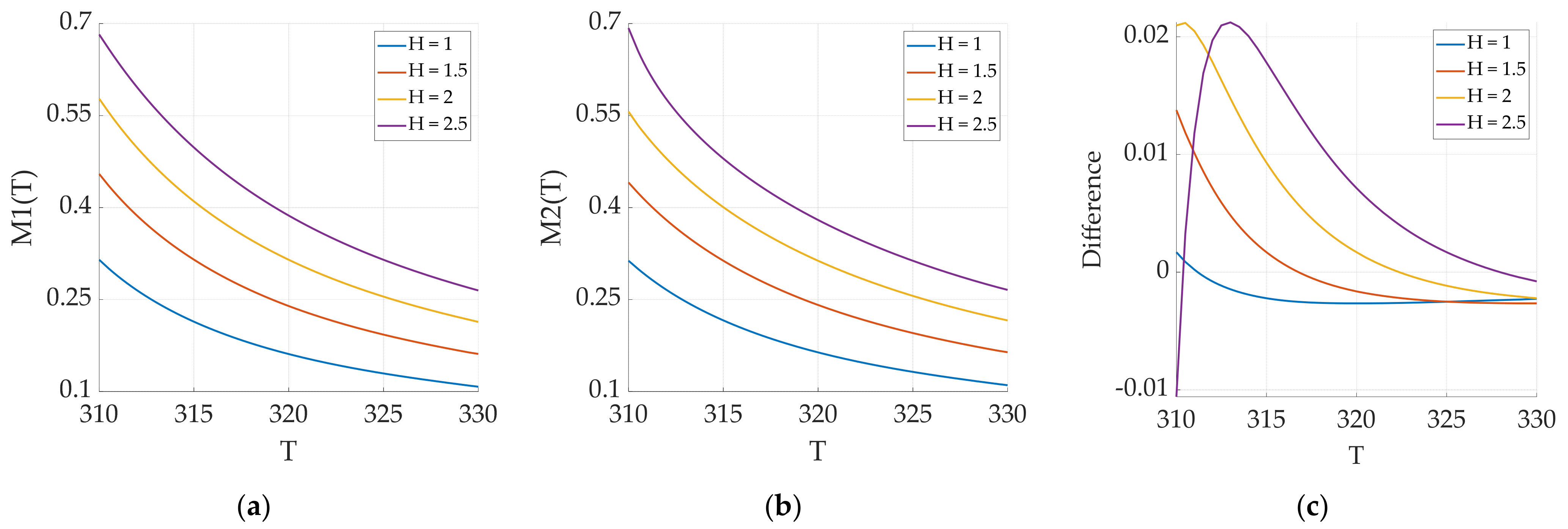
2. Theory and Modeling
3. Methods
3.1. Excitation in Different Magnetic Fields
3.1.1. Low-Frequency AC Magnetic Field Excitation
3.1.2. AC‒DC Superposition Magnetic Field Excitation
3.1.3. Dual-Frequency Superposition Magnetic Field Excitation
3.2. Error Analysis
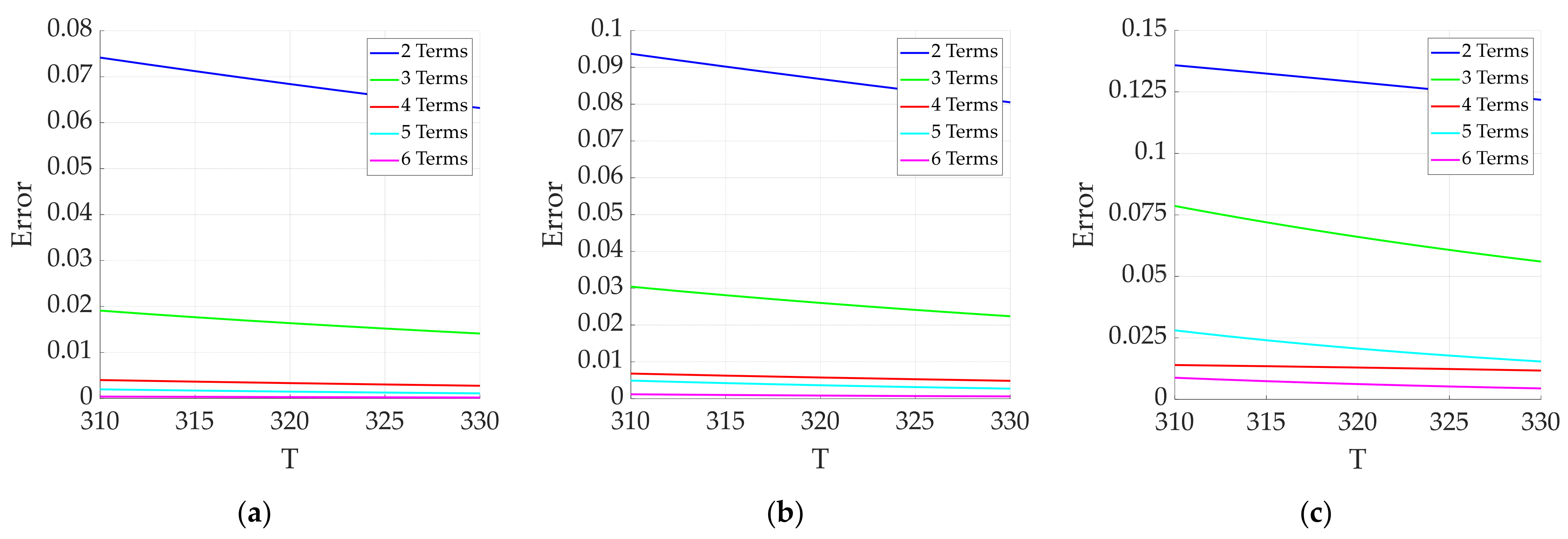
3.2.1. Effect of Truncation Error
3.2.2. Effect of the Excitation Frequency
3.2.3. Effect of Excitation Magnetic Field Amplitude
4. Results
4.1. System Simulation
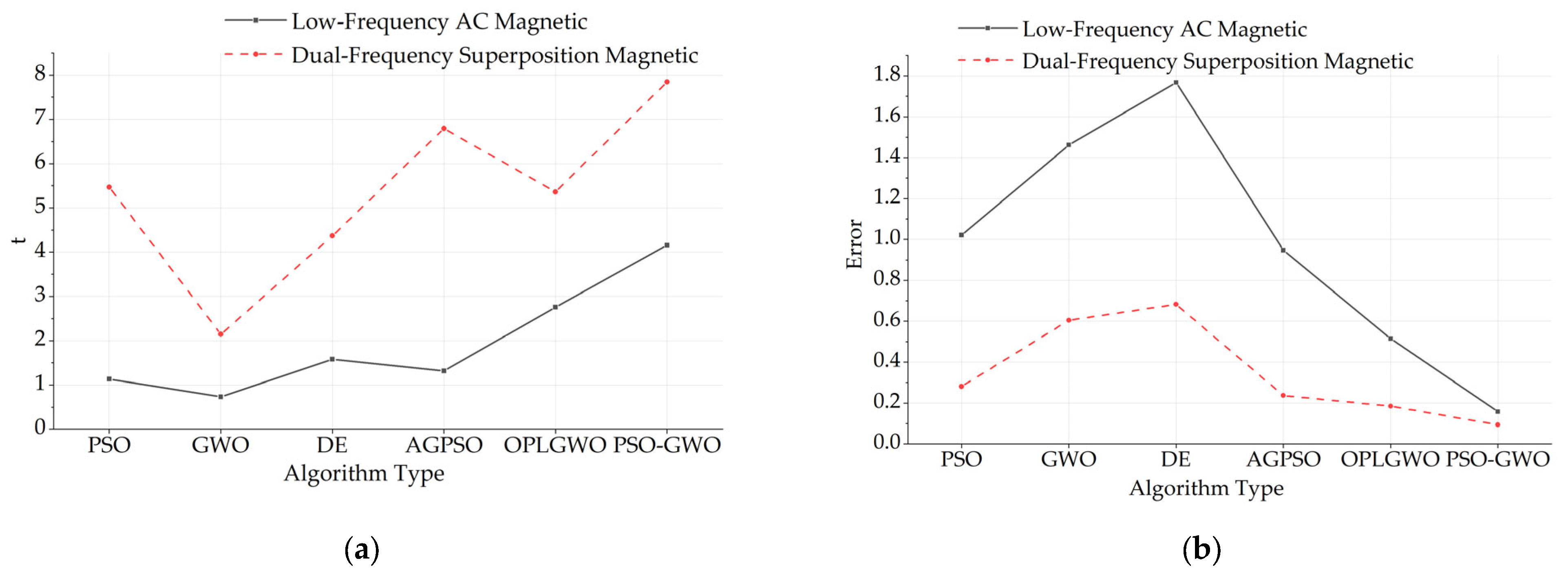
4.2. Temperature Inversion Algorithm
4.3. Data Acquisition and Inversion Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, P.M.; Pan, W.Y.; Wu, C.Y.; Yeh, C.Y.; Korupalli, C.; Luo, P.K.; Chou, C.J.; Chia, W.T.; Sung, H.W. Modulation of tumor microenvironment using a TLR-7/8 agonist-loaded nanoparticle system that exerts low-temperature hyperthermia and immunotherapy for in situ cancer vaccination. Biomaterials 2020, 230, 119629. [Google Scholar] [CrossRef] [PubMed]
- Habash, R.W.; Bansal, R.; Krewski, D.; Alhafid, H.T. Thermal therapy, Part III: Ablation techniques. Crit. Rev. Biomed. Eng. 2007, 35, 37–121. [Google Scholar] [CrossRef] [PubMed]
- Moroz, P.; Jones, S.K.; Gray, B.N. Status of hyperthermia in the treatment of advanced liver cancer. J. Surg. Oncol. 2001, 77, 259–269. [Google Scholar] [CrossRef] [PubMed]
- Marelli, G.; Sica, A.; Vannucci, L.; Allavena, P. Inflammation as target in cancer therapy. Curr. Opin. Pharmacol. 2017, 35, 57–65. [Google Scholar] [CrossRef]
- Rosenberg, H.; Pollock, N.; Schiemann, A.; Bulger, T.; Stowell, K. Malignant hyperthermia: A review. Orphanet J. Rare Dis. 2015, 10, 93. [Google Scholar] [CrossRef]
- Kobayashi, T. Cancer hyperthermia using magnetic nanoparticles. Biotechnol. J. 2011, 6, 1342–1347. [Google Scholar] [CrossRef]
- Hilger, I.; Hiergeist, R.; Hergt, R.; Winnefeld, K.; Schubert, H.; Kaiser, W.A. Thermal Ablation of Tumors Using Magnetic Nanoparticles: An In Vivo Feasibility Study. Investig. Radiol. 2002, 37, 580–586. [Google Scholar] [CrossRef]
- Datta, N.R.; Puric, E.; Klingbiel, D.; Gomez, S.; Bodis, S. Hyperthermia and Radiation Therapy in Locoregional Recurrent Breast Cancers: A Systematic Review and Meta-analysis. Int. J. Radiat. Oncol. Biol. Phys. 2016, 94, 1073–1087. [Google Scholar] [CrossRef]
- Gota, C.; Okabe, K.; Funatsu, T.; Harada, Y.; Uchiyama, S. Hydrophilic fluorescent nanogel thermometer for intracellular thermometry. J. Am. Chem. Soc. 2009, 131, 2766–2767. [Google Scholar] [CrossRef]
- Wust, P.; Hildebrandt, B.; Sreenivasa, G.; Rau, B.; Gellermann, J.; Riess, H.; Felix, R.; Schlag, P.M. Hyperthermia in combined treatment of cancer. Lancet Oncol. 2002, 3, 487–497. [Google Scholar] [CrossRef]
- Espinosa, A.; Di Corato, R.; Kolosnjaj-Tabi, J.; Flaud, P.; Pellegrino, T.; Wilhelm, C. Duality of Iron Oxide Nanoparticles in Cancer Therapy: Amplification of Heating Efficiency by Magnetic Hyperthermia and Photothermal Bimodal Treatment. ACS Nano 2016, 10, 2436–2446. [Google Scholar] [CrossRef] [PubMed]
- Obaidat, I.M.; Issa, B.; Haik, Y. Magnetic Properties of Magnetic Nanoparticles for Efficient Hyperthermia. Nanomaterials 2015, 5, 63–89. [Google Scholar] [CrossRef] [PubMed]
- Neumann, P.; Jakobi, I.; Dolde, F.; Burk, C.; Reuter, R.; Waldherr, G.; Honert, J.; Wolf, T.; Brunner, A.; Shim, J.H. High-precision nanoscale temperature sensing using single defects in diamond. Nano Lett. 2013, 13, 2738–2742. [Google Scholar] [CrossRef] [PubMed]
- Toyli, D.M.; de las Casas, C.F.; Christle, D.J.; Dobrovitski, V.V.; Awschalom, D.D. Fluorescence thermometry enhanced by the quantum coherence of single spins in diamond. Proc. Natl. Acad. Sci. USA 2013, 110, 8417–8421. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Wu, L.-W.; Cao, W.; Huang, Y.-F. Finding a Sensitive Surface-Enhanced Raman Spectroscopic Thermometer at the Nanoscale by Examining the Functional Groups. Anal. Chem. 2022, 94, 6011–6016. [Google Scholar] [CrossRef]
- Li, G.; Xue, Y.; Mao, Q.; Pei, L.; He, H.; Liu, M.; Chu, L.; Zhong, J. Synergistic luminescent thermometer using co-doped Ca2GdSbO6:Mn4+/(Eu3+ or Sm3+) phosphors. Dalton Trans. 2022, 51, 4685–4694. [Google Scholar] [CrossRef]
- Yang, J.-M.; Yang, H.; Lin, L. Quantum dot nano thermometers reveal heterogeneous local thermogenesis in living cells. ACS Nano 2011, 5, 5067–5071. [Google Scholar] [CrossRef]
- Maestro, L.M.; Rodríguez, E.M.; Rodríguez, F.S.; la Cruz, M.C.I.-d.; Juarranz, Á.; Naccache, R.; Vetrone, F.; Jaque, D.; Capobianco, J.A.; Solé, J.G. CdSe quantum dots for two-photon fluorescence thermal imaging. Nano Lett. 2010, 10, 5109–5115. [Google Scholar] [CrossRef]
- Albahrani, S.M.B.; Seoudi, T.; Philippon, D.; Lafarge, L.; Reiss, P.; Hajjaji, H.; Guillot, G.; Querry, M.; Bluet, J.M.; Vergne, P. Quantum dots to probe temperature and pressure in highly confined liquids. RSC Adv. 2018, 8, 22897–22908. [Google Scholar] [CrossRef]
- Pankhurst, Q.A.; Connolly, J.; Jones, S.K.; Dobson, J. Applications of magnetic nanoparticles in biomedicine. J. Phys. D Appl. Phys. 2003, 36, R167–R181. [Google Scholar] [CrossRef]
- Riegler, J.; Liew, A.; Hynes, S.O.; Ortega, D.; O’Brien, T.; Day, R.M.; Richards, T.; Sharif, F.; Pankhurst, Q.A.; Lythgoe, M.F. Superparamagnetic iron oxide nanoparticle targeting of MSCs in vascular injury. Biomaterials 2013, 34, 1987–1994. [Google Scholar] [CrossRef] [PubMed]
- Mohammed, L.; Gomaa, H.; Ragab, D.M.; Zhu, J. Magnetic nanoparticles for environmental and biomedical applications: A review. Particuology 2017, 30, 1–14. [Google Scholar] [CrossRef]
- Weaver, J.B.; Rauwerdink, A.M.; Hansen, E.W. Magnetic nanoparticle temperature estimation. Med. Phys. 2009, 36, 1822–1829. [Google Scholar] [CrossRef]
- Reeves, D.B.; Weaver, J.B. Magnetic nanoparticle sensing: Decoupling the magnetization from the excitation field. J. Phys. D Appl. Phys. 2014, 47, 045002. [Google Scholar] [CrossRef]
- Zhao, Z.; Hu, F.; Cao, Z.; Chi, F.; Wei, X.; Chen, Y.; Duan, C.; Yin, M. Highly uniform and monodisperse β-NaYF4 : Sm3+ nanoparticles for a nanoscale optical thermometer. Opt. Lett. 2018, 43, 835–838. [Google Scholar] [CrossRef]
- Yan, H.; Ni, H.; Jia, J.; Shan, C.; Zhang, T.; Gong, Y.; Li, X.; Cao, J.; Wu, W.; Liu, W.; et al. Smart All-in-One Thermometer-Heater Nanoprobe Based on Postsynthetical Functionalization of a Eu(III)-Metal-Organic Framework. Anal. Chem. 2019, 91, 5225–5234. [Google Scholar] [CrossRef]
- Qu, J.; Liu, G.; Wang, Y.; Hong, R. Preparation of Fe3O4–chitosan nanoparticles used for hyperthermia. Adv. Powder Technol. 2010, 21, 461–467. [Google Scholar] [CrossRef]
- Liu, C.-F.; Leong, W.H.; Xia, K.; Feng, X.; Finkler, A.; Denisenko, A.; Wrachtrup, J.; Li, Q.; Liu, R.-B. Ultra-sensitive hybrid diamond nanothermometer. Natl. Sci. Rev. 2019, 8, nwaa194. [Google Scholar] [CrossRef]
- Bui, T.Q.; Tew, W.L.; Woods, S.I. AC magnetometry with active stabilization and harmonic suppression for magnetic nanoparticle spectroscopy and thermometry. J. Appl. Phys. 2020, 128, 224901. [Google Scholar] [CrossRef]
- Luo, Q.Y.; Zhao, S.; Hu, Q.C.; Quan, W.K.; Zhu, Z.Q.; Li, J.J.; Wang, J.F. High-sensitivity silicon carbide divacancy-based temperature sensing. Nanoscale 2023, 15, 8432–8436. [Google Scholar] [CrossRef]
- Shi, Y.; Weaver, J.B. Concurrent quantification of magnetic nanoparticles temperature and relaxation time. Med. Phys. 2019, 46, 4070–4076. [Google Scholar] [CrossRef] [PubMed]
- Zhong, J.; Liu, W.; Kong, L.; Morais, P.C. A new approach for highly accurate, remote temperature probing using magnetic nanoparticles. Sci. Rep. 2014, 4, 6338. [Google Scholar] [CrossRef] [PubMed]
- Zhong, J.; Liu, W.; Jiang, L.; Yang, M.; Morais, P.C. Real-time magnetic nanothermometry: The use of magnetization of magnetic nanoparticles assessed under low frequency triangle-wave magnetic fields. Rev. Sci. Instrum. 2014, 85, 094905. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Guo, S.; Zhang, P.; Zhong, J.; Liu, W. Iron oxide magnetic nanoparticles based low-field MR thermometry. Nanotechnology 2020, 31, 345101. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, P.; Liu, W.; Guo, S.; Zhang, Y. High-resolution magnetic nanoparticle temperature measurement method based on dual-frequency magnetic field excitation. Meas. Sci. Technol. 2021, 32, 075701. [Google Scholar] [CrossRef]
- Lak, A.; Ludwig, F.; Scholtyssek, J.; Dieckhoff, J.; Fiege, K.; Schilling, M. Size Distribution and Magnetization Optimization of Single-Core Iron Oxide Nanoparticles by Exploiting Design of Experiment Methodology. IEEE Trans. Magn. 2013, 49, 201–207. [Google Scholar] [CrossRef]
- Bogdanov, A.N. Magnetic Domains. The Analysis of Magnetic Microstructures. Low Temp. Phys. 1999, 25, 151–152. [Google Scholar] [CrossRef]
- Ludwig, F.; Eberbeck, D.; Löwa, N.; Steinhoff, U.; Wawrzik, T.; Schilling, M.; Trahms, L. Characterization of magnetic nanoparticle systems with respect to their magnetic particle imaging performance. Biomed. Tech. Biomed. Eng. 2013, 58, 535–545. [Google Scholar] [CrossRef]
- Drbohlavová, J.; Hrdy, R.; Adam, V.; Kizek, R.; Schneeweiss, O.; Hubálek, J. Preparation and Properties of Various Magnetic Nanoparticles. Sensors 2009, 9, 2352–2362. [Google Scholar] [CrossRef]
- Biederer, S.; Knopp, T.; Sattel, T.; Lüdtke-Buzug, K.; Gleich, B.; Gleich, B.; Weizenecker, J.; Borgert, J.; Buzug, T.M. Magnetization response spectroscopy of superparamagnetic nanoparticles for magnetic particle imaging. J. Phys. D Appl. Phys. 2009, 42, 205007. [Google Scholar] [CrossRef]
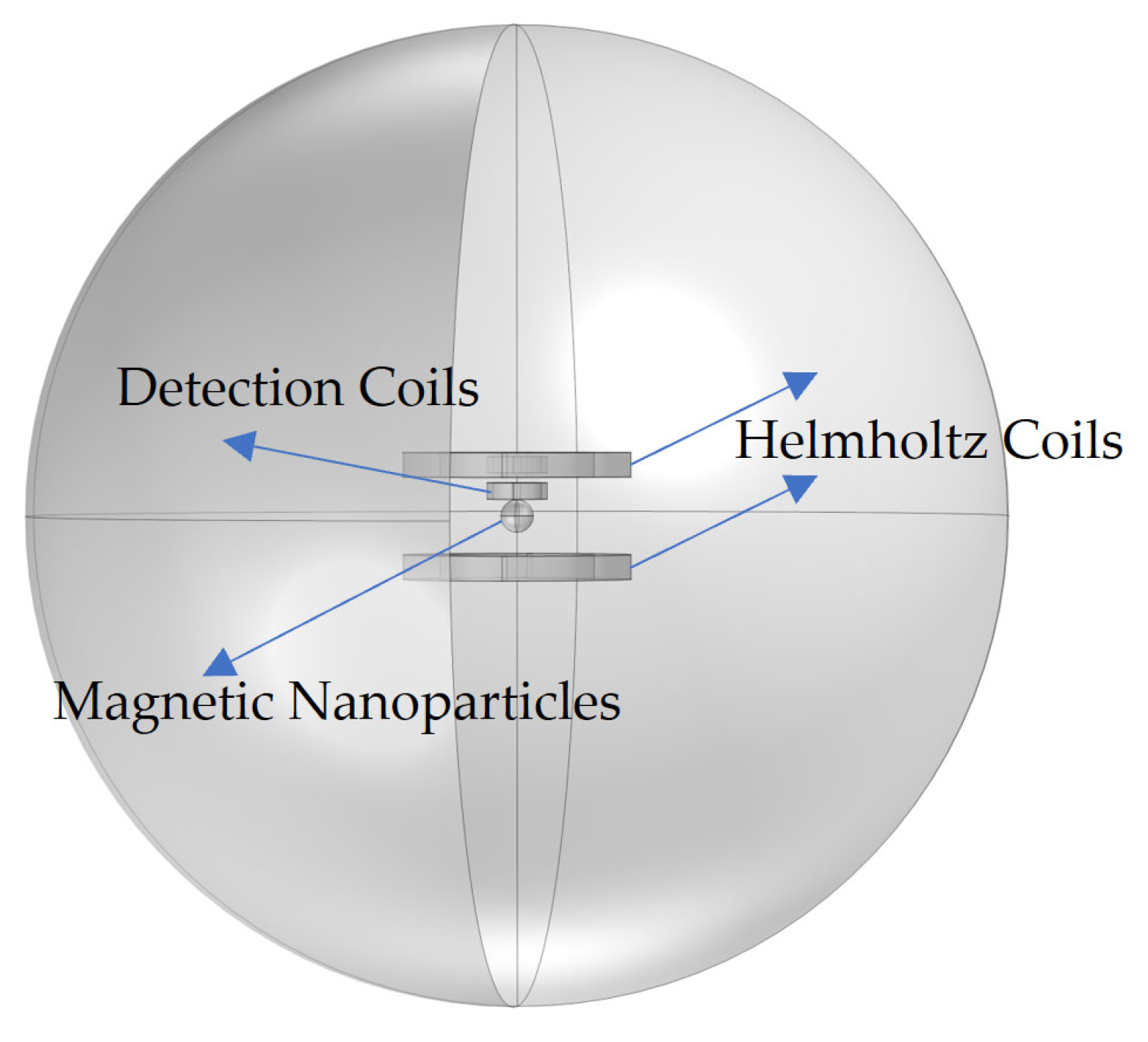


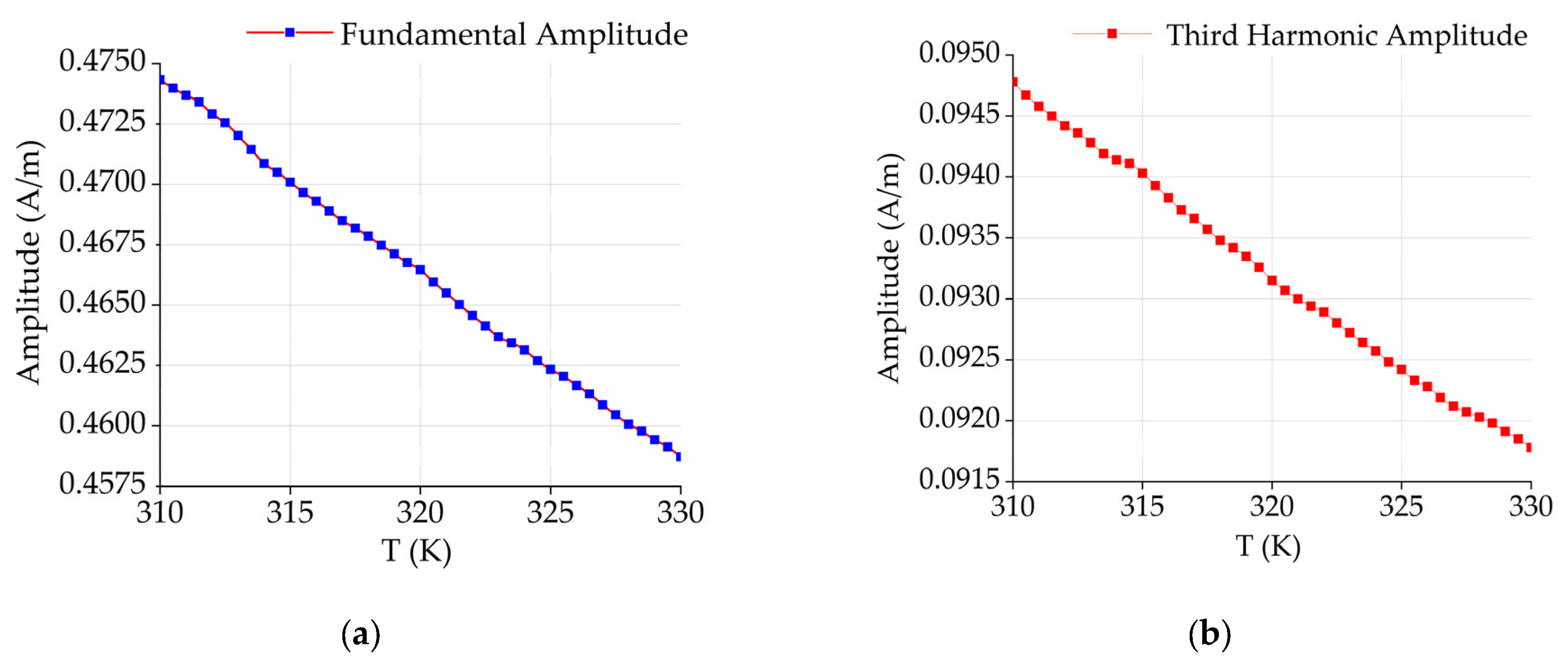
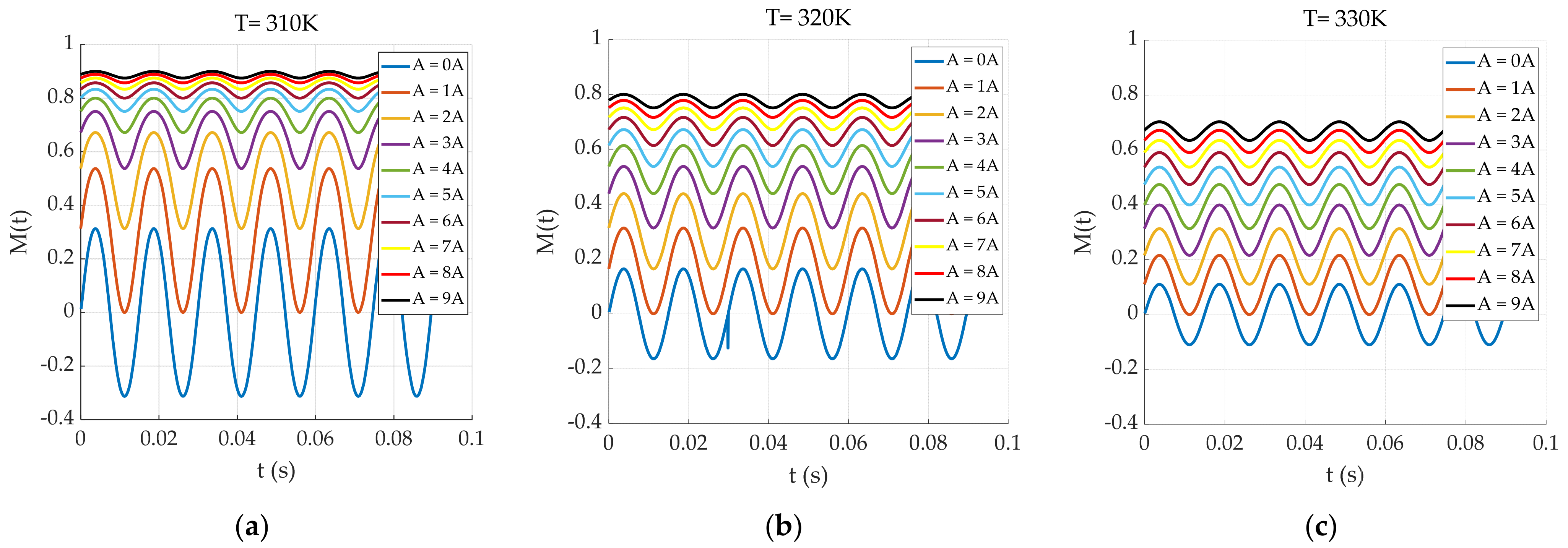
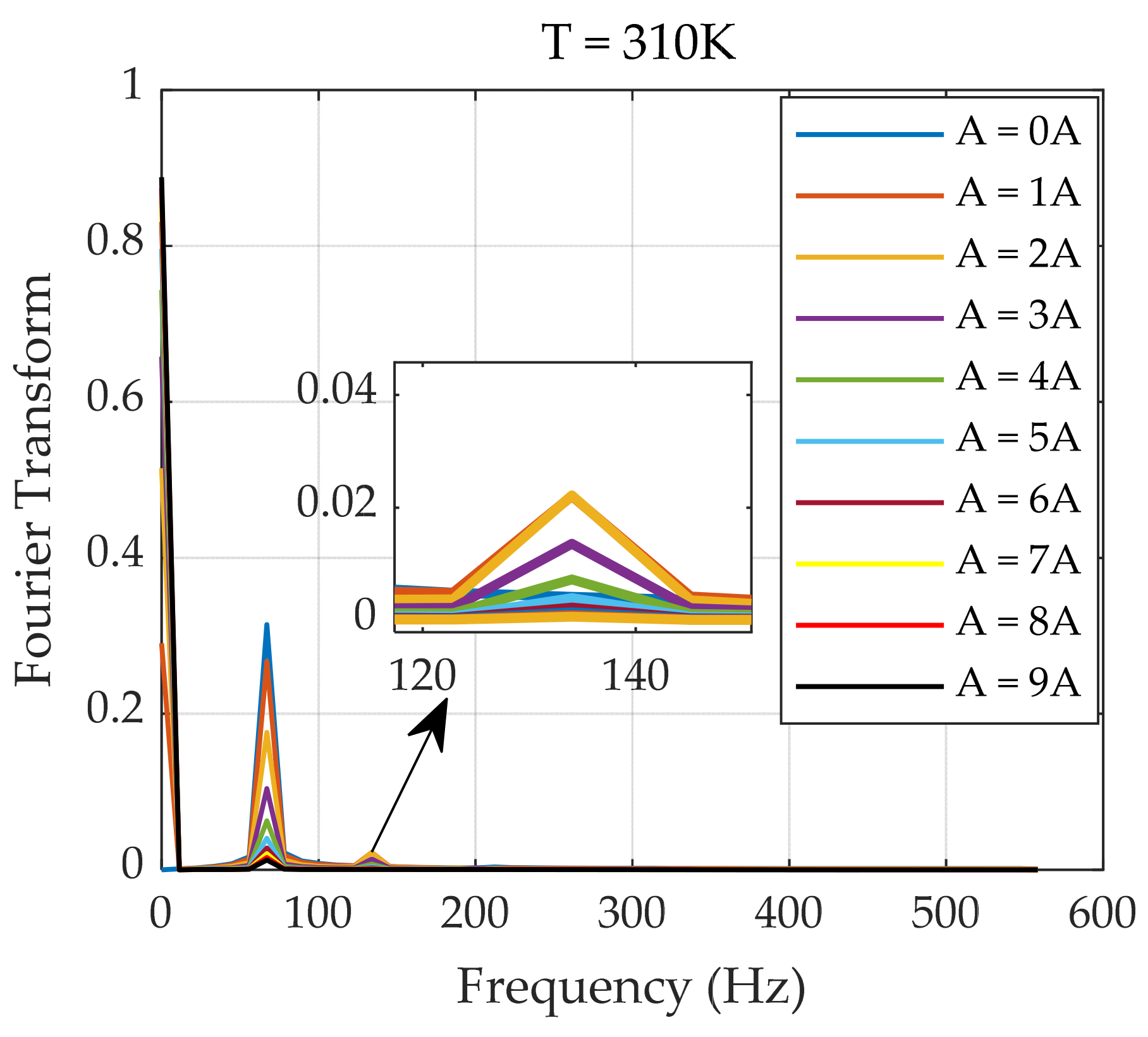
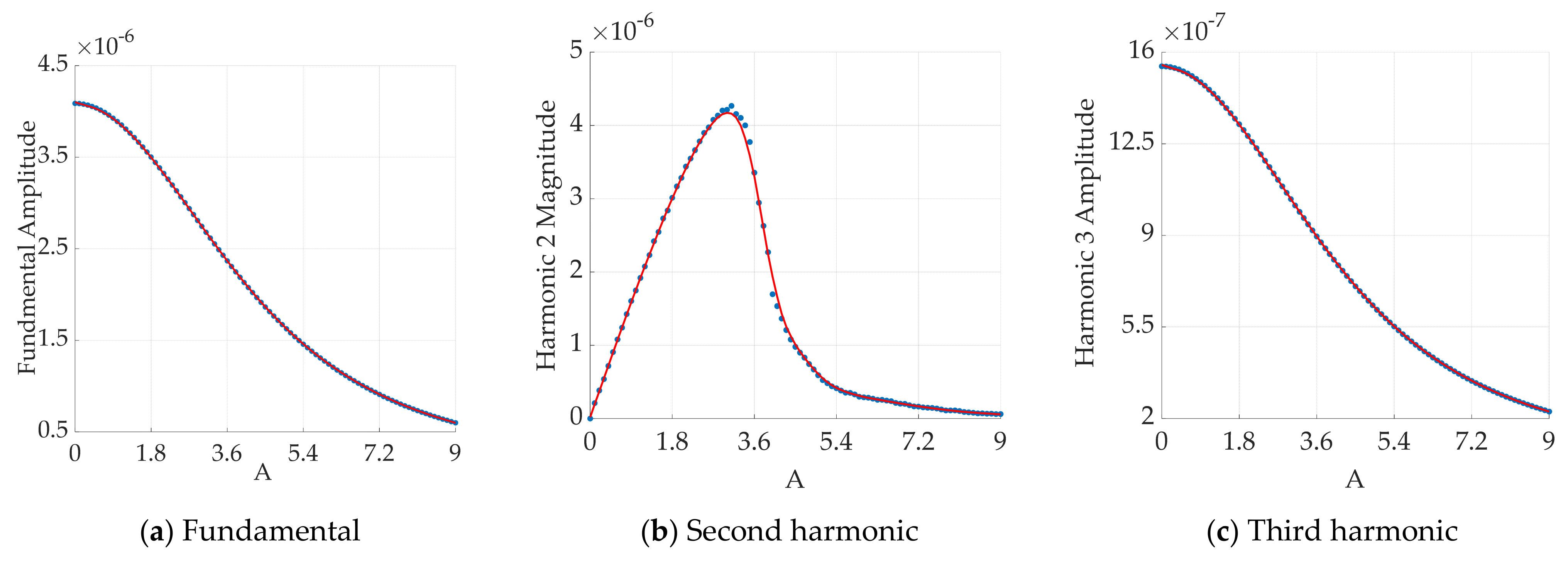

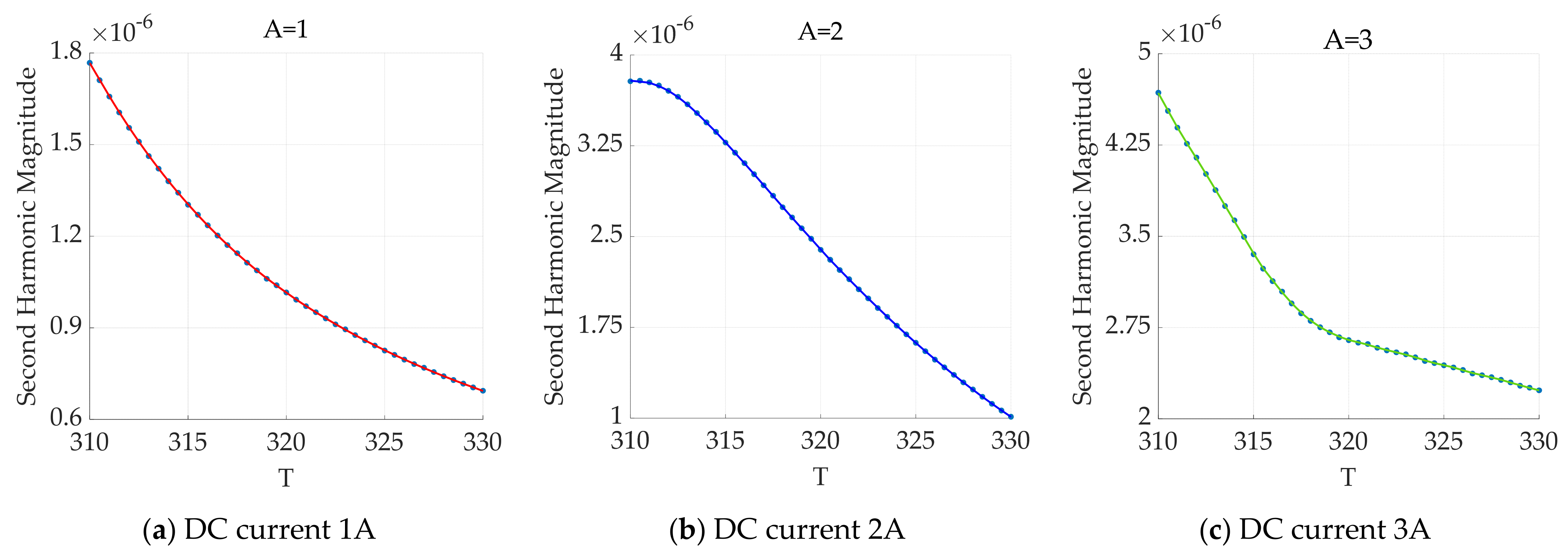
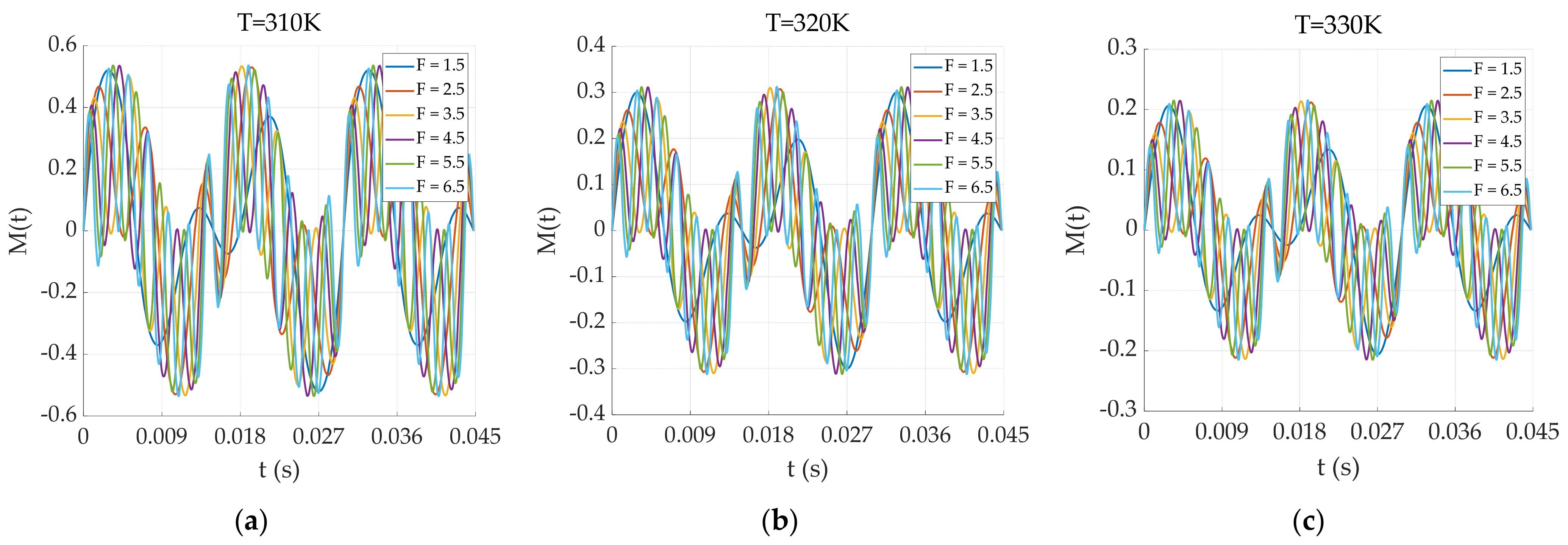
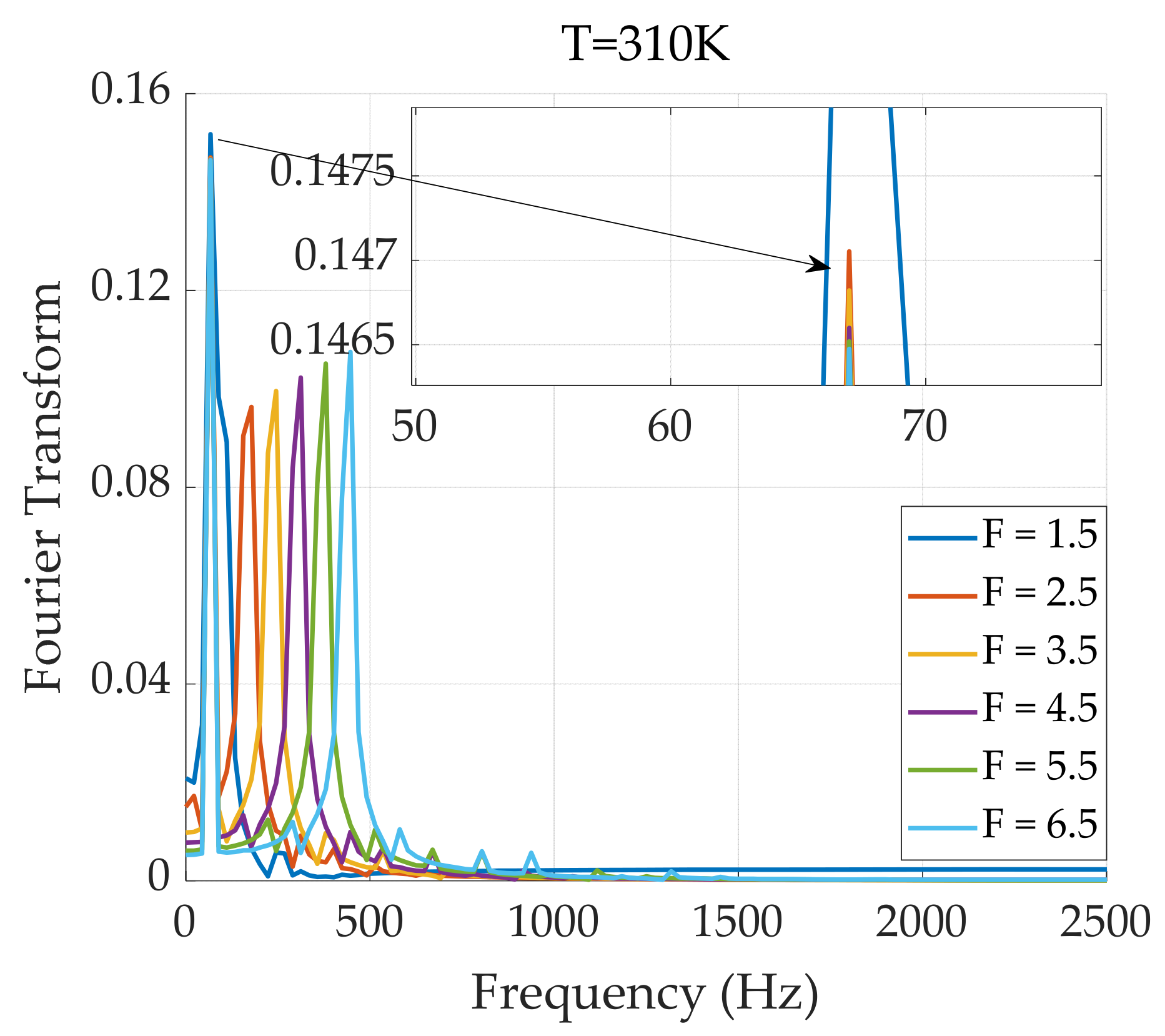
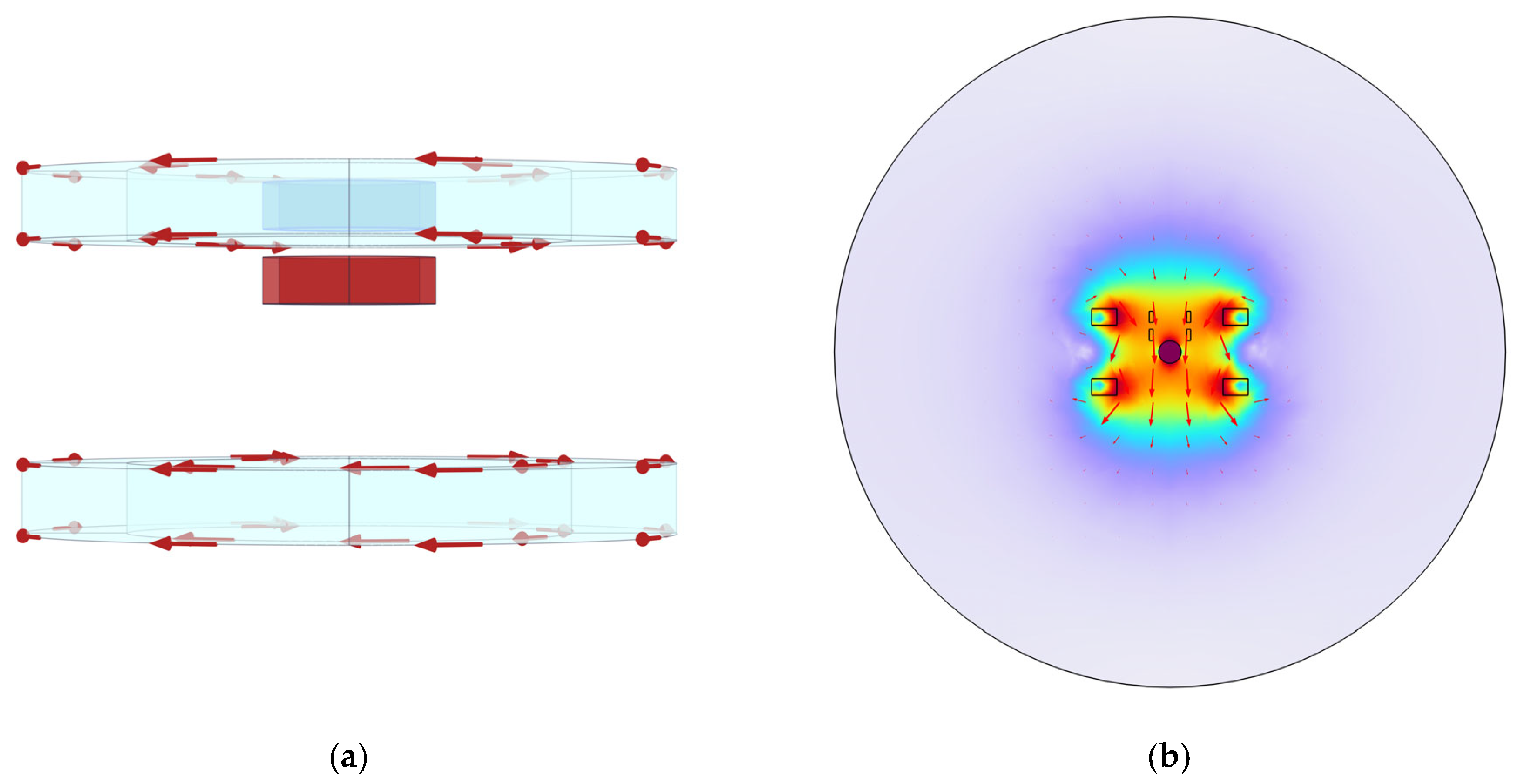




| Number of Turns | Inner Diameter | Outer Diameter | Height | |
|---|---|---|---|---|
| excitation coil | 140 | 47.5 mm | 70 mm | 15 mm |
| detection coils | 62 | 15 mm | 18.5 mm | 10 mm |
| MNPs Diameter | Boltzmann Constant | Air Conductivity |
|---|---|---|
| 30 nm | 0.001 S/m | |
| saturation magnetization | simulation model radius | airspace radius |
| 7000 A/m | 10 mm | 300 mm |
| cross-sectional area of the conductor | relative permeability | relative dielectric constant |
| m2 | 1 | 1 |
| Low-Frequency AC | AC–DC | Dual-Frequency | |
|---|---|---|---|
| PSO | 1.021/1.132 | 0.638/2.037 | 0.281/5.470 |
| GWO | 1.462/0.735 | 1.037/1.412 | 0.605/2.146 |
| DE | 1.768/1.582 | 0.603/2.145 | 0.683/4.368 |
| AGPSO | 0.947/1.318 | 0.394/4.741 | 0.237/6.793 |
| OPLGWO | 0.515/2.756 | 0.291/3.149 | 0.185/5.361 |
| PSO-GWO | 0.158/4.159 | 0.431/3.571 | 0.094/7.846 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Ke, L.; Wei, Y.; Zheng, X. A High-Precision Real-Time Temperature Acquisition Method Based on Magnetic Nanoparticles. Sensors 2024, 24, 7716. https://doi.org/10.3390/s24237716
Zhu Y, Ke L, Wei Y, Zheng X. A High-Precision Real-Time Temperature Acquisition Method Based on Magnetic Nanoparticles. Sensors. 2024; 24(23):7716. https://doi.org/10.3390/s24237716
Chicago/Turabian StyleZhu, Yuchang, Li Ke, Yijing Wei, and Xiao Zheng. 2024. "A High-Precision Real-Time Temperature Acquisition Method Based on Magnetic Nanoparticles" Sensors 24, no. 23: 7716. https://doi.org/10.3390/s24237716
APA StyleZhu, Y., Ke, L., Wei, Y., & Zheng, X. (2024). A High-Precision Real-Time Temperature Acquisition Method Based on Magnetic Nanoparticles. Sensors, 24(23), 7716. https://doi.org/10.3390/s24237716





