ANN-Assisted Beampattern Optimization of Semi-Coprime Array for Beam-Steering Applications
Abstract
1. Introduction
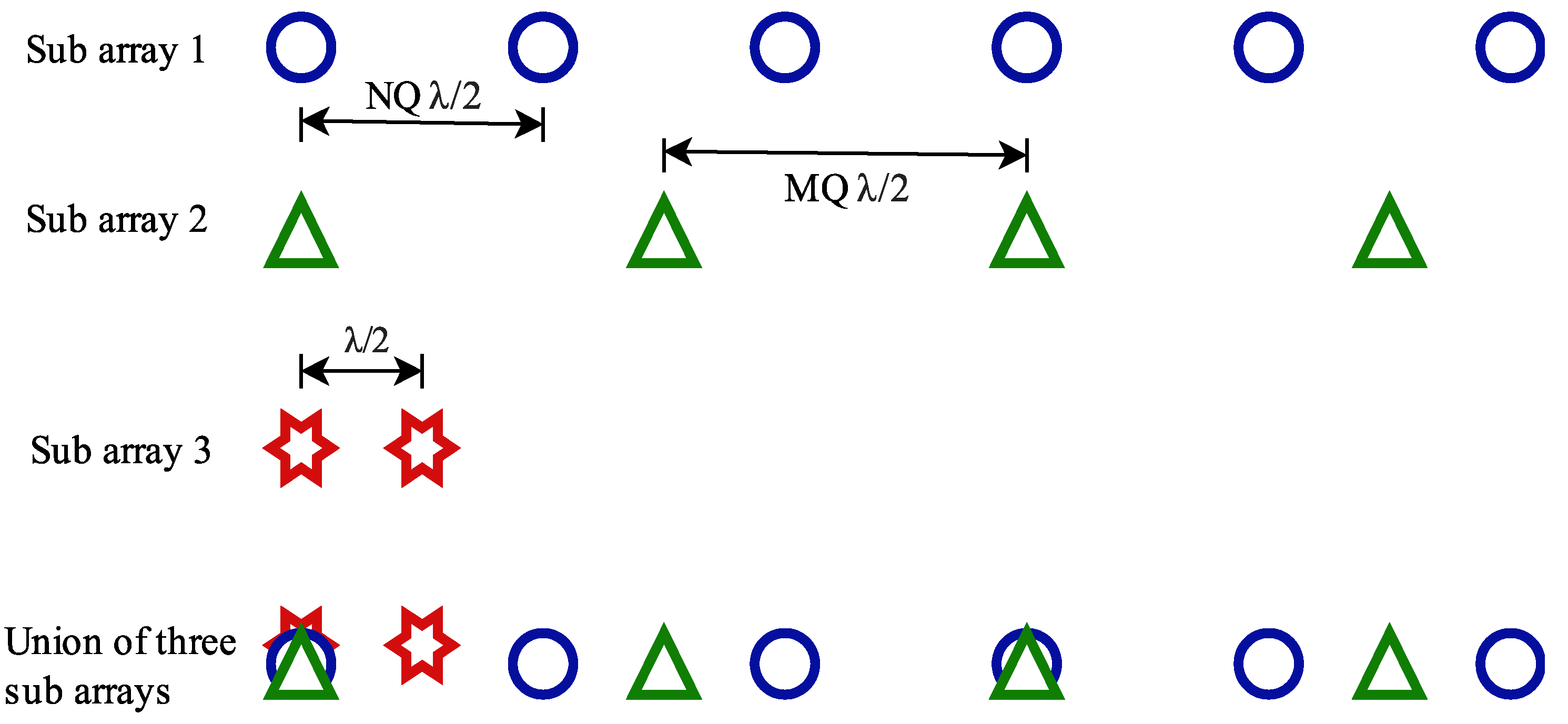
2. An Overview of SCASS and the Associated Challenges
3. Artificial Neural Network: Introduction and Application to the Problem
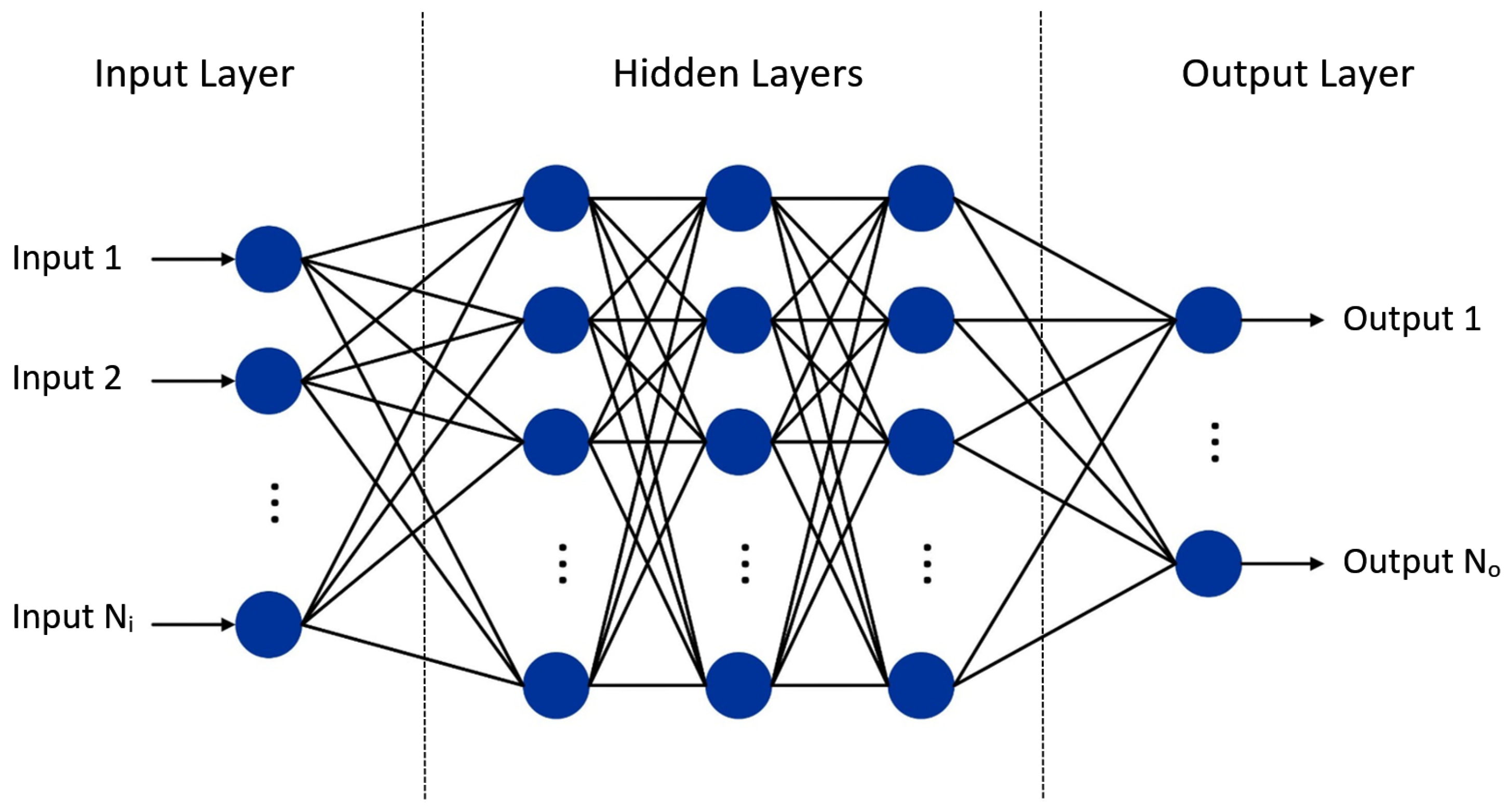
3.1. Basic Architecture of an ANN
3.2. The Dataset Generation
3.3. Training and Architectural Configuration of the Proposed ANN
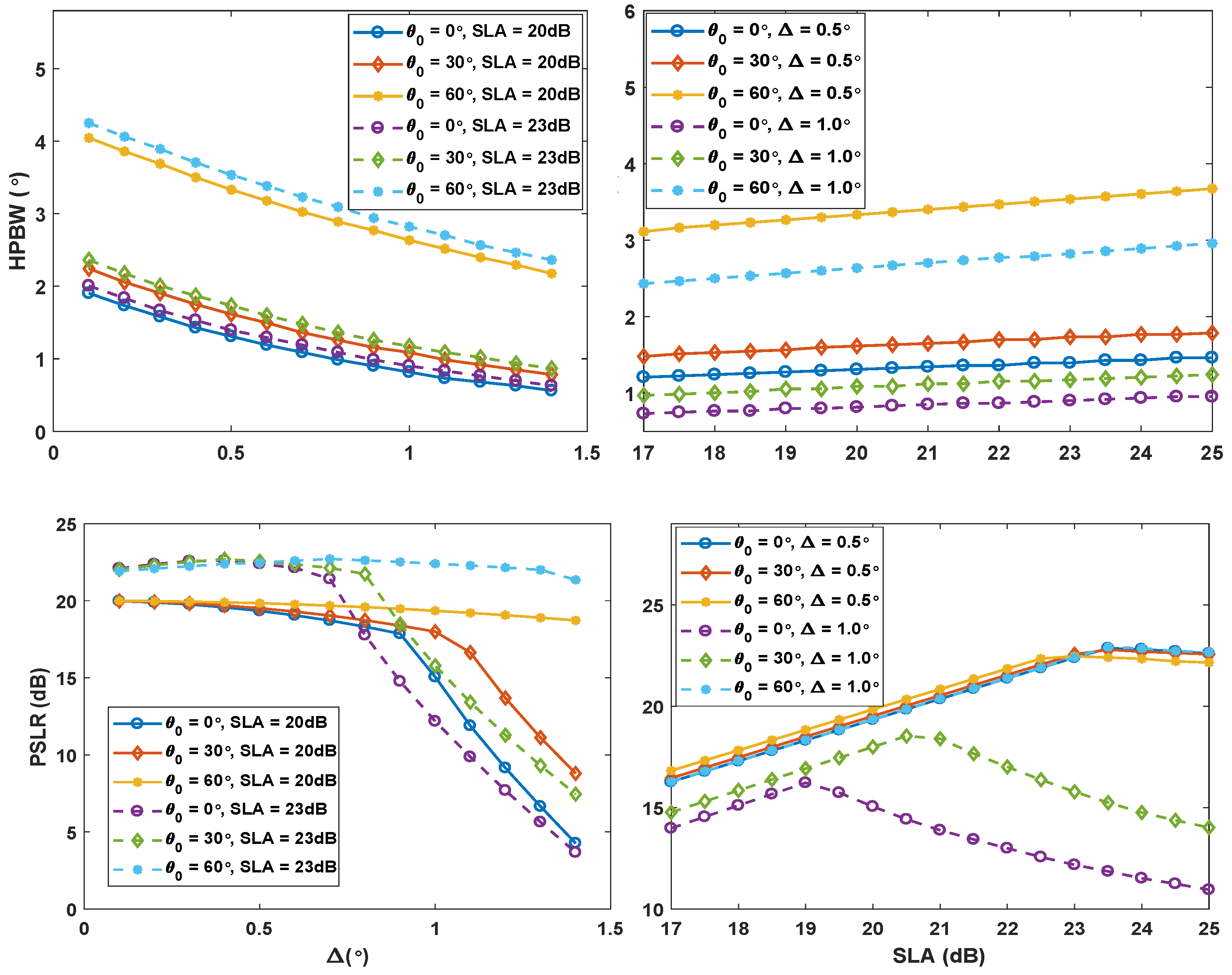
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kenane, E.; Djahli, F. Optimum design of non-uniform symmetrical linear antenna arrays using a novel modified invasive weeds optimization. Arch. Electr. Eng. 2016, 65, 5–18. [Google Scholar] [CrossRef]
- Khalilpour, J.; Ranjbar, J.; Karami, P. A novel algorithm in a linear phased array system for side lobe and grating lobe level reduction with large element spacing. Analog. Integr. Circuits Signal Process. 2020, 104, 265–275. [Google Scholar] [CrossRef]
- Khalaj-Amirhosseini, M. To control the beamwidth of antenna arrays by virtually changing inter-distances. Int. J. Microw.-Comput.-Aided Eng. 2019, 29, e21754. [Google Scholar] [CrossRef]
- Oraizi, H.; Fallahpour, M. Nonuniformly spaced linear array design for the specified beamwidth/sidelobe level or specified directivity/sidelobe level with coupling consideration. Prog. Electromagn. Res. 2008, 4, 185–209. [Google Scholar] [CrossRef]
- Liang, S.; Fang, Z.; Sun, G.; Liu, Y.; Qu, G.; Zhang, Y. Sidelobe reductions of antenna arrays via an improved chicken swarm optimization approach. IEEE Access 2020, 8, 37664–37683. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, W.; Wang, R.; Deng, Y.; Jin, G.; Long, Y. A novel NLFM waveform with low sidelobes based on modified Chebyshev window. IEEE Geosci. Remote Sens. Lett. 2020, 17, 814–818. [Google Scholar] [CrossRef]
- Li, M.; Zhang, Z.; Tang, M.C.; Yi, D.; Ziolkowski, R.W. Compact series-fed microstrip patch arrays excited with Dolph–Chebyshev distributions realized with slow wave transmission line feed networks. IEEE Trans. Antennas Propag. 2020, 68, 7905–7915. [Google Scholar] [CrossRef]
- Elwi, T.A.; Taher, F.; Virdee, B.S.; Alibakhshikenari, M.; Zuazola, I.J.G.; Krasniqi, A.; Kamel, A.S.; Tokan, N.T.; Khan, S.; Parchin, N.O.; et al. On the performance of a photonic reconfigurable electromagnetic band gap antenna array for 5G applications. IEEE Access 2024, 12, 60849–60862. [Google Scholar] [CrossRef]
- Zidour, A.; Ayad, M.; Alibakhshikenari, M.; See, C.H.; Lai, Y.X.; Ma, Y.; Guenad, B.; Livreri, P.; Khan, S.; Pau, G.; et al. Wideband endfire antenna array for 5G mmWave mobile terminals. IEEE Access 2024, 12, 39926–39935. [Google Scholar] [CrossRef]
- Zakeri, H.; Azizpour, R.; Khoddami, P.; Moradi, G.; Alibakhshikenari, M.; Hwang See, C.; Denidni, T.A.; Falcone, F.; Koziel, S.; Limiti, E. Low-cost multiband four-port phased array antenna for sub-6 GHz 5G applications with enhanced gain methodology in radio-over-fiber systems using modulation instability. IEEE Access 2024, 12, 117787–117799. [Google Scholar] [CrossRef]
- Vaidyanathan, P.P.; Pal, P. Sparse sensing with co-prime samplers and arrays. IEEE Trans. Signal Process. 2010, 59, 573–586. [Google Scholar] [CrossRef]
- Adhikari, K. Beamforming with semi-coprime arrays. J. Acoust. Soc. Am. 2019, 145, 2841–2850. [Google Scholar] [CrossRef] [PubMed]
- Adhikari, K.; Drozdenko, B. Design and Statistical Analysis of Tapered Coprime and Nested Arrays for the Min Processor. IEEE Access 2019, 7, 139601–139615. [Google Scholar] [CrossRef]
- Liu, Y.; Buck, J.R. Detecting Gaussian signals in the presence of interferers using the coprime sensor arrays with the min processor. In Proceedings of the 2015 49th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 8–11 November 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 370–374. [Google Scholar]
- Adhikari, K.; Buck, J.R.; Wage, K.E. Extending coprime sensor arrays to achieve the peak side lobe height of a full uniform linear array. EURASIP J. Adv. Signal Process. 2014, 2014, 148. [Google Scholar] [CrossRef]
- Moghadam, G.S.; Shirazi, A.B. Novel method for digital beamforming in co-prime sensor arrays using product and min processors. IET Signal Process. 2019, 13, 614–623. [Google Scholar] [CrossRef]
- Khan, W.; Shahid, S.; Iqbal, W.; Rana, A.S.; Zahra, H.; Alathbah, M.; Abbas, S.M. Semi-Coprime Array with Staggered Beam-Steering of Sub-Arrays. Sensors 2023, 23, 5484. [Google Scholar] [CrossRef] [PubMed]
- Rawat, A.; Yadav, R.; Shrivastava, S. Neural network applications in smart antenna arrays: A review. AEU-Int. J. Electron. Commun. 2012, 66, 903–912. [Google Scholar] [CrossRef]
- Ayestarán, R.G.; Las-Heras, F.; Martínez, J.A. Non Uniform-Antenna Array Synthesis Using Neural Networks. J. Electromagn. Waves Appl. 2007, 21, 1001–1011. [Google Scholar] [CrossRef]
- Al-Bajari, M.; Ahmed, J.M.; Ayoob, M.B. Performance Evaluation of an Artificial Neural Network-Based Adaptive Antenna Array System. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2010; pp. 11–20. [Google Scholar] [CrossRef]
- Zooghby, A.; Christodoulou, C.; Georgiopoulos, M. Neural network-based adaptive beamforming for one- and two-dimensional antenna arrays. IEEE Trans. Antennas Propag. 1998, 46, 1891–1893. [Google Scholar] [CrossRef]
- Wu, X.; Luo, J.; Li, G.; Zhang, S.; Sheng, W. Fast Wideband Beamforming Using Convolutional Neural Network. Remote Sens. 2023, 15, 712. [Google Scholar] [CrossRef]
- Al Kassir, H.; Zaharis, Z.D.; Lazaridis, P.I.; Kantartzis, N.V.; Yioultsis, T.V.; Chochliouros, I.P.; Mihovska, A.; Xenos, T.D. Antenna Array Beamforming Based on Deep Learning Neural Network Architectures. In Proceedings of the 2022 3rd URSI Atlantic and Asia Pacific Radio Science Meeting (AT-AP-RASC), Gran Canaria, Spain, 29 May–3 June 2022; IEEE: Piscataway, NJ, USA, 2022. [Google Scholar] [CrossRef]
- Liao, Z.; Duan, K.; He, J.; Qiu, Z.; Li, B. Robust Adaptive Beamforming Based on a Convolutional Neural Network. Electronics 2023, 12, 2751. [Google Scholar] [CrossRef]
- Roshani, S.; Koziel, S.; Yahya, S.I.; Chaudhary, M.A.; Ghadi, Y.Y.; Roshani, S.; Golunski, L. Mutual Coupling Reduction in Antenna Arrays Using Artificial Intelligence Approach and Inverse Neural Network Surrogates. Sensors 2023, 23, 7089. [Google Scholar] [CrossRef] [PubMed]
- Patnaik, A.; Christodoulou, C. Finding failed element positions in linear antenna arrays using neural networks. In Proceedings of the 2006 IEEE Antennas and Propagation Society International Symposium, Albuquerque, NM, USA, 9–14 July 2006; IEEE: Piscataway, NJ, USA, 2006. [Google Scholar] [CrossRef]
- Patnaik, A.; Choudhury, B.; Pradhan, P.; Mishra, R.K.; Christodoulou, C. An ANN Application for Fault Finding in Antenna Arrays. IEEE Trans. Antennas Propag. 2007, 55, 775–777. [Google Scholar] [CrossRef]
- Southall, H.; Simmers, J.; O’Donnell, T. Direction finding in phased arrays with a neural network beamformer. IEEE Trans. Antennas Propag. 1995, 43, 1369–1374. [Google Scholar] [CrossRef]
- Kumar, A.; Ansari, A.Q.; Kanaujia, B.K.; Kishor, J.; Matekovits, L. A review on different techniques of mutual coupling reduction between elements of any MIMO antenna. Part 1: DGSs and parasitic structures. Radio Sci. 2021, 56. [Google Scholar] [CrossRef]
- Kirtania, S.G.; Elger, A.W.; Hasan, M.R.; Wisniewska, A.; Sekhar, K.; Karacolak, T.; Sekhar, P.K. Flexible antennas: A review. Micromachines 2020, 11, 847. [Google Scholar] [CrossRef]
- Matloff, N. Statistical Regression and Classification From Linear Models to Machine Learning; Taylor and Francis Group: Abingdon, UK, 2017. [Google Scholar]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice Hall PTR: Hoboken, NJ, USA, 1998. [Google Scholar]
- Huber, P.J. Robust Estimation of a Location Parameter. Ann. Math. Stat. 1964, 35, 73–101. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learn; MIT Press: Cambridge, MA, USA, 2016; p. 800. [Google Scholar]
- Qi, J.; Du, J.; Siniscalchi, S.M.; Ma, X.; Lee, C.H. On Mean Absolute Error for Deep Neural Network Based Vector-to-Vector Regression. IEEE Signal Process. Lett. 2020, 27, 1485–1489. [Google Scholar] [CrossRef]


| Parameters | Values |
|---|---|
| () | (3, 2, 3, 3), (4, 3, 3, 2), (5, 2, 3, 3), (6, 5, 3, 2) |
| 0° to 70°, step size = 0.5° | |
| SLA | 17 to 25 dB, step size = 0.1 dB |
| 0° to 2°, step size = 0.1° |
| Inputs of the ANN | Outputs of the ANN | |||||||
|---|---|---|---|---|---|---|---|---|
| PSLR (dB) | SLA (dB) | HPBW (°) | ||||||
| 3 | 2 | 3 | 3 | 14 | 21.29 | 21.5 | 0.3 | 1.701 |
| 3 | 2 | 3 | 3 | 14 | 21.29 | 21.75 | 0.45 | 1.498 |
| 3 | 2 | 3 | 3 | 14 | 21.29 | 22.25 | 0.65 | 1.267 |
| 3 | 2 | 3 | 3 | 14 | 21.29 | 23.5 | 0.7 | 1.253 |
| 3 | 2 | 3 | 3 | 14 | 21.29 | 24 | 0.67 | 1.295 |
| 3 | 2 | 3 | 3 | 14.5 | 21.29 | 21.5 | 0.3 | 1.708 |
| 3 | 2 | 3 | 3 | 14.5 | 21.29 | 22.25 | 0.65 | 1.274 |
| Network Specifications | ANN1 | ANN2 | |
|---|---|---|---|
| Connectivity Type | Fully connected | ||
| Number of Hidden Layers | 1 | 3 | |
| Neurons per Hidden Layer | 16 | 32 | |
| Activation | Input/Output Layers | Linear | |
| Function | Hidden Layers | ReLU | |
| Loss Function | Mean Absolute Error | ||
| M | N | P | Q | PSLR (dB) | SLA (dB) | HPBW (°) | ||
|---|---|---|---|---|---|---|---|---|
| 3 | 2 | 3 | 3 | 5.2 | 17.4 | 19.3 | 0.84 | 0.938 |
| 3 | 2 | 3 | 3 | 5.2 | 19.7 | 21.3 | 0.81 | 1.036 |
| 3 | 2 | 3 | 3 | 5.2 | 22 | 23.1 | 0.68 | 1.211 |
| 3 | 2 | 3 | 3 | 13.15 | 15.9 | 17.8 | 0.84 | 0.938 |
| 3 | 2 | 3 | 3 | 13.15 | 22.2 | 23.2 | 0.68 | 1.26 |
| 3 | 2 | 3 | 3 | 28.87 | 15.5 | 17.5 | 0.95 | 1.015 |
| 3 | 2 | 3 | 3 | 28.87 | 17.7 | 19.6 | 0.96 | 1.085 |
| 3 | 2 | 3 | 3 | 28.87 | 21.7 | 22.8 | 0.79 | 1.358 |
| 3 | 2 | 3 | 3 | 37.19 | 17 | 18.9 | 1.05 | 1.169 |
| 3 | 2 | 3 | 3 | 37.19 | 19.9 | 21.5 | 1.01 | 1.302 |
| 3 | 2 | 3 | 3 | 37.19 | 22.4 | 23.4 | 0.82 | 1.561 |
| 3 | 2 | 3 | 3 | 49.21 | 15.9 | 17.8 | 1.26 | 1.386 |
| 3 | 2 | 3 | 3 | 49.21 | 18.5 | 20.3 | 1.28 | 1.491 |
| 3 | 2 | 3 | 3 | 49.21 | 20.9 | 22.2 | 1.13 | 1.722 |
| 3 | 2 | 3 | 3 | 49.21 | 23 | 23.9 | 0.94 | 1.995 |
| 3 | 2 | 3 | 3 | 58.35 | 16.9 | 18.8 | 1.59 | 1.771 |
| 3 | 2 | 3 | 3 | 58.35 | 21.4 | 22.6 | 1.36 | 2.212 |
| 3 | 2 | 3 | 3 | 58.35 | 23 | 24 | 1.17 | 2.492 |
| Mean Absolute Percentage Error | |||
|---|---|---|---|
| SLA | HPBW | ||
| ANN1 | 0.21% | 1.82% | 1.53% |
| ANN2 | 0.20% | 0.83% | 0.70% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, W.; Shahid, S.; Chaudhry, A.N.; Rana, A.S. ANN-Assisted Beampattern Optimization of Semi-Coprime Array for Beam-Steering Applications. Sensors 2024, 24, 7260. https://doi.org/10.3390/s24227260
Khan W, Shahid S, Chaudhry AN, Rana AS. ANN-Assisted Beampattern Optimization of Semi-Coprime Array for Beam-Steering Applications. Sensors. 2024; 24(22):7260. https://doi.org/10.3390/s24227260
Chicago/Turabian StyleKhan, Waseem, Saleem Shahid, Ali Naeem Chaudhry, and Ahsan Sarwar Rana. 2024. "ANN-Assisted Beampattern Optimization of Semi-Coprime Array for Beam-Steering Applications" Sensors 24, no. 22: 7260. https://doi.org/10.3390/s24227260
APA StyleKhan, W., Shahid, S., Chaudhry, A. N., & Rana, A. S. (2024). ANN-Assisted Beampattern Optimization of Semi-Coprime Array for Beam-Steering Applications. Sensors, 24(22), 7260. https://doi.org/10.3390/s24227260






