Coil-Only High-Frequency Lamb Wave Generation in Nickel Sheets
Abstract
1. Introduction
2. Methodology
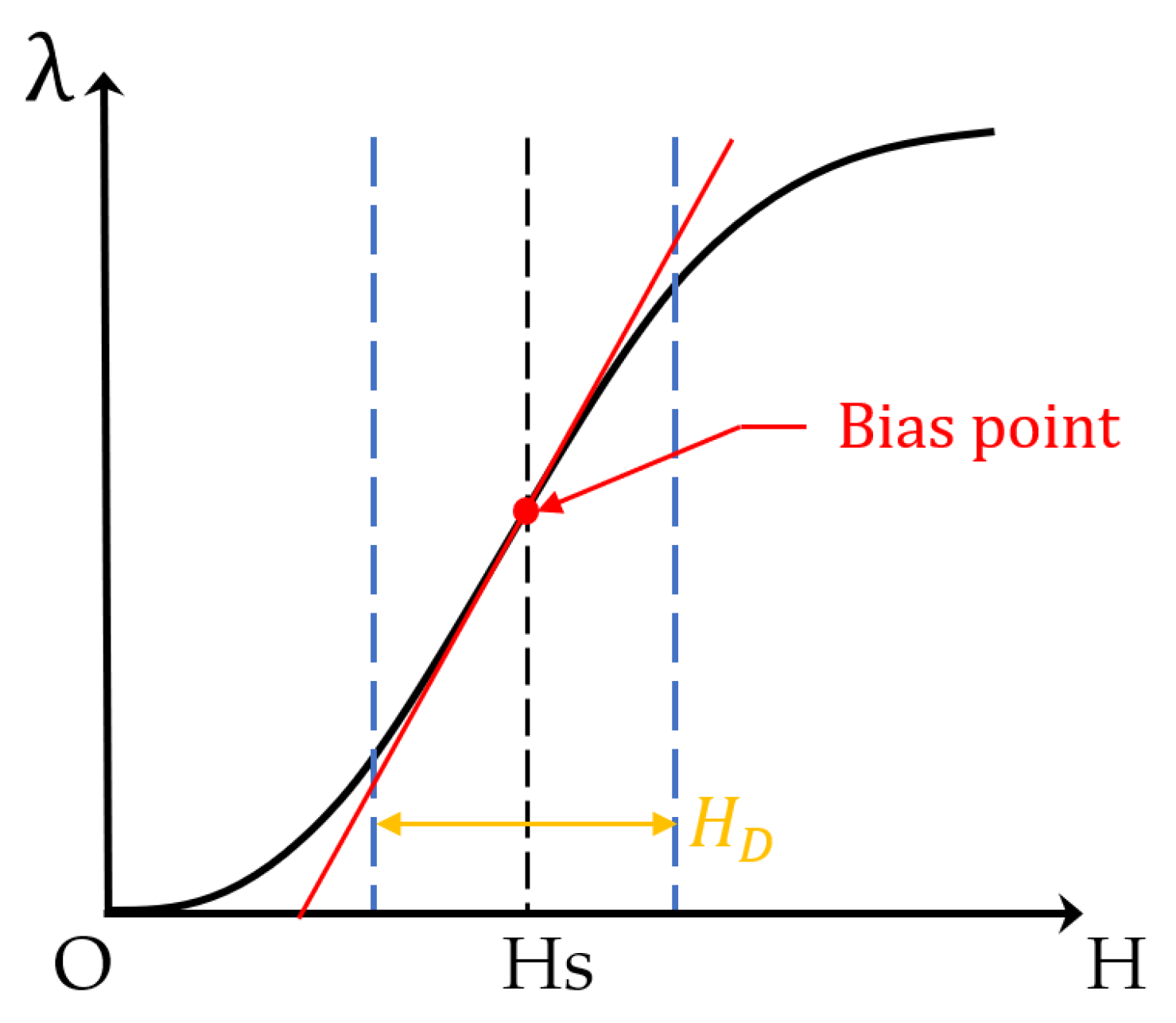
2.1. Magnetostrictive Constitutive Relation
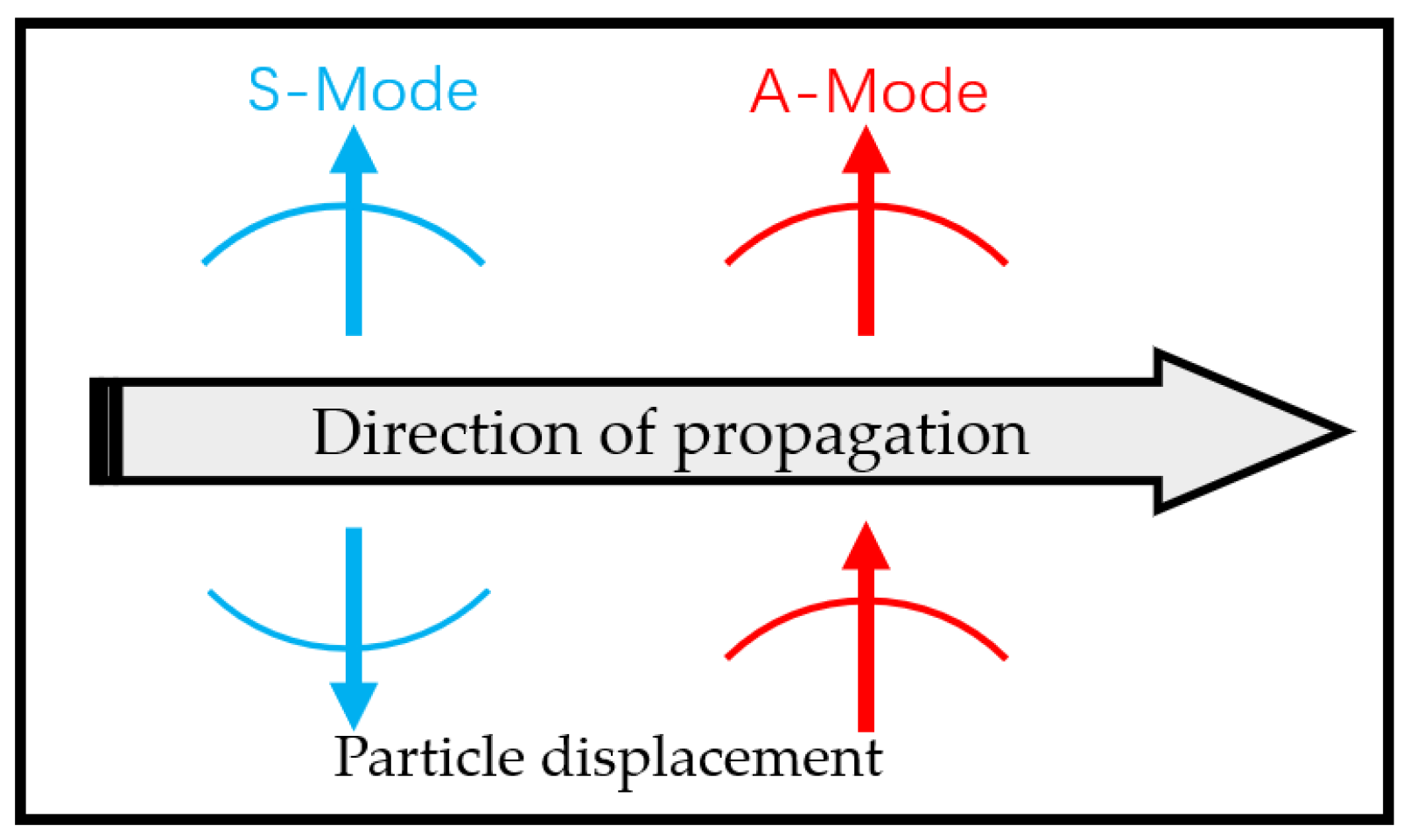
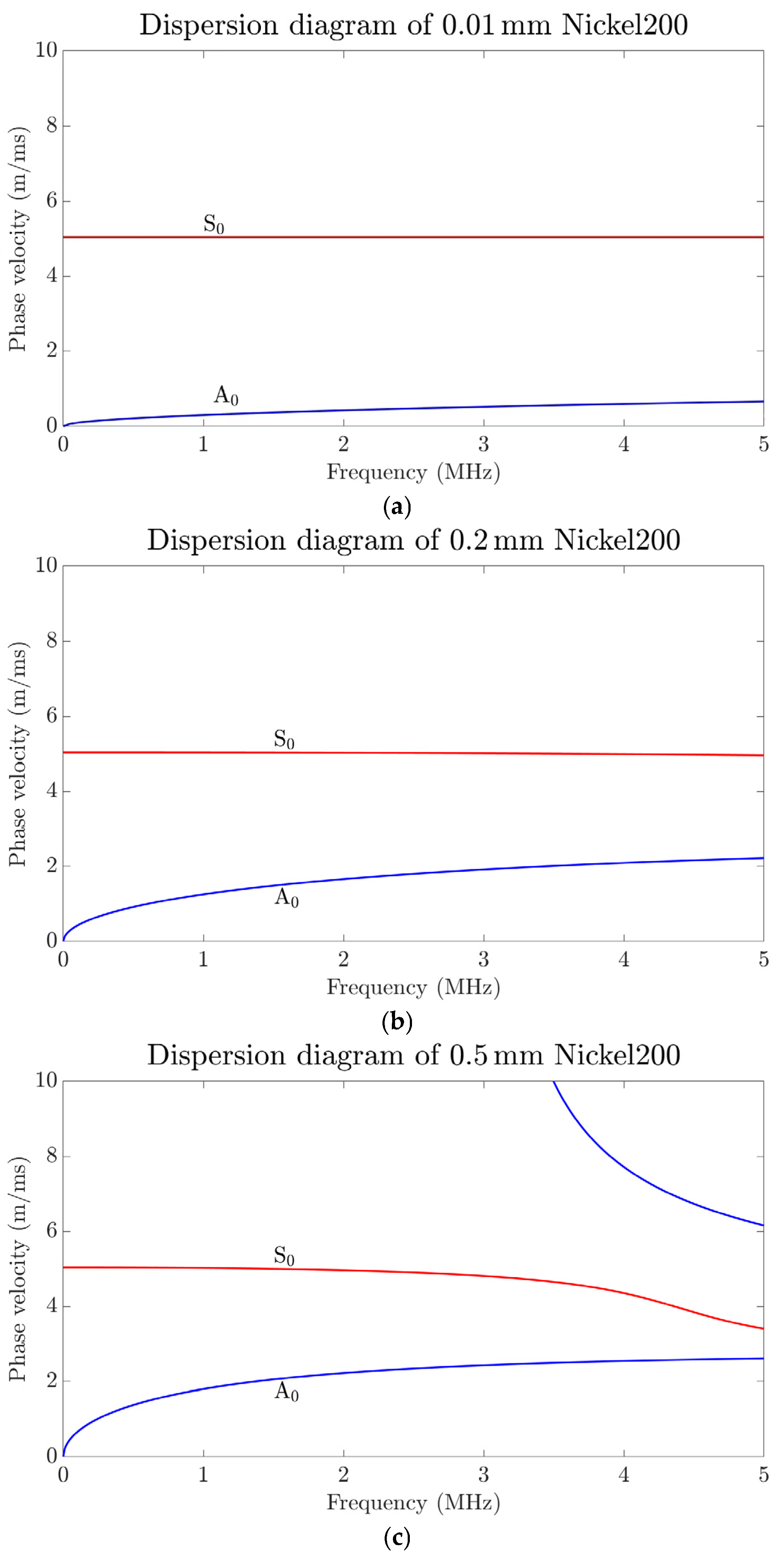
2.2. Dispersion Diagram of Material
3. Experiment & Result Discussion
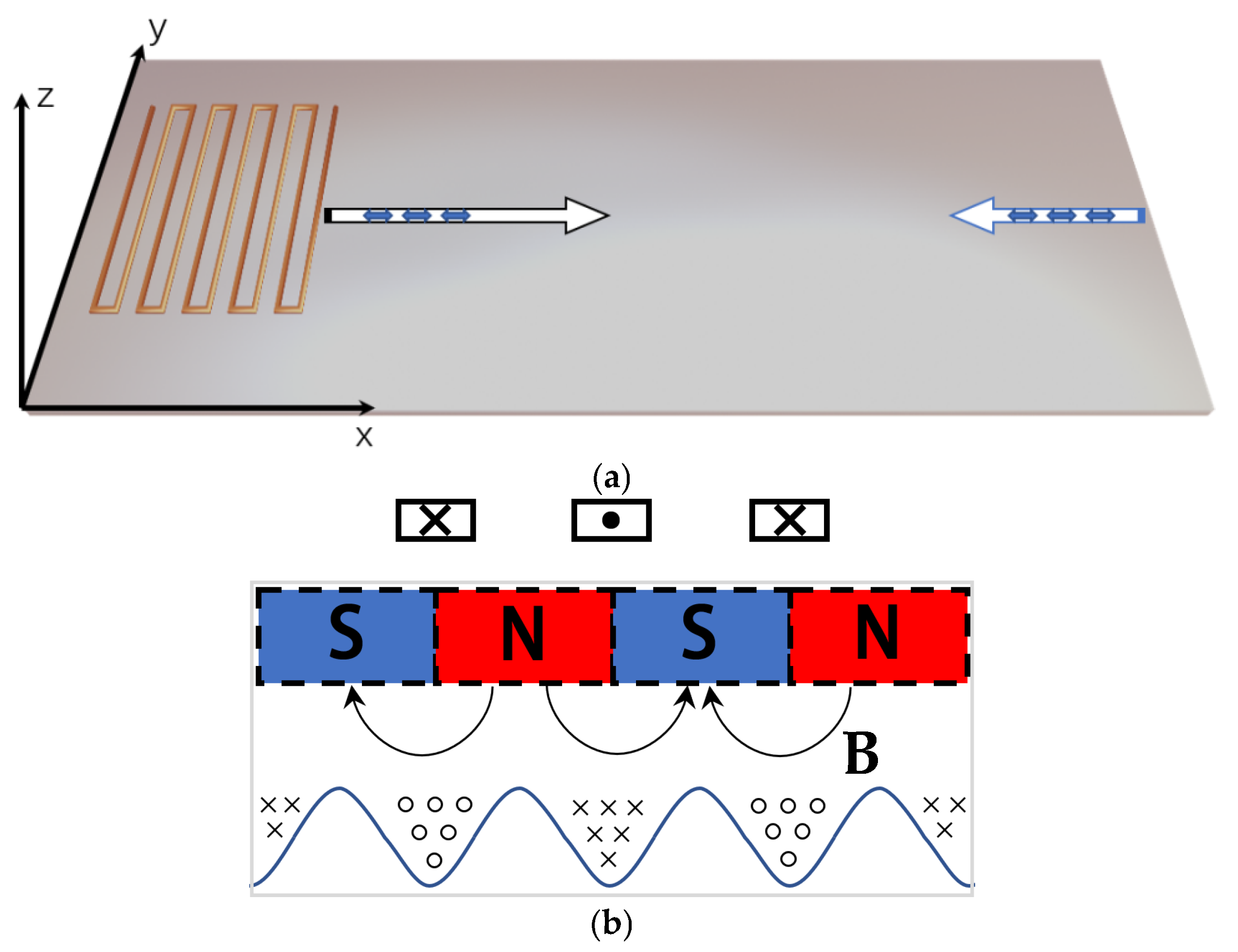
3.1. Experiment Design
3.2. Results of the Experiment
3.2.1. Ultrasonic Velocity of Sound Measurement
3.2.2. Computational Analysis of Experimental Results
4. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guo, X.; Zhu, W.; Qiu, X.; Xiang, Y. A Lorentz Force EMAT Design with Racetrack Coil and Periodic Permanent Magnets for Selective Enhancement of Ultrasonic Lamb Wave Generation. Sensors 2022, 23, 96. [Google Scholar] [CrossRef] [PubMed]
- Del Moral, A. Magnetostriction and Magnetoelasticity Theory: A Modern View. In Handbook of Magnetism and Advanced Magnetic Materials; Wiley: Hoboken, NJ, USA, 2007; ISBN 978-0-470-02218-4. [Google Scholar]
- Murayama, R. Driving Mechanism on Magnetostrictive Type Electromagnetic Acoustic Transducer for Symmetrical Vertical-Mode Lamb Wave and for Shear Horizontal-Mode Plate Wave. Ultrasonics 1996, 34, 729–736. [Google Scholar] [CrossRef]
- Clarke, T.; Cawley, P.; Wilcox, P.D.; Croxford, A.J. Evaluation of the Damage Detection Capability of a Sparse-Array Guided-Wave SHM System Applied to a Complex Structure under Varying Thermal Conditions. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 56, 2666–2678. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.K.; Kim, H.W.; Kim, Y.Y. Omnidirectional Lamb Waves by Axisymmetrically-Configured Magnetostrictive Patch Transducer. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2013, 60, 1928–1934. [Google Scholar] [CrossRef] [PubMed]
- Sun, W.; Liu, G.; Xia, H.; Xia, Z. A Modified Design of the Omnidirectional EMAT for Antisymmetric Lamb Wave Generation. Sens. Actuators A Phys. 2018, 282, 251–258. [Google Scholar] [CrossRef]
- Liu, Z.; Zhong, X.; Xie, M.; Liu, X.; He, C.; Wu, B. Damage Imaging in Composite Plate by Using Double-Turn Coil Omnidirectional Shear-Horizontal Wave Magnetostrictive Patch Transducer Array. Adv. Compos. Mater. 2017, 26, 67–78. [Google Scholar] [CrossRef]
- Murayama, R. Study of Driving Mechanism on Electromagnetic Acoustic Transducer for Lamb Wave Using Magnetostrictive Effect and Application in Drawability Evaluation of Thin Steel Sheets. Ultrasonics 1999, 37, 31–38. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, R.; Feng, B.; Guo, Y.; Kang, Y.; Song, Y.; Ma, H. Magnetostrictive Ultrasonic Torsional Wave Detection Method for High-Density Polyethylene Pipe Weld Status. In Proceedings of the 2024 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Glasgow, UK, 20–23 May 2024; pp. 1–6. [Google Scholar]
- Rueter, D. Induction Coil as a Non-Contacting Ultrasound Transmitter and Detector: Modeling of Magnetic Fields for Improving the Performance. Ultrasonics 2016, 65, 200–210. [Google Scholar] [CrossRef] [PubMed]
- Rueter, D. Experimental Demonstration and Circuitry for a Very Compact Coil-Only Pulse Echo EMAT. Sensors 2017, 17, 926. [Google Scholar] [CrossRef] [PubMed]
- Park, C.I.; Kim, W.; Cho, S.H.; Kim, Y.Y. Surface-Detached V-Shaped Yoke of Obliquely Bonded Magnetostrictive Strips for High Transduction of Ultrasonic Torsional Waves. Appl. Phys. Lett. 2005, 87, 224105. [Google Scholar] [CrossRef]
- Isla, J.; Cegla, F. EMAT Phased Array: A Feasibility Study of Surface Crack Detection. Ultrasonics 2017, 78, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zheng, Z.; Chan, J.; Yeow, J.T.W. Capacitive Micromachined Ultrasound Transducers for Intravascular Ultrasound Imaging. Microsyst. Nanoeng. 2020, 6, 73. [Google Scholar] [CrossRef] [PubMed]
- Birjis, Y.; Swaminathan, S.; Nazemi, H.; Raj, G.C.A.; Munirathinam, P.; Abu-Libdeh, A.; Emadi, A. Piezoelectric Micromachined Ultrasonic Transducers (PMUTs): Performance Metrics, Advancements, and Applications. Sensors 2022, 22, 9151. [Google Scholar] [CrossRef] [PubMed]
- Zang, J.; Fan, Z.; Li, P.; Duan, X.; Wu, C.; Cui, D.; Xue, C. Design and Fabrication of High-Frequency Piezoelectric Micromachined Ultrasonic Transducer Based on an AlN Thin Film. Micromachines 2022, 13, 1317. [Google Scholar] [CrossRef] [PubMed]
- Gandomzadeh, D.; Abbaspour-Fard, M.H. Numerical Study of the Effect of Core Geometry on the Performance of a Magnetostrictive Transducer. J. Magn. Magn. Mater. 2020, 513, 166823. [Google Scholar] [CrossRef]
- Teh, K.-S.; Cheng, Y.-T.; Lin, L. MEMS Fabrication Based on Nickel-Nanocomposite: Film Deposition and Characterization. J. Micromech. Microeng. 2005, 15, 2205–2215. [Google Scholar] [CrossRef][Green Version]
- Weber, N.; Zappe, H.; Seifert, A. An All-Nickel Magnetostatic MEMS Scanner. J. Micromech. Microeng. 2012, 22, 125008. [Google Scholar] [CrossRef]
- Sun, S.; Dai, X.; Sun, Y.; Xiang, X.; Ding, G.; Zhao, X. MEMS-Based Wide-Bandwidth Electromagnetic Energy Harvester with Electroplated Nickel Structure. J. Micromech. Microeng. 2017, 27, 115007. [Google Scholar] [CrossRef]
- Rose, J.L. Ultrasonic Guided Waves in Solid Media, 1st ed.; Cambridge University Press: Cambridge, UK, 2014; ISBN 978-1-107-04895-9. [Google Scholar]



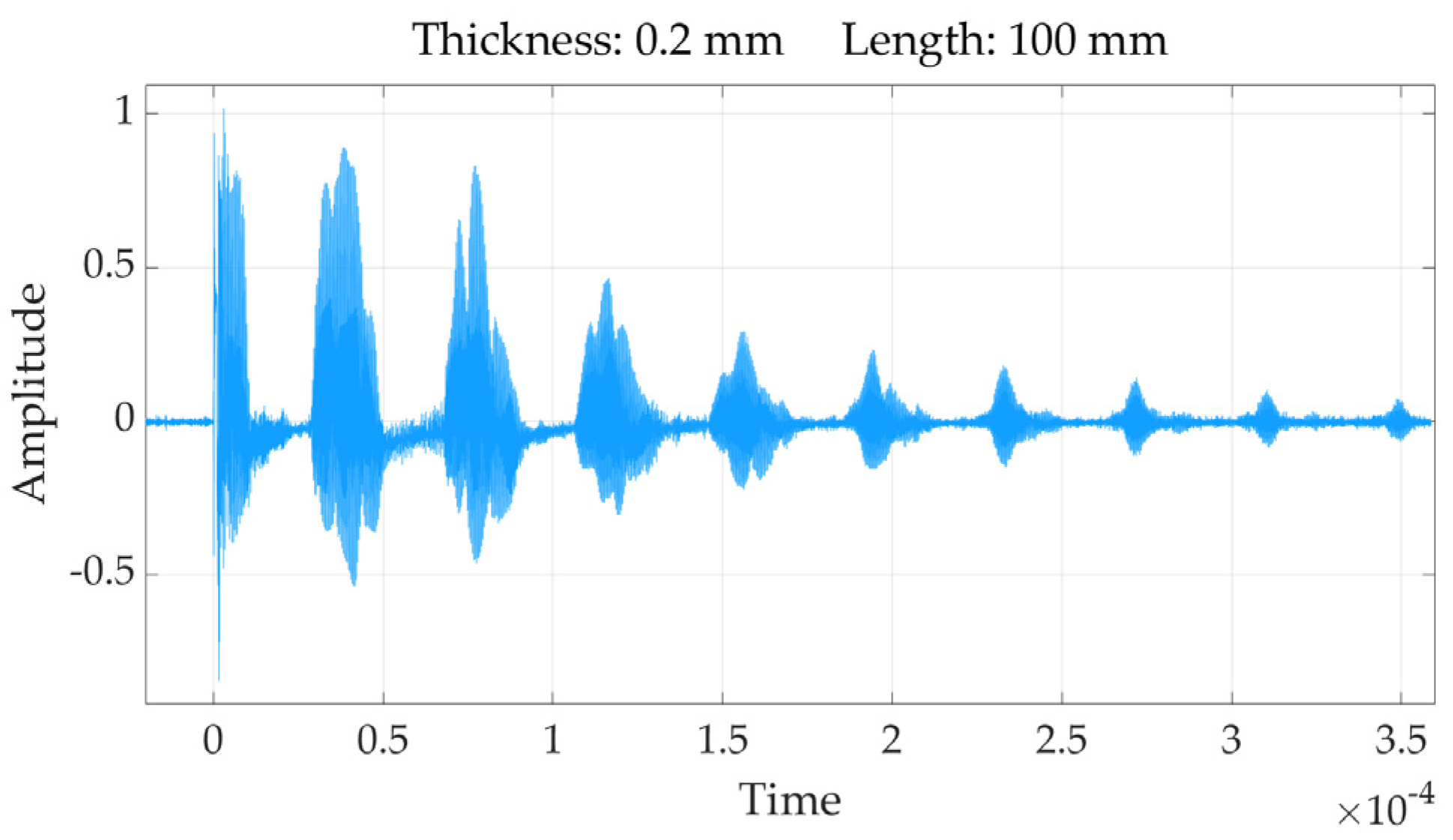
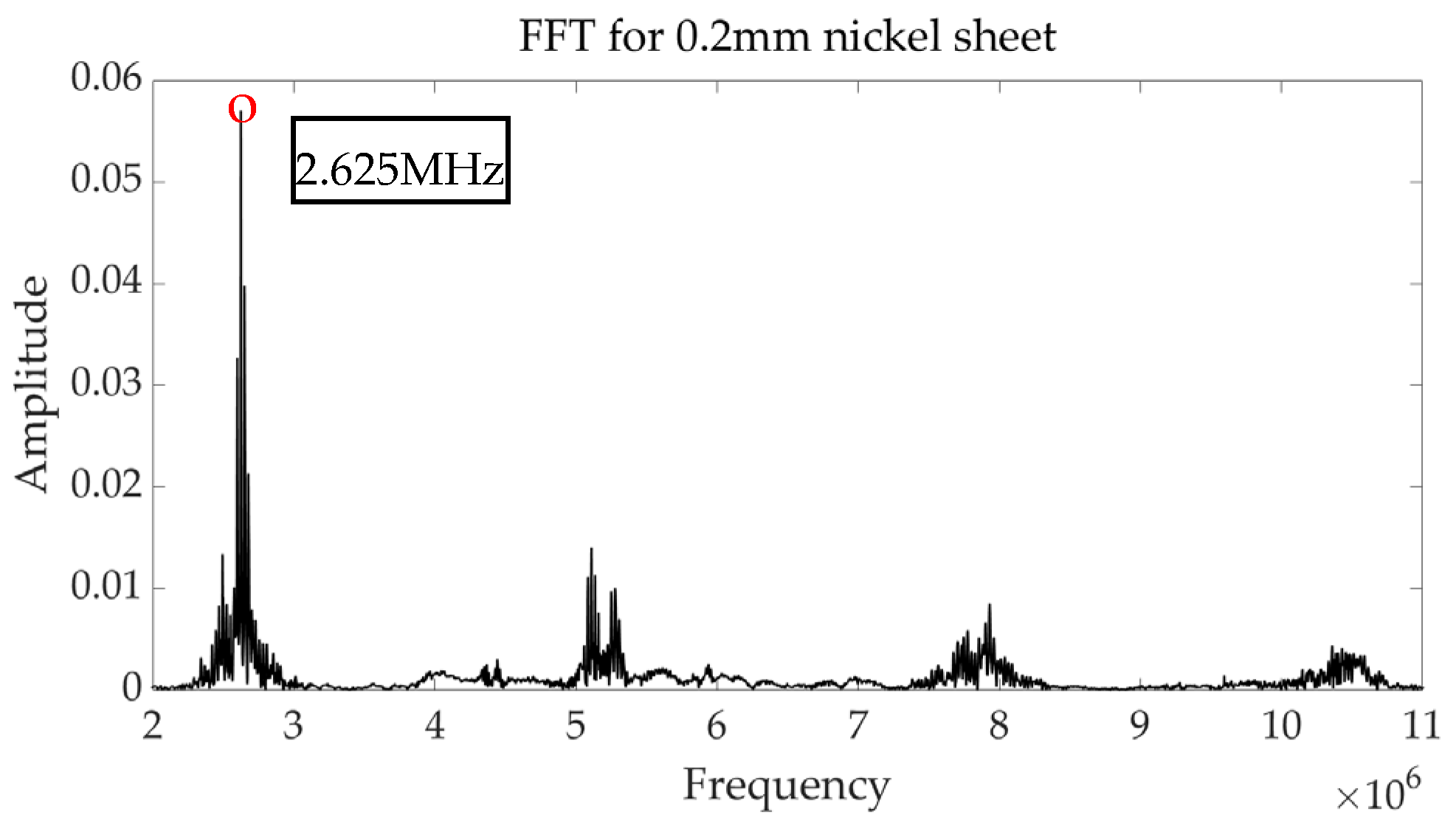
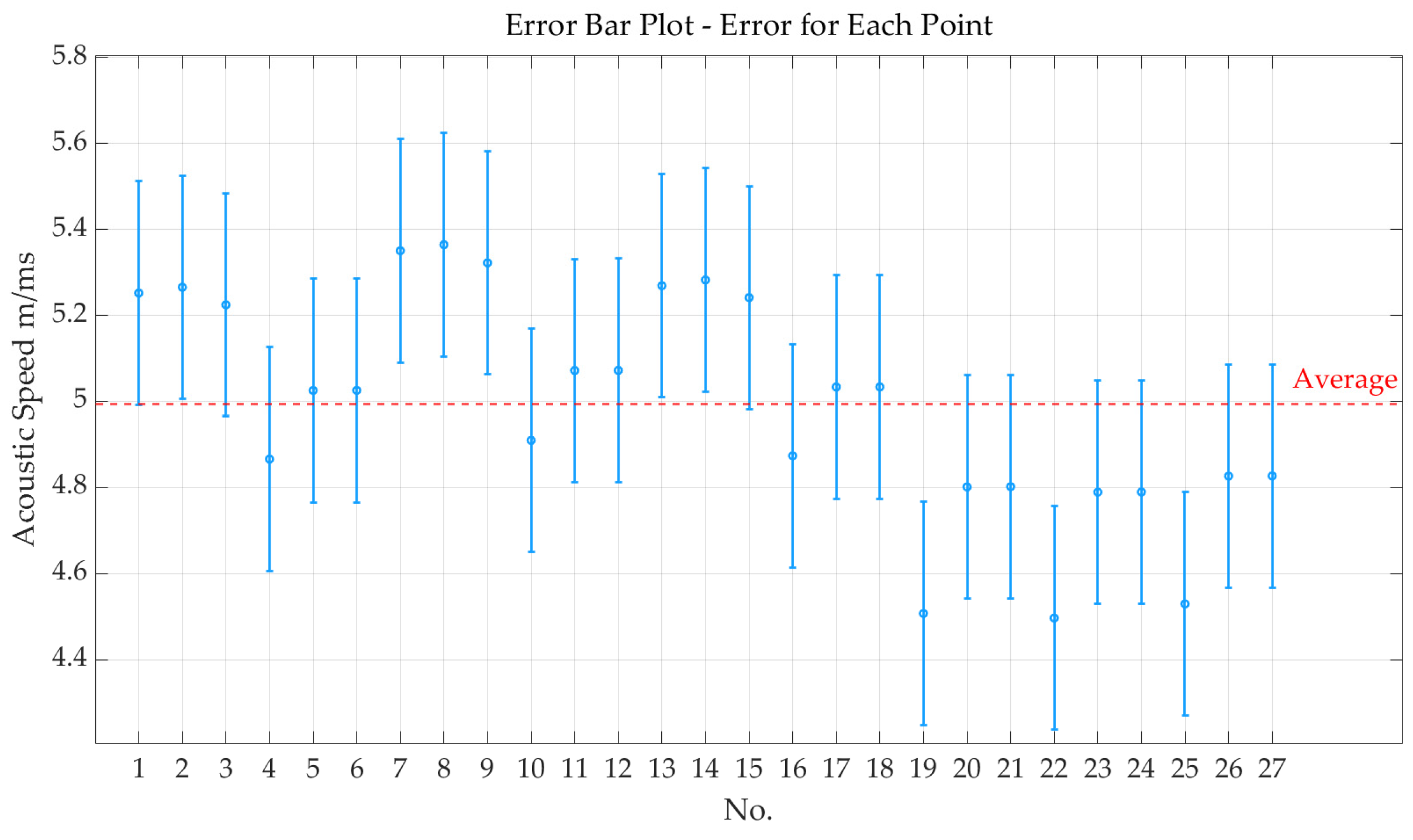
| No. | Thickness (mm) | Length (mm) |
|---|---|---|
| 1; 2; 3 | 0.2 | 100 |
| 4; 5; 6 | 0.2 | 150 |
| 7; 8; 9 | 0.2 | 200 |
| Length | No. | ToP 1 | ToP 2 | ToP 3 | ToP 4 | ToP 5 | ToP 6 | Ave. Time Interval |
|---|---|---|---|---|---|---|---|---|
| 100 mm | 1 | 3.8828 | 7.7274 | 11.652 | 15.614 | 19.427 | 23.274 | 3.8782 |
| 2 | 3.8422 | 7.7247 | 11.646 | 15.529 | 19.377 | 23.263 | 3.9154 | |
| 3 | 3.8422 | 7.7244 | 11.606 | 15.455 | 19.379 | 23.266 | 3.8847 | |
| 153 mm | 4 | 5.7022 | 11.599 | 17.611 | 23.506 | 29.325 | 35.184 | 5.8964 |
| 5 | 5.6990 | 11.709 | 17.601 | 23.478 | 29.335 | 35.155 | 5.8912 | |
| 6 | 5.6222 | 11.593 | 17.602 | 23.459 | 29.337 | 35.157 | 5.9070 | |
| 202 mm | 7 | 7.3573 | 15.377 | 23.781 | 31.569 | / | / | 8.0706 |
| 8 | 7.8166 | 15.779 | 23.727 | 31.629 | / | / | 7.9375 | |
| 9 | 7.8191 | 15.758 | 23.766 | 31.631 | / | / | 7.9373 |
| △L (×10−3 m) | △t (×10−2 ms) | c (m/ms) |
|---|---|---|
| 53 | 2.0054 | 5.2857 |
| 49 | 2.0836 | 4.7034 |
| 102 | 4.0890 | 4.9890 |
| No. | △L (×10−3 m) | △t (×10−2 ms) | c (m/ms) |
|---|---|---|---|
| 1–4 | 53 | 2.0182 | 5.2522 |
| 1–5 | 53 | 2.0130 | 5.2658 |
| 1–6 | 53 | 2.0288 | 5.2248 |
| 1–7 | 102 | 4.1924 | 4.8659 |
| 1–8 | 102 | 4.0593 | 5.0255 |
| 1–9 | 102 | 4.0591 | 5.0257 |
| 2–4 | 53 | 1.9810 | 5.3508 |
| 2–5 | 53 | 1.9758 | 5.3649 |
| 2–6 | 53 | 1.9916 | 5.3224 |
| 2–7 | 102 | 4.1552 | 4.9095 |
| 2–8 | 102 | 4.0221 | 5.0720 |
| 2–9 | 102 | 4.0219 | 5.0722 |
| 3–4 | 53 | 2.0117 | 5.2692 |
| 3–5 | 53 | 2.0065 | 5.2828 |
| 3–6 | 53 | 2.0223 | 5.2416 |
| 3–7 | 102 | 4.1859 | 4.8735 |
| 3–8 | 102 | 4.0528 | 5.0336 |
| 3–9 | 102 | 4.0526 | 5.0338 |
| 4–7 | 49 | 2.1742 | 4.5074 |
| 4–8 | 49 | 2.0411 | 4.8013 |
| 4–9 | 49 | 2.0409 | 4.8018 |
| 5–7 | 49 | 2.1794 | 4.4967 |
| 5–8 | 49 | 2.0463 | 4.7891 |
| 5–9 | 49 | 2.0461 | 4.7896 |
| 6–7 | 49 | 2.1636 | 4.5295 |
| 6–8 | 49 | 2.0305 | 4.8264 |
| 6–9 | 49 | 2.0303 | 4.8269 |
| Guided Waves Mode | Phase Velocity m/ms | Group Velocity m/ms |
|---|---|---|
| S0 | 5.0195 | 4.9802 |
| A0 | 1.8336 | 2.7909 |
| S1 | / | / |
| A1 | / | / |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Y.; Kang, Y.; Wang, K.; Guo, Y.; Tu, J.; Feng, B. Coil-Only High-Frequency Lamb Wave Generation in Nickel Sheets. Sensors 2024, 24, 7141. https://doi.org/10.3390/s24227141
Song Y, Kang Y, Wang K, Guo Y, Tu J, Feng B. Coil-Only High-Frequency Lamb Wave Generation in Nickel Sheets. Sensors. 2024; 24(22):7141. https://doi.org/10.3390/s24227141
Chicago/Turabian StyleSong, Yini, Yihua Kang, Kai Wang, Yizhou Guo, Jun Tu, and Bo Feng. 2024. "Coil-Only High-Frequency Lamb Wave Generation in Nickel Sheets" Sensors 24, no. 22: 7141. https://doi.org/10.3390/s24227141
APA StyleSong, Y., Kang, Y., Wang, K., Guo, Y., Tu, J., & Feng, B. (2024). Coil-Only High-Frequency Lamb Wave Generation in Nickel Sheets. Sensors, 24(22), 7141. https://doi.org/10.3390/s24227141






