GPS-Based Hidden Markov Models to Document Pastoral Mobility in the Sahel
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
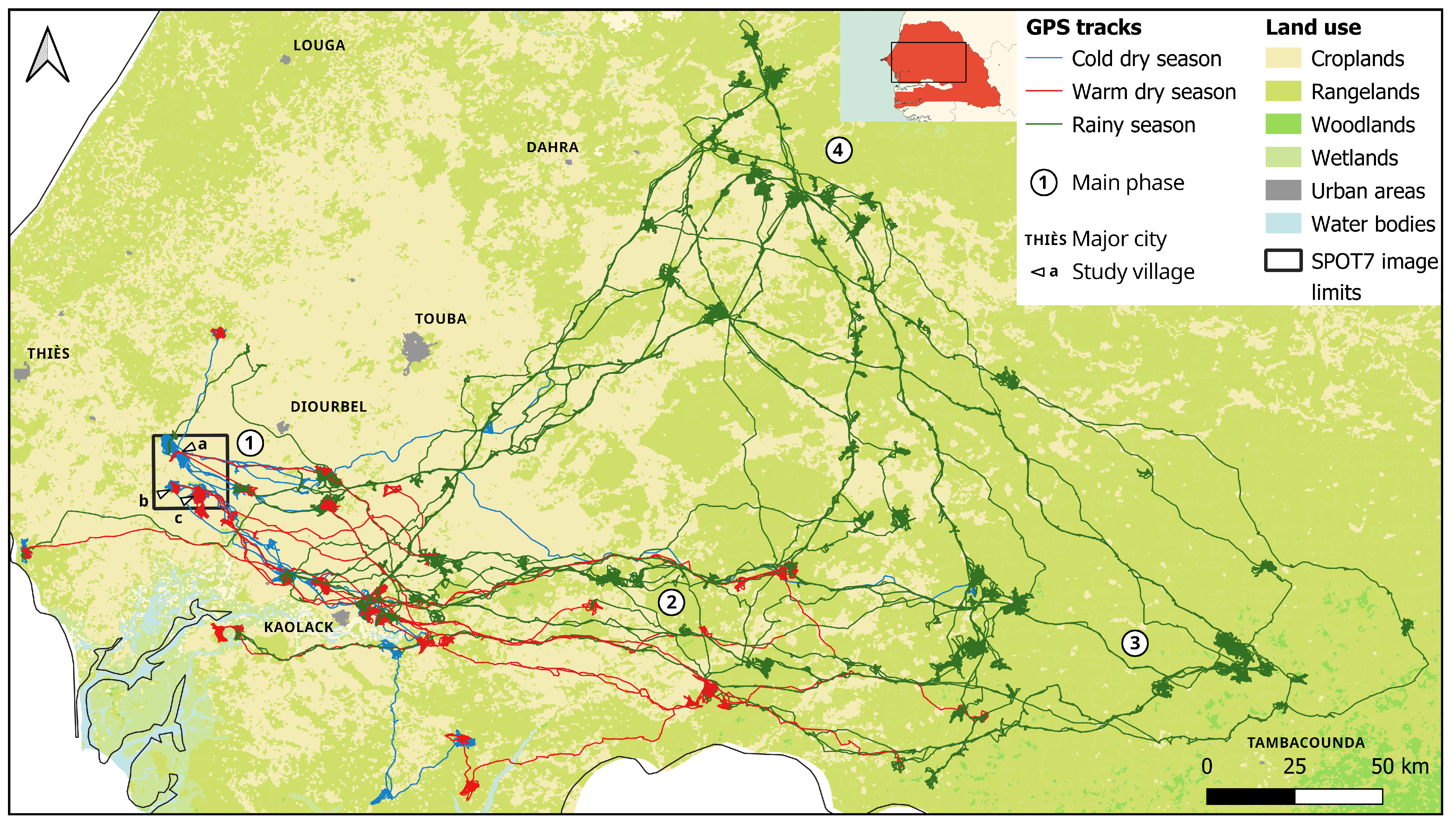
2.1. Case Study: Senegal Pastoral Livestock Systems
2.2. Sampling Design, GPS Collars and Data Collection
2.3. Preparation of GPS and Satellite-Based Land-Use Data
2.4. The Hidden Markov Behaviour Model
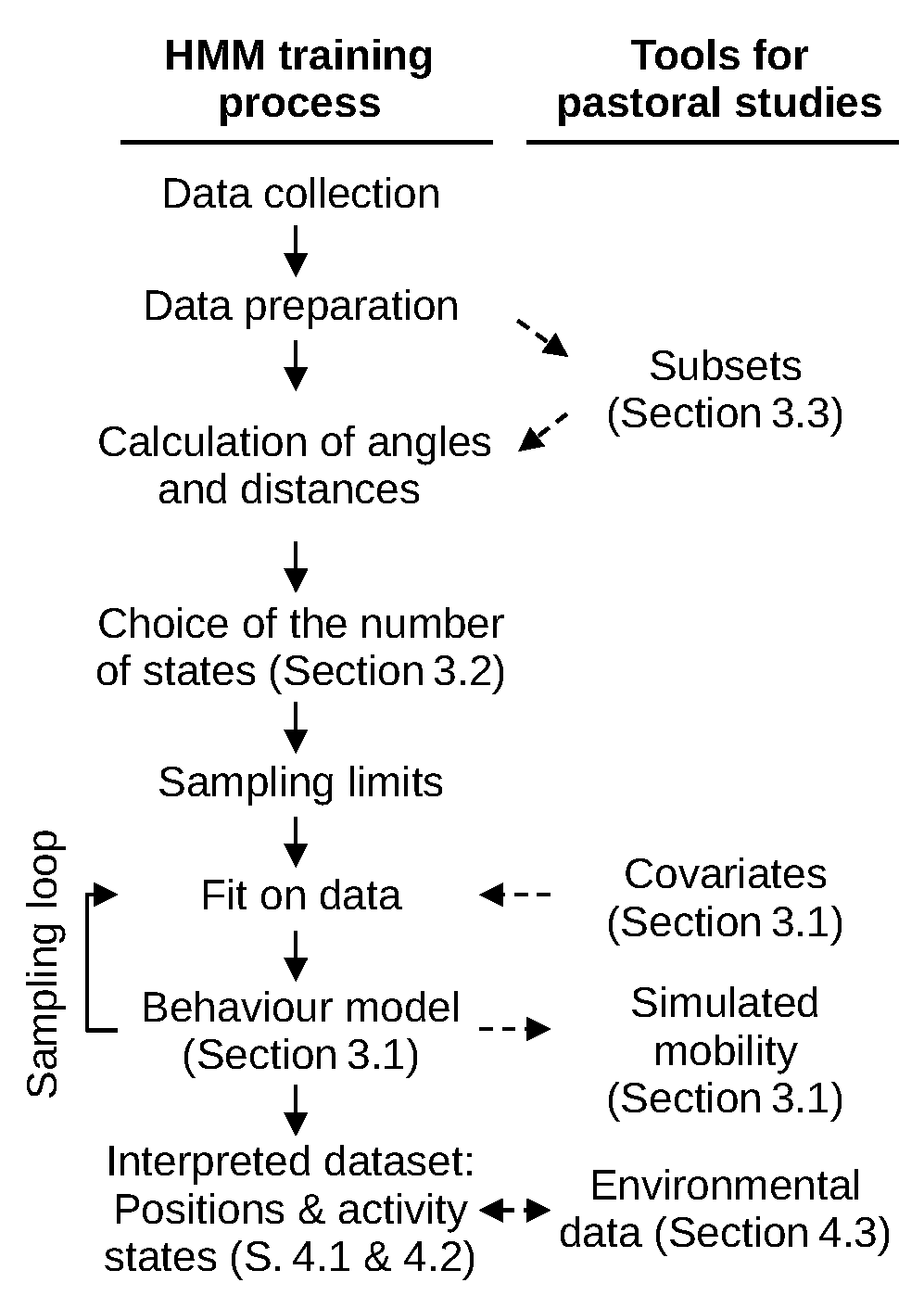
3. Methodological Results—Producing an HMM for West African Pastoral Systems
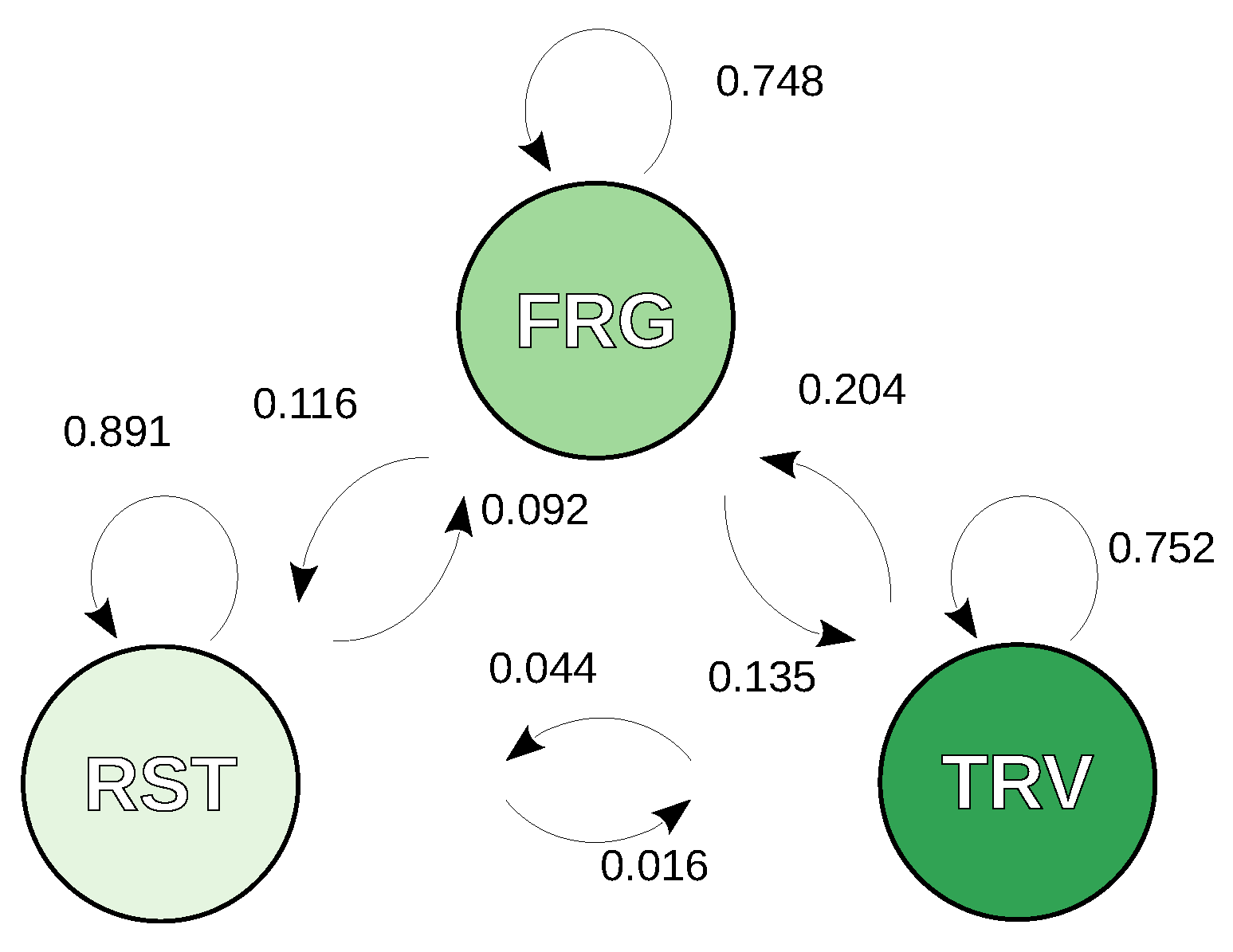
3.1. Activity States Definition and Markov Behavioural Model
3.2. Selecting the Number of States
3.3. Fitting Models on Subsets of Data for Transhumant and Resident Herds
4. Thematic Results—Using the Observed Trajectories and Their Associated Activity States
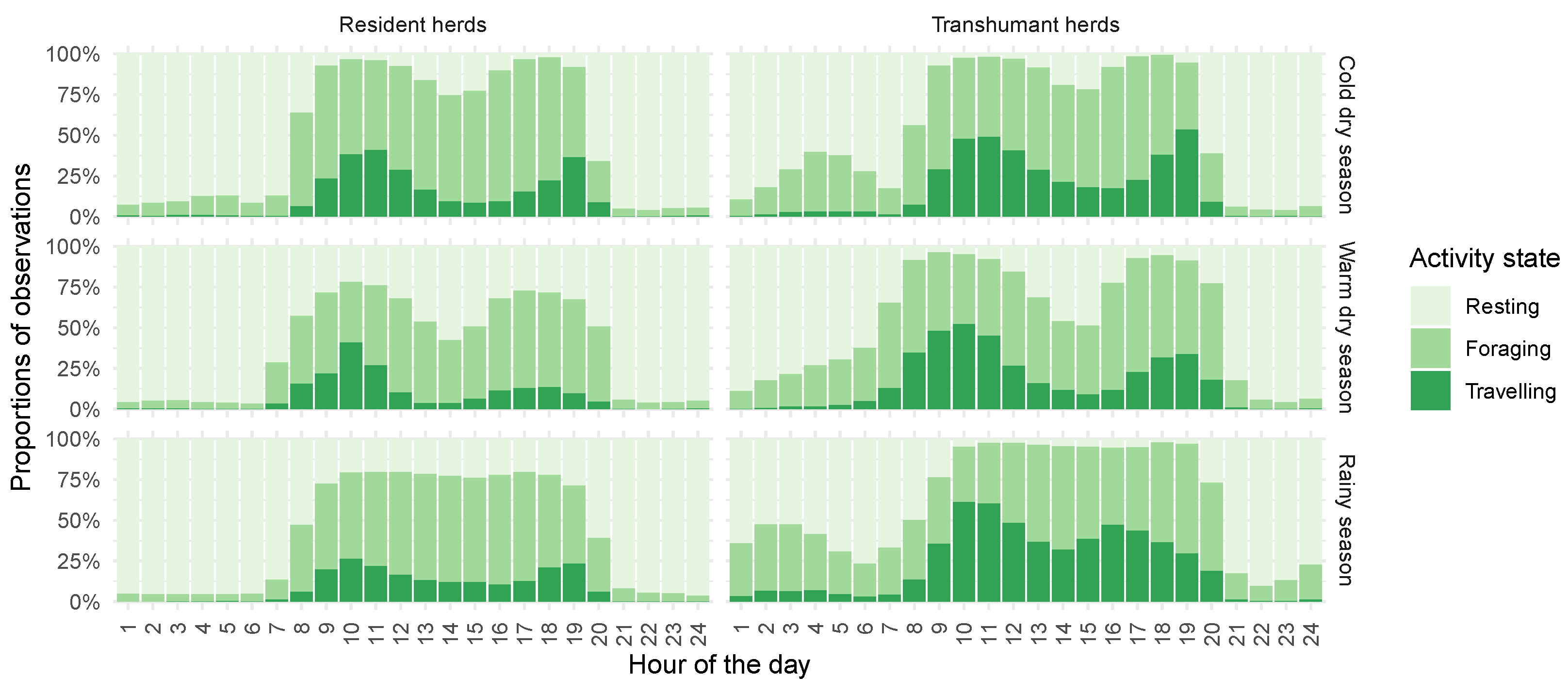
4.1. Identifying Key Features of Herd Behaviour
4.2. Transhumance as Phasic, Seasonal Journeys
4.3. Spatial Repartition of Cattle Activities
5. Discussion
5.1. Limits Inherent to the Data Sources
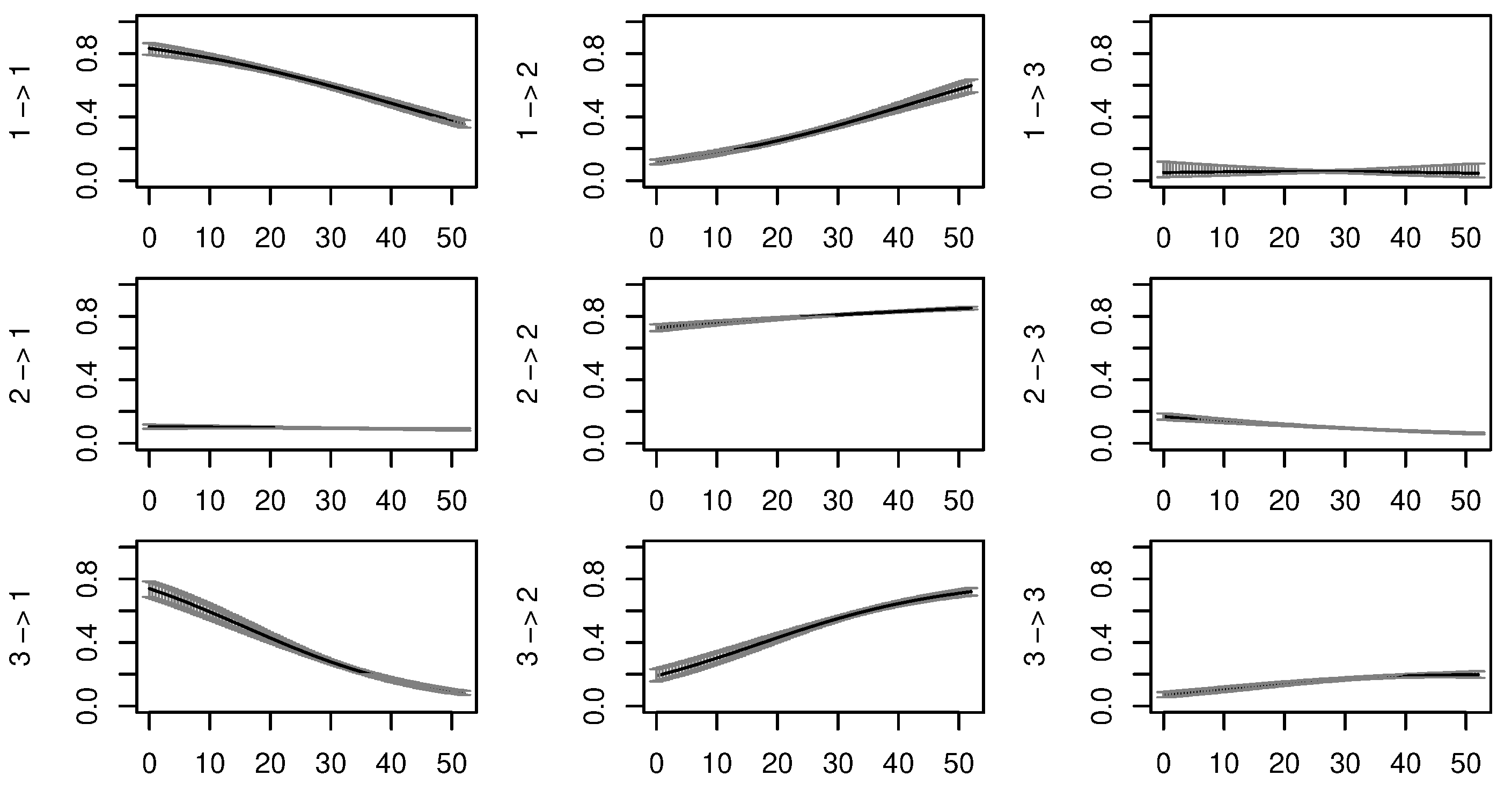
5.2. Model Fit, Validity and Means of Improvement
5.3. Herd Behaviour
5.4. Herding Behaviour and Mobility Patterns in the Transhumance Journey
5.5. A Methodology to Produce Original Insights on Pastoral Practices
5.6. GPS Surveys and HMM for Sahel Pastoralism: Some Prospects
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vayssières, J.; Alary, V.; Aubron, C.; Corniaux, C.; Duteurtre, G.; Ickowicz, A.; Juanès, X.; Messad, S.; Tillard, E.; Wane, A. Multi-Criteria Assessment of Efficiency to Account for the Multifunctionality of Livestock Grazing Systems. In Livestock Grazing Systems and Sustainable Development in the Mediterranean and Tropical Areas: Recent Knowledge on Their Strengths and Weaknesses; Éditions Quae: Versailles, France, 2023. [Google Scholar]
- Dugué, P. Les Transferts de Fertilité dus à l’élevage en Zone de Savane. 1998. Available online: https://agritrop.cirad.fr/390390/ (accessed on 18 June 2024).
- Dugué, P.; Vall, E.; Lecomte, P.; Klein, H.D.; Rollin, D. Évolution des Relations Entre l’Agriculture et l’élevage dans les Savanes d’Afrique de l’Ouest et du Centre: Un Nouveau Cadre d’Analyse pour Améliorer les Modes d’Intervention et Favoriser les Processus d’Innovation. 2004. Available online: https://agritrop.cirad.fr/524553/ (accessed on 18 June 2024).
- Thébaud, B.; Corniaux, C.; François, A.; Powell, A. Etude sur la Transhumance au Sahel (2014-2017)-Dix Constats sur la Mobilité du bétail en Afrique de l’Ouest. 2018. Available online: https://agritrop.cirad.fr/589455/1/Brochure%20FINAL%2018-01-18.pdf (accessed on 13 June 2024).
- Jaikaeo, C.; Jansang, A.; Li-On, S.; Kitisriworapan, S.; Tangtrongpairoj, W.; Phonphoem, A.; Valls-Fox, H.; Menassol, J.B.; Viet, D.H.; Sripiboon, S. Design and Field Test of a Low-Cost Device for Real-Time Livestock Tracking Using GPS/LoRa Communication. Appl. Eng. Agric. 2022, 38, 885–901. [Google Scholar] [CrossRef]
- Scriban, A.; Nabeneza, S.; Salgado, P. Mobility, Behaviour and Land-Use Data from GPS Tracking and Hidden Markov Model Training on Cattle Herds in Sahel Agropastoral Systems. 2024. Available online: https://dataverse.cirad.fr/dataset.xhtml?persistentId=doi:10.18167/DVN1/GHJKQO (accessed on 13 June 2024).
- Scriban, A.; Nabeneza, S.; Cornelis, D.; Salgado, P. Herds Activity Mapping and Analytical Classification; Cirad: Paris, France, 2024; Available online: https://gitlab.cirad.fr/selmet/hamac (accessed on 15 October 2024).
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World Map of the Köppen-Geiger Climate Classification Updated. metz 2006, 15, 259–263. [Google Scholar] [CrossRef] [PubMed]
- Thibaudeau, L.; Garambois, N.; Diop, P.A. Diagnostic Agraire d’une petite région du Bassin Arachidier sénégalais-Bambey. Master’s Thesis, AgroParisTech, Paris, France, 2015. [Google Scholar]
- ClimateData.org. Climate Data for Cities Worldwide. 2024. Available online: https://en.climate-data.org/ (accessed on 18 June 2024).
- Audouin, E.; Vayssières, J.; Odru, M.; Masse, D.; Dorégo, G.; Delaunay, V.; Lecomte, P. Réintroduire l’élevage pour accroître la durabilité des terroirs villageois d’Afrique de l’Ouest: Le cas du bassin arachidier au Sénégal. In Les Sociétés Rurales Face aux Changements Environnementaux en Afrique de l’Ouest; Sultan, B., Lalou, R., Oumarou, A., Sanni, M., Soumaré, A., Eds.; IRD: Marseille, France, 2015; pp. 403–427. Available online: https://horizon.documentation.ird.fr/exl-doc/pleins_textes/divers19-05/010068402.pdf (accessed on 3 December 2020).
- Assouma, M.H.; Hiernaux, P.; Lecomte, P.; Ickowicz, A.; Bernoux, M.; Vayssières, J. Contrasted Seasonal Balances in a Sahelian Pastoral Ecosystem Result in a Neutral Annual Carbon Balance. J. Arid. Environ. 2019, 162, 62–73. [Google Scholar] [CrossRef]
- Faye, A.; Lericollais, A.; Sissokho, M. L’élevage en pays sereer: Du modèle d’intégration aux troupeaux sans pâturages. In Paysans Sereer; Lericollais, A., Ed.; IRD Éditions: Marseille, France, 1999; pp. 299–330. Available online: https://books.openedition.org/irdeditions/15945 (accessed on 15 October 2024).
- Odru, M. Flux de Biomasse et Renouvellement de la Fertilité des Sols à L’échelle du Terroir (Diohine). Master’s Thesis, ISTOM, Cergy Pontoise, France, 2013. [Google Scholar]
- Reiff, C.; Gros, C. Analyse-Diagnostic du systèMe Agraire des Paysans Sérères au Coeur du <<bassin arachidier>>—Sénégal. Master’s Thesis, INA-PG, Paris, France, 2004. [Google Scholar]
- Boffa, J.M.; Sanders, J.; Taonda, S.J.B.; Hiernaux, P.; Bagayoko, M.; Ncube, S.; Nyamangara, J. The Agropastoral Farming System: Achieving Adaptation and Harnessing Opportunities under Duress. In Farming Systems and Food Security in Africa; Routledge: London, UK, 2019. [Google Scholar]
- Marega, O.; Mering, C.; Meunier, V. Sahelian agro-pastoralists in the face of social and environmental changes: New issues, new risks, new transhumance axe. LEspace Geogr. 2018, 47, 235–260. [Google Scholar]
- Timpong-Jones, E.C.; Samuels, I.; Sarkwa, F.O.; Oppong-Anane, K.; Majekodumni, A.O. Transhumance Pastoralism in West Africa–Its Importance, Policies and Challenges. Afr. J. Range Forage Sci. 2023, 40, 114–128. [Google Scholar] [CrossRef]
- Meyer, C. Zébu Gobra-Dictionnaire des Sciences Animales. 2021. Available online: http://dico-sciences-animales.cirad.fr/liste-mots.php?fiche=29402 (accessed on 31 May 2021).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2024. [Google Scholar]
- Michelot, T.; Langrock, R.; Patterson, T.A. moveHMM: An R Package for the Statistical Modelling of Animal Movement Data Using Hidden Markov Models. Methods Ecol. Evol. 2016, 7, 1308–1315. [Google Scholar] [CrossRef]
- Ndiaye, M.L.; Soti, V.; Vayssières, J. Analyse par Télédétection de la Dynamique d’Occupation du sol Dans Trois Terroirs Villageois du Vieux Bassin Arachidier au Sénégal sur la Période 1968–2016; Rapport d’étude; Cirad: Dakar, Sénégal, 2016. [Google Scholar]
- FAO. Land Cover of Senegal-Globcover Regional. 2008. Available online: https://data.apps.fao.org/catalog/iso/325b69b5-69a7-4b86-bbbf-44644d0e0b2b (accessed on 28 June 2024).
- QGIS Development Team. QGIS Geographic Information System; QGIS Association: Berne, Switzerland, 2023; Available online: https://www.qgis.org (accessed on 1 September 2023).
- Nathan, R.; Getz, W.M.; Revilla, E.; Holyoak, M.; Kadmon, R.; Saltz, D.; Smouse, P.E. A Movement Ecology Paradigm for Unifying Organismal Movement Research. Proc. Natl. Acad. Sci. USA 2008, 105, 19052–19059. [Google Scholar] [CrossRef]
- Augustine, D.J.; Derner, J.D. Assessing Herbivore Foraging Behavior with GPS Collars in a Semiarid Grassland. Sensors 2013, 13, 3711–3723. [Google Scholar] [CrossRef]
- Williams, M.L.; James, W.P.; Rose, M.T. Fixed-Time Data Segmentation and Behavior Classification of Pasture-Based Cattle: Enhancing Performance Using a Hidden Markov Model. Comput. Electron. Agric. 2017, 142, 585–596. [Google Scholar] [CrossRef]
- Edelhoff, H.; Signer, J.; Balkenhol, N. Path Segmentation for Beginners: An Overview of Current Methods for Detecting Changes in Animal Movement Patterns. Mov. Ecol. 2016, 4, 21. [Google Scholar] [CrossRef]
- Zampaligré, N. The Role of Ligneous Vegetation for Livestock Nutrition in the Sub-Sahelian and Sudanian Zones of West Africa: Potential Effects of Climate Change. Ph.D. Thesis, University of Kassel, Kassel, Germany, 2012. [Google Scholar]
- Pohle, J.; Langrock, R.; Van Beest, F.M.; Schmidt, N.M. Selecting the Number of States in Hidden Markov Models: Pragmatic Solutions Illustrated Using Animal Movement. JABES 2017, 22, 270–293. [Google Scholar] [CrossRef]
- Sane, Y.; Panthou, G.; Bodian, A.; Vischel, T.; Lebel, T.; Dacosta, H.; Quantin, G.; Wilcox, C.; Ndiaye, O.; Diongue-Niang, A.; et al. Intensity–Duration–Frequency (IDF) Rainfall Curves in Senegal. Nat. Hazards Earth Syst. Sci. 2018, 18, 1849–1866. [Google Scholar] [CrossRef]
- Degrande, R.; Menassol, J.B. Development of a Behavioural Method to Identify Central Individuals in a Domestic Sheep Herd-Master’s Degree Memoir in Ethology. Master’s Thesis, Strasbourg University, Strasbourg, France, 2019. [Google Scholar]
- Etienne, M.P. The Hidden Part of Markovian Stochastic Processes for Biology and Ecology; HDR, Université de Rennes 1: Rennes, France, 2021. [Google Scholar]
- Beumer, L.T.; Pohle, J.; Schmidt, N.M.; Chimienti, M.; Desforges, J.P.; Hansen, L.H.; Langrock, R.; Pedersen, S.H.; Stelvig, M.; Van Beest, F.M. An Application of Upscaled Optimal Foraging Theory Using Hidden Markov Modelling: Year-Round Behavioural Variation in a Large Arctic Herbivore. Mov. Ecol. 2020, 8, 25. [Google Scholar] [CrossRef] [PubMed]
- Franke, A.; Caelli, T.; Hudson, R.J. Analysis of Movements and Behavior of Caribou (Rangifer Tarandus) Using Hidden Markov Models. Ecol. Model. 2004, 173, 259–270. [Google Scholar] [CrossRef]
- Bailey, D.W.; Provenza, F.D. Mechanisms Determining Large-Herbivore Distribution. In Resource Ecology; Prins, H.H.T., Van Langevelde, F., Eds.; Springer: Dordrecht, The Netherlands, 2008; pp. 7–28. [Google Scholar] [CrossRef]
- Turner, M.D.; Schlecht, E. Livestock Mobility in Sub-Saharan Africa: A Critical Review. Pastoralism 2019, 9, 1–15. [Google Scholar] [CrossRef]
- Zampaligré, N.; Schlecht, E. Livestock Foraging Behaviour on Different Land Use Classes along the Semi-Arid to Sub-Humid Agro-Ecological Gradient in West Africa. Environ. Dev. Sustain. 2018, 20, 731–748. [Google Scholar] [CrossRef]
- Leos-Barajas, V.; Photopoulou, T.; Langrock, R.; Patterson, T.A.; Watanabe, Y.Y.; Murgatroyd, M.; Papastamatiou, Y.P. Analysis of Animal Accelerometer Data Using Hidden Markov Models. Methods Ecol. Evol. 2017, 8, 161–173. [Google Scholar] [CrossRef]
- Nams, V.O. Combining Animal Movements and Behavioural Data to Detect Behavioural States. Ecol. Lett. 2014, 17, 1228–1237. [Google Scholar] [CrossRef]
- Cornelis, D. Ecologie du Déplacement du Buffle de Savane Ouest-Africain. Ph.D. Thesis, Montpellier 2 University, Montpellier, France, 2011. [Google Scholar]
- Chirat, G.; Groot, J.C.; Messad, S.; Bocquier, F.; Ickowicz, A. Instantaneous Intake Rate of Free-Grazing Cattle as Affected by Herbage Characteristics in Heterogeneous Tropical Agro-Pastoral Landscapes. Appl. Anim. Behav. Sci. 2014, 157, 48–60. [Google Scholar] [CrossRef]
- Grillot, M.; Guerrin, F.; Gaudou, B.; Masse, D.; Vayssières, J. Multi-Level Analysis of Nutrient Cycling within Agro-Sylvo-Pastoral Landscapes in West Africa Using an Agent-Based Model. Environ. Model. Softw. 2018, 107, 267–280. [Google Scholar] [CrossRef]
- Garenne, M.; Lombard, J. La migration dirigée des Sereer vers les Terres Neuves (Sénégal). In Migration, Changements Sociaux et Développement; JOURNEES DEMOGRAPHIQUES DE I’ORSTO: Paris, France, 1988; pp. 317–332. Available online: https://www.researchgate.net/profile/Michel_Garenne/publication/32983468_La_migration_dirige_des_Sereer_vers_les_Terres_Neuves_(Sngal)/links/02e7e5249c819e9889000000.pdf (accessed on 19 February 2016).
- Shinjo, H.; Hayashi, K.; Abdoulaye, T.; Kosaki, T. Management of Livestock Excreta through Corralling Practice; Sedentary Pastoralists: Sahelian Region, West Africa, 2008; p. 7. [Google Scholar] [CrossRef]
- Guo, Y.; Poulton, G.; Corke, P.; Bishop-Hurley, G.J.; Wark, T.; Swain, D.L. Using Accelerometer, High Sample Rate GPS and Magnetometer Data to Develop a Cattle Movement and Behaviour Model. Ecol. Model. 2009, 220, 2068–2075. [Google Scholar] [CrossRef]
- McClintock, B.T.; Michelot, T. momentuHMM: R Package for Analysis of Telemetry Data Using Generalized Multivariate Hidden Markov Models of Animal Movement. Seattle, USA. 2021. Available online: https://cran.r-project.org/web/packages/momentuHMM/vignettes/momentuHMM.pdf (accessed on 15 October 2024).
- Signer, J.; Fieberg, J.; Avgar, T. Animal Movement Tools (Amt): R Package for Managing Tracking Data and Conducting Habitat Selection Analyses. Ecol. Evol. 2019, 9, 880–890. [Google Scholar] [CrossRef] [PubMed]
- Traore, C.A.D.G.; Delay, E.; Diop, D.; Bah, A. Agent-Based Model for Analyzing the Impact of Movement Factors of Sahelian Transhumant Herds. Hum-Cent Intell. Syst. 2024, 4, 363–381. [Google Scholar] [CrossRef]
- Gersie, S. Predicting Cattle Grazing Distributions: An Agent-Based Modeling Approach. Master’s Thesis, Colorado State University, Fort Collins, CO, USA, 2020. [Google Scholar]
- Searle, K.R.; Hunt, L.P.; Gordon, I.J. Individualistic Herds: Individual Variation in Herbivore Foraging Behavior and Application to Rangeland Management. Appl. Anim. Behav. Sci. 2010, 122, 1–12. [Google Scholar] [CrossRef]
- Assouma, M.H.; Lecomte, P.; Corniaux, C.; Hiernaux, P.; Ickowicz, A.; Vayssières, J. Territoires d’élevage pastoral au Sahel: Un bilan carbone avec un potentiel inattendu d’atténuation du changement climatique. Perspective 2019, 52, 1–4. [Google Scholar] [CrossRef]
- Butt, B. Pastoral Resource Access and Utilization: Quantifying the Spatial and Temporal Relationships between Livestock Mobility, Density and Biomass Availability in Southern Kenya. Land Degrad. Dev. 2010, 21, 520–539. [Google Scholar] [CrossRef]
- Ickowicz, A.; Mbaye, M. Forêts soudaniennes et alimentation des bovins au Sénégal: Potentiel et limites. BOIS FORETS DES TROPIQUES 2001, 270, 47–61. [Google Scholar]
- Pauler, C.M.; Isselstein, J.; Suter, M.; Berard, J.; Braunbeck, T.; Schneider, M.K. Choosy Grazers: Influence of Plant Traits on Forage Selection by Three Cattle Breeds. Funct. Ecol. 2020, 34, 980–992. [Google Scholar] [CrossRef]
- Auerswald, K.; Mayer, F.; Schnyder, H. Coupling of Spatial and Temporal Pattern of Cattle Excreta Patches on a Low Intensity Pasture. Nutr. Cycl. Agroecosyst. 2010, 88, 275–288. [Google Scholar] [CrossRef]
- Chirat, G. Description et Modélisation du Comportement Spatial et Alimentaire de Troupeaux Bovins en Libre Pâture sur Parcours, en Zone Tropicale Sèche. Ph.D. Thesis, Montpellier SupAgro, Montpellier, France, 2010. [Google Scholar]
- Chirat, G.; Ickowicz, A.; Diaf, H.; Bocquier, F. Etude Des Facteurs Clés Du Comportement Spatial et Alimentaire de Troupeaux Bovins En Libre Pâture Sur Un Territoire Agrosylvopastoral Tropical. In Proceedings of the 3R—Rencontres Autour des Recherches sur les Ruminants, Paris, France, 3–4 December 2008. [Google Scholar]
- Jahel, C.; Lenormand, M.; Seck, I.; Apolloni, A.; Toure, I.; Faye, C.; Sall, B.; Lo, M.; Diaw, C.S.; Lancelot, R. Mapping Livestock Movements in Sahelian Africa. Sci. Rep. 2020, 10, 1–12. [Google Scholar] [CrossRef]
- Leclerc, G.; Sy, O. Des indicateurs spatialisés des transhumances pastorales au Ferlo. Cybergeo 2011, 532, 23661. [Google Scholar] [CrossRef]
- Bataille, A.; Salami, H.; Seck, I.; Lo, M.M.; Ba, A.; Diop, M.; Sall, B.; Faye, C.; Lo, M.; Kaba, L.; et al. Combining Viral Genetic and Animal Mobility Network Data to Unravel Peste Des Petits Ruminants Transmission Dynamics in West Africa. PLoS Pathog. 2021, 17, e1009397. [Google Scholar] [CrossRef] [PubMed]
- Blanchard, M.; Valls-Fox, H.; Duong, H.V.; Cesaro, J.D.; Li-On, S.; Phonphoem, A.; Jansang, A.; Jaikaeo, C.; Sripiboon, S.; Sangmalee, A.; et al. Capteurs GPS embarqués à coûts réduits et typologie de systèmes d’élevage en Asie du Sud-Est. In Proceedings of the 3R—Rencontres Autour des Recherches sur les Ruminants, Paris, France, 2–3 December 2020. [Google Scholar]

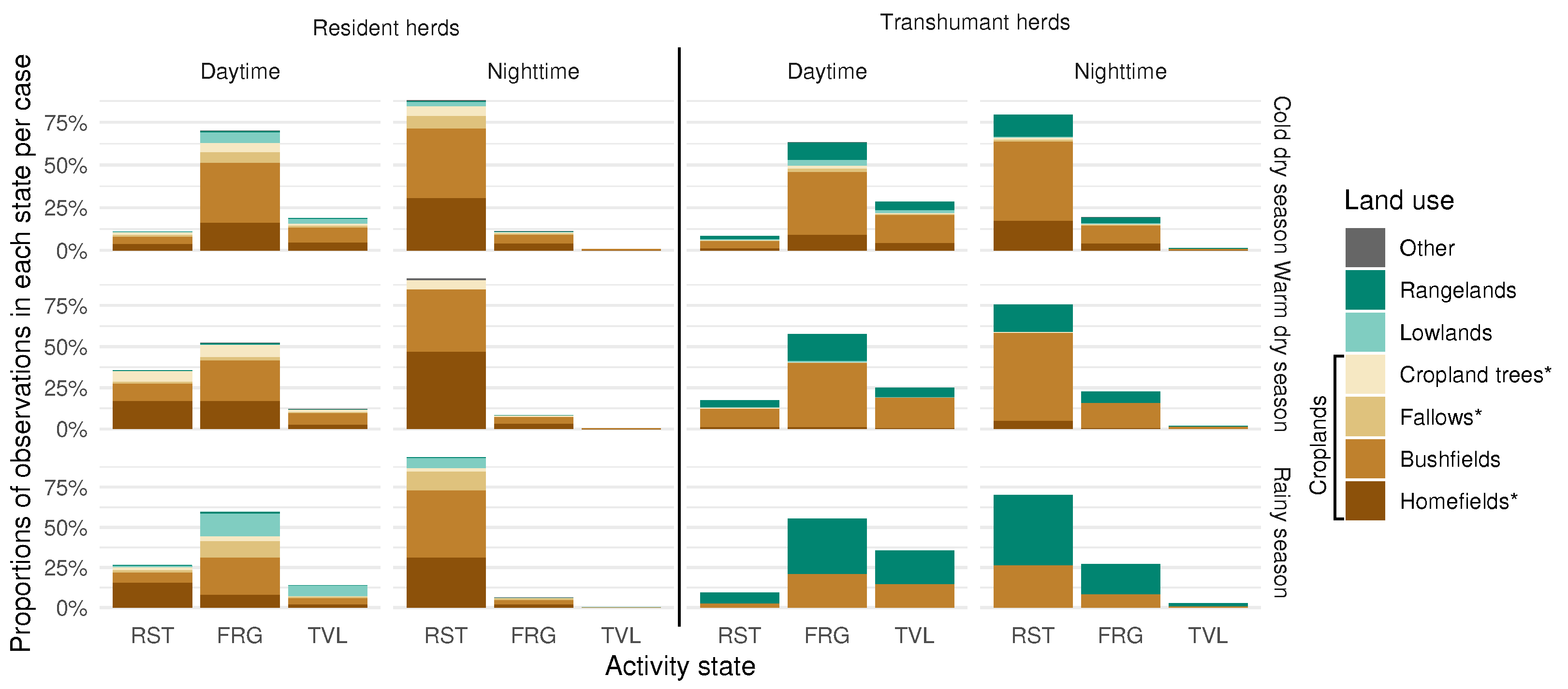
| Resting State | Foraging State | Travelling State | ||||
|---|---|---|---|---|---|---|
| Samp. lim. | Result (±CI 95%) | Samp. lim. | Result (±CI 95%) | Samp. lim. | Result (±CI 95%) | |
| (m/30 min) | 5–100 | 13.53 (13.46–13.61) | 50–250 | 180.1 (178.8–181.5) | 100–1000 | 685.4 (680.6–690.4) |
| (m/30 min) | 5–100 | 11.99 (11.91–12.08) | 50–500 | 149.2 (148.0–150.5) | 100–1000 | 439.8 (436.9–442.9) |
| (rad/30 min) | −3–3 | −3.05 (−3.07–3.03) | −3–3 | 0.00 (−0.0360–0.0361) | −0.5–0.5 | −0.0146 (−0.0211–0.00822) |
| (rad/30 min) | 0.1–1 | 0.29 (0.28–0.30) | 1.5–5 | 0.19 (0.18–0.20) | 1–15 | 1.95 (1.93–1.98) |
| (dimensionless) | (–) | (NA–NA) | (–) | |||
| Simulated trajectories on 10 points |  | 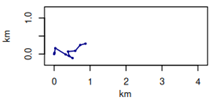 | 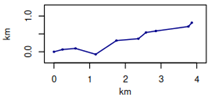 | |||
| St. | Interpretation | ||||||
|---|---|---|---|---|---|---|---|
| m·30 min−1 | m·30 min−1 | rad·30 min−1 | rad·30 min−1 | dimension less | |||
| Two-st. m. (23/44) | 1 | 16 | 14 | −3.06 | 0.32 | Resting | |
| BIC: 488 768 | 2 | 351 | 350 | −0.01 | 0.65 | Moving | |
| Three-state model | 1 | 13 | 12 | −3.05 | 0.29 | Resting | |
| (44/110) | 2 | 180 | 149 | 0.00 | 0.19 | Foraging | |
| BIC: 394 277 | 3 | 685 | 440 | −0.01 | 1.95 | Travelling | |
| Four-state model (6/22) BIC: 337 142 | 1 | 7 | 5 | −3.09 | 0.23 | Resting | |
| 2 | 26 | 19 | −3.03 | 0.38 | Active resting | ||
| 3 | 203 | 174 | 0.03 | 0.22 | Foraging | ||
| 4 | 663 | 458 | −0.02 | 2.11 | Travelling | ||
| 1 | 6 | 4 | −3.09 | 0.23 | Resting | ||
| Five-state model | 2 | 23 | 16 | −3.02 | 0.34 | Active resting | |
| (21/44) | 3 | 144 | 109 | 0.08 | 0.06 | Foraging | |
| BIC: 333 786 | 4 | 472 | 301 | −0.02 | 1.24 | Short travel | |
| 5 | 1421 | 349 | 0.00 | 7.98 | Long travel |
| Resting State | Foraging State | Travelling State | ||||
|---|---|---|---|---|---|---|
| d (m/day) | t (h/day) | d (m/day) | t (h/day) | d (m/day) | t (h/day) | |
| Resident | 116 | 14.9 | 2330 | 6.94 | 3400 | 2.22 |
| Transhu. | 53.2 | 9.57 | 2570 | 8.93 | 6330 | 4.70 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scriban, A.; Nabeneza, S.; Cornelis, D.; Delay, E.; Vayssières, J.; Cesaro, J.-D.; Salgado, P. GPS-Based Hidden Markov Models to Document Pastoral Mobility in the Sahel. Sensors 2024, 24, 6964. https://doi.org/10.3390/s24216964
Scriban A, Nabeneza S, Cornelis D, Delay E, Vayssières J, Cesaro J-D, Salgado P. GPS-Based Hidden Markov Models to Document Pastoral Mobility in the Sahel. Sensors. 2024; 24(21):6964. https://doi.org/10.3390/s24216964
Chicago/Turabian StyleScriban, Arthur, Serge Nabeneza, Daniel Cornelis, Etienne Delay, Jonathan Vayssières, Jean-Daniel Cesaro, and Paulo Salgado. 2024. "GPS-Based Hidden Markov Models to Document Pastoral Mobility in the Sahel" Sensors 24, no. 21: 6964. https://doi.org/10.3390/s24216964
APA StyleScriban, A., Nabeneza, S., Cornelis, D., Delay, E., Vayssières, J., Cesaro, J.-D., & Salgado, P. (2024). GPS-Based Hidden Markov Models to Document Pastoral Mobility in the Sahel. Sensors, 24(21), 6964. https://doi.org/10.3390/s24216964







