A High-Resolution Multipath Delay Measurement Method Using KFSC-WRELAX Algorithm
Abstract
1. Introduction
2. System Architecture
3. Probe Signal Generation
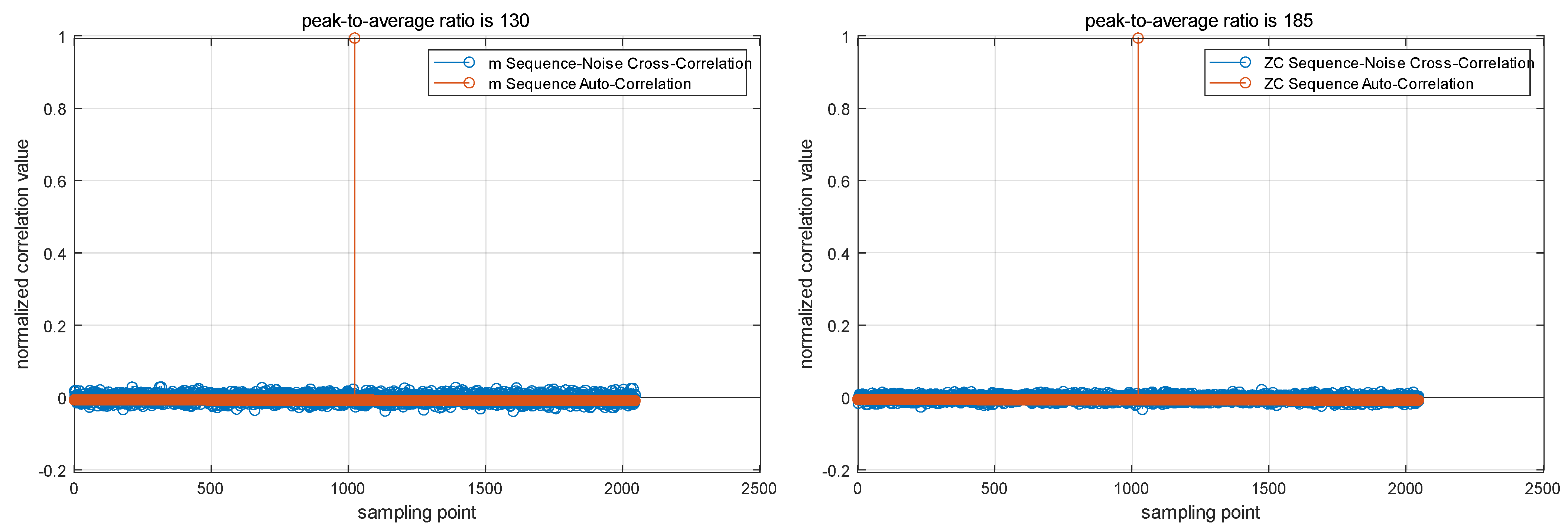
3.1. Pseudorandom Noise Sequence Selection
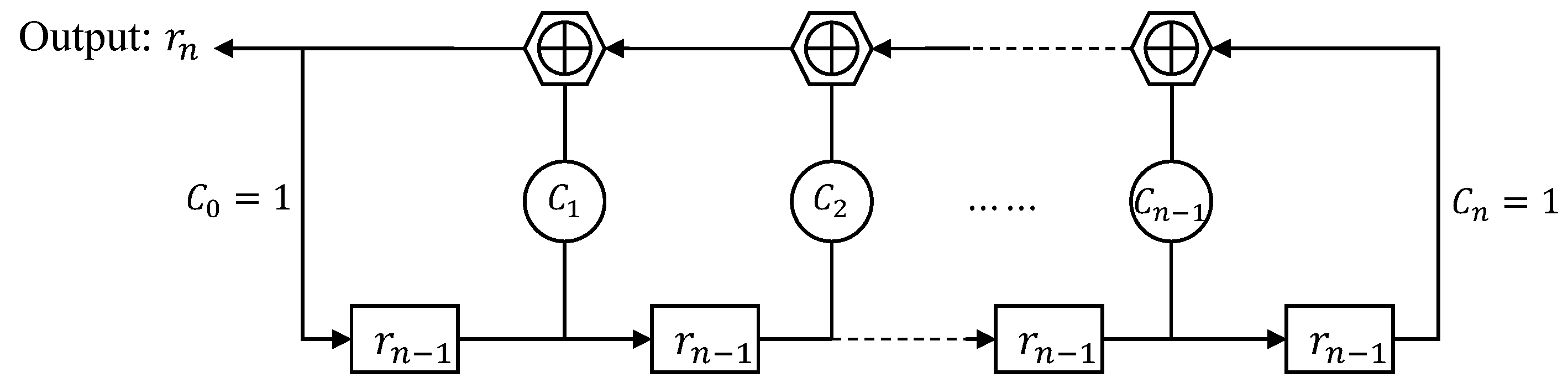
3.2. Linear Feedback Shift Register Generates M-Sequence
3.3. Oversampling and Shaping Filtering
4. Signal Reception Processing
4.1. Multipath Signal Reception
4.2. Kalman Filtering and Sliding Correlation
| Algorithm 1 Implementation of Kalman Filtering |
|
4.3. Channel Parameter Extraction Using the WRELAX Algorithm
- Similarly, when the number of multipath components is L;
5. Simulation Analysis
5.1. The Denoising Performance of the Kalman Filter
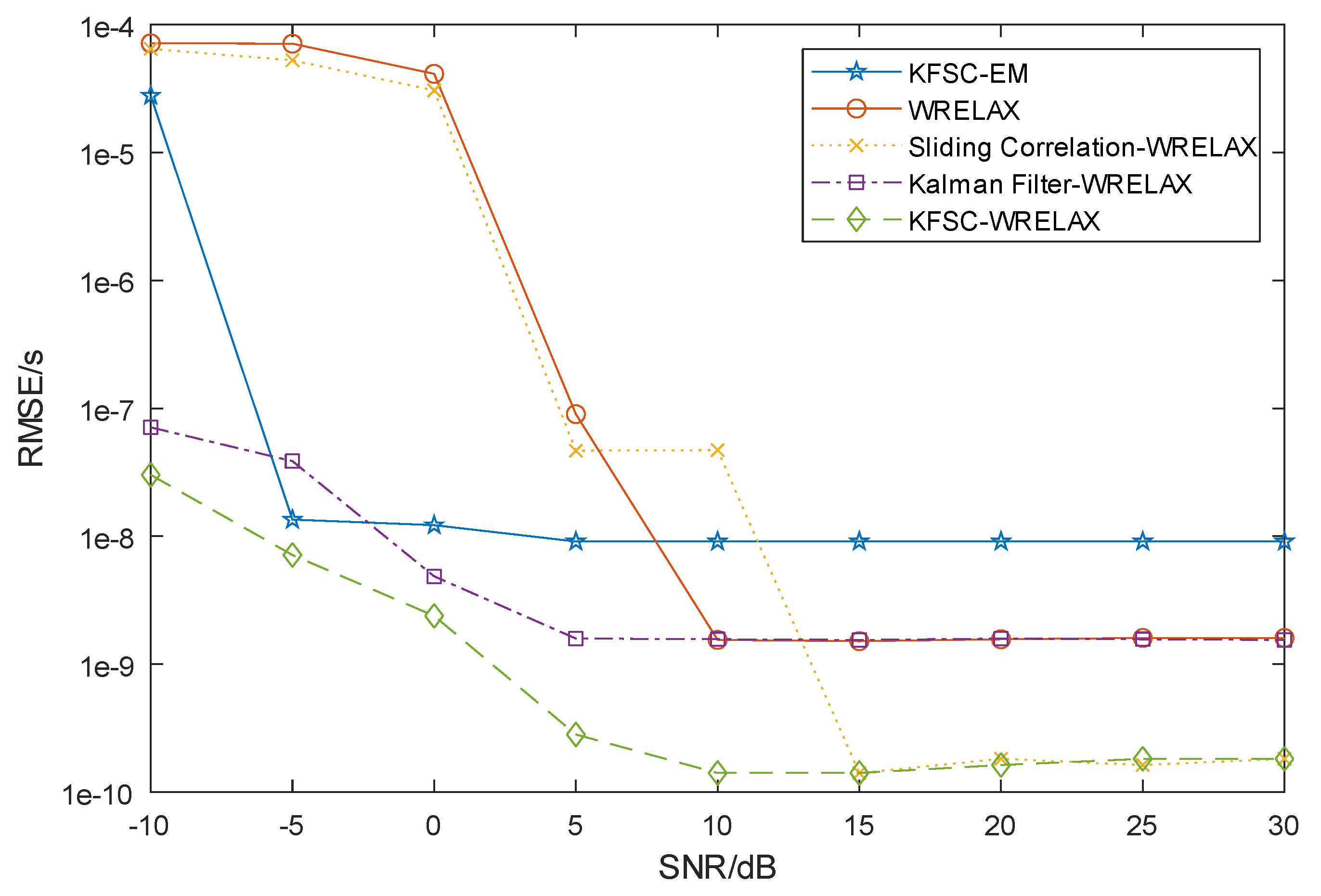
5.2. Simulation Results
5.3. Channel Simulator Test Results
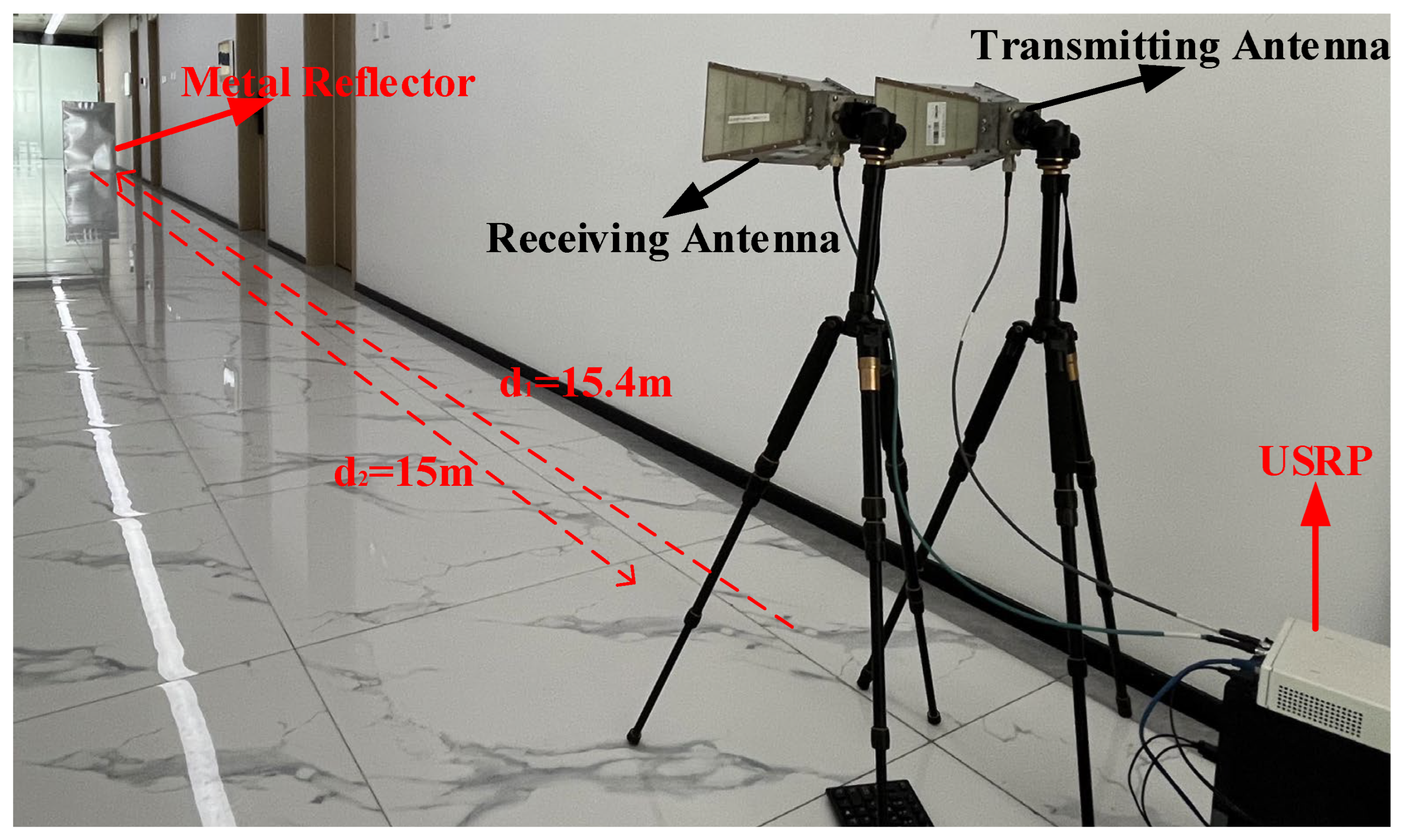
5.4. Corridor Test Results
6. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| WRELAX | Weighted Fourier Transform combined with the RELAXation |
| PN | Pseudorandom Noise |
| KF | Kalman Filtering |
| FZC | Frank Zadoff Chu |
| SNR | Signal-to-Noise Ratio |
| LFSR | Linear Feedback Shift Register |
| ZC | Zadoff-Chu |
| PAPR | Peak-to-Average Power Ratio |
| RMSE | Root Mean Square Error |
References
- Zhang, Z.; Deng, Z.; Liu, J.; Ding, Z.; Liu, B. LJCD-Net: Cross-Domain Jamming Generalization Diagnostic Network Based on Deep Adversarial Transfer. Sensors 2024, 24, 3266. [Google Scholar] [CrossRef] [PubMed]
- Ren, Z.; Li, G.; Ji, C.; Yu, C.; Wang, S.; Wang, R. CASTER: A Computer-Vision-Assisted Wireless Channel Simulator for Gesture Recognition. IEEE Open J. Commun. Soc. 2024, 5, 3185–3195. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, T.; Wei, H. A Single Source-Aided Inertial Integrated Navigation Scheme for Passive Navigation of Autonomous Underwater Vehicles. IEEE Sens. J. 2024, 24, 11237–11245. [Google Scholar] [CrossRef]
- Nabati, M.; Ghorashi, S.A. A real-time fingerprint-based indoor positioning using deep learning and preceding states. Expert Syst. Appl. 2023, 213, 118889–118902. [Google Scholar] [CrossRef]
- Liu, N.; Liu, Z.; Gao, J.; Yuan, Y.; Yan Chan, K. Wi-Fi fingerprint-based indoor location: Multiple fingerprints and multiple classifiers with two-layer fusion weights. Int. J. Commun. Syst. 2024, e5828. [Google Scholar] [CrossRef]
- Sun, M.; Wang, Y.; Xu, S.; Cao, H.; Si, M. Indoor Positioning Integrating PDR/Geomagnetic Positioning Based on the Genetic-Particle Filter. Appl. Sci. 2020, 10, 668. [Google Scholar] [CrossRef]
- Wang, T.; Han, L.; Kong, Q.; Li, Z.; Li, C.; Han, J.; Bai, Q.; Chen, Y. An improved particle filter indoor fusion positioning approach based on Wi-Fi/PDR/geomagnetic field. Def. Technol. 2024, 32, 443–458. [Google Scholar] [CrossRef]
- Marouane, C.; Maier, M.; Feld, S.; Werner, M. Visual positioning systems—An extension to MoVIPS. In Proceedings of the 2014 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Busan, Republic of Korea, 27–30 October 2014; pp. 95–104. [Google Scholar]
- Yuksel, Y. Design and Analysis of Inertial Navigation Systems with Skew Redundant Inertial Sensors. Ph.D. Thesis, University of Calgary, Calgary, AB, Canada, 2011. [Google Scholar]
- Liao, H.; Wang, H.; Zhang, S.; Zang, X. Design of real-time multipath channel sounder system based on GNU Radio. Electron. Meas. Technol. 2020, 43, 148–152. [Google Scholar] [CrossRef]
- Zhao, D.; Duan, H.; Zhang, X.; Liu, C. Research on Multipath Delay Estimation in Wireless Channels. Study Opt. Commun. 2019, 1, 53–58. [Google Scholar] [CrossRef]
- Ren, J. Research on Measurement Method of Wireless Channel Transmission Characteristics in Complicated Mountain Environment. Master’s Thesis, Southwest University of Science and Technology, Mianyang, China, 2022. [Google Scholar] [CrossRef]
- Li, H. Research on Optimization of Channel Estimation Algorithm Based on Machine Learning. Master’s Thesis, University of Electronic Science and Technology of China, Chengdu, China, 2020. [Google Scholar] [CrossRef]
- Liu, H.; Liang, J.; Chen, K.; Liao, T. Wireless Channel Simulation and Measurement of Maglev Tunnel. In Proceedings of the 2022 3rd Information Communication Technologies Conference (ICTC), Nanjing, China, 6–8 May 2022; pp. 25–32. [Google Scholar]
- Ness, G.J.; Helleseth, T. A New Three-Valued Cross Correlation Between m-Sequences of Different Lengths. IEEE Trans. Inf. Theory 2006, 52, 4695–4701. [Google Scholar] [CrossRef]
- Cui, G.; He, Y.; Li, P.; Wang, W. Enhanced Timing Advanced Estimation With Symmetric Zadoff-Chu Sequences for Satellite Systems. IEEE Commun. Lett. 2015, 19, 747–750. [Google Scholar] [CrossRef]
- Wittig, S.; Peter, M.; Keusgen, W. Channel estimation with Zadoff–Chu sequences in the presence of phase errors. Electron. Lett. 2023, 59, e12996. [Google Scholar] [CrossRef]
- Xu, R.; Xu, F.; Song, Y.; Duan, L.; Song, Y.; Tan, S.; Liu, Z. Impact of spectral filtering on pulse breaking-up and noise-like pulse generation in all-normal dispersion fiber lasers. Opt. Express 2020, 28, 21348–21358. [Google Scholar] [CrossRef] [PubMed]
- Bao, L.; Li, K.; Lee, J.; Dong, W.; Li, W.; Shin, K.; Kim, W. An Enhanced Indoor Three-Dimensional Localization System with Sensor Fusion Based on Ultra-Wideband Ranging and Dual Barometer Altimetry. Sensors 2024, 24, 3341. [Google Scholar] [CrossRef] [PubMed]
- Garcia, R.V.; Pardal, P.C.P.M.; Kuga, H.K.; Zanardi, M.C. Nonlinear filtering for sequential spacecraft attitude estimation with real data: Cubature Kalman Filter, Unscented Kalman Filter and Extended Kalman Filter. Adv. Space Res. 2019, 63, 1038–1050. [Google Scholar] [CrossRef]
- Vedel-Larsen, E.; Fuglø, J.; Channir, F.; Thomsen, C.E.; Sørensen, H.B. A comparative study between a simplified Kalman filter and Sliding Window Averaging for single trial dynamical estimation of event-related potentials. Comput Methods Programs Biomed. 2010, 99, 252–260. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Wu, R. An efficient algorithm for time delay estimation. IEEE Trans. Signal Process. 1998, 46, 2231–2235. [Google Scholar] [CrossRef]
- Jia, Q.; Wu, R.; Wang, W.; Wang, D.; Li, J. Multipath interference mitigation in GNSS via WRELAX. GPS Solut. 2017, 21, 487–498. [Google Scholar] [CrossRef]
- Feder, M.; Weinstein, E. Parameter estimation of superimposed signals using the EM algorithm. IEEE Trans. Acoust. Speech Signal Process. 1988, 36, 477–489. [Google Scholar] [CrossRef]
- Kuroda, M.; Geng, Z.; Sakakihara, M. Improving the vector [Math Processing Error] acceleration for the EM algorithm using a re-starting procedure. Comput Stat. 2015, 30, 1051–1077. [Google Scholar] [CrossRef]
- Wang, Y.; Chai, J.; Li, N.; Chen, P.; Wang, W. An Implementation of Fading Channel Simulator for Discrete-Time Wireless Communication Based on USRP Platform. In Proceedings of the 2023 IEEE 6th International Conference on Electronic Information and Communication Technology (ICEICT), Qingdao, China, 21–24 July 2023; pp. 788–792. [Google Scholar]
- Taotao, Z.; Yunge, T.; Huidong, Q.; Jianling, C.; Shuli, D. Design And Implementation of an Efficient Wireless Channel Simulator. In Proceedings of the 2021 IEEE 4th Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Chongqing, China, 18–20 June 2021; pp. 2175–2178. [Google Scholar]
- Zhou, Z.; Zhang, L.; Chen, X.; Wang, C.-X.; Huang, J. Multi-Frequency Wireless Channel Measurements and Characteristics Analysis in Indoor Corridor Scenarios. In Proceedings of the 2021 IEEE 94th Vehicular Technology Conference (VTC2021-Fall), Norman, OK, USA, 27–30 September 2021; pp. 1–5. [Google Scholar]
- Hui, X.; Wuxiong, Z.; Yang, Y. Channel Measurement and Modeling for the 15-GHz Radio Band in an Indoor Corridor Environment. J. Commun. Inf. Netw. 2016, 1, 102–108. [Google Scholar]

| Set SNR | −20 dB | −10 dB | 0 dB | 10 dB | 20 dB | 30 dB |
|---|---|---|---|---|---|---|
| Post-Filtering SNR | −12.33 dB | −2.76 dB | 6.99 dB | 16.83 dB | 26.71 dB | 36.62 dB |
| SNR Improvement | 7.67 dB | 7.24 dB | 6.99 dB | 6.83 dB | 6.71 dB | 6.62 dB |
| Two-Path Delay Difference | Two-Path Amplitude Attenuation | Measured Delay Difference | Measured Amplitude Attenuation | Number of Iterations |
|---|---|---|---|---|
| 73 ns | −15 dB | 72.73 ns | −14.04 dB | 26 |
| 110 ns | −7 dB | 109.82 ns | −7.45 dB | 19 |
| 110 ns | 0 dB | 109.09 ns | −0.54 dB | 13 |
| First Path: d | Second Path: d | Absolute Delay | Measured Delay Points | Measured Absolute Delay |
|---|---|---|---|---|
| 0.4 m | 30.4 m | 100 ns | 11 | 100.22 ns |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Y.; Zhang, Z. A High-Resolution Multipath Delay Measurement Method Using KFSC-WRELAX Algorithm. Sensors 2024, 24, 4968. https://doi.org/10.3390/s24154968
Dong Y, Zhang Z. A High-Resolution Multipath Delay Measurement Method Using KFSC-WRELAX Algorithm. Sensors. 2024; 24(15):4968. https://doi.org/10.3390/s24154968
Chicago/Turabian StyleDong, Yu, and Zhizhong Zhang. 2024. "A High-Resolution Multipath Delay Measurement Method Using KFSC-WRELAX Algorithm" Sensors 24, no. 15: 4968. https://doi.org/10.3390/s24154968
APA StyleDong, Y., & Zhang, Z. (2024). A High-Resolution Multipath Delay Measurement Method Using KFSC-WRELAX Algorithm. Sensors, 24(15), 4968. https://doi.org/10.3390/s24154968





