A Comparative Study of Causality Detection Methods in Root Cause Diagnosis: From Industrial Processes to Brain Networks
Abstract
1. Introduction
- A
- RCA problem in industrial processes
- B
- Source analysis in brain networks
2. Materials
2.1. Industrial Process Case: Root Cause Analysis of Plant-Wide Oscillations
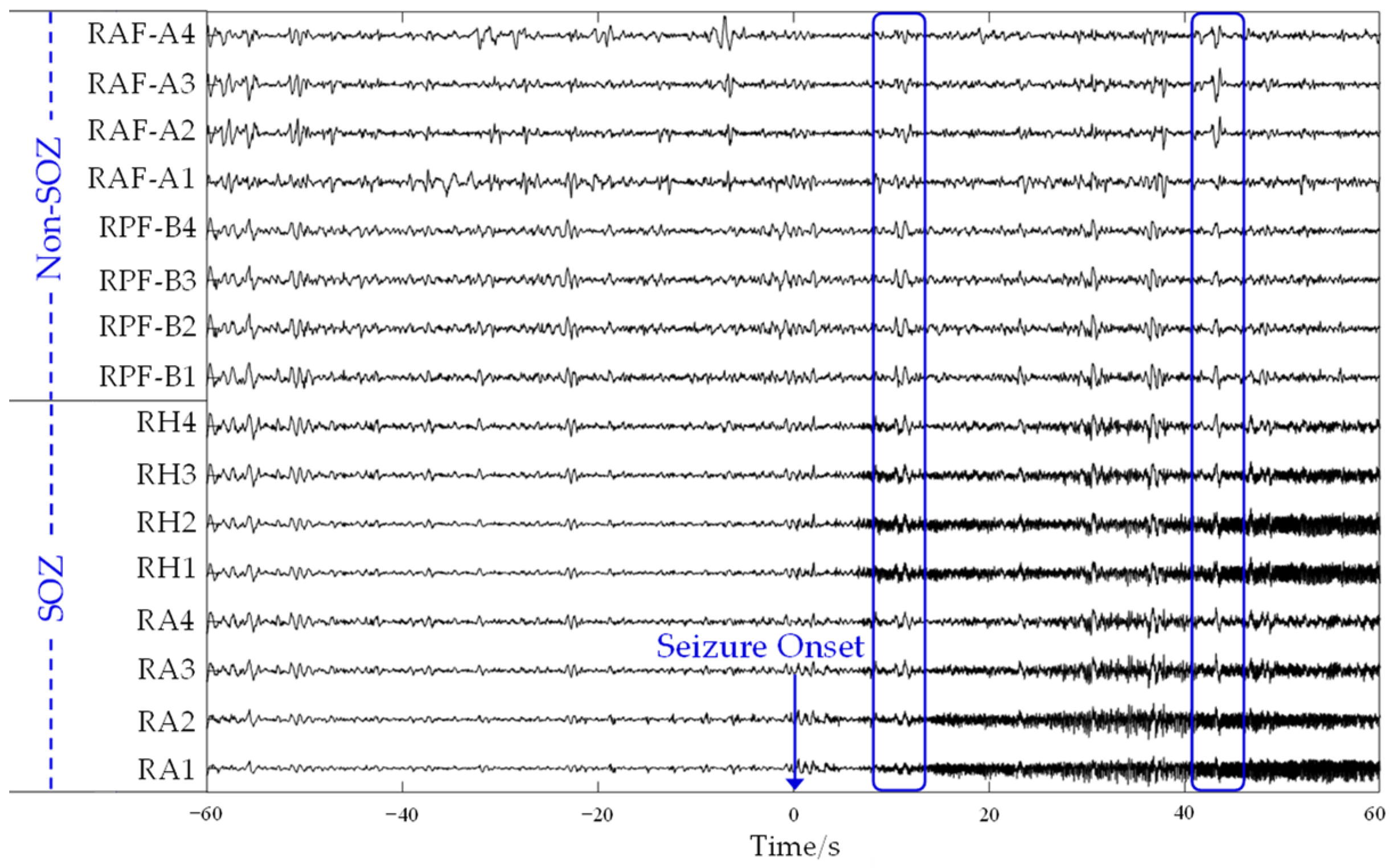
2.2. Brain Network Case: Localization of Seizure Onset Zones in the Human Brain
3. Methods and Results
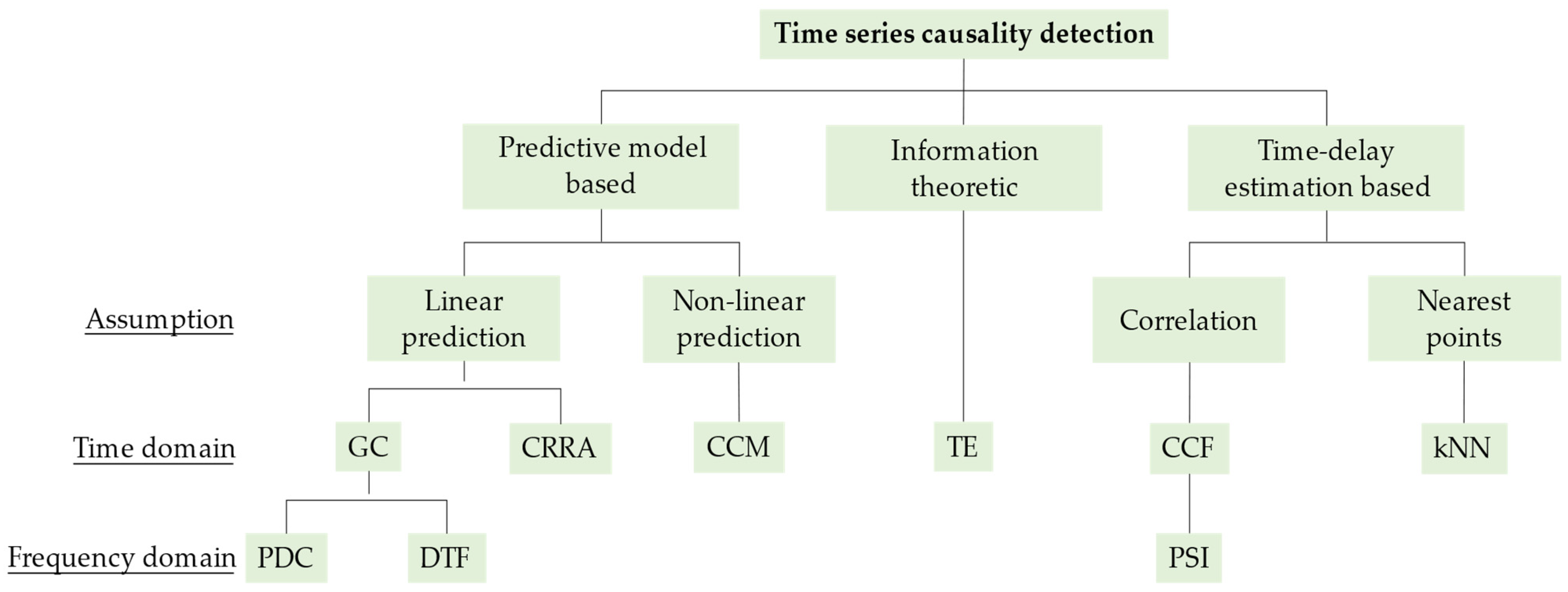
3.1. Taxonomy of Causality Detection Methods
3.1.1. Predictive Model-Based Branch
- A.
- Linear prediction
- (1)
- GC and MVGC
- (2)
- DTF and PDC
- B.
- Nonlinear prediction
- (1)
- CCM
3.1.2. Information-Theoretic Branch
- (1)
- TE
3.1.3. Time Delay Estimation-Based Branch
- (1)
- CCF
- (2)
- PSI
3.2. RCA of Plant-Wide Oscillations
3.2.1. Time-Domain Methods
3.2.2. Frequency-Domain Methods
3.2.3. Improved Frequency-Domain Methods
3.3. Localization of SOZs in the Human Brain
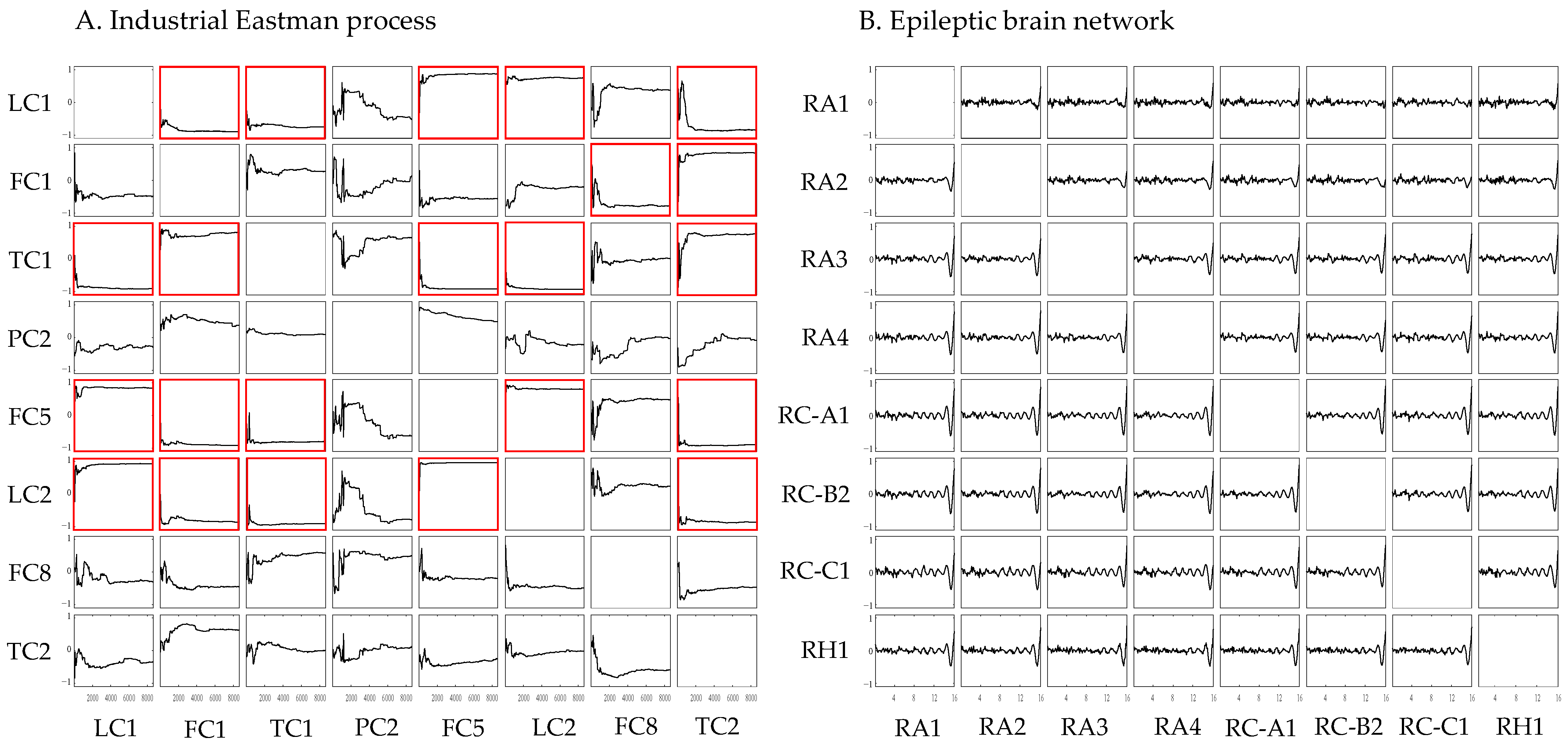
3.4. CCM in Both Cases
4. Discussion
4.1. RCA of Plant-Wide Oscillations
4.2. Localization of SOZs in the Human Brain
- i.
- The GC and TE methods, which are widely used for identifying the root cause of fault in industrial processes, work poorly on brain networks. On one hand, bivariate causality detection methods (TE, GC, and PSI) cannot rule out indirect, redundant causal relations. As a consequence, the causal information outflow that results from any of them shows similar trends across SOZ and non-SOZ channels, making it difficult to identify the SOZ. On the other hand, to address the requirement for stationarity of the time series used in the causal inference in this case, we used sliding windows whose width was limited. However, both TE and GC have a high requirement for the number of samples.
- ii.
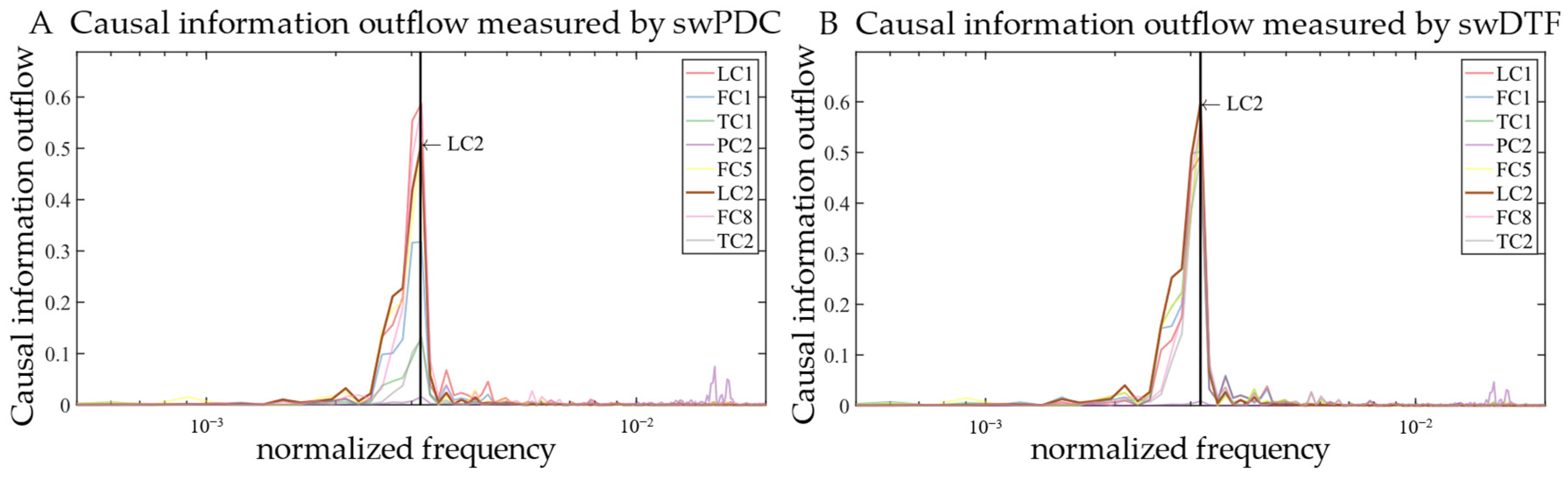
- Multivariate methods (ffDTF, swPDC, and MVGC) are more effective. Of those methods, the ffDTF and swPDC, which detect causal effects in the frequency domain, produced the most promising results.
- iii.
- As for PSI, it may be inapplicable in this case. Bidirectional interactions are the dominant interaction scenario in the majority of cortico–cortical connections. In such situations, the interpretation of the phase difference spectrum (and consequently PSI) as well as the CCF becomes complicated and may fail at correctly describing the directionality. See Witham et al. (2011) and Vinck et al. (2015) for further discussion [68,69].
- iv.
- In brain networks, CCM does not converge and consequently fails to discover causations. A possible reason for the nonconvergence is that CCM assumes that the dynamic system is described by a nonlinear model and has a specific trajectory. However, the dynamics of the brain connectivity pattern changes with time.
4.3. Summary
4.4. Discussions of Interpretative Pitfall
4.5. Future Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Supplementary Introduction to Time Series Causality Detection Methods
| Parameter/Variable | Meaning |
| “Cause” variable in bivariate causal relations | |
| “Effect” variable in bivariate causal relations | |
| “Cause” variable in multivariate causal relations | |
| “Effect” variable in multivariate causal relations | |
| Order of AR or MVAR model | |
| Dimension of the shadow manifold or embedding vector | |
| Time delay of the shadow manifold or embedding vector | |
| Number of neighbors used in prediction of CCM or k-NN |
Appendix A.1. Significance Test of GC
Appendix A.2. Improvements of DTF and PDC
Appendix A.3. Calculation of TE
Appendix A.4. DTE

References
- Spinney, R.E.; Lizier, J.T.; Prokopenko, M. Transfer entropy in physical systems and the arrow of time. Phys. Rev. E 2016, 94, 022135. [Google Scholar] [CrossRef] [PubMed]
- Duan, P.; Yang, F.; Chen, T.; Shah, S.L. Direct Causality Detection via the Transfer Entropy Approach. IEEE Trans. Control Syst. Technol. 2013, 21, 2052–2066. [Google Scholar] [CrossRef]
- Bauer, M.; Thornhill, N.F. A practical method for identifying the propagation path of plant-wide disturbances. J. Process. Control 2008, 18, 707–719. [Google Scholar] [CrossRef]
- Basti, A.; Pizzella, V.; Chella, F.; Romani, G.L.; Nolte, G.; Marzetti, L. Disclosing large-scale directed functional connections in MEG with the multivariate phase slope index. NeuroImage 2018, 175, 161–175. [Google Scholar] [CrossRef] [PubMed]
- Yao, W.; Wang, J. Multi-scale symbolic transfer entropy analysis of EEG. Phys. A Stat. Mech. Its Appl. 2017, 484, 276–281. [Google Scholar] [CrossRef]
- Liu, H.; Lei, M.; Zhang, N.; Du, G. The causal nexus between energy consumption, carbon emissions and economic growth: New evidence from China, India and G7 countries using convergent cross mapping. PLoS ONE 2019, 14, e0217319. [Google Scholar] [CrossRef]
- Bennett, A.; Nijssen, B.; Ou, G.; Clark, M.; Nearing, G. Quantifying Process Connectivity with Transfer Entropy in Hydrologic Models. Water Resour. Res. 2019, 55, 4613–4629. [Google Scholar] [CrossRef]
- Bildirici, M.E. Cement production, environmental pollution, and economic growth: Evidence from China and USA. Clean Technol. Environ. Policy 2019, 21, 783–793. [Google Scholar] [CrossRef]
- Huang, Y.; Franzke, C.L.E.; Yuan, N.; Fu, Z. Systematic identification of causal relations in high-dimensional chaotic systems: Application to stratosphere-troposphere coupling. Clim. Dyn. 2020, 55, 2469–2481. [Google Scholar] [CrossRef]
- Lucke, M.; Chioua, M.; Thornhill, N.F. From oscillatory to non-oscillatory disturbances: A comparative review of root cause analysis methods. J. Process Control 2022, 113, 42–67. [Google Scholar] [CrossRef]
- Neuberg, L.G. CAUSALITY: MODELS, REASONING, AND INFERENCE, by Judea Pearl, Cambridge University Press, 2000. Econom. Theory 2003, 19, 675–685. [Google Scholar] [CrossRef]
- Spirtes, P.; Glymour, C.; Scheines, R. Causation, Prediction, and Search; The MIT Press: Boston, MA, USA, 2001. [Google Scholar]
- Imbens, G.W.; Rubin, D.B. Causal Inference for Statistics, Social, and Biomedical Sciences: An Introduction; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Peters, J.; Janzing, D.; Schlkopf, B. Elements of Causal Inference: Foundations and Learning Algorithms; The MIT Press: Boston, MA, USA, 2017. [Google Scholar]
- Alinezhad, H.S.; Roohi, M.H.; Chen, T. A review of alarm root cause analysis in process industries: Common methods, recent research status and challenges. Chem. Eng. Res. Des. 2022, 188, 846–860. [Google Scholar] [CrossRef]
- Cao, J.; Zhao, Y.; Shan, X.; Wei, H.; Guo, Y.; Chen, L.; Erkoyuncu, J.A.; Sarrigiannis, P.G. Brain functional and effective connectivity based on electroencephalography recordings: A review. Hum. Brain Mapp. 2021, 43, 860–879. [Google Scholar] [CrossRef] [PubMed]
- Balaji, S.S.; Parhi, K.K. Seizure Onset Zone Identification from iEEG: A Review. IEEE Access 2022, 10, 62535–62547. [Google Scholar] [CrossRef]
- Laubach, Z.M.; Murray, E.J.; Hoke, K.L.; Safran, R.J.; Perng, W. A biologist’s guide to model selection and causal inference. Proc. R. Soc. B-Biol. Sci. 2021, 288, 20202815. [Google Scholar] [CrossRef] [PubMed]
- Shams, L.; Beierholm, U. Bayesian causal inference: A unifying neuroscience theory. Neurosci. Biobehav. Rev. 2022, 137, 104619. [Google Scholar] [CrossRef]
- Capisani, L.M.; Ferrara, A.; de Loza, A.F.; Fridman, L.M. Manipulator Fault Diagnosis via Higher Order Sliding-Mode Observers. IEEE Trans. Ind. Electron. 2012, 59, 3979–3986. [Google Scholar] [CrossRef]
- Benmoussa, S.; Bouamama, B.O.; Merzouki, R. Bond Graph Approach for Plant Fault Detection and Isolation: Application to Intelligent Autonomous Vehicle. IEEE Trans. Autom. Sci. Eng. 2013, 11, 585–593. [Google Scholar] [CrossRef]
- Zhou, S.; Qian, S.; Chang, W.; Xiao, Y.; Cheng, Y. A Novel Bearing Multi-Fault Diagnosis Approach Based on Weighted Permutation Entropy and an Improved SVM Ensemble Classifier. Sensors 2018, 18, 1934. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, J.; Tao, Q.; Li, A.; Chen, Y. An unknown wafer surface defect detection approach based on Incremental Learning for reliability analysis. Reliab. Eng. Syst. Saf. 2024, 244, 109966. [Google Scholar] [CrossRef]
- Wan, Y.; Yang, F.; Lv, N.; Xu, H.; Ye, H.; Li, W.; Xu, P.; Song, L.; Usadi, A.K. Statistical root cause analysis of novel faults based on digraph models. Chem. Eng. Res. Des. 2013, 91, 87–99. [Google Scholar] [CrossRef]
- Jiang, H.; Patwardhan, R.; Shah, S.L. Root cause diagnosis of plant-wide oscillations using the concept of adjacency matrix. J. Process Control 2009, 19, 1347–1354. [Google Scholar] [CrossRef]
- Zhu, Q.-X.; Meng, Q.-Q.; Wang, P.-J.; He, Y.-L. Novel Causal Network Modeling Method Integrating Process Knowledge with Modified Transfer Entropy: A Case Study of Complex Chemical Processes. Ind. Eng. Chem. Res. 2017, 56, 14282–14289. [Google Scholar] [CrossRef]
- Shao, H.-M.; Wang, J.-G.; Yao, Y. In A copula-based Granger causality analysis method for root cause diagnosis of plant-wide oscillation. In Proceedings of the International Conference on Image, Video Processing and Artificial Intelligence, Shanghai, China, 21–23 August 2020. [Google Scholar]
- He, R.; Chen, G.; Sun, S.; Dong, C.; Jiang, S. Attention-Based Long Short-Term Memory Method for Alarm Root-Cause Di-agnosis in Chemical Processes. Ind. Eng. Chem. Res. 2020, 59, 11559–11569. [Google Scholar] [CrossRef]
- Chen, H.-S.; Yan, Z.; Yao, Y.; Huang, T.-B.; Wong, Y.-S. Systematic Procedure for Granger-Causality-Based Root Cause Diagnosis of Chemical Process Faults. Ind. Eng. Chem. Res. 2018, 57, 9500–9512. [Google Scholar] [CrossRef]
- Hu, J.; Zhang, L.; Wang, A.; Li, S. Accident prevention by fault propagation analysis and causal fault diagnosis based on granger causality test. In Proceedings of the 2017 13th International Conference on Natural Computation, Fuzzy Systems and Knowledge Discovery (ICNC-FSKD), Guilin, China, 29–31 July 2017; pp. 1554–1558. [Google Scholar]
- Sun, J.; Taylor, D.; Bollt, E.M. Causal Network Inference by Optimal Causation Entropy. SIAM J. Appl. Dyn. Syst. 2015, 14, 73–106. [Google Scholar] [CrossRef]
- Runge, J.; Nowack, P.; Kretschmer, M.; Flaxman, S.; Sejdinovic, D. Detecting and quantifying causal associations in large nonlinear time series datasets. Sci. Adv. 2019, 5, eaau4996. [Google Scholar] [CrossRef] [PubMed]
- Duan, P.; Yang, F.; Shah, S.L.; Chen, T. Transfer Zero-Entropy and Its Application for Capturing Cause and Effect Relationship Between Variables. IEEE Trans. Control Syst. Technol. 2014, 23, 855–867. [Google Scholar] [CrossRef]
- Guo, C.; Yang, F.; Yu, W. A Causality Capturing Method for Diagnosis Based on Transfer Entropy by Analyzing Trends of Time Series. IFAC-PapersOnLine 2015, 48, 778–783. [Google Scholar] [CrossRef]
- Rashidi, B.; Singh, D.S.; Zhao, Q. Data-driven root-cause fault diagnosis for multivariate non-linear processes. Control Eng. Pract. 2017, 70, 134–147. [Google Scholar] [CrossRef]
- Zhang, X.; Hu, W.; Yang, F. Detection of Cause-Effect Relations Based on Information Granulation and Transfer Entropy. Entropy 2022, 24, 212. [Google Scholar] [CrossRef] [PubMed]
- Bressler, S.L.; Menon, V. Large-scale brain networks in cognition: Emerging methods and principles. Trends Cogn. Sci. 2010, 14, 277–290. [Google Scholar] [CrossRef] [PubMed]
- Kanal, E.; Ozkurt, T.; Sclabassi, R.J.; Sun, M. Detecting granger causality in the corticostriatal learning and rewards network using MEG. In Proceedings of the 2009 IEEE 35th Annual Northeast Bioengineering Conference, Cambridge, MA, USA, 3–5 April 2019; pp. 1–2. [Google Scholar]
- Menon, V. Large-scale brain networks and psychopathology: A unifying triple network model. Trends Cogn. Sci. 2011, 15, 483–506. [Google Scholar] [CrossRef] [PubMed]
- David, O.; Guillemain, I.; Saillet, S.; Reyt, S.; Deransart, C.; Segebarth, C.; Depaulis, A. Identifying Neural Drivers with Functional MRI: An Electrophysiological Validation. PLoS Biol. 2008, 6, e315–e397. [Google Scholar] [CrossRef] [PubMed]
- Hu, M.; Liang, H. A copula approach to assessing Granger causalitylle. Neuroimage 2014, 100, 125–134. [Google Scholar] [CrossRef] [PubMed]
- Marinazzo, D.; Liao, W.; Chen, H.; Stramaglia, S. Nonlinear connectivity by Granger causality. NeuroImage 2010, 58, 330–338. [Google Scholar] [CrossRef] [PubMed]
- Al-Ezzi, A.; Yahya, N.; Kamel, N.; Faye, I.; Alsaih, K.; Gunaseli, E. In Social Anxiety Disorder Evaluation using Effective Connectivity Measures: EEG Phase Slope Index Study. In Proceedings of the IEEE-EMBS Conference on Biomedical Engineering and Sciences (IECBES)—Leading Modern Healthcare Technology Enhancing Wellness, Electr Network, Langkawi Island, Malaysia, 1–3 March 2021. [Google Scholar]
- Pagnotta, M.F.; Plomp, G. Time-varying MVAR algorithms for directed connectivity analysis: Critical comparison in simula-tions and benchmark EEG data. PLoS ONE 2018, 13, e0198846. [Google Scholar] [CrossRef] [PubMed]
- Pascucci, D.; Rubega, M.; Plomp, G. Modeling time-varying brain networks with a self-tuning optimized Kalman filter. PLOS Comput. Biol. 2020, 16, e1007566. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Qiao, R.; Shi, Y.; Tang, Y.; Hou, Z.; Tian, Y. The effects of attention in auditory–visual integration revealed by time-varying networks. Front. Neurosci. 2023, 17, 1235480. [Google Scholar] [CrossRef]
- Yang, J.; Li, B.; Dong, W.; Gao, X.; Lin, Y. Time-varying EEG networks of major depressive disorder during facial emotion tasks. Cogn. Neurodynamics 2024, 1–15. [Google Scholar] [CrossRef]
- Malladi, R.; Kalamangalam, G.; Tandon, N.; Aazhang, B. Identifying Seizure Onset Zone from the Causal Connectivity Inferred Using Directed Information. IEEE J. Sel. Top. Signal Process 2016, 10, 1267–1283. [Google Scholar] [CrossRef]
- Li, G.; Qin, S.J.; Yuan, T. Data-driven root cause diagnosis of faults in process industries. Chemom. Intell. Lab. Syst. 2016, 159, 1–11. [Google Scholar] [CrossRef]
- Song, X.; Su, M.; Chen, X.; Xu, M.; Ming, D. Phantom Experiment-Based Validation for Time-Varying Acoustoelectric Brain Imaging with Non-Stationary Current Source Characteristics. IEEE Sens. J. 2022, 22, 4215–4223. [Google Scholar] [CrossRef]
- Piccinini, J.; Ipiñna, I.P.; Laufs, H.; Kringelbach, M.; Deco, G.; Perl, Y.S.; Tagliazucchi, E. Noise-driven multistability vs deterministic chaos in phenomenological semi-empirical models of whole-brain activity. Chaos 2021, 31, 023127. [Google Scholar] [CrossRef] [PubMed]
- Fortela, D.L.B.; Mikolajczyk, A.P. Detecting Plant-Wide Oscillation Propagation Effects of Disturbances and Faults in a Chemical Process Plant Using Network Topology of Variance Decompositions. Processes 2023, 11, 1747. [Google Scholar] [CrossRef]
- Shine, J.M. The thalamus integrates the macrosystems of the brain to facilitate complex, adaptive brain network dynamics. Prog. Neurobiol. 2020, 199, 101951. [Google Scholar] [CrossRef]
- Thornhill, N.F.; Cox, J.W.; Paulonis, M.A. Diagnosis of plant-wide oscillation through data-driven analysis and process understanding. Control Eng. Pract. 2003, 11, 1481–1490. [Google Scholar] [CrossRef]
- Jiang, H.; Choudhury, M.S.; Shah, S.L. Detection and diagnosis of plant-wide oscillations from industrial data using the spectral envelope method. J. Process Control 2007, 17, 143–155. [Google Scholar] [CrossRef]
- Crépon, B.; Navarro, V.; Hasboun, D.; Clemenceau, S.; Martinerie, J.; Baulac, M.; Adam, C.; Le Van Quyen, M. Mapping interictal oscillations greater than 200 Hz recorded with intracranial macroelectrodes in human epilepsy. Brain 2009, 133, 33–45. [Google Scholar] [CrossRef]
- Arunkumar, N.; Ramkumar, K.; Venkatraman, V.; Abdulhay, E.; Fernandes, S.L.; Kadry, S.; Segal, S. Classification of focal and non focal EEG using entropies. Pattern Recognit. Lett. 2017, 94, 112–117. [Google Scholar] [CrossRef]
- Adkinson, J.A.; Karumuri, B.; Hutson, T.N.; Liu, R.; Alamoudi, O.; Vlachos, I.; Iasemidis, L. Connectivity and Centrality Characteristics of the Epileptogenic Focus Using Directed Network Analysis. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 27, 22–30. [Google Scholar] [CrossRef] [PubMed]
- Bernabei, J.M.; Li, A.; Revell, A.Y.; Smith, R.J.; Gunnarsdottir, K.M.; Ong, I.Z.; Davis, K.A.; Sinha, N.; Sarma, S.; Litt, B. HUP iEEG Epilepsy Dataset. OpenNeuro. 2023. Available online: https://openneuro.org/datasets/ds004100/versions/1.1.1 (accessed on 14 January 2024).
- Granger, C.W.J. Investigating Causal Relations by Econometric Models and Cross-spectral Methods. Econometrica 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Kaminski, M.J.; Blinowska, K.J. A new method of the description of the information flow in the brain structures. Biol. Cybern. 1991, 65, 203–210. [Google Scholar] [CrossRef] [PubMed]
- Baccalá, L.A.; Sameshima, K. Partial directed coherence: A new concept in neural structure determination. Biol. Cybern. 2001, 84, 463–474. [Google Scholar] [CrossRef] [PubMed]
- Al-Ezzi, A.; Kamel, N.; Faye, I.; Gunaseli, E. Analysis of Default Mode Network in Social Anxiety Disorder: EEG Resting-State Effective Connectivity Study. Sensors 2021, 21, 4098. [Google Scholar] [CrossRef]
- Sugihara, G.; May, R.; Ye, H.; Hsieh, C.-H.; Deyle, E.; Fogarty, M.; Munch, S. Detecting Causality in Complex Ecosystems. Science 2012, 338, 496–500. [Google Scholar] [CrossRef]
- Schreiber, T. Measuring Information Transfer. Phys. Rev. Lett. 2000, 85, 461–464. [Google Scholar] [CrossRef]
- Xu, Z.; Li, Q.; Qian, L.; Wang, M. Multi-Sensor Fault Diagnosis Based on Time Series in an Intelligent Mechanical System. Sensors 2022, 22, 9973. [Google Scholar] [CrossRef] [PubMed]
- Nolte, G.; Ziehe, A.; Nikulin, V.V.; Schlögl, A.; Krämer, N.; Brismar, T.; Müller, K.-R. Robustly Estimating the Flow Direction of Information in Complex Physical Systems. Phys. Rev. Lett. 2008, 100, 234101. [Google Scholar] [CrossRef]
- Witham, C.L.; Riddle, C.N.; Baker, M.R.; Baker, S.N. Contributions of descending and ascending pathways to corticomuscular coherence in humans. J. Physiol. 2011, 589, 3789–3800. [Google Scholar] [CrossRef]
- Vinck, M.; Huurdeman, L.; Bosman, C.A.; Fries, P.; Battaglia, F.P.; Pennartz, C.M.; Tiesinga, P.H. How to detect the Granger-causal flow direction in the presence of additive noise? Neuroimage 2015, 108, 301–318. [Google Scholar] [CrossRef] [PubMed]
- Franaszczuk, P.J.; Bergey, G.K. Application of the Directed Transfer Function Method to Mesial and Lateral Onset Temporal Lobe Seizures. Brain Topogr. 1998, 11, 13–21. [Google Scholar] [CrossRef] [PubMed]
- Astolfi, L.; Cincotti, F.; Mattia, D.; Marciani, M.G.; Baccala, L.A.; Fallani, F.d.V.; Salinari, S.; Ursino, M.; Zavaglia, M.; Ding, L.; et al. Comparison of different cortical connectivity estimators for high-resolution EEG recordings. Hum. Brain Mapp. 2006, 28, 143–157. [Google Scholar] [CrossRef]
- Korzeniewska, A.; Mańczak, M.; Kamiński, M.; Blinowska, K.J.; Kasicki, S. Determination of information flow direction among brain structures by a modified directed transfer function (dDTF) method. J. Neurosci. Methods 2003, 125, 195–207. [Google Scholar] [CrossRef] [PubMed]
- Wilke, C.; Ding, L.; He, B. Estimation of Time-Varying Connectivity Patterns Through the Use of an Adaptive Directed Transfer Function. IEEE Trans. Biomed. Eng. 2008, 55, 2557–2564. [Google Scholar] [CrossRef] [PubMed]
- Van Mierlo, P.; Carrette, E.; Hallez, H.; Raedt, R.; Meurs, A.; Vandenberghe, S.; Van Roost, D.; Boon, P.; Staelens, S.; Vonck, K. Ictal-onset localization through connectivity analysis of intracranial EEG signals in patients with refractory epilepsy. Epilepsia 2013, 54, 1409–1418. [Google Scholar] [CrossRef]
- Plomp, G.; Quairiaux, C.; Michel, C.M.; Astolfi, L. The physiological plausibility of time-varying Granger-causal modeling: Normalization and weighting by spectral power. NeuroImage 2014, 97, 206–216. [Google Scholar] [CrossRef]





| Propagation Networks of Faults in Industrial Processes | Effective Connectivity Networks of Human Brains | |
|---|---|---|
| Stationarity of time series | Nearly stationary or nonstationary [49] | Nonstationary [50] |
| Stability of connection pattern | Relatively stable in a given state | Transient and unstable |
| System dynamics | Linear or nonlinear | Nonlinear and with chaos behaviors [40,51] |
| Network characteristic | Regular or complex [52] | Complex [53] |
| A priori knowledge | Piping and instrumentation diagrams (P&IDs), etc. [25] | Lacking |
| Method | Parameter Settings |
|---|---|
| GC MVGC |
|
| TE DTE |
|
| CCM |
|
| Parameter Settings in DTF and PDC | |
|---|---|
| MVAR model |
|
| Significance determination |
|
| Method | Parameter Settings | |
|---|---|---|
| TE |
| |
| MVGC |
| |
| ffDTF swDTF swPDC |
| |
| PSI |
| |
| LC1 | FC1 | TC1 | PC2 | FC5 | LC2 | FC8 | TC2 | |
|---|---|---|---|---|---|---|---|---|
| LC1 | −0.90 | −0.75 | \ | 0.87 | 0.75 | 0.37 | −0.84 | |
| FC1 | −0.48 | 0.28 | \ | −0.55 | −0.19 | −0.77 | 0.84 | |
| TC1 | −0.91 | 0.81 | 0.66 | −0.91 | −0.93 | 0.01 | 0.78 | |
| PC2 | −0.30 | 0.38 | 0.10 | \ | \ | \ | \ | |
| FC5 | 0.83 | −0.91 | −0.79 | \ | 0.80 | 0.49 | −0.89 | |
| LC2 | 0.93 | −0.85 | −0.90 | \ | 0.96 | 0.24 | −0.86 | |
| FC8 | −0.31 | −0.45 | 0.58 | 0.51 | −0.19 | −0.49 | −0.46 | |
| TC2 | \ | 0.64 | \ | \ | \ | −0.01 | −0.59 |
| TE | GC | -NN | CRRA | CCM | CCF | DTF | PDC | PSI | |
|---|---|---|---|---|---|---|---|---|---|
| Time domain | √ | √ | √ | √ | √ | √ | |||
| Frequency domain | √ | √ | √ | ||||||
| Linear relation | √ | √ | √ | √ | √ | √ | √ | √ | |
| Nonlinear relation | √ | √ | |||||||
| Parameterized | √ | √ | √ | √ | |||||
| Nonparametric | √ | √ | √ | √ | √ | ||||
| Bivariate | √ | √ | √ | √ | √ | √ | √ | √ | √ |
| Multivariate | √ | √ | √ | √ | √ | ||||
| Number of samples required | high | high | low | high | medium | low | high | high | low |
| Computational load | high | low | medium | low | medium | low | medium | medium | low |
| Insensitive to noise | √ | √ | √ | √ | |||||
| Direct causality | √ a | √ b | √ | √ | |||||
| Number of a priori parameters c | ) | ) | ) | ) | ) | 0 | ) | ) | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, S.; Cai, H.; Chen, H.; Ye, L. A Comparative Study of Causality Detection Methods in Root Cause Diagnosis: From Industrial Processes to Brain Networks. Sensors 2024, 24, 4908. https://doi.org/10.3390/s24154908
Zhou S, Cai H, Chen H, Ye L. A Comparative Study of Causality Detection Methods in Root Cause Diagnosis: From Industrial Processes to Brain Networks. Sensors. 2024; 24(15):4908. https://doi.org/10.3390/s24154908
Chicago/Turabian StyleZhou, Sun, He Cai, Huazhen Chen, and Lishan Ye. 2024. "A Comparative Study of Causality Detection Methods in Root Cause Diagnosis: From Industrial Processes to Brain Networks" Sensors 24, no. 15: 4908. https://doi.org/10.3390/s24154908
APA StyleZhou, S., Cai, H., Chen, H., & Ye, L. (2024). A Comparative Study of Causality Detection Methods in Root Cause Diagnosis: From Industrial Processes to Brain Networks. Sensors, 24(15), 4908. https://doi.org/10.3390/s24154908






