Comparison Analysis of Roundness Measurement of Small Cylindrical Workpieces with Different Styluses
Abstract
1. Introduction
2. Principle and Experiments
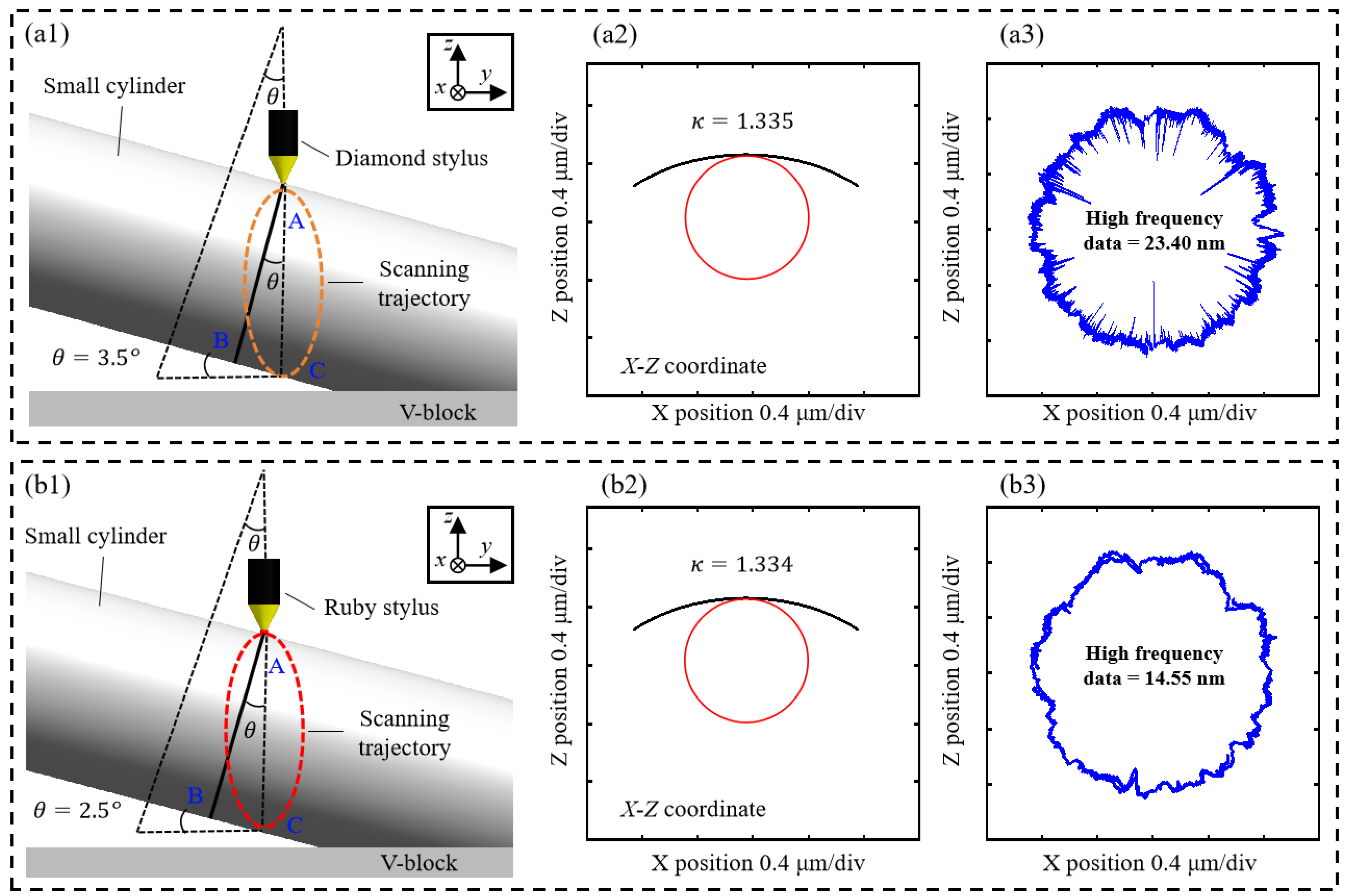
3. Comparison Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Polák, P.; Mikuš, R.; Kročko, V. Monitoring of conditions of agricultural machines’ parts in operation. Res. Agric. Eng. 2014, 60, S57–S65. [Google Scholar] [CrossRef]
- Aliakbari, K. Failure Analysis of Ductile Iron Crankshaft in Four-Cylinder Diesel Engine. Int. J. Met. 2021, 15, 1223–1237. [Google Scholar] [CrossRef]
- Sanaei, N.; Fatemi, A.; Phan, N. Defect characteristics and analysis of their variability in metal L-PBF additive manufacturing. Mater. Des. 2019, 182, 108091. [Google Scholar] [CrossRef]
- Adamczak, S.; Zmarzły, P.; Janecki, D. Theoretical and Practical Investigations Of V-Block Waviness Measurement of Cylindrical Parts. Metrol. Meas. Syst. 2015, 22, 181–192. [Google Scholar] [CrossRef]
- Khaeroman, K.; Haryadi, G.D.; Ismail, R.; Kim, S.J. Failure analysis and evaluation of a six cylinders crankshaft for marine diesel generator. AIP Conf. Proc. 2017, 1788, 030064. [Google Scholar]
- Lee, D. Experimental Investigation of Laser Ablation Characteristics on Nickel-Coated Beryllium Copper. Metals 2018, 8, 211. [Google Scholar] [CrossRef]
- Bleicher, F.; Biermann, D.; Drossel, W.G.; Moehring, H.C.; Altintas, Y. Sensor and actuator integrated tooling systems. CIRP Ann. 2023, 72, 673–696. [Google Scholar] [CrossRef]
- Swiderski, J.; Makiela, W.; Dobrowolski, T.; Stepien, K.; Zuperl, U. The study of the roundness and cylindricity deviations of parts produced with the use of the additive manufacturing. Int. J. Adv. Manuf. Technol. 2022, 121, 7427–7437. [Google Scholar] [CrossRef]
- Pellegrini, G.; Ravasio, C. Study of the Law Motion of the Micro-EDM Drilling Process. J. Manuf. Mater. Process. 2023, 7, 165. [Google Scholar] [CrossRef]
- Liu, F.; Liang, L.; Xu, G.; Hou, C.; Liu, D. Measurement and evaluation of cylindricity deviation in Cartesian coordinates. Meas. Sci. Technol. 2020, 32, 035018. [Google Scholar] [CrossRef]
- Rangappa, R.; Patel, G.C.M.; Chate, G.R.; Lokare, D.; Lakshmikanthan, A.; Giasin, K.; Pimenov, D.Y. Coaxiality error analysis and optimization of cylindrical parts of CNC turning process. Int. J. Adv. Manuf. Technol. 2022, 120, 6617–6634. [Google Scholar] [CrossRef]
- Jiang, K.; Chen, S.; Li, Z.; Ma, T.; Ren, J.; Mao, Z. Cylindrical-cam modulation instantaneous angular speed sensor for reciprocating-rotary machine. Mech. Syst. Signal Process. 2023, 205, 110860. [Google Scholar] [CrossRef]
- Maropoulos, P.G.; Ceglarek, D. Design verification and validation in product lifecycle. CIRP Ann. 2010, 59, 740–759. [Google Scholar] [CrossRef]
- Chen, X.; Dai, Y.; Hu, H.; Tie, G.; Guan, C. Research on High Precision and Deterministic Figuring for Shaft Parts Based on Abrasive Belt Polishing. Materials 2019, 12, 1389. [Google Scholar] [CrossRef] [PubMed]
- Çiçek, A.; Kıvak, T.; Ekici, E. Optimization of drilling parameters using Taguchi technique and response surface methodology (RSM) in drilling of AISI 304 steel with cryogenically treated HSS drills. J. Intell. Manuf. 2013, 26, 295–305. [Google Scholar] [CrossRef]
- Zhu, W.-L.; Beaucamp, A. Compliant grinding and polishing: A review. Int. J. Mach. Tools Manuf. 2020, 158, 103634. [Google Scholar] [CrossRef]
- Ma, Y.Z.; Wang, X.H.; Li, H.M.; Dong, X.; Kang, Y.H. A New Capacitive Sensing System for Roundness Measurement. Adv. Mater. Res. 2013, 662, 754–757. [Google Scholar] [CrossRef]
- Duan, B.; Yin, Z.; Chai, N.; Meng, S.; Yao, J. A new single probe scanning method for on-machine measurement of roundness error. Int. J. Adv. Manuf. Technol. 2021, 116, 2861–2871. [Google Scholar] [CrossRef]
- Liang, J.; Sun, Z. Air conditioning compressor crankshaft roundness measurement based on a laser profiler. Meas. Sci. Technol. 2024, 35, 055010. [Google Scholar] [CrossRef]
- Bai, J.; Wang, Y.; Wang, X.; Zhou, Q.; Ni, K.; Li, X. Three-Probe Error Separation with Chromatic Confocal Sensors for Roundness Measurement. Nanomanuf. Metrol. 2021, 4, 247–255. [Google Scholar] [CrossRef]
- Oertel, E.; Manske, E. Radius and roundness measurement of micro spheres based on a set of AFM surface scans. Meas. Sci. Technol. 2021, 32, 044005. [Google Scholar] [CrossRef]
- Okuyama, E.; Fukuda, T. Roundness Profile Measurement Using a Combination Method of Three-Point Method for Roundness Profile Measurement and Integration Method for Straightness Profile Measurement. Int. J. Autom. Technol. 2024, 18, 77–83. [Google Scholar] [CrossRef]
- Küng, A.; Meli, F.; Thalmann, R. Ultraprecision micro-CMM using a low force 3D touch probe. Meas. Sci. Technol. 2007, 18, 319–327. [Google Scholar] [CrossRef]
- Gao, W.; Kim, S.W.; Bosse, H.; Haitjema, H.; Chen, Y.L.; Lu, X.D.; Kunzmann, H. Measurement technologies for precision positioning. CIRP Ann. 2015, 64, 773–796. [Google Scholar] [CrossRef]
- Bai, J.; Li, J.; Wang, X.; Zhou, Q.; Ni, K.; Li, X. A new method to measure spectral reflectance and film thickness using a modified chromatic confocal sensor. Opt. Lasers Eng. 2022, 154, 107019. [Google Scholar] [CrossRef]
- Bai, J.; Li, X.; Wang, X.; Wang, J.; Ni, K.; Zhou, Q. Self-reference dispersion correction for chromatic confocal displacement measurement. Opt. Lasers Eng. 2021, 140, 106540. [Google Scholar] [CrossRef]
- Bai, J.; Li, X.; Wang, X.; Zhou, Q.; Ni, K. Chromatic Confocal Displacement Sensor with Optimized Dispersion Probe and Modified Centroid Peak Extraction Algorithm. Sensors 2019, 19, 3592. [Google Scholar] [CrossRef] [PubMed]
- Bai, J.; Li, X.; Zhou, Q.; Ni, K.; Wang, X. Improved chromatic confocal displacement-sensor based on a spatial-bandpass-filter and an X-shaped fiber-coupler. Opt. Express 2019, 27, 10961–10973. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Shimizu, Y.; Saito, T.; Matsukuma, H.; Cai, Y.; Gao, W. Improvement of a Stitching Operation in the Stitching Linear-Scan Method for Measurement of Cylinders in a Small Dimension. Appl. Sci. 2021, 11, 4705. [Google Scholar] [CrossRef]
- Li, Q.; Shimizu, Y.; Saito, T.; Matsukuma, H.; Gao, W. Measurement Uncertainty Analysis of a Stitching Linear-Scan Method for the Evaluation of Roundness of Small Cylinders. Appl. Sci. 2020, 10, 4750. [Google Scholar] [CrossRef]
- Li, Q.; Shimizu, Y.; Wang, X.; Li, X.; Gao, W. High-accuracy roundness measurement of small cylindrical workpieces by a high-frequency filtering method. Precis. Eng. 2024, 85, 241–246. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Y.; Li, J.; Wang, X.; Li, X. Non-contact ultra-precision metrology of superfine cylinders with a developed two-dimensional coordinate measuring device. Measurement 2023, 223, 113727. [Google Scholar] [CrossRef]
- Gao, W.; Haitjema, H.; Fang, F.Z.; Leach, R.K.; Cheung, C.F.; Savio, E.; Linares, J.M. On-machine and in-process surface metrology for precision manufacturing. CIRP Ann. 2019, 68, 843–866. [Google Scholar] [CrossRef]
- Gao, W.; Kiyono, S.; Sugawara, T. High-accuracy roundness measurement by a new error separation method. Precis. Eng. 1997, 21, 123–133. [Google Scholar] [CrossRef]
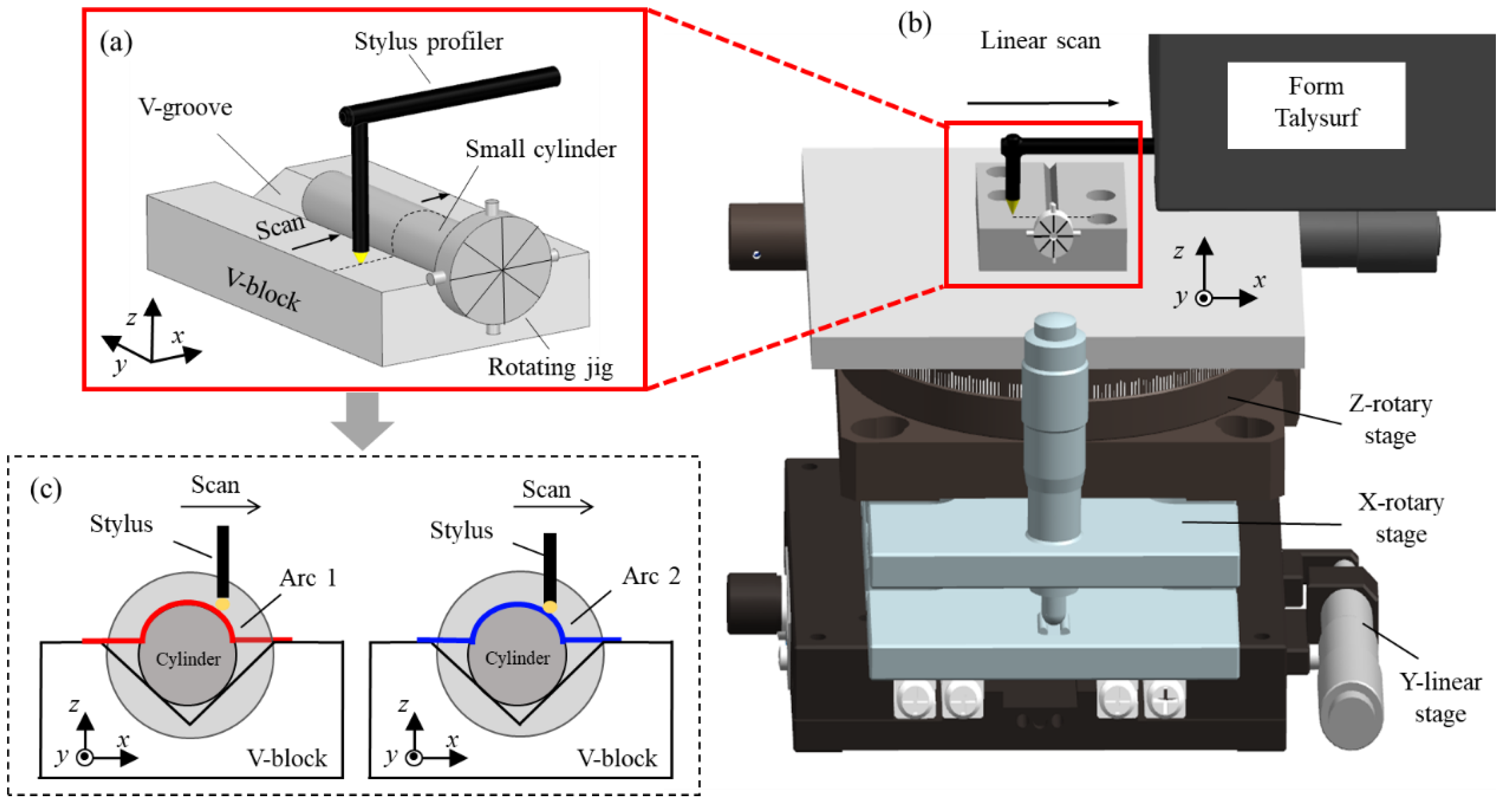


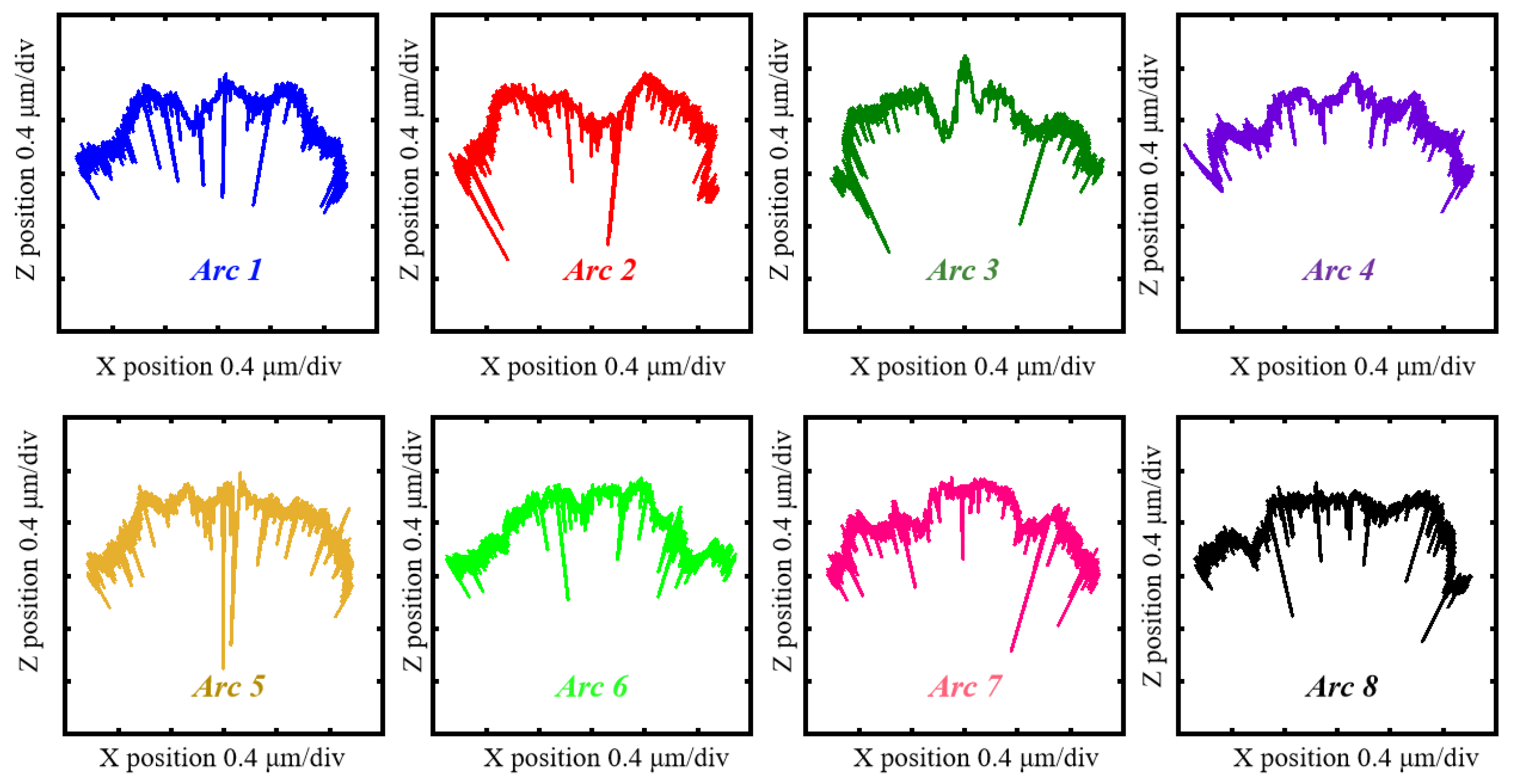
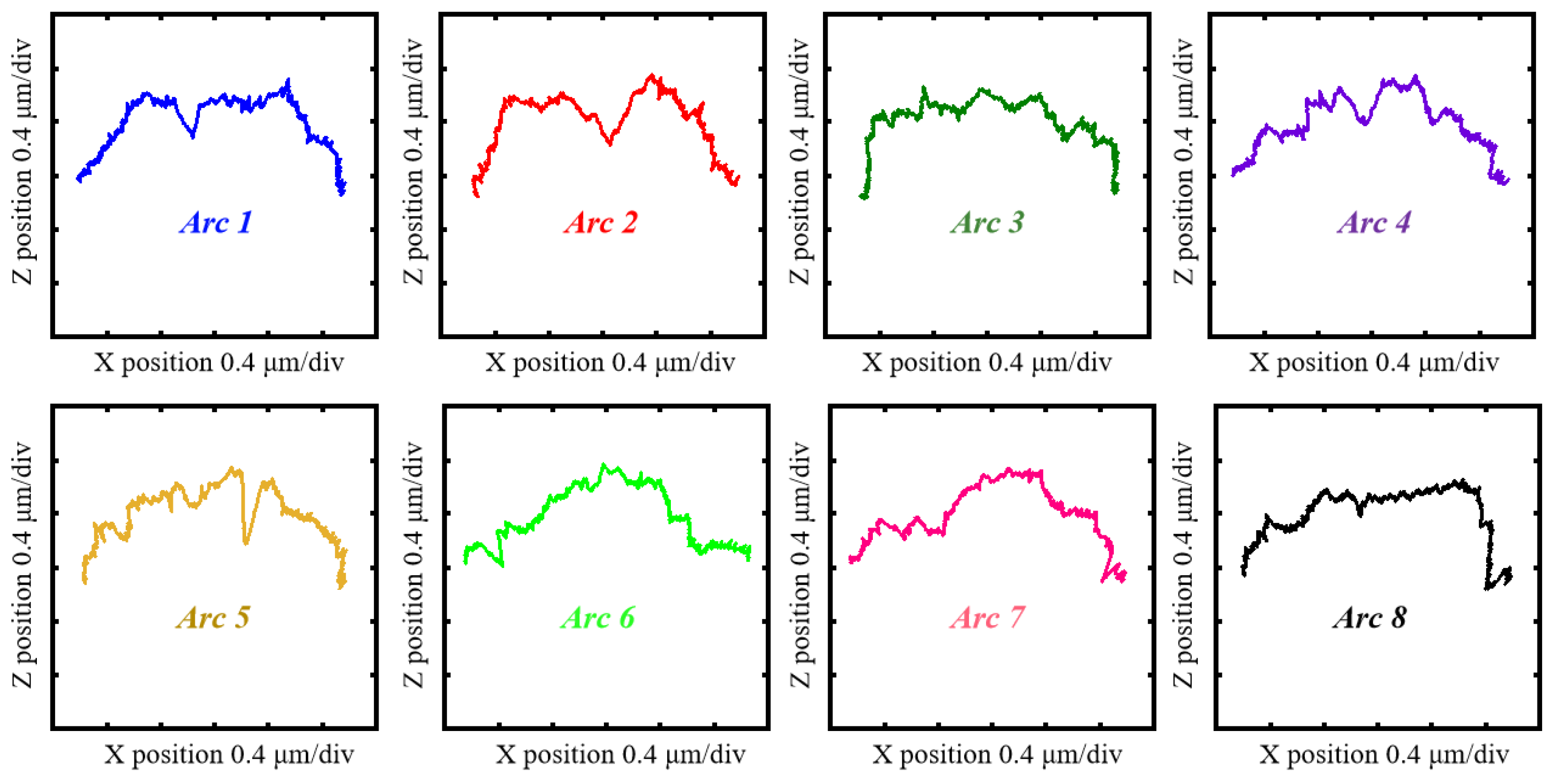
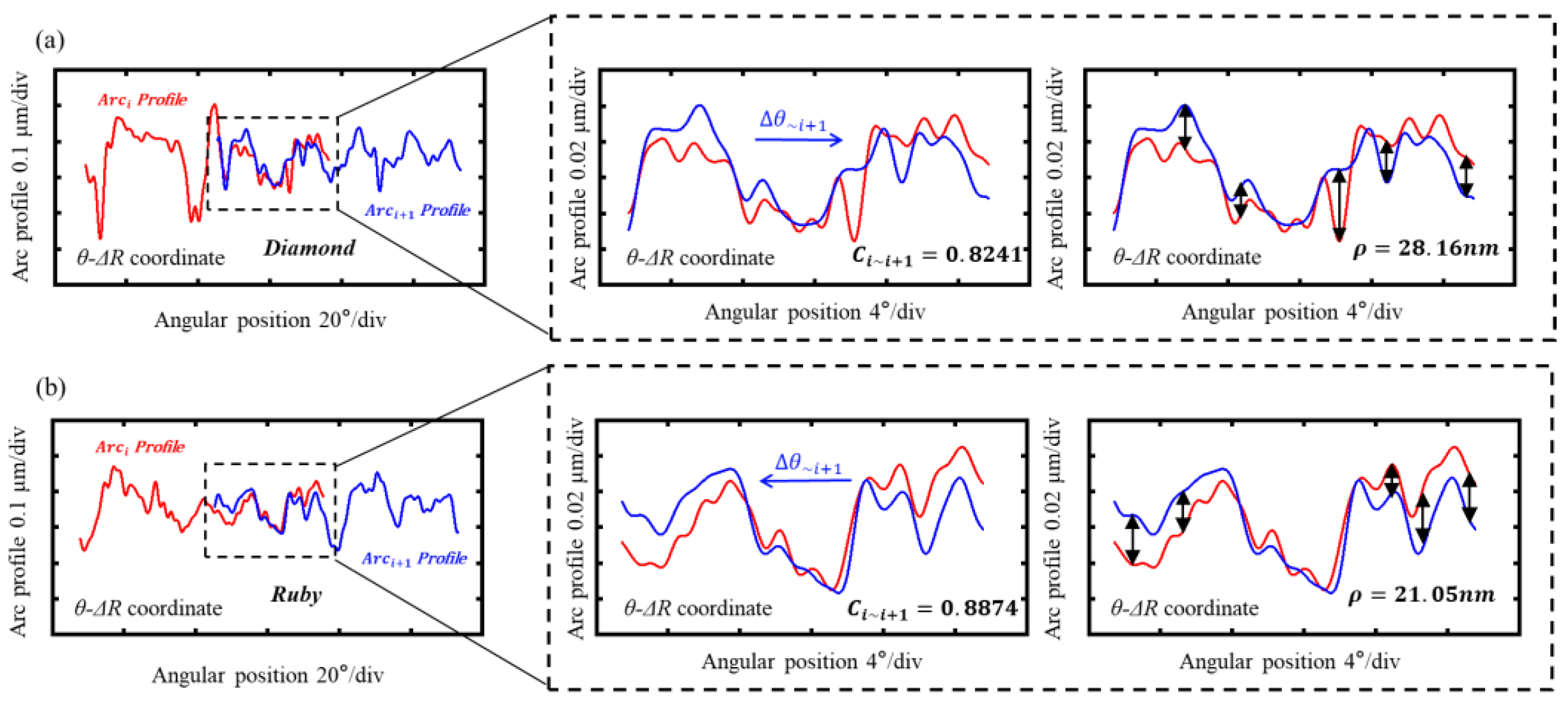


| Item | Resolution (Z) | Measuring Range (Z) | Measuring Range (X) | Sampling Step (X) | Scanning Speed |
|---|---|---|---|---|---|
| Value | 3.2 | 4 | 120 | 0.125 | 0.1 |
| Unit | nm | mm | mm | μm | mm/s |
| Matching Coefficient | Euclidean Distance | High-Frequency Data | Position Error | Mean Curvature | |
|---|---|---|---|---|---|
| Diamond stylus | 0.78 | 26.44 nm | 23.40 nm | 3.5° | 1.335 |
| Ruby ball stylus | 0.85 | 24.48 nm | 14.55 nm | 2.3° | 1.334 |
| Tip Radius | Diameter of Needle Roller | Roundness of Needle Roller | |
|---|---|---|---|
| Diamond stylus | 2 μm | 1.497 mm | 0.16 μm |
| Ruby ball stylus | 150 μm | 1.499 mm | 0.14 μm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, B.; Zeng, C.; Li, Q. Comparison Analysis of Roundness Measurement of Small Cylindrical Workpieces with Different Styluses. Sensors 2024, 24, 3819. https://doi.org/10.3390/s24123819
Wu B, Zeng C, Li Q. Comparison Analysis of Roundness Measurement of Small Cylindrical Workpieces with Different Styluses. Sensors. 2024; 24(12):3819. https://doi.org/10.3390/s24123819
Chicago/Turabian StyleWu, Borong, Chuang Zeng, and Qiaolin Li. 2024. "Comparison Analysis of Roundness Measurement of Small Cylindrical Workpieces with Different Styluses" Sensors 24, no. 12: 3819. https://doi.org/10.3390/s24123819
APA StyleWu, B., Zeng, C., & Li, Q. (2024). Comparison Analysis of Roundness Measurement of Small Cylindrical Workpieces with Different Styluses. Sensors, 24(12), 3819. https://doi.org/10.3390/s24123819







